Известия РАН. Теория и системы управления, 2021, № 4, стр. 74-83

Введение. Данная работа продолжает исследования, начатые в [1, 2]. В [1] оценка последствий каждого разрушения производилась по двум критериям: число разъединенных пар и/или уменьшение пропускной способности каналов связи между узлами источник-приемник. Величина ущерба вычислялась как разность максимальных значений потока между каждой парой вершин в исходной и поврежденной сети. В [2] основное внимание уделено получению гарантированных [3] оценок уязвимости сети. Для оценки ущерба от каждого повреждения определялось: общее число разъединенных пар и все направления связи, пропускная способность по которым оказывалась меньше заданного нормативного значения. Расчеты по указанным критериям позволили получить представительные векторные оценки для маркировки наиболее опасных в смысле предложенных критериев разрушающих воздействий. Предложенные в [2] методы можно рассматривать как возможные подходы к решению классической задачи исследования операций: в условиях неопределенности о намерениях нападающего оценить возможные последствия целенаправленных атак [4, 5].

В работе на модели многопользовательской сети связи [6] продолжен процесс изучения изменений предельно допустимых потоков между всеми парами узлов при разрушающих воздействиях. В качестве критического повреждения [1, 2] рассматривается подмножество ребер, при удалении которых хотя бы для одной пары узлов разрываются все возможные пути соединения. Для каждой пары вершин источник-приемник по двум критериям проводится оценка уменьшения потока при каждом повреждении из заданного множества. На первом шаге определяются все разрушающие воздействия, при которых максимально возможный поток для некоторой выделенной пары узлов становится равным нулю (первый критерий). На следующем шаге для данной пары находятся повреждения, при которых максимальный поток оказывается ниже допустимого уровня, но больше нуля (второй критерий). На основе полученных данных формируются диаграммы предельно допустимых потоков между каждой парой вершин при всех критических повреждениях из заданного множества. Граничные точки на диаграммах соответствуют наиболее уязвимым парам узлов, для них показатели потерь оказываются недоминируемыми хотя бы по одному из критериев. Вычислительные эксперименты проводились для всех возможных комбинаций пар вершин источник-приемник с учетом направления передачи. Анализируются результаты последствий разрушающих воздействий на сетевые системы с различными структурными особенностями.

1. Математическая модель. Для описания многопользовательской сетевой системы используется математическая запись модели передачи многопродуктового потока [1, 2]. Структура сети $G({\mathbf{d}})$ задается множествами $\left\langle {V,R,U} \right\rangle $: узлов (вершин) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $. Ребро ${{r}_{k}} = ({{v}_{{{{n}_{k}}}}},{{v}_{{{{j}_{k}}}}})$ соединяет вершины ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$ (инцидентно вершинам ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$), которые для него служат концевыми. Предполагается, что в сети отсутствуют петли и сдвоенные ребра. Ребру r_k ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ прямого и обратного направления из множества ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют направление передачи потока по ребру r_k между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$.

Обозначим через $S({{v}_{n}})$ множество номеров исходящих дуг, по которым поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{v}_{n}}$. Состав множеств $S({{v}_{n}})$, $T({{v}_{n}})$ однозначно определяется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами n и  j, такими, что n < j. Тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$ считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, ориентированная дуга ${{u}_{{k + E}}} = ({{v}_{j}},{{v}_{n}})$ – входящей для ${{v}_{n}}$ и ее номер k + E помещается в список $T({{v}_{n}})$. Дуга u_k является входящей для ${{v}_{j}}$ и ее номер k попадает в $T({{v}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер k + E вносится в список исходящих дуг $S({{v}_{j}})$.

Предполагается, что в сети между любой парой узлов могут передаваться потоки разных видов. Назовем парой узлов-корреспондентов p_m упорядоченную пару вершин ${{p}_{m}} = ({{v}_{{{{s}_{m}}}}},{{v}_{{{{t}_{m}}}}})$, где вершина с номером ${{s}_{m}}$ является источником, а с номером t_m – стоком или приемником потока $m$-го вида. В настоящей работе, как и в [1, 2], в сети из $N$ узлов рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных потоков различных видов, которые передаются между парами узлов из множества $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $.

Пусть ${{x}_{{mk}}}$ – величина потока m-го вида, который передается по дуге ${{u}_{k}}$ в прямом, а ${{x}_{{m(k + E)}}}$ – величина потока m-го вида, который передается по дуге ${{u}_{{k + E}}}$ в обратном направлении, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $. Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число d_k, определяющее суммарный предельно допустимый поток, который можно передать по ребру r_k в обоих направлениях. В исходной сети компоненты вектора пропускных способностей – ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектором d определяются следующие ограничения на все потоки, передаваемые по ребру r_k:

Обозначим через z_m величину потока m-го вида, который поступает в сеть в узле с номером s_m и покидает из узла с номером t_m.

Во всех узлах сети ${{v}_{n}} \in V$, $n = \overline {1,N} $, для всех видов потоков должны выполняться условия сохранения потоков:

Величина z_m равна входному потоку m-го вида, который пропускается от источника к стоку пары p_m при распределении потоков x_mi по дугам сети.

Ограничения (1.1), (1.2) задают множество допустимых значений компонент векторов потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:

2. Формирование множества структурных повреждений. В настоящей работе, как и в [1, 2], рассматриваются три типа повреждений: разрушение минимального разреза, разделяющего пару источник-приемник в неповрежденной сети, разрушение минимального разреза в сети с единичными пропускными способностями и разрушение всех ребер, инцидентных вершине.

Для построения множества повреждений первого типа для некоторой произвольной пары ${{p}_{a}} \in P$ решается задача поиска максимально возможного потока, который можно передать в сети $G({\mathbf{d}})$ из вершины с номером s_a в вершину с номером t_a без учета всех остальных.

Задача 1. Для фиксированного a найти максимальный поток

Решению задачи 1 (максимальному значению потока $z_{a}^{0}$) соответствует набор ребер – минимальный разрез R_a, ${{R}_{a}} \subset R$ [7]. Множество номеров ребер, образующих разрез R_a, обозначим

здесь R_a – минимальное по суммарной пропускной способности подмножество ребер, таких, что при удалении их из сети максимальный поток из ${{v}_{{{{s}_{a}}}}}$ в ${{v}_{{{{t}_{a}}}}}$ становится равным нулю, т.е. в графе $G({\mathbf{d}}){{\backslash }}{{R}_{a}}$ между вершинами ${{v}_{{{{s}_{a}}}}}$ и ${{v}_{{{{t}_{a}}}}}$ нет пути.

Последовательно для всех ${{p}_{m}} \in P$ решаются цепочки задач 1 и формируются вектор максимальных потоков:

а также множество повреждений первого типа: где $h(m)$ – набор номеров ребер, входящих в минимальный разрез ${{R}_{m}}$, ${{R}_{m}} \subset R$, ${{p}_{m}} \in P$. При решении задачи 1 для некоторой фиксированной пары p_a максимальному потоку $z_{a}^{0}$ ставится в соответствие единственный минимальный разрез $R({{z}_{a}})$ и набор номеров ребер h(a).

Для построения критически опасных повреждений второго типа – минимальных разрезов единичной сети, в ходе вычислительного эксперимента пропускные способности всех ребер исходной сети полагаются равными единице:

Сеть с единичными пропускными способностями обозначим через G(1), а множество достижимых потоков (1.3) – $\mathcal{Z}(x,1)$:

Для определения минимального разреза для каждой пары ${{p}_{m}} \in P$ решается задача о максимальном потоке в единичной сети.

Задача 2. Для некоторой фиксированной пары p_m найти максимальный поток

Решение задачи 2 – максимальный целочисленный поток $z_{m}^{1}$ из вершины с номером s_m в вершину с номером t_m. Величина $z_{m}^{1}$ равна числу ребер в минимальном по суммарной пропускной способности разрезе $R(z_{m}^{1})$, $z_{m}^{1} = {\text{|}}R(z_{m}^{1}){\text{|}}$. В настоящей работе максимальному потоку $z_{m}^{1}$ ставится в соответствие единственный разрез $R(z_{m}^{1})$ со списком номеров ребер

При удалении $R(z_{m}^{1})$ из G(1) максимальный поток $z_{m}^{1}$ из ${{v}_{{{{s}_{m}}}}}$ в ${{v}_{{{{t}_{m}}}}}$ становится равным нулю.

Множество повреждений второго типа

состоит из наборов номеров ребер, входящих в минимальные разрезы $R(z_{m}^{1})$, $m = \overline {1,M} $.

Множество повреждений третьего типа

состоит из наборов номеров ребер, инцидентных вершине ${{v}_{n}}$: где $R({{v}_{n}})$ – множество ребер, инцидентных ${{v}_{n}}$.

Для сокращения объема необходимых вычислений элементы множеств $H( \cdot )$, $Q( \cdot )$, $Y( \cdot )$ сравниваются между собой, производится удаление повторяющихся повреждений любого типа и формирование множества уникальных повреждений:

которое не содержит одинаковых элементов.

3. Оценки повреждений. При проведении вычислительных экспериментов при некотором повреждении w_l  пропускная способность ребер сети $G({\mathbf{d}}(l))$ задается следующим образом:

В поврежденной сети $G(d(l))$ для всех ${{p}_{m}} \in P$ последовательно для каждого $m = \overline {1,M} $ определяется возможный максимальный поток.

Задача 3. При некоторых заданных l и m найти

Задача 3 решается последовательно для всех p_m, ${{p}_{m}} \in P$, и всех ${{w}_{l}} \in W$. Для найденных максимальных потоков $z_{m}^{0}(l)$, $m = \overline {1,M} $, $l = \overline {1,L} $, рассчитываются индикаторные показатели:

Для каждой пары ${{p}_{m}} \in P$ и всех ${{w}_{l}} \in W$ вычисляется

– доля от общего числа повреждений W, при которых максимальный поток для данной пары p_m становится равен нулю.

Для каждой пары p_m, для которой $z_{m}^{0}(l) > 0$ при повреждении w_l, и некоторого наперед заданного значения g рассчитывается индикаторная функция:

Значение параметра γ задается априори в диапазоне $0 < \gamma < 1$. При заданном γ для некоторой пары p_m и всех повреждений из W, таких, что $z_{m}^{0}(l) > 0$, определяется

равная доле от общего числа повреждений из W, при которых максимальный поток для данной пары p_m становится меньше или равен заданному критическому пороговому значению γ.

На основе значений $(\rho (m),\varphi (m,\gamma ))$ для всех пар ${{p}_{m}} \in P$ строятся диаграммы, которые позволяют оценить влияние каждого из повреждений на потоки между всеми парами вершин источник-приемник. Недоминируемые значения – точки на внешней границе диаграмм, они указывают на пары-корреспонденты, которым повреждения из W наносят наибольший ущерб хотя бы по одному из показателей.

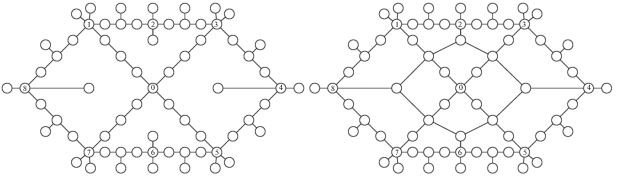
4. Вычислительный эксперимент. Вычислительный эксперимент проводился на моделях сетевых систем, представленных на рис. 1: слева – базовая сеть, а справа – кольцевая. Пропускные способности выбирались случайным образом из отрезка [900, 999] и были равны для совпадающих ребер в обеих сетях. Пропускная способность каждого из дополнительных ребер на рис. 1 справа равна 900. Число повреждений – элементов множества W – составляет 125 для базовой сети и 118 – для кольцевой. Для формирования множества W было найдено порядка 10⁴ минимальных разрезов, из которых менее 100 (около 1%) оказались уникальными.

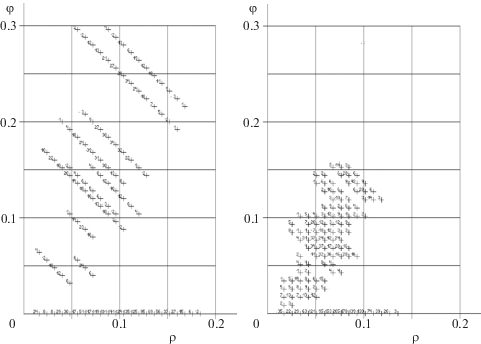
На рис. 2 слева изображена диаграмма расчетных значений $(\rho (m),\varphi (m,\gamma ))$ при $\gamma = 0.6$ для базовой сети, а справа – для кольцевой. Каждый значок плюс на диаграммах относится к одной паре узлов p_m, а цифра рядом означает число пар источник-приемник с совпадающими значениями $(\rho (m),\varphi (m,\gamma ))$. Большое количество точек-плюсов на оси абсцисс $\rho (m)$ относится к парам узлов, для которых $z_{m}^{0}(l) = 0$, оставшиеся значения $z_{m}^{0}(l) > 0.6$, т.е. больше заданного критического значения γ.

Для всех пар узлов оценки ущерба проводятся для всех повреждений из множества W. Значение $\rho (m)$ – относительный показатель – доля от общего числа повреждений, при которых максимальный поток становится равным нулю для данной пары. Величина $\rho (m)$ не зависит от значений γ, а определяется структурой сети и составом множества повреждений W.

На рис. 2 значения $\varphi (m,\gamma )$ по оси ординат значительно отличаются для разных сетей. В кольцевой сети больше обходных путей и максимальные потоки оказываются больше $\gamma = 0.6$ у большего числа пар-корреспондентов.

Точки-плюсы, расположенные вдоль северо-восточной границы диаграммы, соответствуют парам узлов, для которых потери потока оказываются недоминируюмыми хотя бы по одному показателю ущерба $\rho (m)$ или $\varphi (m,\gamma )$. Для кольцевой сети линия северо-восточной границы проходит значительно ближе к началу координат. Последнее означает, что ущерб в кольцевой сети меньше, чем в базовой, даже для самых “уязвимых” пар с наибольшими потерями.

В обеих сетях для большинства пар источник-приемник существует либо один, либо два пути соединения. На рис. 2 точки-плюсы оси абсцисс $\rho (m)$ относятся в основном к парам, имеющим один или три пути соединения. Точки на диаграмме отвечают парам узлов p_m, для которых $z_{m}^{0}(l) \leqslant 0.6z_{m}^{0}$, и относятся к парам с двумя возможными путями соединения. Значение $\gamma = 0.6$ выделяет все такие пары, поскольку относительные потери потока при повреждении одного из путей в среднем составляет 0.5.

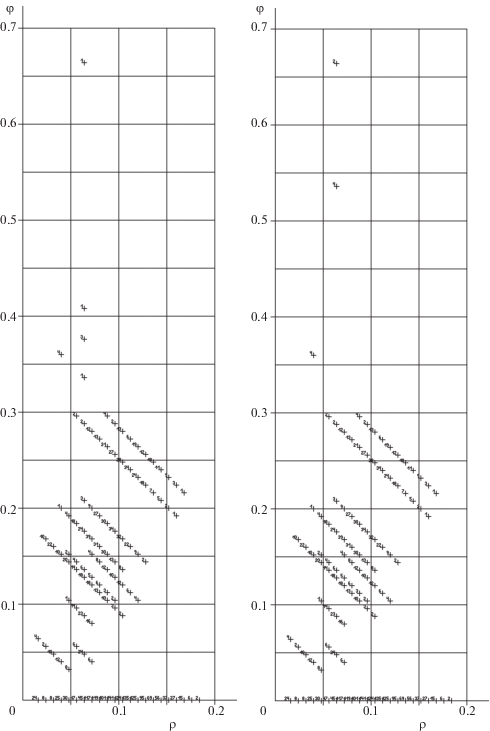
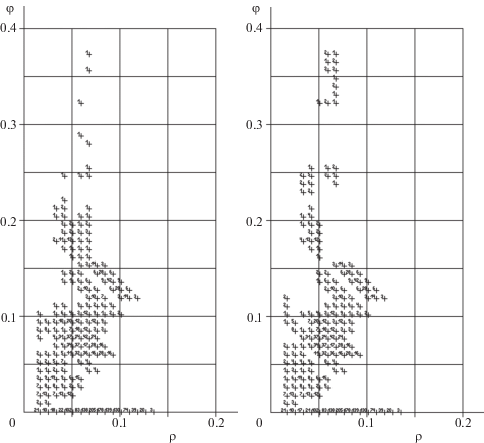
На рис. 3, 4 представлены четыре диаграммы: слева для значений $\gamma = 0.673$, а справа – для $\gamma = 0.7$, на рис. 3 – для базовой сети, на рис. 4 – для кольцевой. Указанные диаграммы разительно отличаются от рис. 2 при $\gamma = 0.6$. Дело в том, что при $\gamma = 0.7$ критическими потерями считается уменьшение максимального потока на 30%, что возможно при разрушении даже одного из трех путей соединения. В результате для некоторых пар узлов, у которых $\varphi (m,\gamma ) = 0$ при $\gamma = 0.6$, фиксируются потери потока, и для пар p_m соответствующие точки-плюсы $\varphi (m,\gamma ) > 0$ оказываются недоминируемым показателем ущерба.

Для тех пар, для которых значение максимального потока в поврежденной сети

при $\gamma = 0.673$ не фиксируются потери потока. В результате общее число точек-плюсов на верхних  ярусах  диаграммы уменьшается и меняется состав (список) пар с недоминируемыми показателями ущерба. Проведенные расчеты и внешние различия диаграммы позволяют достаточно подробно анализировать последствия разрушающих воздействий. В частности, расчеты при различных γ дают возможность определять число разрушенных путей соединения. Подобрав значения γ, можно выделить группы пар-корреспондентов с разными потерями при разрушении одинакового числа путей.

Заключение. В последние годы значительно возрос интерес к более предметному и комплексному анализу уязвимости сложных взаимосвязанных сетевых систем, функционирующих как единое территориально-распределенное образование [8–11]. В [9] прослеживается, как эволюционировали модели и методы исследования уязвимости и живучести: теоретико-графовые, вероятностные, эвристические, имитационные, оптимизационные и др. В [10] основное внимание уделяется специальным моделям уязвимости сетей, отмечается необходимость отдельного анализа террористических действий и/или спланированных хакерских атак, а также влияния человеческого фактора при авариях. В [11] приведен обзор возможных стратегий защиты сетей от природных катастроф.

Различные критерии и методы используются для поиска критических элементов сети [12–18]. В [12] рассматривается задача поиска множества дуг взвешенной сети, удаление которых из сети минимизирует два критерия: максимальный поток и стоимость разрушения. Парето-оптимальные решения этой задачи определяются с помощью специализированного алгоритма ветвей и границ, а также применения релаксации Лагранжа к последовательности однокритериальных задач о поиске максимального потока и минимального разреза. В [13] изучается проблема идентификации подмножества элементов (узлов, дуг, путей, клик и т.д.), удаление которых минимизирует заданную меру связности в поврежденной сети. Приводится обзор некоторых методов, в том числе использующих эвристики, математическое программирование, алгоритмы аппроксимации и подходы динамического программирования. В [14] изучаются предельные функциональные возможности многопродуктовой сети и их изменения при повреждениях сетевых элементов – минимальных разрезов трех основных типов. В частности, рассчитываются две группы количественных характеристик последствий каждого повреждения: доля разделенных пар узлов и уменьшение максимально возможного потока для каждой пары. Указанные показатели используются для двухкритериального ранжирования повреждений. Полученные агрегированные оценки ущерба позволяют также находить критически опасные структурные повреждения сети в рамках предложенных критериев.

В [15–18] рассматривается так называемая проблема определения критических вершин, которая состоит в поиске подмножества из K вершин связного графа, удаление которых ведет к минимизации выбранного критерия связности. В [15] задача решается с использованием методов целочисленного линейного программирования, в [16] – формулируется как двухкритериальная, в [17] изучается ее NP-сложность, а также анализируются результаты проведенных вычислительных экспериментов. В [18] представлен обширный обзор по указанной теме.

Проблема уязвимости кластерных объединений при отказах различных сетевых элементов рассматривается в [19, 20]. В [19] вводится понятие среднего коэффициента кластеризации, проблема формулируется как оптимизационная, доказывается ее NP-полнота и немонотонность, а также предлагается два алгоритма, позволяющих идентифицировать вершины, ключевые для кластерных объединений. В [20] изучается устойчивость структур кластерных связей и исследуется проблема ранжирования повреждений для заданного класса сетевых систем по трем критериям, включая мощность разреза.

В настоящей работе продолжено изучение потокового метода априорного анализа структурной неуязвимости сети при разрушениях определенного вида [1, 2]. Выбор в качестве структурных повреждений разрезов, минимальных по пропускной способности и числу ребер, а также отделяющих некоторую вершину от сети, определяется логикой исследования. Поиск наиболее уязвимых пар источник-приемник для указанных повреждений ведется по двум критериям (обнуление потока и падение потока ниже наперед заданного уровня), что позволяет заранее оценить, насколько структура сохраняет нормативную работоспособность сетевой системы после разрушения. При проведении вычислительного эксперимента использовались методы потокового программирования с полиномиальной оценкой вычислительной сложности [7, 21]. Как уже отмечалось в [2], суммарные вычислительные затраты не превышают $O({{N}^{7}})$, где $N$ – число узлов сети. Предложенная схема проведения расчетов проста и поддается распараллеливанию, поэтому при исследовании уязвимости больших сетей могут быть использованы кластеры из персональных компьютеров с различными операционными системами.