Известия РАН. Теория и системы управления, 2021, № 4, стр. 57-73
УПРАВЛЕНИЕ ПОДВИЖНОЙ МАССОЙ С НАЧАЛЬНЫМ И КОНЕЧНЫМ ПОЛОЖЕНИЕМ НА ГРАНИЦЕ ОБЛАСТИ ДВИЖЕНИЯ С ЦЕЛЬЮ НАИСКОРЕЙШЕГО ПОВОРОТА ТВЕРДОГО ТЕЛА
А. М. Шматков *
Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: shmatkov@ipmnet.ru
Поступила в редакцию 16.09.2020
После доработки 24.09.2020
Принята к публикации 30.11.2020
Аннотация
В плоском случае рассмотрена задача поворота твердого тела на заданный угол за минимально возможное время с помощью взаимодействующей с ним подвижной массы, движения которой ограничены внутренностью заданного круга. Исследована соответствующая двухточечная задача оптимального быстродействия для системы с тремя фазовыми переменными при наличии фазового ограничения. Показано наличие континуума как кривых, удовлетворяющих необходимым условиям оптимальности, так и искомых оптимальных траекторий. В случае, когда подвижная масса начинает и заканчивает свое движение на границе круга, получены оптимальные траектории и длительности ее перемещения. Исследование основано на анализе одномерной механической системы, движения которой соответствуют решениям уравнений трехмерной задачи для оптимальных управлений.
Введение. В агрессивных и ранимых средах при изменении пространственной ориентации робототехнических систем ряд существенных затруднений возникает из-за наличия внешних по отношению к корпусу робота движителей: колес, пропеллеров, ног и т.п. Один из возможных способов решения проблемы – использованиe для переориентации внутренних подвижных масс, что позволяет делать корпус герметичным [1–4]. Тогда возникает ограничение на допустимые положения внутренней массы, состоящее в том, что она не может находиться от центра масс корпуса дальше, чем на некотором заданном расстоянии, зависящем от габаритов устройства. Тот же самый подход может быть применен для управления вращением космических аппаратов [5] без использования реактивных двигателей и гиростабилизирующих систем.
При известных предположениях об особенностях маневра можно пренебречь влиянием внешних сил и полагать соответствующую механическую систему замкнутой, т.е. состоящей только из объекта управления и движущейся массы. Это позволяет упростить математическую модель и получить в аналитическом виде, например, решение задачи о пространственной переориентации тела по заданной программе [6]. Кроме того, для плоского случая, когда оба объекта могут осуществлять только плоскопараллельные движения, оказывается возможным провести подробный анализ некоторых задач оптимального управления, который будет изложен ниже.
Данная работа включает в себя обобщение и анализ кратко изложенных ранее результатов [7].
1. Уравнения движения. Рассмотрим механическую систему, состоящую из твердого тела массы $M$ и материальной точки массы $m$. Допустим, что все внешние силы отсутствуют, и не будем делать никаких предположений о внутренних силах, действующих на оба объекта. Пусть сначала твердое тело и материальная точка покоятся. Тогда на основании законов сохранения количества движения и углового момента, а также того обстоятельства, что общий центр масс системы никогда не движется, можно получить уравнения [4]
(1.1)
$\dot {x} = u,\quad \dot {y} = {v},\quad \dot {\varphi } = \frac{{\mu (yu - x{v})}}{{{{a}^{2}} + \mu ({{x}^{2}} + {{y}^{2}})}},\quad {{u}^{2}} + {{{v}}^{2}} \leqslant {{V}^{2}},\quad {{x}^{2}} + {{y}^{2}} \leqslant {{R}^{2}}.$В (1.1) фазовые переменные x и y – декартовы координаты материальной точки в связанной с твердым телом системе координат, имеющей начало в его центре масс. Последний также является центром круга радиуса $R > 0$, пределы которого материальная точка никогда не должна покидать. Управления u и ${v}$ – проекции вектора скорости материальной точки на оси введенной системы координат, причем длина этого вектора не может превышать некоторой заданной величины V. Еще одна фазовая переменная – угол поворота твердого тела φ. Через $a = \sqrt {J{\text{/}}M} $ обозначен радиус инерции тела, где J – главный центральный момент инерции, а $\mu = m{\text{/}}(M + m)$.
В общем случае граничные условия для системы (1.1) можно записать в форме
(1.2)
$\begin{array}{*{20}{c}} {x(0) = {{x}_{0}},\quad y(0) = {{y}_{0}},\quad \varphi (0) = {{\varphi }_{0}},\quad x_{0}^{2} + y_{0}^{2} \leqslant {{R}^{2}},} \\ {x(T) = {{x}_{T}},\quad y(T) = {{y}_{T}},\quad \varphi (T) = {{\varphi }_{T}},\quad x_{T}^{2} + y_{T}^{2} \leqslant {{R}^{2}}.} \end{array}$Заменим переменные в (1.1), согласно [8]:
Сохраним старые обозначения переменных и получим
(1.3)
$\dot {x} = u,\quad \dot {y} = v,\quad \dot {\varphi } = \frac{{yu - xv}}{{1 + {{x}^{2}} + {{y}^{2}}}},\quad {{u}^{2}} + {{v}^{2}} \leqslant 1,\quad {{x}^{2}} + {{y}^{2}} \leqslant {{R}^{2}}.$Потом перейдем к полярным переменным
(1.4)
$\dot {r} = \hat {u},\quad \dot {\alpha } = \frac{{\hat {v}}}{r},\quad \dot {\varphi } = - \frac{{r\hat {v}}}{{1 + {{r}^{2}}}},\quad {{\hat {u}}^{2}} + {{\hat {v}}^{2}} \leqslant 1,\quad r \leqslant R,$Граничные условия (1.2) для общего случая можно заменить на [8]
Далее будут рассмотрены задачи оптимального быстродействия для системы (1.4) с различными вариантами граничных условий.
2. Оптимальное управление для участков траектории, не лежащих на ограничении. Запишем гамильтониан [9] для системы (1.4):
(2.1)
$H = {{p}_{0}} + {{p}_{r}}\hat {u} + \zeta \hat {v},\quad {{p}_{0}} = {\text{const}} \leqslant 0,\quad \zeta = \frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}.$В (2.1) через ${{p}_{r}}$, ${{p}_{\alpha }}$ и ${{p}_{\varphi }}$ обозначены переменные, сопряженные к фазовым переменным $r$, $\alpha $ и $\varphi $ соответственно. Сопряженные переменные pα и pφ постоянны, поскольку
Заметим, что гамильтониан (2.1) можно рассматривать как сумму константы ${{p}_{0}}$ и скалярного произведения вектора управления с компонентами $\hat {u}$ и $\hat {v}$ на некоторый вектор $\psi $ с компонентами ${{p}_{r}}$ и $\zeta $. Согласно принципу максимума, на оптимальной траектории величина H должна достигать максимума как функция вектора управления, а потому последний должен
быть сонаправлен вектору $\psi $, а также иметь максимально возможную норму, которая в данной задаче (1.4) равна единице.
Кроме того, на оптимальной траектории гамильтониан равен нулю. Следовательно, скалярное
произведение единичного вектора управления и сонаправленного ему вектора ψ постоянно
и равно $ - {{p}_{0}}$. Тогда норма вектора ψ постоянна и равна ${{p}_{0}}$, причем ${{p}_{0}} \ne 0$, так как вектор 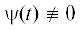 . Отсюда имеем интеграл движения ${{\psi }^{2}} = p_{r}^{2} + {{\zeta }^{2}} = p_{0}^{2}$ и оптимальные управления в форме
. Отсюда имеем интеграл движения ${{\psi }^{2}} = p_{r}^{2} + {{\zeta }^{2}} = p_{0}^{2}$ и оптимальные управления в форме
(2.2)
${{\hat {u}}_{*}} = \frac{{{{p}_{r}}}}{{ - {{p}_{0}}}},\quad {{\hat {v}}_{*}} = \frac{\zeta }{{ - {{p}_{0}}}}.$Поскольку вектор сопряженных переменных определен с точностью до ненулевого скалярного множителя, в дальнейшем положим ${{p}_{0}} = - 1$. Получаем систему дифференциальных уравнений, которой должна удовлетворять оптимальная траектория:
(2.3)
$\begin{array}{*{20}{c}} {\dot {r} = {{p}_{r}},\quad \mathop {\dot {p}}\nolimits_r = \left( {\frac{{{{p}_{\alpha }}}}{{{{r}^{2}}}} + \frac{{{{p}_{\varphi }}(1 - {{r}^{2}})}}{{\mathop {(1 + {{r}^{2}})}\nolimits^2 }}} \right)\left( {\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}} \right),} \\ {\dot {\alpha } = \frac{{{{p}_{\alpha }}}}{{{{r}^{2}}}} - \frac{{{{p}_{\varphi }}}}{{1 + {{r}^{2}}}},\quad \dot {\varphi } = \frac{{ - {{p}_{\alpha }}}}{{1 + {{r}^{2}}}} + \frac{{{{p}_{\varphi }}{{r}^{2}}}}{{\mathop {(1 + {{r}^{2}})}\nolimits^2 }}} \end{array}$(2.4)
$p_{r}^{2} + \mathop {\left( {\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 = 1.$Соотношение (2.4) позволяет, в частности, исключить переменную ${{p}_{r}}$:
(2.5)
${{p}_{r}} = \pm \sqrt {1 - \mathop {\left( {\frac{{{{p}_{\alpha }}}}{r} - \frac{{{{p}_{\varphi }}r}}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 } .$Положительный знак в формуле (2.5) соответствует тем участкам траекторий, на которых расстояние $r$ увеличивается, а отрицательный – тем, на которых оно уменьшается.
Заметим, что вследствие обратимости времени в механических системах уравнения (2.3) инвариантны относительно замены переменных
(2.6)
$\alpha \to - \alpha ,\quad \varphi \to - \varphi ,\quad {{p}_{r}} \to - {{p}_{r}},\quad t \to - t.$Другими словами, если твердое тело поворачивается на угол $\varphi (T)$ при движении материальной точки из начального положения в конечное, то при прохождении той же самой траектории в обратном направлении угол поворота твердого тела составит $ - \varphi (T)$.
3. Задача со свободным правым концом траектории. Это случай, когда значения переменных $r$ и $\alpha $ в конечный момент времени $T$ не заданы. Тогда условия трансверсальности [9] дают ${{p}_{r}}(T) = 0$ и ${{p}_{\alpha }} = 0$. Соответствующее решение найдено в [8, 10]. Оптимальная траектория представляет собой спираль, которая с ростом φ при ${{r}_{0}} < 1$ монотонно асимптотически приближается к единичной окружности изнутри, а при ${{r}_{0}} > 1$ – снаружи. Уравнение кривой имеет вид
(3.1)
$\alpha (r) = \pm \int\limits_{{{r}_{0}}}^r \,\frac{{d\rho }}{{\sqrt {\psi (\rho )} }},\quad \psi (\rho ) = \frac{{r_{T}^{2}\mathop {(1 + {{\rho }^{2}})}\nolimits^2 }}{{\mathop {(1 + r_{T}^{2})}\nolimits^2 }} - {{\rho }^{2}},\quad {{r}_{T}} = r(T).$Неизвестное значение ${{r}_{T}}$ можно найти из уравнения
(3.2)
${{\varphi }_{T}} = \mp \int\limits_{{{r}_{0}}}^{{{r}_{T}}} \,\frac{{{{\rho }^{2}}d\rho }}{{(1 + {{\rho }^{2}})\sqrt {\psi (\rho )} }}.$Заметим, что интегралы в (3.1) и (3.2) являются эллиптическими [11].
4. Движение по прямой. Так как модуль оптимальной скорости равен единице, то время движения равно длине пройденного участка кривой [12]. Пусть в конечный момент времени T величина угла поворота твердого тела ${{\varphi }_{T}}$ не задана. Следовательно, в этом случае требуется найти самую короткую траекторию, соединяющую две заданные точки, а потому решением является отрезок прямой. Для нахождения соответствующей зависимости $\varphi = \varphi (r)$ используем условие трансверсальности ${{p}_{\varphi }} = 0$. Из (2.3) имеем
(4.1)
$rcos(\alpha - {{C}_{p}}) = {{p}_{\alpha }},\quad {{C}_{p}} = {\text{arctg}}\frac{{\sqrt {r_{0}^{2} - p_{\alpha }^{2}} }}{{{{p}_{\alpha }}}}.$Следовательно, величина ${\text{|}}{{p}_{\alpha }}{\text{|}}$ равна расстоянию от начала координат до прямой, содержащей рассматриваемый отрезок. На основании (2.3) получаем
(4.2)
$\varphi (r) = \frac{{ - {{p}_{\alpha }}}}{{\sqrt {1 + p_{\alpha }^{2}} }}{\text{arctg}}\sqrt {\frac{{{{r}^{2}} - p_{\alpha }^{2}}}{{1 + p_{\alpha }^{2}}}} - {{C}_{\varphi }},$5. Траектории на оптимальных кривых, проходящих через начало координат. Как следует из (2.3), движения могут включать точку r = 0 лишь при ${{C}_{\alpha }} = 0$. В этом случае система (2.3) примет вид [13]
(5.1)
$\ddot {r} = \frac{{ - p_{\varphi }^{2}r(1 - {{r}^{2}})}}{{\mathop {(1 + {{r}^{2}})}\nolimits^3 }},\quad \dot {\alpha } = \frac{{ - {{p}_{\varphi }}}}{{1 + {{r}^{2}}}},\quad \dot {\varphi } = \frac{{{{p}_{\varphi }}{{r}^{2}}}}{{\mathop {(1 + {{r}^{2}})}\nolimits^2 }}.$В свою очередь соотношения (5.1) можно записать в форме
(5.2)
$\frac{{{{d}^{2}}\eta }}{{d{{\alpha }^{2}}}} + sin\eta = 0,\quad \frac{{d\varphi }}{{d\alpha }} = \frac{1}{8}(cos\eta - 1),\quad \eta = 4{\text{arctg}}\,r.$Первое из уравнений системы (5.2) описывает колебания маятника [14]. В качестве параметра семейства можно использовать, например, значения производной функции $\eta = \eta (\alpha )$ в начальный момент времени. В дальнейшем, если явно не указано обратное, будем полагать ${{C}_{\alpha }} \ne 0$.
6. Связь с одномерной механической системой. Запишем (2.4) в форме
(6.1)
$\mathop {\left( {\frac{{{{p}_{r}}}}{{{{p}_{\varphi }}}}} \right)}\nolimits^2 + \mathop {\left( {\frac{{{{C}_{\alpha }}}}{r} - \frac{r}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 = \frac{1}{{p_{\varphi }^{2}}},\quad {{C}_{\alpha }} = \frac{{{{p}_{\alpha }}}}{{{{p}_{\varphi }}}}.$Заметим, что интеграл (6.1) можно рассматривать как гамильтониан одномерной консервативной механической системы, состоящей из материальной точки с массой, равной 2, движущейся в центральном поле [15] под действием потенциальной силы со скоростью ${{p}_{r}}{\text{/}}{{p}_{\varphi }}$, причем потенциальная энергия равна
(6.2)
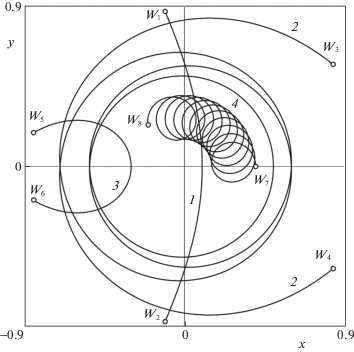
$\Pi = \mathop {\left( {\frac{{{{C}_{\alpha }}}}{r} - \frac{r}{{1 + {{r}^{2}}}}} \right)}\nolimits^2 .$Функция $\Pi = \Pi (r)$ стремится к нулю при $r \to + \infty $ и $\Pi (r) \to + \infty $ при $r \to 0$. На рис. 1 показан характерный вид зависимостей $\Pi = \Pi (r)$ при различных величинах параметра ${{C}_{\alpha }}$, а на рис. 2 – некоторые траектории движения материальной точки, согласно (2.3). График 1 на рис. 1 соответствует случаю ${{C}_{\alpha }} < - 1{\text{/}}8$. Производная потенциальной энергии при этом всюду отрицательна, а потому все движения точки инфинитны [15]. Такой кривой принадлежит, в частности, траектория 1 на рис. 2. Если ${{C}_{\alpha }} = - 1{\text{/}}8$, то зависимость $\Pi (r)$ имеет точку перегиба при ${{r}_{*}} = \sqrt 3 {\text{/}}3$, как показано на графике 2 рис. 1, причем $\Pi ({{r}_{*}}){\kern 1pt} {\text{ = 27/}}64$. Следовательно, при ${{C}_{\alpha }} = - 1{\text{/}}8$, кроме инфинитных, существует единственное финитное движение точки – по окружности с центром в начале координат и радиусом ${{r}_{*}}$. При ${{C}_{\alpha }} \geqslant - 1{\text{/}}8$ точка может двигаться по гораздо более сложным инфинитным кривым, чем при меньших ${{C}_{\alpha }}$, что видно на примере траектории 2 рис. 2, построенной для ${{C}_{\alpha }}$ = –1/8, тогда как траектории 1 рис. 2 соответствует ${{C}_{\alpha }} = - 0.3$.
Рис. 1.
Зависимости $\Pi = \Pi (r)$, характерные для различных значений параметра ${{C}_{\alpha }}$ и занумерованные в порядке его возрастания
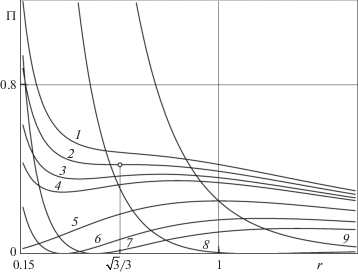
Рис. 2.
Траектории, удовлетворяющие необходимым условиям оптимальности: 1–3 лежат на инфинитных кривых, а 4 – на финитной кривой
Зависимость $\Pi (r)$ для $ - 1{\text{/}}8 < {{C}_{\alpha }} < 1$ всегда имеет локальный минимум при $r = {{r}_{ - }}$ и локальный максимум при $r = {{r}_{ + }}$, удовлетворяющие в случае $ - 1{\text{/}}8 < {{C}_{\alpha }} \leqslant 0$ биквадратному уравнению
(6.3)
${{C}_{\alpha }} = \frac{{(r_{ \mp }^{2} - 1)r_{ \mp }^{2}}}{{\mathop {(r_{ \mp }^{2} + 1)}\nolimits^2 }},\quad {{r}_{ - }} < {{r}_{ + }},\quad {{r}_{ + }} > \frac{{\sqrt 3 }}{3},$(6.4)
$\Pi ({{r}_{ \mp }}) = \frac{{4r_{ \mp }^{2}}}{{\mathop {(1 + r_{ \mp }^{2})}\nolimits^4 }} = \frac{{16{{{({{C}_{\alpha }} - 1)}}^{2}}\mathop {(2{{C}_{\alpha }} + 1 \mp \sqrt {8{{C}_{\alpha }} + 1} )}\nolimits^2 }}{{\mathop {(3 \mp \sqrt {8{{C}_{\alpha }} + 1} )}\nolimits^4 }}.$Как следует из соотношения (6.3) и видно из графиков 3 и 4 на рис. 1, с увеличением значения ${{C}_{\alpha }}$ и приближением его к нулю величина ${{r}_{ - }}$ монотонно уменьшается и также стремится к нулю, причем $\Pi ({{r}_{ - }}) > 0$, а величина ${{r}_{ + }}$ монотонно растет и стремится к единице. При ${{C}_{\alpha }} = 0$ минимум $\Pi ({{r}_{ - }} = 0)$ = 0 и максимум $\Pi ({{r}_{ + }} = 1) = 1{\text{/}}4$, а соответствующая зависимость показана на графике 5 рис. 1. Как видно из графиков 6–8 на рис. 1, по мере дальнейшего роста величины ${{C}_{\alpha }}$ и приближении ее к единице потенциальная энергия $\Pi ({{r}_{ - }})$ по-прежнему равна нулю, а значение $r_{ - }^{2}$ монотонно растет и удовлетворяет линейному уравнению
в то время как монотонно растущее значение ${{r}_{ + }} > 1$ по-прежнему удовлетворяет соотношению (6.3). Как и при ${{C}_{\alpha }} < - 1{\text{/}}8$, для ${{C}_{\alpha }} \geqslant 1$ производная потенциальной энергии всюду отрицательна и все движения инфинитны, что показано на графике 9 рис. 1 в случае ${{C}_{\alpha }} = 1$.Равенство нулю потенциальной энергии при $0 < {{C}_{\alpha }} < 1$ в точке $r = {{r}_{ - }}$ означает равенство единице составляющей скорости вдоль радиус-вектора точки, т.е. существование проходящей через начало координат касательной к траектории. Это отличает движения точки при ${{C}_{\alpha }} < 0$ от движений при ${{C}_{\alpha }} > 0$, что видно на рис. 2 из сравнения траекторий 1 и 2 с траекторией 3, которая построена для случая инфинитного движения при ${{C}_{\alpha }} > 0$.
Наличие потенциальной ямы для $ - 1{\text{/}}8 < {{C}_{\alpha }} < 1$ означает существование оптимальных финитных движений при ${{r}_{ - }} \leqslant r(t) \leqslant {{r}_{ + }}$. Таковыми, в частности, являются окружности с радиусами ${{r}_{ - }}$ и ${{r}_{ + }}$. В отличие от них остальные финитные движения замкнуты только в исключительных ситуациях, когда за период колебания одномерной механической системы с гамильтонианом (6.1) угол α меняется на величину $2\pi i{\text{/}}j$, где i и j – целые числа. Если $ - 1{\text{/}}8 < {{C}_{\alpha }} < 0$, то кривые финитных движений охватывают начало координат и имеют качественное сходство с классическими решениями для неодномерной задачи [15]. В случае $0 < {{C}_{\alpha }} < 1$ соответствующие кривые всегда смещены, как, например, траектория 4 на рис. 2.
7. Выбор параметров. В общем случае оптимальная траектория зависит от постоянных ${{p}_{\alpha }}$ и ${{p}_{\phi }}$. Однако другая пара величин может оказаться более удобной.
Каждое финитное или инфинитное движение содержит хотя бы одну точку поворота [15]. Выберем из них любую, расстояние ${{r}_{{{\text{min}}}}} > 0$ от которой до точки r = 0 минимально для всей кривой. Тогда последнюю можно разбить на две ветви, симметричные относительно прямой, которая проходит через начало координат и указанную точку поворота. Кроме того, в этой точке кинетическая энергия в гамильтониане (6.1) равна нулю, откуда следует выражение
(7.1)
${{p}_{\phi }} = \pm \frac{{{{r}_{{{\text{min}}}}}(1 + r_{{{\text{min}}}}^{2})}}{{{{C}_{\alpha }}(1 + r_{{{\text{min}}}}^{2}) - r_{{{\text{min}}}}^{2}}}.$Выбор знака в соотношении (7.1) зависит от выбора нужной ветви и направления движения по ней (2.5), что связано с обычной для автономных задач оптимального управления инвариантностью системы (2.3) относительно замены:
Вместо параметров ${{p}_{\alpha }}$ и ${{p}_{\varphi }}$ будем использовать ${{C}_{\alpha }}$ и ${{r}_{{{\text{min}}}}}$, поскольку величина ${{r}_{{{\text{min}}}}}$ имеет очевидный физический смысл, а свойства движения существенно зависят от значения Cα. Например, при ${{C}_{\alpha }} < - 1{\text{/}}8$ и ${{C}_{\alpha }} \geqslant 1$ все кривые инфинитны для любой величины rmin.
Заметим, что для каждого значения rmin существует множество значений параметра Cα:
(7.2)
$\begin{array}{*{20}{c}} {\frac{{r_{{{\text{min}}}}^{2}}}{{2(1 + r_{{{\text{min}}}}^{2})}} - \frac{{{{r}_{{{\text{min}}}}}}}{{2\sqrt {1 + r_{{{\text{min}}}}^{2}} }} < {{C}_{\alpha }} < \frac{{r_{{{\text{min}}}}^{2}}}{{2(1 + r_{{{\text{min}}}}^{2})}} + \frac{{{{r}_{{{\text{min}}}}}}}{{2\sqrt {1 + r_{{{\text{min}}}}^{2}} }},} \\ {{{C}_{\alpha }} \ne 0,\quad {{C}_{\alpha }} \ne \frac{{r_{{{\text{min}}}}^{2}}}{{1 + r_{{{\text{min}}}}^{2}}},} \end{array}$(7.3)
$\begin{array}{*{20}{c}} {{{r}_{{max}}} = - {{f}_{k}} + {{f}_{D}},\quad {{r}_{b}} = - {{f}_{k}} - {{f}_{D}},\quad {{C}_{\alpha }} < 0;} \\ {{{r}_{{max}}} = {{f}_{k}} - {{f}_{D}},\quad {{r}_{b}} = - {{f}_{k}} - {{f}_{D}},\quad 0 < {{C}_{\alpha }} < \frac{{r_{{{\text{min}}}}^{2}}}{{1 + r_{{{\text{min}}}}^{2}}};} \\ {{{r}_{{max}}} = {{f}_{k}} + {{f}_{D}},\quad {{r}_{b}} = {{f}_{k}} - {{f}_{D}},\quad {{C}_{\alpha }} > \frac{{r_{{{\text{min}}}}^{2}}}{{1 + r_{{{\text{min}}}}^{2}}},} \end{array}$При $ - 1{\text{/}}8 \leqslant {{C}_{\alpha }} < 1$, когда существуют как инфинитные, так и финитные движения, для любой финитной кривой точка, наиболее удаленная от начала координат, находится от него на расстоянии rmax.
8. Условия финитности оптимальной кривой. Получим дополнительные условия, которым при каждом выбранном значении rmin должна удовлетворять величина $ - 1{\text{/}}8 \leqslant {{C}_{\alpha }} < 1$ для того, чтобы движение было финитным. Поскольку зависимость потенциальной энергии (6.4) от ${{C}_{\alpha }}$ в точке локального максимума имеет сложный вид, сначала найдем ограничения на значения ${{r}_{ + }}$.
Как следует из анализа одномерной системы, для финитности движения необходимо, чтобы ${{r}_{{{\text{min}}}}} \leqslant {{r}_{ + }}$ и $\Pi ({{r}_{{{\text{min}}}}}) \leqslant \Pi ({{r}_{ + }})$, т.е. точка должна иметь возможность находиться в области потенциальной ямы с полной энергией $\Pi ({{r}_{{{\text{min}}}}})$, не превышающей высоты потенциального барьера $\Pi ({{r}_{ + }})$. Используя формулу (6.3) для ${{r}_{ + }}$ и соотношение (6.4) для $\Pi ({{r}_{ + }})$, находим ограничение сверху при всех ${{r}_{{{\text{min}}}}}$:
Для всех остальных значений ${{r}_{{{\text{min}}}}} \geqslant \sqrt 3 {\text{/}}3$ получаем ${{r}_{ + }} \geqslant {{r}_{{{\text{min}}}}}$.
Однако этих условий недостаточно для того, чтобы соответствующее движение было финитным. Еще нужно, чтобы хотя бы одна точка кривой находилась от начала координат на расстоянии, не превышающем ${{r}_{ + }}$. Иначе движение будет инфинитным, а расстояние до точки, ближайшей к началу координат, будет равно не значению rmin, a величине ${{r}_{b}}$, вычисляемой по формулам (7.3). Причина в потенциальном барьере, разделяющем при полученных дополнительных условиях значения r на лежащие внутри потенциальной ямы $r \leqslant {{r}_{ + }}$ и находящиеся снаружи $r > {{r}_{ + }}$. Траектория должна лежать целиком либо с одной, либо с другой стороны локального максимума потенциальной энергии. В случае двухточечной задачи проверку нужно проводить как для начального, так и для конечного значений переменной $r$. Если они оказываются по разные стороны от точки ${{r}_{ + }}$, то для выбранного значения ${{r}_{{{\text{min}}}}}$ решения не существует.
Поскольку, согласно (6.3), величина ${{C}_{\alpha }}$ монотонно растет при увеличении ${{r}_{ + }}$, то для нее нетрудно записать полученные ограничения. Имеем при всех ${{r}_{{{\text{min}}}}}$
9. Поиск допустимых значений параметров в задаче с фазовым ограничением. При наличии ограничивающей окружности радиуса $R$ с центром в начале координат для любых траекторий появляется дополнительное условие ${{r}_{{{\text{min}}}}} \leqslant R$, которое далее для сокращения формул не будем указывать.
Найдем такие условия на параметр ${{C}_{\alpha }}$, при которых полная энергия $\Pi ({{r}_{{{\text{min}}}}})$ одномерного движения не меньше потенциальной энергии $\Pi ({{r}_{a}})$ в некоторой точке ${{r}_{a}}$ соответствующей кривой. Получим, что величина ${{C}_{\alpha }}$ должна удовлетворять либо ограничению
(9.1)
${{C}_{\alpha }} \leqslant \frac{{{{r}_{{{\text{min}}}}}{{r}_{a}}({{r}_{{{\text{min}}}}}{{r}_{a}} - 1)}}{{(1 + r_{{{\text{min}}}}^{2})(1 + r_{a}^{2})}},\quad {{r}_{{{\text{min}}}}} \leqslant {{r}_{a}},$(9.2)
${{C}_{\alpha }} \geqslant \frac{{{{r}_{{{\text{min}}}}}{{r}_{a}}({{r}_{{{\text{min}}}}}{{r}_{a}} + 1)}}{{(1 + r_{{{\text{min}}}}^{2})(1 + r_{a}^{2})}},\quad {{r}_{{{\text{min}}}}} \leqslant {{r}_{a}}.$При ${{C}_{\alpha }} < - 1{\text{/}}8$ и ${{C}_{\alpha }} \geqslant 1$ все траектории лежат на инфинитных кривых, а потому не выходят за пределы заданного круга тогда и только тогда, когда их начала и концы находятся в тех же самых пределах. Следовательно, полная энергия $\Pi ({{r}_{{{\text{min}}}}})$ не может быть меньше потенциальной энергии в начальной и конечной точках траектории. Тогда значения параметра ${{C}_{\alpha }}$ должны дополнительно удовлетворять хотя бы одному из условий (9.1), (9.2) как при ${{r}_{a}} = r(0)$, так и при ${{r}_{a}} = r(T)$. Эти ограничения остаются справедливыми и в случае $ - 1{\text{/}}8 \leqslant {{C}_{\alpha }} < 1$ для траекторий, лежащих на инфинитных кривых.
Финитные кривые могут полностью находиться внутри заданного круга радиуса $R$ только при $\Pi ({{r}_{{{\text{min}}}}}) \leqslant \Pi (R)$. Для них должны быть выполнены полученные выше условия финитности оптимальной кривой и, кроме того, значения параметра ${{C}_{\alpha }}$ должны принадлежать следующему множеству:
В случае, когда финитная кривая лишь частично удовлетворяет фазовому ограничению, соответствующие явные условия для параметров получить невозможно, а потому необходимо использовать свойства конкретной задачи или просто следить за текущим расстоянием r(t) в процессе численного интегрирования системы (2.3) и отбрасывать те траектории, которые нарушают ограничение. Для понимания существа проблемы рассмотрим пример, когда ограничивающая окружность пересекает кривую, фрагмент которой показан на рис. 2 под номером 4. В общем случае невозможно выяснить, выходит ли за пределы круга некоторый участок этой кривой, соединяющий заданные в условии задачи граничные точки, без вычисления эллиптических интегралов, к которым может быть сведено решение уравнений (2.3).
10. Оптимальное управление в точке выхода на ограничение. Запишем фазовое ограничение $r \leqslant R$ из (1.4) в форме
Введем полную производную по времени $\chi $ функции g в силу системы дифференциальных уравнений (1.4):
(10.2)
$\chi (r,\alpha ,\varphi ,\hat {u},\hat {v}) = ({\text{grad}}\,g,f) = \frac{{\partial g}}{{\partial r}}\hat {u} + \frac{{\partial g}}{{\partial \alpha }}\frac{{\hat {v}}}{r} + \frac{{\partial g}}{{\partial \varphi }}\frac{{ - r\hat {v}}}{{1 + {{r}^{2}}}} = \hat {u}.$Градиент в (10.2) вычисляется по вектору с компонентами, являющимися фазовыми переменными $r$, $\alpha $ и $\varphi $, а вектор f имеет компоненты, равные производным этих переменных по времени, согласно (1.4). Из (10.2) видно, что градиент функции $\chi $ по вектору управления с компонентами $\hat {u}$ и $\hat {v}$ для любых значений последних представляет собой ненулевой вектор с компонентами 1 и 0.
Рассмотрим участок траектории, где фазовое ограничение (10.1) обращается в тождество $g(t) \equiv 0$. Он представляет собой дугу окружности радиуса $R$ с центром в начале координат. Функция $\chi $ на нем равна нулю, поскольку в этом случае управление $\hat {u}$, согласно (1.4), равно нулю. Запишем ограничение на управление из (1.4) в виде
Из (10.3) следует, что градиент функции q по вектору управления с компонентами $\hat {u}$ и $\hat {v}$ является вектором с компонентами $2\hat {u}$ и $2\hat {v}$. На рассматриваемом участке траектории $\hat {u} = 0$, а значение $\hat {v} = 0$ не представляет интереса, поскольку в этом случае механическая система покоится. Тогда градиенты функций $\chi $ и q по вектору управления линейно независимы при $g(t) \equiv 0$. Следовательно, при $g(t) \equiv 0$ все траектории движения системы (1.4) регулярны.
Найдем оптимальное управление для этого участка. Из принципа максимума Понтрягина, формулы (2.1) и ограничения (10.3) следует, что управления $\hat {u}$ и ${\hat {v}}$ на оптимальной траектории равны
В точке стыка, соответствующей моменту времени $\tau $, должно выполняться условие скачка в одной из двух форм:
(10.5)
$p(\tau + 0) = p(\tau - 0) + \lambda {\text{grad}}\,g(r(\tau ),\alpha (\tau ),\varphi (\tau )),\quad {{p}_{0}}(\tau + 0) = {{p}_{0}}(\tau - 0),$(10.6)
$p(\tau - 0) + \lambda {\text{grad}}\,g(r(\tau ),\alpha (\tau ),\varphi (\tau )) = 0,\quad {{p}_{0}}(\tau - 0) = 0,\quad \lambda \ne 0.$В (10.5) и (10.6) скаляр λ – действительное число, p – вектор с компонентами ${{p}_{r}}$, ${{p}_{\alpha }}$ и ${{p}_{\varphi }}$, вектор $p(\tau - 0)$ равен пределу слева вектора $p(t)$ в точке, соответствующей моменту $\tau $, вектор $p(\tau + 0)$ равен аналогичному пределу справа, таким же образом определены и значения константы p0, записанные в форме ${{p}_{0}}(\tau - 0)$ и ${{p}_{0}}(\tau + 0)$.
Предположим, что условие скачка выполняется в форме (10.6). Так как функция (10.1) зависит от $r$ и не зависит от $\alpha $ и $\varphi $, то из (10.6) получаем
(10.7)
${{p}_{0}}(\tau - 0) = 0,\quad {{p}_{r}}(\tau - 0) = - \lambda \ne 0,\quad {{p}_{\alpha }}(\tau - 0) = 0,\quad {{p}_{\varphi }}(\tau - 0) = 0.$Соответствующий предел гамильтониана (2.1) с учетом (2.2) и (10.7) есть
(10.8)
$H(\tau - 0) = - \lambda {{\hat {u}}_{*}}(\tau - 0) = - \lambda \frac{{ - \lambda }}{{{\text{|}}\lambda {\text{|}}}} = {\text{|}}\lambda {\text{|}}.$Значение гамильтониана на оптимальном решении постоянно и равно нулю. Тогда предел (10.8) должен быть равен нулю, но, с другой стороны, как указано в (10.6), $\lambda \ne 0$. Следовательно, мы пришли к противоречию и условие скачка должно выполняться в форме (10.5).
По аналогии с (10.7) из (10.5) получаем, что все сопряженные переменные, кроме ${{p}_{r}}$, в точке стыка должны быть непрерывны:
(10.9)
${{p}_{r}}(\tau + 0) = {{p}_{r}}(\tau - 0) + \lambda ,\quad {{p}_{\alpha }}(\tau + 0) = {{p}_{\alpha }}(\tau - 0),\quad {{p}_{\varphi }}(\tau + 0) = {{p}_{\varphi }}(\tau - 0).$Кроме того, оптимальная траектория непрерывна и $r(\tau \pm 0) = R$. Тогда
(10.10)
$H(\tau \pm 0) = {{p}_{0}} + {{p}_{r}}(\tau \pm 0){{\hat {u}}_{*}}(\tau \pm 0) + \zeta (\tau \pm 0){{\hat {v}}_{*}}(\tau \pm 0),$(10.11)
$\zeta (\tau \pm 0) = \frac{{{{p}_{\alpha }}}}{R} - \frac{{{{p}_{\varphi }}R}}{{1 + {{R}^{2}}}}.$Значения ${{\hat {u}}_{*}}(\tau - 0)$ и ${{\hat {v}}_{*}}(\tau - 0)$ определены формулами (2.2), а значения ${{\hat {u}}_{*}}(\tau + 0)$ и ${{\hat {v}}_{*}}(\tau + 0)$ – формулами (10.4). Гамильтониан (2.1) на оптимальном решении непрерывен. Следовательно, в точке стыка имеем $H(\tau - 0) = H(\tau + 0)$, а потому из (10.10) для момента времени $\tau $ следует уравнение
(10.12)
${{p}_{r}}(\tau - 0)\frac{{{{p}_{r}}(\tau - 0)}}{{ - {{p}_{0}}}} + \zeta (\tau - 0)\frac{{\zeta (\tau - 0)}}{{ - {{p}_{0}}}} = \zeta (\tau + 0){\text{sign}}\,\zeta (\tau + 0).$Из (2.4) вытекает равенство
Из (10.4) и условия ${{\hat {u}}_{{*0}}} + {{\hat {v}}_{{*0}}} = 1$ следует неравенство $\zeta (\tau + 0) \ne 0$. Тогда из (10.12) получаем $\zeta (\tau + 0)$ = –p0. Но, согласно (10.11), имеем $\zeta (\tau - 0) = \zeta (\tau + 0)$ и находим ${{p}_{r}}(\tau - 0) = 0$ из (10.13). Следовательно, ${{p}_{r}}(\tau - 0) = 0$ на любой оптимальной траектории, имеющей точку стыка.
Поскольку можно, обратив время, поменять местами начальное и конечное состояния, не меняя траекторию, то это означает, что значение pr равно нулю как при выходе оптимальной траектории на ограничение, так и при сходе с него. Согласно (2.2), получаем, что оптимальная траектория выходит на ограничивающую окружность и сходит с нее, касаясь этой окружности.
В качестве примера рассмотрим задачу со свободным правым концом траектории и выходом на фазовое ограничение [7]. Когда конечное положение материальной точки не задано, то, как показано в [8], при $r(0) > 1$ на оптимальной траектории значение $r(t)$ всегда больше единицы и монотонно уменьшается с ростом ${\text{|}}\alpha (t){\text{|}}$, а при $r(0) = 1$ оптимальная траектория – единичная окружность с центром в начале координат. Поэтому при $R \geqslant 1$ фазовое ограничение можно игнорировать и рассматривать только случай R < 1.
Пусть $\tau $ – момент времени, в который траектория выходит на ограничивающую окружность. Согласно (10.9), сопряженные переменные ${{p}_{\alpha }}$ и ${{p}_{\varphi }}$ непрерывны на всей траектории, причем ${{p}_{\alpha }} = 0$ в силу соответствующего условия трансверсальности. Кроме того, согласно изложенному выше, ${{p}_{r}}(\tau ) = 0$ при $r(\tau ) = R$. Тогда участок траектории от начальной точки до точки выхода на ограничение описывается формулой (3.1) при $r(T) = R$.
11. Оптимальные траектории, начинающиеся и заканчивающиеся на ограничивающей окружности. В рассматриваемом случае из проведенного выше анализа одномерной механической системы вытекает, что $\Pi ({{r}_{{{\text{min}}}}}) \geqslant \Pi (R)$ для всех оптимальных кривых, которые по этой причине удобно разделить на два подмножества $\Psi $ и $\Phi $: принадлежащие к первому существуют при $\Pi ({{r}_{{{\text{min}}}}})$ > Π(R), а ко второму – при $\Pi ({{r}_{{{\text{min}}}}}) = \Pi (R)$. В первом случае ${{p}_{r}}(0) \ne 0$, а во втором ${{p}_{r}}(0) = 0$.
Кривые из подмножества $\Psi $ должны удовлетворять одному из условий (9.1), (9.2) для ${{r}_{a}} = R$, причем в формулах (9.1) и (9.2) необходимо заменить нестрогие неравенства на строгие. По значениям ${{r}_{{{\text{min}}}}}$ и ${{C}_{\alpha }}$, удовлетворяющим этим неравенствам, можно найти соответствующие значения ${{p}_{\varphi }}$, согласно (7.1), где для любой траектории достаточно ограничиться положительным знаком, поскольку отрицательный знак соответствует той же самой траектории, пройденной в обратном направлении и дающей те же самые терминальные значения ${{\alpha }_{T}} = \alpha (T)$ и ${{\varphi }_{T}} = \varphi (T)$, только взятые с обратным знаком. Далее можно получить ${{p}_{\alpha }} = {{C}_{\alpha }}{{p}_{\varphi }}$, после чего правые части дифференциальных уравнений в системе (2.3) полностью определены.
Для рассматриваемого подмножества ${{p}_{r}}(0) \ne 0$ и в формуле (2.5) всегда следует выбирать отрицательный знак, поскольку в начале движения скорость материальной точки всегда направлена внутрь окружности. Тогда можно строить оптимальные траектории, интегрируя систему (2.3) при условиях $r(0) = R$, $\alpha (0) = 0$ и $\varphi (0) = 0$ вплоть до точки, где переменная $r$ снова станет равной R. То, что хотя бы одна такая точка обязательно существует, следует из описанных выше свойств одномерной механической системы. Время движения $T$ будет равно времени оптимального быстродействия. В результате будут получены зависимости ${{\alpha }_{T}} = {{\alpha }_{T}}({{r}_{{{\text{min}}}}},{{C}_{\alpha }})$, ${{\varphi }_{T}} = {{\varphi }_{T}}({{r}_{{{\text{min}}}}},{{C}_{\alpha }})$ и $T = T({{r}_{{{\text{min}}}}},{{C}_{\alpha }})$. Обратные функции ${{r}_{{{\text{min}}}}} = {{r}_{{{\text{min}}}}}({{\alpha }_{T}},{{\varphi }_{T}})$ и ${{C}_{\alpha }} = {{C}_{\alpha }}({{\alpha }_{T}},{{\varphi }_{T}})$ можно аппроксимировать обычными методами и использовать для поиска значений параметров ${{r}_{{{\text{min}}}}}$ и ${{C}_{\alpha }}$ по заданным значениям ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$.
Все кривые из подмножества $\Phi $ являются финитными и полностью лежат внутри ограничивающей окружности. Заметим, что каждое движение зависит только от значения ${{C}_{\alpha }}$, так как параметр ${{r}_{{{\text{min}}}}}$ можно исключить благодаря равенству $\Pi ({{r}_{{{\text{min}}}}}) = \Pi (R)$. Поскольку в начальный момент времени кинетическая энергия в гамильтониане (6.1) равна нулю, из анализа функции (6.2) вытекает, что материальная точка одномерной системы может двигаться в сторону меньших значений переменной $r$ только тогда, когда величина радиуса $R$ ограничивающей окружности лежит между локальным минимумом и локальным максимумом потенциальной энергии, т.е. ${{r}_{ - }} < R < {{r}_{ + }}$. Из этого условия получаем следующее множество значений параметра ${{C}_{\alpha }}$ для рассматриваемого подмножества кривых:
Для построения можно применять тот же самый численный метод, что и для кривых из первого подмножества, только в формуле (7.1) нужно заменить ${{r}_{{{\text{min}}}}}$ на $R$ и всегда полагать ${{p}_{r}}(0) = 0$.
Отыскание оптимальных траекторий на кривых из подмножества $\Phi $ осложнено тем, что для них величина ${{p}_{r}}$ в граничных точках равна нулю, т.е. траектория в начале и конце касается окружности радиуса R, а потому удовлетворяет там полученному выше условию для точки выхода на ограничение. Следовательно, необходимым условиям оптимальности удовлетворяет и траектория, состоящая из любого целого количества таких кусков. Более того, можно без нарушения этих условий дополнительно вставить любые участки движения по ограничению между любыми двумя кусками, а также как перед первым, так и после последнего куска.
12. Пример. Для случая, когда все искомые траектории должны начинаться и заканчиваться на ограничивающей окружности радиуса $R$, были выполнены вычисления при $R = 1{\text{/}}2$.
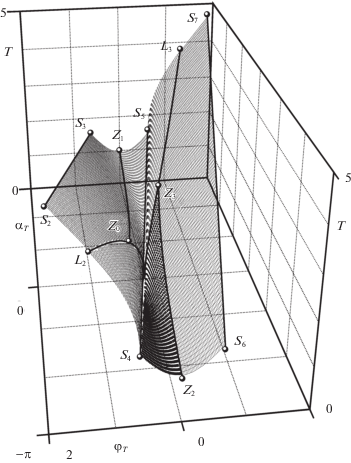
Рисунок 3 иллюстрирует зависимость выбора оптимального управления от конечного положения материальной точки на ограничивающей окружности, заданного углом ${{\alpha }_{T}}$, и соответствующей величинe угла поворота твердого тела ${{\varphi }_{T}}$. Заметим, что на рис. 3 показана только область $ - \pi \leqslant {{\alpha }_{T}} \leqslant \pi $, $ - \pi \leqslant {{\varphi }_{T}} \leqslant \pi $, а для остальных значений ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ она должна быть периодически продолжена по обеим координатным осям. Тогда, в частности, точка ${{L}_{1}}$ будет отождествлена с точкой ${{L}_{2}}$, как и ${{L}_{3}}$ с ${{L}_{4}}$. В результате все точки Ln при $n = 0, \ldots ,5$ окажутся на одной непрерывной кривой и будут расположены на ней в порядке возрастания номеров $n$ слева направо. То же самое относится и к точкам Sn при $n = 0, \ldots ,9$, которые лягут на одну прямую, представленную на рис. 3 пятью отрезками. Точки этой прямой соответствуют траекториям, полностью лежащим на ограничивающей окружности, и представляют собой решения
(12.1)
${{\varphi }_{T}} = - \frac{{{{R}^{2}}}}{{1 + {{R}^{2}}}}{{\alpha }_{T}},\quad - 5\pi \leqslant {{\alpha }_{T}} \leqslant 5\pi $(12.2)
${{\varphi }_{T}} = - \frac{{{{R}^{2}}}}{{1 + {{R}^{2}}}}\left( {{{\alpha }_{T}} + 2\pi (n - 2)} \right),\quad - \pi \leqslant {{\alpha }_{T}} \leqslant \pi $Рис. 3.
Множество значений углов ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$, разделенное на области действия различных законов оптимального управления
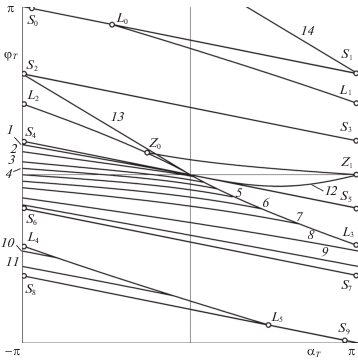
Заметим, что процесс перемещения подвижной массы можно отображать на плоскости параметров ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ как движение точки по некоторой кривой, только пока в качестве соответствующего участка траектории для массы используется дуга какой-либо окружности.
Кривая ${{L}_{2}}{{L}_{3}}$, проходящая через начало координат и симметричная относительно него, разделяет область возможных значений ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ на два множества. Каждая точка, принадлежащая одному из них, соответствует прохождению подвижной массы по какой-либо оптимальной траектории в одном направлении, а точка, симметричная относительно начала координат и принадлежащая другому множеству, – в противоположном. Таким свойством обладают и точки на самой кривой ${{L}_{2}}{{L}_{3}}$. Вследствие инвариантности (2.6) достаточно описать только одно из этих множеств, например, лежащее ниже ${{L}_{2}}{{L}_{3}}$.
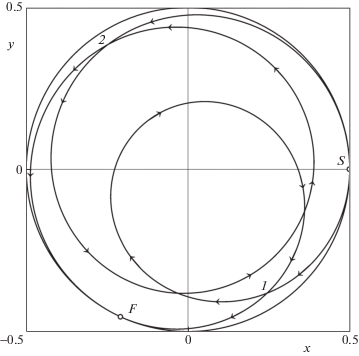
Для точек на ${{L}_{2}}{{L}_{3}}$ оптимальны траектории без участков движения по границе, находящиеся на кривых из описанного выше подмножества $\Phi $ и состоящие из единственного куска. Например, траектории 1 на рис. 4 соответствует точка кривой ${{L}_{2}}{{L}_{3}}$ на рис. 3 с абсциссой ${{\alpha }_{T}} = - 2$ и ординатой ${{\varphi }_{T}} \approx 0.903$.
Рис. 4.
Две оптимальные траектории, касающиеся ограничивающей окружности в начальной точке S и конечной точкe F; направление движения показано стрелками. Для первой время движения $T \approx 2.90$, а для второй – $T \approx 4.65$
Точкам в области, лежащей на рис. 3 ниже кривой ${{L}_{2}}{{L}_{3}}$ и выше отрезка прямой ${{S}_{4}}{{S}_{5}}$, соответствуют оптимальные траектории, состоящие из двух кусков. Первый из них представляет собой дугу ограничивающей окружности, а второй соответствует точке пересечения прямой, параллельной отрезку ${{S}_{4}}{{S}_{5}}$ и проходящей через рассматриваемую точку, с кривой ${{L}_{2}}{{L}_{3}}$. При этом величина центрального угла, опирающегося на дугу первого участка, равна разности абсцисс точки пересечения и рассматриваемой точки, а движение по этому участку происходит по часовой стрелке. Заметим, что значение ${{\alpha }_{T}}$ для любой точки пересечения положительно.
Как следует из сказанного выше при описании подмножества $\Phi $, указанные два куска можно поменять местами. Более того, первый кусок может быть в произвольном месте разбит на две части и тогда второй должен быть вставлен между двумя этими частями. Все полученные таким способом траектории имеют одну и ту же длину, а также удовлетворяют одним и тем же граничным условиям, т.е. подвижная масса приходит за одно и то же время в одну и ту же точку, а твердое тело при этом поворачивается на один и тот же угол.
Далее рассмотрим область, лежащую ниже отрезка ${{S}_{4}}{{S}_{5}}$ и кривой ${{L}_{2}}{{L}_{3}}$, но выше кривой, обозначенной номером 5. Точки последней соответствуют траекториям [13] при оптимальных движениях, проходящих через точку $r = 0$. Заметим, что кривая 5 симметрична ${{Z}_{0}}{{Z}_{1}}$ относительно начала координат. Точка ${{Z}_{0}}$, как и симметричная ей общая точка кривых 5 и ${{L}_{2}}{{L}_{3}}$, соответствует траектории, которая включает точку $r = 0$ и обладает теми же свойствами, что и прочие для кривой ${{L}_{2}}{{L}_{3}}$. Точка ${{Z}_{1}}$ и все лежащие на оси абсцисс рис. 3 отвечают случаям, когда перемещение подвижной массы в новое положение не приводит к изменению ориентации твердого тела. Для ${{Z}_{1}}$ речь идет о траектории в виде отрезка прямой, проходящей через центр масс тела. Остальные отрезки, начала и концы которых лежат на ограничении, тоже являются оптимальными траекториями. На рис. 3 они соответствуют точкам кривой 12, а также симметричной ей относительно начала координат, которая лежит в рассматриваемой области и на рис. 3 не показана. Для вычислений была использована формула
Рис. 5.
Три оптимальные траектории, не касающиеся ограничивающей окружности и полученные для величины ${{r}_{{{\text{min}}}}} = 0.35$ при значениях ${{C}_{{1\alpha }}} \approx - 0.1861$, ${{C}_{{2\alpha }}} \approx - 0.1659$ и ${{C}_{{2\alpha }}} \approx - 0.1030$. Для первой время движения $T \approx 1.24$, для второй – $T \approx 1.35$, а для третьей – $T \approx 4.05$. Направление движения из начальной точки S в конечную точку $F$ по траектории 3 показано стрелками.
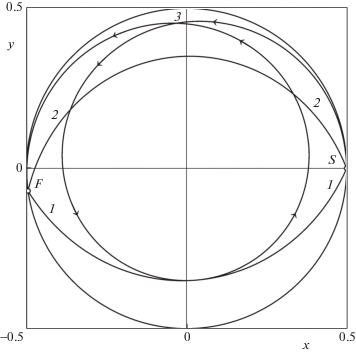
Как и только что рассмотренная область, множество, лежащее на рис. 3 ниже кривых 5 и ${{L}_{2}}{{L}_{3}}$, но выше отрезка ${{S}_{6}}{{S}_{7}}$, целиком заполнено точками, соответствующими оптимальным траекториям из подмножества $\Psi $. Кривые 6–9 на рис. 3 получены при тех же значениях параметра ${{r}_{{{\text{min}}}}}$, что и кривые 1–4, но взятых в обратном порядке. Например, траектория 2 на рис. 5 соответствует точке с той же самой абсциссой ${{\alpha }_{T}} = - 3$, что и траектория 1, но на кривой 8, а не 2.
Теперь рассмотрим область, лежащую на рис. 3 ниже отрезка ${{S}_{6}}{{S}_{7}}$, но выше кривой ${{L}_{4}}{{L}_{5}}$ и отрезка, обозначенного точками ${{S}_{8}}$ и ${{S}_{9}}$. Траектории, соответствующие точкам на кривой ${{L}_{4}}{{L}_{5}}$, обладают теми же свойствами, что и для кривой ${{L}_{2}}{{L}_{3}}$. Например, траектории 2 на рис. 4 соответствует точка кривой ${{L}_{4}}{{L}_{5}}$ на рис. 3 с ординатой ${{\varphi }_{T}} \approx - 2.66$ и той же самой абсциссой ${{\alpha }_{T}} = - 2$, что и в случае траектории 1 на рис. 4.
Возьмем какую-либо внутреннюю точку из рассматриваемой области и проведем через нее прямую, параллельную отрезку ${{S}_{6}}{{S}_{7}}$, как было описано ранее для точек, лежащих ниже кривой ${{L}_{2}}{{L}_{3}}$ и выше отрезка ${{S}_{4}}{{S}_{5}}$. В случае, когда эта прямая пересекает кривую ${{L}_{4}}{{L}_{5}}$, оптимальная траектория также состоит из двух кусков: дуги ограничивающей окружности и траектории, соответствующей точке пересечения, причем центральный угол, на который опирается дуга, равен разности абсцисс рассматриваемой точки и точки пересечения. Различие лишь в том, что в данном случае подвижная масса перемещается по дуге против часовой стрелки. Если пересечение отсутствует, то нужно сперва взять на прямой точку с абсциссой $ - \pi $ и перейти к другой точке, симметричной взятой относительно оси ординат, а затем провести через нее прямую, параллельную отрезку ${{S}_{6}}{{S}_{7}}$. Она обязательно пересечет кривую ${{L}_{2}}{{L}_{3}}$. Искомая траектория снова будет состоять из двух кусков, один из которых будет соответствовать точке пересечения и обладать всеми свойствами, описанными выше применительно к кривой ${{L}_{2}}{{L}_{3}}$, а второй будет опять дугой ограничивающей окружности. Величина центрального угла для нее равна увеличенной на $2\pi $ разности абсцисс рассматриваемой точки и точки пересечения. Перемещение массы опять будет происходить против часовой стрелки.
На рис. 3 ниже кривой ${{L}_{4}}{{L}_{5}}$ и выше отрезка ${{S}_{8}}{{L}_{5}}$ находится область, все точки которой соответствуют оптимальным траекториям из подмножества $\Psi $. Кривые 10 и 11 получены при значениях параметра ${{r}_{{{\text{min}}}}}$, равных $0.35$ и $0.45$, т.е. чем больше величина ${{r}_{{{\text{min}}}}}$, тем ниже находится график. Пример оптимальной траектории для рассматриваемой области показан на рис. 5 под номером 3. Эта траектория соответствует точке с такой же абсциссой ${{\alpha }_{T}} = - 3$, что и траектории 1 и 2 на рис. 5, но лежит на кривой 10 рис. 3.
Наконец рассмотрим область, лежащую на рис. 3 ниже отрезка, обозначенного точками ${{S}_{8}}$ и ${{S}_{9}}$. Траектории, соответствующие всем точкам этой области, относятся к подмножеству $\Phi $ и состоят из дуги ограничивающей окружности и куска, соответствующего некоторой точке кривых ${{L}_{2}}{{L}_{3}}$ и ${{L}_{4}}{{L}_{5}}$. Как и раньше, для отыскания последней проведем через рассматриваемую точку прямую, параллельную указанному отрезку. Возьмем на ней точку с абсциссой $ - \pi $ и перейдем к точке, симметричной относительно оси ординат, после чего будем действовать точно так, как и при описанном выше анализе области, лежащей ниже отрезка ${{S}_{6}}{{S}_{7}}$, но выше кривой ${{L}_{4}}{{L}_{5}}$ и отрезка, обозначенного точками ${{S}_{8}}$ и ${{S}_{9}}$. Единственное отличие заключается в том, что полученную для этой области величину центрального угла нужно увеличить на $\pi $ и значение абсциссы рассматриваемой точки.
Было также вычислено время движения по оптимальным траекториям $T = T({{\alpha }_{T}},{{\varphi }_{T}})$. На рис. 6 эта функция показана для области значений ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$, лежащей на рис. 3 между отрезками ${{S}_{2}}{{S}_{3}}$ и ${{S}_{6}}{{S}_{7}}$. Проекция кривой ${{Z}_{2}}{{Z}_{3}}$ рис. 6 на плоскость параметров ${{\alpha }_{T}}$, ${{\varphi }_{T}}$ совпадает с кривой 5 на рис. 3. Смысл всех остальных обозначений на рис. 6 тот же, что и соответствующих им на рис. 3.
На рис. 7 показаны интервалы значений функции Беллмана. Все обозначения на рис. 7 имеют тот же смысл, что и соответствующие им на рис. 3 и 6.
Рис. 7.
Диапазоны значений времени оптимального быстродействия как функции ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$, показанные оттенками серого
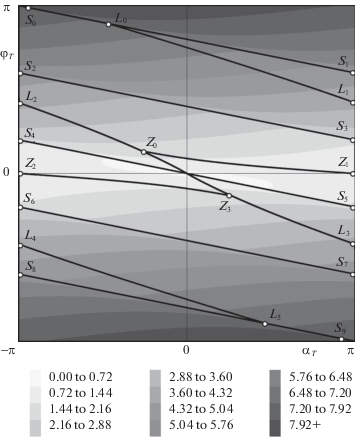
В данной задаче функция Беллмана всюду непрерывна, но имеет разрывы первой производной на отрезках, отмеченных точками ${{S}_{n}}$ для $n = 0, \ldots ,9$. Поясним этот эффект. Сначала напомним, что фактически речь идет о едином при $ - 5\pi \leqslant {{\alpha }_{T}} \leqslant 5\pi $ отрезке (12.1), который разбит на пять частей (12.2) для $ - \pi \leqslant {{\alpha }_{T}} \leqslant \pi $. Теперь рассмотрим какие-либо две точки с одинаковыми абсциссами, лежащие на небольших расстояниях по разные стороны от отрезка ${{L}_{5}}{{S}_{9}}$ на рис. 3 и 7. Нижней точке соответствует траектория, которая включает в себя, как показано выше, короткий кусок, похожий на траекторию 1 рис. 4, а вся остальная часть движения происходит по ограничивающей окружности. Для верхней точки эта последняя часть незначительна, но другая часть гораздо больше по длине и ближе к траектории 2 рис. 4. Длина же траекторий того типа, который показан на рис. 4, быстрее увеличивается с ростом углового расстояния между начальной и конечной точками при малых значениях этого расстояния. Поэтому по мере удаления вверх от отрезка ${{L}_{5}}{{S}_{9}}$ на рис. 3 время движения для соответствующих траекторий увеличивается быстрее, чем при удалении вниз, хотя при приближении к данному отрезку эти времена стремятся к одному и тому же значению – длине некоторой дуги ограничивающей окружности. Рисунок 7 показывает, что первая производная функции Беллмана непрерывна на всех остальных кривых рис. 3.
13. Неединственность решения. На плоскости параметров ${{\alpha }_{T}}$ и ${{\varphi }_{T}}$ есть точки, которым соответствуют не только указанные выше траектории, но и иные, также удовлетворяющие необходимым условиям оптимальности. Как следует из описания подмножества $\Phi $, каждая траектория, соответствующая произвольной точке на кривых ${{L}_{{2n}}}{{L}_{{2n + 1}}}$ рис. 3 при $n = 0,1,2$, может быть куском траектории, которая состоит из любого целого числа таких кусков и удовлетворяет необходимым условиям оптимальности. На той части рис. 3, которая выше кривой ${{L}_{2}}{{L}_{3}}$, такие точки лежат в двух областях: между ней и кривой 13, соединяющей начало координат с точкой ${{S}_{2}}$, а также между кривыми 14 и ${{S}_{0}}{{L}_{0}}{{L}_{1}}$. Координаты этих точек можно вычислить, умножая абсциссу и ординату каждой точки кривых ${{L}_{{2n}}}{{L}_{{2n + 1}}}$, $n = 0,1,2$, на произвольное натуральное число $l$, увеличивая длины соответствующих траекторий в $l$ раз и получая при каждом значении $l$ новый набор кривых на рис. 3. Если $l \to \infty $, то последние становятся отрезками прямой, угол наклона которой равен углу наклона касательной к кривой ${{L}_{2}}{{L}_{3}}$ в начале координат. Вычисления при $R = 1{\text{/}}2$ показывают, что величины времени движения для всех соответствующих им точек больше, чем при использовании траекторий, описанных выше при анализе различных областей на рис. 3. Отсюда следует и невозможность использования таких кривых в качестве кусков оптимальных траекторий, включающих участки ограничивающей окружности. Это связано с быстрым ростом длины кривой, похожей на траекторию 4 рис. 2, по мере увеличения количества “петель” на ней.
Заключение. В общем случае оптимальные траектории в задаче о наискорейшем повороте твердого тела с помощью подвижной массы имеют нетривиальный вид и каждая из них требует вычисления эллиптических интегралов. Решение соответствующей системы из трех дифференциальных уравнений, помимо постоянных интегрирования, зависит от двух параметров, значения которых необходимо искать, учитывая пять граничных условий: две координаты для начального положения подвижной массы, столько же для конечного и требуемый угол поворота твердого тела. Наличие ограничения, не позволяющего массе выйти за заданные пределы, еще более усложняет проблему. Это делает затруднительным сугубо вычислительный подход, основанный, скажем, на прямом переборе по двум углам множества начальных значений сопряженных переменных [13], поскольку заранее неизвестен общий вид получаемой кривой, который может кардинально меняться при малом изменении каждого из параметров задачи. Исследование движения одномерной механической системы, связанной со свойствами оптимальных траекторий, позволило установить их основные качественные характеристики и найти ограничения на их параметры, что дало возможность, в частности, рассмотреть все варианты для случая, когда как в начале, так и в конце движения подвижная масса находится на ограничивающей окружности.
Список литературы
Schmoeckel F., Worn H. Remotely Controllable Microrobots Acting as Nano Positioners and Intelligent Tweezers in Scanning Electron Microscopes (SEMs) // Proc. Intern. Conf. Robotics and Automation, IEEE. V. 4. N.Y., 2001. P. 3903–3913.
Vartholomeos P., Papadopoulos E. Dynamics, Design and Simulation of a Novel Microrobotic Platform Employing Vibration Microactuators // Transactions of ASME. J. Dynamical Systems, Measurement and Control. 2006. V. 128. P. 122–133.
Chernousko F. L. Two-dimensional Motions of a Body Containing Internal Moving Masses // Meccanica. 2016. V. 51. № 12. P. 3203–3209.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // ДАН. 2018. Т. 480. № 5. С. 528–532.
Левский М.В. Синтез оптимального управления ориентацией космического аппарата с использованием комбинированного критерия качества // Изв. РАН ТиСУ. 2019. № 6. С. 139–162.
Шматков А.М. Изменение пространственной ориентации твердого тела с помощью подвижной массы // Изв. РАН ТиСУ. 2020. № 4. С. 151–159.
Шматков А.М. Влияние габаритов управляемого устройства на оптимальный по быстродействию поворот с помощью подвижной внутренней массы // ДАН. 2019. Т. 486. № 3. С. 292–296.
Шматков А.М. Поворот тела за кратчайшее время перемещением точечной массы // ДАН. 2018. Т. 481. № 5. С. 498–502.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969. 384 с.
Черноусько Ф.Л., Шматков А.М. Оптимальное управление поворотом твердого тела при помощи внутренней массы // Изв. РАН ТиСУ. 2019. № 3. С. 10–23.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1962. 1100 с.
Рашевский П.К. Курс дифференциальной геометрии. М.; Л.: ГИТТЛ, 1950. 428 с.
Шматков А.М. Периодические решения задачи оптимального управления поворотом твердого тела с помощью внутренней массы // Вестн. МГУ. Математика, механика. 2020. № 3. С. 63–67.
Маркеев А.П. Теоретическая механика. М.: ЧеРо, 1999. 572 с.
Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1988. 216 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления