Известия РАН. Теория и системы управления, 2021, № 4, стр. 142-156
АНАЛИТИЧЕСКОЕ КВАЗИОПТИМАЛЬНОЕ РЕШЕНИЕ ЗАДАЧИ МИНИМАЛЬНОГО ПО ВРЕМЕНИ ПОВОРОТА КОСМИЧЕСКОГО АППАРАТА
А. В. Молоденков a, *, Я. Г. Сапунков a
a Институт проблем точной механики и управления РАН
Саратов, Россия
* E-mail: molalexei@yandex.ru
Поступила в редакцию 13.03.2020
После доработки 13.08.2020
Принята к публикации 28.12.2020
Аннотация
В кватернионной постановке рассматривается задача оптимального по быстродействию поворота космического аппарата как твердого тела произвольной динамической конфигурации при произвольно заданных граничных условиях. В классе обобщенных конических движений произведена модификация задачи оптимального поворота, которая позволила получить ее аналитическое решение. Аналитическое решение модифицированной задачи может рассматриваться как приближенное (квазиоптимальное) решение традиционной задачи оптимального поворота. Дается алгоритм квазиоптимального поворота космического аппарата. Приводятся числовые примеры, показывающие, что решение модифицированной задачи хорошо аппроксимирует решение традиционной задачи оптимального поворота космического аппарата.
Введение. Построение управления пространственной переориентацией космического аппарата (КА) как твердого тела в традиционной постановке включает задачи программного углового движения (поворота), программного управления и поиска управления, стабилизирующего программу углового движения в малом. Задача расчета программного углового движения и реализующего его управления во многих случаях решается с помощью методов теории оптимального управления. Аналитическое решение этой задачи для наиболее часто используемых функционалов оптимизации при произвольных граничных условиях по угловому положению и угловой скорости КА не найдено даже в случае сферической симметрии КА, не говоря уже о его произвольной динамической конфигурации. Известны лишь некоторые частные случаи решения задачи (например, [1–8]); в общем случае приходится рассчитывать только на приближенные численные методы. Между тем аналитическое решение задачи оптимального поворота в замкнутой форме имеет не только теоретический, но и большой практический интерес, так как позволяет использовать на борту КА готовые законы программного управления и изменения оптимальной траектории.
В настоящей статье (разд. 1–3) в традиционной постановке рассматривается задача оптимального по быстродействию программного поворота КА как твердого тела произвольной динамической конфигурации при произвольно заданных граничных условиях по угловому положению и угловой скорости КА с ограниченной функцией управления. С применением кватернионов на основании принципа максимума Понтрягина получены выражения для структуры оптимального управления, функции Гамильтона–Понтрягина и сопряженной системы уравнений для исходной задачи. В разд. 4 дается краткое описание численного решения традиционной задачи [9] и приведены наводящие соображения, обосновывающие переход от традиционной задачи оптимальной переориентации КА к так называемой модифицированной задаче оптимального разворота. В разд. 5, 6 представлено аналитическое решение модифицированной задачи оптимального по быстродействию поворота КА при произвольных граничных условиях по угловому положению и угловой скорости КА, доведенное до алгоритма. В классе обобщенных конических движений произведена модификация классической задачи оптимального по быстродействию поворота, которая позволила получить аналитические решения для уравнений движения, содержащие произвольные постоянные и две произвольные скалярные функции (параметры обобщенного конического движения). Относительно этих функций и их производных формулируется и решается оптимизационная задача с функционалом быстродействия, в которой в качестве управлений выступают вторые производные от этих двух функций. Найденное аналитическое решение модифицированной задачи может рассматриваться как приближенное (кавазиоптимальное) решение классической задачи оптимального поворота КА при произвольных граничных условиях. Получены явные выражения для вектора угловой скорости, управляющего момента и траектории движения КА. Вектор управляющего момента получается из вектора угловой скорости на основе решения обратной задачи динамики твердого тела. Следует отметить, что для случаев аналитической разрешимости традиционной задачи оптимального поворота при сферической симметрии КА, когда наложены ограничения на краевые условия задачи, – плоский эйлеров поворот, коническое движение – решения традиционной и модифицированной задач полностью совпадают. В разд. 7 приводятся численные примеры, показывающие близость решений традиционной и модифицированной задач оптимального поворота произвольного КА (твердого тела) при произвольных граничных условиях. Среди примеров рассматриваются повороты Международной космической станции (МКС) и КА “Спейс Шаттл”.
Статья продолжает исследования, начатые в [10–13]. В [10, 11] были получены аналитические решения задач оптимальных по быстродействию поворотов сферически-симметричного КА и осесимметричного КА в классах конических движений, а в [12, 13] – квазиоптимальные решения задач минимальных по энергии и в смысле комбинированного функционала поворотов произвольного КА.
Отметим, что в литературе известно квазиоптимальное решение задачи поворота КА [14], которое получено с помощью принципа оптимальности Р. Беллмана на основе решения задачи оптимальной переориентации КА в кинематической постановке, где функцией управления выступает вектор угловой скорости КА. Направление вектора угловой скорости КА при этом определяется граничными условиями по угловому положению КА.
1. Постановка традиционной задачи. Движение КА как твердого тела произвольной динамической конфигурации вокруг центра масс описывается уравнениями [1]
(1.2)
$\dot {\omega } = {{{\mathbf{I}}}^{{ - 1}}}{\mathbf{M}} - {{{\mathbf{I}}}^{{ - 1}}}\left[ {\omega ,{\mathbf{I}}\omega } \right],$На управляющий момент наложено ограничение
Заданы произвольные граничные условия по угловому положению
и угловой скорости КАНеобходимо определить оптимальное управление ${{{\mathbf{M}}}^{{{\text{опт}}}}}(t)$ системой (1.1), (1.2) при ограничении (1.3) и граничных условиях (1.4), (1.5), доставляющее минимум функционалу (задача быстродействия)
2. Переход к безразмерным переменным. Перейдем от размерных переменных задачи к безразмерным по формулам
Далее будем иметь в виду постановку задачи в безразмерных переменных и верхние индексы у них будут опущены.
3. Применение принципа максимума. Выполним процедуру принципа максимума Понтрягина [1, 15]. Введем вспомогательные функции $\Psi (t)$ (кватернион) и $\varphi (t)$ (вектор), сопряженные к фазовым переменным ${\mathbf{\Lambda }}(t),\omega (t)$. Составим функцию Гамильтона–Понтрягина
(3.1)
$H = \left( {\Psi ,\Lambda \circ \omega } \right){\text{/}}2 + (\varphi ,{{{\mathbf{I}}}^{{ - 1}}}{\mathbf{M}} - {{{\mathbf{I}}}^{{ - 1}}}\left[ {\omega ,{\mathbf{I}}\omega } \right]),$Сопряженная система:
(3.2)
$\left\{ \begin{gathered} 2\dot {\Psi } = \Psi \circ \omega , \hfill \\ \dot {\varphi } = {{ - {\text{vect}}(\tilde {\Lambda } \circ \Psi )} \mathord{\left/ {\vphantom {{ - {\text{vect}}(\tilde {\Lambda } \circ \Psi )} 2}} \right. \kern-0em} 2} - [{{{\mathbf{I}}}^{{ - 1}}}\varphi ,{\mathbf{I}}\omega ] + {\mathbf{I}}[{{{\mathbf{I}}}^{{ - 1}}}\varphi ,\omega ], \hfill \\ \end{gathered} \right.$Используя это и введя обозначение [1]
(3.4)
${\mathbf{p}} = {\text{vect}}(\tilde {\Lambda } \circ {\mathbf{\Psi }}) = \tilde {\Lambda } \circ {{{\mathbf{c}}}_{v}} \circ \Lambda ,$(3.5)
$\left\{ \begin{gathered} {\mathbf{p}} = {\mathbf{\tilde {\Lambda }}} \circ {{{\mathbf{c}}}_{v}} \circ {\mathbf{\Lambda }}, \hfill \\ \dot {\varphi } = {{ - {\mathbf{р}}} \mathord{\left/ {\vphantom {{ - {\mathbf{р}}} 2}} \right. \kern-0em} 2} - [{{{\mathbf{I}}}^{{ - 1}}}\varphi ,{\mathbf{I}}\omega ] + {\mathbf{I}}[{{{\mathbf{I}}}^{{ - 1}}}\varphi ,\omega ]. \hfill \\ \end{gathered} \right.$Следует отметить, что применение этого приема [1], основанного на самосопряженности дифференциальной кватернионной системы уравнений (1.1) (замена кватернионной сопряженной переменной $\Psi $ на векторную переменную p (3.4)), позволяет понизить размерность краевой задачи, получаемой после принципа максимума, на четыре.
Условие максимума функции Гамильтона–Понтрягина (3.1) на компактном множестве (2.1) дает следующую структуру оптимального управления:
(3.6)
${{{\mathbf{M}}}^{{{\text{опт}}}}} = {{{\mathbf{I}}}^{{ - 1}}}\varphi {\text{/}}\left| {{{{\mathbf{I}}}^{{ - 1}}}\varphi } \right|.$Функция Гамильтона–Понтрягина (3.1) с учетом новой переменной ${\mathbf{p}}$ (4.4) примет вид
(3.7)
$H = \left( {{\mathbf{p}},\omega } \right){\text{/}}2 + (\varphi ,{{{\mathbf{I}}}^{{ - 1}}}{\mathbf{M}} - {{{\mathbf{I}}}^{{ - 1}}}\left[ {\omega ,{\mathbf{I}}\omega } \right]).$4. Наводящие соображения. В данном разделе приводятся примеры численного решения традиционной задачи оптимального по быстродействию поворота для различных вариантов динамической конфигурации КА и соображения, основанные на этих примерах. Среди примеров рассмотрены повороты КА “Спейс Шаттл” [16] и МКС [17].
Численное решение задачи оптимального поворота (1.1), (1.2), (1.4)–(1.6), (2.1), сводится к решению краевой задачи для системы дифференциальных уравнений:
(4.1)
$\left\{ \begin{gathered} 2\dot {\Lambda } = \Lambda \circ \omega \hfill \\ \dot {\omega } = {{{\mathbf{I}}}^{{ - 1}}}{\mathbf{M}} - {{{\mathbf{I}}}^{{ - 1}}}\left[ {\omega ,{\mathbf{I}}\omega } \right], \hfill \\ \dot {\varphi } = {{ - {\mathbf{р}}} \mathord{\left/ {\vphantom {{ - {\mathbf{р}}} 2}} \right. \kern-0em} 2} - [{{{\mathbf{I}}}^{{ - 1}}}\varphi ,{\mathbf{I}}\omega ] + {\mathbf{I}}[{{{\mathbf{I}}}^{{ - 1}}}\varphi ,\omega ], \hfill \\ {\mathbf{p}} = \tilde {\Lambda } \circ {{{\mathbf{c}}}_{v}} \circ \Lambda ,\quad {{{\mathbf{c}}}_{v}} = {\mathbf{const}}, \hfill \\ \end{gathered} \right.$(4.4)
${{{\mathbf{M}}}^{{{\text{опт}}}}} = {{{\mathbf{I}}}^{{ - 1}}}\varphi {\text{/|}}{{{\mathbf{I}}}^{{ - 1}}}\varphi {\text{|}}\,,$(4.5)
${{H}^{{{\text{опт}}}}}\left( T \right) = \left( {\omega ,{\mathbf{p}}} \right){\text{/}}2 + (\varphi ,{{{\mathbf{I}}}^{{ - 1}}}{{{\mathbf{M}}}^{{{\text{опт}}}}} - {{{\mathbf{I}}}^{{ - 1}}}\left[ {\omega ,{\mathbf{I}}\omega } \right])\left| {_{{t = T}}} \right. = 1,$Конечное условие (4.3) необходимо переписать в семимерном фазовом пространстве $\Lambda \times \omega $ в виде
(4.6)
${\text{vect}}(\Lambda (T) \circ {{\tilde {\Lambda }}_{T}}) = 0,\quad \omega (T) = {{\omega }_{T}}.$Для решения краевой задачи (4.1), (4.2), (4.4)–(4.6) разработан итерационный численный метод [9], представляющий собой комбинацию методов Рунге–Кутты, Ньютона и градиентного спуска. Важно отметить, что условие совпадения кватерниона ориентации твердого тела в конечный момент времени с кватернионом, определяющим заданную конечную ориентацию твердого тела (условие (4.3)), заменено условием обращения в нуль векторной части кватернионного произведения $\Lambda (T) \circ {{\tilde {\Lambda }}_{T}}$ (4.6). В [16, 18] авторы пытались выполнить условие $\Lambda (T) = {{\Lambda }_{T}}$, что приводило к вырождению матриц частных производных от невязок. В качестве первого приближения по недостающим начальным условиям при решении краевой задачи (4.1), (4.2), (4.4)–(4.6) оптимального управления с произвольными граничными условиями по угловому положению и угловой скорости твердого тела берутся начальные условия по переменным $\varphi ,{\mathbf{p}}$, полученные при решении задачи оптимального поворота сферически-симметричного КА в классе плоских эйлеровых поворотов.
Для твердых тел (КА) с различным распределением масс сравним кинематические характеристики оптимального движения в задачах оптимального поворота с одними и теми же граничными условиями.
Например:
Тело 1. Сферически-симметричное твердое тело ${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 1.0$.
Тело 2. Произвольное тело ${{I}_{1}} = 0.9869,$ ${{I}_{2}} = 1.1843,$ ${{I}_{3}} = 0.7895$.
Тело 3. Произвольное тело ${{I}_{1}} = 0.9506,$ ${{I}_{2}} = 1.3308,$ ${{I}_{3}} = 0.5704$.
Тело 4. МКС как произвольное твердое тело ${{I}_{1}} = 4853000$ кг ⋅ м2, ${{I}_{2}} = 23601000$ кг ⋅ м2, ${{I}_{3}} = 26278000$ кг ⋅ м2 (размерные моменты инерции) или ${{I}_{1}} = 0.2358,$ ${{I}_{2}} = 1.1466,$ ${{I}_{3}} = 1.2766$ (безразмерные величины).
Тело 5. КА “Спейс Шаттл” (динамические характеристики КА “Спейс Шаттл” такие же, как у почти осесимметричного твердого тела): ${{I}_{1}} = 3400648$ кг ⋅ м2, ${{I}_{2}} = 21041672$ кг ⋅ м2 или ${{I}_{1}}$ = = 0.1967, ${{I}_{2}} = 1.2168;$ ${{I}_{3}} \approx {{I}_{2}}$.
Время быстродействия $T_{k}^{{{\text{опт}}}},$ где $k = \overline {1,\,5} $, означает номер тела (КА), в каждом из случаев:
В табл. 1 приведены кинематические характеристики (компоненты кватерниона положения КА и вектора угловой скорости) для указанных КА в промежуточных точках tk интервалов времени движения $[0,T_{k}^{{{\text{опт}}}}]$ при решении задачи оптимального управления с граничными условиями (4.7)–(4.9) в традиционной постановке. Промежуточные точки tk выбирались максимально близкими друг к другу (насколько позволяет программа численного решения задачи с переменным шагом вычисления по времени t) и ориентированы на приблизительную середину наибольшего интервала $[0,T_{1}^{{{\text{опт}}}}]{\text{:}}$
Таблица 1
| КА | ${{\lambda }_{0}}$ | ${{\lambda }_{1}}$ | ${{\lambda }_{2}}$ | ${{\lambda }_{3}}$ | ${{\omega }_{1}}$ | ${{\omega }_{2}}$ | ${{\omega }_{3}}$ |
|---|---|---|---|---|---|---|---|
| Тело 1 (${{t}_{1}}$) | 0.80437 | 0.36758 | –0.37955 | 0.27171 | –0.03412 | –0.03576 | –0.55873 |
| Тело 2 (${{t}_{2}}$) | 0.80480 | 0.36812 | –0.37874 | 0.27082 | –0.03497 | –0.03416 | –0.57245 |
| Тело 3 (${{t}_{3}}$) | 0.80582 | 0.36894 | –0.37740 | 0.26853 | –0.03943 | –0.03158 | –0.60068 |
| Тело 4 (${{t}_{4}}$) | 0.80405 | 0.36949 | –0.38005 | 0.26935 | –0.04073 | –0.04253 | –0.58311 |
| Тело 5 (${{t}_{5}}$) | 0.80311 | 0.37231 | –0.37877 | 0.27006 | –0.02850 | –0.04501 | –0.58950 |
В табл. 2 рассмотрим кинематические характеристики оптимального движения тел 1, 4, 5 для случая, когда граничные условия по угловому положению определяются выражениями (4.7), (4.8), а по угловой скорости они нулевые (поворот из положения покоя в положение покоя):
Таблица 2
| КА | ${{\lambda }_{0}}$ | ${{\lambda }_{1}}$ | ${{\lambda }_{2}}$ | ${{\lambda }_{3}}$ | ${{\omega }_{1}}$ | ${{\omega }_{2}}$ | ${{\omega }_{3}}$ |
|---|---|---|---|---|---|---|---|
| Тело 1 ($t_{1}^{0}$) | 0.83121 | 0.36278 | –0.35560 | 0.22588 | 0.02843 | –0.04552 | –0.60910 |
| Тело 4 ($t_{4}^{0}$) | 0.82396 | 0.35523 | –0.36235 | 0.25220 | 0.02834 | –0.05283 | –0.61018 |
| Тело 5 ($t_{5}^{0}$) | 0.82698 | 0.35296 | –0.36222 | 0.24560 | 0.02813 | –0.04666 | –0.61162 |
Время быстродействия при этом $T_{1}^{{{\text{опт}}}} = 1.3916,$ $T_{4}^{{{\text{опт}}}} = 1.5645,$ $T_{5}^{{{\text{опт}}}} = 1.5278.$ Промежуточные точки $t_{k}^{0}$, ориентированные на приблизительную середину наибольшего интервала $[0,T_{4}^{{{\text{опт}}}}],$ таковы:
Аналогичные расчеты проводились и для других начальных и конечных состояний КА. Из табл. 1, 2 и других проведенных расчетов с другими граничными условиями видно, что кинематические характеристики оптимального движения КА независимо от их динамической конфигурации, достаточно похожи. Отметим, что в задаче оптимального по энергии поворота произвольного твердого тела с фиксированным временем [13] это проявляется более явно, так как интервал времени движения твердого тела и его промежуточная (срединная) точка одинаковы во всех примерах. Отсюда следует, что, используя кинематические характеристики тела со сферической симметрией, из динамических уравнений Эйлера с учетом моментов инерции произвольных тел можно вычислить управляющие моменты для движения произвольных тел. Такие моменты можно рассматривать как квазиоптимальные управляющие моменты для перевода КА из начального состояния в конечное состояние. Выражения для траектории углового движения и угловой скорости КА можно построить аналитически в явном виде на основе решения так называемой модифицированной задачи оптимального поворота, а управляющий момент определить исходя из решения обратной задачи динамики твердого тела. Покажем это.
5. Модифицированная задача оптимального поворота. Движение КА по-прежнему описывается соотношениями (1.1), (1.2), (1.4)–(1.6), (2.1), при этом начальное и конечное значения по угловому положению и угловой скорости КА произвольны и заданы.
Одной из основных проблем при построении аналитического решения в задаче оптимального поворота твердого тела является разрешимость классической задачи Дарбу – аналитического определения ${\mathbf{\Lambda }}(t)$ из уравнения (1.1) при известных ${{{\mathbf{\Lambda }}}_{0}}$, ${\mathbf{\omega }}(t)$.
Для кватернионного дифференциального уравнения (2.1) при условии, что вектор угловой скорости ${\mathbf{\omega }}(t)$ задается выражением
(5.1)
$\omega (t) = {{{\mathbf{i}}}_{1}}\dot {f}(t)\sin g(t) + {{{\mathbf{i}}}_{2}}\dot {f}(t)\cos g(t) + {{{\mathbf{i}}}_{3}}\dot {g}(t),$(5.2)
$\Lambda (t) = {{\Lambda }_{0}} \circ {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{3}}g(0){\text{/}}2\} \circ {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{2}}f(0){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{2}}f(t){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{3}}g(t){\text{/}}2\} ,$Заметим [19], что задачу Дарбу с произвольно заданным вектором угловой скорости $\omega (t)$ с помощью замен переменных можно свести к решению уравнения типа (2.1) с угловой скоростью:
Другими словами, предлагаемая структура угловой скорости (5.1) хорошо соотносится с концепцией Пуансо, что всякое произвольное угловое движение твердого тела вокруг неподвижной точки можно рассматривать как некоторое обобщенное коническое движение твердого тела.
Выражение (5.1) и решение (5.2) можно обобщить, добавив поворот на постоянный угол вокруг некоторой оси. Такой поворот задается с помощью кватерниона ${\mathbf{К}}$, $\left\| {\mathbf{К}} \right\| = 1$. Тогда вектор ${\mathbf{\omega }}$ и кватернион ${\mathbf{\Lambda }}$ будут определяться соотношениями
(5.3)
$\omega = {\mathbf{\tilde {К}}} \circ ({{{\mathbf{i}}}_{1}}\dot {f}(t)\sin g(t) + {{{\mathbf{i}}}_{2}}\dot {f}(t)\cos g(t) + {{{\mathbf{i}}}_{3}}\dot {g}(t)) \circ {\mathbf{К}},$(5.4)
$\Lambda = {{\Lambda }_{0}} \circ {\mathbf{\tilde {К}}} \circ {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{3}}g(0)/2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{2}}(f(t) - f(0)){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{3}}g(t){\text{/}}2\} \circ {\mathbf{К}}.$Будем рассматривать вторые производные от функций f и g в качестве управляющих параметров. Тогда если ввести обозначения
то можно составить систему дифференциальных уравнений, описывающих управляемую систему:(5.6)
$\dot {f} = {{f}_{1}},\quad \dot {g} = {{g}_{1}},\quad {{\dot {f}}_{1}} = {{u}_{1}},\quad {{\dot {g}}_{1}} = {{u}_{2}},$Ограничимся случаем, когда кватернион ${\mathbf{К}}$ представляется в виде произведения:
(5.7)
${\mathbf{К}} = {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}},\quad {{{\mathbf{К}}}_{1}} = {\mathbf{exp}}\{ {{{\mathbf{i}}}_{1}}{{\alpha }_{1}}{\text{/}}2\} ,\quad {{{\mathbf{К}}}_{2}} = {\mathbf{exp}}\{ {{{\mathbf{i}}}_{2}}{{\alpha }_{2}}{\text{/}}2\} ,$(5.8)
${\mathbf{\tilde {К}}} = {{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}},\quad {{{\mathbf{\tilde {К}}}}_{1}} = {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{1}}{{\alpha }_{1}}{\text{/}}2\} ,\quad {{{\mathbf{\tilde {К}}}}_{2}} = {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{2}}{{\alpha }_{2}}{\text{/}}2\} .$Условия того, что выражения для $\omega $, $\Lambda $ (5.3), (5.4) удовлетворяют граничным условиям (1.4), (1.5) с учетом (5.7), (5.8), запишутся как
(5.9)
${{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}} \circ ({{{\mathbf{i}}}_{1}}{{f}_{1}}(0)\sin g(0) + {{{\mathbf{i}}}_{2}}{{f}_{1}}(0)\cos g(0) + {{{\mathbf{i}}}_{3}}{{g}_{1}}(0)) \circ {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} = {{\omega }_{0}},$(5.10)
${{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}} \circ ({{{\mathbf{i}}}_{1}}{{f}_{1}}(T)\sin g(T) + {{{\mathbf{i}}}_{2}}{{f}_{1}}(T)\cos g(T) + {{{\mathbf{i}}}_{3}}{{g}_{1}}(T)) \circ {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} = {{\omega }_{T}},$(5.11)
${{\Lambda }_{0}} \circ {{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}} \circ {\mathbf{exp}}\{ - {{{\mathbf{i}}}_{3}}g(0){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{2}}(f(Т) - f(0)){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{3}}g(Т){\text{/}}2\} \circ {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} = {{\Lambda }_{Т}}.$Управляющий момент, соответствующий решению модифицированной задачи оптимального поворота КА, определяется из (1.2), (5.1), (5.5), (5.6) по формуле
(5.12)
$\begin{gathered} {\mathbf{М}} = {\mathbf{I}}\dot {\omega } + [\omega ,{\mathbf{I}}\omega ] = {\mathbf{I}}({\mathbf{\tilde {К}}} \circ (({{{\mathbf{i}}}_{1}}({{u}_{1}}{\text{sin}}g + {{f}_{1}}{{g}_{1}}{\text{cos}}g) + {{{\mathbf{i}}}_{2}}({{u}_{1}}{\text{cos}}g - {{f}_{1}}{{g}_{1}}{\text{sin}}g) + {{{\mathbf{i}}}_{3}}{{u}_{2}}) \circ {\mathbf{К}}) + \\ \, + [{\mathbf{\tilde {К}}} \circ ({{{\mathbf{i}}}_{1}}{{f}_{1}}{\text{sin}}g + {{{\mathbf{i}}}_{2}}{{f}_{1}}{\text{cos}}g + {{{\mathbf{i}}}_{3}}{{g}_{1}}) \circ {\mathbf{К}},{\mathbf{I}}({\mathbf{\tilde {К}}} \circ ({{{\mathbf{i}}}_{1}}{{f}_{1}}{\text{sin}}g + {{{\mathbf{i}}}_{2}}{{f}_{1}}{\text{cos}}g + {{{\mathbf{i}}}_{3}}{{g}_{1}}) \circ {\mathbf{К}})]. \\ \end{gathered} $Ограничение на модуль вектора М выражается через $\omega $, $\dot {\omega }$по (2.1):
(5.13)
$\left| {\mathbf{M}} \right| = \sqrt {{{{({\mathbf{I}}\dot {\omega })}}^{2}} + 2({\mathbf{I}}\dot {\omega },[\omega ,{\mathbf{I}}\omega ]) + {{{[\omega ,{\mathbf{I}}\omega ]}}^{2}}} \leqslant 1.$Учитывая (5.7), компоненты векторов ${\mathbf{\omega }}$ и ${\mathbf{\dot {\omega }}}$имеют явный вид:
(5.14)
${{\omega }_{2}} = {{f}_{1}}(\sin g\sin {{\alpha }_{1}}\sin {{\alpha }_{2}} + \cos g\cos {{\alpha }_{1}}) + {{g}_{1}}\sin {{\alpha }_{1}}\cos {{\alpha }_{2}},$(5.15)
$\begin{gathered} {{{\dot {\omega }}}_{2}} = {{u}_{1}}(\sin g\sin {{\alpha }_{1}}\sin {{\alpha }_{2}} + \cos g\cos {{\alpha }_{1}}) + \\ \, + {{f}_{1}}{{g}_{1}}(\cos g\sin {{\alpha }_{1}}\sin {{\alpha }_{2}} - \sin g\cos {{\alpha }_{1}}) + {{u}_{2}}\sin {{\alpha }_{1}}\cos {{\alpha }_{2}}, \\ \end{gathered} $Чтобы выполнить условие (5.13) на управляющие параметры ${{u}_{1}}$, ${{u}_{2}}$ системы (5.6), наложим ограничение
где величина ${{u}_{*}}$ ($0 < {{u}_{*}} < 1$) выбирается из требования выполнения условия (5.13).Тогда для управляемой системы (5.6) можно сформулировать следующую задачу оптимального управления, решение которой можно рассматривать как приближенное (квазиоптимальное) решение исходной задачи (1.1), (1.2), (1.4)–(1.6), (2.1). Требуется найти оптимальные управления ${{и}_{1}}(t),{{u}_{2}}(t)$, удовлетворяющие ограничению (5.16), которые за минимальный промежуток времени переводят управляемую систему (5.6) из начального состояния
в конечное состояние и удовлетворяющие соотношениям (5.9)–(5.11), в которых ${{\alpha }_{1}},{{\alpha }_{2}}$ выступают как параметры, подлежащие определению.Соотношения (5.9)–(5.11) можно переписать в виде
(5.19)
${{{\mathbf{i}}}_{1}}{{f}_{1}}(0)\sin g(0) + {{{\mathbf{i}}}_{2}}{{f}_{1}}(0)\cos g(0) + {{{\mathbf{i}}}_{3}}{{g}_{1}}(0) = {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} \circ {{{\mathbf{\omega }}}_{0}} \circ {{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}},$(5.20)
${{{\mathbf{i}}}_{1}}{{f}_{1}}(T)\sin g(T) + {{{\mathbf{i}}}_{2}}{{f}_{1}}(T)\cos g(T) + {{{\mathbf{i}}}_{3}}{{g}_{1}}(T) = {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} \circ {{{\mathbf{\omega }}}_{Т}} \circ {{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}},$(5.21)
${\mathbf{exp}}\{ - {{{\mathbf{i}}}_{3}}g(0){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{2}}(f(Т) - f(0)){\text{/}}2\} \circ {\mathbf{exp}}\{ {{{\mathbf{i}}}_{3}}g(Т){\text{/}}2\} = {{{\mathbf{К}}}_{2}} \circ {{{\mathbf{К}}}_{1}} \circ {{\tilde {\Lambda }}_{0}} \circ {{\Lambda }_{Т}} \circ {{{\mathbf{\tilde {К}}}}_{1}} \circ {{{\mathbf{\tilde {К}}}}_{2}}.$Такую задачу оптимального управления будем называть модифицированной задачей оптимального поворота КА.
6. Решение задачи с помощью принципа максимума. Функция Гамильтона–Понтрягина для управляемой системы (5.6) в случае задачи быстродействия имеет вид
(6.1)
$H = - 1 + {{\psi }_{1}}{{f}_{1}} + {{\psi }_{2}}{{g}_{1}} + {{\psi }_{3}}{{u}_{1}} + {{\psi }_{4}}{{u}_{2}},$(6.2)
${{\dot {\psi }}_{1}} = 0,\quad {{\dot {\psi }}_{2}} = 0,\quad {{\dot {\psi }}_{3}} = - {{\psi }_{1}},\quad {{\dot {\psi }}_{4}} = - {{\psi }_{2}}.$Общее решение уравнений (6.2), содержащее произвольные постоянные ${{с}_{1}},\,.\,.\,.\,,\,{{с}_{4}}$, имеет вид
(6.3)
${{\psi }_{1}} = {{с}_{1}},\quad {{\psi }_{2}} = {{с}_{2}},\quad {{\psi }_{3}} = - {{с}_{1}}t + {{c}_{3}},\quad {{\psi }_{4}} = - {{с}_{2}}t + {{c}_{4}}.$Из условия максимума для функции Гамильтона–Понтрягина (6.1) с учетом ограничения (5.16) определяется оптимальное управление
(6.4)
$\begin{gathered} {{u}_{1}} = {{u}_{*}}( - {{с}_{1}}t + {{c}_{3}}){\text{/}}\sqrt {{{{( - {{с}_{1}}t + {{c}_{3}})}}^{2}} + {{{( - {{с}_{2}}t + {{c}_{4}})}}^{2}}} , \\ {{u}_{2}} = {{u}_{*}}( - {{с}_{2}}t + {{c}_{4}}){\text{/}}\sqrt {{{{( - {{с}_{1}}t + {{c}_{3}})}}^{2}} + {{{( - {{с}_{2}}t + {{c}_{4}})}}^{2}}} . \\ \end{gathered} $После подстановки (6.4) в систему уравнений (5.6) находится общее решение для фазовых координат, содержащее восемь произвольных постоянных ${{с}_{1}},\,.\,.\,.\,,\,{{с}_{8}}$:
(6.5)
${{f}_{1}} = - {{с}_{1}}{{u}_{*}}[F(t) + B\ln \left( {t - A + F(t)} \right){{c}_{2}}{\text{/}}{{c}_{1}}]{\text{/}}С + {{c}_{5}},$Так как c6 входит в функцию f как аддитивная постоянная, то из формулы (5.4) видно, что эта постоянная не оказывает влияние; по этой причине постоянную c6 можно положить равной нулю. Таким образом, для определения девяти неизвестных постоянных задачи ${{с}_{1}},\,.\,.\,.\,,\,{{с}_{5}},\,\,{{с}_{7}},\,{{с}_{8}},{{\alpha }_{1}},\,{{\alpha }_{2}}$ и времени Т служит девять уравнений из системы (5.19)–(5.21) (отметим, что в кватернионном уравнении (5.21) независимыми являются только три уравнения в скалярной форме из-за нормированности кватерниона $\Lambda $) и условие равенства нулю функции Гамильтона–Понтрягина (6.1) при t = T. Если формулы (6.5) подставить в (5.3), (5.4), то будут получены аналитические выражения для определения законов изменения оптимальной угловой скорости и оптимальной траектории КА. Эти выражения определят оптимальный по быстродействию поворот КА в классе обобщенных конических движений. Формула (5.12) с учетом (6.4), (6.5) найдет аналитическое решение для управляющего момента, соответствующего решению модифицированной задачи. Модифицированная задача оптимального поворота КА, тем самым, решена полностью.
Следует отметить, что решения для управляющих параметров ${{u}_{1}},{{u}_{2}}$ и фазовых координат $f,g,{{f}_{1}},{{g}_{1}}$, которые определяются соотношениями (6.4), (6.5), при условии, что ${{с}_{1}}{{с}_{4}} - {{с}_{2}}{{с}_{3}} \ne 0$, соответствуют непрерывным управляющим параметрам ${{u}_{1}},{{u}_{2}}$ и, следовательно, непрерывным управляющим моментам М, согласно (5.12). Если ${{с}_{1}}{{с}_{4}} - {{с}_{2}}{{с}_{3}} = 0$, то допускаются разрывные решения для управляющих параметров ${{u}_{1}},{{u}_{2}}$ и управляющих моментов М. В последнем случае для ${{с}_{1}},{{с}_{2}},{{с}_{3}},{{с}_{4}}$ выполняется соотношение
Тогда выражения (6.4) для управляющих параметров представляются в виде кусочно-постоянных функций
(6.7)
$\begin{gathered} {{u}_{1}} = - {{с}_{1}}{{u}_{*}}\,{\text{sign}}(t - {{t}_{*}}){\text{/}}\sqrt {с_{1}^{2} + с_{2}^{2}} , \\ {{u}_{2}} = - {{с}_{2}}{{u}_{*}}\,{\text{sign}}(t - {{t}_{*}}){\text{/}}\sqrt {с_{1}^{2} + с_{2}^{2}.} \\ \end{gathered} $Из формул (6.7) следует, что если ${{t}_{*}}$ будет располагаться внутри отрезка времени [0,T], то оптимальное управление будет состоять из двух этапов, на каждом из которых управляющие параметры сохраняют постоянные значения. В противном случае оптимальное управление будет состоять из одного этапа с постоянными значениями управляющих параметров. Решение для фазовых координат с учетом (6.7) будет определяться полиномами первой и второй степени по t:
(6.8)
$\begin{gathered} g = - {{с}_{2}}{{u}_{*}}{{(t - {{t}_{*}})}^{2}}sign(t - {{t}_{*}}){\text{/}}2C + {{c}_{7}}(t - {{t}_{*}}) + {{c}_{8}}, \\ {{f}_{1}} = - {{с}_{1}}{{u}_{*}}(t - {{t}_{*}})sign(t - {{t}_{*}}){\text{/}}C + {{c}_{5}} = - {{с}_{1}}{{u}_{*}}\left| {t - {{t}_{*}}} \right|{\text{/}}C + {{c}_{5}}, \\ \end{gathered} $Решение (6.8) построено с учетом непрерывности фазовых координат в точке разрыва управляющих параметров при $t = {{t}_{*}}$. Отметим, что постоянная c6 может быть положена равной нулю, а c1 – равной +1 или –1 (так как формулы (6.7), (6.8) можно привести к виду, в котором ${{с}_{2}},\;{{с}_{3}},\;{{с}_{4}}$ будут присутствовать в виде отношений этих величин к c1). Следовательно, выражения (6.7), (6.8) содержат пять произвольных постоянных ${{с}_{2}},\;{{с}_{5}},\;{{с}_{7}},\;{{с}_{8}},\;{{t}_{*}}$. Для определения постоянных ${{с}_{2}},\;{{с}_{5}},\;{{с}_{7}},\;{{с}_{8}},\;{{t}_{*}}$ и неизвестных величин $Т,\,\,{{\alpha }_{1}},\,\,{{\alpha }_{2}}$ служат девять скалярных соотношений (5.19)–(5.21). Из них следует, что решения задачи с разрывом управляющих параметров ${{u}_{1}},\,\,{{u}_{2}}$ будут возникать только при определенной связи между заданными величинами ${{\Lambda }_{0}},\,\,{{\omega }_{0}},\,{{\Lambda }_{Т}},\,\,{{\omega }_{Т}}$. Если произвольным образом менять величины ${{с}_{2}},\;{{с}_{5}},\,\,{{с}_{7}},\;{{с}_{8}},\;{{t}_{*}},\;Т,\,\,{{\alpha }_{1}},\,\,{{\alpha }_{2}}$, то из соотношений (5.19)–(5.21) может быть получено множество значений ${{\omega }_{0}},\;{{\Lambda }_{Т}},\,\,{{\omega }_{Т}}$, при которых возможно решение задачи оптимального разворота с разрывом управляющих параметров ${{u}_{1}},{{u}_{2}}$ и, следовательно, с разрывным управляющим моментом М.
Следует отметить, что при сферической симметрии КА (${{I}_{1}} = \,{{I}_{2}} = \,{{I}_{3}}$) квадрат модуля безразмерного управляющего момента традиционной задачи выражается по (5.12), (5.14), (5.15) через управляющие параметры и фазовые координаты модифицированной задачи следующим образом:
Если в задаче оптимального по быстродействию поворота сферически-симметричного КА векторы граничных условий по угловой скорости ${{\omega }_{0}},\,\,{{\omega }_{Т}}$ положить параллельными ${\text{vect}}({{\tilde {\Lambda }}_{0}} \circ {{\Lambda }_{T}})$ (плоский эйлеров поворот КА), то решения задач в традиционной и модифицированной постановках полностью совпадут. То же самое можно сказать и о случае, когда решение традиционной задачи оптимального поворота сферически-симметричного КА получено в классе конических движений [10]. В этих случаях слагаемое $f_{1}^{2}g_{1}^{2}$ в (6.9) обращается в нуль и модуль вектора М в модифицированной задаче постоянен (равен величине ограничения).
При решении традиционной задачи оптимального поворота КА из условия максимума для функции Гамильтона–Понтрягина следует, согласно (3.6), что $\left| {\mathbf{M}} \right| \equiv 1$. В модифицированной задаче быстродействия также из условия максимума для функции Гамильтона–Понтрягина, согласно (6.4), имеем $\sqrt {u_{1}^{2} + u_{2}^{2}} = {{u}_{*}}$, где ${{u}_{*}}$ определяется из условия, чтобы вычисленный управляющий момент удовлетворял условию $\left| {\mathbf{M}} \right| \leqslant 1$. Управляющий момент, полученный при квазиоптимальном решении задачи, может не удовлетворять условию $\left| {\mathbf{M}} \right| \equiv 1$. По этой причине время движения в квазиоптимальной задаче может немного отличаться от времени решения традиционной задачи.
Приведем алгоритм решения задачи оптимального по быстродействию поворота КА произвольной динамической конфигурации при произвольно заданных граничных условиях в классе обобщенных конических движений в безразмерных переменных.
Шаг 1. По заданным граничным условиям по угловому положению ${{\Lambda }_{0}},\;{{\Lambda }_{Т}}$ (1.4), угловой скорости ${{\omega }_{0}},\;{{\omega }_{Т}}$ (1.5) из формул (5.7), (5.8), девяти скалярных уравнений системы (5.19)–(5.21) и условия равенства нулю выражения (6.1) при t = T с учетом (6.3)–(6.5) определяются девять неизвестных постоянных задачи ${{с}_{1}},...,{{с}_{5}},\;{{с}_{7}},\;{{с}_{8}},\;{{\alpha }_{1}},\;{{\alpha }_{2}}$ и время Т, а также строятся функции f, ${{f}_{1}}$, $g$, ${{g}_{1}}$.
Шаг 2. Используя формулы (5.7), находим компоненты кватерниона ${\mathbf{К}}$.
Шаг 3. По формуле (5.3)
Шаг 4. По формуле (5.4)
Шаг 5. Используя формулу (5.12), вычисляется вектор управляющего момента КА.
7. Численные примеры. В данном разделе рассматриваются сравнительные результаты численных решений традиционной и модифицированной задач оптимального по быстродействию поворота КА. Для модифицированной задачи выполнялись расчеты по аналитическому алгоритму разд. 6. Значения постоянных ${{\alpha }_{1}},{{\alpha }_{2}}$, ${{с}_{1}},...,{{с}_{5}},{{с}_{7}},{{с}_{8}}$, входящих в аналитическое решение модифицированной задачи, и ограничивающей модуль управления величины ${{u}_{*}}$ для разворотов тел 1–5 с граничными условиями (4.7)–(4.9) приведены в табл. 3.
Таблица 3
| Постоянные | КА | ||||
|---|---|---|---|---|---|
| Тело 1 | Тело 2 | Тело 3 | Тело 4 | Тело 5 | |
| ${{с}_{1}}$ | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| ${{с}_{2}}$ | –1.03798 | –1.04032 | –1.04032 | –0.97083 | –0.96543 |
| ${{с}_{3}}$ | 0.67161 | 0.67114 | 0.67114 | 0.68530 | 0.68641 |
| ${{с}_{4}}$ | –0.70520 | –0.70617 | –0.70617 | –0.67693 | –0.67460 |
| ${{с}_{5}}$ | 0.01875 | 0.01877 | 0.01877 | 0.01837 | 0.01835 |
| ${{с}_{7}}$ | –0.73653 | –0.73683 | –0.73683 | –0.72792 | –0.72725 |
| ${{с}_{8}}$ | –0.73932 | –0.73947 | –0.73947 | –0.79459 | –0.73418 |
| ${{\alpha }_{1}}$ | –0.04218 | –0.04218 | –0.04218 | –0.04218 | –0.04218 |
| ${{\alpha }_{2}}$ | –0.22280 | –0.22280 | -0.22280 | –0.22280 | –0.22280 |
| ${{u}_{ * }}$ | 0.99450 | 0.99570 | 0.99570 | 0.96050 | 0.95780 |
Время быстродействия модифицированной задачи ${{T}_{k}},$ где $k = \overline {1,\,5} $, означает номер тела, в каждом из случаев составило:
Решения традиционной (разд. 4) и модифицированной задач оказались близки. Для примера в табл. 4 приведем значения компонент кватерниона $\Lambda $ и вектора $\omega $ для КА в промежуточных точках τk интервалов времени движения [0, Tk] при решении задачи разворота с граничными условиями (4.7)–(4.9) в модифицированной постановке. Точки τk выбирались максимально близкими к рассмотренным ранее в традиционной задаче точкам ${{t}_{k}}$ (насколько позволяет программа численной реализации алгоритма с переменным шагом вычисления по времени t)
Таблица 4
| КА | ${{\lambda }_{0}}$ | ${{\lambda }_{1}}$ | ${{\lambda }_{2}}$ | ${{\lambda }_{3}}$ | ${{\omega }_{1}}$ | ${{\omega }_{2}}$ | ${{\omega }_{3}}$ |
|---|---|---|---|---|---|---|---|
| Тело 1 (${{\tau }_{1}}$) | 0.80452 | 0.36763 | –0.37817 | 0.27309 | –0.02646 | –0.02650 | –0.55603 |
| Тело 2 (${{\tau }_{2}}$) | 0.80453 | 0.36761 | –0.37817 | 0.27309 | –0.02645 | –0.02655 | –0.55654 |
| Тело 3 (${{\tau }_{3}}$) | 0.80453 | 0.36761 | –0.37817 | 0.27309 | –0.02645 | –0.02655 | –0.55654 |
| Тело 4 (${{\tau }_{4}}$) | 0.80424 | 0.36816 | –0.37822 | 0.27313 | –0.02681 | –0.02529 | –0.54140 |
| Тело 5 (${{\tau }_{5}}$) | 0.80422 | 0.36820 | –0.37823 | 0.27313 | –0.02684 | –0.02519 | –0.54021 |
В табл. 5–8 рассмотрим значения компонент вектора ${\mathbf{М}}(t)$ на концах и в промежуточных точках при решении традиционной (${\mathbf{М}}_{{}}^{{{\text{традиц}}}}$) и модифицированной (${\mathbf{М}}_{{}}^{{{\text{модиф}}}}$) задач для тел 1–4.
Таблица 5
| t | ${\text{М}}_{1}^{{{\text{традиц}}}}$ | ${\text{М}}_{2}^{{{\text{традиц}}}}$ | ${\text{М}}_{3}^{{{\text{традиц}}}}$ | t | ${\text{М}}_{1}^{{{\text{модиф}}}}$ | ${\text{М}}_{2}^{{{\text{модиф}}}}$ | ${\text{М}}_{3}^{{{\text{модиф}}}}$ |
|---|---|---|---|---|---|---|---|
| 0 | –0.65603 | 0.48884 | –0.57503 | 0 | –0.63762 | 0.51267 | –0.57285 |
| ${{t}_{1}}$ | –0.70530 | 0.41389 | –0.57554 | ${{\tau }_{1}}$ | –0.72143 | 0.38795 | –0.56710 |
| $Т_{{\text{1}}}^{{{\text{опт}}}}$ | 0.78625 | –0.29616 | 0.54230 | ${{Т}_{1}}$ | 0.84240 | –0.07923 | 0.52813 |
Таблица 6
| t | ${\text{М}}_{1}^{{{\text{традиц}}}}$ | ${\text{М}}_{2}^{{{\text{традиц}}}}$ | ${\text{М}}_{3}^{{{\text{традиц}}}}$ | t | ${\text{М}}_{1}^{{{\text{модиф}}}}$ | ${\text{М}}_{2}^{{{\text{модиф}}}}$ | ${\text{М}}_{3}^{{{\text{модиф}}}}$ |
|---|---|---|---|---|---|---|---|
| 0 | –0.66476 | 0.57169 | –0.48090 | 0 | –0.63803 | 0.51278 | –0.51437 |
| ${{t}_{2}}$ | –0.72876 | 0.48752 | –0.48086 | ${{\tau }_{2}}$ | –0.71825 | 0.46267 | –0.44870 |
| $Т_{{\text{2}}}^{{{\text{опт}}}}$ | 0.82962 | –0.32708 | 0.45249 | ${{Т}_{2}}$ | 0.83165 | –0.09390 | 0.41841 |
Таблица 7
| t | ${\text{М}}_{1}^{{{\text{традиц}}}}$ | ${\text{М}}_{2}^{{{\text{традиц}}}}$ | ${\text{М}}_{3}^{{{\text{традиц}}}}$ | t | ${\text{М}}_{1}^{{{\text{модиф}}}}$ | ${\text{М}}_{2}^{{{\text{модиф}}}}$ | ${\text{М}}_{3}^{{{\text{модиф}}}}$ |
|---|---|---|---|---|---|---|---|
| 0 | –0.66247 | 0.64225 | –0.38554 | 0 | –0.63803 | 0.51278 | –0.51437 |
| ${{t}_{3}}$ | –0.74532 | 0.54519 | –0.38375 | ${{\tau }_{3}}$ | –0.69743 | 0.52222 | –0.32400 |
| $Т_{{\text{3}}}^{{{\text{опт}}}}$ | 0.86416 | –0.34931 | 0.36223 | ${{Т}_{3}}$ | 0.80104 | –0.10551 | 0.30229 |
Таблица 8
| t | ${\text{М}}_{1}^{{{\text{традиц}}}}$ | ${\text{М}}_{2}^{{{\text{традиц}}}}$ | ${\text{М}}_{3}^{{{\text{традиц}}}}$ | t | ${\text{М}}_{1}^{{{\text{модиф}}}}$ | ${\text{М}}_{2}^{{{\text{модиф}}}}$ | ${\text{М}}_{3}^{{{\text{модиф}}}}$ |
|---|---|---|---|---|---|---|---|
| 0 | –0.12849 | 0.57345 | –0.80910 | 0 | –0.14290 | 0.60640 | –0.78220 |
| ${{t}_{4}}$ | –0.17884 | 0.53974 | –0.82261 | ${{\tau }_{4}}$ | –0.16535 | 0.42109 | –0.67304 |
| $Т_{{\text{4}}}^{{{\text{опт}}}}$ | 0.20885 | –0.56190 | 0.80041 | ${{Т}_{4}}$ | 0.19680 | –0.08921 | 0.60627 |
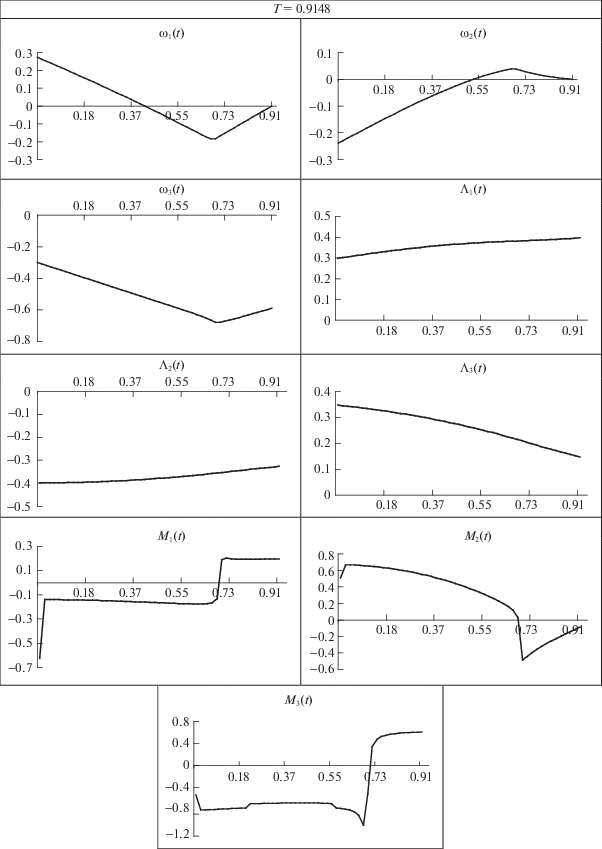
Для тела 4 (МКС) на рис. 1 представлены графики изменения во времени компонент угловой скорости ${{\omega }_{i}}(t),$ $i = \overline {1,3} ,$ векторной части кватерниона ориентации ${{\Lambda }_{i}}(t),$ $i = \overline {1,3} $, и компонент вектора управляющего момента $М_{i}^{{}}(t),$ $i = \overline {1,3} $, в модифицированной задаче оптимального поворота при произвольных заданных граничных условиях (4.7)–(4.9).
Проводились расчеты по решению задач поворотов КА в модифицированной постановке из положения покоя в положение покоя с граничными условиями (4.7), (4.8), (4.10). При этом значения постоянных величин модифицированной задачи для тел 1, 4, 5 указаны в табл. 9. Время быстродействия модифицированной задачи Т в каждом из случаев составило:
Таблица 9
| Постоянные | КА | ||
|---|---|---|---|
| Тело 1 | Тело 4 | Тело 5 | |
| ${{с}_{1}}$ | 1.0 | 1.0 | 1.0 |
| ${{с}_{2}}$ | –0.31037 | –0.54929 | –0.058406 |
| ${{с}_{3}}$ | 0.69640 | 0.78734 | 0.77096 |
| ${{с}_{4}}$ | –0.21614 | –0.43247 | –0.45029 |
| ${{с}_{5}}$ | 0.65875 | 0.53523 | 0.53857 |
| ${{с}_{7}}$ | –0.20446 | –0.29399 | –0.20446 |
| ${{с}_{8}}$ | –1.13081 | –0.84609 | –0.31456 |
| ${{\alpha }_{1}}$ | 0.36003 | 0.50562 | 0.46559 |
| ${{\alpha }_{2}}$ | 1.30935 | 1.07055 | 1.05114 |
| ${{u}_{ * }}$ | 0.99045 | 0.77560 | 0.80900 |
Решения традиционной и модифицированной задач опять же оказались близкими. В табл. 10 приведем значения компонент кватерниона $\Lambda $ и вектора $\omega $ для тел 1, 4, 5 в промежуточных точках $\tau _{k}^{0}$ интервалов времени движения $[0,{{T}_{k}}]$ при решении модифицированной задачи поворота из положения покоя в положение покоя. Точки $\tau _{k}^{0}$ взяты максимально близкими к рассмотренным ранее в традиционной задаче промежуточным точкам $t_{k}^{0}$:
Таблица 10
| КА | ${{\lambda }_{0}}$ | ${{\lambda }_{1}}$ | ${{\lambda }_{2}}$ | ${{\lambda }_{3}}$ |
${{\omega }_{1}}$ | ${{\omega }_{2}}$ | ${{\omega }_{3}}$ |
|---|---|---|---|---|---|---|---|
| Тело 1 ($\tau _{k}^{0}$) | 0.83228 | 0.36140 | –0.35278 | 0.22855 | 0.02987 | –0.05517 | –0.60373 |
| Тело 4 ($\tau _{k}^{0}$) | 0.82742 | 0.35058 | –0.35897 | 0.25222 | 0.03185 | –0.04695 | –0.60802 |
| Тело 5 ($\tau _{k}^{0}$) | 0.82750 | 0.35052 | –0.35880 | 0.25227 | 0.03263 | –0.04792 | –0.62100 |
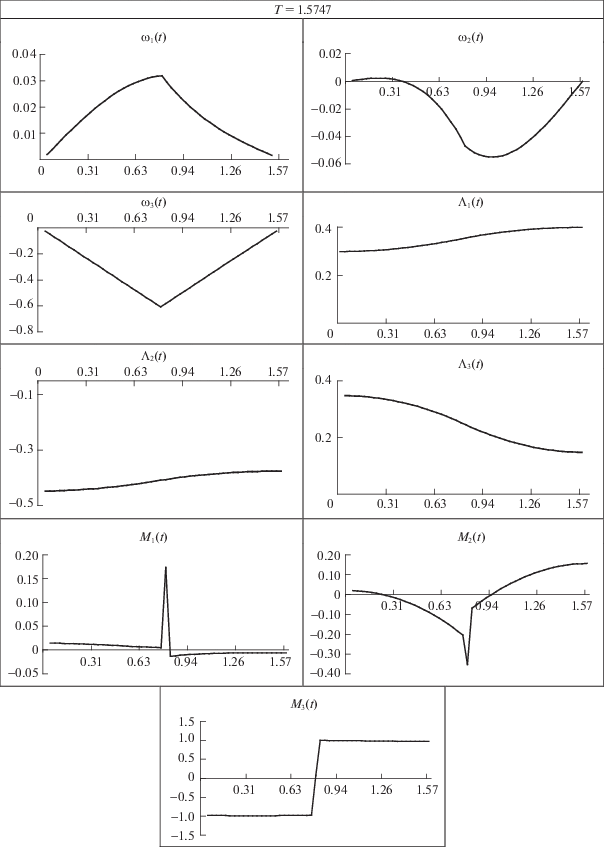
Для тела 4 на рис. 2 представлены графики решения модифицированной задачи поворота МКС из положения покоя в положение покоя с граничными условиями (4.7), (4.8), (4.10).
Рис. 2.
Результаты решения модифицированной задачи при повороте из положения покоя в положение покоя
Отметим, что кватернион ориентации КА ${\mathbf{\Lambda }}(t)$ может быть двузначным [1], т.е. ${\mathbf{\Lambda }}$ и $ - {\mathbf{\Lambda }}$ соответствуют одному и тому же угловому положению КА в пространстве.
Заключение. Представленное в статье аналитическое квазиоптимальное решение задачи поворота КА произвольной динамической конфигурации при произвольных граничных условиях по угловому положению и угловой скорости может найти свое применение при построении систем управления КА, как и известные аналитические решения задачи оптимальной переориентации сферически-симметричного КА в классе плоских эйлеровых поворотов [1].
Полученные результаты на основе решения обратной задачи динамики твердого тела могут быть обобщены на случай управления КА при наличии в постановке задачи различных возмущений.
Список литературы
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973.
Scrivener S.L., Thompson R.C. Survey of Time-Optimal Attitude Maneuvers // J. Guidance, Control, and Dynamics. 1994. V. 17. № 2.
Петров Б.Н., Боднер В.А., Алексеев К.Б. Аналитическое решение задачи управления пространственным поворотным маневром // ДАН СССР. 1970. Т. 192. № 6.
Левский М.В. Ограниченное квадратично оптимальное управление разворотом космического аппарата за фиксированное время // Изв. РАН. ТиСУ. 2019. № 1.
Челноков Ю.Н. Кватернионное решение кинематических задач управления ориентацией твердого тела: уравнения движения, постановка задач, программное движение и управление // Изв. РАН. МТТ. 1993. № 4.
Левский М.В. Синтез оптимального управления ориентацией космического аппарата с использованием комбинированного критерия качества // Изв. РАН. ТиСУ. 2019. № 6.
Молоденков А.В., Сапунков Я.Г. Новый класс аналитических решений в задаче оптимального разворота сферически-симметричного твердого тела // Изв. РАН. МТТ. 2012. № 2.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального разворота сферически-симметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2013. № 3.
Сапунков Я.Г., Молоденков А.В. Численное решение задачи оптимальной переориентации вращающегося космического аппарата // Мехатроника, автоматизация, управление. 2008. № 6.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота сферически-симметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2014. № 2.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2018. № 2.
Молоденков А.В., Сапунков Я.Г. Аналитическое приближенное решение задачи оптимального разворота космического аппарата при произвольных граничных условиях // Изв. РАН. ТиСУ. 2015. № 3.
Молоденков А.В., Сапунков Я.Г. Аналитическое квазиоптимальное решение задачи разворота произвольного твердого тела при произвольных граничных условиях // Изв. РАН. МТТ. 2019. № 2.
Акуленко Л.Д., Лилов Л.К. Синтез квазиоптимальной системы переориентации и стабилизации КА // Космич. исслед. 1990. Т. 28. № 2.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1961.
Li. F., Bainum P.M. Numerical Approach for Solving Rigid Spacecraft Minimum Time Attitude Maneuvers // J. Guidance, Control, and Dynamics. 1990. V. 13. № 1.
Банит Ю.Р., Беляев М.Ю., Добринская Т.А., Ефимов Н.И., Сазонов В.В., Стажков В.М. Определение тензора инерции международной космической станции по телеметрической информации. Препринт № 57. М.: ИПМ им. М.В. Келдыша РАН. 2002.
Lastman G.J. A Shooting Method for Solving Two-Point Boundary-Value Problems Arising from Non-Singular Bang-Bang Optimal Control Problems // Intern. J. Control. 1978. V. 27. № 4.
Молоденков А.В. К решению задачи Дарбу // Изв. РАН. МТТ. 2007. № 2.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления