Известия РАН. Теория и системы управления, 2021, № 4, стр. 130-141
МЕТОД АНАЛИЗА ВЛИЯНИЯ ПОГРЕШНОСТЕЙ ГИРОСКОПИЧЕСКОГО КАНАЛА БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ НА ПОГРЕШНОСТИ ИНЕРЦИАЛЬНОГО СЧИСЛЕНИЯ
А. А. Голован a, В. Ю. Мишин b, А. В. Молчанов c, *, М. В. Чиркин b
a ФГБОУ ВО “Московский государственный университет им. М.В. Ломоносова”
Москва, Россия
b ФГБОУ ВО “Рязанский государственный радиотехнический университет им. В.Ф. Уткина”
Рязань, Россия
c ПАО “Московский институт электромеханики и автоматики”
Москва, Россия
* E-mail: a.v.molchanov@mail.ru
Поступила в редакцию 08.11.2020
После доработки 08.12.2020
Принята к публикации 25.01.2021
Аннотация
Описан метод, позволяющий анализировать влияние погрешностей гироскопического канала бесплатформенной инерциальной навигационной системы на погрешности инерциального счисления. Метод был реализован с помощью компьютерного имитатора бесплатформенной инерциальной навигационной системы. Развит общий подход к процедуре моделирования погрешностей в компьютерном имитаторе с проведением нулевого теста. Моделирование дало возможность выделить погрешности инерциального счисления в случаях различных типов траекторий летательного аппарата при применении цифровой обработки данных в гироскопических каналах лазерных датчиков угловой скорости.
Введение. Методы математического моделирования широко используются при исследовании прикладных задач навигации и управления. Соответствующие компьютерные имитаторы являются важной составляющей разработки и тестирования программно-математического обеспечения (ПМО) бесплатформенных инерциальных навигационных систем (БИНС). В частности, они востребованы в задаче анализа влияния погрешностей инерциальных датчиков – акселерометров и гироскопов (датчиков угловой скорости (ДУС)) – на точность инерциального счисления БИНС. Такая задача, в частности, возникает на стадиях проектирования системы, применения новых, перспективных программно-аппаратных решений.
Вопросами компьютерной имитации прикладных задач навигации и управления занимаются во многих научно-производственных организациях и учебных заведениях соответствующего профиля. Среди предметных публикаций по этой тематике выделим (не претендуя на полноту) монографии [1–3], статью [4]. Среди зарубежных разработок имитаторов для тестирования интегрированных инерциально-спутниковых навигационных систем выделим продукт SimINERTIAL компании Spirent (www.spirentgnss.com, www.spirentgnss.ru).
Очевидны требования, предъявляемые к математическому обеспечению компьютерного имитатора: алгоритмы должны обеспечивать универсальность и полноту имитационного моделирования, оставаясь достаточно простыми в вычислительном плане и использующими минимальный набор исходных данных для моделирования.
Как известно [5], любая инерциальная навигационная система предназначена для определения движения материальной точки – приведенной чувствительной массы блока ньютонометров или акселерометров (далее акселерометров) – и движения приборной системы координат, отождествляемой с корпусом объекта. Движение материальной точки и приборной системы координат удовлетворяет известным уравнениям теоретической механики, которые должны учитывать принятые в навигации модели формы Земли, ее поля тяготения, вращение Земли и т.п. Опора на эти инвариантные механические объекты и понятия определяет универсальность имитатора.
С практической точки зрения это означает, что имитатор без каких-либо модификаций может быть использован для моделирования разноплановых задач функционирования БИНС разного класса точности: от точных систем, построенных на лазерных, волоконно-оптических, твердотельных волновых гироскопах, до грубых систем на MEMS-датчиках. Это достигается за счет имитации первичной навигационной информации – идеальных показаний идеально установленных инерциальных датчиков (в общем случае – интегрирующих): акселерометров, измеряющих удельную внешнюю силу, и гироскопов, измеряющих абсолютную угловую скорость объекта.
При моделировании важно обеспечить выполнение так называемого нулевого теста, когда по сформированным показаниям идеальных инерциальных датчиков бортовые алгоритмы БИНС воспроизводят исходную траекторию (координаты, линейные скорости, углы ориентации) с максимальной точностью, в идеале, абсолютно точно. Для обеспечения нулевого теста необходимо решение задач механики: определения движения по известным силам и скоростям (прямая задача), определения сил и скоростей движения по известной траектории (обратная задача). Задача выполнения нулевого теста при кажущейся простоте и очевидности содержит, однако, ряд тонкостей, которые потребовали проведения аккуратного исследования, подробно описанное в [6]. В разработанном имитаторе исключительно важную роль играют алгоритмы формирования идеальных показаний акселерометров и ДУС для в общем случае интегрирующих датчиков и последующая тщательная проверка нулевого теста. Это обстоятельство выделяет данный имитатор от других аналогичных разработок.
Очевиден пример использования нулевого теста – имитация возмущенного режима работы БИНС. Имитируя инструментальные погрешности инерциальных датчиков в соответствии с классом точности инерциальной системы, либо используя стендовые записи реализаций инструментальных погрешностей конкретной БИНС, можно простым суммированием идеальных показаний и реализаций инструментальных погрешностей сымитировать “реальные” измерения инерциальных датчиков. Уровень “не выполнения” нулевого теста будет отражать точностные характеристики конкретной автономной БИНС на заданной траектории движения объекта.
Применительно к рассматриваемой в настоящей статье задаче тестирования алгоритмов цифровой обработки квадратурных сигналов лазерного гироскопа с механической вибрационной частотной подставкой имитируемые идеальные показания ДУС служат входной информацией для соответствующей математической модели блока лазерных ДУС. Выходная информация блока моделирования будет служить входной информацией для нулевого теста, уровень “не выполнения” которого будет отражать точностные характеристики алгоритмов цифровой обработки данных.
Важной составляющей компьютерного имитатора служит исходная траектория объекта, например, записи географических координат, компонент вектора линейной скорости, углов ориентации корпуса объекта. Среди указанных траекторных параметров нет угловых скоростей ${{\omega }_{z}}$ корпуса объекта и компонент вектора удельной внешней силы fz, являющихся полезными сигналами для инерциальных датчиков. Эти параметры вычисляются отдельно при помощи описываемых далее алгоритмов.
Существуют два способа формирования исходных траекторных данных. Первый способ предполагает явное аналитическое задание траекторных параметров как функций времени. Второй способ основан на зарегистрированных экспериментально телеметрических данных конкретного навигационного эксперимента, например полетных данных. Использование телеметрической информации много предпочтительней первого варианта, поскольку последующее моделирование в этом случае будет осуществляться на характерном классе траекторных движений объекта. Далее рассмотрен вариант применения телеметрических данных.
1. Состав исходной траекторной информации для моделирования, предобработка. Выше упоминался необходимый и достаточный состав исходной траекторной информации: время ${{t}_{j}}$, географическая широта φ, долгота $\lambda $, высота h, компоненты восточной ${{V}_{E}}$, северной ${{V}_{N}}$, вертикальной ${{V}_{{up}}}$ относительной скорости, углы истинного курса ψ, крена γ и тангажа ${v}$. Информационный поток телеметрических данных часто имеет низкую частоту регистрации, например 1 Гц, и может содержать записи выходных параметров нескольких БИНС, установленных на объекте, а также данные приемника сигналов спутниковых навигационных систем (СНС). Здесь также возможна многовариантность регистрируемой информации, когда записываются данные автономного (шулеровского) режима функционирования БИНС и данные так называемого комплексного канала БИНС.
Предобработка исходных телеметрических данных для последующего моделирования включает следующие этапы:
– предварительная проверка исходной информации на наличие сбоев регистрации и синхронизации. В случае выявленных дефектов входной информации осуществляется (если возможно) ее корректировка;
– регистрация финального состава траекторной телеметрической информации из многовариантных наборов позиционной, скоростной, угловой информации БИНС и СНС;
– оконное сглаживание телеметрической информации для ослабления возмущений, вызванных ошибками квантования при записи данных, рассинхронизацией разнородных информационных потоков;
– интерполяция кубическими сплайнами телеметрических данных с низкой частоты (например, 1 Гц) на задаваемую более высокую частоту (например, 2400 Гц), обусловленная постановкой задачи проводимого исследования.
Результатом начальной стадии моделирования является опорная, идеальная траектория объекта при нужной частоте “регистрации”, регистрации без ошибок, синхронизации и т.п., включающая в себя упомянутый выше состав траекторной информации.
2. Задача моделирования показаний идеальных инерциальных датчиков БИНС с проведением нулевого теста. Моделирование показаний идеальных инерциальных датчиков БИНС следует за предобработкой телеметрических данных и содержит две составляющие. Первая – собственно моделирование идеальных показаний инерциальных датчиков. Вторая – проведение нулевого теста, когда сымитированные идеальные показания являются входом для типовых бортовых алгоритмов БИНС при отсутствии ошибок начальной выставки системы. Выполнение нулевого теста заключается в том, что алгоритмы инерциального счисления БИНС должны восстановить исходную траекторию с высокой точностью, например с точностью первых десятков сантиметров для координат.
2.1. Моделирование показаний гироскопов [6–8]. Задача ставится следующим образом. В моменты времени tj, ${{t}_{{j + 1}}}$ предполагаются известными координаты φ, λ, h точки M, отождествляемой с объектом, и параметры ориентации ψ, γ, υ приборного трехгранника Mz, также отождествляемого со связанной с корпусом объекта системой координат. Требуется вычислить значения вектора ${{\omega }_{z}} = {{({{\omega }_{{{{z}_{1}}}}},{{\omega }_{{{{z}_{2}}}}},{{\omega }_{{{{z}_{3}}}}})}^{{\text{т}}}}$ абсолютной угловой скорости трехгранника Mz, соответствующего его переходу из углового положения, которое трехгранник занимал в момент времени tj, в угловое положение, которое он займет в момент времени ${{t}_{{j + 1}}}$.
Один из вариантов численного решения этой задачи основан на частном случае интегрируемости уравнения Пуассона:
(2.1)
${{\dot {A}}_{z}} = {{\hat {\omega }}_{z}}{{A}_{z}},\quad {{\hat {\omega }}_{z}} = \left( {\begin{array}{*{20}{c}} 0&{{{\omega }_{{{{z}_{3}}}}}}&{ - {{\omega }_{{{{z}_{2}}}}}} \\ { - {{\omega }_{{{{z}_{3}}}}}}&0&{{{\omega }_{{{{z}_{1}}}}}} \\ {{{\omega }_{{{{z}_{2}}}}}}&{ - {{\omega }_{{{{z}_{1}}}}}}&0 \end{array}} \right)$Если вектор угловой скорости ${{\omega }_{z}}$ не меняет своего направления на интервале времени [tj, ${{t}_{{j + 1}}}$], то интеграл
(2.2)
${{A}_{z}}\left( {{{t}_{{j + 1}}}} \right) = \left( {E + \frac{{\sin \gamma }}{\gamma }{{{\hat {\gamma }}}_{z}} + \frac{{1 - \cos \gamma }}{\gamma }\hat {\gamma }_{z}^{2}} \right){{A}_{z}}\left( {{{t}_{j}}} \right),\quad \gamma = \sqrt {\gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2}} .$Здесь и далее ${{\hat {\gamma }}_{z}}$ – кососимметрическая матрица вида (2.1), поставленная в соответствии вектору ${{\gamma }_{z}}$, E – единичная (3 × 3)-матрица.
В [6] приведено описание численного алгоритма, определяющего на основе уравнения (2.2) вектор ${{\gamma }_{z}}$ при помощи значений ${{A}_{z}}\left( {{{t}_{j}}} \right)$, ${{A}_{z}}\left( {{{t}_{{j + 1}}}} \right)$ матрицы ориентации. Окончательно интегрально среднее значение вектора ${{\omega }_{z}}$ абсолютной угловой скорости на интервале [tj, ${{t}_{{j + 1}}}$] определяется так: ${{\omega }_{z}} = {{{{\gamma }_{z}}} \mathord{\left/ {\vphantom {{{{\gamma }_{z}}} {\Delta t}}} \right. \kern-0em} {\Delta t}}$, где $\Delta t = {{t}_{{j + 1}}} - {{t}_{j}}$. Далее величина ${{\omega }_{z}}$ отождествляется с идеальным измерением абсолютной угловой скорости блока ДУС на этом интервале.
2.2. Моделирование показаний акселерометров [6, 8]. В моменты времени tj, ${{t}_{{j + 1}}}$ предполагаются известными координаты φ, λ, h точки M, отождествляемой с объектом, значение вектора скорости в момент времени tj, параметры ориентации ψ, γ, ν приборного трехгранника Mz. Требуется вычислить в осях приборного трехгранника Mz значения вектора ${{f}_{z}} = {{\left( {\begin{array}{*{20}{c}} {{{f}_{{{{z}_{1}}}}},}&{{{f}_{{{{z}_{2}}}}},}&{{{f}_{{{{z}_{3}}}}}} \end{array}} \right)}^{{\text{т}}}}$ внешней удельной силы, которая соответствует переходу точки M из ее положения в момент времени tj в положение, которое она займет в момент времени ${{t}_{{j + 1}}}$. При этом учитывается навигационная модель удельной силы тяготения ${{\bar {g}}^{0}}$, действующей на точку M во время ее движения.
Один из вариантов численного решения сформулированной задачи основан на частном случае интегрируемости динамических уравнений движения, записанных в осях сопровождающего географического трехгранника Mx:
(2.3)
${{\dot {A}}_{x}} = {{\hat {\omega }}_{x}}{{A}_{x}},\quad {{{\dot {v}}}_{x}} = {{\hat {\omega }}_{x}}{{{v}}_{x}} + {{f}_{x}} + g_{x}^{0}.$Здесь Ax – матрица ориентации географического трехгранника Mx относительно инерциального Oξ, ${{\omega }_{x}}$ – вектор его абсолютной угловой скорости, ${{{v}}_{x}}$ – вектор абсолютной линейной скорости точки M в осях Mx, $g_{x}^{0}$ – вектор удельной силы тяготения в осях Mx, ${{f}_{x}}$ – искомый вектор удельной силы, измеряемый блоком акселерометров, если бы их оси чувствительности совпадали с осями Mx.
Будем считать, что векторы ${{f}_{x}} + g_{x}^{0}$ и ${{\omega }_{x}}$ не меняют своего направления на интервале времени [tj, ${{t}_{{j + 1}}}$]. Тогда уравнение (2.3) интегрируется в явном виде:
(2.4)
$\begin{gathered} {{{v}}_{x}}\left( {{{t}_{{j + 1}}}} \right) = \left( {E + \frac{{\sin \gamma }}{\gamma }{{{\hat {\gamma }}}_{x}} + \frac{{1 - \cos \gamma }}{\gamma }\hat {\gamma }_{x}^{2}} \right){{{v}}_{x}}\left( {{{t}_{j}}} \right) + \left( {E + \frac{{1 - \cos \gamma }}{{\gamma _{{}}^{2}}}{{{\hat {\gamma }}}_{x}} + \frac{{\sin \gamma }}{{\gamma _{{}}^{3}}}\hat {\gamma }_{x}^{2}} \right)\Delta F, \\ \Delta F = \int\limits_{{{t}_{j}}}^{{{t}_{{j + 1}}}} {({{f}_{x}} + g_{x}^{0})\left( \tau \right)d\tau } \quad \gamma = \sqrt {\gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2}} . \\ \end{gathered} $В (2.4) неизвестным параметром является вектор $\Delta F$ и ${{f}_{x}} + g_{x}^{0} = {{\Delta F} \mathord{\left/ {\vphantom {{\Delta F} {\Delta t}}} \right. \kern-0em} {\Delta t}}$. В [6] приведено подробное описание численного алгоритма определения вектора $\Delta F$ и в итоге – искомого вектора fz внешней удельной силы в проекциях уже на оси приборного трехгранника Mz.
2.3. Нулевой тест. “Показания” ${{\omega }_{z}}$, fz блоков ДУС и акселерометров далее используются в штатных алгоритмах инерциального счисления БИНС при отсутствии ошибок начальной выставки БИНС и при идеальных параметрах ее вертикального канала. Интегрируются кинематические уравнения для счисления географических координат и параметров ориентации приборного трехгранника Mz, динамические уравнения для счисления линейной скорости движения точки M. Параметры полученной траектории сравниваются с аналогичными параметрами опорной траектории, которая использована в качестве основы моделирования.
Опыт применения имитатора для телеметрических полетных данных показал высокую точность выполнения нулевого теста.
3. Математическая модель лазерного ДУС с цифровой обработкой выходной информации. В качестве прецизионных датчиков угловой скорости широко используются гироскопы на основе кольцевых гелий-неоновых лазеров. Погрешность лазерного гироскопа содержит несколько составляющих [9]. Математическое моделирование позволяет выделить влияние каждой из них на погрешности инерциального счисления.
В соответствии с результатами работы [10] при временах усреднения выходного сигнала лазерного ДУС, превышающих 1000 с, доминирует нестабильность дрейфа гироскопа. Если время усреднения находится в диапазоне 0.01–100 с и используется цифровая обработка квадратурных сигналов [11], доминирует случайная погрешность, обратно пропорциональная квадратному корню из времени осреднения, которая вызвана связью встречных волн в кольцевом резонаторе [12] в условиях применения знакопеременной частотной подставки. В данной работе именно эта составляющая проанализирована при моделировании влияния погрешностей гироскопического канала на результаты инерциального счисления.
Известно, что источником информации о движении кольцевого лазера является изменение фазы Саньяка – разности фаз ψ генерируемых лазером встречных волн. Последовательный теоретический подход к описанию динамики кольцевого лазера с учетом связи встречных волн основан на теории Лэмба [9]. Предполагая, что кольцевой лазер идеален, а его информационные сигналы зависят только от мгновенной разности фаз встречных волн, можно создать упрощенную модель кольцевого лазера, учитывающую связь встречных волн [11–15] с помощью дифференциального уравнения:
(3.1)
$\frac{{d\psi }}{{dt}} = \frac{{8\pi A}}{{\lambda L}}({{\omega }_{{{{z}_{i}}}}}\left( t \right) + {{\omega }_{i}}\left( t \right) - {{\omega }_{L}}\sin \left( {\psi + \gamma } \right)),$В качестве отсчетов угловой скорости ${{\omega }_{i}}\left( t \right)$, с которой колеблется кольцевой лазер, используются сигналы, экспериментально зарегистрированные для кольцевых лазеров с механическими вибрационными частотными подставками [16, 17]. В процессе выполнения измерений эти датчики находились в режиме измерений проекций угловой скорости вращения Земли, на оси чувствительности лазерных гироскопов. Для каждого массива ${{\omega }_{{{{z}_{i}}}}}\left( t \right)$ использованы различные реализации ${{\omega }_{i}}\left( t \right)$, отличающиеся центральной частотой, на которой происходят колебания кольцевого лазера.
Численное решение дифференциального уравнения (3.1) осуществляется методом Рунге–Кутта четвертого порядка. Поскольку в уравнении (3.1) имеется слагаемое, пропорциональное $\sim {\kern 1pt} \sin \left( \psi \right)$, а заданная угловая скорость ${{\omega }_{{{{z}_{i}}}}}$ может изменяться в широких пределах (±400 град/с), то шаг, с которым ищется решение, должен быть достаточно мал. В [15] показано, что спектры первичных сигналов кольцевого лазера с механической вибрационной частотной подставкой, испытывающего вращение с угловой скоростью до ±400 град/с, содержат гармоники вплоть до частот, близких к 2 МГц. Чтобы исключить явление “элайзинга” (маскировка частот), частота дискретизации должна, как минимум, в 2 раза превышать верхнюю границу занимаемой сигналом полосы частот. Поэтому частота дискретизации первичных сигналов кольцевого лазера и восстановленной фазы Саньяка ψ выбрана заведомо больше указанного предела (4.8 МГц).
Первичные информационные сигналы ${{U}_{c}}\left( t \right)$, ${{U}_{s}}\left( t \right)$ с фазой Саньяка ψ связаны следующими соотношениями:
(3.2)
${{U}_{c}}\left( t \right) = {{U}_{{c,0}}} + {{U}_{{c,m}}}\cos \left( {\psi + {{\varphi }_{c}}} \right),\quad {{U}_{s}}\left( t \right) = {{U}_{{s,0}}} + {{U}_{{s,m}}}\sin \left( {\psi + {{\varphi }_{s}}} \right),$Чтобы из первичных сигналов (3.2) извлечь информацию об угловой скорости, использован алгоритм обработки квадратурных сигналов, развитый в работах [11, 15, 16] применительно к лазерной гироскопии. Цифровая обработка включает следующие стадии:
– дискретизация первичных сигналов;
– аппроксимация эллипсом множества точек, соответствующих первичным отсчетам на плоскости переменных ${{U}_{c}}$, ${{U}_{s}}$;
– определение параметров квадратурных сигналов ${{U}_{{c,0}}}$, ${{U}_{{s,0}}}$, ${{U}_{{s,m}}}$, ${{U}_{{c,m}}}$, ${{\varphi }_{c}}$ и ${{\varphi }_{s}}$;
– определение разности фаз ψ встречных волн, генерируемых кольцевым лазером;
– подавление с помощью режекторного фильтра составляющей выходного сигнала, связанной с колебаниями кольцевого лазера (вибрационной подставкой).
Выходные данные модели лазерного гироскопа представляют собой восстановленные отсчеты угловой скорости $\omega _{{{{z}_{i}}}}^{'}$ с частотой дискретизации 2400 Гц.
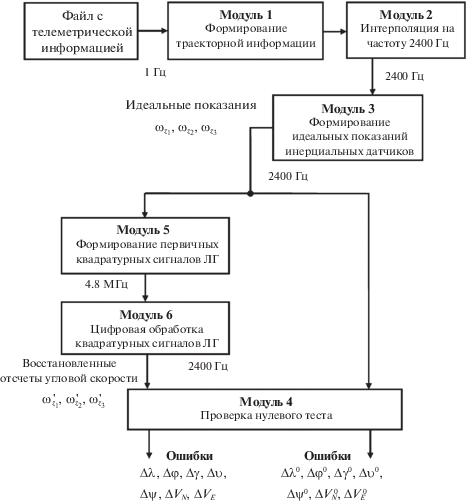
4. Описание процедуры моделирования. Процедура моделирования выполняется с помощью нескольких программных модулей (рис. 1). На первом этапе выбирается файл, содержащий телеметрическую информацию, записанную с частотой дискретизации 1 Гц во время реального полета летательного аппарата. В процессе моделирования данные, содержащиеся в файле, подвергались требуемой обработке.
Первый модуль выделяет из входного файла телеметрическую информацию, необходимую для последующего моделирования. Состав траекторной информации: время tj, долгота λ, широта φ, высота h, восточная ${{V}_{E}}$, северная ${{V}_{N}}$, вертикальная ${{V}_{{UP}}}$ составляющие скорости, углы курса ψ, крена γ и тангажа ${v}$. Эти данные представляют собой последовательности отсчетов с частотой 1 Гц.
Реализована мультивариантность выбора траекторной информации, поскольку в телеметрическом файле содержатся:
– позиционные, скоростные данные СНС;
– позиционные, скоростные, угловые данные автономного “шулеровского” режима БИНС;
– позиционные, скоростные, угловые данные комплексного режима БИНС.
Второй модуль интерполирует данные БИНС с частоты 1 Гц на задаваемую более высокую частоту. Интерполяция осуществляется с помощью кубических сплайнов. Для каждой дискретной функции рассчитывается кусочно-непрерывная функция, состоящая из полиномов третьей степени. Задается новый массив времени t с постоянным шагом, который определяется заданной частотой дискретизации $\tau = 1{\text{/}}{{f}_{s}}$. С помощью рассчитанных интерполирующих функций создаются новые массивы траекторных данных (время tj, географические координаты λ, φ, h, скорости ${{V}_{E}}$, ${{V}_{N}}$, ${{V}_{{UP}}}$, углы ψ, γ, ${v}$), имеющих более высокую частоту дискретизации${{f}_{s}}$. При интерполяции (как и при предварительном сглаживании) учитывались возможные переходы значений углов курса, тангажа, крена через особые точки: ±π, ±π/2. В работе осуществлялась интерполяция данных на частоту 2400 Гц, соответствующую частоте данных на выходе исследуемой системы.
Третий модуль осуществляет вычисление и запись в выходные файлы идеальных показаний инерциальных датчиков: датчиков абсолютной угловой скорости (${{\omega }_{{{{z}_{1}}}}}$, ${{\omega }_{{{{z}_{2}}}}}$, ${{\omega }_{{{{z}_{3}}}}}$) и акселерометров (${{f}_{{{{z}_{1}}}}}$, ${{f}_{{{{z}_{2}}}}}$, ${{f}_{{{{z}_{3}}}}}$). Сжатое описание этих алгоритмов было представлено выше. Результаты работы третьего модуля, отсчеты абсолютной угловой скорости ${{\omega }_{{{{z}_{1}}}}}$, ${{\omega }_{{{{z}_{2}}}}}$, ${{\omega }_{{{{z}_{3}}}}}$ используются для проверки разработанных алгоритмов цифровой обработки квадратурных сигналов лазерного гироскопа с механической вибрационной частотной подставкой.
Четвертый модуль производит проверку выполнения “нулевого теста”, когда при помощи идеальных показаний акселерометров и гироскопов алгоритмы счисления инерциальной навигации восстанавливают опорную траекторию, которая служит основой моделирования идеальных показаний инерциальных датчиков ${{f}_{{{{z}_{1}}}}}$, ${{f}_{{{{z}_{2}}}}}$, ${{f}_{{{{z}_{3}}}}}$, ${{\omega }_{{{{z}_{1}}}}}$, ${{\omega }_{{{{z}_{2}}}}}$, ${{\omega }_{{{{z}_{3}}}}}$. Результатом работы данного модуля являются ошибки “восстановленной” опорной траектории: ошибки координат ($\Delta \lambda $, $\Delta \varphi $), ошибки компонент относительной скорости в восточном и северном направлении ($\Delta {{V}_{E}}$, $\Delta {{V}_{N}}$) и ошибки определения углов курса $\Delta \psi $, крена $\Delta \gamma $ и тангажа $\Delta \nu $.
Четвертый модуль организован так, что для него входной информацией может служить отдельный файл с показаниями блока ДУС, полученными путем преобразований исходных идеальных показаний блока ДУС. Тем самым этот модуль позволяет осуществить тестирование используемых алгоритмов цифровой обработки сигналов ДУС в режиме автономного “шулеровского” инерциального счисления (для горизонтальных каналов БИНС).
В пятом модуле для каждого из заданных массивов имитируемых идеальных показаний ДУС ${{\omega }_{{{{z}_{i}}}}}$ выполняется решение дифференциального уравнения (3.1), формируются отсчеты разности фаз встречных волн ψi, по которым моделируются первичные квадратурные сигналы кольцевых лазеров (3.2).
Шестой модуль реализует выбранный алгоритм обработки [11, 13, 15] первичных квадратурных сигналов, сформированных в модуле 5. Выходными данными модуля являются массивы показаний ДУС $\omega _{{{{z}_{i}}}}^{'}$, которые включают погрешности, задаваемые в модели кольцевого лазера и вносимые выбранным алгоритмом обработки первичных сигналов.
Далее с помощью четвертого модуля осуществлялась проверка выполнения “нулевого теста”, когда при помощи идеальных показаний акселерометров (${{f}_{{{{z}_{1}}}}}$, ${{f}_{{{{z}_{2}}}}}$, ${{f}_{{{{z}_{3}}}}}$) и восстановленных показаний гироскопов ($\omega _{{{{z}_{i}}}}^{'}$, $\omega _{{{{z}_{2}}}}^{'}$, $\omega _{{{{z}_{3}}}}^{'}$), алгоритмы счисления инерциальной навигации восстанавливают опорную траекторию. Результатом являются ошибки определения координат, компонент относительной скорости в восточном и северном направлении и углов курса, крена и тангажа, обусловленные используемым методом обработки первичных сигналов лазерного гироскопа.
5. Результаты моделирования. При моделировании погрешностей инерциального счисления в гироскопических каналах БИНС задавались одинаковые погрешности, реализовывались идентичные алгоритмы подавления составляющей выходного сигнала, связанной с колебаниями кольцевого лазера (частотной подставкой). Использованы одинаковые амплитуды частотных подставок и законы их ошумления; центральные частоты колебаний кольцевых лазеров различались на заданную величину разноса частот: 400 ± 20 Гц.
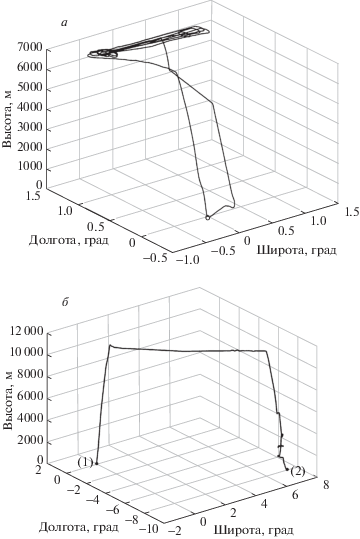
Моделирование погрешностей инерциального счисления выполнено для двух типов траекторий полета. Первый тип: маневренный полет, который содержит взлет и набор высоты, динамичный участок с маневрами, снижение и возврат в начальную точку (рис. 2, а). Второй тип: перелет из одной точки в другую, который содержит взлет и набор высоты, участок полета с минимальными эволюциями, снижение и посадка (рис. 2, б).
Рис. 2.
Типовые траектории, для которых выполнено моделирование: а – маневренный полет с возвратом в исходную точку, б – перелет из точки 1 в точку 2
На первом этапе решалась задача подтверждения комплексной работоспособности исследованного программно-математического обеспечения лазерного ДУС с цифровой обработкой (программные модули 5 и 6) и имитатора БИНС, реализованного в программных модулях 1–4. В качестве тестовой траектории была использована траектория первого типа. Случайная погрешность измерения угловой скорости в модели лазерного ДУС была задана равной нулю (статический порог синхронизации ωL принят нулевым). Параметры режекторного фильтра: ширина полосы 20 Гц, коэффициент подавления 60 дБ. Результаты моделирования показали, что используемый метод обработки первичных сигналов лазерного гироскопа приводит к появлению ошибок, которые не превышают:
– 0.7 м по модулю в определении координат,
– 0.012 м/с компонент относительной скорости в восточном и северном направлениях,
– 1–2 угл. с по углам курса, крена и тангажа.
Полученные результаты хорошо соотносятся с результатами моделирования погрешностей углов ориентации при высокоскоростных маневрах с угловыми ускорениями, превышающих 100 град/с2 [13].
На втором этапе в математическую модель лазерного ДУС вводилась величина ненулевого порога захвата и определялись погрешности инерциального счисления. Моделирование проводилось для траекторий первого и второго типа с теми же параметрами режекторного фильтра, что и на первом этапе. Величина статического порога синхронизации лазерного ДУС ωL = 0.01 град/c. Выбранная величина ωL является характерным нижним пределом для лазерных ДУС КЛ-3, серийно выпускаемых для комплектации систем БИНС-СП2.
Результаты моделирования для типовых траекторий представлены на рис. 3–6. Введение случайной погрешности в гироскопические каналы приводит к появлению погрешностей координат, линейных скоростей и углов ориентации. Отклонения от “истинных” значений увеличиваются и составляют:
Рис. 3.
Ошибки определения координат: красный цвет – маневренный полет, синий цвет – перелет, сплошные кривые – широта, пунктирные кривые – долгота
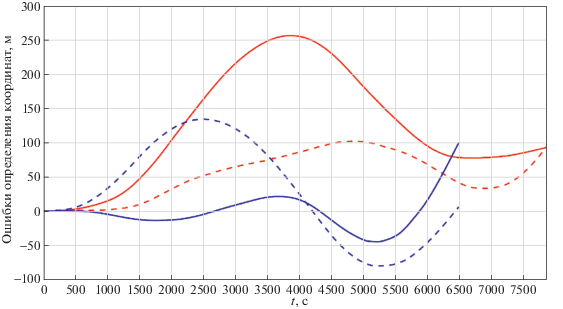
Рис. 4.
Ошибки определения скоростей: красный цвет – маневренный полет, синий цвет – перелет, сплошные кривые – ΔVE, две пунктирные кривые – ΔVN
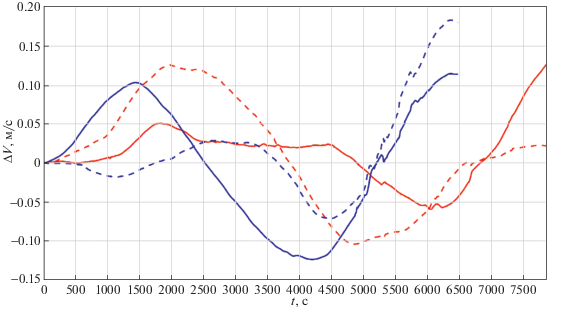
Рис. 5.
Ошибки определения углов (а) (маневренный полет): красный цвет – курс, синий цвет – тангаж, черный цвет – крен; угловые ускорения по крену (б)
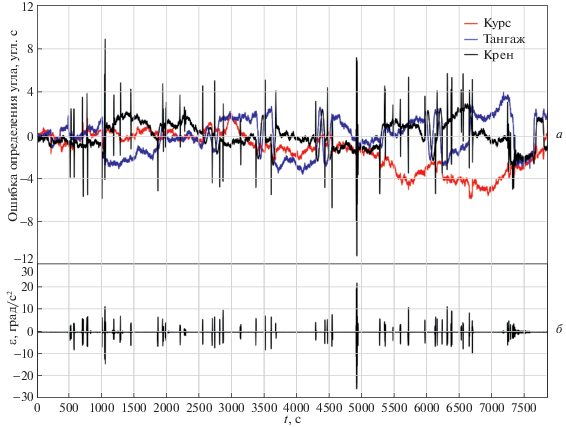
Рис. 6.
Ошибки определения углов (перелет): красная кривая – курс, синяя кривая – тангаж, черная кривая – крен
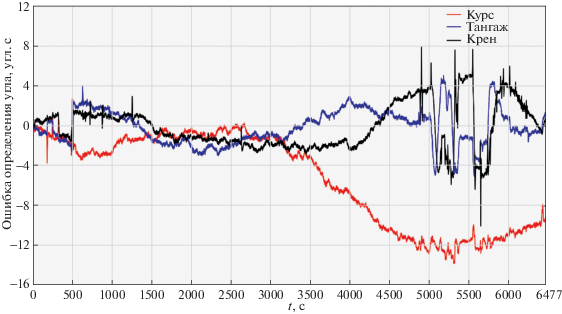
– для координат 100–250 м по модулю;
– для линейных скоростей 0.05–0.2 м/с;
– для углов курса, крена и тангажа 5 угл. с с выбросами до 12 угл. с.
Ошибки определения линейных скоростей и углов ориентации увеличились на порядок, ошибки определения координат возрастают в сотни раз. Масштаб обнаруженных отклонений характерен для обоих типовых траекторий и с запасом укладывается в требования к системам класса точности БИНС-СП2 [18].
Однако очевидны и различия. В случае маневренного полета отклонения углов пространственной ориентации от истинных значений содержат большое количество выбросов, в особенности для угла крена. Их появление отражает более сложную динамику объекта, характеризующуюся значительными изменениями составляющих угловой скорости. Частые изменения курсового угла (виражи в горизонтальной плоскости, рис. 2, а) сопровождаются быстрыми изменениями угла крена и колебаниями соответствующей составляющей углового ускорения с большими амплитудами, что неизбежно сопровождается погрешностями, вносимыми в результат режекторной фильтрацией потока выходных данных лазерного ДУС [13]. Данный процесс хорошо иллюстрирует график изменения углового ускорения по каналу крена, приведенный на рис. 5, б. Однако накопление с течением времени погрешностей определения углов в данном случае не наблюдается.
В случае простого перелета количество и размах выбросов на графиках ошибок определения углов значительно меньше. Однако через 3000 с появляются явные признаки накопления погрешности определения курсового угла, величина которой в конце полета приближается к значимой для БИНС величине 12 угл. с.
Обнаруженные особенности изменения погрешностей для разных типов траекторий объекта требуют отдельного анализа, что выходит за рамки статьи, основная задача которой заключается в описании метода анализа погрешностей гироскопического канала БИНС на основе компьютерной имитации задачи.
Примененный метод анализа погрешностей гироскопического канала с помощью компьютерного имитатора БИНС позволил оценить погрешности счисления при введении режекторной фильтрации вибрационной подставки лазерного ДУС и величины случайной компоненты ухода в угле.
Полученные результаты, с одной стороны, подтверждают возможность применения такого подхода в обработке выходной информации с лазерного ДУС в инерциальных навигационных системах с погрешностью определения координат лучше 1.85 км (2σ), а с другой – демонстрируют возможности данного подхода для оценки целесообразности применения новых программно-аппаратных решений в других задачах инерциально-спутниковой навигации.
Заключение. Для двух качественно различающихся траекторий летательного аппарата определено влияние режекторной фильтрации вибрационной подставки лазерного ДУС и величины случайной компоненты ухода в угле на погрешности инерциального счисления БИНС. Фильтрация приводит к появлению ошибок, которые не превышают: 0.7 м для координат, 0.012 м/с для компонент относительной скорости в восточном и северном направлениях, 2 угл. с по углам курса, крена и тангажа. Введение случайной погрешности в гироскопические каналы, вызванной связью встречных волн в кольцевом лазере и ошумлением вибрационной подставки, сопровождается увеличением погрешностей определения линейных скоростей до 0.2 м/с, углов ориентации до 5 угл. с, а ошибки определения координат возрастают до 250 м.
Развитый подход создает предпосылку для исследования вкладов составляющих погрешностей инерциальных датчиков и особенностей алгоритмов обработки их первичных сигналов на погрешность инерциального счисления БИНС. Выгодное преимущество подобного моделирования заключается в возможности исследовать влияние каждого из факторов по отдельности и распространить анализ, например, на нестабильность дрейфа выходного сигнала гироскопа [10].
Описанный метод тщательной компьютерной имитации для оценки погрешностей гироскопического канала БИНС без каких-либо серьезных изменений может быть использован в других задачах инерциально-спутниковой навигации, возникающих при сравнительном анализе возможностей инерциальных датчиков различных типов или для оценки целесообразности применения новых программно-аппаратных решений.
Список литературы
Матвеев В.В., Распопов В.Я. Основы построения бесплатформенных инерциальных навигационных систем. СПб.: Концерн “ЦНИИ “Электроприбор”, 2009. 280 с.
Емельянцев Г.И., Степанов А.П. Интегрированные инерциально-спутниковые системы ориентации и навигации. СПб.: Концерн “ЦНИИ “Электроприбор”, 2016. 393 с.
Веремеенко К.К., Желтов С.Ю., Ким Н.В., Себряков Г.Г., Красильщиков М.Н. Современные информационные технологии в задачах навигации и наведения беспилотных маневренных летательных аппаратах. М.: Физматлит, 2009. 556 с.
Тихомиров В.А., Александров С.Ю. Моделирование информационного потока бесплатформенной инерциальной системы самолета // Ученые записки Комсомольского-на-Амуре государственного технического ун-та. 2014. Т. 1. № 4. С. 23–35.
Голован А.А., Парусников Н.А. Математические основы навигационных систем. Ч. I. Математические модели инерциальной навигации. 3-е изд., испр. и доп. М.: МАКС Пресс, 2011. 136 с.
Богданов О.Н. Методика согласованного моделирования измерений инерциальных датчиков, траекторных параметров объекта с приложением к задачам инерциальной и спутниковой навигации: Дис. … канд. физ.-мат. наук. М., 2015. 146 с.
Богданов О.Н., Фомичев А.В. Имитация показаний идеальных датчиков угловой скорости БИНС на основе телеметрических данных движения объекта // Вестн. МГУ. Сер. 1. Математика, механика. 2014. № 3. С. 40–47.
Баранов Э.В., Богданов О.Н., Голован А.А., Кокорев С.М., Куликов Д.Ю., Пестраков М.И. Имитатор спутниковых радиосигналов с блоком универсального моделирования работы БИНС // Новости навигации. 2016. № 1. С. 22–27.
Aronovitz F. Fundamentals of the Ring Laser Gyro // Optical Gyros and their Application // RTO-AG-339. 1999. P. 3-1–3-45.
Molchanov A.V., Serebryakov A.E., Klimakov V.V., Dao H.N., Mishin V.Yu., Chirkin M.V. The Effect of Slow Fluctuation Processes in the Ring Laser Gyroscope on its Bias Instability // Proc. 25-th Saint Petersburg Intern. Conf. on Integrated Navigation Systems. St. Petersburg, Russia, 2018. P. 302–305.
Molchanov A.V., Belokurov V.A., Chirkin M.V., Koshelev V.I., Mishin V.Yu., Morozov D.A. Precision Laser Gyro with a Digital Channel for Quadrature Signal Processing // Proc. 22nd Saint Petersburg Intern. Conf. on Integrated Navigation Systems. St. Petersburg, Russia, 2015. P. 307–314.
Молчанов А.В., Степанов А.Ю., Чиркин М.В. Статистические характеристики подложек зеркал и случайная погрешность лазерного гироскопа // Авиакосмическое приборостроение. 2008. № 3. С. 9–17.
Chirkin M.V., Mishin V.Yu., Morozov D.A., Golovan A.A., Molchanov A.V. Filtering Output Signals of a Laser Gyro Triad // Proc. 21 Saint Petersburg Intern. Conf. on Integrated Navigation Systems. St. Petersburg, Russia, 2014. P. 388–390.
Алексеев С.Ю., Чиркин М.В., Мишин В.Ю., Морозов Д.А., Борисов М.В., Молчанов А.В., Захаров М.А. Методика измерения порога синхронизации при изготовлении и эксплуатации прецизионных кольцевых лазеров // Гироскопия и навигация. 2013. № 2. С. 75–83.
Мишин В.Ю., Молчанов А.В., Чиркин М.В. Проблема цифровой обработки первичных квадратурных сигналов в лазерных гироскопах // Приборы. 2013. № 1 (151). С. 33–38.
Molchanov A.V., Belokurov V.A., Chirkin M.V., Kagalenko M.B., Koshelev V.I., Mishin V.Yu., Morozov D.A. The Application of Advanced Processing Technique to the Triad of Precision Laser Gyroscopes // Proc. of 23rd Saint Petersburg Intern. Conf. on Integrated Navigation Systems. St. Petersburg, Russia, 2016. P. 120–122.
Зимин В.С., Мишин В.Ю., Морозов Д.А. Особенности функционирования вибрационной частотной подставки в триаде лазерных гироскопов // “Современные технологии в науке и образовании – СТНО-2017”. Сб. тр. Междунар. науч.-техн. и науч.-метод. конф. В 4 т. Рязань, 2017. С. 249–253.
ГОСТ РВ 52 339-2005. Системы бесплатформенные инерциально-навигационные на лазерных гироскопах. М., 2005. С. 15.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления