Известия РАН. Теория и системы управления, 2021, № 4, стр. 7-26
ДИНАМИКА ГИСТЕРЕЗИСНО-СВЯЗАННЫХ ОСЦИЛЛЯТОРОВ ВАН-ДЕР-ПОЛЯ: МЕТОД МАЛОГО ПАРАМЕТРА
А. Л. Медведский a, П. А. Мелешенко b, c, В. А. Нестеров d, О. О. Решетова b, М. Е. Семенов b, e, f, *
a Федеральное государственное унитарное предприятие “Центральный аэрогидродинамический институт
им. проф. Н.Е. Жуковского”
Жуковский, Россия
b Воронежский государственный ун-т
Воронеж, Россия
c Целевая поисковая лаборатория прорывных технологий радиосвязи Фонда перспективных исследований
Воронеж, Россия
d МАИ (национальный исследовательский ун-т)
Москва, Россия
e ФГБУН Федеральный исследовательский центр “Единая геофизическая служба Российской академии наук”
Обнинск, Россия
f Воронежский государственный технический ун-т
Воронеж, Россия
* E-mail: mkl150@mail.ru
Поступила в редакцию 10.07.2020
После доработки 20.11.2020
Принята к публикации 25.01.2021
Аннотация
Основные результаты работы связаны с изучением динамики осциллятора Ван-дер-Поля, находящегося под воздействием вынуждающей силы и гистерезисного воздействия, формализуемого посредством феноменологической модели Боука–Вена. Установлена регуляризирующая роль гистерезисного звена в части редукции хаотических режимов. Основные результаты получены в рамках метода асимптотических разложений (метода малого параметра).
Рассмотрена система двух связанных осцилляторов Ван-дер-Поля в условиях воздействия вынуждающей силы на один из них: в аналитической форме была установлена зависимость между амплитудами и частотами собственных колебаний осцилляторов. Также в работе описана система перекрестно-связанных осцилляторов Ван-дер-Поля, в которой вынуждающая сила, действующая на один из них, определяется выходом гистерезисного преобразователя, на вход которого подается рассогласование между скоростями осцилляторов. Установлено, что существенное влияние на синхронизацию в системе оказывает параметр связи между осцилляторами, а также параметр, определяющий влияние гистерезисного звена.
Введение. Уравнение Ван-дер-Поля – классическое уравнение теории колебаний, посредством которого описывается универсальный механизм возникновения автоколебательных режимов через бифуркацию Андронова–Хопфа. Кроме того, известна возможность появления как квазигармонических, так и релаксационных колебаний.
К настоящему времени число автоколебательных систем, поведение которых моделируется при помощи уравнения Ван-дер-Поля, достаточно велико: различные системы в радиотехнике, такие, как триодный генератор и генератор на туннельном диоде, динамика кардиоритмов, а также разнообразные приложения в робототехнике, в частности, модели поворачивающегося робота [1] и мн. др. [2, 3]. Системы связанных осцилляторов Ван-дер-Поля успешно применялись для анализа сложных систем, в том числе и с распределенными параметрами (тропические циклоны, где было использовано свойство осцилляторов генерировать автоколебательные режимы), а также при описании ионизационных волн [4] и в широком спектре задач, связанных с моделированием процессов, протекающих в человеческом организме.
Весьма обширное направление, связанное с моделированием процессов в организме человека, также основывается на свойствах осциллятора Ван-дер-Поля. По-видимому, в одной из первых работ [5] в указанном направлении динамика сокращений сердечной мышцы моделировалась посредством трех связанных осцилляторов Ван-дер-Поля. С помощью этой модели удалось объяснить многие виды аритмии и даже предсказать ряд новых, обнаруженных впоследствии. В настоящее время активно продолжаются исследования, в которых динамика кардиостимуляторов моделируется уравнениями осцилляторов Ван-дер-Поля. Так, например, в работе [6] предлагается модель, позволяющая воспроизвести несколько известных электрокардиологических явлений, таких, как тахикардия, полная блокада сердца, трепетание предсердий и фибрилляцию желудочков. В [7] исследуется феноменологическая модель сердцебиения, состоящая из двух связанных осцилляторов Ван-дер-Поля, позволяющая проанализировать синхронизацию ритмов. В [8] представлена модель сердечно-сосудистой системы, которая является комбинацией уравнения Ван-дер-Поля и информационной модели в форме сети Вольтерры.
Недавние исследования показали, что динамику осциллятора голосовой связки возможно моделировать с помощью уравнения Ван-дер-Поля. Оказалось, что указанная модель упрощает ее анализ и в должной степени соответствует основным принципам функционирования [9]. Отметим также работу [10], где осциллятор Ван-дер-Поля применяется для моделирования процессов, возникающих при отоакустической эмиссии, т.е. звуков, генерируемых в наружном слуховом проходе колебаниями волосковых клеток ушной улитки.
Так как перемещение людей и животных носит ритмичный характер, то для моделирования походки, а также движений конечностей часто применяют системы связанных осцилляторов Ван-дер-Поля. В [11] показано, что бипедальное передвижение возможно моделировать с помощью взаимосвязанных осцилляторов Ван-дер-Поля, более того, варьируя параметры осцилляторов, можно управлять длиной шага и частотой ходьбы. Работа [12] предлагает модель, состоящую из нескольких осцилляторов Ван-дер-Поля, Дуффинга и Рэлея, что позволяет описать силу контакта между ногами человека и жесткой поверхностью. Параметры модели были получены на основе обработки экспериментальных данных. Анализ устойчивости проводился с использованием метода энергетического баланса и метода возмущений. В [13] изучается биомеханическая модель реакции моста на движение пешеходов, при этом моделирование походки пешехода осуществляется посредством осциллятора Ван-дер-Поля. Показано, что при некотором критическом значении числа пешеходов, зависящем от физических параметров моста, амплитуда его колебаний резко возрастает. Отметим, что этот факт находится в полном соответствии с наблюдаемыми явлениями.
Одним из фундаментальных свойств нелинейных систем является синхронизация, т.е. установление определенных соотношений между характерными временами, частотами или фазами колебаний систем в результате их взаимодействия. Синхронизация автоколебаний исследовалась как в технических системах, например, синхронизация электронных часов внешним воздействием высокостабильного генератора, в результате чего обеспечивается высокая точность времени в системе транспорта, так и в биологических, социальных, экономических. В частности, синхронизация колебаний мембранного потенциала моделей взаимодействующих биологических нейронов использовалась в задачах сегментации зашумленных изображений [14]. В классических работах [15, 16] рассматривались фундаментальные вопросы теории синхронизации периодических и квазипериодических колебаний. Отметим в этой связи, что система связанных осцилляторов Ван-дер-Поля является эталоном для реализации различных режимов синхронизации.
Известно, что в системе связанных осцилляторов Ван-дер-Поля могут реализовываться как регулярные, так и хаотические режимы движения [17]. Одной из классических задач, связанной со сложной динамикой, является задача управления. В [18, 19] описывались алгоритмы управления техническими системами, основанные на вариациях внутренних параметров и параметров внешнего воздействия. В [20, 21] рассматривались методы управления механическими системами, где желаемым был периодический режим. Управление хаотической динамикой, основанное на различных модификациях принципа обратной связи в сочетании с методами теории уравнений с запаздывающим аргументом, приведено в [22, 23]. Один из перспективных методов управления хаотической динамикой основан на использовании гистерезисных преобразователей в контуре управления [24].
Явления гистерезисной природы возникают в различных технических системах как на уровне отдельных блоков, так и на уровне управляющих воздействий. Динамике систем с гистерезисом посвящено значительное количество публикаций, из которых отметим [25–27]. В указанных работах рассматриваются нелинейные динамические системы и их отклик на гистерезисное воздействие, описываемое в рамках феноменологического похода (модель Боука-Вена и ее вариации). В области моделирования технических систем с гистерезисом отметим, прежде всего, работу [28], в которой приводится динамическая модель двуногого робота с точечными опорами. В рамках этой модели гистерезис проявляется в связях между динамическими характеристиками. В [29] описывается гистерезисное поведение в осцилляторе Ван-дер-Поля–Дуффинга вблизи субгармонического резонанса 3:1, исследуется влияние на зоны синхронизации и резонанса. Отметим, что гистерезисные явления, свойственны не только физическим и техническим системам, но имеют место также и в области экономики и социологических наук. В частности, в публикациях [30, 31] описываются модели экономических и социальных систем, наблюдаемые характеристики которых (уровень безработицы, уровень стресса и т.д.) демонстрируют ярко выраженное гистерезисное поведение.
Гистерезисные преобразователи в управляющих элементах рассматривались в работах [32–34], в качестве составляющих колебательных систем – в [35, 36]. Отметим, что при описании моделей гистерезиса традиционно используются два подхода: первый из них основан на операторной трактовке носителей гистерезисных свойств в терминах преобразователей с пространством состояний и входно-выходными соответствиями [37, 38]. Второй основан на феноменологическом подходе, в котором гистерезисная петля описывается посредством дифференциальных и алгебраических соотношений – наиболее популярной в этом смысле является модель Боука–Вена. Детальный анализ этой модели содержится в ряде работ [39–42]. Модель Боука–Вена является удобным, с точки зрения алгоритмической реализации, инструментом формализации гистерезисных зависимостей, особенно в случаях, когда гистерезисные элементы являются частями сложной системы.
1. Динамика осциллятора Ван-дер-Поля с внешним воздействием гистерезисной природы. 1.1. Осциллятор Ван-дер-Поля с периодическим внешним воздействием. Следуя классическим методам исследования осциллятора Ван-дер-Поля, основанных на идеях метода малого параметра, приведем необходимые для дальнейшего изложения результаты [16]. Для этого запишем уравнение Ван-дер-Поля в следующем виде:
(1.1)
$\ddot {x} - \mu (1 - \alpha {{x}^{2}})\dot {x} + \omega _{0}^{2}x = \omega _{0}^{2}B{\text{cos}}(\omega t).$Формально введем в это уравнение малый параметр:
(1.2)
$\ddot {x} + \omega _{0}^{2}x = \varepsilon (\omega _{0}^{2}B{\text{cos}}(\omega t) + \mu (1 - \alpha {{x}^{2}})\dot {x}).$Очевидно, что при ε = 1 уравнение (1.2) эквивалентно (1.1). Однако для дальнейших построений удобно считать ε малым ($\left| \varepsilon \right| \ll 1$) параметром. В этом случае, следуя классическим схемам [16], решение уравнения (1.2) ищется в виде формального степенного ряда по $\varepsilon $ в виде
(1.3)
$x = A\cos \psi + \varepsilon {{u}_{1}}(A,\psi ) + {{\varepsilon }^{2}}{{u}_{2}}(A,\psi ) + ...,$(1.4)
$\dot {A} = \varepsilon {{f}_{1}}(A,\varphi ) + {{\varepsilon }^{2}}{{f}_{2}}(A,\varphi ) + ...,\quad \dot {\varphi } = - \Delta + \varepsilon {{F}_{1}}(A,\varphi ) + {{\varepsilon }^{2}}{{F}_{2}}(A,\varphi ) + ...\;.$Здесь $\Delta = \omega - {{\omega }_{0}}$ – расстройка частоты, ${{F}_{1}}$, ${{F}_{2}}$, ${{f}_{1}}$, ${{f}_{2}}$ – неизвестные функции, которые следует определить из условий отсутствия резонансных членов для функции ${{u}_{1}}$. Ниже ограничимся поиском лишь приближенного решения соответствующего линейным по ε слагаемым.
Следуя [16], подставим (1.3) и (1.4) в (1.2) и, приравняв к нулю резонансные слагаемые при $\varepsilon $ в первой степени, получим следующую систему, определяющую динамику амплитуды и фазы свободных колебаний:
(1.5)
$\dot {A} = - \frac{{{{\omega }_{0}}B}}{2}\sin \varphi + \frac{\mu }{2}A\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right),\quad \dot {\varphi } = \Delta - \frac{{{{\omega }_{0}}B}}{{2A}}{\text{cos}}\varphi ,$В синхронном режиме можно положить $\dot {A} = 0$, $\dot {\varphi } = 0$. Исключая из полученных уравнений $\varphi $, найдем уравнение для определения A:
(1.6)
${{\left( {{{{\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right)}}^{2}} + 4\frac{{{{\Delta }^{2}}}}{{{{\mu }^{2}}}}} \right)}^{2}}\frac{{{{A}^{2}}}}{{A_{0}^{2}}} = {{b}^{2}},\quad {\text{где}}\quad b = \frac{{{{\omega }_{0}}B}}{{{{A}_{0}}}}.$В следующих разделах будет проведен сравнительный анализ результатов справедливых для классического уравнения Ван-дер-Поля, с результатами, полученными для уравнения, которое содержит гистерезисное звено.
1.2. Осциллятор Ван-дер-Поля с гистерезисным звеном в контуре обратной связи. Рассмотрим уравнение Ван-дер-Поля, содержащее в правой части, помимо внешнего гармонического воздействия, гистерезисный блок, формализованный посредством феноменологической модели Боука–Вена. В [43] было показано, что включение гистерезисного звена в правую часть аналогичных систем существенным образов влияет на их динамические особенности. Это объясняется в первую очередь тем, что выход гистерезисного преобразователя (как в рамках конструктивного, так и феноменологического представления) зависит не только от входа в настоящий момент времени, но и от всей его предыстории.
Модель Боука–Вена определяется следующими соотношениями:
(1.7)
$\left\{ {\begin{array}{*{20}{l}} {{{\Phi }_{{BW}}}(x,t) = \alpha x(t) + (1 - \alpha )Dz(t),} \\ {\dot {z}(t) = {{A}_{1}}\dot {x}(t) - \beta \left| {\dot {x}(t)} \right|{{{\left| {z(t)} \right|}}^{{n - 1}}}z(t) - \gamma \dot {x}(t){{{\left| {z(t)} \right|}}^{n}},} \end{array}} \right.$Осциллятор Ван-дер-Поля с гистерезисным звеном будет формализован при помощи уравнения
(1.8)
$\ddot {x} - \mu (1 - \lambda {{x}^{2}})\dot {x} + \omega _{1}^{2}x = B\omega _{1}^{2}\cos (\omega t) + {{\Phi }_{{BW}}}(x,t).$Для дальнейшего исследования перепишем уравнение (1.8) следующим образом:
где $G(t) = B\omega _{1}^{2}\cos (\omega t) + {{\Phi }_{{BW}}}(x,t)$. Здесь, как и ранее, решение ищем в виде (1.3). Далее, формально дифференцируя это соотношение по времени, получим(1.10)
$\dot {x} = \dot {A}\cos \psi - A\sin \psi \dot {\psi } + \varepsilon {{\dot {u}}_{1}}\omega + ...{\text{ }},$(1.11)
$\ddot {x} = \ddot {A}\cos \psi - 2\dot {A}\sin \psi \dot {\psi } - A\cos \psi {{\dot {\psi }}^{2}} - A\sin \psi \ddot {\psi } + \varepsilon {{\ddot {u}}_{1}}{{\omega }^{2}} + ...\;.$Подставляя найденные соотношения в уравнение (1.9) и ограничившись линейными по $\varepsilon $ слагаемым, получим соотношение
(1.12)
${{\omega }^{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{\psi }^{2}}}} + \omega _{1}^{2}{{u}_{1}} = \left( {2{{\omega }_{1}}{{f}_{{`1}}} - A\frac{{\partial {{F}_{1}}}}{{\partial \phi }}\Delta } \right){\text{sin}}\psi - \left( {2{{\omega }_{1}}A{{F}_{{`1}}} - A\frac{{\partial {{f}_{1}}}}{{\partial \phi }}\Delta } \right){\text{cos}}\psi - \mu A\Delta \left( {1 - \frac{{{{A}^{2}}\alpha }}{4}} \right){\text{sin}}\psi - G(t){\text{ }}.$Из условия отсутствия резонансных слагаемых в правой части (1.12) определим следующую систему для амплитуды и фазы:
(1.13)
$\left\{ {\begin{array}{*{20}{l}} {2{{f}_{1}} - A\frac{\Delta }{{{{\omega }_{0}}}}\frac{{\partial {{F}_{1}}}}{{\partial \varphi }} = - {{G}_{{\sin }}}(t) + \mu A\Delta \left( {1 - \frac{{{{A}^{2}}\alpha }}{4}} \right),} \\ {2A{{F}_{1}} + \frac{\Delta }{{{{\omega }_{0}}}}\frac{{\partial {{f}_{1}}}}{{\partial \varphi }} = - {{G}_{{\cos }}}(t),} \end{array}} \right.$Примем, что преобразователь Боука–Вена применяется исключительно к нулевому решению ${{x}_{0}} = A{\text{cos}}(\omega t + \varphi ),$ первую гармонику разложение в ряд Фурье выхода оператора Боука–Вена можно представить следующим образом:
(1.14)
${{\Phi }_{{BW}}}(A\cos (\omega t + \varphi )) = \frac{{{{a}_{0}}}}{2} + {{a}_{1}}\cos \varphi + {{b}_{1}}\sin \varphi .$Так как ${{a}_{0}}{\text{/}}2 = 0$, то ${{F}_{{\sin }}}(t)$ и ${{F}_{{\cos }}}(t)$ принимают вид
(1.15)
${{F}_{{\sin }}}(t) = \omega _{0}^{2}B\sin \varphi + {{b}_{1}}\sin \varphi ,\quad {{F}_{{\cos }}}(t) = \omega _{0}^{2}B\cos \varphi + {{a}_{1}}\cos \varphi .$Из системы уравнений (1.13) с учетом (1.15) получим уравнения для определения амплитуды и фазы колебаний:
(1.16)
$\left\{ {\begin{array}{*{20}{l}} {\dot {A} = - \frac{{\omega _{0}^{2}B + {{b}_{1}}}}{{2{{\omega }_{0}}}}\sin \varphi + \frac{\mu }{2}A\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right){\text{ }},} \\ {\dot {\varphi } = \Delta - \frac{{\omega _{0}^{2}B + {{а}_{1}}}}{{2{{\omega }_{0}}А}}{\text{cos}}\varphi {\text{ }}.} \end{array}} \right.$В синхронном режиме полагая $\dot {A} = 0$, $\dot {\varphi } = 0$ и исключая из (1.16) $\varphi $, найдем уравнение для определения $A$:
(1.17)
$\left( {{{{\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right)}}^{2}} + 4\frac{{{{\Delta }^{2}}}}{{{{\mu }^{2}}}}\frac{{{{{(\omega _{0}^{2}B + {{b}_{1}})}}^{2}}}}{{{{{(\omega _{0}^{2}B + {{a}_{1}})}}^{2}}}}} \right)\frac{{{{A}^{2}}}}{{A_{0}^{2}}} = \alpha \frac{{{{{(\omega _{0}^{2}B + {{b}_{1}})}}^{2}}}}{{4\omega _{0}^{2}{{\mu }^{2}}}}.$Для определим значений коэффициентов при разложении в ряд Фурье ${{a}_{1}}$ и ${{b}_{1}}$, воспользуемся методом гармонического баланса:
(1.18)
${{a}_{1}} = \frac{\omega }{\pi }\int\limits_0^{2\pi /\omega } {{{\Phi }_{{BW}}}\left( {A\cos (\omega t + \varphi )} \right)} \cos (\omega t + \varphi )dt,\quad {{b}_{1}} = \frac{\omega }{\pi }\int\limits_0^{2\pi /\omega } {{{\Phi }_{{BW}}}\left( {A\cos (\omega t + \varphi )} \right)} \sin (\omega t + \varphi )dt.$Если коэффициент системы (1.7) α = 0, то в первом уравнении остается только гистерезисная составляющая. Второе уравнение системы (1.7) перепишем как
(1.19)
$\dot {z}(t) = \dot {x}(t)({{A}_{1}} - \left[ {\beta {\text{sgn}}\left( {\dot {x}(t)z(t)} \right) + \gamma } \right]{{\left| {z(t)} \right|}^{n}}),$Параметр n в модели Боука–Вена существенным образом влияет на форму гистерезисной петли. В общем случае аналитическое представление, даже первого приближения, получить крайне затруднительно, поэтому ниже рассматриваются три разных случая, соответствующие различным значениям параметра n модели Боука–Вена.
В первом из них положим $n = 1$, определяя вход как $x(t) = A\cos (\omega t + \varphi )$, а выход – как $z(t) = b\cos (\omega t + \varphi )$. Рассмотрим частный случай, когда параметр модели Боука–Вена ${{A}_{1}} = 1$:
(1.20)
$\dot {z}(t) = - A\omega \sin (\omega t + \varphi )\left( {1 - \left[ {\beta \operatorname{sgn} \left( { - A\omega \sin (\omega t + м)b\cos (\omega t + \varphi )} \right) + \gamma } \right]{\text{ }}\left| {b\cos (\omega t + \varphi )} \right|} \right).$Умножим на $\sin (\omega t + \phi )$левую и правую части уравнения (1.20) и проинтегрируем их по периоду:
(1.21)
$\begin{gathered} \int\limits_0^{2\pi /\omega } {\dot {z}(t)} \sin (\omega t + \varphi )dt = \\ \, = \int\limits_0^{2\pi /\omega } { - A\omega {{{\sin }}^{2}}(\omega t + \varphi )(1 - \left[ {\beta \operatorname{sgn} \left( { - A\omega \sin (\omega t + \varphi )b\cos (\omega t + \varphi )} \right) + \gamma } \right]\left| {b\cos (\omega t + \varphi )} \right|)dt} {\text{.}} \\ \end{gathered} $Вычислив интегралы, запишем соотношение
(1.22)
$ - b\pi = - A\pi + \frac{{4Ab}}{3}(\beta {{\sin }^{3}}\varphi + \gamma {{\cos }^{3}}\varphi ).$Откуда для $b$ получим
(1.23)
$b = \frac{{3A\pi }}{{4A(\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }}.$Следовательно, первое приближение выхода гистерезисного преобразователя принимает вид
(1.24)
$z(t) = \frac{{3A\pi }}{{4A(\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }}\cos (\omega t + \varphi ).$Вернемся к уравнениям (1.18) и определим коэффициенты a1 и ${{b}_{1}}$:
(1.25)
$\begin{gathered} {{a}_{1}} = \frac{\omega }{\pi }\int\limits_0^{2\pi /\omega } {\frac{{3A\pi }}{{4A(\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }}\cos (\omega t + \varphi )} \cos (\omega t + \varphi )dt; \\ {{b}_{1}} = \frac{\omega }{\pi }\int\limits_0^{2\pi /\omega } {\frac{{3A\pi }}{{4A(\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }}\cos (\omega t + \varphi )} \sin (\omega t + \varphi )dt. \\ \end{gathered} $Интегрируя эти выражения, получим
(1.26)
${{a}_{1}} = \frac{{3A\pi }}{{4A{\kern 1pt} {\kern 1pt} (\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }};\quad {{b}_{1}} = 0.$Выполним подстановку в уравнение (1.17). Тогда зависимость амплитуды решения от амплитуды внешнего воздействия будет определяться как
(1.27)
$\left( {{{{\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right)}}^{2}} + 4\frac{{{{\Delta }^{2}}}}{{{{\mu }^{2}}}}\frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{{{{\left( {\omega _{0}^{2}B + \frac{{3A\pi }}{{4A(\beta {{{\sin }}^{3}}\varphi + \gamma {{{\cos }}^{3}}\varphi ) + 3\pi }}} \right)}}^{2}}}}} \right)\frac{{{{A}^{2}}}}{{A_{0}^{2}}} = \alpha \frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{4\omega _{0}^{2}{{\mu }^{2}}}}.$Теперь рассмотрим случай $n = 2$. Тогда уравнение (1.19) примет вид
(1.28)
$\dot {z}(t) = - A\omega \sin (\omega t + \varphi )(1 - \left[ {\beta \operatorname{sgn} \left( { - A\omega \sin (\omega t + \varphi )b\cos (\omega t + \varphi )} \right) + \gamma } \right]{{\left( {b\cos (\omega t + \varphi )} \right)}^{2}}).$Выполнив аналогичные с (1.21) преобразования, получим уравнение относительно b:
Запишем соотношение для положительного корня уравнения (1.29):
где коэффициенты ${{a}_{1}}$ и ${{b}_{1}}$ имеют вид:Подставим ${{a}_{1}}$ и ${{b}_{1}}$ в уравнение (1.17), тогда зависимость амплитуды решения от амплитуды внешнего воздействия определена как
(1.32)
$\left( {{{{\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right)}}^{2}} + 4\frac{{{{\Delta }^{2}}}}{{{{\mu }^{2}}}}\frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{{{{\left( {\omega _{0}^{2}B + \frac{2}{{\gamma A}}( - 1 + \sqrt {1 + {{A}^{2}}\gamma } )} \right)}}^{2}}}}} \right)\frac{{{{A}^{2}}}}{{A_{0}^{2}}} = \alpha \frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{4\omega _{0}^{2}{{\mu }^{2}}}}.$Теперь рассмотрим третий случай, когда $n = 3{\text{/}}2$. Уравнение (1.19) примет вид
(1.33)
$\dot {z}(t) = - A\omega \sin (\omega t + \varphi )(1 - \left[ {\beta \operatorname{sgn} \left( { - A\omega \sin (\omega t + \varphi )b\cos (\omega t + \varphi )} \right) + \gamma } \right]{{\left| {b\cos (\omega t + \varphi )} \right|}^{{3/2}}}).$Проинтегрируем (1.33):
(1.34)
$\begin{gathered} - b\pi = - A\pi + \frac{4}{{21}}{\text{ }}A{{b}^{{3/2}}}{\text{ }}\left( {(\beta + \gamma )F\left[ {\pi + \frac{\varphi }{2},2} \right] + (\beta - \gamma )F\left[ {\frac{\varphi }{2},2} \right]} \right. + \\ \, + \left. {2\beta F\left[ {\frac{{\pi + \varphi }}{2},2} \right] + ( - \beta + \gamma )F\left[ {\frac{1}{4}(\pi + 2\varphi ),2} \right] - (\beta + \gamma )F\left[ {\frac{1}{4}(3\pi + 2\varphi ),2} \right]} \right), \\ \end{gathered} $Проведем преобразования, аналогичные (1.23)–(1.26), и найдем коэффициенты ${{a}_{1}}$ и ${{b}_{1}}$. После подстановки последних в уравнение (1.17) получим зависимость между амплитудой решения и амплитудой внешнего воздействия для случая $n = 3{\text{/}}2$:
(1.35)
$\begin{gathered} \left( {{{{\left( {1 - \frac{{{{A}^{2}}}}{{A_{0}^{2}}}} \right)}}^{2}} + 4\frac{{{{\Delta }^{2}}}}{{{{\mu }^{2}}}}\frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{{{{(\omega _{0}^{2}B + {{a}_{1}})}}^{2}}}}} \right)\frac{{{{A}^{2}}}}{{A_{0}^{2}}} = \alpha \frac{{{{{(\omega _{0}^{2}B)}}^{2}}}}{{4\omega _{0}^{2}{{\mu }^{2}}}}, \\ {{a}_{1}} = {\text{ }}7056{{A}^{2}}{\text{ }}\left( {(\beta + \gamma )F\left[ {\pi + \frac{\varphi }{2},2} \right] + (\beta - \gamma )F\left[ {\frac{\varphi }{2},2} \right] + 2\beta F\left[ {\frac{{\pi + \varphi }}{2},2} \right]} \right. + \\ \, + {{\left. {( - \beta + \gamma )F\left[ {\frac{1}{4}(\pi + 2\varphi ),2} \right] - (\beta + \gamma )F\left[ {\frac{1}{4}(3\pi + 2\varphi ),2} \right]} \right)}^{2}}. \\ \end{gathered} $На рис. 1, 2 приведены графики зависимости амплитуды решения от амплитуды внешнего воздействия, а также параметра μ для полученных соотношений (1.27) и (1.32).
Рис. 1.
Зависимости амплитуд решения $A$ от амплитуды вынуждающей силы $\omega _{0}^{2}B$ для различных значений $\mu $: а – для уравнения, не содержащего гистерезисный блок; б – при значении параметра модели Боука–Вена n = 1; в – при значении параметра модели Боука–Вена n = 2
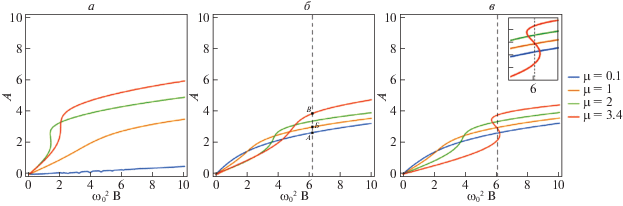
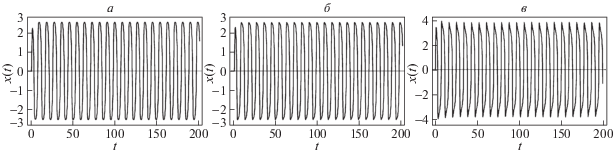
Рис. 2.
Численное решение системы (1.8) при значениях параметров n = 1, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $ и различных значениях $\mu $: а – $\mu = 0.1$, б – $\mu = 1$, в – $\mu = 3.4$
Особо отметим, что при значениях параметра $\mu = 3.4$ и $\omega _{0}^{2}B \approx 2\pi $ (параметры численного решения систем (1.1) и (1.8)) имеет место неоднозначная зависимость амплитуды колебаний от амплитуды внешнего воздействия, т.е. при одной и той же внешней вынуждающей силе возможно два устойчивых режима колебаний, отличающиеся амплитудой.
На рис. 1, б отмечены некоторые значения параметров, которым соответствуют графики решений, приведенные на рис. 2 (точкам А, Б и В соответствуют рис. 2, а–в). Сопоставление соответствующих рисунков показывает, что с точностью до 3% амплитуда собственных колебаний осциллятора совпадает с результатами теоретических расчетов.
1.3. Различные режимы динамики осциллятора Ван-дер-Поля. Известно, что в осцилляторе Ван-дер-Поля, находящегося под воздействием внешней периодической силы, могут реализовываться различные режимы динамики: периодический, квазипериодический, хаотический. Так для значений $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$ и $\omega _{0}^{2} = \pi $ в системе (1.1) спектр показателей Ляпунова, вычисленных с помощью стандартного алгоритма Вольфа, имеет значения [0.109414, –2.41502, 0.0], которые соответствуют хаотическому режиму.
В настоящем разделе исследуется влияние гистерезисного звена на режимы колебаний осциллятора Ван-дер-Поля. Известно, что гистерезисное слагаемое способно регуляризировать сложные, в том числе, и хаотические движения. В этой связи одна из задач настоящей работы заключается в исследовании возможности управления, в том числе и хаотической динамикой, посредством гистерезисного блока.
На следующих графиках (рис. 3, 4) отражена динамика решения системы (1.1) и (1.8) и их фазовые портреты.
Рис. 3.
Решение систем (1.1), (1.8) при значениях $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $
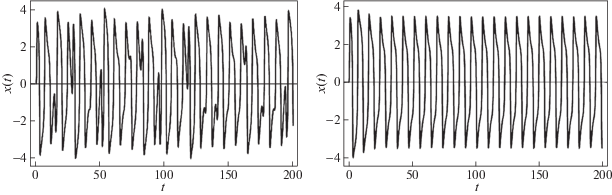
Рис. 4.
Фазовые портреты (1.1), (1.8) при значениях $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $
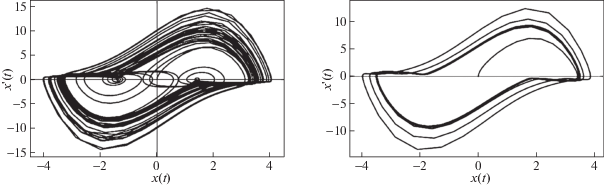
Как следует из результатов численного моделирования (уравнения решались в среде MatLab с использованием метода Рунги–Кутты четвертого порядка с шагом интегрирования 0.01), системы (1.1) и (1.8) имеют существенные отличия в динамике. Объяснить это можно тем, что включение гистерезисного звена приводит к диссипации энергии и, как следствие, к изменению динамических характеристик рассматриваемой системы. Как видно из рис. 3, б и 4, б, в системе (1.8) устанавливаются периодические колебания. Этот факт также подтверждают показатели Ляпунова: для уравнения (1.8) при значениях параметров $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $ они будут равны [0.00018, –0.935628, –11.1694].
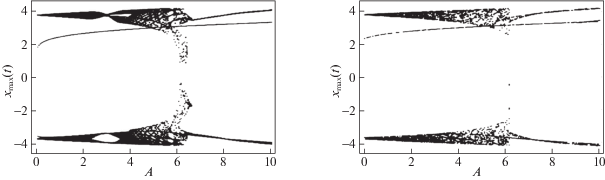
На рис. 5 представлены бифуркационные диаграммы для систем (1.1) и (1.8) в зависимости от амплитуды внешнего воздействия.
Рис. 5.
Бифуркационные диаграммы в зависимости от амплитуды внешнего воздействия для систем (1.1), (1.8) при значениях $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $
На рис. 6 приведены спектры решения систем (1.1) и (1.8).
Рис. 6.
Спектральные характеристики для систем (1.1) и (1.8) при значении параметров $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega = 0.7$, $\omega _{0}^{2} = \pi $
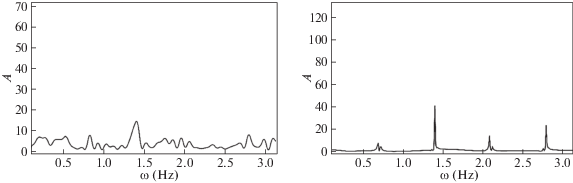
Спектр решения системы (1.1) является непрерывным, что, как известно, соответствует хаотическому поведению, в то время как спектр уравнения (1.8) демонстрирует четырехчастотное движение.
1.4. Синхронизация собственных колебаний осциллятора с частотой вынуждающей силы. Моделирование динамики системы (1.1) показало, что при значениях параметров $\mu = 3.4$, $\omega _{0}^{2} = \pi $ и существенном влиянии периодической внешней силы $\omega _{0}^{2}B = 2\pi $ в области значения параметра $\omega \in [0.8,1.8]$ происходит синхронизация собственных колебаний с частотой вынуждающей силы. Отметим, что синхронизация по амплитуде внешнего воздействия при этом не возникает. Добавление гистерезисного звена, формализованного моделью Боука–Вена при указанных параметрах сдвигает интервал синхронизации $\omega \in \left[ {0.7,{\text{ }}1.7} \right]$, что связано с регуляризирующей ролью гистерезисного звена.
На рис. 7–9 приведены графики решения уравнений (1.1) и (1.8) и соответствующие им графики поведения возмущающей силы, а также бифуркационные диаграммы в зависимости от параметра $\omega $.
Рис. 7.
Численное решение системы (1.1) и возмущающая сила при значении параметров $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega _{0}^{2} = \pi $, $\omega = 0.8$
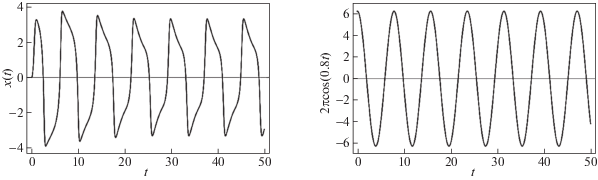
Рис. 8.
Численное решение системы (1.8) и возмущающая сила при значении параметров $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega _{0}^{2} = \pi $, $\omega = 0.7$

Рис. 9.
Бифуркационные диаграммы в зависимости частоты внешнего воздействия для систем (1.1) и (1.8) при значении параметров $\mu = 3.4$, $\omega _{0}^{2}B = 2\pi $, $\omega _{0}^{2} = \pi $
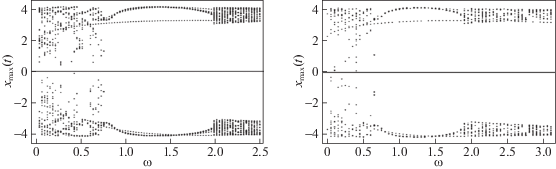
Отметим, что увеличение амплитуды внешнего воздействия в уравнении (1.8) приводит к увеличению полосы синхронизации. Так, значению B = 3 соответствует интервал $\omega \in \left[ {0.4,{\text{ }}2.1} \right]$, а значению $B = 4$ – $\omega \in \left[ {0.2,{\text{ }}2.4} \right]$.
2. Система связанных осцилляторов Ван-дер-Поля с гистерезисной внешней силой. 2.1. Математическая модель. Рассмотрим систему вида
(2.1)
$\left\{ {\begin{array}{*{20}{l}} {\ddot {x} - \mu (1 - \lambda {{x}^{2}})\dot {x} + \omega _{1}^{2}x = B\omega _{1}^{2}\cos ({{\omega }_{v}}t),} \\ {\ddot {y} - \mu (1 - \lambda {{y}^{2}})\dot {y} + \omega _{1}^{2}y = \nu x,} \end{array}} \right.$Исследуем взаимную синхронизацию осцилляторов x и y. Отметим, что в системе (2.1) осциллятор $x$ будет являться ведущим, а $y$ – ведомым.
Решение уравнений будем искать в виде $x = {{A}_{1}}\cos (\omega t + {{\varphi }_{1}})$, $y = {{A}_{2}}\cos (\omega t + {{\varphi }_{2}})$, где $\omega = ({{\omega }_{1}} + {{\omega }_{2}}){\text{/}}2$, а ${{A}_{1}}$, ${{A}_{2}}$и ${{\varphi }_{1}}$, ${{\varphi }_{2}}$ – медленно меняющиеся функции времени.
Для удобства применения метода малого параметра, представим систему (2.1) в виде
(2.2)
$\left\{ {\begin{array}{*{20}{l}} {\ddot {x} + \omega _{1}^{2}x = \mu (1 - \lambda {{x}^{2}})\dot {x} + B\omega _{1}^{2}\cos ({{\omega }_{v}}t),} \\ {\ddot {y} + \omega _{1}^{2}y = \mu (1 - \lambda {{y}^{2}})\dot {y} + \nu x.} \end{array}} \right.$Учитывая порядок малости, вычислим $\dot {x}$, $\ddot {x}$, $\dot {y}$ и $\ddot {y}$. Так как равенства будут одинаковые с точностью до коэффициентов, приведем только два соотношения:
(2.3)
$\dot {x} = {{\dot {A}}_{1}}\cos (\omega t + {{\varphi }_{1}}) - {{\dot {A}}_{1}}\sin (\omega t + {{\varphi }_{1}})(\omega + {{\dot {\varphi }}_{1}}),$(2.4)
$\ddot {x} = - 2{{\dot {A}}_{1}}\omega \sin (\omega t + {{\varphi }_{1}}) - {{\dot {A}}_{1}}\cos (\omega t + {{\varphi }_{1}})({{\omega }^{2}} + 2\omega {{\dot {\varphi }}_{1}}).$Используя соотношения (2.3) и (2.4), преобразуем отдельно левую и правую части уравнений системы (2.2) для осциллятора $x$:
(2.5)
$\ddot {x} + \omega _{1}^{2}x = - 2{{\dot {A}}_{1}}\omega \sin (\omega t + {{\varphi }_{1}}) - \cos (\omega t + {{\varphi }_{1}})({{\dot {A}}_{1}}({{\omega }^{2}} + 2\omega {{\dot {\varphi }}_{1}}) + \omega _{1}^{2}{{\dot {A}}_{1}}),$(2.6)
$\mu (1 - \lambda {{x}^{2}})\dot {x} + B\omega _{1}^{2}\cos ({{\omega }_{v}}t) = B\omega _{1}^{2}\cos ({{\omega }_{v}}t) - \sin (\omega t + {{\varphi }_{1}})\left( {\mu \omega {{A}_{1}} - \frac{{A_{1}^{3}\omega }}{4}} \right).$С учетом аналогичных преобразований для осциллятора $y$ запишем систему (2.2) в следующем виде:
(2.7)
$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} - 2{{{\dot {A}}}_{1}}\omega \sin (\omega t + {{\varphi }_{1}}) - \cos (\omega t + {{\varphi }_{1}})({{{\dot {A}}}_{1}}({{\omega }^{2}} + 2\omega {{{\dot {\varphi }}}_{1}}) + \omega _{1}^{2}{{A}_{1}}) = \hfill \\ \, = B\omega _{1}^{2}\cos ({{\omega }_{{v}}}t) - \sin (\omega t + {{\varphi }_{1}})\left( {\mu \omega {{A}_{1}} - \frac{{{{A}_{1}}^{3}\omega }}{4}} \right){\text{ }}, \hfill \\ \end{gathered} \\ \begin{gathered} - 2{{{\dot {A}}}_{2}}\omega \sin (\omega t + {{\varphi }_{2}}) - \cos (\omega t + {{\varphi }_{2}})({{{\dot {A}}}_{2}}({{\omega }^{2}} + 2\omega {{{\dot {\varphi }}}_{2}}) + \omega _{2}^{2}{{A}_{2}}) = \hfill \\ \, = \nu {{A}_{1}}\cos (\omega t + {{\varphi }_{1}}) - \sin (\omega t + {{\varphi }_{2}})\left( {\mu \omega {{A}_{2}} - \frac{{{{A}_{2}}^{3}\omega }}{4}} \right){\text{ }}. \hfill \\ \end{gathered} \end{array}} \right.$Соотношения для амплитуды и фазы первого осциллятора были получены ранее в разд. 1.1:
Выполним преобразования для осциллятора y в системе (2.7) и получим эквивалентную систему для определения ${{\dot {A}}_{2}}$ и ${{\dot {\varphi }}_{2}}$:
(2.8)
$\left\{ {\begin{array}{*{20}{l}} { - 2{{{\dot {A}}}_{2}}{\text{cos}}{{\varphi }_{2}} + {\text{sin}}{{\varphi }_{2}}({{A}_{2}}({{\omega }^{2}} + 2\omega {{{\dot {\varphi }}}_{2}}) + \omega _{2}^{2}{{A}_{2}}) = \nu {{A}_{{\text{1}}}}{\text{sin}}{{\varphi }_{1}} - {\text{cos}}{{\varphi }_{2}}\left( {\mu \omega {{A}_{2}} - \frac{{{{A}_{2}}^{3}\omega }}{4}} \right),} \\ { - 2{{{\dot {A}}}_{2}}\omega {\text{sin}}{{\varphi }_{2}} - {\text{cos}}{{\varphi }_{2}}({{A}_{2}}({{\omega }^{2}} + 2\omega {{{\dot {\varphi }}}_{2}}) + \omega _{2}^{2}{{A}_{2}}) = \nu {{A}_{1}}{\text{cos}}{{\varphi }_{1}} - {\text{sin}}{{\varphi }_{2}}\left( {\mu \omega {{A}_{2}} - \frac{{{{A}_{2}}^{3}\omega }}{4}} \right).} \end{array}} \right.$Запишем соотношения для амплитуды и фазы осциллятора $y$:
(2.9)
${{\dot {A}}_{2}} = {{A}_{2}}\left( {\frac{\mu }{2} - \frac{{A_{2}^{2}}}{8}} \right) - \frac{{\nu {{A}_{1}}}}{{2\omega }}\sin \Phi ,\quad {{\dot {\varphi }}_{2}} = - \frac{\Delta }{2} + \frac{{\nu {{A}_{1}}}}{{2\omega {{A}_{2}}}}\cos \Phi ,\quad \Phi = {{\varphi }_{1}} - {{\varphi }_{2}}.$В синхронном режиме, приравнивая (2.9) к нулю, получим следующее выражение:
(2.10)
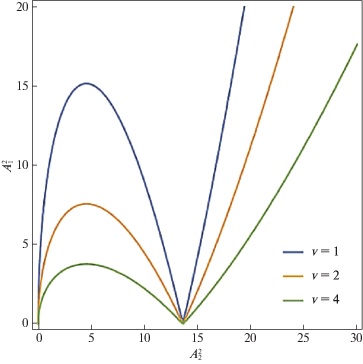
${{\left( {\frac{{{{A}_{2}}\omega \mu }}{{\nu {{A}_{1}}}}\left( {1 - \frac{{A_{2}^{2}}}{{4\mu }}} \right)} \right)}^{2}} + {{\left( {\frac{{{{A}_{2}}\omega \Delta }}{{\nu {{A}_{1}}}}} \right)}^{2}} = 1.$Для получения зависимости между квадратами амплитуд $A_{1}^{2}$ и $A_{2}^{2}$ при различных значениях параметра $\nu $ приведем уравнение (2.9) к виду
(2.11)
$A_{2}^{6}{{\omega }^{2}}{{\mu }^{2}} - 8A_{2}^{4}{{\omega }^{2}}{{\mu }^{3}} + A_{2}^{2}(16{{\omega }^{2}}{{\mu }^{4}} - {{\omega }^{2}}{{\Delta }^{2}}) = 16{{\mu }^{2}}{{\nu }^{2}}A_{1}^{2}.$На рис. 10 приведена зависимость $A_{1}^{2}$ от $A_{2}^{2}$ при различных значениях $\nu $.
2.2. Система связанных осцилляторов Ван-дер-Поля с гистерезисным блоком. Рассмотрим систему, аналогичную (2.1), с гистерезисным блоком в первом уравнении:
(2.12)
$\left\{ {\begin{array}{*{20}{l}} {\ddot {x} - \mu (1 - \lambda {{x}^{2}})\dot {x} + \omega _{1}^{2}x = B\omega _{1}^{2}\cos (\omega _{v}^{{}}t) + b{{\Phi }_{{BW}}}(x,t),} \\ {\ddot {y} - \mu (1 - \lambda {{y}^{2}})\dot {y} + \omega _{2}^{2}y = \nu x.} \end{array}} \right.$Уравнение для осциллятора $x$ было подробно исследовано в разд. 2.2. Таким образом, соотношения для определения амплитуды и фазы колебаний для осциллятора $x$ совпадают с уравнениями (1.16). Уравнение для осциллятора y осталось неизменным относительно системы (2.1), следовательно, амплитуда и фаза колебаний могут быть определены согласно уравнениям (2.9).
При рассмотрении систем (2.1) и (2.12) особое значение представляет динамика осциллятора $y$ в зависимости от параметра, определяющего влияние гистерезисного звена. На рис. 11 приведены бифуркационные диаграммы осциллятора $y$ в зависимости от параметра $\nu $ для систем (2.1) и (2.12).
2.3. Численное моделирование системы связанных осцилляторов Ван-дер-Поля. Приведем результаты численного моделирования решения систем (2.1) и (2.12). Динамика осцилляторов $x$ и $y$, а также их фазовые портреты отражены на рис. 12–15.
Рис. 12.
Решения системы (2.1) при значениях $\mu = 3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi $, $B = 2,$ $\omega = 0.7,$ $\nu = 2$
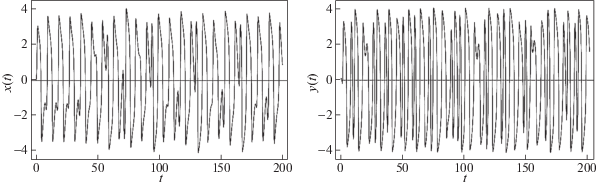
Рис. 13.
Динамика осцилляторов $x$ и $y$ системы (2.12) при значении параметров $\mu = 3.4,$ $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $B = 2,$ $\omega = 0.7,$ $b = 1.7,$ $\nu = 2$
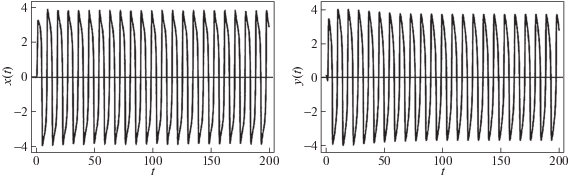
Рис. 14.
Фазовые портреты осцилляторов $x$ и $y$ системы (2.1) при значении параметров $\mu = 3.4,$ $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $B = 2,$ $\omega = 0.7,$ $\nu = 2$
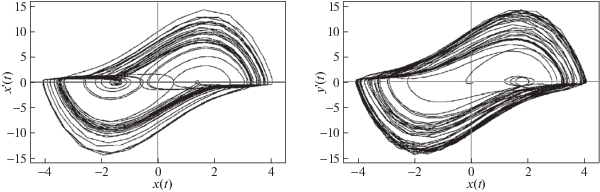
Рис. 15.
Фазовые портреты $x$ и $y$ системы (2.12) при значении параметров $\mu = 3.4,$ $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $B = 2,$ $\omega = 0.7,$ $b = 1.7,$ $\nu = 2$
Из анализа аналитических и численных результатов для систем (2.1) и (2.12) следует вывод о регуляризирующей роли гистерезисного блока в системе. Для иллюстрации этого факта приведем спектр показателей Ляпунова. Для системы (2.1) при значении параметров μ = 3.4, $\omega _{1}^{2} = \omega _{2}^{2}$ = π, $B = 2$, $\omega = 0.7$ и $\nu = 2$ были получены следующие значения: [0.110291857, –0.15691426, –2.417233756, –4.93154012], что соответствует хаотическому режиму а для системы (2.12) при тех же значениях параметров, а также при $b = 1.7$ был получен следующий спектр: [0.000193202, –0.18328, –0.935938, –5.54008, –11.1454], т.е. устойчивый цикл (старший показатель незначимо отличается от нуля).
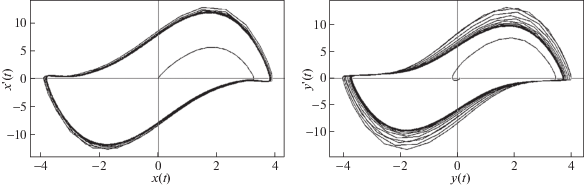
2.4. Синхронизация в системах связанных осцилляторов Ван-дер-Поля. Динамика систем (2.1) и (2.12), а также динамика вынуждающей силы отражены на графиках рис. 16, 17. При указанных значениях параметров наблюдается как взаимная синхронизация осцилляторов $x$ и $y$, так и вынужденная синхронизация по частоте с внешним воздействием. Отметим, что в отличие от случая, когда рассматривался единственный осциллятор (1.1) и (1.8), область значения параметра ${{\omega }_{v}}$ отличается. В частности, если говорить о взаимной синхронизации в системе (2.1), то значение параметра ${{\omega }_{v}} \in [0.8,{\text{ }}1.8]$, однако в случае вынужденной синхронизации значения ${{\omega }_{v}}$ принадлежит отрезку $[0.8,{\text{ }}1.1]$. В системе (2.12) взаимная синхронизация происходит при значении параметра ${{\omega }_{v}} \in [0.7,{\text{ }}1.7]$, а вынужденная синхронизация – при ${{\omega }_{v}} \in [0.7,{\text{ }}1]$. Существенное влияние на полосу синхронизации осцилляторов оказывает параметр линейной связи $\nu $. С увеличением параметра полоса синхронизации становится значительно уже при $\nu = 3.6$, взаимная синхронизация осцилляторов в системе (2.1) происходит при ${{\omega }_{v}} \in [0.7,{\text{ }}1.4]$, а вынужденная синхронизация – при ${{\omega }_{v}} \in [0.7,{\text{ }}0.9]$. Для системы (2.12) ${{\omega }_{v}} \in [0.8,{\text{ }}1.3]$ и ${{\omega }_{v}} \in [0.8,{\text{ }}1]$ соответственно.
Рис. 16.
Поведение осциллятора: а – $x$ в системе (2.1); б – $y$ в системе (2.1); в – возмущающая сила при значении параметров $\mu = 3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $\nu = 2.6$, $B = 2$, ${{\omega }_{{v}}} = 0.8$
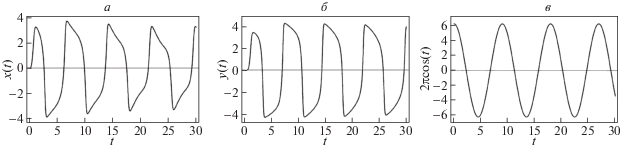
Рис. 17.
Поведение осциллятора: а – $x$ в системе (2.12); б –$y$ в системе (2.12); в – возмущающая сила при значении параметров $\mu = 3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $\nu = 2.6$, $B = 2$, $b = 1.7$, ${{\omega }_{{v}}} = 0.8$

На рис. 18, 19 приведены бифуркационные диаграммы поведения осцилляторов $x$ и $y$ в системах (2.1) и (2.12) в зависимости от параметра ${{\omega }_{v}}$.
Рис. 18.
Бифуркационные диаграммы в зависимости частоты внешнего воздействия для системы (2.1) для осциллятора $x$ (слева) и для осциллятора $y$ (справа) при значении параметров $\mu = 3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $\nu = 2.6$, $B = 2$
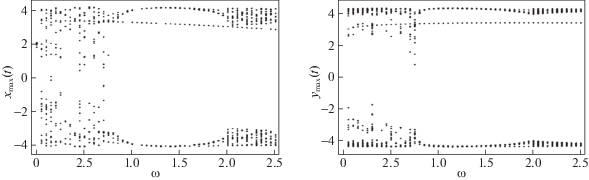
Рис. 19.
Бифуркационные диаграммы в зависимости частоты внешнего воздействия для системы (2.12) для осциллятора $x$ (слева) и для осциллятора $y$ (справа) при значении параметров $\mu = 3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi ,$ $\nu = 2.6$, $b = 1.7$, $B = 2$
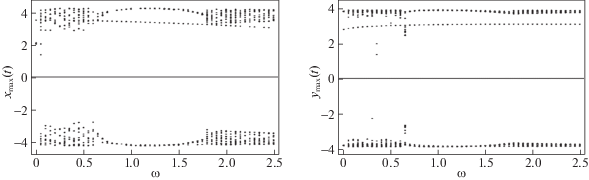
Поясним результаты, полученные выше. В системе (2.12) на вход гистерезисного блока подается сигнал, который представляет собой сумму, состоящую из собственных колебаний системы и отклика системы на внешнее периодическое воздействие. Синхронизация с внешним воздействием представляется затруднительной в силу того, что система обладает собственными сильными колебаниями, имеющими определенный период и “неправильную” форму. В том случае, когда спектральные характеристики собственных колебаний имеют ярко выраженную доминирующую частоту, происходит синхронизация (выход гистерезисного преобразователя имеет частоту).
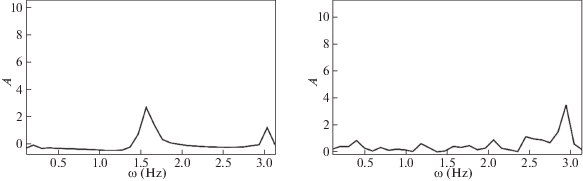
На рис. 20 представлен спектр выхода гистерезисного преобразователя в зависимости от различных значений параметров ${{\omega }_{{v}}}$.
Рис. 20.
Спектральная характеристика выхода гистерезисного преобразователя в уравнении (2.12) при значениях параметра, принадлежащих интервалу синхронизации осцилляторов $x$ и y, ${{\omega }_{{v}}}$ = 0.8 (слева), и при значениях параметра, не принадлежащих интервалу синхронизации ${{\omega }_{{v}}}$ = 1.9 (справа)
2.5. Система перекрестно-связанных осцилляторов Ван-дер-Поля с гистерезисным блоком. Рассматривается система перекрестно-связанных осцилляторов Ван-дер-Поля с несимметричной связью, в которой вынуждающая сила, действующая на первый из них, определяется выходом гистерезисного преобразователя, на вход которого подается рассогласование между скоростями осцилляторов:
(2.13)
$\left\{ {\begin{array}{*{20}{l}} {\ddot {x} - \mu (1 - \lambda {{x}^{2}})\dot {x} + \omega _{1}^{2}x = B\omega _{1}^{2}\cos (\omega _{v}^{{}}t) + b{{\Phi }_{{BW}}}(\dot {y} - \dot {x}),} \\ {\ddot {y} - \mu (1 - \lambda {{y}^{2}})\dot {y} + \omega _{2}^{2}y = \nu x.} \end{array}} \right.$Численное решение системы (2.13) показало, что для осцилляторов $x$ и $y$ характерны различные режимы поведения. Приведем бифуркационные диаграммы в зависимости от различных параметров системы (рис. 21).
Рис. 21.
Бифуркационные диаграммы поведения осциллятора $y$: a – в зависимости от коэффициента перед гистерезисным блоком $b$; б – в зависимости от амплитуды внешнего воздействия $B\omega _{1}^{2}$; в – в зависимости от параметра $\nu $ при $\mu = 1$, $\lambda = 1$, $\omega _{1}^{2} = \omega _{2}^{2} = 1$
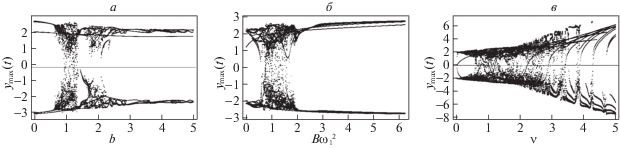
Рис. 22.
Динамика поведения: а – осциллятора $x$; б – осциллятора $y$ при значениях параметров μ = 1, $\lambda = 1$, $\omega _{1}^{2} = \omega _{2}^{2} = 1$, $B\omega _{1}^{2} = 1.2$, ${{\omega }_{{v}}} = 1$, $b = 1.3$, $\nu = 1$
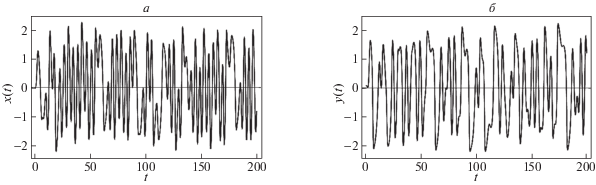
Рис. 23.
Фазовый портрет: а – осциллятора $x$; б – осциллятора $y$ при значениях параметров μ = 1, $\lambda = 1$, $\omega _{1}^{2} = \omega _{2}^{2} = 1$, $B\omega _{1}^{2} = 1.2$, ${{\omega }_{{v}}} = 1$, $b = 1.3$, $\nu = 1$
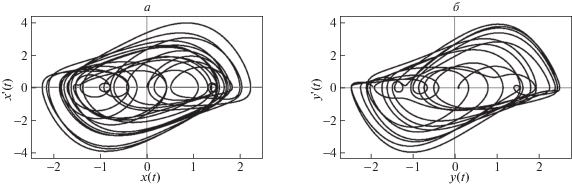
Также были вычислены показатели Ляпунова, при этом параметрам системы μ = 1, λ = 1, $\omega _{1}^{2} = \omega _{2}^{2}$ = 1, $B\omega _{1}^{2} = 1.2$, ${{\omega }_{v}} = 1$, ν = 1 соответствуют значения [0.11806, –0.0392802, –0.317961, –0.621109, –2.03704]. Поведение осцилляторов $x$ и $y$ при соответствующих параметрах отражено на графиках рис. 22, 23.
В отличие от рассмотренного выше случая (2.1) и (2.12) с линейной связью между осцилляторами $x$ и $y$ синхронизация в системе (2.13) затруднительна, так как вынуждающая сила, действующая на первый осциллятор, определяется выходом гистерезисного преобразователя, вход которого в свою очередь зависит от рассогласования между скоростями осцилляторов. Однако были определены параметры системы, при которых возможна как внешняя, так и внутренняя синхронизация. Отметим, что внешняя синхронизация системы происходит только по частоте, тогда как при внутренней синхронизации частота и амплитуда совпадают. Параметры системы (2.13) $\mu = 3.4$, $\lambda = 1{\text{/}}3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi $, $B\omega _{1}^{2} = 2\pi $, $b = 1.7$, $\nu = 2.6$ при значении частоты внешнего гармонического воздействия ${{\omega }_{{v}}} = 1$ соответствуют интервалу внешней и внутренней синхронизаций осцилляторов $x$ и $y$. На рис. 24 приведены графики, иллюстрирующие соответствующую динамику.
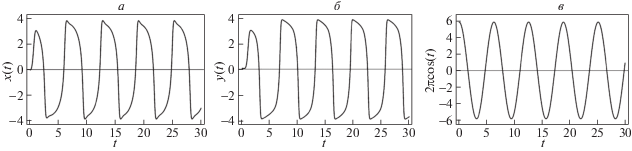
Рис. 24.
Поведение осциллятора: а – $x$ в системе (2.13); б – $y$ в системе (2.13); в – возмущающая сила при значении параметров $\mu = 3.4$, $\lambda = 1{\text{/}}3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi $, $B\omega _{1}^{2} = 2\pi $, $b = 1.7$, $\nu = 2.6$, ${{\omega }_{{v}}} = 1$
Исследование интервалов внешней синхронизации показало, что с увеличением параметра $\nu $ полоса синхронизации увеличивается. Так, параметрам $\mu = 3.4$, $\lambda = 1{\text{/}}3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi $, $B\omega _{1}^{2} = 2\pi $, $b = 1.7$, $\nu = 2.6$ соответствуют значения, принадлежащие интервалу ${{\omega }_{v}} \in [0.6,{\text{ }}1.9]$, а в случае $\nu = 3.6$ синхронизация возможна при ${{\omega }_{{v}}} \in [0.4,{\text{ }}2.2]$. Также удалось установить, что с увеличением влияния гистерезисного звена, т.е. с увеличением параметра $b$, полоса внешней синхронизации будет уменьшаться, а именно параметрам $\mu = 3.4$, $\lambda = 1{\text{/}}3.4$, $\omega _{1}^{2} = \omega _{2}^{2} = \pi $, $B\omega _{1}^{2} = 2\pi $, $\nu = 2.6$, b = 3 соответствует интервал ${{\omega }_{{v}}} \in [0.6,{\text{ }}1.7]$. Аналогичные результаты справедливы и для внутренней синхронизации: с увеличением параметра $\nu $ интервал увеличивается, а с увеличением параметра $b$ интервал уменьшается.
Заключение. В работе рассмотрены различные динамические режимы осциллятора Ван-дер-Поля в условиях периодического воздействия при наличии гистерезисного блока в контуре обратной связи. С использованием техники асимптотических разложений (метода малого параметра) было получено аналитическое решение для уравнения осциллятора Ван-дер-Поля, находящегося под воздействием вынуждающей силы и гистерезисного воздействия, формализуемого посредством феноменологической модели Боука–Вена. Также была установлена регуляризирующая роль гистерезисного звена в части редукции хаотических режимов. Идентифицирован диапазон значений параметров, соответствующих хаотическим и регулярным режимам движения, а также определены параметры, отвечающие синхронизации собственных колебаний осциллятора с внешней вынуждающей силой.
При рассмотрении системы двух связанных осцилляторов Ван-дер-Поля в условиях воздействия вынуждающей силы на один из них в аналитической форме получена зависимость между амплитудами и частотами собственных колебаний осцилляторов. Также было установлено, что гистерезисный блок существенным образом влияет как на внешнюю, так и на внутреннюю синхронизацию. Другими словами интервал внутренней синхронизации заметно увеличивается, при этом синхронизация с внешним воздействием оказывается затруднительна.
Исследована динамика системы перекрестно-связанных осцилляторов Ван-дер-Поля с несимметричной связью, в которой вынуждающая сила определяется выходом гистерезисного преобразователя, на вход которого подается рассогласование между скоростями осцилляторов. Рассмотрены различные режимы динамики системы, а также синхронизация осцилляторов. Получены количественные оценки влияния на синхронизацию параметра связи между осцилляторами, а также параметра, определяющего влияние гистерезисного звена.
Представленные в статье результаты ориентированы в первую очередь на расширение классов систем, динамика которых моделируется осцилляторами (системами связанных осцилляторов) Ван-дер-Поля. Как было отмечено выше, список реальных технических систем, а также биологических, экономических систем, систем различных органов в организме человека и животных, поведение которых моделируется посредством систем связанных осцилляторов Ван-дер-Поля, достаточно широк. При этом гистерезисные особенности естественным образом проявляются в динамике механических (роботизированных) систем вследствие старения и износа их составляющих (действительно, люфты и упоры – преобразователи гистерезисной природы могут быть конструктивно инсталлированы в соответствующие системы или проявиться в них с течением времени). В связи с этим возможность учитывать на модельном уровне гистерезисные свойства роботизированных систем расширяет возможности идентификации их разнообразных динамических режимов, что в конечном итоге повышает адекватность соответствующих математических моделей. Применительно к задачам экономики, биологии, медицины, в которых исследуются модели автоколебательных систем, включение в указанные модели гистерезисных блоков позволит учесть такую важную их особенность, как локальная память. Действительно, для многих систем из указанных предметных областей типична ситуация, когда будущее зависит не только от текущего состояния и формализованных связей, но и от предыстории. Это свойство внутренне присуще гистерезисным преобразователям. Кроме того гистерезисные блоки, как было показано в работе, обладают фильтрующими свойствами, что позволяет рассматривать их как один из инструментов управления динамическими системами.
Список литературы
Veskos P., Demiris Y. Developmental Acquisition of Entrainment Skills in Robot Swinging Using van der Pol Oscillators // Proc. Fifth International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems Lund University Cognitive Studies. Nara, Japan. 2005. P. 87.
Yabuno H., Kaneko H., Kuroda M., Kobayashi T. Van der Pol Type Self-excited Micro-cantilever Probe of Atomic Force Microscopy // Nonlinear Dyn. 2008. № 54. P. 137.
Dutra M.S., de Pina Filho A.C., Romano V.F. Modeling of a Bipedal Locomotor Using Coupled Nonlinear Oscillators of Van der Pol // Biol. Cybern. 2003. V. 88. P. 286.
Klinger T., Piel A., Seddighi F., Wilke C. Van der Pol Dynamics of Ionization Waves // Physics Letters A. 1993. V. 182. № 2, 3. P. 312.
Van der Pol B., Van der Mark J. The Heartbeat Considered as a Relaxation Oscillation, and an Electrical Model of the Heart // Philosophical Magazine & Journal of Science. 1928. V. 6. № 38. P. 763.
Ryzhii E., Ryzhii M. Modeling of Heartbeat Dynamics with a System of Coupled Nonlinear Oscillators // Communications in Computer and Information Science. 2014. V. 404. P. 67–75.
Dos Santos Angela M., Lopes Sergio R., Viana R.L.Ricardo L. Rhythm Synchronization and Chaotic Modulation of Coupled Van der Pol Oscillators in a Model for the Heartbeat // Physica A: Statistical Mechanics and its Applications, Elsevier. 2004. V. 338 (3). P. 335–355.
Булдаков Н.С., Самочетова Н.С., Ситников А.В., Суятинов С.И. Моделирование связей в системе “сердце-сосуды” // Наука и образование. Электронный научно-технический журнал. 2013. № 1. С. 123.
Lucero J., Schoentgen J. Modeling Vocal Fold Asymmetries with Coupled van der Pol Oscillators // Proceedings of Meetings on Acoustics. 2013. V. 19 (1). P. 060165.
Long G.R., Tubis A., Jones K.L. Modeling Synchronization and Suppression of Spontaneous Otoacoustic Emissions Using Van der Pol oscillators: Effects of Aspirin Administration // J. Acoust. Soc. Am. 1991. V. 89. № 3. P. 1201.
Dutra M.S., de Pina Filho A.C., Romano V.F. Modeling of a Bipedal Locomotor Using Coupled Nonlinear Oscillators of Van der Pol // Biol. Cybern. 2003. V. 88. P. 286.
Kumar P., Kumar A., Racic V., Erlicher S. Modelling Vertical Human Walking Forces Using Self-sustained Oscillator // Mechanical Systems and Signal Processing. 2018. V. 99. P. 345–363.
Belykh I., Jeter R., Belykh V. Foot Force Models of Crowd Dynamics on a Wobbly Bridge // Science Advances. 2017. V. 3. № 11. P. e1701512.
Соловьёв А.М., Кабулова Е.Г., Семёнов М.Е. Модель динамики биологической нейронной сети с гистерезисными связями // Вестн. Воронежск. гос. ун-та. Сер. Системный анализ и информационные технологии. 2018. № 1. С. 133–141.
Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. Под ред. Н.А. Железцова. 2-е изд. М.: Наука, 1981. 914 с.
Ланда П.С. Автоколебания в системах с конечным числом степеней свободы. М.: Наука, 1980. 360 с.
Кузнецов С.П. Динамический хаос и однородно гиперболические аттракторы: от математики к физике // УФН. 2011. Т. 181. № 2. С. 121–149.
Ананьевский И.М., Ишханян Т.А. Управление твердым телом, несущим диссипативные осцилляторы, в присутствии возмущений // Изв. РАН. ТиСУ. 2019. № 1. С. 42–51.
Глебов С.Г., Зотов А.Н. Управление системой с двумя степенями свободы посредством потенциальных сил // Изв. РАН. ТиСУ. 2020. № 1. С. 161–167.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Pyragas K. Continuous Control of Chaosby Self-Controlling Feedback // Phys. Lett. 1992. V. 170. P. 421–427.
Магницкий Н.А. О стабилизации неподвижных точек хаотических отображений // Докл. РАН. 1996. Т. 351. № 2. С. 175–177.
Semenov M.E., Reshetova O.O., Solovyov A.M., Meleshenko P.A., Sobolev V.A., Bogaychuk A.N. The van der Pol Oscillator Under Hysteretic Control: Regular and Chaotic Dynamics // J. Physics: Conference Series. 2019. V. 1368. P. 042030.
Arena A., Carboni B., Lacarbonara W. Nonlinear Dynamic Response of Hysteretic Wire Ropes: Modeling and Experiments // ASME 2018 Intern. Design Engineering Technical Conf. and Computers and Information in Engineering Conf. Quebec City, Canada, 2018. P. V008T10A050.
Antonelli M., Carboni B., Lacarbonara W., Bernardini D., Kalmar-Nagy T. Quantifying Rate-Dependence of a Nonlinear Hysteretic Device // Nonlinear Dynamics of Structures, Systems and Devices. 2020. V. 1. P. 347–355.
Carboni B., Lacarbonara W., Brewick P., Masri S. Dynamical Response Identification of a Class of Nonlinear Hysteretic Systems // J. Intelligent Material Systems and Structures. 2018. V. 29. P. 2795–2810.
Yudaev S., Rachinskii D., Sobolev V. Asymptotic Solution for a Biped Walker Model: Slow-Fast Systems and Hysteresis: Theory and Applications // Extended Abstracts Summer. 2018. V. 10. P. 95–99.
Fahsi A., Belhaq M. Hysteresis Suppression and Synchronization Near 3:1 Subharmonic Resonance // Chaos, Solitons & Fractals. 2009. V. 42. P. 1031–1036.
Rios L., Rachinskii D., Cross R. A Model of Hysteresis Arising From Social Interaction Within a Firm // J. Physics: Conference Series. 2017. V. 811. P. 012011.
Rios L., Rachinskii D., Cross R. On the Rationale for Hysteresis in Economic Decisions // J. Physics: Conference Series. 2017. V. 811. P. 012012.
Semenov M.E., Solovyov A.M., Meleshenko P.A., Balthazar J.M. Nonlinear Damping: From Viscous to Hysteretic Dampers // Recent Trends in Applied Nonlinear Mechanics and Physics. Springer Proceedings in Physics, Cham: Springer, 2018. V. 199. P. 259–275.
Semenov M.E., Solovyov A.M., Meleshenko P.A. Stabilization of Coupled Inverted Pendula: From Discrete to Continuous Case // J. Vibration and Control. 2020. April. https://doi.org/10.1177/1077546320923436
Семенов М.Е., Матвеев М.Г., Лебедев Г.Н., Соловьёв А.М. Стабилизация обратного гибкого маятника с гистерезисными свойствами // Мехатроника, автоматизация, управление. 2017. № 8. С. 516–525.
Семенов М.Е., Матвеев М.Г., Мелешенко П.А., Соловьев А.М. Динамика демпфирующего устройства на основе материала Ишлинского// Мехатроника, автоматизация, управление. 2019. № 20. С. 106–113.
Semenov M.E., Solovyov A.M., Meleshenko P.A., Reshetova O.O. Efficiency of Hysteretic Damper in Oscillating Systems // Mathematical Modelling of Natural Phenomena. 2020. V. 15. P. 43.
Semenov M.E., Reshetova O.O., Tolkachev A.V., Solovyov A.M., Meleshenko P.A. Oscillations Under Hysteretic Conditions: From Simple Oscillator to Discrete Sine-Gordon Model // Topics in Nonlinear Mechanics and Physics. V. 228. Singapore: Springer, 2019. P. 229–253.
Красносельский М.А., Покровский А.В. Системы с гистерезисом. М.: Наука, 1983. 272 с.
Ikhouane F., Rodellar J. On the Hysteretic Bouc–Wen Model // Nonlinear Dyn. 2005. V. 42. P. 63–78.
Ikhouane F., Rodellar J. Systems with Hysteresis: Analysis, Identification and Control Using the Bouc-Wen Model. N.Y.: John Wiley & Sons, 2007.
Charalampakis A.E., Koumousis V.K. Identification of Bouc–Wen Hysteretic Systems by a Hybrid Evolutionary Algorithm // J. Sound and Vibration. 2008. V. 314. P. 571–585.
Charalampakis A.E., Koumousis V.K. A Bouc–Wen Model Compatible With Plasticity Postulates // J. Sound and Vibration. 2009. V. 322. P. 954–968.
Семенов М.Е., Мелешенко П.А., Решетова О.О. Неограниченные и диссипативные колебания в системах с релейными нелинейностями // Вестн. Воронежск. гос. ун-та. Сер. Физика. Математика. 2018. № 3. С. 158–171.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления