Известия РАН. Теория и системы управления, 2021, № 4, стр. 27-45
СВОЙСТВО СТАБИЛЬНОСТИ В ИГРОВОЙ ЗАДАЧЕ О СБЛИЖЕНИИ ПРИ НАЛИЧИИ ФАЗОВЫХ ОГРАНИЧЕНИЙ
А. А. Зимовец a, *, А. Р. Матвийчук a, **, А. В. Ушаков a, ***, В. Н. Ушаков a, ****
a Институт математики и механики им. Н.Н. Красовского УрО РАН
Екатеринбург, Россия
* E-mail: aazimovets@gmail.com
** E-mail: matv@uran.ru
*** E-mail: aushakov.pk@gmail.com
**** E-mail: ushak@imm.uran.ru
Поступила в редакцию 18.11.2019
После доработки 29.11.2020
Принята к публикации 29.03.2021
Аннотация
Рассматривается нелинейная конфликтно управляемая система на конечном промежутке времени и в конечномерном пространстве, стесненная нестационарными фазовыми ограничениями. Изучается игровая задача о сближении в фиксированный момент времени с компактом в фазовом пространстве системы. Исследуется центральное в теории позиционных дифференциальных игр свойство стабильности. Приведены некоторые модификации определения u-стабильного моста и аппроксимирующей этот мост системы множеств. Эти модификации ориентированы на разработку алгоритмов приближенного вычисления решений в конкретных игровых задачах о сближении при наличии фазовых ограничений на систему. Описаны две конкретные задачи о сближении, для которых проведено математическое моделирование и представлены результаты моделирования.
Введение. Рассматривается нелинейная конфликтно управляемая система на конечном промежутке времени. Фазовый вектор системы принадлежит конечномерному евклидову пространству и стеснен нестационарным фазовым ограничением. Изучается игровая задача о сближении системы с компактным целевым множеством в фиксированный момент времени в рамках теории позиционных дифференциальных игр [1–4]. Исследуется центральное в этой теории свойство стабильности, введенное в дифференциальные игры Н.Н. Красовским [1, 2]. Предлагается схема приближенного конструирования максимального u-стабильного моста – множества разрешимости в задаче о сближении.
Отметим, что задача о сближении в игровой постановке является одной из центральных и наиболее важных задач теории управления динамическими системами, функционирующими в условиях неопределенности [1–9]. Она актуальна во многих приложениях. Многие задачи управления из механики, экономики и физики могут быть формализованы и решаться как игровые задачи управления нелинейными динамическими системами на конечном промежутке времени [9–13].
В работе рассматриваются две конкретные задачи управления нелинейными динамическими системами – задача об управлении механической системой “маятник на тележке” и задача об управлении четырехколесным автомобилем (машиной Дубинса) при наличии подвижных фазовых ограничений. В этих задачах моделируется численно построение множеств разрешимости, разрешающих управлений и траекторий на конечном промежутке времени, приводится графическое сопровождение результатов численного моделирования.
По своей тематике работа близка к [1–16].
1. Постановка задачи. Пусть задана конфликтно управляемая система, поведение которой на промежутке времени $[{{t}_{0}},\vartheta ]$, ${{t}_{0}} \leqslant \vartheta < \infty $ описывается дифференциальным уравнением
Здесь x – m-мерный фазовый вектор из евклидова пространства ${{\mathbb{R}}^{m}}$, u – управление первого игрока, ${v}$ – управление второго игрока, $P \in {\text{comp(}}{{\mathbb{R}}^{p}})$, $Q \in {\text{comp(}}{{\mathbb{R}}^{q}})$, где ${\text{comp(}}{{\mathbb{R}}^{k}})$ – метрическое пространство компактов в ${{\mathbb{R}}^{k}}$ с хаусдорфовой метрикой.
Предполагается, что выполнены следующие условия на функцию $f(t,x,u,v) = {{f}^{{(1)}}}(t,x,u)$ + + ${{f}^{{(2)}}}(t,x,v)$.
Условие A. Вектор-функции ${{f}^{{(1)}}}(t,x,u)$ и ${{f}^{{(2)}}}(t,x,v)$ определены и непрерывны на $[{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}} \times P$ и $[{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}} \times Q$ соответственно, и для любого компакта ${\mathbf{D}} \subset [{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}}$ найдется такая постоянная ${\mathbf{L}} = {\mathbf{L}}({\mathbf{D}}) \in (0,\infty )$, что
(1.2)
$\begin{gathered} \left\| {{{f}^{{(1)}}}(t,{{x}^{{(1)}}},u) - {{f}^{{(1)}}}(t,{{x}^{{(2)}}},u)} \right\| \leqslant {\mathbf{L}}\left\| {{{x}^{{(1)}}} - {{x}^{{(2)}}}} \right\|, \\ \left\| {{{f}^{{(2)}}}(t,{{x}^{{(1)}}},{v}) - {{f}^{{(2)}}}(t,{{x}^{{(2)}}},{v})} \right\| \leqslant {\mathbf{L}}\left\| {{{x}^{{(1)}}} - {{x}^{{(2)}}}} \right\| \\ \end{gathered} $Условие B. Существует такая постоянная $\mu \in (0,\infty )$, что
Считаем, что, наряду с системой (1.1), заданы целевое множество $M \in {\text{comp(}}{{\mathbb{R}}^{m}})$ и множество $\Phi $ – ограниченная замкнутая область в $[{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}}$, удовлетворяющая следующим условиям:
а) $\Phi (t) = \{ x \in {{\mathbb{R}}^{m}}:(t,x) \in \Phi \} \ne \emptyset $, $t \in [{{t}_{0}},\vartheta ]$;
б) многозначное отображение $t \mapsto \Phi (t)$ непрерывно на $[{{t}_{0}},\vartheta ]$ в хаусдорфовой метрике;
в) $M \subset \Phi (\vartheta )$.
Рассматриваемая здесь игровая задача заключается в следующем.
Задача о сближении. Первому игроку требуется выбором управления $u = u(t)$ обеспечить приведение движения $x(t)$ системы (1.1) в момент $\vartheta $ на множество M, как бы ни действовал второй игрок в рамках допустимых позиционных управлений $v = v(t,x)$. При этом до момента $\vartheta $ управление первого игрока $u = u(t)$ должно обеспечивать включение
Решение задачи о сближении требуется обеспечить в классе позиционных стратегий $u(t,x)$ первого игрока или в классе позиционных процедур управления этого игрока.
В [2] показано, что для сформулированной игровой задачи о сближении справедливо следующее утверждение: существует такое замкнутое множество ${{W}^{0}} \subset \Phi $, называемое множеством позиционного поглощения, что для всех исходных позиций $({{t}_{*}},{{x}_{*}}) \in {{W}^{0}}$ разрешима задача о сближении и для всех исходных позиций $({{t}_{*}},{{x}_{*}}) \in \Phi {{\backslash }}{{W}^{0}}$ задача о сближении не разрешима.
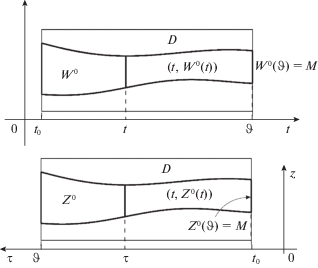
Установлено, что множество W 0 есть максимальный (по включению) $u$-стабильный мост. Свойство стабильности было введено в дифференциальные игры в работах [1, 2]. Это свойство можно облечь в различные формулировки; самая ранняя его формулировка дана в этих публикациях.
Множество W 0, которое для простоты будем называть множеством разрешимости задачи о сближении, допускает аналитическое описание в немногих случаях, поэтому важен вопрос о приближенном построении W 0. Вопросу о приближенном конструировании W 0 посвящены работы [14–16]. При приближенном конструировании W 0 используется не непосредственно свойство $u$-стабильности, а некоторые его модификации.
2. Свойство $u$-стабильности, $u$-стабильные мосты и $u$-стабильные тракты в задаче о сближении. Свойство $u$-стабильности – ключевое при выделении множества W 0 в фазовом ограничении $\Phi $. Для какого-либо замкнутого множества W в $\Phi $ его $u$-стабильность означает слабую инвариантность W относительно некоторого набора дифференциальных включений, индуцированных системой (1.1) на промежутке $[{{t}_{0}},\vartheta ]$. Как известно, свойство слабой инвариантности множеств относительно дифференциальных включений хорошо изучено, например [3].
Упомянутый набор дифференциальных включений (д.в.) зададим ниже.
Для этого введем некоторую ограниченную замкнутую цилиндрическую область D = $[{{t}_{0}},\vartheta ]$ × Ω, $\Omega \in {{\mathbb{R}}^{m}}$, настолько большую, что в ней будут заведомо содержаться все элементы разрешающей задачу о сближении конструкции. В том числе в этой области содержатся множество M* = = $(\vartheta ,M) = \left\{ {(\vartheta ,x):x \in M} \right\}$, фазовое ограничение $\Phi $ и множество разрешимости W 0 задачи о сближении – максимальный $u$-стабильный мост.
Итак, считаем, что все элементы разрешающей конструкции содержатся в ${\mathbf{D}} \subset [{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}}$.
Для любых $(t,x,v) \in {\mathbf{D}} \times Q$ определим множество
Замечание. Существует такая положительная функция $\omega {\kern 1pt} *(\delta ),$ $\delta \in (0,\infty )$ ($\omega {\kern 1pt} *(\delta ) \downarrow 0$ при $\delta \downarrow 0$), что
Здесь ${\mathbf{L}}$ – постоянная Липшица из условия A, отвечающая области ${\mathbf{D}}$; $d({{F}_{*}},F{\kern 1pt} *)$ – хаусдорфово расстояние между ${{F}_{*}}$ и $F{\kern 1pt} *$ из ${\text{comp(}}{{\mathbb{R}}^{m}})$.
Введем в рассмотрение д.в.
Дадим определение оператора $u$-стабильного поглощения в задаче о сближении, выраженное на языке многозначных отображений $(t,x) \to {{F}_{{v}}}(t,x),$ ${v} \in Q$ и д.в. (2.1) (см., например, [14]).
Предварительно введем обозначения: ${{X}_{{v}}}(t{\kern 1pt} *,{{t}_{*}},{{x}_{*}})$ – множество достижимости д.в. (2.1) в момент $t{\kern 1pt} *$ $({{t}_{0}} \leqslant {{t}_{*}} < t{\kern 1pt} * \leqslant \vartheta )$ с начальным условием $x({{t}_{*}}) = {{x}_{*}}$;
Здесь ${{X}_{*}}$ и $X{\kern 1pt} *$ – множества из ${{\mathbb{R}}^{m}}$.
Определение 1 (см. [14]). Оператором u-стабильного поглощения π в задаче о сближении (разд. 1) назовем многозначное отображение $({{t}_{*}},t{\kern 1pt} *,X{\kern 1pt} *) \to \pi ({{t}_{*}},t{\kern 1pt} *,X{\kern 1pt} *) \subset {{\mathbb{R}}^{m}}$, $({{t}_{*}},t{\kern 1pt} *,X{\kern 1pt} *) \in \Delta {\kern 1pt} * \times {{2}^{{{{\mathbb{R}}^{m}}}}},$ заданное соотношением
Определение 2 (см. [14]). Замкнутое множество $W \subset \Phi $ назовем $u$-стабильным мостом в задаче о сближении, если
Введем время $\tau = {{t}_{0}} + \vartheta - t,$ $t \in [{{t}_{0}},\vartheta ],$ которое назовем обратным временем.
Представим конфликтно управляемую систему (1.1) в терминах обратного времени в виде
(2.2)
$\frac{{dz}}{{d\tau }} = h(\tau ,z,u,v) = - f({{t}_{0}} + \vartheta - \tau ,z,u,{v}),\quad \tau \in [{{t}_{0}},\vartheta ],\quad z \in {{\mathbb{R}}^{m}}.$Вектор-функцию $h(\tau ,z,u,{v})$ запишем как
гдеНаряду с системой (2.2) рассмотрим д.в.
(2.3)
$\frac{{dz}}{{d\tau }} \in {{H}_{{v}}}(\tau ,z) = - {{F}_{{v}}}({{t}_{0}} + \vartheta - \tau ,z),\quad \tau \in [{{t}_{0}},\vartheta ],\quad z \in {{\mathbb{R}}^{m}},\quad {v} \in Q.$Введем обозначения при ${{t}_{0}} \leqslant {{\tau }_{*}} < \tau {\kern 1pt} * \leqslant \vartheta {\text{:}}$
${{Z}_{{v}}}(\tau {\kern 1pt} *,{{\tau }_{*}},z{{{\kern 1pt} }_{*}})$ – множество достижимости в момент $\tau {\kern 1pt} *$ д.в. (2.3) c начальным условием $z({{\tau }_{*}})\, = \,z{{{\kern 1pt} }_{*}};$
Введем также отображение $(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}}) \to Z(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}})$ на множестве {(τ*, ${{\tau }_{*}},{{Z}_{*}})$ : ${{t}_{0}} \leqslant {{\tau }_{*}} < \tau {\kern 1pt} * \leqslant \vartheta $, ${{Z}_{*}} \subset {{\mathbb{R}}^{m}}\} .$ Задав между тройками $({{t}_{*}},t{\kern 1pt} *,X{\kern 1pt} *)$ и $(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}})$ соответствие с помощью равенств
Определение 3. Оператором $u$-стабильного поглощения $\chi $ в задаче о сближении назовем многозначное отображение $(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}}) \to \chi (\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}})$, $({{t}_{0}} \leqslant {{\tau }_{*}} < \tau {\kern 1pt} * \leqslant \vartheta $, ${{Z}_{*}} \subset {{\mathbb{R}}^{m}})$, заданное соотношением
Определение 4. Замкнутое множество $Z \subset \Phi $ назовем $u$-стабильным трактом в задаче о сближении, если
(2.4)
$Z({{t}_{0}}) \subset M,\quad Z(\tau {\kern 1pt} *) \subset \chi (\tau {\kern 1pt} *,{{\tau }_{*}},Z({{\tau }_{*}})),\quad {{t}_{0}} \leqslant {{\tau }_{*}} < \tau {\kern 1pt} * \leqslant \vartheta .$Определение 5. Множество ${{Z}^{0}} \subset {\mathbf{D}}$, где ${{Z}^{0}}(\tau ) = {{W}^{0}}(t),$ $t + \tau = {{t}_{0}} + \vartheta ,$ $\tau \in [{{t}_{0}},\vartheta ],$ назовем максимальным $u$-стабильным трактом системы (2.2).
В самом деле, Z 0 есть максимальный по включению $u$-стабильный тракт системы (2.2).
Множества W 0 и Z 0 изображены на рис. 1.
3. Аппроксимирующая система $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ в ${{\mathbb{R}}^{m}}$. Пользуясь конструкциями обратного времени $\tau $, сведем приближенное вычисление максимального $u$-стабильного моста W 0 к приближенному вычислению максимального $u$-стабильного тракта Z 0 системы (2.2).
В связи с этим введем в этом разделе аппроксимирующую систему $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ множеств ${{\tilde {Z}}^{\Gamma }}({{\tau }_{i}})$ в пространстве ${{\mathbb{R}}^{m}}$. Аппроксимирующая система $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ есть то понятие, которое составляет теоретическую основу для разработки алгоритма приближенного вычисления множества Z0 в задаче о сближении. Это понятие возникает при подмене непрерывной (по времени) схемы, отвечающей промежутку $[{{t}_{0}},\vartheta ]$, дискретной схемой, отвечающей конечному разбиению $\Gamma $ промежутка $[{{t}_{0}},\vartheta ]$. А именно, вместо промежутка $[{{t}_{0}},\vartheta ]$ рассматривается двоичное разбиение $\Gamma = \{ {{\tau }_{0}} = {{t}_{0}},{{\tau }_{1}},{{\tau }_{2}},...,{{\tau }_{i}},...,{{\tau }_{N}} = \vartheta \} $ $(N = {{2}^{r}}$, $r \in \mathbb{N})$, и множества ${{Z}_{{v}}}(\tau {\kern 1pt} *,{{\tau }_{*}},z{{{\kern 1pt} }_{*}}),$ $v \in Q$ из разд. 2 подменяются более удобными для вычисления выпуклыми множествами ${{z}_{*}} + \delta {{H}_{{v}}}({{\tau }_{*}},z{{{\kern 1pt} }_{*}}),$ $\delta = \tau {\kern 1pt} * - {{\tau }_{*}},$ $v \in Q.$ Соответственно этому определения множеств $Z(\tau {\kern 1pt} *,{{\tau }_{*}},z{{{\kern 1pt} }_{*}})$ и $Z(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}})$ трансформируются в определения множеств, задействованных в дискретной схеме приближенного вычисления ${{Z}^{0}}$.
Прежде чем определить аппроксимирующую систему $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $, введем в рассмотрение “промежуточную” систему $\{ {{Z}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ в ${{\mathbb{R}}^{m}}$, также отвечающую разбиению $\Gamma $ промежутка $[{{t}_{0}},\vartheta ]$. Заметим при этом, что система $\{ {{Z}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ не задействована в приближенных вычислениях множества ${{Z}^{0}}$, а является лишь вспомогательной системой в наших рассуждениях, обосновывающих корректность (аппроксимирующую сущность) системы $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} .$
Итак, пусть $\Gamma = \{ {{\tau }_{0}} = {{t}_{0}},{{\tau }_{1}},{{\tau }_{2}},...,{{\tau }_{i}},...,{{\tau }_{N}} = \vartheta \} $ – двоичное разбиение промежутка $[{{t}_{0}},\vartheta ]$ с диаметром $\Delta = \Delta (\Gamma ) = {{N}^{{ - 1}}}(\vartheta - {{t}_{0}}),$ $N = {{2}^{r}},$ где $r \in \mathbb{N}$. Разбиению $\Gamma $ сопоставим систему $\{ {{Z}^{0}}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ множеств ${{Z}^{0}}({{\tau }_{i}}) = \{ z \in {{\mathbb{R}}^{m}}:({{\tau }_{i}},z) \in {{Z}^{0}}\} $ – временны́х сечений множества ${{Z}^{0}}$. Наряду с системой $\{ {{Z}^{0}}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ определим систему $\{ {{Z}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ при помощи рекуррентного соотношения ${{Z}^{\Gamma }}({{\tau }_{i}}) = Z({{\tau }_{i}},{{\tau }_{{i - 1}}},{{Z}^{\Gamma }}({{\tau }_{{i - 1}}})),$ $i = \overline {1,N} $, где ${{Z}^{\Gamma }}({{\tau }_{0}}) = M.$
Так как, согласно определению множества ${{Z}^{0}}$, его сечения ${{Z}^{0}}({{\tau }_{i}})$ удовлетворяют соотношениям
(3.1)
${{Z}^{0}}({{\tau }_{0}}) = M,\quad {{Z}^{0}}({{\tau }_{i}}) \subset Z({{\tau }_{i}},{{\tau }_{{i - 1}}},{{Z}^{0}}({{\tau }_{{i - 1}}})),\quad i = \overline {1,N} ,$Введем последовательность двоичных разбиений ${{\Gamma }^{{(n)}}} = \{ \tau _{0}^{{(n)}} = {{t}_{0}},\tau _{1}^{{(n)}},...,\tau _{i}^{{(n)}},...,\tau _{{N(n)}}^{{(n)}} = \vartheta \} ,$ $n \in \mathbb{N}$ промежутка $[{{t}_{0}},\vartheta ],$ где $N(n) = {{2}^{{n - 1}}}$.
В этой последовательности каждое последующее разбиение содержит предыдущие разбиения.
Для упрощения обозначений полагаем ${{Z}^{{(n)}}}(\tau _{i}^{{(n)}}) = {{Z}^{{{{\Gamma }^{{(n)}}}}}}(\tau _{i}^{{(n)}}),$ $i = \overline {0,N(n)} ,$ и каждому разбиению ${{\Gamma }^{{(n)}}}$ по аналогии с разбиением $\Gamma $ сопоставляем систему $\{ {{Z}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $ множеств
Для любого двоичного момента ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$ справедливы включения
(3.3)
${{Z}^{0}}({{\tau }_{*}}) \subset {{Z}^{{(n)}}}({{\tau }_{*}}),\quad {{Z}^{{(k)}}}({{\tau }_{*}}) \subset {{Z}^{{(n)}}}({{\tau }_{*}}),\quad {\text{где}}\quad n < k,\quad {{\tau }_{*}} \in {{\Gamma }^{{(n)}}}.$Пусть ${{\tau }_{*}}$ – двоичный момент из $[{{t}_{0}},\vartheta ].$ Принимая во внимание включения (3.3), получаем, что последовательность $\{ {{Z}^{{(n)}}}({{\tau }_{*}})\} $ сходится в хаусдорфовой метрике к компакту
Это означает, что для любой точки ${{z}_{*}} \in \hat {Z}({{\tau }_{*}})$ найдется последовательность $\{ z_{*}^{{(n)}}\} $ ($z_{*}^{{(n)}}\, \in \,{{Z}^{{(n)}}}({{\tau }_{*}}),$ $n \in \mathbb{N}$), сходящаяся к ${{z}_{*}}$, и, с другой стороны, любая сходящаяся последовательность $\{ z_{*}^{{(n)}}\} $ $(z_{*}^{{(n)}} \in {{Z}^{{(n)}}}({{\tau }_{*}})$, $n \in \mathbb{N})$ имеет в пределе точку ${{z}_{*}} \in \hat {Z}({{\tau }_{*}})$.
Распространим определение множества $\hat {Z}({{\tau }_{*}})$ с двоичных моментов ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$ на все остальные моменты ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ].$ Полагаем для этого ${{t}_{n}}({{\tau }_{*}}) = \max \{ \tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}:\tau _{i}^{{(n)}} \leqslant {{\tau }_{*}}\} .$
Пусть ${{\tau }_{*}}$ – недвоичный момент из $[{{t}_{0}},\vartheta ].$ Определим $\hat {Z}({{\tau }_{*}})$ как множество всех точек ${{z}_{*}}\, \in \,\Phi ({{\tau }_{*}}),$ для каждой из которых найдется последовательность $\{ ({{t}_{n}}({{\tau }_{*}}),z_{*}^{{(n)}})\} $ ($z_{*}^{{(n)}} \in {{Z}^{{(n)}}}({{t}_{n}}({{\tau }_{*}})),$ $n \in \mathbb{N}$), сходящаяся к $({{\tau }_{*}},{{z}_{*}})$ при $n \to \infty .$ Вместе с тем введем множество
(3.4)
$\hat {Z} = \bigcup\limits_{{{\tau }_{*}} \in [{{t}_{0}},\vartheta ]} {({{\tau }_{*}},\hat {Z}({{\tau }_{*}}))} \subset \Phi \subset D.$Так как множество $\hat {Z}$ получено из последовательности систем $\{ {{Z}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $, $n \in \mathbb{N}$, с использованием некоторых предельных переходов, то будем писать
Справедливо следующее утверждение.
Лемма 1. $\hat {Z} = {{Z}^{0}}.$
Доказательство. Докажем сначала включение $\hat {Z} \subset {{Z}^{0}}.$ Для этого покажем, что $\hat {Z}$ удовлетворяет соотношениям вида (2.4), т.е. соотношениям
(3.5)
$\hat {Z}({{t}_{0}}) \subset M,\quad \hat {Z}(\tau {\kern 1pt} *) \subset \chi (\tau {\kern 1pt} *,{{\tau }_{*}},\hat {Z}({{\tau }_{*}})),\quad {{t}_{0}} \leqslant {{\tau }_{*}} < \tau {\kern 1pt} * \leqslant \vartheta .$В самом деле, $\hat {Z}({{\tau }_{0}}) = {{Z}^{0}}({{\tau }_{0}}) = M.$
Покажем теперь, что выполнено второе из соотношений (3.5). Пусть выбраны произвольно ${{\tau }_{*}},$ τ*, $({{\tau }_{*}},\tau {\kern 1pt} *) \in \Delta {\kern 1pt} *$, $\Delta {\kern 1pt} * = \{ ({{\tau }_{*}},\tau {\kern 1pt} *) \in [{{t}_{0}},\vartheta ] \times [{{t}_{0}},\vartheta ]:$ ${{t}_{0}} \leqslant {{\tau }_{*}} \leqslant \tau {\kern 1pt} * \leqslant \vartheta \} $ – двоичные моменты из $[{{t}_{0}},\vartheta ]$ и точка $z{\kern 1pt} * \in \hat {Z}(\tau {\kern 1pt} *)$. Поскольку $z{\kern 1pt} * \in {{Z}^{{(n)}}}(\tau {\kern 1pt} *) = Z(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}^{{(n)}}}({{\tau }_{*}})),$ $n \in \mathbb{N},$ то $z{\kern 1pt} * \in {{Z}_{{v}}}(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}^{{(n)}}}({{\tau }_{*}}))$ при любых ${v} \in Q,$ $n \in \mathbb{N}$ и $z{\kern 1pt} * \in \Phi (\tau {\kern 1pt} *)$. Значит, при любых $v \in Q$ и $n \in \mathbb{N}$ существует такая точка $z_{*}^{{(n)}} \in {{Z}^{{(n)}}}({{\tau }_{*}})$, которая является начальной для некоторого решения $z_{{v}}^{{(n)}}(\tau )$ д.в. $\frac{{dz}}{{d\tau }} \in {{H}_{{v}}}(\tau ,z),$ $\tau \in [{{\tau }_{*}},\tau {\kern 1pt} *],$ удовлетворяющего $z_{v}^{{(n)}}(\tau {\kern 1pt} *) = z{\kern 1pt} *$.
Не нарушая общности рассуждений, считаем, что последовательность $\{ z_{{v}}^{{(n)}}(\tau )\} $ на $[{{\tau }_{*}},\tau {\kern 1pt} *]$ равномерно сходится к некоторой функции $z_{{v}}^{{}}(\tau )$ на $[{{\tau }_{*}},\tau {\kern 1pt} *]$. Очевидно, что $z_{{v}}^{{}}(\tau ),$ $\tau \in [{{\tau }_{*}},\tau {\kern 1pt} *]$ является решением д.в. (2.3), удовлетворяющим краевым условиям
Эти соотношения означают, что
(3.6)
$z{\kern 1pt} * \in {{Z}_{{v}}}(\tau {\kern 1pt} *,{{\tau }_{*}},\hat {Z}({{\tau }_{*}})),\quad {v} \in Q.$Учитывая (3.6), а также включение $z{\kern 1pt} * \in \Phi (\tau {\kern 1pt} *)$ и произвольный выбор точки $z{\kern 1pt} *$ в $\hat {Z}(\tau {\kern 1pt} *),$ получаем, что выполняется второе из соотношений (3.5). Соотношение (3.5) доказано для двоичных моментов ${{\tau }_{*}},$ $\tau {\kern 1pt} *$ из $[{{t}_{0}},\vartheta ]$.
Пусть теперь ${{\tau }_{*}}$ и $\tau {\kern 1pt} *$ – недвоичные моменты из $[{{t}_{0}},\vartheta ]$. Выберем произвольную точку $(\tau {\kern 1pt} *,z{\kern 1pt} *)\, \in \,\hat {Z},$ и пусть $\{ ({{t}_{n}}(\tau {\kern 1pt} *),z_{n}^{*})\} $ – последовательность из $\hat {Z}$, сходящаяся к $(\tau {\kern 1pt} *,z{\kern 1pt} *)$.
Выберем последовательность $\{ {{t}_{n}}({{\tau }_{*}})\} ,$ сходящуюся к ${{\tau }_{*}}$ слева. Так как ${{t}_{n}}({{\tau }_{*}}),$ ${{t}_{n}}(\tau {\kern 1pt} *)$ – двоичные моменты разбиения ${{\Gamma }^{{(n)}}}$, то
Отсюда следует, что существует такая точка $z_{*}^{{(n)}} \in {{Z}^{{(n)}}}({{t}_{n}}({{\tau }_{*}})),$ $n \in \mathbb{N},$ что некоторое решение $z_{{v}}^{{(n)}}(\tau ),$ $\tau \in [{{t}_{n}}({{\tau }_{*}}),{{t}_{n}}(\tau {\kern 1pt} *)]$ д.в. $\frac{{dz}}{{d\tau }} \in {{H}_{{v}}}(\tau ,z),$ $z_{{v}}^{{(n)}}({{t}_{n}}({{\tau }_{*}})) = z_{*}^{{(n)}}$ удовлетворяет равенству $z_{{v}}^{{(n)}}({{t}_{n}}(\tau {\kern 1pt} *)) = z_{n}^{*}$.
Не нарушая общности рассуждений, считаем, что последовательность $\{ z_{{v}}^{{(n)}}(\tau )\} $ на $[{{\tau }_{*}},\tau {\kern 1pt} *]$ равномерно сходится к некоторой функции $z{\kern 1pt} _{{v}}^{{}}(\tau ),$ $\tau \in [{{\tau }_{*}},\tau {\kern 1pt} *]$ (здесь мы доопределили $z_{{v}}^{{(n)}}(\tau )$ на промежутке $[{{t}_{n}}(\tau {\kern 1pt} *),\tau {\kern 1pt} *]$ с помощью равенства $z_{{v}}^{{(n)}}(\tau ) = z_{n}^{*},$ $n \in \mathbb{N}$).
Вектор-функция $z_{{v}}^{{}}(\tau ),$ $\tau \in [{{\tau }_{*}},\tau {\kern 1pt} *]$ является решением д.в. (2.3) и удовлетворяет условиям
Также из включения $z_{n}^{*} \in Z({{t}_{n}}(\tau {\kern 1pt} *)) \subset \Phi ({{t}_{n}}(\tau {\kern 1pt} *))$ и непрерывности многозначного отображения $\tau \to \Phi (\tau ),$ $\tau \in [{{\tau }_{*}},\tau {\kern 1pt} *]$ следует включение $z{\kern 1pt} * \in \Phi (\tau {\kern 1pt} *)$.
Следовательно, $z{\kern 1pt} * \in \Phi (\tau {\kern 1pt} *) \cap {{Z}_{{v}}}(\tau {\kern 1pt} *{{\tau }_{*}},\hat {Z}({{\tau }_{*}})),$ $v \in Q$. Поскольку $v \in Q$ и $z{\kern 1pt} * \in \hat {Z}(\tau {\kern 1pt} *)$ выбраны произвольно, то
(3.7)
$\hat {Z}(\tau {\kern 1pt} *) \subset Z(\tau {\kern 1pt} *,{{\tau }_{*}},\hat {Z}({{\tau }_{*}}))$Аналогично доказывается включение (3.7) в случае, когда один из моментов ${{\tau }_{*}},$ $\tau {\kern 1pt} *$ двоичный, а другой – нет.
Итак, для всевозможных пар $({{\tau }_{*}},\tau {\kern 1pt} *) \in \Delta {\kern 1pt} *$ установлены соотношения (3.5), откуда вытекает $\hat {Z} \subset {{Z}^{0}}.$
Докажем включение ${{Z}^{0}} \subset \hat {Z}.$
В самом деле, для любого двоичного момента ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$ справедливо включение
Пусть теперь ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$ – недвоичный момент и $({{\tau }_{*}},z{{{\kern 1pt} }_{*}}) \in {{Z}^{0}}$.
Рассмотрим последовательность $\{ {{t}_{n}}({{\tau }_{*}})\} $ двоичных моментов ${{t}_{n}}({{\tau }_{*}})$, входящих в такие разбиения ${{\Gamma }^{{(n)}}}$, что ${{\Delta }^{{(n)}}} = \Delta ({{\Gamma }^{{(n)}}}) \downarrow 0$ при $n \to \infty .$
Так как ${{Z}^{0}}({{\tau }_{*}}) \subset Z({{\tau }_{*}},{{t}_{n}}({{\tau }_{*}}),{{Z}^{0}}({{t}_{n}}({{\tau }_{*}}))),$ $n \in \mathbb{N},$ то $z{{{\kern 1pt} }_{*}}\, \in Z({{\tau }_{*}},{{t}_{n}}({{\tau }_{*}}),{{Z}^{0}}({{t}_{n}}({{\tau }_{*}}))),$ $n \in \mathbb{N}$.
Выберем некоторое $v \in Q$. Имеет место
$z{{{\kern 1pt} }_{*}}\, \in \Phi ({{\tau }_{*}}) \cap {{Z}_{{v}}}({{\tau }_{*}},{{t}_{n}}({{\tau }_{*}}),{{Z}^{0}}({{t}_{n}}({{\tau }_{*}}))),$ $n \in \mathbb{N}.$
Значит, существует такая последовательность $\{ z({{t}_{n}}({{\tau }_{*}}))\} $ точек $z({{t}_{n}}({{\tau }_{*}})) \in {{Z}^{0}}({{t}_{n}}({{\tau }_{*}})) \subset \hat {Z}({{t}_{n}}({{\tau }_{*}})),$ $n \in \mathbb{N},$ что некоторое решение $z_{{v}}^{{(n)}}(\tau )$, $\tau \in [{{t}_{n}}({{\tau }_{*}}),{{\tau }_{*}}]$ д.в. $dz{\text{/}}d\tau = {{H}_{{v}}}(\tau ,z)$, $z_{{v}}^{{(n)}}({{t}_{n}}({{\tau }_{*}})) = z({{t}_{n}}({{\tau }_{*}}))$ удовлетворяет условию $z{\kern 1pt} _{v}^{{(n)}}({{\tau }_{*}}) = z{{{\kern 1pt} }_{*}}$, $n \in \mathbb{N}$.
Справедливо предельное соотношение
Принимая во внимание включение ${{Z}^{0}}({{\tau }_{*}}) \subset \hat {Z}({{\tau }_{*}})$ при двоичных ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ],$ получаем, что (3.8) справедливо при всех ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$ и, значит, ${{Z}^{0}} \subset \hat {Z}$. Из включений $\hat {Z} \subset {{Z}^{0}}$, ${{Z}^{0}} \subset \hat {Z}$ следует ${{Z}^{0}} = \hat {Z}$. Лемма 1 доказана.
В лемме 1 утверждается, что максимальный u-стабильный тракт Z0 есть предел
Бесперспективность точного вычисления множеств ${{Z}^{{(n)}}}(\tau _{i}^{{(n)}})$ обусловлена тем, что мы не можем в сколько-нибудь нетривиальных случаях вычислить точно множества достижимости $Z(\tau {\kern 1pt} *,{{\tau }_{*}},{{Z}_{*}})$, ${{Z}_{*}}\, \subset \,{{\mathbb{R}}^{m}}$. Поэтому возникает необходимость в подмене множеств $Z(\tau _{i}^{{(n)}},\tau _{{i - 1}}^{{(n)}},{{Z}^{{(n)}}}(\tau _{{i - 1}}^{{(n)}}))$ такими множествами, которые были бы близки в некотором смысле (например, в смысле хаусдорфовой метрики) к множествам $Z(\tau _{i}^{{(n)}},\tau _{{i - 1}}^{{(n)}},{{Z}^{{(n)}}}(\tau _{{i - 1}}^{{(n)}}))$ и которые к тому же можно было бы точно вычислить.
Задавшись целью определить такие вычислимые множества, введем аппроксимирующую систему $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ множеств ${{\tilde {Z}}^{\Gamma }}({{\tau }_{i}})$ в ${{\mathbb{R}}^{m}}$.
Поясним, какой смысл мы вкладываем в понятие аппроксимирующей системы $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $. Мы считаем, что задано двоичное разбиение $\Gamma = \{ {{\tau }_{0}} = {{t}_{0}},{{\tau }_{1}},...,{{\tau }_{i}},...,{{\tau }_{N}} = \vartheta \} $ промежутка $[{{t}_{0}},\vartheta ]$. Каждому полуинтервалу $[{{\tau }_{i}},{{\tau }_{{i + 1}}})$ разбиения $\Gamma $ сопоставим д.в.:
(3.9)
$\begin{gathered} \frac{{dz}}{{d\tau }} \in {{H}_{{v}}}({{\tau }_{i}},{{z}^{{(i)}}}) + \varphi (\Delta ){\mathbf{B}},\quad z({{\tau }_{i}}) = {{z}^{{(i)}}} \in {{\mathbb{R}}^{m}}, \\ \tau \in [{{\tau }_{i}},{{\tau }_{{i + 1}}}),\quad v \in Q; \\ \end{gathered} $Пусть $({{\tau }_{i}},{{z}^{{(i)}}})$ и $({{\tau }_{i}},{{Z}^{{(i)}}})$ из ${\mathbf{D}}$ и ${v} \in Q$.
Введем обозначения: $\bar {Z}_{{v}}^{\Gamma }({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}}) = {{z}^{{(i)}}} + \Delta {{H}_{{v}}}({{\tau }_{i}},{{z}^{{(i)}}})$ – множество достижимости в момент ${{\tau }_{{i + 1}}}$ д.в. $dz{\text{/}}d\tau \in {{H}_{{v}}}({{\tau }_{i}},{{z}^{{(i)}}})$, $\tau \in [{{\tau }_{i}},{{\tau }_{{i + 1}}}]$, $z({{\tau }_{i}}) = {{z}^{{(i)}}}$;
Как известно, при ${{\tau }_{i}}$, ${{\tau }_{{i + 1}}}$ из $\Gamma $, $({{\tau }_{i}},{{z}^{{(i)}}}) \in {\mathbf{D}}$, и ${v} \in Q$ справедлива оценка
(3.10)
$d({{Z}_{{v}}}({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}}),{{\bar {Z}}_{{v}}}({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}})) \leqslant \omega (\Delta ).$Из (3.10) следует включение
(3.11)
${{Z}_{{v}}}({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}}) \subset \bar {Z}_{{v}}^{\Gamma }({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}}) + \omega (\Delta ){\mathbf{B}} = \tilde {Z}_{{v}}^{\Gamma }({{\tau }_{{i + 1}}},{{\tau }_{i}},{{z}^{{(i)}}}).$Из (3.11) вытекает
(3.12)
$\begin{gathered} {{Z}_{{v}}}({{\tau }_{{i + 1}}},{{\tau }_{i}},{{Z}^{{(i)}}}) \subset \tilde {Z}_{{v}}^{\Gamma }({{\tau }_{{i + 1}}},{{\tau }_{i}},{{Z}^{{(i)}}}), \\ ({{\tau }_{i}},{{Z}^{{(i)}}}) = {\mathbf{D}},\quad {{\tau }_{i}}\;\;{\text{и}}\;\;{{\tau }_{{i + 1}}}\;\;{\text{из}}\;\;\Gamma ,\;\;{v} \in Q. \\ \end{gathered} $Из (3.12) получаем
(3.13)
$\begin{gathered} Z({{\tau }_{{i + 1}}},{{\tau }_{i}},{{Z}^{{(i)}}}) \subset {{{\tilde {Z}}}^{\Gamma }}({{\tau }_{{i + 1}}},{{\tau }_{i}},{{Z}^{{(i)}}}) \\ ({{\tau }_{i}},{{Z}^{{(i)}}}) \subset {\mathbf{D}},\quad {{\tau }_{i}}\;\;{\text{и}}\;\;{{\tau }_{{i + 1}}}\;\;{\text{из}}\;\;\Gamma . \\ \end{gathered} $Введем аппроксимирующую систему $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $. Аппроксимирующая система $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ предназначена для аппроксимации множеств Z 0.
Определение 6. Аппроксимирующей системой $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ множеств ${{\tilde {Z}}^{\Gamma }}({{\tau }_{i}})$ в ${{\mathbb{R}}^{m}}$, соответствующей двоичному разбиению $\Gamma = \{ {{\tau }_{0}} = {{t}_{0}},{{\tau }_{1}},...,{{\tau }_{i}},...,{{\tau }_{N}} = \vartheta \} $ промежутка $[{{t}_{0}},\vartheta ]$, назовем набор множеств
(3.14)
${{\tilde {Z}}^{\Gamma }}({{\tau }_{0}}) = M,\quad {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}) = {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}},{{\tau }_{{i - 1}}},{{\tilde {Z}}^{\Gamma }}({{\tau }_{{i - 1}}})),\quad i = \overline {1,N} .$Теперь сравним системы $\{ {{Z}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ и $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $, отвечающие одному и тому же разбиению $\Gamma $.
Принимая во внимание ${{\tilde {Z}}^{\Gamma }}({{\tau }_{0}}) = {{Z}^{\Gamma }}({{\tau }_{0}}) = M$ и включения (3.13), получаем
(3.15)
${{Z}^{\Gamma }}({{\tau }_{i}}) \subset {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}),\quad {{\tau }_{i}} \in \Gamma .$Вместе с тем справедливы включения
Таким образом, аппроксимирующая система $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ является мажорантой для набора сечений $\{ {{Z}^{0}}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ множества Z 0.
Сосредоточимся на рассмотрении двоичных разбиений ${{\Gamma }^{{(n)}}} = \{ \tau _{0}^{{(n)}} = {{t}_{0}},\tau _{1}^{{(n)}},...,\tau _{i}^{{(n)}},...,\tau _{{N(n)}}^{{(n)}} = \vartheta \} $, $n \in \mathbb{N}$. Для упрощения введем обозначение ${{\tilde {Z}}^{{(n)}}}({{\tau }_{*}}) = {{\tilde {Z}}^{{{{\Gamma }^{{(n)}}}}}}({{\tau }_{*}})$, ${{\tau }_{*}} \in {{\Gamma }^{{(n)}}}$, $n \in \mathbb{N}$. Аппроксимирующая система $\{ {{\tilde {Z}}^{{{{\Gamma }^{{(n)}}}}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $ запишется в виде $\{ {{\tilde {Z}}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $.
Введем в рассмотрение множество Ω0 всех тех точек $({{\tau }_{*}},{{z}_{*}}) \in {\mathbf{D}}$, каждая из которых представима в виде $({{\tau }_{*}},{{z}_{*}}) = \mathop {\lim }\limits_{n \to \infty } ({{t}_{n}}({{\tau }_{*}}),{{z}_{n}})$, где $\{ ({{t}_{n}}({{\tau }_{*}}),{{z}_{n}})\} $ – некоторая последовательность точек $({{t}_{n}}({{\tau }_{*}}),{{z}_{n}}) \in ({{t}_{n}}({{\tau }_{*}}),{{\tilde {Z}}^{{(n)}}}({{t}_{n}}({{\tau }_{*}})))$, $n \in \mathbb{N}$. При таком определении справедливо равенство ${{\Omega }^{0}}(\tau _{0}^{{(n)}}) = {{\Omega }^{0}}({{t}_{0}}) = M$.
Так как при любых ${{\tau }_{*}} \in {{\Gamma }^{{(n)}}}$, $n \in \mathbb{N}$ имеет место
то из определения Ω0 и ${{Z}^{0}} = \mathop {\lim }\limits_{n \to \infty } ({{Z}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in \Gamma )$ вытекает включение при любом недвоичном ${{\tau }_{*}} \in [{{t}_{0}},\vartheta ]$. Следовательно, имеет место включениеКроме того, по той же самой схеме рассуждений, что и для Z0, доказывается включение
(3.19)
${{\Omega }^{0}}(\tau {\kern 1pt} *) \subset Z(\tau {\kern 1pt} *,{{\tau }_{*}},{{\Omega }^{0}}({{\tau }_{*}}))$Учитывая равенство ${{\Omega }^{0}}({{t}_{0}}) = M$ и (3.19), получаем, что замкнутое множество Ω0 в D есть u-стабильный тракт системы (2.2). Следовательно, справедливо включение
Из (3.18) и (3.20) следует следующее утверждение.
Лемма 2. ${{Z}^{0}} = {{\Omega }^{0}}$.
Объединяем леммы 1 и 2.
Теорема. ${{Z}^{0}} = \hat {Z} = {{\Omega }^{0}}$.
Теорема представляет собой теоретическое обоснование возможности использования аппроксимирующих систем $\{ {{\tilde {Z}}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $ для приближенного вычисления максимального $u$-стабильного тракта Z0 и, стало быть, максимального $u$-стабильного моста W0 в игровой задаче о сближении системы (1.1) с M в момент $\vartheta $ при наличии фазового ограничения $\Phi $.
Заметим, однако, что сама система $\{ {{\tilde {Z}}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $ не может быть реализована в точности в процессе приближенных вычислений (в конкретных игровых задачах о сближении), поскольку в нетривиальных конфликтно управляемых системах даже при множествах $M \subset {{\mathbb{R}}^{m}}$ и $\Phi \subset [{{t}_{0}},\vartheta ] \times {{\mathbb{R}}^{m}}$ с простой геометрией несчетные множества ${{\tilde {Z}}^{{(n)}}}(\tau _{i}^{{(n)}})$, $\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}$ имеют непростую геометрическую структуру. Эти множества определяются соотношениями вида
Таким образом, можно сделать вывод, что для проведения эффективных приближенных вычислений максимального $u$-стабильного тракта Z 0 сама система $\{ {{\tilde {Z}}^{{(n)}}}(\tau _{i}^{{(n)}}):\tau _{i}^{{(n)}} \in {{\Gamma }^{{(n)}}}\} $ требует корректировки, что является важной отдельной задачей.
4. Вычисление приближенных решений в конкретных игровых задачах. В этом пункте рассматриваются две задачи о сближении конкретных динамических систем на конечном промежутке времени $[{{t}_{0}},\vartheta ]$.
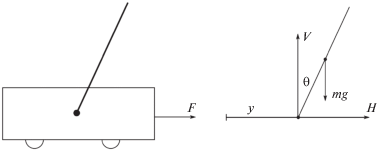
Задача 1. Задана механическая управляемая система – обратный маятник с точкой подвеса, находящейся на тележке, которая передвигается по горизонтальной плоскости [13].
На тележку воздействует в горизонтальном направлении тяговое усилие величины F. Обратный маятник подвержен силе гравитации $m\vec {g}$, приложенной к его центру тяжести, а также находится под действием горизонтальной $\vec {H}$ и вертикальной $\vec {V}$ составляющих сил реакции в опорной точке маятника; $m$ – масса маятника, $m{\kern 1pt} *$ – масса тележки, $\vec {g}$ – гравитационная постоянная (рис. 2).
Полагаем, что $L$ – расстояние между центром тяжести маятника и его опорной точкой, $y$ – смещение опорной точки маятника, $\alpha $ – угол наклона маятника по отношению к вертикальной оси, I – момент инерции маятника относительно центра массы. Введем переменные ${{x}_{1}} = \alpha $, ${{x}_{2}} = \dot {\alpha }$, ${{x}_{3}} = y$, ${{x}_{4}} = \dot {y}$. Допустим также, что $u = u(t)$ – величина тягового усилия $\vec {F}(t)$ на промежутке $[{{t}_{0}},\vartheta ]$, где ${\text{|}}\vec {F}(t){\text{|}} \leqslant \mu $, $\mu $ – заданное положительное число; $k$ – коэффициент трения горизонтальной поверхности.
Считаем, что $u = u(t)$ находится в распоряжении первого игрока и может выбираться как позиционное управление $u(t,x)$ (${\text{|}}u(t,x){\text{|}} \leqslant \mu $), где $(t,x) = (t,{{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}})$ – позиция системы тележка–маятник. Считаем также, что коэффициент трения $k = k(t)$, который рассматриваем как управление ${v} = {v}(t) = k(t)$ второго игрока, неизвестен первому игроку. Мы не исключаем, что он может быть реализован как функция $k(t) = {v}(t,x(t))$, где функция ${v}(t,x)$ удовлетворяет неравенству ${\text{|}}{v}(t,x(t)){\text{|}} \leqslant \zeta $, а $x(t)$ – движение системы (4.1), $\zeta $ – заданное положительное число.
При таких обозначениях уравнение системы тележка–маятник принимает вид
(4.1)
$\begin{gathered} {{{\dot {x}}}_{1}} = {{x}_{2}},\quad {{{\dot {x}}}_{2}} = - \frac{1}{{\Delta ({{x}_{1}})}}\{ (m + m{\kern 1pt} *)mgL\sin {{x}_{1}} - mL\cos {{x}_{1}}(u + mLx_{2}^{2}\sin {{x}_{1}} - {v}{{x}_{2}})\} , \\ {{{\dot {x}}}_{3}} = {{x}_{4}},\quad {{{\dot {x}}}_{4}} = - \frac{1}{{\Delta ({{x}_{1}})}}\{ - mL\cos {{x}_{1}}mgL\sin {{x}_{1}} + (I + m{{L}^{2}})(u + mLx_{2}^{2}\sin {{x}_{1}} - {v}{{x}_{2}})\} ; \\ \end{gathered} $Рассматривается игровая задача о сближении системы (4.1) с целевым множеством $M = \{ x \in {{\mathbb{R}}^{4}}:\left\| x \right\| \leqslant 0.5\;{\text{м\} }}$ ($x = ({{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}})$) при наличии стационарного фазового ограничения $\Phi = [{{t}_{0}},\vartheta ] \times \Omega $, ${{t}_{0}} = 0,$ $\vartheta = 2.5,$ Ω = $\{ x \in {{\mathbb{R}}^{4}}: - 0.3\;{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}} \leqslant {{x}_{2}} \leqslant 0.3$ рад/c, $ - 0.5\;{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}} \leqslant {{x}_{4}} \leqslant 0.5\;{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}\} $ со следующими значениями входящих в (4.1) параметров: $m = 0.25$ кг, $m{\kern 1pt} * = 2$ кг, $g = 9.81$ м/с2, $L = 1$ м, $I = 1$ кг ⋅ м2, ${{x}^{{(0)}}} = ( - 0.257\;{\text{рад, 0}}{\text{.048}}\;{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} {\text{с}}}} \right. \kern-0em} {\text{с}}},0.050\;{\text{м,}} - {\kern 1pt} {\text{0}}{\text{.028}}\;{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}) \in {{\mathbb{R}}^{4}}$, $Q = [0$ кг/м, 0.39 кг/м], P = = ${\text{[}}{\kern 1pt} - {\kern 1pt} {\text{1Н, 1Н]}}$, $\tilde {Q} = \{ {{v}^{{(l)}}} \in Q:{{v}^{{(l)}}} = l \cdot 0.03,{\text{ }}l \in \overline {1,13} \} $, $\tilde {P} = \{ {{u}^{{(s)}}} \in P:$ ${{u}^{{(s)}}} = s \cdot 0.25{\text{Н}},$ $s \in - \overline {4,4} \} $. Здесь обозначено
Вычислить точно множество разрешимости W0 рассматриваемой игровой задачи о сближении для системы (4.1) не представляется возможным, поэтому осуществим приближенное вычисление W0, согласно изложенной в разд. 3 методике.
Именно система (4.1) записывается в терминах обратного времени $\tau = {{t}_{0}} + \vartheta - t$, $t \in [{{t}_{0}},\vartheta ]$:
(4.2)
$\begin{gathered} {{{\dot {z}}}_{1}} = - {{z}_{2}},\quad {{{\dot {z}}}_{2}} = \frac{1}{{\Delta ({{z}_{1}})}}\{ (m + m{\kern 1pt} *)mgL\sin {{z}_{1}} - mL\cos {{z}_{1}}(u + mLz_{2}^{2}{\text{sin}}{{z}_{2}} - v{{z}_{2}})\} , \\ {{{\dot {z}}}_{3}} = - {{z}_{4}},\quad {{{\dot {z}}}_{4}} = \frac{1}{{\Delta ({{z}_{1}})}}\{ - mL{\text{cos}}{{z}_{1}}mgL{\text{sin}}{{z}_{1}} + (I + m{{L}^{2}})(u + mLz_{2}^{2}{\text{sin}}{{z}_{1}} - {v}{{z}_{2}})\} . \\ \end{gathered} $Затем вводится конечное разбиение $\Gamma = \{ {{\tau }_{0}} = {{t}_{0}},{{\tau }_{1}},...,{{\tau }_{i}},...,{{\tau }_{{N - 1}}},{{\tau }_{N}} = \vartheta \} $ промежутка $[{{t}_{0}},\vartheta ]$, где $\Delta = \Delta (\Gamma ) = {{\Delta }_{i}} = {{\tau }_{{i + 1}}} - {{\tau }_{i}} = {{N}^{{ - 1}}}(\vartheta - {{t}_{0}}),$ $i = \overline {0,N - 1} $, – диаметр разбиения $\Gamma $.
Система $\{ {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}):{{\tau }_{i}} \in \Gamma \} $ в ${{\mathbb{R}}^{4}}$, аппроксимирующая максимальный $u$-стабильный тракт ${{Z}^{0}}$, определяется рекуррентными соотношениями
(4.3)
${{\tilde {Z}}^{\Gamma }}({{\tau }_{0}}) = M,\quad {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}}) = {{\tilde {Z}}^{\Gamma }}({{\tau }_{i}},{{\tau }_{{i - 1}}},{{\tilde {Z}}^{\Gamma }}({{\tau }_{{i - 1}}})) = \bigcap\limits_{{v} \in Q} {\tilde {Z}_{{v}}^{\Gamma }({{\tau }_{i}},{{\tau }_{{i - 1}}},{{{\tilde {Z}}}^{\Gamma }}({{\tau }_{{i - 1}}}))} \cap \Omega ,\quad i = \overline {1,N} .$Так как множества ${{\tilde {Z}}^{\Gamma }}({{\tau }_{i}})$ несчетны и имеют сложную геометрию, то их точное вычисление невозможно; каждое из них приходится рассчитывать приближенно как некоторое конечное (состоящее из конечного числа точек) множество ${{\tilde {\mathcal{Z}}}^{\Gamma }}({{\tau }_{i}})$ в ${{\mathbb{R}}^{4}}$. В частности, и ${{\tilde {Z}}^{\Gamma }}({{\tau }_{0}}) = M$ вычисляем приближенно как некоторое конечное множество ${{\tilde {\mathcal{Z}}}^{\Gamma }}({{\tau }_{0}})$ в ${{\mathbb{R}}^{4}}$.
Так как в (4.3) входят множество $\Omega = \Phi ({{\tau }_{i}})$ и множества P и Q – ограничения на управления игроков, то их также аппроксимируем некоторыми конечными множествами $\tilde {\Omega }$ и $\tilde {P}$, $\tilde {Q}$ в пространствах ${{\mathbb{R}}^{4}}$ и ${{\mathbb{R}}^{1}}$ соответственно. При этом операции пересечения множеств, входящих в (4.3), ставится в соответствие некоторая операция над конечными множествами $\tilde {\mathcal{Z}}_{v}^{\Gamma }({{\tau }_{i}},{{\tau }_{{i - 1}}},{{\tilde {\mathcal{Z}}}^{\Gamma }}({{\tau }_{{i - 1}}}))$ и $\tilde {\Omega }$.
После того, как вычислили множества ${{\tilde {\mathcal{Z}}}^{\Gamma }}({{\tau }_{i}})$, $i = \overline {0,N} $, в пространстве ${{\mathbb{R}}^{4}},$ определяем в этом пространстве набор конечных множеств ${{\tilde {\mathcal{W}}}^{\Gamma }}({{\tau }_{i}})$, отвечающий разбиению Γ = $\{ {{t}_{0}},{{t}_{1}},...,{{t}_{j}},...,{{t}_{{N - 1}}},{{t}_{N}}$ = ϑ}: ${{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}}) = {{\tilde {\mathcal{Z}}}^{\Gamma }}({{\tau }_{i}})$, ${{t}_{j}} = {{t}_{0}} + \vartheta - {{\tau }_{i}}$, $i = N,N - 1,...,0$. Согласно изложенной в разд. 3 теории, набор $\{ {{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}}):{{t}_{j}} \in \Gamma \} $ аппроксимирует множество разрешимости ${{W}^{0}}$ в игровой задаче о сближении системы (4.1) с $M$.
Имея в своем распоряжении аппроксимирующий набор $\{ {{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}}):{{t}_{j}} \in \Gamma \} $, первый игрок приступает ко второму этапу конструирования приближенного решения задачи о сближении для системы (4.1) – реализации стратегии экстремального прицеливания [2] на набор $\{ {{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}}):{{t}_{j}} \in \Gamma \} $. Предполагаем при этом, что второй игрок выбирает некоторое управление $v(t)$ – постоянное на полуинтервалах $[{{t}_{j}},{{t}_{{j + 1}}})$ разбиения $\Gamma $. Управление $v(t)$ на $[{{t}_{0}},\vartheta ]$ может по ходу времени формироваться по принципу обратной связи:
Далее заметим, что, имея выбранную начальную позицию $({{t}_{0}},{{x}^{{(0)}}})$ системы (4.1), первый игрок выбирает произвольно вектор $u({{t}_{0}}) \in \tilde {P}$ в качестве управления на начальном промежутке $[{{t}_{0}},{{t}_{1}})$:
При этом в системе (4.1) присутствует в качестве управления $v(t)$ на $[{{t}_{0}},{{t}_{1}})$ некоторый вектор ${{v}^{{(0)}}} \in \tilde {Q}$:
Для проведения последующих выкладок правую часть системы обозначим через $f(t,x,u,v) \in {{\mathbb{R}}^{4}}$, а также полагаем
Движение системы (4.1) на полуинтервале $[{{t}_{0}},{{t}_{1}})$ моделируем как звено ломаной Эйлера: $\tilde {x}(t) = {{x}^{{(0)}}} + (t - {{t}_{0}})f({{t}_{0}},{{x}^{{(0)}}},u({{t}_{0}}),{{v}^{{(0)}}})$, $t \in [{{t}_{0}},{{t}_{1}})$. Далее, имея в распоряжении в момент ${{t}_{1}}$ фазовый вектор $\tilde {x}({{t}_{1}})$, вычисляем ближайшую к $\tilde {x}({{t}_{1}})$ на ${{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{1}})$ точку $\tilde {y}({{t}_{1}})$ и вектор $s({{t}_{1}}) = \tilde {y}({{t}_{1}}) - \tilde {x}({{t}_{1}}) \in {{\mathbb{R}}^{4}}$. Затем первый игрок вычисляет управление $u{\kern 1pt} {\text{*}}(t) = {{u}^{e}}({{t}_{1}})$, $t \in [{{t}_{1}},{{t}_{2}})$ из условия экстремального прицеливания движения системы (4.1) из точки $\tilde {x}({{t}_{1}})$ на множество ${{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{1}})$:
Движение системы (4.1) на промежутке $[{{t}_{1}},{{t}_{2}}]$ моделируем как звено ломаной Эйлера:
Продолжаем вычисление разрешающих управлений $u{\kern 1pt} {\text{*}}(t) = {{u}^{e}}({{t}_{j}})$ на последующих промежутках $[{{t}_{j}},{{t}_{{j + 1}}})$, $j = \overline {3,N - 1} $, разбиения $\Gamma $ в соответствии с правилом экстремального прицеливания [2]:
Движение системы (4.1) на промежутках $[{{t}_{j}},{{t}_{{j + 1}}}]$ моделируем как звено ломаной Эйлера:
Для реализовавшейся в ходе вычислений ломаной Эйлера $\tilde {x}(t)$, $t \in [{{t}_{0}},\vartheta ]$, получаем, что величина
Следует полагать, что правило экстремального прицеливания будет также эффективно действовать и в отношении реального движения $x(t)$, $t \in [{{t}_{0}},\vartheta ]$ системы (4.1), которое на промежутках $[{{t}_{j}},{{t}_{{j + 1}}})$ разбиения $\Gamma $ описывается соотношением
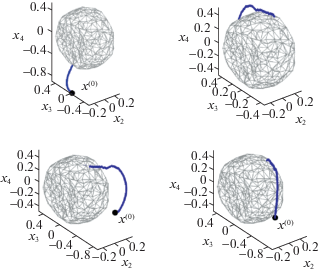
Представим графическое сопровождение результатов математического моделирования решения задачи 1 (рис. 3–5).
Рис. 3.
Проекции множеств ${{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}})$, (${{t}_{j}} = 0,{\text{ }}1,{\text{ }}1.5,{\text{ }}2,{\text{ }}2.2,{\text{ }}2.5$) на подпространство переменных ${{x}_{2}}$, ${{x}_{3}}$, ${{x}_{4}}$ фазового пространства ${{\mathbb{R}}^{4}}$

Рис. 4.
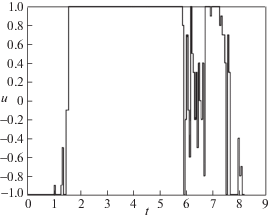
Графики управления u*(t) на [0, 2.5], вычисленного по правилу экстремального прицеливания на множества ${{\tilde {\mathcal{W}}}^{\Gamma }}({{t}_{j}})$, и произвольно выбранного управления $v(t)$ на [0, 2.5] второго игрока
Рис. 5.
Проекции на трехмерные подпространства из ${{\mathbb{R}}^{4}}$ движения $x(t)$, $x(0) = {{x}^{{(0)}}}$ системы (4.2), порожденного управлениями u*(t) и $v(t)$
Задача 2. Задана управляемая система, описывающая динамику движения четырехколесной тележки на горизонтальной плоскости [11, 12]:
(4.4)
$\left\{ {\begin{array}{*{20}{c}} {{{{\dot {x}}}_{1}} = \cos {{x}_{3}},} \\ {{{{\dot {x}}}_{2}} = \sin {{x}_{3}},} \\ {{{{\dot {x}}}_{3}} = u{\text{ }}.} \end{array}} \right.$Здесь $({{x}_{1}},{{x}_{2}})$ – координаты точки на тележке, расположенной посередине между задними колесами тележки, x3 – угол поворота тележки, $u$ – управляющее воздействие, которое может принимать значения в диапазоне [–1, 1].
В данном случае тележку мы идентифицируем с точкой, имеющей координаты $({{x}_{1}},{{x}_{2}})$, т.е. не рассматриваем тележку как протяженный объект.
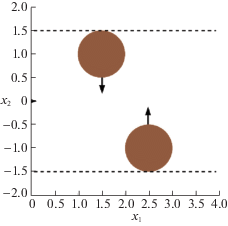
Требуется перевести управляемую систему (4.4) из точки ${{x}^{{(0)}}} = (0,0,0)$ на одноточечное множество $M = \{ (0,0,\pi )\} $ в момент времени $\vartheta = 8.2$, т.е. необходимо развернуть тележку на 180°, обходя при этом подвижные препятствия. Эти препятствия для фазовой точки $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ представляют собой в каждый момент $t \in [{{t}_{0}},\vartheta ]$ круговые цилиндры $\mathbb{Z}{\kern 1pt} {\text{*}}(t)$ и $\mathbb{R}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*(}}t)$ с осями, параллельными оси ${{x}_{3}}$ и основаниями в плоскости ${{x}_{1}},{{x}_{2}}$ – кругами $K{\kern 1pt} {\text{*}}(t)$ и $K{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$, совершающими периодические движения, параллельные оси x2, между прямыми линиями ${{x}_{2}} = - 1.5$ и ${{x}_{2}} = 1.5$ со скоростью, равной 1, начиная каждый от своей линии (см. рис. 6, 7). Считаем при этом, что фазовая точка x системы (4.4) может соприкасаться с цилиндрами $\mathbb{Z}{\kern 1pt} {\text{*}}(t)$ и $\mathbb{Z}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t)$ по их границам. Таким образом, в рассматриваемой задаче фазовое ограничение $\Phi $ в ${{\mathbb{R}}^{3}}$ представимо равенством
где $\Phi (t) = {{\mathbb{R}}^{3}}{{\backslash }}(\operatorname{int} \mathbb{Z}{\kern 1pt} {\text{*}}(t) \cup \operatorname{int} \mathbb{Z}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t))$, t = 0, $\vartheta = 8.2$.Рис. 6.
Объединение замкнутых цилиндров $\mathbb{Z}{\kern 1pt} {\text{*}}(t)$ и $\mathbb{Z}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*(}}t)$ в ${{\mathbb{R}}^{3}}$, таких, что $\operatorname{int} (\mathbb{Z}{\kern 1pt} {\text{*}}(t) \cup \mathbb{Z}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t))$ является препятствием в момент t для фазовой точки $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ системы (4.4)
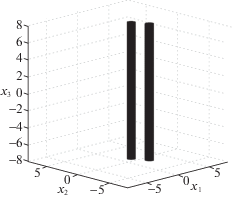
Рис. 7.
Проекция препятствия $\operatorname{int} (\mathbb{Z}{\kern 1pt} {\text{*}}({{t}_{0}}) \cup \mathbb{Z}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}({{t}_{0}}))$ на плоскость переменных ${{x}_{1}},\;{{x}_{2}}$
В этой задаче управления системой (4.4) полагаем, что помеха $v = v(t)$ отсутствует, т.е. $v = v(t) = 0$, $t \in [{{t}_{0}},\vartheta ]$. В связи с отсутствием помехи ${v}$ здесь предполагается иной подход к решению задачи. Этот подход, так же как и подход к решению задачи 1, реализует приближенное решение. Он включает в себя три основных этапа и предполагает приближенное вычисление множеств достижимости $X({{t}_{j}},{{t}_{0}},{{x}^{{(0)}}})$ системы (4.4), отвечающих моментам tj из некоторого конечного разбиения $\Gamma = \{ {{t}_{0}},{{t}_{1}},...,{{t}_{j}},...,{{t}_{{N - 1}}},{{t}_{N}} = \vartheta \} $ промежутка $[{{t}_{0}},\vartheta ]$. Эти множества ${{\tilde {X}}^{\Gamma }}({{t}_{j}})$ в ${{\mathbb{R}}^{3}}$ вычисляются как конечные (т.е. состоящие из конечного числа точек) множества по рекуррентной формуле
Таким образом, эти множества развиваются во времени $t$ от начальной точки ${{x}^{{(0)}}}$, отвечающей начальному моменту ${{t}_{0}}$, с учетом изменяющегося во времени фазового ограничения $\Phi (t)$. В момент $\vartheta = 8.2$ выполняется включение ${{x}^{f}} = (0,0,\pi ) \in {{\tilde {X}}^{\Gamma }}(\vartheta )$. На втором этапе решения, пятясь в прямом времени $t$ от конечной точки x f и перебирая множества достижимости ${{\tilde {X}}^{\Gamma }}({{t}_{j}})$, $j = N,N - 1,...,0$, приходим в конечном итоге в некоторую точку $\tilde {x}({{t}_{0}}) = {{\tilde {x}}^{{(0)}}}$, близкую с большой степенью точности к ${{x}^{{(0)}}}$. На третьем этапе решения из точки ${{x}^{{(0)}}}$ (как из начальной) вычисляем движение $x(t)$ системы (4.4), порожденное программным кусочно-постоянным (постоянным на полуинтервалах $[{{t}_{j}},{{t}_{{j + 1}}})$) управлением $u{\kern 1pt} *(t)$, $t \in [{{t}_{0}},\vartheta ]$, максимально сдвигаясь в направлении на ломаную $\tilde {x}(t)$ в каждый момент ${{t}_{j}} \in \Gamma $. В результате применения управления $u{\kern 1pt} *(t)$, $t \in [{{t}_{0}},\vartheta ]$ приходим в момент $\vartheta $ в точку $x(\vartheta )$, очень близкую к финальной точке ${{x}^{f}} = (0,0,\pi )$. Отметим, что хорошая близость $x(\vartheta )$ к x f обусловлена простотой динамики управляемой системы (4.4) и малой размерностью системы. Эти ее особенности позволили провести весьма точные приближенные вычисления множеств достижимости ${{X}^{\Gamma }}({{t}_{j}})$, $j = \overline {1,N} $, в виде множеств ${{\tilde {X}}^{\Gamma }}({{t}_{j}})$ и тем самым обеспечили условия для построения траектории $x(t)$, $t \in [{{t}_{0}},\vartheta ]$, подходящей близко к финальной точке x f в момент $\vartheta = 8.2$.
Ниже представлены элементы графического сопровождения результатов математического моделирования решения задачи 2 (рис. 8–10).
Рис. 8.
Множества ${{\tilde {X}}^{\Gamma }}({{t}_{j}},{{t}_{0}},{{x}^{{(0)}}}) \subset {{\mathbb{R}}^{3}}$ и множества $\operatorname{int} (\mathbb{Z}{\text{*}}({{t}_{j}}) \cup \mathbb{Z}{\text{**}}({{t}_{j}}))$ в моменты ${{t}_{j}} = 2,\;4,\;6,\;8.2$
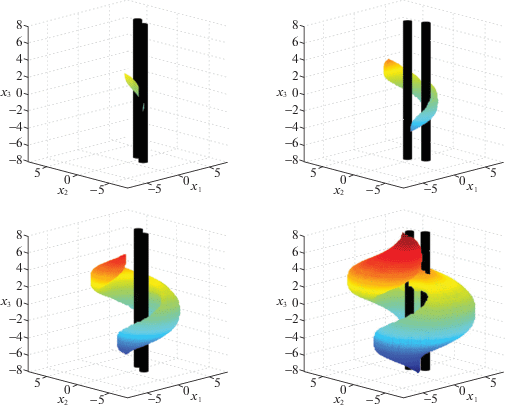
Рис. 9.
Проекция движения $x(t)$ системы (4.4), порожденного управлением u*(t), на плоскость ${{x}_{1}},\;{{x}_{2}}$ и множества $K{\kern 1pt} {\text{*}}({{t}_{j}}) \cup K{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}({{t}_{j}})$ в моменты ${{t}_{j}} = 2,\;4,\;6,\;8.2$
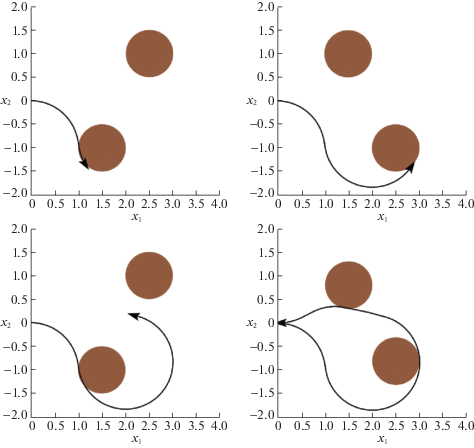
Заключение. Для конечномерной управляемой системы рассмотрена игровая задача о сближении с целевым множеством в фазовом пространстве системы. Предложен метод приближенного конструирования множества разрешимости. В конкретной задаче управления механической системой “тележка–маятник на тележке” конструируется разрешающее управление на основе принципа Н.Н. Красовского экстремального прицеливания на множество разрешимости. Описана задача управления движением четырехколесной тележки на горизонтальной плоскости. По условиям задачи тележка стеснена подвижными фазовыми ограничениями. Требуется за фиксированное время осуществить разворот тележки на 180°, соблюдая фазовые ограничения. В задаче управления тележкой построено разрешающее программное управление. Предложенный в работе метод построения приближенных решений применим к широкому кругу конкретных задач управления.
Список литературы
Красовский Н.Н. Игровые задачи о встрече движений. М.: Наука, 1970.
Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974.
Куржанский А.Б. Избранные труды. М.: Изд-во МГУ, 2009.
Осипов Ю.С. Избранные труды. М.: Изд-во МГУ, 2009.
Понтрягин Л.С. Математическая теория оптимальных процессов и дифференциальные игры // Тр. МИАН. 1985. Т. 169. С. 119–158.
Черноусько Ф.Л., Меликян А.А. Игровые задачи управления и поиска. М.: Наука, 1978.
Никольский М.С. Об альтернированном интеграле Л.С. Понтрягина // Мат. cб. 1981. Т. 116. № 1. С. 136–144.
Половинкин Е.С. Стабильность терминального множества и оптимальность времени преследования в дифференциальных играх // Дифференц. уравнения. 1984. Т. 20. № 3. С. 433–446.
Кряжимский А.В., Максимов В.И. Задача ресурсосберегающего слежения на бесконечном промежутке времени // Дифференц. уравнения. 2011. Т. 47. № 7. С. 993–1002.
Ананьевский И.М., Решмин С.А., Черноусько Ф.Л. Методы управления нелинейными механическими системами. М.: Физматлит, 2006.
Dubins L.S. On Curves of Minimal Length with a Constraint of Average Curvature and with Prescribed Initial and Terminal Positions and Tangents // American J. Math. 1957. V. 79. № 79. P. 407–516.
Пацко В.С., Федотов А.А. Множество достижимости в момент для машины Дубинса в случае одностороннего поворота // Тр. Ин-та математики и механики. 2018. Т. 24. № 1. С. 143–155.
Халил Х.К. Нелинейные системы, 3-е изд. Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, Ин-т компьютерных исследований, 2009.
Тарасьев А.М., Ушаков В.Н., Хрипунов А.П. Об одном вычислительном алгоритме решения игровых задач управления // ПММ. 1987. Т. 51. № 2. С. 216–222.
Ушаков В.Н., Хрипунов А.П. О приближенном построении решений в игровых задачах управления // ПММ. Т. 61. Вып. 3. 1997. С. 413–421.
Ушаков В.Н., Успенский А.А. Об одном дополнении к свойству стабильности в дифференциальных играх // Тр. МИАН. 2010. С. 299–318.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления