1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 5, 2021

Известия РАН. Теория и системы управления, 2021, № 5, стр. 162-176

О МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ ДИНАМИКИ МНОГОЗВЕННЫХ СИСТЕМ И ЭКЗОСКЕЛЕТОВ

А. В. Борисов a, b, *, И. Е. Каспирович a, b, **, Р. Г. Мухарлямов a, b, ***

a Филиал ФГБОУ ВО НИУ “МЭИ”
Смоленск, Россия

b Российский университет дружбы народов
Москва, Россия

* E-mail: BorisowAndrej@yandex.ru
** E-mail: kaspirovich.ivan@mail.ru
*** E-mail: robgar@mail.ru

Поступила в редакцию 20.06.2020
После доработки 24.12.2020
Принята к публикации 29.03.2021

Полный текст (PDF)

Аннотация

Приводится обзор известных публикаций и излагаются некоторые результаты исследований авторов по моделированию динамики систем твердых тел и экзоскелетов. Описываются различные подходы к проблеме моделирования динамики многозвенных систем, включая задачи построения уравнений движений и решения задач управления. Рассматриваются матричные и рекуррентные методы составления уравнений динамики антропоморфных механизмов и экзоскелетов, а также задачи моделирования плоских и пространственных систем, содержащих звенья переменной длины. Результаты исследований по аналитическому конструированию экзоскелетов, антропоморфных механизмов и их аналогов представляются актуальными для проектирования систем, предназначенных для усиления двигательных функций человека и разработки робототехнических систем различного назначения.

Введение. В работе будут использованы следующие понятия и определения.

Эндоскелет – механизм, обеспечивающий опору, поддержание формы тела, движение за счет внутреннего каркаса. В качестве примера эндоскелета можно указать костные системы животных и человека.

Экзоскелет – механизм, предназначенный для передвижения в нем человека и увеличения возможностей пользователя за счет внешнего каркаса. Экзоскелет соответствует биомеханике человека или различным видам животных.

Звено переменной длины – часть механизма, способная изменять свою длину вдоль направления между шарнирами-суставами без деформации изгиба и кручения. Оно может иметь достаточно сложную механическую конструкцию и реализовывать растяжение-сжатие.

Шарнир-сустав – модель биологического сустава в виде шарнира, в котором может создаваться необходимый управляющий момент.

Обеспечение комфортной окружающей среды для лиц с ограниченными двигательными возможностями невозможно без создания высокотехнологичной продукции робототехники, обеспечивающей повышение их социальной, физической адаптации и эффективности работы организма в целом. Разработка пространственных моделей человеко-машинных систем в виде экзоскелета, обеспечивающего устойчивое, целенаправленное, комфортабельное передвижение в нем человека и доступного для непосредственной технической реализации, являются актуальными вызовами, стоящими перед исследователями и конструкторами.

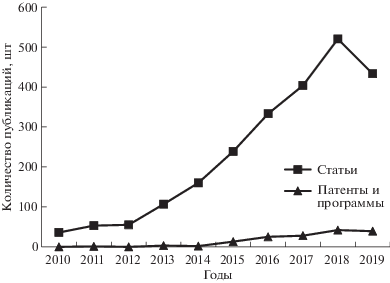
Актуальность разработки экзоскелетов в Российской Федерации прослеживается по количеству публикаций, в Российском индексе научного цитирования (РИНЦ), возрастающих в последние 10 лет практически экспоненциально (рис. 1). На рис. 1 представлены графики результатов поисков по ключевому слову “экзоскелет” с учетом морфологии публикаций (с маркерами в виде квадратов) и патентов вместе с зарегистрированными программами (с маркерами в виде треугольников), в которых учтены модели, соответствующие экзоскелетам для человека или их частям.

Рис. 1.

Количество публикаций в системе РИНЦ за последние 10 лет

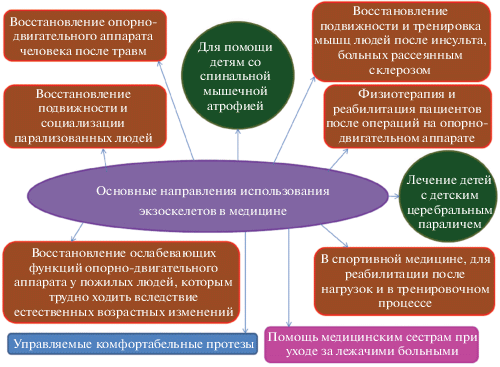
Из рис. 1 видно начало интенсивного роста публикаций по теме экзоскелетов после 2012 г. Рост количества патентов начинается с 2015 г., до этого число патентов было не более двух в год. Некоторый спад в 2019 г. объясняется тем, что анализ публикаций проводился в начале января 2020 г. и, скорее всего, еще не все публикации за 2019 г. поступили в систему РИНЦ. Таким образом, с каждым годом все больше исследователей включается в процесс создания экзоскелетов. Увеличивающееся количество научных статей, патентов, программ и т.п. свидетельствует о том, что эта тема является актуальной, востребованной и популярной. Значительный рост исследований по данной тематике объясняется технологическими возможностями, появившимися в последнее время для создания новых моделей: создание доступных мощных вычислительных систем, датчиков, новых материалов, методов управления. Это подтверждается запаздывающим ростом количества патентов после роста теоретических разработок. Существенное значение имеют широта областей применения экзоскелетов в медицине, промышленности, сельском хозяйстве, военном и спасательном деле, в космосе, в быту и значительные перспективы коммерциализации проектов по их разработке. Так, значимость экзоскелетов в медицине можно оценить по областям применения, представленным на рис. 2.

Рис. 2.

Основные направления применения экзоскелетов в медицине

При создании моделей человекоподобных механизмов используются биологические прототипы из живой природы. Наиболее активно изучаются направления создания экзоскелетов, их частей и робототехнических систем. Исследования антропоморфных роботов и экзоскелетов ведутся в направлении анализа известных пространственных моделей и конструкций экзоскелетов, антропоморфных механических систем. Ниже приводится обзор отечественных и зарубежных публикаций по этим направлениям в той мере, которой удалось достичь авторам. Рассматриваются подходы к изучению эффективных рекуррентных алгоритмов и матричных методов составления уравнений динамики, вопросы ветвления звеньев и моделирования древовидных структур, методы решения задач управления целенаправленным движением. Значимость статьи заключается в описании нового класса транспортных роботизированных устройств антропоморфной структуры, предназначенных для синтеза алгоритмов управления целенаправленным движением и исследования совместного функционирования человеко-машинной системы.

1. Обзор работ отечественных авторов. Разработкам методов математического моделирования антропоморфных механизмов и экзоскелетов существенно способствовало стремительное развитие современных средств вычислительной техники. Появилось значительное число публикаций, посвященных созданию экзоскелетов и антропоморфных роботов. Комбинирование моделей биомеханики опорно-двигательного аппарата и антропоморфных роботов может быть эффективно использовано при создании моделей экзоскелета – робототехнического устройства, функционирующего совместно с человеком.

В историческом плане необходимо отметить модель выдающего русского математика и механика П.Л. Чебышева (1821–1894), основоположника русской школы теории механизмов и машин, предложившего впервые в мире конструкцию “стопоходящей” машины [1], которая получила всеобщее одобрение на Всемирной выставке в Париже 1878 г. Заслуживают внимания работы о целенаправленном движении и моделировании опорно-двигательного аппарата человека [2, 3] с уравнениями Лагранжа в тензорном виде с учетом мышц, вызывающих движение. Предложенные модели построены аналитически без численных расчетов и оценок, равно как и параметров рассматриваемых моделей.

Вопросы моделирования антропоморфных механизмов и управления движением неустойчивых объектов приведены в [4, 5]. Задача управления движением антропоморфных механизмов с пятью и семью звеньями описывается уравнениями Лагранжа в матричной форме и решается в аналитическом виде. Излагаются результаты численных экспериментов с модельными числовыми значениями параметров антропоморфных механизмов, представленных абсолютно твердыми телами. Проблемы динамики и управления двуногих механизмов с невесомыми ногами были исследованы в [6]. Предложены различные способы организации двуногого способа перемещения.

В [7] рассматривается модель шагающего антропоморфного робота, состоящего из 11 весомых звеньев, которые считаются абсолютно твердыми или телескопическими. Механизм состоит из корпуса-балансира и двух одинаковых ног, включающих бедро, голень и стопу. Стопа состоит из пятки, плюсны и фаланги. Однако теория звеньев переменной длины не развита, намечены только основные подходы.

Проблемы построения уравнений динамики механических систем и синтеза управления были сформулированы в [8, 9] как задачи динамического программирования и представлены в качестве обратных задач динамики в [10–12]. Решение задач управления заключается в определении выражений управляющих воздействий, обеспечивающих требуемые свойства движений, и в конечном итоге сводятся к построению уравнений динамики замкнутой системы в той или иной форме [13].

В Брянском государственном техническом университете под руководством Д.Ю. Погорелова создан программный комплекс “Универсальный механизм” [14], позволяющий проводить составление уравнений динамики, численное решение и анимационную визуализацию модели по результатам расчетов. Однако “уравнения формируются программой для компьютерной обработки и недоступны в виде, например, уравнений Лагранжа II рода” [15]. Данный комплекс ориентирован на инженеров и на разработку конкретных моделей в машиностроении и не удобен для аналитических исследований. На его основе проводилось моделирование антропоморфных механизмов, отработка алгоритмов управления с обратной связью для обеспечения устойчивой ходьбы [16, 17].

Вопросам оптимального управления роботами и упругими манипуляторами посвящены работы о моделировании многозвенных стержневых систем с шарнирами на основе уравнений Аппеля [16, 18]. В [19] исследуются походки робота по цилиндрическим поверхностям. Результаты применимы также для манипулирования цилиндром посредством схвата руки робота. В [20–22] проводится моделирование движений шестиногого робота, рассматриваются вопросы управления. Компьютерное моделирование управляемых движений многозвенных роботов проводится с помощью программного комплекса “Универсальный механизм”. Решаются задачи преодоления водных препятствий шестиногим роботом с использованием плота и одновременным переносом груза. Робот типа черепахи за счет манипулирования ногами совершает раскачку и переворот. Детали законов управления авторы не раскрывают. Приводятся только общая идеология и результаты моделирования. Так как насекомые и черепахи имеют экзоскелет, то указанные работы непосредственно относятся к теме данного обзора.

Задачи управления сложными нелинейными механическими системами исследованы в публикациях [23, 24]. В них строятся обобщенные модели управления, которые представляют интерес для применения в антропоморфных механизмах.

Существенное значение для проектирования антропоидов имеет разработка устойчивых систем программного движения и численных методов решения дифференциально-алгебраических уравнений. Методы построения уравнений динамики и решения задач управления динамическими системами предложены в [25–41]. Описаны способы построения уравнений динамики, обеспечивающие стабилизацию связей при численном решении, и методы решения задач управления программным движением систем различного назначения.

Моделированию динамики систем различного назначения и построению алгоритмов управления посвящено значительное число публикаций, из которых упомянем, например, работы [42–55]. В [56–72] предложены различные алгоритмы составления дифференциальных уравнений движения экзоскелетов, антропоморфных механизмов и стержневых систем, включая системы с переменной длиной звеньев. Исследуются вопросы управления такими системами.

В ИПМ им. М.В. Келдыша РАН разработан экспериментальный комплекс роботизированных мехатронных реабилитационных устройств, который может быть использован при лечении пациентов с различной тяжестью заболеваний опорно-двигательного аппарата для тренировки различных групп мышц и суставов. Комплекс состоит из тренажера для разработки голеностопного сустава, модуля для стимуляции стопы, тренажера-вертикализатора и легопулятора (экзоскелета нижних конечностей) человека, специализированного тренажера для ног пациента [73–75]. В Лаборатории бионической робототехники ИПМ им. М.В. Келдыша РАН созданы экзоскелетные устройства ExoArm и ExoChair [76].

Учеными института механики МГУ ведутся исследования по управлению движением экзоскелета, оценке энергетических затрат при ходьбе [77–79], разрабатывается программно-аппаратный комплекс дублирования опорно-двигательного аппарата человека “ПАК Экзоскелетон”. Управление динамикой антропоморфных механизмов осуществляется на основе информации, получаемой видеокамерами [80].

В рамках проекта “ЭкзоАтлет” [81] разработаны перспективные модели пассивных и активных экзоскелетов, в первую очередь ориентированных на социально значимые направления: медицину, спасательные работы и т.п. Проводятся клинические исследования разработанных моделей и внедрение в медицинскую практику [82], начаты продажи экзоскелетов. Общие вложения в “ЭкзоАтлет” составили 130 млн рублей.

К области решения некоторых прикладных задач и использованию экзоскелетов в промышленности относятся работы [83–87]. В медицинских учреждениях России находят практическое применение как отечественные, так и зарубежные разработки экзоскелетов. Так, в региональном сосудистом центре “Республиканская клиническая больница” Министерства здравоохранения Чувашской Республики (г. Чебоксары) [88] для восстановления постинсультных больных применяется экзоскелетный комплекс Locomat Pro Швейцарской фирмы “Hocoma”.

2. Обзор работ зарубежных авторов. В [89] рассматриваются вопросы динамики систем твердых тел, связанных друг с другом идеальными голономными и неголономными, стационарными и нестационарными связями. Автором предложен общий формализм математического описания систем твердых тел, который может использоваться как для аналитических, так и для численных исследований. Приводятся различные типы систем, в частности со структурой дерева, которые применимы для разработки роботов и экзоскелетов.

В публикациях [90, 91] решаются задачи управления манипуляционными и антропоморфными роботами, создаются математические модели шагающих роботов, изучаются модели походок, локомоции человека, записываются дифференциальные уравнения движения. Разрабатываются алгоритмы управления ходьбой и решается проблема устойчивости и стабилизации ходьбы. Производится энергетический анализ и предлагается реализация искусственной ходьбы на примере экзоскелетона с электромеханическим приводом. Приводятся данные по результатам разработки и испытания первого действующего макета шагающего антропоморфного робота типа экзоскелетона.

Первый экзоскелет стали изучать в 60-х годах прошлого века [92] в американской фирме “General Electric”. Это была массивная гидравлическая конструкция под названием “Hardiman”, весившая почти 700 кг. При этом экзоскелет обладал небольшой скоростью и низкой грузоподъемностью. Дальнейшее возрастание интереса к использованию экзоскелетов стимулировал новые разработки. Курс на роботизацию и кибернетизацию в военном деле потребовал в дополнение к существующим роботам новое оснащение для живых бойцов. В США перспективные разработки решили не отдавать одной фирме, а распределили между несколькими конструкторскими коллективами, с выделением по 20 млн долл. в год каждому. Результатом конкуренции стал быстрый и реальный прорыв в области исследований экзоскелетов. Примерно за 10 лет работы ученые представили различные конструкции экзоскелетов. Разработку экзоскелетов финансировал DARPA (defense advanced research projects agency – агентство передовых оборонных исследовательских проектов) – агентство Министерства обороны США, отвечающее за новые технологии для использования в вооруженных силах) [93].

Первой и самой масштабной стала совместная разработка фирм “Raytheon” и “Sarcos”. Экзоскелет XOS представлял собой массивное устройство на основе гидравлики. У представленного в 2008 г. образца имелся целый ряд недостатков: он потреблял много электроэнергии, имел весьма ограниченный набор движений. В 2010 г. “Raytheon” и “Sarcos” представили армейским заказчикам XOS-2, затем еще две версии. Конструкторам удалось вдвое снизить энергопотребление и увеличить двигательные возможности, но даже последняя модель устройства пока не соответствует всем требованиям Darpa [94]. Добиться настоящей автономности так и не удалось – к устройству присоединен силовой кабель. Поэтому возможной сферой применения XOS станет не поле боя, а хозяйственные армейские работы.

Конструкторы из Калифорнийского университета пошли по другому направлению [95]. Они выделили три базовые функции солдата: стрелять, носить и бегать. Для двух последних функций разрабатывается экзоскелет, предназначенный для усиления ног и спины солдата. В 2004 г. началась разработка проекта HULC. К 2010 г. были показаны действующие образцы.

Активно работают над экзоскелетом японские инженеры и ученые. В производстве находится модель HAL-5 (hybrid assistive limb – гибридная вспомогательная конечность) японской корпорации “Cyberdyne” [96], имеющая и ножные, и ручные усилители. Она может работать в автономном режиме, а цена устройства не превышает 60 тыс. долл. Данная модель, созданная в помощь спасательным службам и инвалидам [97], используется для реабилитации и социальной адаптации людей с проблемами опорно-двигательного аппарата. Экзоскелет HAL стал базовой моделью для проведения различных исследований. Так, в роботе-экзоскелете HAL изучили синхронизацию и управление, основанное на изменении положения центра масс и силы реакции. Позже они добавили датчики скорости в систему управления экзоскелетом [98]. Описанный в работе [99] экзоскелет HAL управляется на основе объединения сигналов, создаваемых верхними и нижними конечностями.

Экзоскелеты появились на рынке. Швейцарская компания “Hocoma” [100] разработала Локомат (Lokomat), который является роботизированным экзоскелетом и широко используется для реабилитации больных с различными заболеваниями нижних конечностей. Компания “Honda” создала вспомогательное устройство Honda–Walk Assist And Mobility Devices [101], представляющее собой портативный экзоскелет, который состоит из талии (рамы). К ней крепятся с двух сторон искусственные бедра, каждое из которых имеет одну степень свободы. Ekso фирмы “Ekso Bionics” [102] разработан в лаборатории робототехники и человеческой инженерии в Беркли (Berkeley, Exoskeletons: Robotics & Human Engineering Laboratory) [103]. Ekso представлен в виде бионического костюма, позволяющего людям с ограниченной подвижностью нижних конечностей стоять и ходить. В качестве эволюции экзоскелета можно рассматривать роботов, представленных в [104]. “ReWalk Robotics” выпустил экзоскелет, имеющий четыре звена: бедра и коленные суставы, программируемый с заданной структурой походки, которая обеспечивает необходимую мышечную тренировку для пользователя [105]. “Rex Bionics Group” создала экзоскелет Rex [106]. Устройство обеспечивает полную поддержку веса тела в состоянии равновесия без использования трости.

Роботизированный экзоскелет для больных после инсульта описан в [107]. Индийские ученые разрабатывают экзоскелет для реабилитации и обучения заново ходьбе больных после инсульта [108–110].

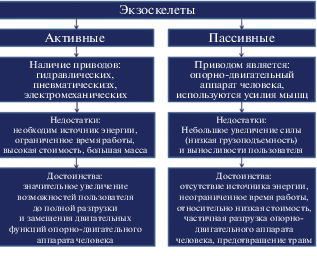
3. Анализ известных конструкций экзоскелетов. Как следует из краткого обзора известных моделей, экзоскелеты можно разделить на две группы: активные и пассивные. Их преимущества и недостатки представлены на рис. 3. Разработчики в зависимости от поставленной задачи выбирают ту или иную модель экзоскелета.

Рис. 3.

Сравнительный анализ активных и пассивных экзоскелетов

Пассивные модели чаще используются в промышленном производстве при выполнении сборочных операций, требующих от работника находиться продолжительное время в одной позе, а также для перераспределения и снижения нагрузок на опорно-двигательный аппарат человека и предотвращения травм на производстве, в сельском хозяйстве, при уходе за лежачими больными, при переноске или подъеме тяжестей. Активные экзоскелеты и их фрагменты находят применение в промышленности и в медицине в процессе реабилитации больных и восстановления двигательных функций.

Большинство роботизированных экзоскелетов сосредоточены на конструкции нижней конечности, предполагают совместное функционирование тазобедренного сустава с голеностопным суставом и состоят из звеньев постоянной длины. Например, в коленном суставе ось вращения не постоянна, а изменяет свое положение. Обычно представленные в публикациях экзоскелеты состоят из механических суставов с простыми поворотными осями, соединенными между собой абсолютно твердыми стержнями. Число степеней свободы в местах подвижных сочленений бывает недостаточно, что создает скованность и неестественность движений. Жесткая конструкция на практике может привести к травме пользователя [111], так как в суставах человека при движении оси вращений не остаются в одном месте, а перемещаются в пространстве. Моделей, учитывающих изменения длин звеньев, на данный момент не выявлено. Учет изменений длин звеньев приводит к увеличению числа степеней свободы и возникают трудности при управлении движением.

Среди публикаций, имеющихся в открытом доступе, не удалось обнаружить описание пространственных механизмов со звеньями переменной длины. Поэтому исследования в этом направлении могут способствовать дальнейшим разработкам новых конструкций экзоскелетов.

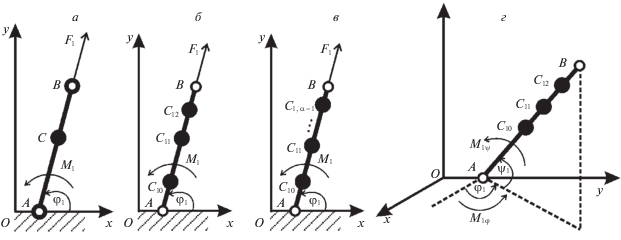
4. Моделирование опорно-двигательного аппарата человека и экзоскелета. Для описания опорно-двигательного аппарата человека могут быть успешно использованы конструкции, содержащие звенья переменной длины с сосредоточенными массами в шарнирах-суставах и между ними (рис. 4, а–г).

Рис. 4.

Модели подвижного звена опорно-двигательного аппарата человека с сосредоточенными массами

Рассмотрим движение звена AB длиной l(t) с неподвижной точкой А, расположенной на оси Ox системы Oxy. Представим звено системой трех точек A, C, B с массами m0, m1, m2 соответственно, две из которых совпадают с концами стержня, третья точка С находится между ними. Положение этой точки будем определять величиной kl(t), k – const, 0 < k < 1, положение звена – углом φ1 относительно оси Ox и длиной l. На звено действует сила тяжести, момент М1 относительно точки О и направленная вдоль AB сила F1, приложенная в точке В. Лагранжиан определяется выражением

(4.1)
$L = T - P,\quad 2T = a({{(\dot {l})}^{2}} + {{l}^{2}}{{({{\dot {\varphi }}_{1}})}^{2}}),\quad P = bglS,$
где a = m1k2 + m2, S = sinφ1, b = m1k + m2.

Для модели, представленной на рис. 4, в, при нумерации точек от 1 до n значения a и b изменятся соответственно:

$a = {{m}_{1}}k_{1}^{2} + {{m}_{2}}k_{2}^{2} + ... + {{m}_{n}}k_{n}^{2},\quad b = {{m}_{1}}{{k}_{1}} + {{m}_{2}}{{k}_{2}} + ... + {{m}_{n}}{{k}_{n}}.$

Движение звена описывается уравнениями Лагранжа

(4.2)
${{l}^{2}}a{{\ddot {\varphi }}_{1}} + glbC + 2la\dot {l}{{\dot {\varphi }}_{1}} = {{M}_{1}},\quad a\ddot {l} - al\dot {\varphi }_{1}^{2} + gbS = {{F}_{1}}$
с начальными условиями при t0 = 0:

(4.3)
${{\varphi }_{1}}\left( {{{t}_{0}}} \right) = \varphi _{1}^{0},\quad {{\dot {\varphi }}_{1}}\left( {{{t}_{0}}} \right) = \dot {\varphi }_{1}^{0},\quad l\left( {{{t}_{0}}} \right) = {{l}^{0}},\quad \dot {l}\left( {{{t}_{0}}} \right) = {{\dot {l}}^{0}},\quad C = \cos \varphi ,\quad S = \sin \varphi .$

Положение звена AB длиной l1(t) в пространстве, определяемом системой координат Oxyz, (рис. 4, г), задается расстоянием от точки A до центра масс, углом φ1 между осью Оx и проекцией звена AB на плоскость Oxy и углом ψ1 между звеном AB и этой плоскостью. Координаты сосредоточенных на звене масс, кинетическая энергия и потенциальная энергия звена находятся так:

${{x}_{C}}_{{1\beta }} = {{l}_{1}}{{n}_{{1\beta }}}C_{1}^{\psi }C_{1}^{\varphi },\quad {{y}_{C}}_{{1\beta }} = {{l}_{1}}{{n}_{{1\beta }}}C_{1}^{\psi }S_{1}^{\varphi },\quad {{z}_{C}}_{{1\beta }} = {{l}_{1}}{{n}_{1}}_{\beta }S_{1}^{\psi },\quad \beta = 0,1,2,$
(4.5)
$C_{1}^{\varphi } = {\text{cos}}{{\varphi }_{1}},\quad C_{1}^{\psi } = {\text{cos}}{{\psi }_{1}},\quad S_{1}^{\varphi } = {\text{sin}}{{\varphi }_{1}},\quad S_{1}^{\psi } = {\text{sin}}{{\psi }_{1}}.$
$L = T - \Pi ,\quad T = \frac{1}{2}{{\zeta }_{1}}[\dot {l}_{1}^{2} + l_{1}^{2}((\dot {\varphi }_{1}^{2}{{(C_{1}^{\psi })}^{2}} + \dot {\psi }_{1}^{2})],\quad \Pi = g{{\eta }_{1}}{{l}_{1}}S_{1}^{\psi },$
(4.6)
${{\zeta }_{1}} = {{m}_{{11}}}n_{{11}}^{2} + {{m}_{{12}}},\quad {{\eta }_{1}} = {{m}_{{11}}}{{n}_{{11}}} + {{m}_{{12}}}.$

Дифференциальные уравнения движения звена переменной длины в трехмерном пространстве описываются уравнениями Лагранжа:

(4.7)
${{\zeta }_{1}}l_{1}^{2}{{(C_{1}^{\psi })}^{2}}{{\ddot {\varphi }}_{1}} + 2{{\zeta }_{1}}{{l}_{1}}{{(C_{1}^{\psi })}^{2}}{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} - 2{{\zeta }_{1}}l_{1}^{2}C_{1}^{\psi }S_{1}^{\psi }{{\dot {\varphi }}_{1}}{{\dot {\psi }}_{1}} = {{M}_{{1\varphi }}},$
(4.8)
${{\zeta }_{1}}l_{1}^{2}{{\ddot {\psi }}_{1}} + {{\zeta }_{1}}l_{1}^{2}C_{1}^{\psi }S_{1}^{\psi }\dot {\varphi }_{1}^{2} + 2{{\zeta }_{1}}{{l}_{1}}{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} + g{{\eta }_{1}}{{l}_{1}}C_{1}^{\psi } = {{M}_{{1\psi }}},$
(4.9)
${{\zeta }_{1}}{{\ddot {l}}_{1}} - {{\zeta }_{1}}{{l}_{1}}{{(C_{1}^{\psi })}^{2}}\dot {\varphi }_{1}^{2} - {{\zeta }_{1}}{{l}_{1}}\dot {\psi }_{1}^{2} + g{{\eta }_{1}}S_{1}^{\psi } = {{F}_{1}}.$

Общее решение системы дифференциальных уравнений движения содержит шесть произвольных постоянных, которые определяются по начальным условиям (4.3) и в дополнение к ним (4.10):

(4.10)
${{\psi }_{1}}\left( {{{t}_{0}}} \right) = \psi _{1}^{0},\quad {{\dot {\psi }}_{1}}\left( {{{t}_{0}}} \right) = \dot {\psi }_{1}^{0}.$

Модель опорно-двигательного аппарата человека при общем рассмотрении содержит точки с ветвлением, например, точки соединения с корпусом опорной ноги, переносимой ноги, руки. В [67] приводятся уравнения динамики моделей с точками ветвления.

Динамика системы n звеньев переменой длины, представленной на рис. 5, описывается системой нелинейных дифференциальных уравнений, представленной в векторно-матричной форме [71, 72]:

(4.11)
$\begin{gathered} {{A}_{\kappa }}(\varphi ,\psi ,l)\ddot {\varphi } + {{B}_{\kappa }}(\varphi ,\psi ,l)\ddot {\psi } + {{\Lambda }_{\kappa }}(\varphi ,\psi ,l)\ddot {l} + {{D}_{\kappa }}(\varphi ,\psi ,l)\dot {\Phi }\dot {\varphi } + {{E}_{\kappa }}(\varphi ,\psi ,l)\dot {\Psi }\dot {\psi } + \\ + 2{{G}_{\kappa }}(\varphi ,\psi ,l)\dot {\Phi }\dot {\psi } + 2{{H}_{\kappa }}(\varphi ,\psi ,l)\dot {\Phi }\dot {l} + 2{{K}_{\kappa }}(\varphi ,\psi ,l)\dot {\Psi }\dot {l} + g{{P}_{\kappa }}(\psi ) = {{M}_{\kappa }}(\varphi ,\psi ,l). \\ \end{gathered} $
Рис. 5.

Фрагмент модели опорно-двигательного аппарата человека с n звеньями переменной длины в пространстве

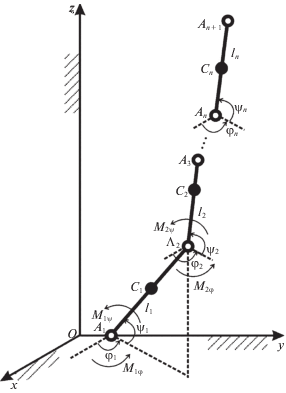
Здесь κ = φ, ψ, l: φ = (φ1, …, φn) и ψ = (ψ1, …, ψn) – векторы угловых координат сосредоточенных масс, l = (l1, …, ln) – вектор длин звеньев, $\dot {\Phi }$ = diag(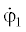, …, ${{\dot {\varphi }}_{n}}$), $\dot {\Psi }$ = diag(${{\dot {\psi }}_{1}}$, …, ${{\dot {\psi }}_{n}}$) – диагональные матрицы; Mκ – обобщенные силы, Aκ(φ, ψ, l), Bκ(φ, ψ, l), Dκ(φ, ψ, l), Eκ(φ, ψ, l), Gκ(φ, ψ, l) – матрицы, учитывающие инерционные свойства, Λκ(φ, ψ, l), Hκ(φ, ψ, l), Kκ(φ, ψ, l) – матрицы, учитывающие переменность длины звеньев; Pκ(ψ) – матрицы, определяемые силами тяжести.

Рассмотрим пример составления дифференциальных уравнений динамики плоской модели, состоящей из четырех звеньев переменной длины (рис. 6).

Рис. 6.

Система с четырьмя подвижными звеньями переменной длины на плоскости

Элементы матрицы A определяются равенствами

${{a}_{{11}}} = l_{1}^{2}\left( {{{m}_{{11}}}n_{{11}}^{2} + {{m}_{{12}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 2}^4 {{{m}_{{k\beta }}}} } } \right),$
${{a}_{{12}}} = {{a}_{{21}}} = {{l}_{1}}{{l}_{2}}\left( {{{m}_{{21}}}{{n}_{{21}}} + {{m}_{{22}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 3}^4 {{{m}_{{k\beta }}}} } } \right)\cos ({{\varphi }_{1}} - {{\varphi }_{2}}),$
(4.12)
${{a}_{{j3}}} = {{a}_{{3j}}} = {{l}_{j}}{{l}_{3}}\left( {{{m}_{{31}}}{{n}_{{31}}} + {{m}_{{32}}} + \sum\limits_{\beta = 0}^2 {{{m}_{{4\beta }}}} } \right)\cos ({{\varphi }_{j}} - {{\varphi }_{3}}),\quad j = 1,2,$
${{a}_{{j4}}} = {{a}_{{4j}}} = {{l}_{j}}{{l}_{4}}({{m}_{{41}}}{{n}_{{41}}} + {{m}_{{42}}})\cos ({{\varphi }_{j}} - {{\varphi }_{4}}),\quad j = 1,2,$
${{a}_{{22}}} = l_{2}^{2}\left( {{{m}_{{21}}}n_{{21}}^{2} + {{m}_{{22}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 3}^4 {{{m}_{{k\beta }}}} } } \right),\quad {{a}_{{33}}} = l_{3}^{2}\left( {{{m}_{{31}}}n_{{31}}^{2} + {{m}_{{32}}} + \sum\limits_{\beta = 0}^2 {{{m}_{{4\beta }}}} } \right),$
${{a}_{{34}}} = {{a}_{{43}}} = {{l}_{3}}{{l}_{4}}({{m}_{{41}}}{{n}_{{41}}} + {{m}_{{42}}})\cos ({{\varphi }_{3}} - {{\varphi }_{4}}),\quad {{a}_{{44}}} = l_{4}^{2}({{m}_{{41}}}n_{{41}}^{2} + {{m}_{{42}}}).$

Аналогично находятся элементы для всех остальных матриц. В итоге первое уравнение принимает вид

(4.13)
${{a}_{{11}}}{{\ddot {\varphi }}_{1}} + {{a}_{{12}}}{{\ddot {\varphi }}_{2}} - {{a}_{{13}}}{{\ddot {\varphi }}_{3}} - {{a}_{{14}}}{{\ddot {\varphi }}_{4}} + ...,$
где многоточием обозначены члены, не содержащие ускорений.

Сравнивая уравнения движения на плоскости и в пространстве, можно получить закономерность записи уравнений трехмерного движения по соответствующему дифференциальному уравнению для двумерной модели. Приведем данные закономерности на примере матрицы А (4.14). Для того, чтобы отличать элементы матриц пространственной и плоской моделей, снабдим их верхними индексами “3D” и “2D” соответственно. Плоская и пространственная модели должны быть одинаковой структуры, т.е. иметь одинаковое количество звеньев, расположение точек ветвления, распределение масс на звене. Формулы для перехода имеют следующий вид:

${}^{{3D}}a_{{11}}^{\varphi } = l_{1}^{2}\left( {{{m}_{{11}}}n_{{11}}^{2} + {{m}_{{12}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 2}^4 {{{m}_{{k\beta }}}} } } \right){\text{co}}{{{\text{s}}}^{2}}{{\psi }_{1}},$
${}^{{3D}}a_{{12}}^{\varphi } = {}^{{3D}}a_{{21}}^{\varphi }~ = {{l}_{1}}{{l}_{2}}\left( {{{m}_{{21}}}{{n}_{{21}}} + {{m}_{{22}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 3}^4 {{{m}_{{k\beta }}}} } } \right){\text{cos}}({{\varphi }_{1}}--{{\varphi }_{2}}){\text{cos}}{{\psi }_{1}}{\text{cos}}{{\psi }_{2}},$
$^{{3D}}a_{{j3}}^{\varphi }~\, = {{\,}^{{3D}}}a_{{3j}}^{\varphi }~ = {{l}_{j}}{{l}_{3}}\left( {{{m}_{{31}}}{{n}_{{31}}} + {{m}_{{32}}} + \sum\limits_{\beta = 0}^2 {{{m}_{{4\beta }}}} } \right){\text{cos}}({{\varphi }_{j}}--{{\varphi }_{3}}){\text{cos}}{{\psi }_{j}}{\text{cos}}{{\psi }_{3}},\quad j = {\text{ }}1,2,$
${}^{{3D}}a_{{j4}}^{\varphi } = {}^{{3D}}a_{{4j}}^{\varphi } = {{l}_{j}}{{l}_{4}}\left( {{{m}_{{41}}}{{n}_{{41}}} + {{m}_{{42}}}} \right){\text{cos}}({{\varphi }_{j}}--{{\varphi }_{4}}){\text{cos}}{{\psi }_{3}}{\text{cos}}{{\psi }_{4}},\quad j = 1,2,$
${}^{{3D}}a_{{22}}^{\varphi } = l_{2}^{2}\left( {{{m}_{{21}}}n_{{21}}^{2} + {{m}_{{22}}} + \sum\limits_{\beta = 0}^2 {\sum\limits_{k = 3}^4 {{{m}_{{4\beta }}}} } } \right){\text{co}}{{{\text{s}}}^{2}}{{\psi }_{2}},$
${}^{{3D}}a_{{33}}^{\varphi } = l_{3}^{2}\left( {{{m}_{{31}}}n_{{31}}^{2} + {{m}_{{32}}} + \sum\limits_{\beta = 0}^2 {{{m}_{{4\beta }}}} } \right){\text{co}}{{{\text{s}}}^{2}}{{\psi }_{3}},$
${}^{{3D}}a_{{34}}^{\varphi } = {}^{{3D}}a_{{43}}^{\varphi } = {{l}_{3}}{{l}_{4}}\left( {{{m}_{{41}}}{{n}_{{41}}} + {{m}_{{42}}}} \right){\text{cos}}({{\varphi }_{3}}--{{\varphi }_{4}}){\text{cos}}{{\psi }_{3}}{\text{cos}}{{\psi }_{4}},$
(4.14)
${}^{{3D}}a_{{44}}^{\varphi } = l_{4}^{2}({{m}_{{41}}}n_{{41}}^{2} + {{m}_{{42}}}){\text{co}}{{{\text{s}}}^{2}}{{\psi }_{4}}.$

Далее построение аналогично выражению (4.13). Описанный метод позволяет довольно просто составить алгоритм записи уравнений динамики.

Разработан рекуррентный алгоритм составления дифференциальных уравнений движения. Ранее были получены обобщающие формулы для матриц, входящих в систему дифференциальных уравнений движения, позволяющие ее записать для экзоскелета с n подвижными звеньями переменной длины [72].

На основе полученных уравнений составлен рекуррентный алгоритм, который по матрицам коэффициентов уравнений системы, содержащей n звеньев, определяет матрицы коэффициентов уравнений системы с n + 1 звеном. По известной матрице

(4.15)
${{A}_{n}} = \left( {{{a}_{{ij}}}} \right),\quad {{a}_{{ij}}} = \left( {{{\eta }_{j}} + \sum\limits_{k = j + 1}^n {{{\theta }_{k}}} } \right){{l}_{i}}{{l}_{j}}{{C}_{{ij}}},\quad i,j = 1, \ldots ,n,\quad {{a}_{{ij}}} = {{\theta }_{{n + 1}}}{{l}_{i}}{{l}_{j}}{{C}_{{ij}}},\quad i,j = 1, \ldots ,n,$
элементы матрицы ${{A}_{{n + 1}}}$ задаются выражениями

(4.16)
$\begin{gathered} {{a}_{{n + 1,j}}} = {{\eta }_{{n + 1}}}{{l}_{{n + 1}}}{{l}_{j}}{{C}_{{n + 1,j}}},\quad {{a}_{{i,n + 1}}} = {{\eta }_{{n + 1}}}{{l}_{{n + 1}}}{{l}_{i}}{{C}_{{i,n + 1}}}, \\ i,j = 1,\; \ldots ,\;n + 1. \\ \end{gathered} $
${{C}_{{ij}}} = {\text{cos}}({{\varphi }_{i}}--{{\varphi }_{j}}),\quad {{\theta }_{n}}_{{ + 1}} = \sum\limits_{\beta = 0}^{\alpha - 1} {{{m}_{{n + 1,\beta }}}} ,\quad {{\eta }_{n}}_{{ + 1}} = \sum\limits_{\beta = 0}^{\alpha - 1} {{{m}_{{n + 1,\beta }}}{{n}_{{n + 1,\beta }}}} ,\quad {{\zeta }_{n}}_{{ + 1}} = \sum\limits_{\beta = 0}^{\alpha - 1} {{{m}_{{n + 1,\beta }}}n_{{n + 1,\beta }}^{2}} .$

Алгоритм построения матрицы трехмерной модели с n + 1 звеном по матрице двумерной модели с n звеньями имеет следующую последовательность действий:

(4.17)
$^{{2D}}{{А}_{n}} \to {{\,}^{{2D}}}{{А}_{n}}_{{ + 1}} \to {{\,}^{{3D}}}{{A}_{n}}_{{ + 1}}.$

Аналогично находятся остальные матрицы.

Таким образом, получен рекуррентный алгоритм составления уравнений движения двумерной стержневой механической системы с n + 1 звеном по известным уравнениям системы со звеньями переменной длины для дальнейшего перехода к трехмерной модели соответствующей структуры. Это позволяет автоматизировать составление системы дифференциальных уравнений движения стержневой механической системы со звеньями переменной длины.

Матричный метод и рекуррентный алгоритм составления дифференциальных уравнений реализован в среде системы компьютерной математики “Mathematica” и пример применения приведен в приложении к статье [69]. При составлении уравнений Лагранжа было затрачено время в секундах для модели с одним подвижным звеном – 0.59, с двумя подвижными звеньями – 5.3, с тремя подвижными звеньями – 37 при использовании матричного метода соответственно 0.46, 0.55 и 0.79 с [67]. Рекуррентный алгоритм для модели с двумя и тремя подвижными звеньями занял 0.59 и 0.86 с. Проводя сравнение с трехмерными моделями, для модели экзоскелета с двумя подвижными звеньями (рис. 5 при n = 2) время, затраченное на составление уравнений Лагранжа, оказалось равным 113.69 с. Использование матричного метода потребовало 1.30 с. Таким образом, видно, что различия в скорости составления системы дифференциальных уравнений движения нарастают с увеличением количества звеньев и перехода к трехмерной модели.

Способы решения различных модельных задач, включая вопросы, связанные с трением в суставах, движения человека в экзоскелете, точности моделирования изложены в [56–58].

Были разработаны: модель звена экзоскелета с одним участком переменной длины и абсолютно твердым весомым стержнем (рис. 7, а), с двумя невесомыми участками переменной длины и одним абсолютно твердым весомым стержнем (рис. 7, б), с двумя весомыми абсолютно твердыми участками и одним невесомым участком переменной длины (рис. 7, в), телескопическая модель звена (рис. 7, г), состоящая из двух весомых абсолютно жестких частей – штока и корпуса, которые совершают движение относительно друг друга вдоль прямой, проходящей через его начало и конец (рис. 7, г). Один из шарниров жестко соединен со штоком, второй – с корпусом. Под действием реакций со стороны опоры и соседних стержней происходит движение штока внутри корпуса, тем самым обеспечивается изменение длины звена.

Рис. 7.

Модели одного звена экзоскелета переменной длины

Все предложенные модели звеньев на плоскости были перенесены в пространство. Для этих моделей звеньев были составлены системы дифференциальных уравнений движения. Далее проводилось исследование многозвенных моделей, составленных из таких звеньев, получены системы дифференциальных уравнений движения в обобщенном векторно-матричном виде, реализован для них рекуррентный метод составления систем дифференциальных уравнений движения. Проводилось математическое моделирование движения экзоскелетов и антропоморфных роботов с использованием разработанных моделей звеньев переменной длины [57, 59–71].

Заключение. Проведен анализ российских и зарубежных публикаций, посвященных исследованиям экзоскелетов. На основании изучения работ библиографической базы РИНЦ установлен факт интенсивного роста публикаций по данной тематике. Выявлены проблемы в области создания экзоскелетов, связанные на данный момент с их низкой функциональностью, недостаточной комфортабельностью. Активным экзоскелетам свойственно высокое энергопотребление и короткое время автономной работы при эксплуатации.

Одним из возможных вариантов повышения качества работы экзоскелетов может оказаться включение в структуры моделей звеньев переменной длины. Предложенные модели могут быть востребованы при изучении экзоскелетов и применены в исследованиях по моделированию опорно-двигательного аппарата человека. Матричные методы и рекуррентные алгоритмы позволяют использовать методы компьютерной алгебры для построения уравнений динамики стержневых систем и решения задач управления целенаправленным движением.

Список литературы

  1. Научное наследие П.Л. Чебышева. Вып. 2. Теория механизмов. М.–Л.: Изд-во. АН СССР, 1945. 192 с.

  2. Коренев Г.В. Очерки механики целенаправленного движения. М.: Наука, 1980. 192 с.

  3. Коренев Г.В. Введение в механику человека. М.: Наука, 1977. 264 с.

  4. Формальский А.М. Управление движением неустойчивых объектов. М.: Физматлит, 2012. 232 с.

  5. Формальский А.М. Перемещение антропоморфных механизмов. М.: Наука, 1982. 368 с.

  6. Белецкий В.В. Двуногая ходьба: модельные задачи динамики и управления. М.: Наука, 1984. 288 с.

  7. Бербюк В.Е. Динамика и оптимизация робототехнических систем. Киев: Наук. думка, 1989. 192 с.

  8. Галиуллин А.С. О задачах динамического программирования // Тр. УДН им. П. Лумумбы. 1964. Т. 5. Вып. 2. С. 3–9.

  9. Галиуллин А.С., Мухаметзянов И.А., Мухарлямов Р.Г., Фурасов В.Д. Построение систем программного движения. М.: Наука, 1971. 352 с.

  10. Галиуллин А.С. Обратные задачи динамики и задачи управления движениями материальных систем // Дифференц. уравнения. 1972. Т. 8. № 9. С. 1535–1541.

  11. Галиуллин А.С. Методы решения обратных задач динамики. М.: Наука, 1986. 224 с.

  12. Галиуллин А.С. Обратные задачи динамики. М.: Наука, 1981. 143 с.

  13. Галиуллин А.С., Гафаров Г.Г., Малайшка Р.П., Хван А.М. Аналитическая динамика систем Гельмгольца, Биркгофа, Намбу // Успехи физ. наук. 1997. 324 с.

  14. http://www.umlab.ru/

  15. http://www.umlab.ru/faq/

  16. Голубев Ю.Ф., Погорелов Д.Ю. Компьютерное моделирование шагающих роботов // Фундаментальная и прикладная математика. 1998. Т. 4. № 2. С. 525–534.

  17. Погорелов Д.Ю. Современные алгоритмы компьютерного синтеза уравнений движения систем тел // Изв. РАН. ТиСУ. 2005. № 4. С. 5–15.

  18. Голубев Ю.Ф. Функция Аппеля в динамике систем твердых тел : Препринты № 58. М.: ИПМ им. М.В. Келдыша, 2014. 16 с. URL: http://library.keldysh.ru/preprint.asp?id=2014-58.

  19. Golubev Yu., Melkumova E. Two-legged Walking Robot Prescribed Motion on a Rough Cylinder // AIP Conf. Proceedings. V. 1959. Published by the American Institute of Physics, 2018. https://doi.org/10.1063/1.5034589.

  20. Голубев Ю.Ф., Корянов В.В. Транспортировка груза на плоту инсектоморфным роботом // Изв. РАН. ТиСУ. 2018. № 5. С. 136–146.

  21. Голубев Ю.Ф., Корянов В.В., Мелкумова Е.В. Приведение инсектоморфного робота в рабочее состояние из аварийного положения “вверх ногами” // Изв. РАН. ТиСУ. 2019. № 6. С. 163–176.

  22. Голубев Ю.Ф., Корянов В.В. Экстремальные локомоционные возможности инсектоморфных роботов. М.: ИПМ им. М.В. Келдыша, 2018. 212 с.

  23. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.

  24. Черноусько Ф.Л., Болотник Н.Н. Локомоция многозвенных систем на плоскости: динамика, управление, оптимизация: Препринт № 1128. М.: Изд-во ИПМех РАН, 2016. 154 с.

  25. Мухарлямов Р.Г. Об уравнениях движения механических систем // Дифференц. уравнения. 1983. Т. 19. № 12. С. 2048–2056.

  26. Mukharlyamov R.G., Ibragimov R.G., Kolesnikov A.P. Control in Adaptive Optical Systems // IFAC Workshop on Evaluation of Adaptive Control Strategies in Industrial Application. Tbilisi, USSR, 17–21 Oct. 1989. Oxford: Pergamonpress, 1990. P. 301–306.

  27. Мухарлямов Р.Г. Управление программным движением адаптивной оптической системы // Вестн. РУДН, Сер. Прикл. матем. и информатика. 1994. № 1. С. 22–40.

  28. Мухарлямов Р.Г. Управление программным движением многозвенного манипулятора // Вестн. РУДН. Сер. Прикл. матем. и информатика. 1998. № 1. С. 22–39.

  29. Мухарлямов Р.Г. О численном решении дифференциально-алгебраических уравнений // Вестн. РУДН. Сер. Прикл. матем. и информатика. 1999. № 1. С. 20–24.

  30. Мухарлямов Р.Г. О построении систем дифференциальных уравнений движения механических систем // Дифференц. уравнения. 2003. Вып. 39. № 3. С. 343–353.

  31. Мухарлямов Р.Г. Стабилизация движений механических систем на заданных многообразиях фазового пространства // ПММ. 2006. Т. 70. № 2. С 236–249.

  32. Mukharlyamov R.G. Reduction of Dynamical Equations for the Systems with Constraints to Given Structure // J. Applied Mathematics and Mechanics. 2007. V. 71. № 3. P. 401–410.

  33. Мухарлямов Р.Г. Дифференциально-алгебраические уравнения программных движений лагранжевых динамических систем // Изв. РАН. МТТ. 2011. № 4. С. 50–61.

  34. Mukharlyamov R.G., Beshaw A.W. Solving Differential Equations of Motion for Constrained Mechanical Systems // Вестн. РУДН. Сер. Математика, информатика, физика. 2013. № 3. С. 81–91.

  35. Мухарлямов Р.Г. Управление программным движением системы с переменными массами // Вестн. Казанск. технологического ун-та. 2013. № 12. С. 278–284.

  36. Мухарлямов Р.Г. Моделирование процессов управления, устойчивость и стабилизация систем с программными связями // Изв. РАН. ТиСУ. 2015. № 1. С. 15–28.

  37. Мухарлямов Р.Г. Управление динамикой систем с позиционными связями // Аналитическая механика, устойчивость и управление: Тр. XI Междунар. Четаевской конф. Т. 3. Секция 3. Управление. Ч. II. Казань : КНИТУ-КАИ, 2017. С. 140–146.

  38. Mukharlyamov R.G., Tleubergenov M.I. Control of System Dynamics and Constraints Stabilization // Distributed Computer and Communication Networks (DCCN 2017) / Eds V. Vishnevskiy, K. Samouylov, Kozyrev D. Communications in Computer and Information Science. V. 700. Cham : Springer, 2017. P. 431–442.

  39. Мухарлямов Р.Г. Управление динамикой системы с дифференциальными связями // Изв. РАН. ТиСУ. 2019. № 4. С. 16–28.

  40. Каспирович И.Е., Мухарлямов Р.Г. О методах построения уравнений динамики с учетом стабилизации связей // Изв. РАН. МТТ. 2019. № 3. С. 124–135.

  41. Kaspirovich I.E. Application of Constraint Stabilization to Nonholonomic mechanics // 2nd Intern. Conf. on Industrial Engineering, Applications and Manufacturing (ICIEAM). Chelyabinsk, 2016. https://doi.org/10.1109/ICIEAM.2016.7910921.

  42. Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. М.: Наука, 1967. 519 с.

  43. Бутенин Н.В., Фуфаев Н.А. Введение в аналитическую динамику: 2-е изд., пер. и доп. М.: Наука, 1991. 250 с.

  44. Калёнова В.И., Карапетян А.В., Морозов В.М., Салмина М.А. Неголономные механические системы и стабилизация движения // Фундаментальная и прикладная математика. 2005. Т. 11. № 7. С. 117–158.

  45. Борисов А.В., Мамаев И.С., Килин А.А. Избранные задачи неголономной механики. Москва–Ижевск: Институт компьютерных исследований, 2005. 289 с.

  46. Baumgarte J. Stabilization of Constraints and Integrals of Motion in Dynamical Systems // Computer Methods in Applied Mechanics and Engineering. 1972. V. 1. Iss. 1. P. 1–16.

  47. Пол Р. Моделирование, планирование траекторий и управление движением робота-манипулятора / Пер. с англ. М.: Наука, Физматлит, 1976. 104 с.

  48. Layton R.A. Principles of Analytical System Dynamics. N.Y.: Springer, 1998. 158 p.

  49. Meiser P., Enge O., Freudenberg H., Kielau G. Electromechanical Interactions in Multibody Systems Containing Electromechanical Drives // Multibody System Dynamics. 1997. № 1. P. 281–302.

  50. Llibre J., Ramirez R. Inverse Problems of Ordinary Differential Equations and Applications. Switzerland: Springer International Publishing, 2016. 266 p.

  51. Amirouche F. Fundamentals of Multibody Dynamics: Theory and Applications. Boston: Birkh user, 2006.

  52. Грдина Я.И. Динамика живых организмов. Екатеринослав: Типография И. Когана, 1911. 108 с.

  53. Раус Э. Дж. Динамика систем твердых тел. М.: Наука, 1983. Т. 1. 463 с.

  54. Юревич Е.И. Управление роботами и робототехническими системами. СПб., 2000. elib.spbstu.ru›dl/326.pdf/download.

  55. Козлов В.В., Макарычев В.П., Тимофеев А.В., Юревич Е.И. Динамика управления роботами. М.: Наука, Физматлит, 1984. 336 с.

  56. Борисов А.В. Проверка возможности использования экспериментально определенных на людях управляющих моментов для управления движением антропоморфного робота // Тр. XXI Междунар. науч.-техн. конф. “Экстремальная робототехника”. СПб.: Политехника-сервис, 2010. С. 327–337.

  57. Борисов А.В. Управление движением одиннадцатизвенного антропоморфного робота на основе информации, экспериментально полученной на биологических объектах // Вестн. Воронежск. гос. технологической академии. Сер. Информационные технологии, моделирование и управление. 2011. № 2. С. 68–71.

  58. Борисов А.В. Динамика эндо- и экзоскелета: монография. Смоленск: Смоленская городская типография, 2012. 296 с.

  59. Борисов А.В. Автоматизация проектирования стержневых экзоскелетов // Мехатроника, автоматизация, управление. 2014. № 10. С. 29–33.

  60. Борисов А.В. Автоматизация разработки трехмерных моделей экзоскелетов со звеньями переменной длины // Мехатроника, автоматизация, управление. 2015. Т. 16. № 12. С. 828–835.

  61. Борисов А.В. Модель телескопического звена экзоскелета // Энергетика, информатика, инновации. 2016. Т. 1. С. 235–238.

  62. Борисов А.В., Розенблат Г.М. Новые алгоритмы составления дифференциальных уравнений движения экзоскелета с переменной длиной звеньев и управлением в шарнирах-суставах // Компьютерные исследования и моделирование. 2017. Т. 9. № 2. С. 201–210.

  63. Борисов А.В. Синтез экзоскелета со звеньями переменной длины для опорно-двигательного аппарата человека // Вопросы оборонной техники. Технические средства противодействия терроризму. 2017. Сер. 16. Вып. 5–6. С. 59–67.

  64. Борисов А.В. Модель экзоскелета и антропоморфного робота с многозвенными стопами // Технология машиностроения и материаловедение: материалы междунар. науч.-практ. конф. 2017. № 1. С. 21–23.

  65. Борисов А.В. Эмпирический и теоретический подходы к управлению движением экзоскелета // Вестн. Балтийского федерального ун-та им. И. Канта. Сер.: Физико-математические и технические науки. 2017. № 3. С. 33–47.

  66. Борисов А.В., Розенблат Г.М. Матричный метод составления дифференциальных уравнений движения экзоскелета и управление им // ПММ. 2017. Т. 81. № 5. С. 511–522.

  67. Борисов А.В., Кончина Л.В. Сравнительный анализ алгоритмов управления экзоскелетом со звеньями переменной длины // Мехатроника, автоматизация, управление. 2017. Т. 18. № 4. С. 238–245.

  68. Борисов А.В., Розенблат Г.М. Моделирование динамики экзоскелета с управляемыми моментами в суставах и переменной длиной звеньев с использованием рекуррентного метода составления дифференциальных уравнений движения // Изв. РАН. ТиСУ. 2018. № 2. С. 148–174.

  69. Борисов А.В., Розенблат Г.М. Автоматизация разработки экзоскелетов и антропоморфных роботов с использованием рекуррентного метода составления дифференциальных уравнений движения // Справочник. Инженерный журнал. 2018. № 1. С. 25–31.

  70. Борисов А.В. Механика пространственной модели экзоскелета и антропоморфного робота // Вопросы оборонной техники. Технические средства противодействия терроризму. 2018. Сер. 16. Вып. 3–4. С. 46–55.

  71. Борисов А.В., Розенблат Г.М. Динамика механических стержневых систем со звеньями переменной длины применительно к эндо-, экзоскелетам и антропоморфным роботам на плоскости и в пространстве // Справочник. Инженерный журнал. 2019. № 10 (начало). С. 1–20.

  72. Борисов А.В., Розенблат Г.М. Динамика механических стержневых систем со звеньями переменной длины применительно к эндо-, экзоскелетам и антропоморфным роботам на плоскости и в пространстве // Справочник. Инженерный журнал. 2019. № 11 (окончание). С. 1–20.

  73. Павловский В.Е., Платонов А.К., Алисейчик А.П. и др. Биомехатронный комплекс нейрореабилитации – концепция, конструкция, модели и управление: Препринт № 111. М.: ИПМ им. М.В. Келдыша, 2014. 19 с. URL: http://library.keldysh.ru/preprint.asp?id=2014-111.

  74. Алисейчик А.П., Орлов И.А., Павловский В.Е., Павловский В.В., Платонов А.К. Механика и управление экзоскелетами нижних конечностей для нейрореабилитации спинальных больных // ХI Всероссийск. съезд по фундаментальным проблемам теоретической и прикладной механики: аннотации докладов. Казань: Изд-во Академии наук РТ, 2015. С. 319.

  75. Павловский В.Е. О разработках шагающих машин: Препринт № 101. М.: ИПМ им. М.В. Келдыша, 2013. 32 с. URL: http://library.keldysh.ru/preprint.asp?id=2013-101.

  76. https://karfidovlab.com/projects/exochair/

  77. Иванов А.В. Исследование математической модели экзоскелетона нижних конечностей // Ломоносовские чтения: тез. докл. науч. конф. М.: Изд-во МГУ, 2012. С. 84.

  78. Лавровский Э.К., Письменная Е.В. Алгоритмы управления экзоскелетоном нижних конечностей в режиме одноопорной ходьбы по ровной и ступенчатой поверхностям // Мехатроника, автоматизация, управление. 2014. № 1. С. 44–51.

  79. Лавровский Э.К., Письменная Е.В. Алгоритм управления, обеспечивающий задание произвольных траекторий экзоскелета нижних конечностей // XII Всероссийск. съезд по фундаментальным проблемам теоретической и прикладной механики: сб. трудов. В 4 т. Т. 1. Уфа : Изд-во Башкирск. гос. ун-та, 2019. С. 218–219.

  80. Комаров П.А. Алгоритмы управления движением шагающего аппарата на плоской поверхности по данным видеокамеры // Ломоносовские чтения: тез. докл. науч. конф. М.: Изд-во МГУ, 2012. С. 96.

  81. https://www.exoatlet.com/

  82. Котов С.В., Исакова Е.В., Лиждвой В.Ю., Секирин А.Б., Письменная Е.В., Петрушанская К.А., Геворкян А.А. Методические рекомендации по нейрореабилитации больных рассеянным склерозом, имеющих нарушения ходьбы, с использованием экзоскелета ExoAtlet. М.: ГБУЗ МО МОНИКИ им. М.Ф. Владимирского, 2018. 26 с.

  83. Яцун С.Ф., Антипов В.М., Карлов А.Е., Аль Манджи Хамиль Хамед Мохаммед. Подъем груза в экзоскелете с гравитационной компенсацией // Изв. Юго-Западного гос. ун-та. 2019. Т. 23. № 2. С. 8–17.

  84. Яцун С.Ф., Антипов В.М., Карлов А.Е. Моделирование подъема груза с помощью промышленного экзоскелета // Изв. Юго-Западного гос. ун-та. 2018. Т. 22. № 6 (81). С. 14–20.

  85. Яцун С.Ф., Савин С.И., Герасимов М.С. Система принятия решений для экзоскелета нижних конечностей на основе сверточных нейронных сетей // Матер. междунар. научно-практической конф. “Прогресс транспортных средств и систем” / Под ред. И.А. Каляева, Ф.Л. Черноусько, В.М. Приходько. Волгоград: Изд-во Волгоградск. гос. техн. ун-та, 2018. С. 198–199.

  86. Яцун С.Ф., Мищенко В.Я., Яцун А.С. Пассивный грузовой экзоскелетон: Патент на полезную модель. RU 190786. 2019.

  87. Яцун С.Ф., Яцун А.С., Постольный А.А., Карлов А.Е., Мищенко В.Я. Стопа экзоскелета: Патент на полезную модель. RU 189145. 2019.

  88. Тихоплав О.А., Иванова В.В., Гурьянова Е.А., Иванов И.Н. Эффективность роботизированной механотерапии комплекса “LOKOMAT PRO” у пациентов, перенесших инсульт // Вестн. восстановительной медицины. 2019. № 5(93). С. 57–64.

  89. Виттенбург Й. Динамика систем твердых тел. М.: Мир, 1980. 296 с.

  90. Вукобратович М., Христич Д. Управление антропоморфическими системами // Управление в пространстве. 1976. Т. 2. С. 180–187.

  91. Вукобратович М., Стокич Д. Управление манипуляцилнными роботами: теория и приложения. М.: Наука, 1985. 383 с.

  92. http://cyberneticzoo.com/wp-content/uploads/2010/04/GE-Hardiman-paper.pdf.

  93. https://darpa.com/

  94. https://www.army-technology.com/projects/raytheon-xos-2-exoskeleton-us/

  95. https://www.army-technology.com/projects/human-universal-load-carrier-hulc/

  96. Tsukahara A., Hasegawa Y., Sankai Y. Gait Support for Complete Spinal Cord Injury Patient by Synchronized Leg-swing with HAL // Proc. IEEE/RSJ Intern. Conf. on Intelligent Robots and Systems (IROS’11). San Francisco, 2011. P. 1737–1742.

  97. http://www.popmech.ru/blogs/post/2356-nachalis-probnyie-postavki-kiberkostyuma-ekzoskeleta-hal-5/

  98. Tsukahara A., Hasegawa Y., Eguchi K., Sankai Y. Restoration of Gait for Spinal Cord Injury Patients Using HAL with Intention Estimator for Preferable Swing Speed // IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2015. V. 23. №. 2. P. 308–318.

  99. Hassan M., Kadone H., Suzuki K., Sankai Y. Exoskeleton Robot Control Based on Cane and Body Joint Synergies // Proc. 25th IEEE/RSJ Intern. Conf. on Robotics and Intelligent Systems (IROS’12). Vilamoura, 2012. P. 1609–1614.

  100. https://www.hocoma.com/solutions/lokomat/

  101. http://corporate.honda.com/innovation/walk-assist/

  102. http://www.eksobionics.com

  103. http://bleex.me.berkeley.edu/research/exoskeleton/

  104. Kazerooni H. Exoskeletons for Human Power Augmentation // Proc. IEEE IRS/RSJ Intern. Conf. on Intelligent Robots and Systems (IROS '05). Edmonton, 2005. P. 3120–3125.

  105. http://www.rewalk.com/

  106. http://www.rexbionics.com/

  107. Bortole M., del Ama A., Rocon E., Moreno J.C., Brunetti F., Pons J.L. A Robotic Exoskeleton for Overground gait Rehabilitation // Proc. IEEE Intern. Conf. on Robotics and Automation (ICRA '13). Karlsruhe, 2013. P. 3356–3361.

  108. Chaudhary K., Chaudhary H. Optimum Balancing of Slider-Crank Mechanism Using Equimomental System of Point-Masses // 2nd Intern. Conf. on Innovations in Automation and Mechatronics Engineering (ICIAME 2014). Springer, 2014. P. 35–42.

  109. Gupta V., Chaudhary H., Saha S.K. Dynamics and Actuating Torque Optimization of Planar Robots // J. Mechanical Science and Technology. 2015. V. 29. P. 2699–2704.

  110. Kumani D.S. Chaudhary H. Hexahedron Point Mass Model and Teaching Learning Based Optimization for Balancing of Industrial Manipulators // 2nd Intern. and 17th National Conf. on Machines and Mechanisms (iNaCoMM 2015). Kanpur, 2015. P. 28–36.

  111. Piña-Martínez E., Rodriguez-Leal E. Inverse Modeling of Human Knee Joint Based on Geometry and Vision Systems for Exoskeleton Applications // Mathematical Problems in Engineering. Vol. 2015. Art. ID 145734. https://doi.org/10.1155/2015/145734

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал