1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 5, 2021

Известия РАН. Теория и системы управления, 2021, № 5, стр. 152-161

ОБ УПРАВЛЕНИИ ФОРМОЙ ДОЖДЕВАЛЬНОЙ МАШИНЫ КРУГОВОГО ДЕЙСТВИЯ И УСТОЙЧИВОСТИ ЕЕ ПРОГРАММНОГО ДВИЖЕНИЯ

Е. С. Брискин a, b, *, Я. В. Калинин a, b, К. Ю. Лепетухин a, А. В. Малолетов a, b, Н. Г. Шаронов a, b

a Волгоградский государственный технический ун-т
Волгоград, Россия

b Центр технологий компонентов робототехники и мехатроники, Университет Иннополис
Иннополис, Россия

* E-mail: dtm@vstu.ru

Поступила в редакцию 29.10.2020
После доработки 12.11.2020
Принята к публикации 25.01.2021

Полный текст (PDF)

Аннотация

Рассматривается задача управления формой секционной дождевальной машины кругового действия и определяются условия достижимости ее оптимальной конфигурации и устойчивости программного движения опорных тяговых тележек, обеспечивающих требуемое движение. Подтверждается и объясняется эффект самоориентации опорных тележек. Предложены методы управления движением группы секций дождевальной машины для обеспечения ее оптимальной конфигурации, состоящие в последовательности регулирования скоростей опорных тележек в соответствии с установленными закономерностями. Показано, что при рациональном построении конфигурации дождевальной машины и оптимальном управлении движением опорных тележек необходимость в наличии приводов поворота опорных тележек относительно секций дождевальной машины отсутствует, что упрощает ее конструкцию и систему управления.

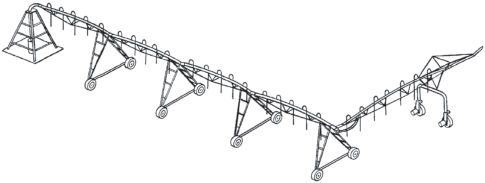
Введение. В сельском хозяйстве широко применяются дождевальные машины кругового действия. Известны как отечественные машины “Кубань”, “Фрегат” и др., так и зарубежные [1–4], в том числе и шагающие на базе машины “Кубань” [5] (рис. 1). Конструктивной особенностью таких машин является то, что они состоят из шарнирно сочлененных секций, каждая из которых опирается на тяговую опорную тележку, установленную перпендикулярно секции. Одним из недостатков дождевальных машин кругового действия является вполне определенная форма орошаемых полей с границей в виде дуги окружности [6] (рис. 2). В связи с этим теряется достаточно большая площадь потенциально плодородных земель. Предлагаемые новые решения [7, 8], направленные на увеличение орошаемых площадей, основаны на рациональном размещении центров таких машин, изменении их габаритов как за счет количества секций, так и за счет их поворота и обработки вполне определенных секторов [9] (рис. 3), или на изменении формы дождевальной машины, вызываемой поворотом ее секций друг относительно друга [10] (рис. 4). Однако в последнем случае опорная тележка должна иметь возможность поворота относительно секции и последующего совместного движения всех секций дождевальной машины как единого твердого тела. Тогда увеличивается число приводов и усложняется конструкция опорной тяговой тележки и системы управления. Поэтому актуальна может быть задача изменения формы дождевальной машины без увеличения числа приводов и усложнения системы управления. Такая задача, в силу необходимости согласованного управления группой опорных тяговых тележек, является разновидностью задач группового управления мобильных роботов, которой в последнее время уделяется повышенное внимание [11, 12], а ее особенность состоит в практической значимости для задач мелиорации.

Рис. 1.

Дождевальная машина “Кубань” с шагающими движителями

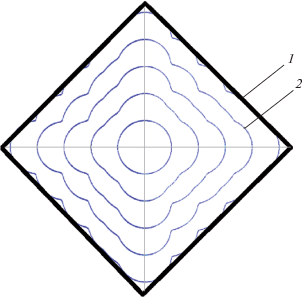
Рис. 2.

Формы круговых полей (космическая фотосъемка): 1 – орошаемые площади, 2 – неорошаемые (потерянные) площади

Рис. 3.

Примеры измененных форм орошаемых полей: 1 – орошаемые площади, 2 – неорошаемые площади

Рис. 4.

Дождевальная машина с изменяемой конфигурацией и концевой консолью

1. Постановка задачи. В качестве расчетной кинематической схемы (рис. 5) дождевальной машины кругового действия (центральная опора 1 неподвижна, обрабатываемое некруглое поле задано кромкой 6) выбирается система 2N твердых тел (секций 2 и опорных тележек 3), соединенных между собой шарнирами 4. Секции 2 машины соединены с соседними секциями шарнирами 4, опорная тяговая тележка 3 – с секцией 2 шарниром 5 (рис. 5, б).

Рис. 5.

Расчетная схема дождевальной машины кругового действия: а – машины в целом, б – узлов соединения секций и подвеса опорной тележки

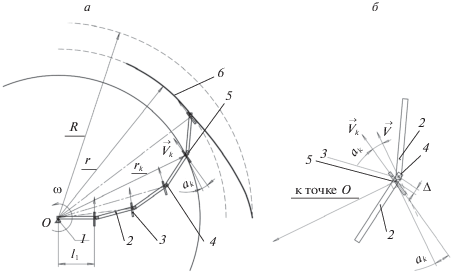
На рассматриваемую механическую систему, состоящую из N секций и N тяговых опорных тележек и совершающую плоскопараллельное движение, накладываются 4N геометрических связей в виде цилиндрических шарниров и N линейных кинематических связей, обусловленных заданием направления скорости Vk оси движителя каждой из тележек вдоль ее продольной оси. Поэтому для обеспечения программного движения достаточно N приводов, причем это приводы курсового движения. Действительно, при отсутствии хотя бы одного из таких приводов движители соответствующей опорной тележки, взаимодействующей с грунтом, не реализуют тягового усилия и могут являться тормозами. Однако в общем случае, в целях обеспечения гарантированного устойчивого программного движения, в шарнирах, соединяющих секции дождевальной машины между собой, могут быть установлены дополнительные управляемые приводы поворота секций или торможения, препятствующие такому повороту. Тогда количество приводов избыточно и равно 2N, что требует своего характерного расчета [13].

Ставится задача определения законов согласованной работы N приводов курсового движения опорных тележек, обеспечивающих заданную форму дождевальной машины в соответствии с известным методом оптимизации формы машины по различным критериям [14]. Определяются условия реализации накладываемых кинематических связей и законы самоориентации опорных тележек на стационарном этапе движения в положение, обеспечивающие движение по окружности точки ее подвеса к секции дождевальной машины при установившейся конфигурации, что характерно для этого этапа движения.

2. Управление формой дождевальной машины. Форма орошаемого поля с минимальным r и максимальным R радиусами обработки рассматривается в виде секторов (рис. 6), соответствующих следующим зонам: I – уменьшение обрабатываемого радиуса, II – движение с оптимальной конфигурацией для требуемого радиуса обработки; III – увеличение обрабатываемого радиуса.

Рис. 6.

Пример управления конфигурацией дождевальной машины

В качестве примера показана дождевальная машина, состоящая из пяти сочлененных секций. Определяются законы движения на трех этапах. Например, может быть рассмотрен следующий алгоритм.

Первый этап соответствует искривлению формы дождевальной машины за счет последовательного поворота секций относительно различных осей и состоит из четырех подэтапов (если машина состоит из N секций, из (N – 1) подэтапов). Так, на первом подэтапе первая секция неподвижна, а все остальные как одно твердое тело поворачиваются вокруг оси, соединяющей ее со следующей. На каждом j-м подэтапе неподвижными остаются все секции с номерами k ≤ j, а секции с номерами k > j поворачиваются как твердое тело вокруг j-й оси. Углы поворота секций определяются в соответствии с установленной оптимальной конфигурацией [14].

На втором стационарном этапе движение наиболее удаленной опорной тележки происходит по границе кромки поля в форме дуги окружности. Машина имеет постоянную конфигурацию и совершает вращательное движение вокруг точки O как твердое тело. В частности, этого можно добиться установкой управляемых тормозов, предотвращающих поворот одной секции относительно другой.

Третий этап соответствует восстановлению прямолинейной формы дождевальной машины. Это можно обеспечить за счет вращательного движения на каждом j-м подэтапе ближайших к центру секций и поступательного движения остальных до тех пор, пока не восстановится прямолинейная конфигурация дождевальной машины. Поступательное движение соответствующих секций можно обеспечить, если скорость Vk каждой k-й тележки будет определяться выражением

(2.1)
${{V}_{k}} = \omega {{r}_{k}}\cos {{\alpha }_{k}}.$

Здесь ω – угловая скорость первых j секций как твердого тела, rk – расстояние от неподвижного центра O до оси сочленения секций k и k + 1 дождевальной машины (приближенно можно считать до оси установки k-й опорной тележки), αk – угол между продольной осью k-й тележки и перпендикуляром к кратчайшему расстоянию до центра О. На рис. 5 соответствующие величины показаны для k = 4.

Простейшие примеры движения машины на каждом из этапов представлены на рис. 6: а – последовательный поворот секций от центральной опоры к крайней до оптимальной конфигурации, последовательный поворот секций от центральной опоры к периферийной до прямой конфигурации; б – последовательный поворот секций от центральной опоры к крайней до оптимальной конфигурации, последовательный поворот секций от крайней опоры к центральной до прямой конфигурации; в – последовательный поворот секций от крайней опоры к центральной до оптимальной конфигурации, последовательный поворот секций от крайней опоры к центральной до прямой конфигурации; г – последовательный поворот секций от крайней опоры к центральной до оптимальной конфигурации, последовательный поворот секций от центральной опоры к периферийной до прямой конфигурации. На рис. 6 приняты следующие обозначения: 1 – полностью выпрямленная конфигурация дождевальной машины; 2 – тележка периферийной секции дождевальной машины; 3 – оптимальная конфигурация дождевальной машины для обработки требуемого радиуса; 4 – траектории движения подвижных опорных тележек на этапе уменьшения радиуса обрабатываемого поля; 5 – траектории движения подвижных опорных тележек на этапе движения с оптимальной конфигурацией для требуемого радиуса обработки; 6 – траектории поступательного движения подвижных опорных тележек в зоне увеличения радиуса обрабатываемого поля; 7 – траектории кругового движения подвижных опорных тележек в зоне увеличения радиуса обрабатываемого поля; 8 – граница обрабатываемого поля; НД – направление движения.

Вариант орошения квадратного поля в соответствии с алгоритмом, представленным на рис. 6, б, показан на рис. 7.

Рис. 7.

Вариант орошения квадратного поля: 1 – граница орошаемого квадратного поля; 2 – траектории движения опорных тяговых тележек дождевальной машины

Алгоритмы управления на каждом из этапов и внутри этапов могут отличаться от приведенного в примере. Это объясняется тем, что на форму машины, имеющую N степеней свободы, накладываются только две связи: задается положение неподвижной геометрической точки О центра машины и траектория периферийной опорной тележки. Поэтому возможно существование нескольких зависящих от числа секций алгоритмов, удовлетворяющих этому условию.

3. Динамика движения тяговой опорной тележки. Метод исследования динамики движения тяговой опорной тележки основан на составлении дифференциальных уравнений опорных тележек в форме уравнений Лагранжа с избыточными координатами и введением кинематических связей, соответствующих представлению о направлении скорости характерной точки движителей (для колеса – его оси) вдоль продольной оси тележки. Расположение этой характерной точки для различных других типов движителей и их количества должно определяться решением задачи о взаимодействии опорной поверхности движителей с деформируемым грунтом.

В качестве расчетной схемы опорной тележки рассматривается стержень массы m с моментом инерции относительно центра масс Jс (рис. 8). Центр масс С находится на расстоянии l от точки A, в которой тележка шарнирно соединена с секцией дождевальной машины. Центр контакта движителя с опорной поверхностью В находится на расстоянии b от центра масс, при чем это расстояние может быть как положительным, так и отрицательным: отрицательному b соответствует положение точки В между точками А и С. Положение точки A относительно неподвижного центра дождевальной машины задается расстоянием R и углом φ, а положение тележки – углом α.

Рис. 8.

Расчетная схема для описания движения опорной тяговой тележки: 1 – опорная тяговая тележка; 2 – секции дождевальной машины

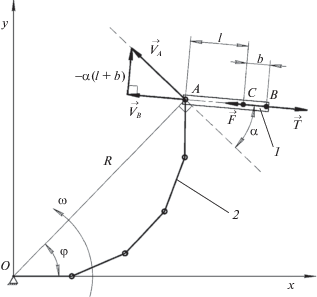
Гипотеза об отсутствии перемещения точки контакта движителя с опорной поверхностью перпендикулярно продольной оси тележки обусловлена значительным размером колеи при движении по переувлажненному грунту.

Подобная расчетная схема применяется при исследовании задачи о движении саней С.А. Чаплыгина [15], при этом в качестве обоснования отсутствия скорости характерной точки в перпендикулярном к продольной оси тележки направлении выступает наличие острой кромки колеса, что соответствует образованию колеи в переувлажненном грунте.

Принятая в качестве расчетной схема подобна используемой в задаче С.А. Чаплыгина о плоском неголономном движении [15], а отличается от нее тем, что:

– учитывается движение одной из точек (точки А);

– на твердое тело в точке контакта движителя с опорной поверхностью (для колеса в пятне контакта, у С.А. Чаплыгина края режущей кромки) действуют силы: движущая F, реализуемая приводом курсового движения (обеспечивается взаимодействием с опорной поверхностью) и направленная вдоль продольной оси тележки, сила сопротивления движению T, направленная в сторону, противоположную силе F, и поперечная сила, учитываемая ниже введением неопределенного множителя Лагранжа в соответствии с принятой гипотезой о связях;

– для повышения устойчивости от опрокидывания ферм дождевальной машины тяговая тележка может быть снабжена дополнительной пассивной опорой, например, в форме “рояльного колеса”, которая в расчетной схеме (рис. 8) не указана, а ее взаимодействие с опорной поверхностью учитывается только вертикальной реакцией. Эта опора расположена также на оси AB или ее продолжении. В математической модели С.А. Чаплыгина также имеются две пассивные опоры, не оказывающие влияние на плоское движение саней [15].

Для составления уравнений динамики движения тяговой опорной тележки ее кинетическая энергия Е определяется выражением

(3.1)
$E = \frac{1}{2}mV_{c}^{2} + \frac{1}{2}{{J}_{c}}{{\left( {\dot {\alpha } + \dot {\varphi }} \right)}^{2}},$
где V c – скорость центра масс стержня.

Если учесть, что

(3.2)
$V_{c}^{2} = {{\left[ { - R\dot {\varphi }\sin \varphi + l\left( {\dot {\varphi } + \dot {\alpha }} \right)\cos \left( {\varphi + \alpha } \right) + \dot {R}\cos \varphi } \right]}^{2}} + {{\left[ {R\dot {\varphi }\cos \varphi + l\left( {\dot {\varphi } + \dot {\alpha }} \right)\sin \left( {\varphi + \alpha } \right) + \dot {R}\sin \varphi } \right]}^{2}},$
то

(3.3)
$E = \frac{1}{2}m{{R}^{2}}{{\dot {\varphi }}^{2}} + \frac{1}{2}(m{{l}^{2}} + {{J}_{c}}){{(\dot {\varphi } + \dot {\alpha })}^{2}} + mRl\left( {\dot {\varphi } + \dot {\alpha }} \right)\dot {\varphi }\sin \alpha + \frac{1}{2}m{{\dot {R}}^{2}} + m\dot {R}l\left( {\dot {\varphi } + \dot {\alpha }} \right)\cos \alpha .$

Для определения обобщенных сил находится виртуальная работа равнодействующей Φ тяговой силы сцепления движителя с грунтом F и силы сопротивления курсовому движению T:

(3.4)
$\delta A = \left( {{{F}_{x}} - {{T}_{x}}} \right)\delta x + \left( {{{F}_{y}} - {{T}_{y}}} \right)\delta y = {{\Phi }_{x}}\delta x + {{\Phi }_{y}}\delta y$,
где Fx, Fy, Tx, Ty – проекции сил F и T на оси координат. Тогда обобщенные силы Qφ, QR, Qα, соответствующие координатам φ, R, α, имеют вид

(3.5)
${{Q}_{\varphi }} = \Phi \;R\cos \alpha ,\;\;\;{{Q}_{R}} = \Phi \;\sin \alpha ,\;{{Q}_{\alpha }} = 0.$

Согласно принятой гипотезe о накладываемых связях, а также учитывая тот факт, что центр масс тележки не совпадает с характерной точкой B движителя, а расстояние между ними равно b, записываются уравнения кинематических неголономных связей:

(3.6)
$\begin{gathered} - \left( {l + b} \right)\left( {\dot {\varphi } + \dot {\alpha }} \right)\cos \alpha - {{V}_{B}}\sin \alpha = \dot {R}, \\ - \left( {l + b} \right)\left( {\dot {\varphi } + \dot {\alpha }} \right)\sin \alpha + {{V}_{B}}\cos \alpha = R\dot {\varphi }, \\ \end{gathered} $
где VB – скорость, развиваемая движителем и направленная вдоль продольной оси тележки.

Имея в виду, что скорость VB является управляющим воздействием, (4.6) удобно представить в форме

(3.7)
$\left\{ \begin{gathered} \dot {R}\cos \alpha + \left( {R\sin \alpha + l + b} \right)\dot {\varphi } + \dot {\alpha }\left( {l + b} \right) = 0, \hfill \\ - \dot {R}\sin \alpha + R\dot {\varphi }\cos \alpha = {{V}_{B}}. \hfill \\ \end{gathered} \right.$

Тогда уравнения Лагранжа с избыточными координатами и линейными неголономными связями имеют вид

(3.8)
$\left\{ \begin{gathered} (m{{R}^{2}} + m{{l}^{2}} + {{J}_{c}} + 2mRl\sin \alpha )\ddot {\varphi } + 2mR\dot {R}\dot {\varphi } + 2m\dot {R}l\dot {\varphi }\sin \alpha + 2mRl\dot {\alpha }\dot {\varphi }\cos \alpha + m\ddot {R}l\cos \alpha + \hfill \\ + \,(m{{l}^{2}} + {{J}_{c}} + mRl\sin \alpha )\ddot {\alpha } + mlR{{{\dot {\alpha }}}^{2}}\cos \alpha = {{\lambda }_{1}}\left( {R\sin \alpha + l + b} \right) + {{\lambda }_{2}}R\cos \alpha + \Phi R\cos \alpha , \hfill \\ m\ddot {R} + ml\ddot {\alpha }\cos \alpha + ml\ddot {\varphi }\cos \alpha - mR{{{\dot {\varphi }}}^{2}} - ml\sin \alpha ({{{\dot {\varphi }}}^{2}} + 2\dot {\varphi }\dot {\alpha } + {{{\dot {\alpha }}}^{2}}) = {{\lambda }_{1}}\cos \alpha - {{\lambda }_{2}}\sin \alpha - \Phi \sin \alpha , \hfill \\ (m{{l}^{2}} + {{J}_{c}} + mRl\sin \alpha )\ddot {\varphi } + (m{{l}^{2}} + {{J}_{c}})\ddot {\alpha } + m\ddot {R}l\cos \alpha + 2m\dot {R}l\dot {\alpha }\sin \alpha - mRl{{{\dot {\varphi }}}^{2}}\cos \alpha = {{\lambda }_{1}}\left( {l + b} \right), \hfill \\ \end{gathered} \right.$
где λ1, λ2 – неопределенные множители Лагранжа, механический смысл которых состоит соответственно в реакции опорной поверхности, перпендикулярной продольной оси опорной тележки, и силе взаимодействия секции дождевальной машины с опорной тележкой, направленной вдоль ее продольной оси.

Таким образом три дифференциальных уравнения (3.8) совместно с двумя уравнениями неголономных связей (3.7) содержат семь функций времени: φ(t), R(t), α(t), λ1(t), λ2(t), Φ(t) = F(t) – T(t), VB(t). Поэтому две из этих функций могут быть заданы.

4. Эффект самоориентации тяговой опорной тележки с постоянной конфигурацией дождевальной машины. Рассматривается движение дождевальной машины на втором этапе (рис. 6), где требуется сохранять ее конфигурацию (форму) и обеспечивать вращательное движение вокруг центра O как твердого тела. Сохранение конфигурации можно обеспечить, в частности, включением тормозов в осях сочленения секций, предотвращающих их относительные перемещения, а вращение с постоянной угловой скоростью – системой управления, реализующей требуемую силу F тяги, а следовательно, и равнодействующую силу Φ. Однако это отдельная задача, которая дополняет задачу о самоориентации опорной тележки, состоящей в определении изменения угла α как функции времени.

Таким образом, изучаемое движение характеризуется дополнительными уравнениями голономных связей:

(4.1)
${{R}_{k}} = {\text{const}}{\text{.}}$

В этом случае уравнения (3.7) и (3.8) упрощаются и имеют вид

(4.2)
$\left\{ \begin{gathered} 2m{{R}_{k}}l\omega {{{\dot {\alpha }}}_{k}}\cos {{\alpha }_{k}} + (m{{l}^{2}} + {{J}_{c}} + m{{R}_{k}}l\sin {{\alpha }_{k}}){{{\ddot {\alpha }}}_{k}} + m{{R}_{k}}l\dot {\alpha }_{k}^{2}\cos {{\alpha }_{k}} = \hfill \\ = {{\lambda }_{1}}\left( {R\sin {{\alpha }_{k}} + l + b} \right) + {{\lambda }_{2}}R\cos {{\alpha }_{k}} + \Phi R\cos {{\alpha }_{k}}, \hfill \\ ml{{{\ddot {\alpha }}}_{k}}\cos {{\alpha }_{k}} - m{{R}_{k}}{{\omega }^{2}} - ml\sin {{\alpha }_{k}}{{(\omega + {{{\dot {\alpha }}}_{k}})}^{2}} = {{\lambda }_{1}}\cos {{\alpha }_{k}} - {{\lambda }_{2}}\sin {{\alpha }_{k}} - \Phi \sin {{\alpha }_{k}} + {{\lambda }_{3}}, \hfill \\ (m{{l}^{2}} + {{J}_{c}}){{{\ddot {\alpha }}}_{k}} - m{{R}_{k}}l{{\omega }^{2}}\cos {{\alpha }_{k}} = {{\lambda }_{1}}\left( {l + b} \right), \hfill \\ {{R}_{k}}\omega \cos {{\alpha }_{k}} = {{V}_{{Bk}}}, \hfill \\ \left( {{{R}_{k}}\sin {{\alpha }_{k}} + l + b} \right)\omega + {{{\dot {\alpha }}}_{k}}\left( {l + b} \right) = 0. \hfill \\ \end{gathered} \right.$

Физический смысл нового неопределенного множителя λ3 обусловленного голономной связью (4.1), состоит в реакции секции, направленной вдоль отрезка OA. Особенность уравнений (4.2) заключается в возможности независимого решения последнего уравнения относительно α(t), а затем определения и остальных неизвестных.

Действительно, из последних двух уравнений можно найти законы изменения угла α и необходимую скорость VB движителя опорной тележки. На графиках рис. 9 представлены соответствующие зависимости для модельной задачи: m = 450 кг, l = 1 м, J = 900 кг ∙ м2, R = 500 м, ω = = 0.000174 с–1 (один оборот за 10 ч), α0 = 30°, что соответствует достаточно удаленной от центра опорной тяговой тележке. Остальные уравнения могут быть использованы для определения развиваемых усилий Φ и реакций λ1, λ2, λ3, которые необходимы для подбора энергоустановки, обеспечивающей движение, и расчета конструкции на прочность и жесткость.

Рис. 9.

Зависимости от времени угла ориентации тележки α (а) и программной скорости VB (б) опорной тележки для различных развиваемых усилий λ2 + Φ(b) при l + b > 0; 1 – b = 0.5 м, 2 – b = 0 м, 3 – b = –0.5 м

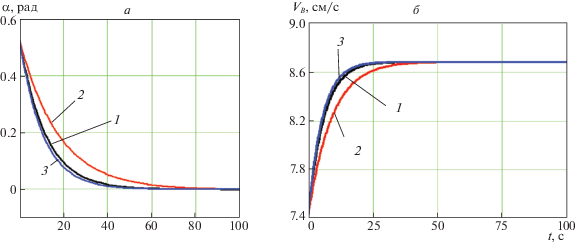
Анализ графиков показывает, что происходит самоориентация опорных тележек, состоящая в том, что продольная ось тележки, первоначально ориентированная в соответствии с движением на предыдущем этапе и составляющая угол α0 с перпендикуляром к оси ОА (рис. 8), с течением времени занимает положение, характеризуемое углом ${{\alpha }_{*}}$:

(4.3)
$\sin {{\alpha }_{*}} = - \frac{{l + b}}{R}.$

С увеличением расстояния l + b от оси крепления опорной тележки до точки приложения равнодействующей силы взаимодействия движителя с опорной поверхностью самоориентация происходит медленнее. Медленнее увеличивается и программная скорость движителя опорной тележки. Тем не менее, в худшем случае (b = –0.5 м) в модельной задаче это происходит примерно за 80 с, что соответствует повороту дождевальной машины на угол φ ≈ 0.8° и перемещению тележки на расстояние Δ S ≈ 7 м.

Если расстояние l + b < 0, т.е. точка приложения равнодействующей силы взаимодействия движителя с опорной поверхностью находится по движению впереди от оси крепления опорной тележки с секцией l + b < 0, то движитель работает в “тянущем” режиме. Такое положение оказывается неустойчивым, и опорная тележка должна разворачиваться на 180°. Однако этого не происходит в силу неограниченного возрастания равнодействующих продольных усилий λ 2 + Φ при α → π/2. Должно измениться и направление скорости движителя. Этот результат объясним, если при ω = const составить уравнения в вариациях для последнего уравнения из (4.2).

Условие устойчивости движения в этом случае имеет вид

(4.4)
$\frac{R}{{l + b}}\cos {{\alpha }_{*}} > 0,$
которое сводится к неравенству
(4.5)
$l + b > 0,$
что и подтверждает установленное явление. Такой режим работы движения будет “толкающим”. Также интересно проанализировать реакции λ1, λ2 опорной поверхности в зависимости от взаимного расположения точек С и В при параметрах модельной задачи (рис. 9), представленные на рис. 10.

Рис. 10.

Зависимости от времени а – поперечных реакций опорной поверхности на движитель опорной тяговой тележки λ1 и б – продольных реакций поверхности на движитель, направленные вдоль оси опорной тяговой тележки λ2: 1 – b = 0; 2 – b = 0.5 м; 3 – b = –0.1 м

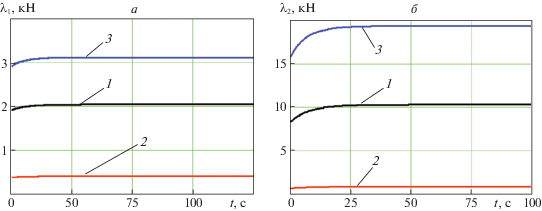
Таким образом, при достаточном удалении тележки от центра поля возникают значительные поперечные реакции величиной 0.4–3 кН. Столь значительные поперечные реакции в опоре на переувлажненном грунте могут быть реализованы колесами низкого давления большого диаметра, обеспечивающими значительную площадь пятна контакта, либо шагающими движителями с соответствующей опорной поверхностью, например лыжеобразные [16] (рис. 1), что предпочтительнее.

Заключение. Предложены методы управления движением группы секций дождевальной машины, обеспечивающие ее оптимальную конфигурацию и состоящие в последовательности регулирования скоростей опорных тележек согласно установленным закономерностям.

Установлен механический эффект самоориентации тяговых опорных тележек дождевальной машины и определены условия его реализации. Если классифицировать режимы работы тележек как “толкающий” и “тянущий”, то устойчивым режимом является “толкающий”. На основании указанного механического эффекта обосновано отсутствие необходимости наличия приводов поворота опорных тележек относительно секций дождевальной машины, что упрощает ее конструкцию и систему управления.

Для обеспечения устойчивого программного движения многосекционных дождевальных машин с изменяемой конфигурацией целесообразно применять тяговые тележки с шагающими движителями, имеющими значительную опорную поверхность.

Список литературы

  1. Фокин Б.П., Носов А.К. Современные проблемы применения многоопорных дождевальных машин. Научное издание. Ставрополь, 2011. 80 с.

  2. Рязанцев А.И., Киселев А.В. К оптимизации параметров ходовой системы дождевальной машины “Фрегат” // Конструирование, использование и надежность машин сельскохозяйственного назначения. 2005. № 1 (4). С. 15–19.

  3. Valin M.I., Cameira M.R., Teodoro P.R. et al. DEPIVOT: A Model for Center-pivot Design and Evaluation // Computers and Electronics in Agriculture. 2012. V. 87. P. 159–170.

  4. Palacin J., Salse J.A., Clua X. et al. Center-pivot Automatization for Agrochemical Use // Computers and Electronics in Agriculture. 2005. V. 49. P. 419–430.

  5. Брискин Е.С., Жога В.В., Чернышев В.В. и др. Динамика и управление движением шагающих машин с цикловыми движителями / Под ред. Е.С. Брискина. М.: Машиностроение, 2009. 191 с.

  6. Штепа Б.Г., Носенко В.Ф., Винникова Н.В. и др. Механизация полива: Справочник. М.: Агропромиздат, 1990. 336 с.

  7. Абезин В.Г., Семененко С.Я., Скрипкин Д.В., Беспалов А.Г. Совершенствование конструкции дождевальных машин кругового действия // Изв. нижневолжского агроуниверситетского комплекса: Наука и высшее профессиональное образование. 2015. № 2 (38). С. 208–212.

  8. Кузнецов П.И. К вопросу модернизации многоопорных дождевальных машин кругового действия // Природоустройство. 2011. № 4. С. 72–75.

  9. Кремнев Ю.А., Лямперт Г.П. Современные задачи развития оросительной техники // Тракторы и сельхозмашины. 1986. № 12. С. 11–14.

  10. Балакай Г.Т., Васильев С.В., Бабичев А.Н. Концепция дождевальной машины нового поколения для прецизионного орошения // Научный журнал Российского НИИ проблем мелиорации. 2017. № 2 (26). С. 1–18.

  11. Каляев И.А., Гайдук А.Р., Капустян С.Г. Модели и алгоритмы коллективного управления в группах роботов. М.: Физматлит, 2009. 280 с.

  12. Белоглазов Д.А., Гайдук А.Р., Косенко Е.Ю. и др. Групповое управление подвижными объектами в неопределенных средах / Под ред. В.Х. Пшихопова. М.: Физматлит, 2015. 305 с.

  13. Брискин Е.С., Шаронов Н.Г. Об управлении движением механических систем с избыточным числом управляющих воздействий // Изв. РАН. ТиСУ. 2019. № 3. С. 48–54.

  14. Лепетухин К.Ю., Малолетов А.В., Брискин Е.С. Об оптимальном управлении взаимным расположением секций дождевальной машины кругового действия при обработке некруглых полей // Мехатроника, автоматизация, управление. 2017. Т. 18. № 2. С. 103–107.

  15. Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. М.: Наука, 1967. 519 с.

  16. Брискин Е.С., Чернышев В.В. Экспериментальные исследования динамики многоопорной шагающей машины с движителями лямбдаобразного вида // Изв. вузов. Машиностроение. 1999. № 4. С. 32–37.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал