Известия РАН. Теория и системы управления, 2021, № 5, стр. 52-73
ЗАДАЧА УПРАВЛЕНИЯ ЛИНЕЙНЫМ ВЫХОДОМ НЕЛИНЕЙНОЙ НЕУПРАВЛЯЕМОЙ СТОХАСТИЧЕСКОЙ ДИФФЕРЕНЦИАЛЬНОЙ СИСТЕМЫ ПО КВАДРАТИЧНОМУ КРИТЕРИЮ
А. В. Босов *
МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: AVBosov@mail.ru
Поступила в редакцию 17.11.2020
После доработки 14.02.2021
Принята к публикации 29.03.2021
Аннотация
Решена задача оптимального управления по квадратичному критерию качества общего вида для неуправляемого диффузионного процесса Ито и линейного управляемого выхода. Управление с обратной связью в предположении наличия полной информации ищется методом динамического программирования. Функция Беллмана представлена в виде квадратичной формы относительно переменной выхода с коэффициентами, нелинейными относительно переменной состояния. Оптимальное управление формируется двумя слагаемыми: линейной функцией выхода и нелинейной функцией состояния. Коэффициенты, не зависящие от состояния, определены матричным уравнением Риккати, коэффициенты-функции состояния – системой уравнений параболического типа. Изучение свойств параболических уравнений приводит к стохастическому представлению описываемых ими коэффициентов в форме условного математического ожидания терминального состояния некоторой вспомогательной стохастической системы. Это представление обеспечивается формулой Фейнмана–Каца. Показано, что в частном случае линейного сноса оптимальное управление является линейным и по состоянию, а коэффициенты определяются системой обыкновенных дифференциальных уравнений. Этот случай иллюстрируется моделью Кокса–Ингерсона–Росса и численным примером для показателя времени отклика сетевого протокола TCP. В рамках численного эксперимента выполнен сравнительный анализ приближенных решений, полученных традиционным методом конечных разностей и альтернативным методом на основе стохастического представления Фейнмана–Каца.
Введение. Рассматриваемая в работе задача может быть отнесена к традиционной задаче оптимального управления дифференциальными стохастическими системами. Задача решается классическими методами, равно как и основанными на них приближенными методами поиска оптимальных управлений [1–3]. Ключевые результаты, составляющие классическую теорию управления, получены более 40 лет назад. Наибольшую полноту и результативность имеет задача управления линейно-гауссовскими стохастическими системами по квадратичному критерию (LQG) [4]. Эта задача дает исходный базис, на котором основано множество успешно исследованных и решенных задач стохастического управления и оптимизации. Множество результатов в этой области как в части моделей, так и в части математического аппарата, имевших место в последующие годы, существенно обогатили теорию управления. Но и до настоящего времени линейные модели и квадратичный критерий, несмотря на всю справедливую критику в отношении их адекватности и гибкости, сохраняют исследовательский интерес и находят современные области приложения.
Не претендуя на сколько-нибудь полное обоснование последнего тезиса, приведем несколько примеров, показавшихся наиболее интересными. Так, в [5] решается линейно-квадратичная задача в игровой постановке с запаздыванием. В близкой по модели работе [6] задача управления ставится в терминах ${{H}_{\infty }}$-робастности. Точнее называть эту тематику H2/H∞-управлением, и работ по этой теме очень много. Аккуратности ради следует уточнить, что под линейными в этой теории понимаются модели с мультипликативными по состоянию возмущениями. Совсем другой класс моделей, особо популярных в последние годы, составляют скачкообразные процессы. Например, линейные уравнения в сочетании с пуассоновскими скачками в [7] используются в моделях, описывающих различные показатели функционирования сетевых протоколов передачи данных транспортного уровня. Надо заметить, что телекоммуникации представляют в последние годы популярный прикладной материал для исследований, работ по этой проблематике множество, математические техники привлекаются самые разные и самые современные, но и линейным моделям место находится. В этой сравнительно новой прикладной области имеются приложения и для методов стохастического оптимального управления [8].
Близкой к области телекоммуникаций являются задачи управления ресурсами программных систем, в качестве которых могут выступать сайты, базы данных и банки знаний, а также традиционные вычислительные ресурсы, такие, как узлы распределенных систем, компоненты центров обработки данных и т.д. Такие ресурсы управляются программами – менеджерами задач, оптимизаторами запросов в системах управления базами данных, системами балансировки нагрузки. Моделями для постановки задач оптимизации функционирования программных систем являются системы массового обслуживания или, при значительном росте числа состояний, их диффузионные аппроксимации [9]. Соответствующая практическая интерпретация в качестве состояния оптимизируемой системы может использовать число пользователей, запросов, буферов памяти, процессорного времени и т.п., описывая его диффузионным процессом. Объем ресурсов при этом – это линейный выход, учитывающий и состояние, и активное действие программной системы, такое, как объем выделенных или освобожденных ресурсов. Отметим, что такая прикладная интерпретация изучаемой задачи ранее была представлена для случая дискретного времени [10, 11].
Исследуемая в статье модель следует традиционному представлению управляемой системы в форме вход-выход. Входная переменная предполагается неуправляемой, оптимизируется выход. Такого рода задачи известны в числе многих исследуемых постановок задач оптимального управления под терминами управление (регулирование) выходом или управление по выходу. Одно из первых применений этой терминологии обнаруживается в [12], где специальным образом записанная классическая LQG-задача используется для математической формализации инженерной задачи “доведения выхода до нуля”.
В качестве примера более современных постановок в терминологии управления выходом можно привести работу [13] (также указан ряд релевантных ссылок аналогичной тематики). Неопределенность там не имеет стохастической природы, а описывается простыми геометрическими ограничениями, что указывает на робастный характер применяемого метода инвариантных эллипсоидов. Изучаемая система при этом является линейной и автономной. Аналогичную модель исследуют авторы [14] с помощью аппарата линейных матричных неравенств. В указанной и других работах оптимизируется квадратичный критерий и используются свойства линейных регуляторов. Исследований, посвященных нелинейным моделям систем с управляемым выходом, обнаруживается немного. Так, довольно популярны постановки в терминах нелинейного адаптивного управления, предлагающие различные варианты задачи стабилизации [15].
В данной работе, как и во многих других, эксплуатируются привлекательные свойства линейных моделей и квадратичного критерия. Обобщение затронуло модель динамики системы. Оптимизируемая динамическая система описывается двумя системами уравнений. Состояние задается системой нелинейных стохастических дифференциальных уравнений Ито, не содержащих управляемой переменной. Возмущения здесь описываются стандартным векторным винеровским процессом, накладываются простые условия существования и единственности решения. Поскольку состояние не управляется, то возможно его интерпретировать еще и как сложное внешнее возмущение. Вторая переменная – управляемый выход – задается системой линейных стохастических дифференциальных уравнений. Цель оптимизации выхода формируется квадратичным критерием общего вида. Формальная постановка задачи дана в разд. 2. Для решения задачи применяется метод динамического программирования, решается уравнение Беллмана [3], используемые общие положения приведены в разд. 1. Соответственно в результате получаются аналитические выражения и для оптимального управления, и для значения функционала качества. Технически традиционный, стандартный подход к задаче обременен, пожалуй, единственной проблемой – поиском верного представления структуры функции Беллмана. Справиться с этой проблемой в большей степени удается за счет результата, полученного при решении дискретного по времени аналога рассматриваемой постановки [11]. Конечные соотношения для оптимального решения, как и во всех подобных задачах, включая классическую LQG, содержат решения определенных дифференциальных уравнений (обыкновенных и в частных производных). Вывод этих уравнений представлен в разд. 3. Решение дает функция Беллмана вида $V(t,y,z) = {{z}^{T}}\alpha (t)z + {{z}^{T}}\beta (t,y) + \gamma (t,y)$, в котором переменная y соответствует вектору состояния, переменная z – выходу, а коэффициенты α(t), $\beta \left( {t,y} \right),$ $\gamma \left( {t,y} \right)$ представлены решениями полученных дифференциальных уравнений (обыкновенного Риккати и системы линейных уравнений в частных производных параболического типа). При определении функции Беллмана получено и выражение для оптимального управления в виде линейной функции z и коэффициента $\beta \left( {t,y} \right).$ Соответственно естественная численная реализация оптимального решения – это приближенное решение методом конечных разностей соответствующих дифференциальных уравнений. При этом применение сеточных методов для параболических уравнений осложняется тем обстоятельством, что имеются только начальные условия для уравнений, определяющих $\beta (t,y),$ $\gamma (t,y),$ оснований для указания граничных условий, нужных для метода конечных разностей, нет. Из-за этого граничные условия в модельном эксперименте, которому посвящен раздел 6, выбираются довольно волюнтаристски, обсуждается экспериментальный анализ их влияния на решение. И хотя удается получить удовлетворительный результат, поиск альтернативного метода для приближенного вычисления коэффициентов функции Беллмана сохраняет актуальность.
Поскольку обсуждаемые коэффициенты описываются линейными уравнениями в частных производных второго порядка параболического типа, то перспективным представлялось опираться в исследовании этой задачи на известные факты, ассоциирующие такие уравнения с уравнениями стохастическими. Видимо самая известная ассоциация такого рода – это уравнение А.Н. Колмогорова [16], которое и было использовано в качестве инструмента для реализации альтернативного метода приближенного вычисления коэффициентов $\beta \left( {t,y} \right),$ $\gamma \left( {t,y} \right).$ Точнее применялось утверждение, которое определяет связь между решением задачи Коши для уравнения А.Н. Колмогорова, с одной стороны, и теоретико-вероятностным представлением ее терминального условия. Использованное в работе интегральное представление этого результата известно как формула Фейнмана–Каца [17]. Такой метод для численного решения параболических уравнений и уравнений даже более общей структуры успешно реализован и исследован [18], так что примененный в статье подход можно считать апробированным. Обсуждению этого результата посвящен раздел 4. Соответственно стохастическая интерпретация $\beta \left( {t,y} \right)$ дает возможность определения этого коэффициента как статистической оценки математического ожидания терминальной переменной вспомогательной динамической системы, формируемой из интегрального представления Фейнмана–Каца. Таким образом, альтернативный метод аппроксимации оптимального решения рассматриваемой задачи сводится к использованию компьютерного моделирования и метода Монте-Карло. Результаты применения этого метода и сравнение с методом конечных разностей приведены в разд. 6, представляющем численный эксперимент.
Практически важный частный случай рассматриваемой задачи, случай линейного сноса, но нелинейной диффузии, обычно характеризуемый как модель с мультипликативными возмущениями, рассмотрен в разд. 5. Оптимальное решение в этом случае не требует интегрирования параболического уравнения, управление линейно по состоянию и выходу, а численная реализация сводится к решению только обыкновенных дифференциальных уравнений. Это дает возможность, во-первых, получить подходящий эталонный пример для сравнительного анализа двух других методов аппроксимации оптимального решения – сеточного и имитационного. Во-вторых, позволяет в полном объеме рассмотреть модельный пример, связанный с выбранной целевой прикладной областью телекоммуникаций. Именно в разд. 6 обсуждаются результаты численного эксперимента, выполненного предложенными методами для модели Кокса–Ингерсона–Росса, описывающей показатель времени сетевого отклика RTT (round-trip time) основного сетевого протокола Интернета TCP (transmission control protocol).
1. Общий подход к решению. Предваряя основной результат, кратко опишем положения, привлекаемые далее к решению задачи, следуя обозначениям и терминологии [3]. Будем рассматривать задачу оптимального управления состоянием $x\left( t \right) \in {{\mathbb{R}}^{n}}$ стохастической динамической системы по полной информации, применяя метод динамического программирования. Допустимыми будем считать управления с обратной связью, т.е. функции вида $u = u\left( {t,x} \right) \in {{\mathbb{R}}^{k}},$ $x \in {{\mathbb{R}}^{n}}$, множество допустимых управлений обозначается $U_{0}^{T} = \{ u\left( {t,x} \right),{\text{\;}}0 \leqslant t \leqslant T,~~x \in {{\mathbb{R}}^{n}}\} $, такие, что реализациями управления $u(t) = u(t,x(t))$ обеспечиваются выполненными условия существования x(t) для $u \in U_{0}^{T}$. Заметим, что использование обозначений $u = u\left( {t,x} \right)$ для управления с обратной связью и $u(t) = u(t,x(t))$ для его реализации, соответствующей траектории x(t), далее будет везде понятно из контекста и не приведет к неоднозначности.
Минимизируемый целевой функционал имеет вид
(1.1)
$J(U_{0}^{T}) = \mathbb{E}\left\{ {\mathop \smallint \limits_0^T L\left( {t,x\left( t \right),u\left( t \right)} \right)dt + l\left( {x\left( T \right)} \right)} \right\},$(1.2)
$dx\left( t \right) = m\left( {t,x\left( t \right),u\left( t \right)} \right)dt + \lambda \left( {t,x\left( t \right)} \right)dW\left( t \right),~\quad 0 \leqslant t \leqslant T,~\quad x\left( 0 \right) = X,$Относительно функций сноса $m\left( {t,x,u} \right)$ и диффузии ${{\lambda }}\left( {t,x} \right)$ в (1.2) будем предполагать выполненными какие-либо условия существования и единственности решения для заданного допустимого управления. Так, учитывая, что допустимыми являются управления с обратной связью, будем считать, что $m\left( {t,x,u\left( {t,x} \right)} \right)$ и $\lambda \left( {t,x} \right)$ удовлетворяют условию линейного роста по x и локальному условию Липшица по x равномерно по t (т.е. условиям Ито). Также относительно функций из целевого функционала $L\left( {t,x,u} \right)$ и l(x) предполагаются выполненными типовые условия существования, например ограничения полиномиального роста по x и u.
Для поиска оптимального управления, минимизирующего $J(U_{0}^{T})$, рассматривается функция Беллмана
(1.3)
$V\left( {t,x} \right) = \mathop {\inf }\limits_{U_{t}^{T}} \mathbb{E}\left. {\left. {\left\{ {\mathop \smallint \limits_t^T L\left( {\tau ,x\left( \tau \right),u\left( \tau \right)} \right)d\tau + l\left( {x\left( T \right)} \right)} \right.} \right|\mathcal{F}_{t}^{x}} \right\},$(1.4)
$\frac{{\partial V}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\lambda }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}}\lambda } \right\} + \mathop {\min }\limits_u \left\{ {{{m}^{{\text{T}}}}\frac{{\partial V}}{{\partial x}} + L} \right\} = 0,\quad ~V\left( {T,x} \right) = l\left( x \right),$Традиционно в рамках применения метода динамического программирования будем предполагать, что функции $L,l,m,\lambda $ обеспечивают существование хотя бы одного решения уравнения (1.4), а следовательно, и оптимального управления
2. Постановка задачи управления выходом. Рассмотрим стохастическую дифференциальную систему, состояние которой представляет диффузионный процесс $y\left( t \right) \in {{\mathbb{R}}^{{{{n}_{y}}}}}$, описываемый системой нелинейных стохастических дифференциальных уравнений Ито
(2.1)
$dy\left( t \right) = A\left( {t,y\left( t \right)} \right)dt + \Sigma \left( {t,y\left( t \right)} \right)d{v}\left( t \right),~\quad y\left( 0 \right) = Y,$Будем считать, что y(t) описывает состояние некоторой динамической системы. Под выходом этой системы понимается процесс $z\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}}}}}$, линейно связанный с состоянием:
(2.2)
$dz\left( t \right) = a\left( t \right)y\left( t \right)dt + b\left( t \right)z\left( t \right)dt + c\left( t \right)u\left( t \right)dt + \sigma \left( t \right)dw\left( t \right),~\quad z\left( 0 \right) = Z,$Качество управления $U_{0}^{T}$ определяется целевым функционалом следующего вида:
(2.3)
$J(U_{0}^{T}) = \mathbb{E}\left\{ {\mathop \smallint \limits_0^T {\text{||}}P\left( t \right)y\left( t \right) + Q\left( t \right)z\left( t \right) + R\left( t \right)u\left( t \right){\text{||}}_{{S\left( t \right)}}^{2}dt + \,{\text{||}}P\left( T \right)y\left( T \right) + Q\left( T \right)z\left( T \right){\text{||}}_{{S\left( T \right)}}^{2}} \right\},$Матричные функции $a\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{y}}}}},$ $b\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{z}}}}},$ $c\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{u}}}}},$ $\sigma \left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{w}}}}}$ ограничены: |a(t)| + $\left| {b(t)} \right| + \left| {c(t)} \right| + \left| {\sigma (t)} \right| \leqslant C$ для всех $0 \leqslant t \leqslant T$. Таким образом, обеспечивается существование решения уравнения (2.2) для любого допустимого управления u. Более того, будем предполагать, что все используемые функции времени $a\left( t \right),b\left( t \right),c\left( t \right),\sigma \left( t \right),P\left( t \right),Q\left( t \right),R\left( t \right),S\left( t \right)$ кусочно-непрерывны, чтобы обеспечить выполнение типовых условий существования решений дифференциальных уравнений, получаемых далее.
Задачу составляет поиск $(U{\text{*}})_{0}^{T} = \{ u{\text{*}}\left( {t,y,z} \right),{\text{\;}}0 \leqslant t \leqslant T,y \in {{\mathbb{R}}^{{{{n}_{y}}}}},z \in {{\mathbb{R}}^{{{{n}_{z}}}}}\} $ – допустимого управления с обратной связью, доставляющего минимум квадратичному функционалу $J(U_{0}^{T}).$
Функционал (2.3) формализует типичную задачу управления выходом. В [12], как уже упоминалось, в качестве примера практического приложения такого типа целевой функции рассматривается задача “доведения выхода до нуля”. Предлагаемый более общий вид целевого функционала отражает практическое содержание упомянутой выше задачи распределения ресурсов. Так, частный вид функционала (2.3)
Поставленная задача очевидным образом формулируется в терминах выражений (1.1)–(1.3), для этого нужно обозначить
Функция Беллмана (1.3) принимает вид $V = V\left( {t,y,z} \right)$, а уравнение (1.4) с обозначениями $\Sigma = \Sigma (t,y),$ $A = A\left( {t,y} \right)$, $a = a\left( t \right),$ $b = b\left( t \right),$ $c = c\left( t \right),$ $u = u\left( t \right),$ $\sigma = \sigma \left( t \right),$ $P = P\left( t \right),$ $Q = Q\left( t \right),$ $R = R\left( t \right),$ $S = S(t),$ записывается как
(2.4)
$\begin{array}{*{20}{c}} {\frac{{\partial V}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}\Sigma + {{\sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{z}^{2}}}}\sigma } \right\} + } \\ { + \mathop {{\text{min}}}\limits_u \left\{ {{{A}^{{\text{T}}}}\frac{{\partial V}}{{\partial y}} + {{{\left( {ay + bz + cu} \right)}}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + \,{\text{||}}Py + Qz + Ru{\text{||}}_{S}^{2}} \right\} = 0,} \\ {V\left( {T,y,z} \right) = {\text{||}}P\left( T \right)y + Q\left( T \right)z{\text{||}}_{{S\left( T \right)}}^{2}.} \end{array}$Существование решения уравнения (2.4) является достаточным условием оптимальности, оптимальное управление при этом получается при минимизации соответствующего слагаемого в фигурных скобках.
3. Динамическое программирование и оптимальное управление. В рассматриваемой постановке линейность выхода и квадратичность критерия дают те же преимущества, что и в классической LQG-задаче [4], а именно позволяют сразу определить вид оптимального управления и фактические условия его существования. Действительно, сохраняя в (2.4) под знаком $\mathop {{\text{min}}}\limits_u $ только члены, зависящие от u, получаем
(3.1)
$\begin{array}{*{20}{c}} {\frac{{\partial V}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}\Sigma + {{\sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{z}^{2}}}}\sigma } \right\} + } \\ { + \,{{A}^{{\text{T}}}}\frac{{\partial V}}{{\partial y}} + {{{\left( {ay + bz} \right)}}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + \,{\text{||}}Py + Qz{\text{||}}_{S}^{2} + } \\ { + \mathop {{\text{min}}}\limits_u \left\{ {{{u}^{{\text{T}}}}\left( {{{c}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + 2{{R}^{{\text{T}}}}S\left( {Py + Qz} \right)} \right) + \,{\text{||}}Ru{\text{||}}_{S}^{2}} \right\} = 0.} \end{array}$Далее из (3.1) с учетом сделанного предположения ${{R}^{{\text{T}}}}SR > 0$, обозначения “A–1” для обратной матрицы A и выражения для минимума квадратичной формы получаем равенство для оптимального управления в предположении существования решения (3.1):
(3.2)
$u{\text{*}} = u{\text{*}}\left( {t,y,z} \right) = - 1{\text{/}}2{{({{R}^{{\text{T}}}}SR)}^{{ - 1}}}\left( {{{c}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + 2{{R}^{{\text{T}}}}S\left( {Py + Qz} \right)} \right).$Это управление доставляет минимум последнему слагаемому в (3.1):
Отметим, что оптимальное управление получается из двух слагаемых: одно слагаемое линейное по состоянию и выходу (как в классической линейно-квадратичной задаче), второе слагаемое нелинейное, определяется производной $\partial V{\text{/}}\partial z$.
Таким образом, функция Беллмана описывается следующим дифференциальным уравнением:
(3.3)
$\begin{array}{*{20}{c}} {\frac{{\partial V}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}\Sigma + {{\sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{z}^{2}}}}\sigma } \right\} + } \\ { + {{A}^{{\text{T}}}}\frac{{\partial V}}{{\partial y}} + {{{\left( {ay + bz} \right)}}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + \,{\text{||}}Py + Qz{\text{||}}_{S}^{2} - } \\ { - 1{\text{/}}4~{{{\left( {{{c}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + 2{{R}^{{\text{T}}}}S\left( {Py + Qz} \right)} \right)}}^{{\text{T}}}}{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}\left( {{{c}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} + 2{{R}^{{\text{T}}}}S\left( {Py + Qz} \right)} \right) = 0.} \end{array}$Преобразуя последнее слагаемое в (3.3), перепишем его в виде
(3.4)
$\begin{array}{*{20}{c}} {\frac{{\partial V}}{{\partial t}} + 1{\text{/}}2{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}\Sigma + {{\sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{z}^{2}}}}\sigma } \right\} + {{A}^{{\text{T}}}}\frac{{\partial V}}{{\partial y}} + } \\ { + \,({{{\left( {ay + bz} \right)}}^{{\text{T}}}} - {{{({{R}^{{\text{T}}}}S\left( {Py + Qz} \right))}}^{{\text{T}}}}{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}})\frac{{\partial V}}{{\partial z}} + } \\ {\begin{array}{*{20}{c}} { + {{{\left( {Py + Qz} \right)}}^{{\text{T}}}}(S - SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}S)\left( {Py + Qz} \right) - } \\ { - 1{\text{/}}4~{{{\left( {\frac{{\partial V}}{{\partial z}}} \right)}}^{T}}c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}}\frac{{\partial V}}{{\partial z}} = 0.} \end{array}} \end{array}$Рассматривая полученное уравнение, предположим, что его решение может быть представлено в как
(3.5)
$V = V\left( {t,y,z} \right) = {{z}^{{\text{T}}}}\alpha \left( t \right)z + {{z}^{{\text{T}}}}\beta \left( {t,y} \right) + \gamma \left( {t,y} \right),$Граничное условие при сделанном предположении (3.5) принимает вид
(3.6)
$\begin{gathered} \alpha \left( T \right) = {{Q}^{{\text{T}}}}\left( T \right)S\left( T \right)Q\left( T \right),~\quad \beta \left( {T,y} \right) = 2{{Q}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y, \\ \gamma \left( {T,y} \right) = {{y}^{T}}{{P}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y. \\ \end{gathered} $При этом поскольку (3.5) дает $\partial V{\text{/}}\partial z = 2\alpha z + \beta $, то само оптимальное управление, определенное выражением (3.2),
(3.7)
$u{\text{*}} = u{\text{*}}\left( {t,y,z} \right) = - 1{\text{/}}2~{{({{R}^{{\text{T}}}}SR)}^{{ - 1}}}({{c}^{{\text{T}}}}\left( {2\alpha z + \beta } \right) + 2{{R}^{{\text{T}}}}S\left( {Py + Qz} \right)).$Дальнейшие преобразования удобнее выполнить, представив V в виде
Раскрывая скобки и формируя слагаемые при ${{z}^{T}}z,~z$ (каждой компоненте ${{z}^{{\left( i \right)}}}$) и ${{z}^{0}} = 1$, имеем
Окончательно требуемая группировка слагаемых записывается с использованием обозначения ${{\left[ A \right]}^{{\left( {ji} \right)}}}$ для элемента j-й строки i-го столбца матрицы A:
Поскольку полученное равенство выполняется для всех $z \in {{\mathbb{R}}^{{{{n}_{z}}}}}$, $y \in {{\mathbb{R}}^{{{{n}_{y}}}}}$, то каждое из трех слагаемых должно быть равно 0, что дает следующие уравнения:
− матричное дифференциальное уравнение для функции $\alpha = \alpha (t)$ (с учетом предположения $\alpha = {{\alpha }^{{\text{T}}}}$):
(3.8)
$\begin{array}{*{20}{c}} {\frac{{d\alpha }}{{dt}} + ({{b}^{{\text{T}}}} - {{Q}^{{\text{T}}}}SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}})\alpha + \alpha (b - c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}SQ) + } \\ { + \,{{Q}^{{\text{T}}}}(S - SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}S)Q - \alpha c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}}\alpha = 0,~\quad \alpha \left( T \right) = {{Q}^{{\text{T}}}}\left( T \right)S\left( T \right)Q\left( T \right),} \end{array}$− систему дифференциальных уравнений в частных производных для функций β(i) = = ${{\beta }^{{(i)}}}(t,y),~i = \overline {1,{{n}_{z}}} $:
(3.9)
$\begin{gathered} \frac{{\partial {{\beta }^{{(i)}}}}}{{\partial t}} + 1{\text{/}}2{\text{tr}}\left\{ {{{\Sigma }^{{\rm T}}}\frac{{{{\partial }^{2}}{{\beta }^{{(i)}}}}}{{\partial {{y}^{2}}}}\Sigma } \right\} + {{A}^{{\text{T}}}}\frac{{\partial {{\beta }^{{(i)}}}}}{{\partial y}} + \\ + \sum\limits_{j = 1}^{{{n}_{z}}} {{{\beta }^{{(j)}}}{{{[b - c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}SQ - c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}}\alpha ]}}^{{(ji)}}} + } \\ + \,2\sum\limits_{j = 1}^{{{n}_{y}}} {{{y}^{{(j)}}}{{{[({{a}^{{\text{T}}}} - {{P}^{{\text{T}}}}SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}})\alpha + {{P}^{{\text{T}}}}(S - SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}S)Q]}}^{{(ji)}}} = 0,} \\ \end{gathered} $− дифференциальное уравнение в частных производных для функции $\gamma = \gamma \left( {t,y} \right)$:
(3.10)
$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{\partial \gamma }}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}\gamma }}{{\partial {{y}^{2}}}}\Sigma } \right\} + {\text{tr}}\{ {{\sigma }^{{\text{T}}}}\alpha \sigma \} + {{A}^{{\text{T}}}}\frac{{\partial \gamma }}{{\partial y}} + {{\beta }^{{\text{T}}}}(a - c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}SP)y + } \\ { + {{y}^{{\text{T}}}}{{P}^{{\text{T}}}}(S - SR{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{R}^{{\text{T}}}}S)Py - 1{\text{/}}4~{{\beta }^{{\text{T}}}}c{{{({{R}^{{\text{T}}}}SR)}}^{{ - 1}}}{{c}^{{\text{T}}}}\beta = 0,} \end{array}} \\ {\gamma \left( {T,y} \right) = {{y}^{{\text{T}}}}{{P}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y.} \end{array}$Вводя дополнительно обозначения
(3.11)
$\frac{{\partial {{\beta }^{{\left( i \right)}}}}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}{{\beta }^{{\left( i \right)}}}}}{{\partial {{y}^{2}}}}\Sigma } \right\} + {{A}^{{\text{T}}}}\frac{{\partial {{\beta }^{{\left( i \right)}}}}}{{\partial y}} + \mathop \sum \limits_{j = 1}^{{{n}_{y}}} {{y}^{{\left( j \right)}}}{{\left[ M \right]}^{{\left( {ji} \right)}}} + \mathop \sum \limits_{j = 1}^{{{n}_{z}}} {{\beta }^{{\left( j \right)}}}{{\left[ N \right]}^{{\left( {ji} \right)}}} = 0,$(3.12)
$\frac{{\partial \gamma }}{{\partial t}} + 1{\text{/2\;tr}}\left\{ {{{\Sigma }^{T}}\frac{{{{\partial }^{2}}\gamma }}{{\partial {{y}^{2}}}}\Sigma } \right\} + {\text{tr}}\{ {{\sigma }^{T}}\alpha \sigma \} + {{A}^{T}}\frac{{\partial \gamma }}{{\partial y}} + K = 0.$Уравнение (3.8) – это матричное уравнение Риккати, точнее его частный случай для квадратной симметричной матрицы α. Сделанных выше предположений достаточно для существования единственного неотрицательного решения для всех $0 \leqslant t \leqslant T$. Этот факт требует дополнительного комментария. Рассмотрим исходную задачу при дополнительных условиях: $a\left( t \right) = {{0}_{{{{n}_{z}} \times {{n}_{v}}}}},$ $P\left( t \right) = {{0}_{{{{n}_{J}} \times {{n}_{y}}}}},$ $S\left( t \right) = E$ для всех $0 \leqslant t \leqslant T$. Это дает
Теперь уравнение (3.8) для α(t) принимает хорошо известный вид
(3.13)
$\frac{{d\alpha }}{{dt}} + {{b}^{{\text{T}}}}\alpha + \alpha b + {{Q}^{{\text{T}}}}Q - \alpha c{{({{R}^{{\text{T}}}}R)}^{{ - 1}}}{{c}^{{\text{T}}}}\alpha = 0,\quad ~\alpha \left( T \right) = {{Q}^{{\text{T}}}}\left( T \right)Q\left( T \right).$В таком случае, как известно [19], существует единственное оптимальное управление – линейное с обратной связью по выходу z(t), с коэффициентом усиления, описываемым уравнением Риккати (3.13). Именно этот результат дают уравнения (3.8)–(3.10) и описываемая ими функция Беллмана (3.5), так как из $a\left( t \right) = 0,P\left( t \right) = 0$ немедленно следует, что ${{\beta }^{{\left( i \right)}}}\left( {t,y} \right) = 0,{\text{\;}}i = \overline {1,{{n}_{z}}} ,$ откуда, в свою очередь, с учетом независимости решения от y следует, что γ не зависит от y и задается уравнением $d{{\gamma /}}dt + {\text{tr}}\{ {{\sigma }^{{\text{T}}}}\alpha \sigma \} = 0,{{\gamma }}\left( T \right) = 0$. Оптимальное управление при этом $u{\text{*}} = - {{({{R}^{{\text{T}}}}R)}^{{ - 1}}}{{c}^{{\text{T}}}}\alpha z,$ т.е. все полностью совпадает с известным классическим решением.
С уравнениями (3.11) и (3.12) ситуация, естественно, обстоит сложнее. Это линейные уравнения в частных производных второго порядка параболического типа, поскольку ${{\Sigma }^{{\text{T}}}}\Sigma \geqslant 0$. Уравнения неоднородные, причем в уравнении (3.12) для $\gamma \left( {t,y} \right)$ участвуют все ${{\beta }^{{\left( i \right)}}}\left( {t,y} \right)$, т.е. сначала должны быть решены уравнения (3.11) и результат подставлен в (3.12). Также в уравнения (3.11) нужно подставить α(t) – решение уравнения (3.8). Далее, в каждом из уравнений (3.11) неоднородность для ${{\beta }^{{\left( i \right)}}}\left( {t,y} \right)$ формируется неизвестными функциями ${{\beta }^{{\left( j \right)}}}\left( {t,y} \right),{\text{\;}}j \ne i$, т.е. параболические уравнения объединены в систему и по отдельности решаться не могут, так что актуален еще и вопрос их приближенного решения. Кроме того, отсутствуют конструктивные условия, гарантирующие существование решений (требовать, чтобы все фигурирующие в уравнениях коэффициенты были представлены аналитическими функциями на всем пространстве значений, вряд ли целесообразно, а в имеющейся системе уравнений, может быть, и не достаточно). Поэтому далее будем предполагать, что уравнения (3.11) и (3.12) имеют на интервале $0 \leqslant t \leqslant T$ хотя бы одно гладкое (непрерывно дифференцируемое по t и дважды непрерывно дифференцируемое по y) решение и именно эти условия можно считать достаточными условиями существования оптимального решения рассматриваемой задачи.
Таким образом, доказана следующая теорема.
Теорема. Пусть для диффузионного процесса (2.1) выполнены условия Ито, для выхода (2.2) ограничены коэффициенты, уравнения (3.8)–(3.10) имеют гладкие решения для $0 \leqslant t \leqslant T$. Тогда минимум функционалу (2.3) доставляет $(U{\text{*}})_{0}^{T}$ – оптимальное управление с полной обратной связью, определенное (3.7).
4. Стохастическое представление коэффициентов функции Беллмана. Для реализации оптимального управления и оценки его качества потребуется решать полученные уравнения (3.8), (3.11), (3.12) приближенно. Решение уравнения (3.8) не представляет трудностей и может быть выполнено любым из множества эффективных численных методов решения обыкновенных дифференциальных уравнений. Несколько сложнее обстоит ситуация с уравнениями (3.11), (3.12). Для уравнений параболического типа также имеются эффективные численные схемы, основанные на методе конечных разностей. Но в рассматриваемом случае трудности в реализации возникают при определении граничных условий, необходимых для этого метода. В рассматриваемой задаче физические основания для определения границы и, тем более граничных условий как для $\beta \left( {t,y} \right),$ так и для $\gamma \left( {t,y} \right)$ отсутствуют. Вариант возможного преодоления этих сложностей обсуждается далее в рамках представления численного эксперимента. Более подходящим и лишенным таких трудностей представляется решение параболического уравнения на основе его ассоциации с уравнением А.Н. Колмогорова, точнее связи между решением задачи Коши с терминальным условием для уравнения А.Н. Колмогорова и теоретико-вероятностным представлением этого терминального условия [16]. Выражением этого результата является формула Фейнмана–Каца [17], непосредственно применимая к уравнению (3.12). С учетом введенных выше обозначений интегральное представление Фейнмана–Каца решения дифференциального уравнения (3.12) имеет вид
(4.1)
$\gamma \left( {t,y} \right) = \mathbb{E}\left\{ {\left. {{{y}^{{\text{T}}}}\left( T \right){{P}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y\left( T \right) + \mathop \smallint \limits_t^T K\left( {\tau ,y\left( \tau \right)} \right)d\tau } \right|\mathcal{F}_{t}^{y}} \right\}.$В предположении, что α(t) и $\beta \left( {t,y} \right)$ известны (вычислены), (4.1) дает основание для применения компьютерного моделирования для аппроксимации $\gamma \left( {t,y} \right)$. Многократно моделируя решение уравнения (2.1), проходящее через точку (t, y) (именно это обозначает σ-алгебра $\mathcal{F}_{t}^{y}$ в условном математическом ожидании), значение $\gamma \left( {t,y} \right)$ можно получить как статистическую оценку функции терминального условия, согласно (4.1). Подробнее этот метод описан далее. Следует отметить, что как в формулировке для уравнения А.Н. Колмогорова, так и в формуле Фейнмана–Каца утверждается существование процесса yt, обеспечивающего равенство (4.1), т.е. формально это другой процесс и задан он на другом пространстве, чем процесс, участвующий в поставленной выше задаче управления. При этом описывается этот процесс таким же уравнением (2.1) и имеет те же вероятностные характеристики, что дает основание использовать уже имеющуюся дифференциальную систему, не вводить новые обозначения.
Такой же подход хотелось бы применить для приближенного вычисления $\beta \left( {t,y} \right).$ Более того, в скалярном случае ${{n}_{z}} = 1$ интегральное представление Фейнмана–Каца решения дифференциального уравнения (3.11) записывается без дополнительных усилий и имеет вид
(4.2)
$\beta \left( {t,y} \right) = \mathbb{E}\left\{ {\left. {\begin{array}{*{20}{c}} {2\exp \left\{ {\mathop \smallint \limits_t^T N\left( \tau \right)d\tau } \right\}{{y}^{{\text{T}}}}\left( T \right){{P}^{{\text{T}}}}\left( T \right)S\left( T \right)Q\left( T \right) + } \\ { + \mathop \smallint \limits_t^T \exp \left\{ {\mathop \smallint \limits_t^\tau N\left( s \right)ds} \right\}{{y}^{{\text{T}}}}\left( \tau \right)M\left( \tau \right)d\tau } \end{array}} \right|\mathcal{F}_{t}^{y}} \right\}.$Далее выводится аналог (4.2) для ${{n}_{z}} > 1.$ Для этого введем новую переменную $\bar {\beta } = \bar {\beta }\left( {t,y} \right) \in {{\mathbb{R}}^{{{{n}_{z}}}}}$ и выполним замену $\beta \left( {t,y} \right) = I\left( t \right)\bar {\beta }\left( {t,y} \right),$ где матрица $I = I\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{z}}}}}$ является решением уравнения $dI(t){\text{/}}dt + {{N}^{{\text{T}}}}(t)I(t) = 0$. Такая замена позволяет исключить из уравнений (3.11) слагаемые с ${{\beta }^{{\left( j \right)}}}$. Действительно, для слагаемых
Следующим действием левая часть полученного равенства разрешается относительно эллиптической части и $\partial{ \bar {\beta }}{\text{/}}\partial t$ умножением на I–1(t)
(4.3)
$\frac{{\partial {{{\bar {\beta }}}^{{\left( i \right)}}}}}{{\partial t}} + 1{\text{/}}2~{\text{tr}}\left\{ {{{\Sigma }^{{\text{T}}}}\frac{{{{\partial }^{2}}{{{\bar {\beta }}}^{{\left( i \right)}}}}}{{\partial {{y}^{2}}}}\Sigma } \right\} + {{A}^{{\text{T}}}}\frac{{\partial {{{\bar {\beta }}}^{{\left( i \right)}}}}}{{\partial y}} + \mathop \sum \limits_{j = 1}^{{{n}_{y}}} {{y}^{{\left( j \right)}}}{{[{{I}^{{ - 1}}}{{M}^{{\text{T}}}}]}^{{\left( {ij} \right)}}} = 0,~\quad i = \overline {1,{{n}_{z}}} .$Теперь для каждого из уравнений (4.3) может быть записана формула Фейнмана–Каца:
Наконец, обратная замена $\bar {\beta }\left( {t,y} \right) = {{I}^{{ - 1}}}\left( t \right)\beta \left( {t,y} \right)$ дает
(4.4)
$\beta \left( {t,y} \right) = \,~\mathbb{E}\left\{ {\left. {\begin{array}{*{20}{c}} {2{{I}^{{ - 1}}}\left( t \right){{I}^{{ - 1}}}\left( T \right){{Q}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y\left( T \right) + } \\ { + {{I}^{{ - 1}}}\left( t \right)\mathop \smallint \limits_t^T {{I}^{{ - 1}}}\left( \tau \right){{M}^{{\text{T}}}}\left( \tau \right)y\left( \tau \right)d\tau } \end{array}} \right|\mathcal{F}_{t}^{y}} \right\}.$Приводя выражения, нужные для расчета по формулам (4.1) и (4.4), в дифференциальный вид, окончательно получаем следующую систему:
(4.5)
$\begin{gathered} dy\left( \tau \right) = A\left( {\tau ,y\left( \tau \right)} \right)d\tau + \Sigma \left( {\tau ,y\left( \tau \right)} \right)d{v}\left( \tau \right),\quad {{y}_{t}} = y,\quad t \leqslant \tau \leqslant T, \\ \frac{{d{{I}^{{ - 1}}}\left( \tau \right)}}{{d\tau }} - {{N}^{{\text{T}}}}\left( \tau \right){{I}^{{ - 1}}}\left( \tau \right) = 0,\quad {{I}^{{ - 1}}}\left( t \right) = \exp \left\{ {\mathop \smallint \limits_0^t {{N}^{{\text{T}}}}\left( s \right)ds} \right\}, \\ \frac{{d{{y}^{\beta }}\left( \tau \right)}}{{d\tau }} = {{I}^{{ - 1}}}\left( \tau \right){{M}^{{\text{T}}}}\left( \tau \right)y\left( \tau \right),\quad ~{{y}^{\beta }}\left( \tau \right) = 0, \\ \beta \left( {t,y} \right) = \mathbb{E}\{ {{I}^{{ - 1}}}\left( t \right){{I}^{{ - 1}}}\left( T \right){{Q}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y\left( T \right) + {{I}^{{ - 1}}}\left( t \right){{y}^{\beta }}\left( T \right)\} , \\ \frac{{d{{y}^{\gamma }}\left( \tau \right)}}{{d\tau }} = K\left( {\tau ,y\left( \tau \right)} \right),~{{y}^{\gamma }}\left( t \right) = 0, \\ \gamma \left( {t,y} \right) = \mathbb{E}\{ {{y}^{{\text{T}}}}\left( T \right){{P}^{{\text{T}}}}\left( T \right)S\left( T \right)P\left( T \right)y\left( T \right) + {{y}^{\gamma }}\left( T \right)\} . \\ \end{gathered} $Здесь для удобства интегрирования введены дополнительные переменные ${{y}^{\beta }}(\tau ) \in {{\mathbb{R}}^{{{{n}_{z}}}}}$, ${{y}^{\gamma }}(\tau )\, \in \,{{\mathbb{R}}^{1}}$ и учтено, что
Полученная дифференциальная система (4.5) дает альтернативный вариант приближенного расчета оптимального управления (3.7) в отношении расчета коэффициентов $\beta \left( {t,y} \right)$ и определения его качества $J((U{\text{*}})_{0}^{T}) = V\left( {0,Y,Z} \right) = \mathbb{E}\{ {{Z}^{{\text{T}}}}\alpha \left( 0 \right)Z + {{Z}^{{\text{T}}}}\beta \left( {0,Y} \right) + \gamma \left( {0,Y} \right)\} $ в отношении расчета коэффициента $\gamma \left( {0,y} \right).$ Именно многократно моделируя решение системы (4.5) для различных начальных условий $\left( {t,y} \right),$ указанные коэффициенты можно оценивать по методу Монте-Карло, заменяя операторы $\mathbb{E}\left\{ \cdot \right\}$ в (4.5) статистическим средним. Детально соответствующий алгоритм приведен в [21]. Заметим, что альтернативным предлагаемый метод квалифицируется по отношению к традиционному способу решения параболических уравнений (3.11), (3.12) методом конечных разностей.
5. Частный случай линейного сноса. Прежде чем перейти к вопросам практической реализации и обсуждению модельного примера, рассмотрим один частный случай, когда оптимальное управление (3.7) может быть найдено аналитически, т.е. без численного решения параболического уравнения (3.11). Очевидно, что частным случаем рассматриваемой задачи является классическая линейно-гауссовская постановка, о чем уже упоминалось выше. В таком случае функция Беллмана (3.5) является квадратичной, что означает линейность коэффициентов $\beta (t,y)$ и квадратичность коэффициента $\gamma \left( {t,y} \right)$ по y, т.е. решения (3.11), (3.12) могут быть найдены в виде $\beta (t,y) = {{\beta }^{a}}(t)y + {{\beta }^{b}}(t)$ и $\gamma (t,y) = {{y}^{{\text{T}}}}{{\gamma }^{a}}(t)y + {{y}^{{\text{T}}}}{{\gamma }^{b}}(t) + {{\gamma }^{c}}(t)$ соответственно, где матрица ${{\beta }^{a}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}} \times {{n}_{y}}}}}$, вектор ${{\beta }^{b}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{z}}}}}$, матрица ${{\gamma }^{a}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{y}} \times {{n}_{y}}}}}$, вектор ${{\gamma }^{b}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{y}}}}}$ и функция ${{\gamma }^{c}}\left( t \right) \in {{\mathbb{R}}^{1}}$ не зависят от y. Такой случай с точки зрения новизны интереса не представляет.
Однако рассматриваемая постановка включает другой более интересный частный вариант. Из-за независимости состояния y(t), заданного уравнением (2.1), от управления u(t), которое входит линейно только в уравнение (2.2) выхода z(t), для линейности коэффициентов $\beta \left( {t,y} \right)$ достаточно линейного сноса $A\left( {t,y} \right)$ в (2.1), а линейность диффузии $\Sigma \left( {t,y} \right)$ не требуется. В отличие от случая LQG функция Беллмана при этом не будет квадратичной, решение уравнения (3.12) в виде $\gamma \left( {t,y} \right) = {{y}^{{\text{T}}}}{{\gamma }^{a}}\left( t \right)y + {{y}^{{\text{T}}}}{{\gamma }^{b}}\left( t \right) + {{\gamma }^{c}}\left( t \right)$ не представляется именно из-за нелинейности $\Sigma \left( {t,y} \right),$ но простое линейное представление оптимального управления (3.7) в этом практически важном частном случае получается.
Итак, в предположении, что $A\left( {t,y} \right) = {{A}^{a}}\left( t \right)y + {{A}^{b}}\left( t \right)$, где матрица ${{A}^{a}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{y}} \times {{n}_{y}}}}}$ и вектор ${{A}^{b}}\left( t \right) \in {{\mathbb{R}}^{{{{n}_{y}}}}}$ не зависят от y, найдем решение (3.11) в виде $\beta \left( {t,y} \right) = {{\beta }^{a}}\left( t \right)y + {{\beta }^{b}}\left( t \right)$. При этом предположении
Кроме того, учтем, что для слагаемых с $\partial {{\beta }^{{\left( i \right)}}}{\text{/}}\partial y$ в (3.11) имеет место
(5.1)
$\frac{{d{{\beta }^{a}}}}{{dt}} + {{\beta }^{a}}{{A}^{a}} + {{M}^{{\text{T}}}} + {{N}^{{\text{T}}}}{{\beta }^{a}} = 0,\quad \frac{{d{{\beta }^{b}}}}{{dt}} + {{\beta }^{a}}{{A}^{b}} + {{N}^{{\text{T}}}}{{\beta }^{b}} = 0,$(5.2)
$u{\text{*}} = u{\text{*}}\left( {t,y,z} \right) = - 1{\text{/}}2~{{({{R}^{{\text{T}}}}SR)}^{{ - 1}}}(2({{c}^{{\text{T}}}}\alpha + {{R}^{{\text{T}}}}SQ)z + ({{c}^{{\text{T}}}}{{\beta }^{a}} + 2{{R}^{{\text{T}}}}SP)y + {{c}^{{\text{T}}}}{{\beta }^{b}}).$6. Вопросы численной реализации и модельный пример. В этом разделе обсуждаются некоторые аспекты практической реализации полученного оптимального управления. С этой целью рассматривается прикладной пример из области телекоммуникаций – популярного современного источника приложений для различных теоретических задач. Далее использована простая модель для показателя RTT сетевого протокола TCP [22]. Рассматривается модельный пример, поэтому параметры подобраны для лучшей выразительности иллюстративного материала. Переменная состояния RTT описывается следующей диффузией:
(6.1)
$dy\left( t \right) = \left( {1 - y\left( t \right)} \right)dt + 2.5\sqrt {y\left( t \right)} d{v}\left( t \right),\quad y\left( 0 \right) = Y\sim \mathbb{N}\left( {15,9} \right).$Здесь $\mathbb{N}\left( {M,D} \right)$ – нормальное распределение со средним M и дисперсией D.
Надо отметить, что такое уравнение (с точностью до варьируемых параметров) изначально известно как модель Кокса–Ингерсона–Росса (Cox–Ingersoll–Ross model) [23] и описывает эволюцию процентных ставок. Конечно, для описания реальных данных RTT модель типа (6.1) представляет не более чем начальное приближение, но оно полезно уже потому, что дает основу для дальнейших обобщений, уточнений модели (см., например, [7]). Свойства процесса y(t) из (6.1) хорошо изучены, в частности имеется свойство неотрицательности выборочных значений $y\left( t \right) > 0$, наличие эргодичности, известно предельное распределение и переходная вероятность. Отметим, что начальные условия в (6.1) выбраны так, что M, D значительно отличаются от моментных характеристик предельного распределения, т.е. управление ведется в рамках переходного процесса, а не в стационарном режиме.
Выход для состояния (6.1) задается уравнением
(6.2)
$dz\left( t \right) = y\left( t \right)dt - z\left( t \right)dt + u\left( t \right)dt + 2.5dw\left( t \right),\quad ~{{z}_{0}} = Z\sim \mathbb{N}\left( {9,9} \right),$(6.3)
$J(U_{0}^{T}) = \mathbb{E}\left\{ {\mathop \smallint \limits_0^T ({{{\left( {y(t) - z(t)} \right)}}^{2}} + {{z}^{2}}(t) + {{u}^{2}}(t))dt + {{{\left( {y\left( T \right) - z\left( T \right)} \right)}}^{2}} + {{z}^{2}}\left( T \right)} \right\}.$Такой выход имитирует выделение некоторого временного ресурса, складывающегося из текущего показателя RTT, управляющего воздействия и возмущения. Соответственно функционал (6.3) ставит целью отслеживание выходной переменной состояния с минимизацией затрат на управляющие воздействия и абсолютное значение выхода. Таким образом, понятная для практики задача отслеживания состояния дополняется учетом значения выхода, которое не позволит ему неограниченно расти в случае роста RTT, и платой за применение управляющих воздействий, которые в реальности связаны с некоторыми изменениями конфигурации оборудования или программного обеспечения.
Моделировалось $N = 1000$ траекторий $y(t),z{\text{*}}(t),~u{\text{*}}(t)$ для T = 5. Здесь через z*(t) обозначен выход (6.2), рассчитанный для оптимального управления с обратной связью $u{\text{*}} = u{\text{*}}(t,y,z)$. Кроме того, моделировались траектории ${{z}^{{(prog)}}}(t),{{u}^{{(prog)}}}(t)$ для программного управления ${{u}^{{(prog)}}}(t) = \mathbb{E}\{ u{\text{*}}(t)\} $ и ${{z}^{{(0)}}}(t),{{u}^{{(0)}}}(t)$ для неуправляемого выхода (6.2), т.е. для $u\left( t \right) = 0$. В каждом случае путем осреднения по пучку траекторий оценивались величины $J(U_{0}^{t})$. Соответственно в результате можно увидеть не только конечные значения целевой функции для разных вариантов управления $J((U{\text{*}})_{0}^{T})$, $J(({{U}^{{\left( {prog} \right)}}})_{0}^{T})$, $~J(({{U}^{{\left( 0 \right)}}})_{0}^{T})$, но и их формирование в динамике.
Описание численных процедур начнем с моделирования. Траектории y(t), z(t) моделировались приближенно, для чего уравнения (6.1), (6.2) дискретизировались по методу Эйлера с шагом ${{\delta }_{t}} = 0.001$ (тем же, что далее использовался при численной аппроксимации $\beta \left( {t,y} \right)$). Соответствующие смоделированные значения $y\left( {t - {{\delta }_{t}}} \right),z{\text{*}}\left( {t - {{\delta }_{t}}} \right)$ применялись в (3.7) для вычисления реализаций управления $u{\text{*}}\left( t \right) = u{\text{*}}(t,y\left( t \right),z{\text{*}}\left( t \right))$.
Далее заметим, что уравнение Риккати (3.8) для α(t) с учетом постоянных коэффициентов в выбранной модели выхода (6.2) и целевом функционале (6.3) решается точно. Именно
Наконец, оптимальное управление u* рассчитывалось тремя способами. Во-первых, поскольку снос в модели (6.1) линейный, то в рассматриваемом примере можно вычислить решение, не интегрируя общее уравнение (3.11) для $\beta \left( {t,y} \right)$, а решая уравнения (5.1) и вычисляя далее управление, согласно (5.2). Система (5.1) линейных уравнений для ${{\beta }^{a}}\left( t \right)$ и ${{\beta }^{b}}\left( t \right)$ решалась неявным методом Эйлера с тем же шагом ${{\delta }_{t}} = 0.001$. Соответствующее приближенное оптимальное управление обозначается далее ${{u}^{{\left( {ref} \right)}}}$, решение уравнение (3.11) – ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)$. Эти аппроксимации в данном примере носят референсный (эталонный) характер.
Второй способ аппроксимации $\beta \left( {t,y} \right)$ – использование традиционного метода конечных разностей для решения параболического уравнения (3.11). Реализованные варианты и особенности применения этого метода ниже обсуждаются подробнее, а соответствующее приближенное решение обозначается ${{u}^{{\left( {net} \right)}}}$, решение уравнения (3.11) – ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right).$
Третий способ – моделирование решений системы (4.5) и замена математического ожидания статистической оценкой (метод Монте-Карло). Соответствующие приближенные решения – ${{u}^{{\left( {MK} \right)}}}$ и ${{\beta }^{{\left( {MK} \right)}}}\left( t \right).$
Оказалось, что на графических иллюстрациях далее визуализировать разницу между реализациями управлений ${{u}^{{\left( {ref} \right)}}}\left( t \right),~{{u}^{{\left( {net} \right)}}}\left( t \right),~{{u}^{{\left( {MK} \right)}}}\left( t \right)$ не удается, поэтому в этих иллюстрациях использовано общее обозначение u*(t).
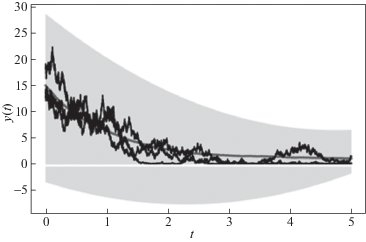
Вопросы применения метода конечных разностей для уравнения параболического типа давно и хорошо изучены [24]. Первое, что надо сделать для расчета ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right),$ – это ограничить область значения аргумента y для формирования численной схемы расчета. С этой целью использовались N смоделированных траекторий (6.1): выборочные значения использовались для оценивания функций математического ожидания и дисперсионной, с помощью которой определялась 3σ-трубка. Рисунок 1 иллюстрирует характерные траектории (6.1), среднее значение процесса и вычисленные границы (закрашенная серым область). В расчетах граница значений $y$ задавалась добавлением еще 10% к границе 3σ-трубки, чтобы уменьшить влияние выбора граничных условий, а также учитывалась положительность y(t), поэтому далее область интегрирования $y \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} ,\bar {y}]$ = [0, 40].
Определение границы, нужное для инициирования любой схемы метода конечных разностей, выявляет проблему отсутствия граничных условий для решаемого уравнения (3.11). Этих условий нет, и нет физических оснований для их обоснованного выбора. Из-за этого граница $\bar {y}$ была сдвинута дополнительно, а сами граничные условия приходилось выбирались волюнтаристски в надежде на нечувствительность решения в отношении этих граничных условий.
Выбор граничного условия и анализ его влияния на решение выполнялся следующим образом. Были взяты два традиционных варианта граничных условий – в задаче Дирихле: ${{\left. {\beta (t,y)} \right|}_{{y = \bar {y}}}}$ = 0, т.е. условие поглощения, и в задаче Неймана: ${{\left. {\partial \beta \left( {t,y} \right){\text{/}}\partial y} \right|}_{{y = \bar {y}}}} = 0$, т.е. условие отражения. Причем наличие в данном примере эталонного решения ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)$ позволяет видеть, что оба варианта далеки от точного. Далее уравнение (3.11) решалось методом конечных разностей с использованием явной и неявной численных схем сначала для одного граничного условия, затем для второго и полученные решения сравнивались. Устойчивость в таком случае означает совпадение (близость) решений в области, выделенной по результатам моделирования, т.е. для $y \in \left[ {0,30} \right].$
Для численного интегрирования в выбранной области $\left[ {0,T} \right] \cup [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} ,\bar {y}]$ формировалась сетка $\left\{ {{{t}_{k}},{{y}_{i}}} \right\}$ с шагами δt (для интегрирования по переменной t) и δy (для интегрирования по переменной y). С использованием обозначения $\beta _{i}^{k}$ для значения $\beta \left( {t,y} \right)$ в узле $\left( {{{t}_{k}},{{y}_{i}}} \right)$ производные аппроксимировались следующим образом:
Шаги интегрирования δt, δy при анализе влияния граничных условий и устойчивости схем аппроксимации выбирались разными, например явная схема обсчитывалась для ${{\delta }_{t}} = 0.0002$ и ${{\delta }_{y}} = 0.1$, в том числе с учетом того, что для нее самой вопрос устойчивости ограничивает вариации шагов. Главное, что в итоге подтвердилось отсутствие влияния выбора граничных условий на результаты численного интегрирования уравнения (3.11) для $\beta \left( {t,y} \right),$ по крайней мере, для выбранной модели, а также для комбинации шагов δt, δy, обеспечивающей устойчивость схем аппроксимации. Итоговый расчет выполнен для неявной схемы с шагами ${{\delta }_{t}} = 0.001$ и ${{\delta }_{y}} = 0.01,$ и именно это решение обозначено ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right)$, т.е. сетка содержала ${{N}_{T}} = 5000$ точек разбиения отрезка [0, T] и ${{N}_{y}} = 4000$ точек разбиения отрезка $[\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} ,\bar {y}]$.
Наконец, последний третий метод расчета на основании стохастического представления коэффициентов функции Беллмана дал приближенное решение ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right)$. Использовалась та же сетка $\left\{ {{{t}_{k}},{{y}_{i}}} \right\}$ с ${{\delta }_{t}} = 0.001$ и ${{\delta }_{y}} = 0.01$, что и в итоговом расчете методом конечных разностей, и выборка из $N \cdot {{N}_{T}} \cdot {{N}_{y}} = 2 \times {{10}^{{10}}}$ фрагментов траекторий y(t), аппроксимирующих (4.5) согласно явному методу Эйлера.
Результаты расчетов иллюстрируют рис. 2–4, на которых приведены примеры траекторий для выхода и управлений $z{\text{*}}\left( t \right),~u{\text{*}}\left( t \right)$, ${{z}^{{\left( {prog} \right)}}}\left( t \right),~{{u}^{{\left( {prog} \right)}}}\left( t \right)$ и ${{z}^{{\left( 0 \right)}}}\left( t \right),~{{u}^{{\left( 0 \right)}}}\left( t \right)$.
Рис. 2.
Выборочные траектории: а – z*(t), б – ${{z}^{{\left( {prog} \right)}}}\left( t \right),$ в – ${{z}^{{\left( 0 \right)}}}\left( t \right)$
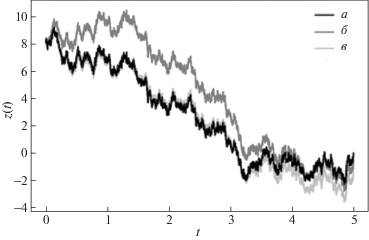
Рис. 3.
Выборочные траектории: а – u*(t), б – ${{u}^{{\left( {prog} \right)}}}\left( t \right),$ в – ${{u}^{{\left( 0 \right)}}}\left( t \right)$
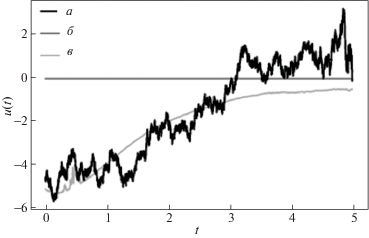
Рис. 4.
Динамика целевого функционала а – $J((U{\text{*}})_{0}^{t}),$ б – $J(({{U}^{{(prog)}}})_{0}^{t}),$ в – $J(({{U}^{{(0)}}})_{0}^{t})$

Рисунок 4 демонстрирует ожидаемый проигрыш неуправляемой системы ${{z}^{{\left( 0 \right)}}}\left( t \right),{{u}^{{\left( 0 \right)}}}\left( t \right)$ и хорошее качество программного управления ${{u}^{{\left( {prog} \right)}}}\left( t \right)$. Последнее обстоятельство, конечно, объясняется исключительно выбранными параметрами рассматриваемого модельного примера.
Остается сравнить результаты трех методов аппроксимации оптимального управления u*. Лучшей иллюстрацией является сравнение аппроксимаций $\beta \left( {t,y} \right)$, т.е. поверхностей ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right),$ ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right),$ ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right).$ Выполненные расчеты иллюстрируются на рис. 5–7, представляющих эти поверхности в точках $t = $ 0, 1, 2, 3, 4, 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 4.95, 5.0 (точки выбраны там, где изменения поверхности более выражены и иллюстрации более выразительны) и целочисленных точках отрезка $y \in \left[ {0,30} \right].$
Как уже отмечалось, визуально оценить данные на этих рисунках затруднительно, но качественно можно отметить, что, с одной стороны, поверхности похожи, с другой – поверхность ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right)$ отличается некоторым “дрожанием” в сравнении с гладкими ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)$ и ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right),$ что является очевидным следствием аппроксимации значений $\beta \left( {t,y} \right)$ статистическими оценками по моделируемым данным.
Несколько более информативны графические материалы, приведенные на рис. 8–10. Это сечения поверхностей ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right),$ ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right)$ и ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right)$ в тех же точках t. Причем в точном решении, представленном ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right),$ это прямые линии. Также прямой $\beta \left( {T,y} \right) = - 2y$ отвечает терминальное условие.
Числовые значения, иллюстрирующие отклонения $\left| {{{\beta }^{{(net)}}}(t,y) - {{\beta }^{{(ref)}}}(t,y)} \right|$ и $\left| {{{\beta }^{{(MK)}}}(t,y) - {{\beta }^{{(ref)}}}(t,y)} \right|$ в некоторых точках t, y, представлены в табл. 1 и 2. В табл. 3 приведены значения ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)$, чтобы можно было оценить относительные отклонения. По всей совокупности полученных данных можно сказать, что отклонения ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right)$ от эталонной поверхности ${{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)$ несколько (2–3%) меньше в большинстве точек, чем отклонения ${{\beta }^{{\left( {net} \right)}}}\left( {t,y} \right)$. Но поверхность, рассчитанная методом конечных разностей, и ее отклонения от эталона носят более регулярный характер. Точнее, в некоторых узлах относительные отклонения $\left| {{{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right) - {{\beta }^{{\left( {ref} \right)}}}\left( {t,y} \right)} \right|$ составляют до 10% и в целом, как и самой поверхности ${{\beta }^{{\left( {MK} \right)}}}\left( {t,y} \right)$, им свойственно некоторое “дрожание”, характерное для оценок Монте-Карло. Объективную оценку проводимого сравнения, конечно, дает значение целевого функционала (6.3), доставляемое управлениями ${{u}^{{\left( {ref} \right)}}},$ ${{u}^{{\left( {net} \right)}}}$ и ${{u}^{{\left( {MK} \right)}}}$. Эти данные приведены в табл. 4 и подтвердили не только высокую точность расчетов, но и превосходство метода аппроксимации, основанного на стохастическом представлении коэффициентов функции Беллмана. И хотя последний вывод сделан в отношении цели решаемой задачи управления, т.е. качества аппроксимации управления u*, данные в табл. 4 можно интерпретировать и как косвенное свидетельство о более высокой точности аппроксимации $\beta \left( {t,y} \right).$
Таблица 1.
Отклонения $\left| {{{\beta }^{{(net)}}}(t,y) - {{\beta }^{{(ref)}}}(t,y)} \right|$
| t, y | 0.0 | 3.0 | 5.0 | 10.0 | 15.0 | 25.0 |
|---|---|---|---|---|---|---|
| 4.95 | 0.0233 | 0.0404 | 0.0829 | 0.1892 | 0.2955 | 0.5080 |
| 4.9 | 0.0196 | 0.2237 | 0.3599 | 0.7001 | 1.0404 | 1.7208 |
| 4.8 | 0.0329 | 0.2804 | 0.4454 | 0.8580 | 1.2706 | 2.0936 |
| 4.7 | 0.0409 | 0.2735 | 0.4285 | 0.8162 | 1.2038 | 1.9742 |
| 4.6 | 0.0448 | 0.2429 | 0.3749 | 0.7051 | 1.0353 | 1.6890 |
| 4.5 | 0.0457 | 0.2056 | 0.3122 | 0.5788 | 0.8453 | 1.3713 |
| 4.4 | 0.0445 | 0.1691 | 0.2521 | 0.4598 | 0.6673 | 1.0759 |
| 4.3 | 0.0420 | 0.1364 | 0.1993 | 0.3566 | 0.5138 | 0.8225 |
| 4.2 | 0.0386 | 0.1084 | 0.1550 | 0.2713 | 0.3875 | 0.6151 |
| 4.1 | 0.0349 | 0.0853 | 0.1190 | 0.2030 | 0.2870 | 0.4508 |
| 4.0 | 0.0310 | 0.0666 | 0.0903 | 0.1496 | 0.2089 | 0.3237 |
| 3.0 | 0.0061 | 0.0049 | 0.0042 | 0.0022 | 0.0002 | 0.0060 |
| 2.0 | 0.0009 | 0.0005 | 0.0003 | 0.0003 | 0.0010 | 0.0046 |
| 1.0 | 0.0001 | 0.0001 | 0.0001 | 0.0000 | 0.0001 | 0.0027 |
| 0.0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0025 |
Таблица 2.
Отклонения $\left| {{{\beta }^{{(MK)}}}(t,y) - {{\beta }^{{(ref)}}}(t,y)} \right|$
| t, y | 0.0 | 3.0 | 5.0 | 10.0 | 15.0 | 25.0 |
|---|---|---|---|---|---|---|
| 4.95 | 0.0285 | 0.0105 | 1.0764 | 0.2761 | 0.5671 | 0.6918 |
| 4.9 | 0.0089 | 0.2988 | 0.4090 | 0.7194 | 1.0914 | 1.1994 |
| 4.8 | 0.1142 | 0.3755 | 0.1529 | 2.6940 | 0.7033 | 0.3248 |
| 4.7 | 0.1229 | 0.2741 | 0.6190 | 0.1041 | 2.8318 | 1.9781 |
| 4.6 | 0.0350 | 0.1291 | 0.3174 | 0.9699 | 1.2111 | 2.1372 |
| 4.5 | 0.0879 | 0.4242 | 0.5385 | 0.0298 | 0.4110 | 2.8989 |
| 4.4 | 0.0574 | 0.1915 | 0.7325 | 0.0092 | 0.7438 | 0.4403 |
| 4.3 | 0.1234 | 0.3271 | 0.2571 | 0.7245 | 2.7593 | 0.3966 |
| 4.2 | 0.0195 | 0.4084 | 0.1320 | 0.0601 | 0.7345 | 0.2707 |
| 4.1 | 0.1129 | 0.2158 | 0.1640 | 0.0178 | 0.6478 | 0.6370 |
| 4.0 | 0.0300 | 0.0933 | 0.0546 | 0.5945 | 0.2144 | 0.9019 |
| 3.0 | 0.0243 | 0.0657 | 0.0551 | 0.3454 | 0.0940 | 0.1782 |
| 2.0 | 0.0468 | 0.0200 | 0.1190 | 0.0636 | 0.1032 | 0.8721 |
| 1.0 | 0.0626 | 0.1975 | 0.1085 | 0.1386 | 0.0987 | 0.4386 |
| 0.0 | 0.0036 | 0.0828 | 0.0301 | 0.0288 | 0.0860 | 0.3083 |
Таблица 3.
Поверхность ${{\beta }^{{(ref)}}}(t,y)$
| t, y | 0.0 | 3.0 | 5.0 | 10.0 | 15.0 | 25.0 |
|---|---|---|---|---|---|---|
| 4.95 | –0.0592 | –4.8340 | –8.0172 | –15.9752 | –23.9332 | –39.8493 |
| 4.9 | –0.1183 | –3.6679 | –6.0344 | –11.9504 | –17.8665 | –29.6985 |
| 4.8 | –0.1658 | –2.3944 | –3.8802 | –7.5947 | –11.3091 | –18.7380 |
| 4.7 | –0.1805 | –1.6625 | –2.6506 | –5.1208 | –7.5909 | –12.5312 |
| 4.6 | –0.1798 | –1.2315 | –1.9326 | –3.6855 | –5.4384 | –8.9442 |
| 4.5 | –0.1723 | –0.9759 | –1.5116 | –2.8510 | –4.1903 | –6.8689 |
| 4.4 | –0.1625 | –0.8256 | –1.2676 | –2.3727 | –3.4778 | –5.6880 |
| 4.3 | –0.1525 | –0.7392 | –1.1302 | –2.1079 | –3.0856 | –5.0411 |
| 4.2 | –0.1435 | –0.6917 | –1.0572 | –1.9709 | –2.8845 | –4.7119 |
| 4.1 | –0.1358 | –0.6678 | –1.0224 | –1.9090 | –2.7957 | –4.5690 |
| 4.0 | –0.1295 | –0.6577 | –1.0099 | –1.8904 | –2.7708 | –4.5317 |
| 3.0 | –0.1118 | –0.6910 | –1.0772 | –2.0425 | –3.0079 | –4.9386 |
| 2.0 | –0.1127 | –0.7006 | –1.0925 | –2.0723 | –3.0520 | –5.0116 |
| 1.0 | –0.1132 | –0.7016 | –1.0939 | –2.0746 | –3.0553 | –5.0167 |
| 0.0 | –0.1132 | –0.7017 | –1.0940 | –2.0748 | –3.0555 | –5.0170 |
Таблица 4.
Динамика функционалов $J(({{U}^{{(ref)}}})_{0}^{T})$, $J(({{U}^{{(net)}}})_{0}^{T}),$ $J(({{U}^{{(MK)}}})_{0}^{T})$
| t | $J(({{U}^{{(ref)}}}))_{0}^{t})$ | $J(({{U}^{{(net)}}})_{0}^{t})$ | $J(({{U}^{{(MK)}}})_{0}^{t})$ | $\frac{{{\text{|}}J(({{U}^{{(ref)}}})_{0}^{t}) - J(({{U}^{{(net)}}})_{0}^{t}){\text{|}}}}{{J(({{U}^{{(ref)}}})_{0}^{t})}}$100% | $\frac{{{\text{|}}J(({{U}^{{(ref)}}})_{0}^{t}) - J(({{U}^{{(MK)}}})_{0}^{t}){\text{|}}}}{{J(({{U}^{{(ref)}}})_{0}^{t})}}$100% |
|---|---|---|---|---|---|
| 1 | 112.7 | 120.6 | 116.0 | 7.0 | 2.9 |
| 2 | 157.4 | 170.3 | 161.0 | 8.2 | 2.3 |
| 3 | 174.6 | 190.0 | 179.9 | 8.8 | 3.1 |
| 4 | 186.4 | 200.9 | 192.1 | 7.8 | 3.1 |
| 5 | 202.1 | 215.7 | 208.6 | 6.7 | 3.2 |
Заключение. Представленные в работе результаты в полном объеме описывают решение задачи управления линейным выходом векторного диффузионного процесса Ито по квадратичному критерию качества. Оптимальное решение – управление с полной обратной связью – задано замкнутой системой уравнений, приближенное решение которых может быть получено известными численными методами решения обыкновенных дифференциальных уравнений и уравнений в частных производных параболического типа. Свойства оптимального управления описаны стохастическим представлением коэффициентов найденной функции Беллмана на основе формулы Фейнмана–Каца. Это стохастическое представление позволило реализовать альтернативный метод приближенного решения задачи, базирующийся на имитационном компьютерном моделировании оптимизируемой системы. Численный пример показал работоспособность обоих методов аппроксимации и небольшое преимущество метода, основанного на стохастическом представлении коэффициентов функции Беллмана.
Для дальнейшего изучения важны следующие два направления. Во-первых, интересна задача с неполной информацией, т.е. постановка, в которой диффузионный процесс (2.1) предполагается ненаблюдаемым непосредственно, а доступным только косвенным наблюдениям (2.2). В этом направлении решение в общем виде получить не удастся. Причиной являются трудности в решении возникающей в такой постановке вспомогательной задачи оценивания – оптимальной фильтрации состояния y(t) по наблюдениям z(t). Субоптимальная фильтрация позволяет предлагать приближенные решения, практически пригодные, но не очень содержательные для теоретического изучения [25].
Второе перспективное направление развития исследованной задачи – это обобщение модели диффузии на случай смешанных непрерывно-дискретных возмущений. Это важное обобщение сделает постановку более практически содержательной. Так в использованном здесь модельном примере обобщается и становится более соответствующей потребностям практики модель RTT.
Список литературы
Kushner H.J., Dupuis P.G. Numerical Methods for Stochastic Control Problems in Continuous Time. N.Y.: Springer-Verlag, 2001.
Bertsekas D.P. Dynamic Programming and Optimal Control. Cambridge: Athena Scientific, 2013.
Флеминг У., Ришел Р. Оптимальное управление детерминированными и стохастическими системами / Пер. с англ. М.: Мир, 1978.
Athans M. The Role and Use of the Stochastic Linear-Quadratic-Gaussian Problem in Control System Design // IEEE Trans. Automat. Control. 1971. V. 16. № 6. P. 529–552.
Wu Z. Forward-backward Stochastic Differential Equations, Linear Quadratic Stochastic Optimal Control and Nonzero Sum Differential Games // J. Syst. Sci. Complexity. 2005. V. 18. № 2. P. 179–192.
Chen B.S., Zhang W. Stochastic H2/H1 Control with State-dependent Noise // IEEE Trans. Automat. Control. 2004. V. 49. № 1. P. 45–56.
Bohacek S. A Stochastic Model of TCP and Fair Video Transmission // Proc. IEEE INFOCOM. 2003. P. 1134–1144.
Миллер Б.М., Авраченков К.Е., Степанян К.В., Миллер Г.Б. Задача оптимального стохастического управления потоком данных по неполной информации // Пробл. передачи информ. 2005. Т. 41. № 2. С. 89–110.
Боровков А.А. Асимптотические методы в теории массового обслуживания. М.: Наука, 1980.
Босов А.В. Обобщенная задача распределения ресурсов программной системы // Информатика и ее применения. 2014. Т. 8. Вып. 2. С. 39–47.
Босов А.В. Управление линейным выходом дискретной стохастической системы по квадратичному критерию // Изв. РАН. ТиСУ. 2016. № 3. С. 19–35.
Athans M., Falb P.L. Optimal Control: An Introduction to the Theory and Its Applications. N.Y., Sydney: McGraw-Hill, 1966.
Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних возмущений: управление по выходу // АиТ. 2008. № 5. С. 72–90.
Баландин Д.В., Коган М.М. Минимаксный подход к синтезу оптимального управления при неопределенных начальных условиях // АиТ. 2009. № 11. С. 3–12.
Мирошник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное управление сложными динамическими системами. СПб.: Наука, 2000.
Gihman I.I., Skorohod A.V. The Theory of Stochastic Processes III. N.Y.: Springer-Verlag, 2012.
Øksendal B. Stochastic Differential Equations. An Introduction with Applications. N.Y.: Springer-Verlag, 2003.
Fahim A., Touzi N., Warin, X. A Probabilistic Numerical Method for Fully Nonlinear Parabolic Pdes // Annals of Applied Probability. 2011. V. 21. № 4. P. 1322–1364.
Девис М.Х.А. Линейное оценивание и стохастическое управление / Пер. с англ. М.: Наука, 1984.
Bhatia R. Matrix Analysis. T. 169. N.Y.: Springer, 1997.
Босов А.В., Стефанович А.И. Управление выходом стохастической дифференциальной системы по квадратичному критерию. IV. Альтернативное численное решение // Информатика и ее применения. 2020. Т. 14. Вып. 1. С. 24–30.
Bohacek S., Rozovskii B. A Diffusion Model of Roundtrip Time // Computational Statistics & Data Analysis. 2004. V. 45. Iss. 1. P. 25–50.
Cox J.C., Ingersoll J.E., Ross S.A. A Theory of the Term Structure of Interest Rates // Econometrica. 1985. V. 53. Iss. 2. P. 385–407.
Саульев В.К. Интегрирование уравнений параболического типа методом сеток. М.: Физматлит, 1960.
Босов А.В. Применение условно-оптимального фильтра для синтеза субоптимального управления в задаче оптимизации выхода нелинейной дифференциальной стохастической системы // АиТ. 2020. № 11. С. 34–47.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления