Известия РАН. Теория и системы управления, 2021, № 5, стр. 74-90

Введение. Важным направлением в теории управления является развитие методов оптимизации движения систем с распределенными параметрами. В случае выпуклых функционалов математическое обоснование для задач оптимального управления динамическими системами, определяемыми линейными дифференциальными уравнениями в частных производных (УЧП), заложено во многом научной школой Лионса [1]. Вопросы управляемости систем с УЧП гиперболического типа рассматривались и другими авторами [2, 3]. Вводный обзор теории управления распределенными колебаниями дан в [4]. Управляемые колебания в сетевых моделях исследуются, в частности, в [5–7]. Актуальность достоверного математического моделирования динамических систем с распределенными параметрами ускорило развитие новых подходов к решению прямых и обратных задач механики.

Можно указать на два важных направления изучения задач оптимального управления для распределенных процессов. Для первого из них в иностранной литературе распространен термин “поздняя дискретизация” (late lumping). Согласно этому подходу, законы оптимального управления строятся непосредственно для исходной динамической системы, описываемой УЧП. Только на последнем этапе управляющие функции и само решение могут аппроксимироваться с применением подходящего конечномерного пространства. В этом случае оптимизация может опираться, например, на спектральную теорию линейных операторов [8, 9]. Иногда для относительно простых систем используют [10] метод разделения переменных и декомпозиции на основе метода Фурье, что позволяет находить квазиоптимальные ограниченные воздействия, за конечное время приводящие систему в заданное состояние. Альтернативный метод в решении задач оптимального управления с УЧП связан с методом выбора [11]. В общем случае даже для несложных систем, описывающих, скажем, движения замкнутой струны, получение управления в явном виде и последующее доказательство его оптимальности невозможно без привлечения развитых математических подходов [12]. Важный вопрос в обратных задачах динамики для систем с распределенными параметрами – это управляемость и, как следствие, возможность или невозможность точного приведения изучаемой системы в заданное состояние за конечное время и дальнейшего удержания в этом состоянии с помощью ограниченных воздействий [13, 14].

Второе развитое направление в изучении динамики и управления распределенными системами называется “ранней дискретизацией” (early lumping) и широко используется для построения численных решений. В этом случае начально-краевая задача уже на начальном этапе дискретизируется и сводится к системе либо алгебраических, либо обыкновенных дифференциальных уравнений (ОДУ). Для этой цели развиваются метод конечных элементов (МКЭ), методы конечного объема и конечных разностей [16, 15 ]. В случае МКЭ алгоритмы решения могут основываться на методе коллокации, методе Бубнова–Галеркина [18], подходе Петрова–Галеркина [19], методе наименьших квадратов [20] и т.д. В этом ряду численных подходов при рассмотрении задач управления динамикой системы спектральный анализ обеспечивает важные преимущества [9] в случае, когда собственные функции системы находятся в явном виде. Для неоднородных систем могут применяться численные методы нахождения собственных функций [21].

На основе метода интегродифференциальных соотношений (МИДС) для описания и оптимизации колебаний в упругих и вязкоупругих системах предложены и проанализированы различные вариационные и проекционные формулировки задач оптимального управления [22]. Одна из этих формулировок используется в работе для определения необходимых свойств гладкости (непрерывности) решения. Эффективный алгоритм численного построения решения в задачах оптимального управления линейной упругости на основе метода Ритца и МКЭ был предложен в [23] и развит в [24] для случая продольных движений однородных и неоднородных упругих стержней с различными типами краевых условий.

В циклах статей авторов [25, 26] и др. исследуются задачи управления, близкие по постановке к рассмотренной далее задаче. В отличие от упомянутых публикаций, в этой статье предложена оригинальная обобщенная формулировка начально-краевой задачи, основанная на минимизации функционала невязки уравнений состояния. В этой постановке решение ищется в более широком классе и не требуются явные предположения о гладкости следов решения на границах пространственно-временной области (начальных, терминальных и краевых условий). Другой особенностью данного исследования является сама задача оптимального управления при условии минимизации энергетического функционала, который естественным образом соответствует требованиям к гладкости решения обобщенной задачи. Еще одна отличительная черта этой работы – нахождение оптимального решения как вариации бегущих волн в представлении Даламбера, что позволяет представить управление и состояние системы в единой компактной форме на всей области определения искомых функций. Проблема гладкости следов решения часто встречается при постановке обобщенной задачи в энергетических пространствах [27, 28]. В настоящей работе она решена за счет введения так называемой динамической функции (потенциала), дополнительной к функции перемещений точек упругой системы, и определения решения как пары неизвестных: упругих перемещений и динамического потенциала.

В этой работе, по сравнению с [24], хотя и рассматривается случай однородного упругого стержня с достаточно простыми краевыми условиями второго рода, получено точное оптимальное решение для важного случая минимизации средней механической энергии системы. На основе предложенного метода декомпозиции решения и представления Даламбера задачу управления удалось свести к классической вариационной задаче с фиксированными концами и построить в явном виде как оптимальный закон программного управления, так и соответствующие движения точек стержня. Более того, как показывают наши исследования, данная методика распространяется и на более широкий класс целевых функционалов, а также может быть обобщена на случай ограниченных управляющих воздействий. В статье обсуждается важный с теоретической точки зрения факт существования критического значения времени управления, за которое система может быть приведена в состояние покоя, но в общем случае не может прийти в нулевое состояние. Как будет показано ниже, это обуславливает как строго монотонное убывание средней энергии стержня при увеличении времени управления, так и стремление значения механической энергии к бесконечности при приближении времени управления к критической величине.

1. Постановка начально-краевой задачи. Рассмотрим продольные движения тонкого прямолинейного упругого стержня, схематически изображенного на рис. 1. Уравнение движения выражается через функцию $v:\overline \Omega \to \mathbb{R}$, определяемую на пространственно-временной области Ω = = $(0,T) \times ( - \ell ,\ell )$, согласно [30], уравнением

Здесь $T$ – время окончания рассматриваемого процесса, $\ell $ – полудлина стержня, нижние индексы t и x обозначают соответственно частные производные по времени и пространству, $\rho :[ - \ell ,\ell ] \to \mathbb{R}$ – линейная плотность, а $\kappa :[ - \ell ,\ell ] \to \mathbb{R}$ – продольная жесткость стержня.

В классической постановке, рассмотренной в работе, начальные условия накладываются на положения и скорости точек стержня в момент времени t = 0:

где ${{v}_{0}}$ и ${{\dot {v}}_{0}}$ – известные достаточно гладкие функции [30, 31]. На концах $x = \pm \ell $ заданы нормальные силы в поперечном сечении как неизвестные входные управляющие воздействия ${{u}_{ \pm }}(t)$ в форме

Для того чтобы перейти, согласно МИДС [22], к обобщенной формулировке начально-краевой задачи (1.1)–(1.3), введем на пространственно-временной области $\Omega $ неизвестные функции линейной плотности импульса $p:\overline \Omega \to \mathbb{R}$ и нормальной силы в поперечном сечении $s:\overline \Omega \to \mathbb{R}$. Закон изменения импульса (второй закон Ньютона) выразится через эти переменные как

Потребуются также два закона состояния, которые связывают плотность импульса p и скорости точек стержня ${{v}_{t}}$, а также нормальную силу s с продольной деформацией ${{v}_{x}}$:

Замыкают систему начально-краевые условия, заданные на $t \in [0,T]$, $x \in [ - \ell ,\ell ]$ и выраженные через переменные $v$, $p$, $s$ как

Для необходимого нам в дальнейшем упрощения представления системы с распределенными параметрами введем специальную функцию $r:\overline \Omega \to \mathbb{R}$, назовем ее динамическим “потенциалом” или динамической переменной в отличие от кинематической переменной $v$. Эта новая переменная заменяет функции импульса и силы:

Непосредственной подстановкой (1.7) в (1.4) можно показать, что при такой замене второй закон Ньютона выполняется тождествено:

Также необходимо переписать в новых терминах уравнения состояния (1.5), заданные на $(t,x) \in \overline \Omega $ как

Через кинематическую и динамическую переменные выражаются и начально-краевые соотношения (1.6), а именно

Отметим важную деталь такого представления состояния системы: динамическая переменная r определена с точностью до произвольной константы ${{c}_{0}}$, значение которой не влияет на форму движения упругого тела. В (1.10) вводятся две новые функции времени ${{U}_{ \pm }}$ как интегралы от функций управления ${{u}_{ \pm }}$. Две константы управления ${{r}_{0}}( \pm \ell )$ выбираются так, чтобы обеспечить необходимую, как будет показано далее, непрерывность решения обобщенной задачи. Другими словами, эти константы обеспечивают совместность начальных и краевых условий при t = 0 и $x = \pm \ell $.

2. Вариационная формулировка задачи. Согласно МИДС, локальные законы состояния (1.9), выраженные в УЧП и требующие C²-гладкости решения [31], заменяются одним интегральным соотношением, который, как показано в [22], может быть сведен к минимизации энергетического функционала:

при выполнении существенных ограничений и фиксированных управляющих функциях ${{U}_{ \pm }}$. В (2.1) $d\Omega = dtdx$ для выбранной системы координат $t$ и $x$. Там же введены вспомогательные функции состояния g, h, квадраты которых имеют размерность линейной плотности энергии. При этом сам функционал $\Phi $ имеет размерность энергии и его значение определяет близость аппроксимации к точному решению ${{v}_{*}},\;{{r}_{*}}$, на котором достигается абсолютный минимум $\Phi $ по переменным $v$ и $r$.

Если обратить внимание на структуру подынтегрального выражения, то можно отметить, что в него входят квадраты частных производных по $t$ и $x$ неизвестных $v$ и r. Это означает, что с учетом достаточной гладкости и отделимости от нуля параметров $\rho $, $\kappa $ эти производные должны существовать в обобщенном смысле как функции, интегрируемые в квадратах. Из этого факта следует [29], что решение ${{v}_{*}}$, ${{r}_{*}}$ вариационной задачи (2.1), (2.2) в случае его существования принадлежит гильбертову пространству H¹:

Таким образом, введение функционала (2.1) позволяет существенно ослабить требования к гладкости решения, оставаясь при этом, как будет показано далее, в рамках непрерывных функций при выбранных достаточно гладких начальных и терминальных условиях, что имеет важное значение для конструктивного решения задачи управления.

3. Задача оптимального управления. В дальнейшем рассматривается частный случай однородного упругого стержня, механические параметры которого $\rho (x) = {\text{const}}$ и $\kappa (x) = {\text{const}}$ не зависят от пространственной координаты. В этом случае для упрощения описания системы лучше перейти к безразмерным переменным:

Далее индекс $ * $ опускается.

В безразмерных переменных

следовательно, обобщенная начально-краевая задача (2.1), (2.2) переписывается в виде

Ставится следующая задача оптимального управления. Найти такие функции $U_{ \pm }^{*}$, которые задаются на фиксированном интервале времени $t \in [0,T]$, минимизируют с учетом ограничений (3.3) среднюю запасенную механическую энергию стержня, определяемую как

и приводят систему в терминальное состояние

Решение (3.3)–(3.5) – это вектор-функция $(v,r)$, поэтому в выражение для энергии E, которая является частью квадрата нормы упорядоченной пары $(v,r)$ в ${{H}^{1}}(\Omega )$, входят все частные производные $v$ и $r$.

В (3.4) введена функция линейной плотности энергии $e:\Omega \to \mathbb{R}$. Условия существования допустимого управления $\left( {{{U}_{ - }}(t),{{U}_{ + }}(t)} \right)$, приводящего систему в терминальное состояние (3.5), изучаются ниже. Обсудим сами терминальные условия.

Первое, оптимальное движение зависит от константы ${{r}_{1}}$ лишь неявно, влияя на значение целевого функционала E. При этом механический смысл терминальных условий не меняется при изменении величины ${{r}_{1}}$. Поэтому этот параметр необходимо рассматривать как свободный параметр оптимизации.

Второе, если константа ${{p}_{1}}$ не равна нулю (${{p}_{1}} \ne 0$), а ${{v}_{1}}$ – произвольна, это означает, что стержень приводится в состояние движения как жесткого целого без упругих колебаний. Если при этом терминальные значения плотности импульса ${{p}_{1}}$ и положения ${{v}_{1}}$ не важны для задачи управления, возникают еще два свободных параметра оптимизации.

Третье, если зафиксировать нулевой импульс (${{p}_{1}} = 0$), а положение ${{v}_{1}}$ задать или оставить свободным параметром, то целью управления является приведение системы в состояниe покоя с нулевой внутренней энергией.

Наконец последний случай, когда ${{p}_{1}} = 0$ и ${{v}_{1}} = 0$, означает, что целью процесса управления является приведение механической системы в нулевое состояние. Этот случай и будет рассматриваться в дальнейшем.

Следует еще раз подчеркнуть, что в зависимости от того, какие из трех терминальных констант зафиксированы или свободны, будут изменяться значение функционала, оптимальное управление $(U_{ - }^{*}(t),U_{ + }^{*}(t))$ и соответствующее решение $(v{\kern 1pt} *(t,x),r{\kern 1pt} *(t,x))$.

Отметим сходство структуры двух функционалов цены E и состояния $\Phi $, последний из которых представим в виде

где функция $\varphi :\Omega \to \mathbb{R}$ представляет собой квадрат плотности невязки уравнений состояния в которых переменные g и $h$ определены в (2.1).

4. Решение прямой задачи динамики. Будем искать решение $(v,r)$ задачи (3.3) в представлении Даламбера (в виде бегущих волн). Для этого вводятся две одномерные функции

такие, что

Чтобы представить геометрически, как две одномерные функции определяют решение на области $\Omega $, обратимся к рис. 2. Непосредственной подстановкой показывается, что функционал состояния $\Phi $ равен нулю при выполнении соотношений (4.2), так как ${{r}_{x}} = {{v}_{t}},$ ${{r}_{t}} = {{v}_{x}}.$

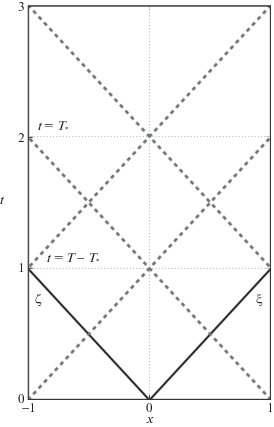
Для большей компактности окончательных результатов вводятся новые координаты, связанные с характеристическими линиями решения, т.е. отрезками в области $\Omega $, на которых не меняются значения функций ${{w}_{ \pm }}(t \pm x)$. Новые и старые координаты связаны друг с другом следующими линейными преобразованиями:

В новых координатах решение примет вид

Можно непосредственно убедиться, что переменные $\xi (t,x)$ и $\zeta (t,x)$ пробегают в области $\Omega = (0,T) \times ( - 1,1)$ все допустимые значения интервала $( - 1,T + 1)$.

Краевые условия $r(t, \pm 1) = {{U}_{ \pm }}(t)$ из (3.3) выполняются, если выбрать интегралы управления в виде

Начальные и терминальные условия частично определяют функции ${{w}_{ \pm }}$. Из начальных условий в (3.3) и из (4.3), (4.4) следует, что

В свою очередь терминальные условия из (3.3) задают функции Даламбера ${{w}_{ \pm }}$ на другом подынтервале области определения:

Важно отметить, что, как видно из (4.3), (4.4), функции ${{w}_{ \pm }}$ свободны на открытых интервалах области определения $\zeta \in (1,T - 1)$ и $\xi \in (1,T - 1)$.

Из (4.6), (4.7) следует, что для полной совместности краевых условий при t = 0 и $t = T$ достаточно, чтобы суммарное время управления было больше критического: $T > {{T}_{*}} = 2$. Этот временной интервал необходим, чтобы сигнал управления от одного конца стержня достиг другого конца, отразился и вернулся обратно. При $T \leqslant {{T}_{*}}$ начальные и терминальные условия пересекаются и в общем случае произвольных ${{v}_{0}}$, ${{r}_{0}}$ и ${{p}_{1}}$, ${{v}_{1}}$, ${{r}_{1}}$ несовместны.

При выборе некоторых допустимых значений функций ${{w}_{ + }}(\xi ),$ ${{w}_{ - }}(\zeta )$ на участке $(1,T - 1)$ полностью доопределяются, согласно (4.5), допустимые внешние воздействия ${{U}_{ \pm }}$ при $t \in [0,T],$ а также решение $(v,r)$ в области $\Omega $ в соответствии с (4.2) или (4.4) в зависимости от выбора координат.

Таким образом, получено решение прямой задачи динамики (3.3), (3.5) при некотором допустимом законе управления. Произвол в выборе этого закона используется далее для минимизации целевого функционала средней энергии E.

5. Декомпозиция средней энергии. Обращая внимание на структуру функции плотности энергии $e$, определенной в (3.4), и замечая, что ${{r}_{t}} = {{v}_{x}}$ и ${{r}_{x}} = {{v}_{t}}$ на решении (4.4), получим

Здесь штрихом обозначены производные функций ${{w}_{ \pm }}$ по своим аргументам. В итоге, слагаемые ${{e}_{ \pm }}$ в функции плотности энергии $e$ зависят от одного из двух аргументов. Так как функционал средней энергии E строится из функции e через линейное преобразование (интегрированием), то и он в свою очередь распадается на две независимые части:

Здесь величина ${{E}_{ + }}$ определена, если задана функция ${{w}_{ + }}(\xi )$, а значение ${{E}_{ - }}$ известно, если заданы значения ${{w}_{ - }}(\zeta )$.

Подставляя выражение для ${{e}_{ + }}$ из (5.1) в ${{E}_{ + }}$, получаем

где кусочно-линейная функция $\Delta \zeta $ возникает в результате первичного интегрирования по координате $\zeta $:

Ее значения проверяются геометрически (см. рис. 2), если учесть разбиение области $\Omega $ угловыми характеристиками ξ = 1, $\xi = T - 1$, $\zeta = 1$, $\zeta = T - 1$ (штриховые линии) и определить длины отрезков интегрирования по переменной ζ.

Принимая во внимание заданные участки функций ${{w}_{ \pm }}$, согласно (4.6) и (4.7), приходим к формуле для одной из частей декомпозированной средней энергии:

Для второго слагаемого ${{E}_{ - }}$ аналогично выводим

Подобным же образом получаем симметрично относительно замены аргумента $\xi $ на $\zeta $ и функции ${{w}_{ + }}$ на ${{w}_{ - }}$ окончательное выражение для второго слагаемого целевого функционала:

Как видно, оба слагаемых ${{E}_{ \pm }}$ зависят соответственно от начальных, терминальных и свободных значений функций Даламбера ${{w}_{ \pm }}$.

Согласно последней строке (5.1), после декомпозиции в выражение для средней энергии (5.2) входят квадраты первых производных по $\xi $ и $\zeta $ функций бегущих волн ${{w}_{ + }}(\xi )$ и ${{w}_{ - }}(\zeta )$. Существование интегралов ${{E}_{ \pm }}$ означает, что должны существовать обобщенные производные этих функций, т.е.

Как следует из вида зависимости ${{w}_{ \pm }}$ от начальных функций ${{v}_{0}},\;{{r}_{0}}$, требование принадлежности ${{w}_{ \pm }}$ пространству Соболева ${{H}^{1}}$ влечет за собой ограничение на начальные условия, а именно ${{v}_{0}},{{r}_{0}} \in {{H}^{1}}( - 1,1).$ Вложенность одномерных функций из гильбертова пространства ${{H}^{1}}$ в пространство непрерывных функций

согласно лемме Соболева [32], означает, что функции ${{w}_{ + }}$ или ${{w}_{ - }}$ могут быть продолжены на замыкание $[ - 1,T + 1]$ и их значения, заданные на различных участках, должны непрерывно стыковаться в точках ξ = 1, $\xi = T - 1$ и ζ = 1, $\zeta = T - 1$ соответственно.

6. Вывод оптимального решения. Из вида функционалов ${{E}_{ \pm }}$ следует, что для их независимой минимизации необходимо проварьировать свободные значения функции ${{w}_{ + }}(\xi )$ или ${{w}_{ - }}(\zeta )$ на интервалах аргумента $\zeta \in (1,T - 1)$ или $\xi \in (1,T - 1)$. Таким образом возникает классическая задача вариационного исчисления [33]. При этом надо учесть краевые условия, вытекающие из свойства непрерывности ${{w}_{ \pm }}$ в точках $\xi ,\zeta = 1,T - 1$:

Необходимые условия существования минимума независимых функционалов ${{E}_{ \pm }}$ – это соответствующие линейные уравнения Эйлера второго порядка:

Эта система интегрируема, и общее решение выражается как линейный многочлен соответствующих аргументов. Из граничных условий (6.1) получаем выражения для экстремалей

на участках $\xi \in (1,T - 1)$ и $\zeta \in (1,T - 1)$ соответственно. Из линейности системы уравнений следуют достаточные условия оптимальности и единственность решения.

Итак, все требуемые оптимальные выражения получаются следующим образом. Сперва восстанавливаются значения функций ${{w}_{ + }}(\xi )$ и ${{w}_{ - }}(\zeta )$ на областях определения $\xi \in [ - 1,T + 1]$, $\zeta \in [ - 1$, T + 1] с использованием выражений (4.6) и (4.7) и (6.3). Затем с помощью формул (4.5) находятся интегралы управления $U_{ - }^{*}(t)$ и $U_{ + }^{*}(t)$ на временном интервале $t \in [0,T]$. Производные этих функций дают значения оптимальных внешних сил $u_{ - }^{*}(t) = (U_{ - }^{*}){\kern 1pt} '(t)$ и $u_{ + }^{*}(t) = (U_{ + }^{*}){\kern 1pt} '(t)$. По формулам (4.2) получаем оптимальные кинематическую ($v{\kern 1pt} *$) и динамическую ($r{\kern 1pt} *$) функции состояния системы и по (1.7) восстаналиваем плотность импульса $p{\kern 1pt} * = r_{x}^{*}$ и нормальные силы $s{\kern 1pt} * = r_{t}^{*}$.

7. Допустимое решение на критическом интервале времени. Рассмотрим особый случай, когда время управления равно критическому значению $T = {{T}_{*}} = 2$. Область определения задается как ${{\Omega }_{ * }} = (0,2) \times ( - 1,1)$. Как видно из рис. 3, варьируемые области исчезают и решение (4.2) терминальной задачи (3.3) определяется однозначно, с точностью до терминальных констант ${{v}_{1}}$, ${{r}_{1}}$, ${{p}_{1}}$ из (3.5).

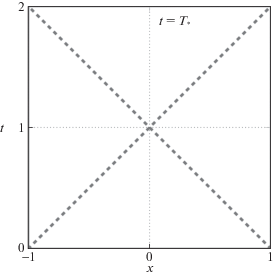
Функции Даламбера выражаются следующим образом:

Точкой пересечения областей определения этих функций являются значения координат характеристик ξ = 1, ζ = 1 с заданными в них условиями непрерывности:

Из (7.2) получаем, что

Из этих условий следует два вывода. Во-первых, терминальный параметр ${{r}_{1}}$ динамической функции определен однозначно из системы (7.3) и равен ${{r}_{1}} = \tfrac{1}{2}{{r}_{0}}(1) + \tfrac{1}{2}{{r}_{0}}( - 1)$. Во-вторых, так как ${{v}_{1}} - {{p}_{1}} = \tfrac{1}{2}{{v}_{0}}(1) + \tfrac{1}{2}{{v}_{0}}( - 1)$, нельзя привести систему в нулевое состояние за критическое время ${{T}_{*}}$, если ${{v}_{0}}(1) \ne - {{v}_{0}}( - 1)$. Отметим также, что оптимальный по энергии параметр ${{p}_{1}} = 0$. Поэтому всегда более выгодное с энергетической точки зрения движение – это приведение системы в терминальное состояние покоя.

Теперь рассмотрим конкретный пример допустимого движения для начальных условий и терминальных параметров:

Из (7.3) и (7.4) следует, что ${{r}_{1}} = 0$, а ${{v}_{1}} = \tfrac{1}{2}{{{v}}_{0}}(1) + \tfrac{1}{2}{{{v}}_{0}}( - 1) = cos(3) \approx - 0.99$. На рис. 4 показан график функции перемещений $v(t,x)$. Как видно, в конечный момент времени система прибывает в состояние покоя (ненулевое положение). Вследствие постановки вариационной задачи найденная функция $v$ непрерывна, что следует из явных линейных выражений (4.2) для $v$ в терминах ${{w}_{ \pm }}$ и соответствует гипотезе непрерывности упругой среды.

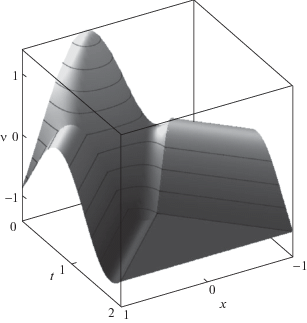
Значения динамической функции (потенциала) $r(t,x)$ представлены на рис. 5. Эти функции равны нулю при t = 0, $t = T$ для выбранных начальных и терминальных ${{r}_{0}}$ и ${{r}_{1}}$. Функция r, согласно (4.2), является линейной комбинацией непрерывных функций ${{w}_{ \pm }}$, т.е. сама непрерывна, что наглядно иллюстрируется ее графиком. При этом порожденные ею механические поля импульса и силы могут иметь разрывы значений. Это подтверждается наличием угловых точек на линиях характеристик ξ = 1, ζ = 1, обозначенных на рис. 3 пунктирными линиями. Угловые точки распространяются по этим характеристикам и на графике функции $v$ (см. рис. 4).

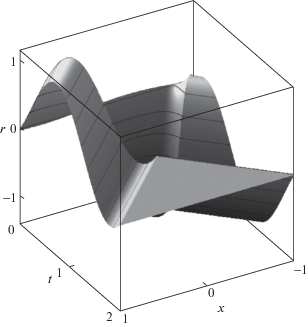
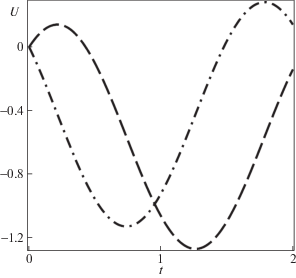
Допустимые интегралы управления ${{U}_{ - }}(t)$ и ${{U}_{ + }}(t)$ показаны на рис. 6 штриховой и штрихпунктирной линиями соответственно. Их тригонометрический характер определен выбранными для примера начальными условиями.

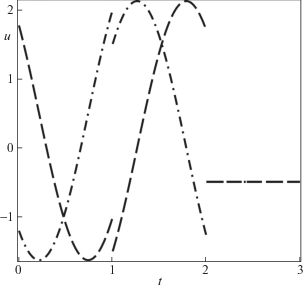
Последние графики на рис. 7 показывают вид исходных управляющих воздействий – внешних сил ${{u}_{ - }}(t)$ и ${{u}_{ + }}(t)$, которые представляют собой производные от функций ${{U}_{ - }}(t)$ и ${{U}_{ + }}(t)$. По построению ${{U}_{ - }}(0) = {{U}_{ + }}(0) = 0$, в то же время на управления ${{u}_{ - }}(t)$ и ${{u}_{ + }}(t)$ не накладываются какие-либо начальные или терминальные условия.

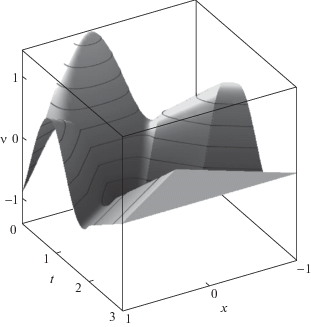
8. Пример оптимального движения. Для наглядности рассмотрим пример оптимального управления продольными перемещениями упругого стержня при времени управления $T = 3 > {{T}_{ * }}$. В качестве начальных значений опять выберем функции из (7.4). Оптимальное распределение перемещений показано на рис. 8. Как видно из графика, к конечному моменту времени стержень приходит в нулевое состояние как по энергии, так и по положению. Видны угловые точки, расположенные по характеристикам, которые изображены на рис. 2 штриховыми линиями.

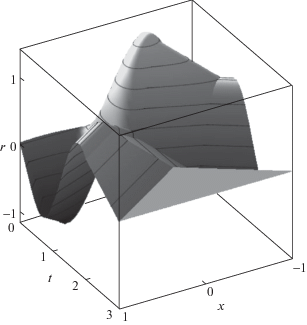
На рис. 9 показаны оптимальные значения динамического потенциала $r(t,x)$. Снова оптимальным терминальным значением для r является нулевое распределение. Напомним, что значение этой функции дается с точностью до начальной константы c₀, введенной в (1.10). В данном примере ее значение равно нулю. Следует подчеркнуть, что хотя в классической постановке движение полностью определяется функцией перемещения, в обобщенной вариационной постановке, используемой в этой работе, динамическая функция $r$ – неотъемлемая часть решения, которая обязательно представляет вторую позицию в упорядоченной паре $({v},r)$.

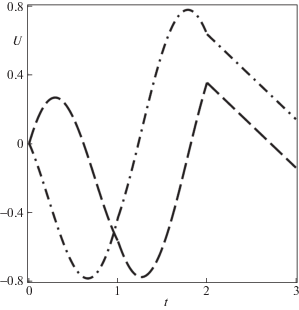
Оптимальные интегралы управления ${{U}_{ - }}(t)$ и ${{U}_{ + }}(t)$ изображены на рис. 10 штриховой и штрихпунктирной линиями соответственно. Это непрерывные функции с нулевыми начальными значениями, что следует из линейности соотношений (4.5). На последнем участке при $t \in [2,3]$ закон оптимального управления имеет линейный характер, что обусловлено видом оптимальных функций Даламбера (бегущих волн) как линейных многочленов. На остальных участках $t \in [0,1]$ и $t \in [1,2]$ интегралы управления представляют собой линейные комбинации тригонометрических и полиномиальных функций, согласно выбранным начальным условиям (7.4).

Завершает этот пункт рисунок 11, на котором показаны оптимальные функции управления ${{u}_{ - }}(t)$ и ${{u}_{ + }}(t)$ штриховой и штрихпунктирной линиями соответственно. На трех равных по длине интервалах времени $t \in (0,1)$, $t \in (1,2)$, $t \in (2,3)$ управления задаются аналитическими функциями, причем на третьем этапе оба управления равны одной константе ${{u}_{ - }}(t) = {{u}_{ + }}(t) = \frac{1}{2}cos(3)$. В точках t = 1 и $t = 2$ видны разрывы функций управления.

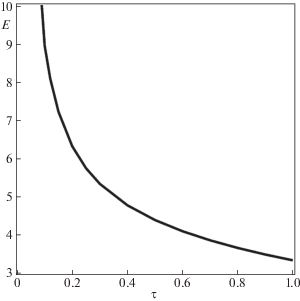
9. Анализ поведения средней энергии. Изучим поведение оптимального значения средней механической энергии системы при изменении времени управления T. Для удобства представления вводится вспомогательный параметр $\tau = T - {{T}_{*}}$, который определяет расстояние между временем управления и его критическим значением.

На рис. 12 представлены результаты расчетов оптимальных значений функционала E для различных значений параметра $\tau \in (0,1]$ при фиксированных начальных условиях (7.4). Как видно из графика, значение целевого функционала убывает строго монотонно и, как показывают проведенные расчеты, стремится к нулю при $\tau \to \infty $. С другой стороны, значение средней энергии стремится к бесконечности при $\tau \to 0,$ т.е. при $T \to {{T}_{ * }}$. Это косвенно подтверждает невозможность с энергетической точки зрения приведения при выбранных начальных условиях упругого стержня в нулевое состояние для заданного класса гладкости обобщенного решения при $T = {{T}_{ * }}$, как это и было показано в разд. 7.

Заключение. В работе исследованы продольные перемещения тонкого прямолинейного упругого стержня. Дана обобщенная формулировка начально-краевой задачи, решение которой ищется относительно кинематической и динамической переменных в энергетическом пространстве. Для случая однородного стержня, управляемого с помощью приложенных с обоих концов внешних сил, определено критическое время, за которое система может быть приведена в состояние покоя и в общем случае показана невозможность для произвольных начальных условий приведения точек стержня в нулевое состояние. Для фиксированных интервалов времени, больших критического, решена задача оптимального управления о приведении системы в нулевое состояние. Целевой функционал – средняя механическая энергия, запасаемая стержнем во время движения. Поставленная двумерная по пространству и времени задача управления сведена к классической одномерной квадратичной вариационной задаче с фиксированными концами. Оптимальное управление и соответствующие движения стержня найдены в явном виде как комбинации бегущих волн. Исследована зависимость средней энергии, запасаемой в системе, от времени управления.