Известия РАН. Теория и системы управления, 2021, № 5, стр. 128-136
АНАЛИЗ НАДЕЖНОСТИ: ОТ ДЕРЕВА ОТКАЗОВ К ДЕРЕВУ КАТАСТРОФ
Д. И. Кательников a, Л. В. Пустыльник b, А. П. Ротштейн c, d, *
a Винницкий национальный технический ун-т
Винница, Украина
b Тель-Авивский академический инженерный колледж – Афека
Тель-Авив, Израиль
c Иерусалимский политехнический ин-т – Махон Лев
Иерусалим, Израиль
d Донецкий национальный ун-т им. Василия Стуса
Винница, Украина
* E-mail: rothstei@g.jct.ac.il
Поступила в редакцию 06.02.2021
После доработки 25.03.2021
Принята к публикации 31.05.2021
Аннотация
Предлагается метод анализа дерева катастроф, который является аналогом классического метода анализа дерева отказов, не требующим знания вероятностей событий. Вместо понятия “вероятность отказа” используется понятие “возможность бифуркации”, которая оценивается числом в интервале [0, 1] с помощью теории катастроф и соответствует функции принадлежности нечеткого множества. Расчет возможности бифуркации (или катастрофы) системы выполняется с помощью специально введенных правил агрегации возможностей бифуркаций для различных логических операций дерева отказов. Иллюстрация метода анализа катастроф выполнена на примере дерева отказов для дорожной аварии на T-образном перекрестке.
Введение. Метод дерева отказов (fault tree analysis – FTA), предложенный в 1962 г. и подробно изложенный в [1], до сих пор является одним из основных методов анализа надежности, безопасности и риска не только в технических, но и в социально-экономических, военных и других системах [2, 3].
Вероятностные модели FTA предусматривают бинарную концепцию отказов системы и ее элементов: 1 – нет отказа, 0 – есть отказ. Поэтому событие “отказ” можно трактовать как бифуркацию, т.е. перескок из одного устойчивого состояния (нет отказа) в другое устойчивое состояние (есть отказ). Подход к моделированию и оптимизации надежности на основе вилок бифуркаций из теории хаоса рассмотрен в [4, 5].
Специальным математическим аппаратом моделирования бифуркаций служит теория катастроф [6–8], которая является развитием теории нелинейных колебаний [9]. Несмотря на широкое распространение теории катастроф в различных областях, работы по ее применению в моделях надежности отсутствуют.
В статье предлагается метод анализа дерева катастроф (catastrophe tree analysis – CTA), который есть аналог классического метода FTA, не требующий знания вероятностей событий. Вместо понятия “вероятность отказа” используется понятие “возможность бифуркации”, которая оценивается числом в интервале [0, 1] с помощью теории катастроф и соответствует функции принадлежности нечеткого множества [10–12]. Расчет возможности бифуркации (или катастрофы) системы выполняется с помощью специально введенных правил агрегации возможностей бифуркаций для различных логических операций дерева отказов.
Статья организована следующим образом. В разд. 1 приводятся понятия характеристической функции и функции принадлежности, необходимые для понимания различий между вероятностью и возможностью отказа, которые вычисляются на основе структурной функции надежности. В разд. 2 рассматривается пример описания бифуркации с помощью функции принадлежности нечеткого множества. Раздел 3 содержит основные соотношения теории катастроф, которые используются в методе анализа дерева катастроф. В разд. 4 предлагаются правила агрегации уровней бифуркаций для логических операций дерева катастроф. Раздел 5 иллюстрирует метод дерева катастроф на примере дорожной аварии.
1. Структурная функция: вероятность и возможность отказа. Формальной основой дерева отказов является булева функция, которую в теории надежности принято называть структурной функцией [1]. Она связывает бинарные характеристические функции системы и ее элементов:
(1.1)
${{\chi }_{S}} = {{f}_{L}}\left( {{{\chi }_{1}},{{\chi }_{2}}, \ldots ,{{\chi }_{n}}} \right),$Зная вероятности этих состояний
При этом используются следующие правила перехода к вероятности:
Если в (1.1) характеристические функции χi и χS заменить функциями принадлежности нечетких множеств, то получаем нечетко-логическую функцию
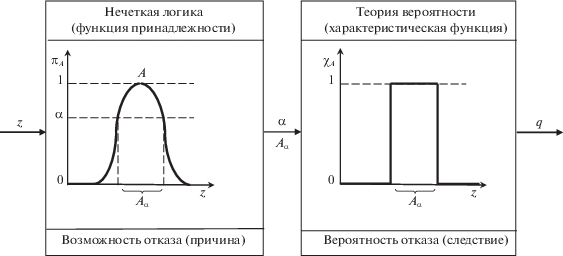
которая позволяет оценивать возможность безотказной работы системы ${{\pi }_{S}} \in \left[ {0,1} \right]$ на основе возможностей ${{\pi }_{i}} \in \left[ {0,1} \right]$ безотказной работы ее элементов. При этом используются следующие правила вычислений:Взаимосвязь возможности и вероятности в моделях надежности показана на рис. 1, где z – параметр, от которого зависит надежность элемента, $z \in \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} ,\bar {z}} \right]$, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} \left( {\bar {z}} \right)$ – нижнее (верхнее) значение интервала допустимых значений; А – нечеткое множество “возможность надежной работы элемента в зависимости от параметра z''; ${{\pi }_{A}}\left( z \right)$ – функция принадлежности параметра z к нечеткому множеству A. Согласно [10], функция ${{\pi }_{A}}\left( z \right)$ трактуется как распределение возможности надежной работы элемента; α – число в интервале [0, 1], которое задает минимально необходимый уровень возможности надежной работы; ${{A}_{\alpha }}$ – множество α-уровня, определяющее значения параметра z, для которых возможность надежной работы не ниже α, т.е.
2. Функция принадлежности к бифуркации. Событие “отказ” нами трактуется как бифуркация, т.е. потеря устойчивости. В теории колебаний [9] принято использовать определение устойчивости по Ляпунову, которое требует внутреннего описания системы с помощью дифференциальных уравнений.
Покажем, что при отсутствии внутреннего описания устойчивость можно определить с помощью нечетких множеств, которые лежат в основе теории возможностей [10].
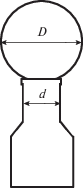
На рис. 2 показан шарик диаметром D, который сохраняет устойчивость на горлышке бутылки диаметром d. Предполагается, что величина диаметра D может изменяться.
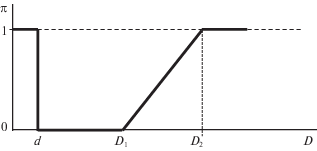
Бифуркация, т.е. падение шарика с бутылки, описывается функцией принадлежности (рис. 3), где имеются следующие области:
(a) как только $D < d$, то шарик проваливается в бутылку и степень принадлежности к бифуркации π = 1.
(б) если $D \in \left[ {d,{{D}_{1}}} \right]$, то шарик сохраняет устойчивость, π = 0.
(в) при $D \in \left[ {{{D}_{1}},{{D}_{2}}} \right]$ шарик находится на нечетком переходе “устойчиво – не устойчиво”, что соответствует возрастанию π от 0 к 1.
(г) при $D > {{D}_{2}}$ шарик падает с бутылки и π = 1.
3. Необходимые соотношения теории катастроф. Теория катастроф – это математическая дисциплина для моделирования нелинейных объектов “вход–выход”, в которых незначительные изменения входов (причин) приводят к большим изменениям выходов (следствий) [6–8]. Эта теория позволяет напрямую изучать прерывистое поведение системы без знания ее внутренней структуры. Для этого используется понятие потенциальной функции, которая в механике называется энергетической функцией или функцией Ляпунова в теории устойчивости (второй метод Ляпунова).
В каждый момент времени система стремится минимизировать свой потенциал, который меняется в зависимости от внешних (управляющих) параметров (минимизация локальная). При изменении этих параметров некоторые локальные минимумы могут “исчезать”, что приводит к скачкам, которые соответствуют бифуркациям или катастрофам. Наглядной моделью этой ситуации служит шарик на неровной поверхности, который под воздействием силы тяжести стремится в самое нижнее положение среди других, находящихся поблизости.
В табл. 1 приведены потенциальные функции, которые будут использованы при построении дерева катастроф, соответствующего дереву отказов.
Таблица 1.
Возможности бифуркаций для различных потенциальных функций
| Модель катастрофы | Потенциальная функция | Число входов | Нормализованные формулы |
|---|---|---|---|
| С (Cusp) | $V\left( x \right) = {{x}^{4}} + a{{x}^{2}} + bx$ | 2 | ${{x}_{a}} = \sqrt a $, ${{x}_{b}} = \sqrt[3]{b}$ |
| S (Swallowtail) | $V\left( x \right) = {{x}^{5}} + a{{x}^{3}} + b{{x}^{2}} + cx$ | 3 | ${{x}_{a}} = \sqrt a $, ${{x}_{b}} = \sqrt[3]{b}$, ${{x}_{c}} = \sqrt[4]{c}$ |
| B (Butterfly) | $V\left( x \right) = {{x}^{6}} + a{{x}^{4}} + b{{x}^{3}} + c{{x}^{2}} + dx$ | 4 | ${{x}_{a}} = \sqrt a $, ${{x}_{b}} = \sqrt[3]{b}$, ${{x}_{c}} = \sqrt[4]{c}$, ${{x}_{d}} = \sqrt[5]{d}$ |
В каждой потенциальной функции V(x) имеется переменная состояния системы (x) и управляемые (входные) переменные (a, b, c, d), которые изменяются в интервалах их допустимых значений. При стремлении потенциальной функции к минимуму могут возникать бифуркации, множество которых определяется из системы уравнений: $V{\kern 1pt} '(x) = 0$, $V{\kern 1pt} ''(x) = 0$. Множеству бифуркаций соответствуют нормализованные формулы, позволяющие вычислить уровни бифуркации (${{x}_{a}}$, $~{{x}_{b}}$, …, $~{{x}_{d}}$) по входным переменным (a, b, …, d). Вывод нормализованных формул описан в работе [13]. Они получены исходя из требования, что входные переменные и уровни бифуркаций изменяются в интервале [0, 1]. Это допускает интерпретацию в терминах теории возможности [10]:
a, b, …, d – возможности событий, соответствующих входным переменным;
${{x}_{a}}$, $~{{x}_{b}}$, …, $~{{x}_{d}}$ – возможности бифуркаций по входным переменным.
Следует отметить, что операциям извлечения корней в нормализованных формулах соответствуют лингвистические модификаторы (достаточно, более-менее и др.), которые используются для растяжения функций принадлежности в теории нечетких множеств. Этим достигается увеличение функции при небольших значениях аргумента.
Например, пусть ${{\pi }_{p}}\left( y \right) = y$ – функция принадлежности переменной $y \in \left[ {0,1} \right]$ к нечеткому множеству “перфектность $\left( p \right)$”. Тогда модифицированные нечеткие множества “достаточно перфектно $\left( {fp} \right)$” и “более-менее перфектно $\left( {mlp} \right)$” описываются функциями принадлежности:
Поскольку входные переменные $a,~b,~c,~d$ в потенциальных функциях (табл. 1) изменяются в интервале [0, 1] и имеют смысл степеней принадлежности, то операции извлечения корней (правый столбец табл. 1) можно трактовать как растяжение степеней принадлежности с помощью лингвистических модификаторов.
4. Дерево катастроф. Будем предполагать, что известно дерево отказов, в котором используются только два логических узла: AND (∧) и OR (∨). Кроме того, ограничимся случаем, когда в каждый из логических узлов входит не более четырех аргументов (стрелок). Методика построения дерева катастроф будет показана на примере в разд. 5.
При переходе от дерева отказов к дереву катастроф будем использовать следующие модели, представленные в табл. 2:
Таблица 2.
Правила агрегации на дереве катастроф
| Логический узел | Катастрофа | Обозначение на дереве катастроф | Формула агрегации |
|---|---|---|---|
| C | 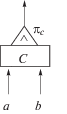 |
$\pi _{C}^{{}} = \left\{ \begin{gathered} \min (\sqrt a ,\sqrt[3]{b}), \hfill \\ \sqrt {\sqrt a \cdot \sqrt[3]{b}} \hfill \\ \end{gathered} \right.$ | |
| AND ($ \wedge $) |
S |  |
$\pi _{S}^{{}} = \left\{ \begin{gathered} \min (\sqrt a ,\sqrt[3]{b},\sqrt[4]{c}), \hfill \\ \sqrt[3]{{\sqrt a \cdot \sqrt[3]{b} \cdot \sqrt[4]{c}}} \hfill \\ \end{gathered} \right.$ |
| B | 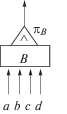 |
$\pi _{B}^{{}} = \left\{ \begin{gathered} \min (\sqrt a ,\sqrt[3]{b},\sqrt[4]{c},\sqrt[5]{d}), \hfill \\ \sqrt[4]{{\sqrt a \cdot \sqrt[3]{b} \cdot \sqrt[4]{c} \cdot \sqrt[5]{d}}} \hfill \\ \end{gathered} \right.$ | |
| С | 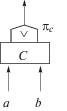 |
$\pi _{C}^{{}} = \left\{ \begin{gathered} \max (\sqrt a ,\sqrt[3]{b}), \hfill \\ \frac{1}{2}(\sqrt a + \sqrt[3]{b}) \hfill \\ \end{gathered} \right.$ | |
| OR ($ \vee $) |
S | 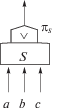 |
$\pi _{S}^{{}} = \left\{ \begin{gathered} \max (\sqrt a ,\sqrt[3]{b},\sqrt[4]{c}), \hfill \\ \frac{1}{3}(\sqrt a + \sqrt[3]{b} + \sqrt[4]{c}) \hfill \\ \end{gathered} \right.$ |
| B |  |
$\pi _{B}^{{}} = \left\{ \begin{gathered} \max (\sqrt a ,\sqrt[3]{b},\sqrt[4]{c},\sqrt[5]{d}), \hfill \\ \frac{1}{4}(\sqrt a + \sqrt[3]{b} + \sqrt[4]{c} + \sqrt[5]{d}) \hfill \\ \end{gathered} \right.$ |
Сборка (C) – для логических узлов с двумя входными стрелками;
Ласточкин хвост (S) – для логических узлов с тремя входными стрелками;
Бабочка (B) – для логических узлов с четырьмя входными стрелками.
Каждый из узлов дерева катастроф представляет собой преобразователь “входы–выход” по правилам агрегации “вектор–скаляр”, которые приведены в табл. 2. В теории нечетких множеств используются различные методы агрегации функций принадлежности, над которыми выполняются операции AND и OR. Применение каждого из этих методов может давать различные результаты. В частности, в [14] рассмотрен пример необходимости замены операции min операцией умножения. Окончательное решение о результатах анализа дерева катастроф для конкретного объекта целесообразно принимать путем сравнения нескольких методов агрегации “вектор–скаляр”. Поэтому в табл. 2, наряду с традиционными для теории нечетких множеств операциями min и max, приводятся среднее геометрическое и среднее арифметическое. Однако это не исключает возможности применения других известных методов агрегации.
Предполагается, что при нумерации входных стрелок дерева катастроф, соответствующих терминальным вершинам дерева отказов, соблюдается условие $a \leqslant b \leqslant c \leqslant d$. Это необходимо для получения min и max${\text{\;}}$ при выполнении операций AND и OR.
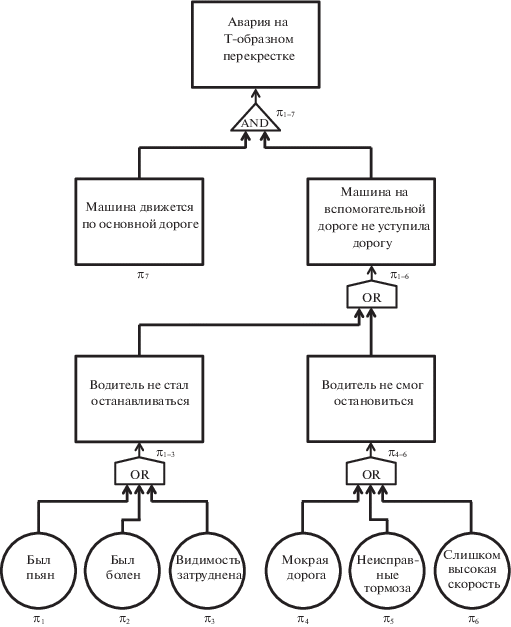
5. Пример применения. На рис. 4 представлено дерево отказов, для аварии на T-образном перекрестке, где обозначены: ${{\pi }_{1}},{{\pi }_{2}}, \ldots ,{{\pi }_{6}},{{\pi }_{7}}$ – возможности первичных событий, которые соответствуют терминальным вершинам дерева; ${{\pi }_{{1 - 3}}},{{\pi }_{{4 - 5}}},{{\pi }_{{1 - 6}}}$ – возможности промежуточных (не терминальных) событий; ${{\pi }_{{1 - 7}}}$ – возможность аварии.
Пользуясь табл. 2, от дерева отказов (рис. 4) переходим к дереву катастроф (рис. 5), которому соответствуют расчетные формулы:
Исходные данные для расчета по этим формулам задаются экспертно либо с помощью функций принадлежности по известным количественным значениям параметра, влияющего на возможность события. При выборе функций принадлежности можно воспользоваться методом нечеткой перфектности [14].
В табл. 3 приведены результаты расчета возможности аварии ${{\pi }_{{1 - 7}}}$ для семи сценариев, каждый из которых представляет собой вектор возможностей $\left( {{{\pi }_{1}},{{\pi }_{2}}, \ldots ,{{\pi }_{7}}} \right)$ терминальных событий дерева отказов (рис. 4).
Таблица 3.
Возможность аварии для различных сценариев
| Сценарии | ${{\pi }_{1}}$ | ${{\pi }_{2}}$ | ${{\pi }_{3}}$ | ${{\pi }_{4}}$ | ${{\pi }_{5}}$ | ${{\pi }_{6}}$ | ${{\pi }_{7}}$ | ${{\pi }_{{1 - 7}}}$ | |
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | ||||||||
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 0.00 | 0.00 |
| 2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.32 | 0.42 |
| 3 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.45 | 0.51 |
| 4 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.3 | 0.55 | 0.57 |
| 5 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.4 | 0.63 | 0.63 |
| 6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.5 | 0.71 | 0.68 |
| 7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.6 | 0.77 | 0.71 |
По табл. 3 необходимо сделать пояснение: столбец (1) соответствует агрегации с использованием мin и max, а столбец (2) – применению среднего геометрического и среднего арифметического. Из табл. 3 видно, что если машина двигается по основной дороге $\left( {{{\pi }_{7}} \ne 0} \right)$, то отсутствие аварии $\left( {{{\pi }_{{1 - 7}}} = 0} \right)$ возможно только при ${{\pi }_{1}} = {{\pi }_{2}} = \ldots = {{\pi }_{6}} \approx 0$, т.е. когда нет нарушений, связанных с водителем, видимостью, дорогой, тормозами и скоростью. Наличие хотя бы одного из таких нарушений приводит к резкому возрастанию возможности аварии.
Заключение. Статья является первой работой, в которой теория катастроф применяется для моделирования возможности нежелательных событий на основе известного в задачах надежности и безопасности метода деревьев отказов.
Понятие “отказ” рассматривается как бифуркация, т.е. перескок между устойчивыми состояниями, и оценивается нормализованными формулами из теории катастроф. Понятие “возможность отказа” оценивается числом в интервале [0, 1] и моделируется по правилам нечеткой логики.
Результатом работы является метод анализа дерева катастроф, которое соответствует дереву отказов. Суть предложенного метода состоит в сформулированных правилах агрегации возможностей бифуркаций для различных логических узлов дерева.
Иллюстрация метода анализа катастроф выполнена на примере дерева отказов, моделирующего дорожную аварию на T-образном перекрестке.
Метод дерева катастроф не отменяет метод дерева отказов, а дополняет его следующими новыми качествами:
1. Отсутствует необходимость проведения трудоемких экспериментов, связанных с получением вероятностей первичных событий, которые влияют на вероятность отказа системы. Вместо вероятностей используются возможности первичных событий, уровни которых оцениваются экспертно или на основе измеряемых параметров и соответствующих функций принадлежности.
2. Наблюдение за динамикой изменения входных параметров позволяет переходить к on-line мониторингу уровня возможности отказа системы.
3. Применение моделей теории катастроф позволяет наблюдать нелинейные эффекты, связанные с резким увеличением возможности отказа при незначительных изменениях входных параметров.
Список литературы
Barlow R., Proschan F. Statistical Theory of Reliability and Life Testing. Rinehart and Winston: Holt, 1975.
Ryabinin I.A. Reliability and Safety of Structurally Complex Systems. St. Petersburg: SPb Polytechnics, 2000.
Solozhentsev E.D. Scenario Logic and Probabilistic Management of Risk in Business and Engineering. St. Petersburg: Business-press, 2004.
Ротштейн А.П. Интеграция подходов нечеткой логики и теории хаоса в моделировании и оптимизации надежности // Изв. РАН ТиСУ. 2012. № 4 (51). С. 77–87.
Rotshtein A.P., Katielnikov D.I., Pustylnik L.V. Reliability Modeling and Optimization Using Fuzzy Logic and Chaos Theory // International J. of Quality, Statistics, and Reliability. 2012. V. 2012. Article ID 847416. 9 p. https://doi.org/10.1155/2012/847416
Thom R. Structural Stability and Morphogenesis. W. A. Benjamin, Reading, Mass, 1975.
Zeeman E.C. Catastrophe Theory // Scientific American. 1976. V. 234: P. 65–83.
Arnold V.I. Catastrophe Theory. Berlin: Springer-Verlag, 1992.
Andronov A.A., Vitt A.A., Khaikin S.E. Theory of Oscillators. Pergamon Press, 1966.
Zadeh L.A. Fuzzy Sets as a Basis for a Theory of Possibility // Fuzzy Sets and Systems. 1978. V. 1. P. 3–28.
Ротштейн А.П. Алгебра алгоритмов и нечеткая логика в анализе надежности систем // Изв. РАН ТиСУ. 2010. № 2 (49). С. 87–99.
Кательников Д.И., Ротштейн А.П. Нечетко-алгоритмическое моделирование надежности: оптимизация ресурсов контроля и коррекции // Изв. РАН ТиСУ. 2010. № 6 (49). С. 138–142.
Ching-Hsue Cheng, Ying-Hua Liu, Yin Lin. Evaluating a Weapon System Using Catastrophe Series Based on Fuzzy Scales // Soft Computing in Intelligent Systems and Information Processing// Asian Fuzzy Systems Symposium. Kenting, Taiwan, 1996. P. 212–217. https://doi.org/10.1109/AFSS.1996.58359.
Ротштейн А.П. Выбор условий деятельности человека на основе нечеткой перфектности // Изв. РАН ТиСУ. 2018. № 6 (57). С. 108–119.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления