Известия РАН. Теория и системы управления, 2021, № 5, стр. 120-127
РАСПРЕДЕЛЕНИЕ НЕОДНОРОДНОГО НАБОРА РЕСУРСОВ ПРИ СОСТАВЛЕНИИ МНОГОПРОЦЕССОРНОГО РАСПИСАНИЯ
М. Г. Фуругян *
Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
* E-mail: rtsccas@yandex.ru
Поступила в редакцию 20.12.2020
После доработки 08.02.2021
Принята к публикации 29.03.2021
Аннотация
Рассматривается задача составления многопроцессорного расписания для комплекса работ при наличии ресурсов двух видов – возобновляемых (процессоров) и невозобновляемых. Доступные объемы ресурсов могут изменяться во времени. Работы характеризуются объемами и директивными интервалами. Допускается параллельное выполнение работы несколькими процессорами. Решаются следующие задачи: существования и построения допустимого расписания при заданных объемах ресурсов; минимизации стоимости ресурсов, при наличии которых существует допустимое расписание.
Введение. Задачи планирования выполнения работ и составления расписаний возникают во многих областях деятельности человека: при создании, возведении и сопровождении сложных технических объектов (летательные аппараты, атомные реакторы), проведении различных испытаний в реальном масштабе времени, проектировании систем противовоздушной и противоракетной обороны, при обработке больших массивов информации технического, экономического и экологического характера, в других областях. В середине прошлого века американскими исследователями были разработаны системы ПЕРТ (program evaluation and review technique – метод оценки и пересмотра планов) и МКП (critical path method – метод критического пути) [1, 2], которые успешно применялись при создании вооружений для военно-морских сил США и строительстве военных и гражданских объектов. При этом решались задачи распределения невозобновляемых ресурсов (финансы, топливо, электроэнергия, различные материалы, оперативная память электронно-вычислительной машины, закрепленная за определенными программными модулями). Предполагалось, что длительности работ линейно зависят от величины выделенного им ресурса.
Возобновляемые ресурсы (процессоры, машины, исполнительные механизмы, приборы, рабочие), в отличие от невозобновляемых, могут использоваться многократно. Проблемам распределения возобновляемых ресурсов посвящено большое количество публикаций. Отметим такие фундаментальные работы, как [3–5], в которых исследованы различные задачи теории расписаний (планирование прерываемых и непрерываемых заданий, решение задач с директивными сроками и задач на быстродействие, составление однопроцессорных и многопроцессорных расписаний). В [6] рассмотрены задачи распределения возобновляемых ресурсов с нефиксированными параметрами. В некоторых случаях задачи планирования работ могут быть сведены к сетевому планированию [2, 7] и минимаксным задачам [8–11].
В настоящей статье рассматривается задача планирования комплекса работ (заданий), использующих как возобновляемые, так и невозобновляемые ресурсы. Доступные объемы ресурсов могут изменяться во времени. Каждая работа характеризуется объемом и директивным интервалом. Исследуются следующие случаи:
– все работы допускают прерывания и переключения с одного процессора на другой;
– комплекс содержит как прерываемые, так и непрерываемые задания;
– в фиксированный момент времени работа может выполняться не более чем одним процессором;
– допускается параллельное выполнение работы несколькими процессорами.
Для указанных случаев решаются задачи поиска допустимого расписания и минимизации стоимости используемых ресурсов. Методика решения указанных задач основана на сведении их к потоковым задачам в сетях специального вида.
1. Постановка задачи. Имеется комплекс работ (заданий) $W = \{ {{w}_{1}},\;{{w}_{2}},...,{{w}_{n}}\} ,\;$подлежащих выполнению во временном интервале планирования [0; T] с применением двух видов ресурсов – возобновляемых (процессоров) и невозобновляемых. Интервал $[0;T]$ разбивается на p непересекающихся интервалов ${{I}_{1}}$, ${{I}_{2}}$, …, ${{I}_{p}}$ (${{I}_{j}} = [{{\tau }_{j}},\;\;{{\tau }_{{j + 1}}}]$, $j = \overline {1,\;p} $, $0 = {{\tau }_{1}} < {{\tau }_{2}} < \;...\; < {{\tau }_{p}} < {{\tau }_{{p + 1}}} = T$), пусть ${{\delta }_{j}} = {{\tau }_{{j + 1}}} - {{\tau }_{j}}$ – длина интервала Ij. Доступные объемы ресурсов в каждый момент времени определяются следующим образом. В интервале Ij для выполнения работ имеется ${{m}_{j}}$ процессоров, производительности которых ${{s}_{{j1}}} \leqslant {{s}_{{j2}}} \leqslant \;...\; \leqslant {{s}_{{j{{m}_{j}}}}}$ (${{S}_{j}} = {{s}_{{j1}}} + {{s}_{{j2}}} + \;...\; + {{s}_{{j{{m}_{j}}}}}$ – их суммарная производительность), и K типов невозобновляемых ресурсов. Доступный объем невозобновляемого ресурса k-го типа в интервале Ij составляет ${{R}_{{jk}}}$, $j = \overline {1,\;p} $, $k = \overline {1,\;K} $.
Каждая работа ${{w}_{i}} \in W$ может выполняться с использованием обоих видов ресурсов (возобновляемых и невозобновляемых), допускает прерывания и переключения (не требующие временных затрат) с одного процессора на другой и параллельную реализацию несколькими процессорами (при определенных ограничениях). Задание ${{w}_{i}} \in W$ имеет следующие характеристики: ${{Q}_{i}}$ – объем; $[{{b}_{i}};{{f}_{i}}]$ – директивный интервал, ${{b}_{i}},\;{{f}_{i}} \in \{ {{\tau }_{1}},\;{{\tau }_{2}},\;...\;,\;{{\tau }_{{p + 1}}}\} $ (т.е. задание ${{w}_{i}}$ может исполняться только в этом интервале); $q_{{ij}}^{0}$ – максимально допустимый объем работы процессоров, выполняющих задание ${{w}_{i}}$ в интервале ${{I}_{j}}$; $r_{{ijk}}^{0}$ – максимальный объем невозобновляемого ресурса k-го типа, который может быть выделен заданию ${{w}_{i}}$ в интервале Ij.
Если процессоры с суммарной производительностью s в интервале Ij выполняют некоторое задание в течение временного отрезка длиной $\delta $, то объем производимый ими работы при этом составляет ${{a}_{j}}{\kern 1pt} \delta {\kern 1pt} s$, а стоимость эксплуатации этих процессоров равна ${{c}_{j}}{\kern 1pt} {{a}_{j}}{\kern 1pt} \delta {\kern 1pt} s$. В фиксированный момент времени каждый процессор может исполнять не более одного задания. Использование в интервале Ij невозобновляемого ресурса k-типа в количестве ${{r}_{{jk}}}$ обеспечивает объем работы, равный ${{b}_{{jk}}}{\kern 1pt} {{r}_{{jk}}}$, а его стоимость равна ${{d}_{{jk}}}{\kern 1pt} {{b}_{{jk}}}{\kern 1pt} {{r}_{{jk}}}$ (здесь ${\kern 1pt} {{a}_{j}},\;{{c}_{j}},\;{{b}_{{jk}}},\;{{d}_{{jk}}}$ – заданные положительные величины).
Ресурсы каждого вида могут быть выделены работе ${{w}_{i}}$ в интервале Ij только в том случае, когда ${{I}_{j}} \subseteq [{{b}_{i}};\;{{f}_{i}}]$. Если в интервале Ij суммарный объем работы процессоров по выполнению задания ${{w}_{i}}$ составляет ${{q}_{{ij}}}$, то должны быть верны следующие соотношения:
(1.2)
$\sum\limits_{i = 1}^n {{{q}_{{ij}}}} \leqslant {{a}_{j}}{\kern 1pt} {{S}_{j}}{{\delta }_{j}},\quad j = \overline {1,p} .$Если в интервале Ij заданию ${{w}_{i}}$ выделен невозобновляемый ресурс k-го типа в объеме ${{r}_{{ijk}}}$, то должны удовлетворяться следующие соотношения:
(1.3)
${{r}_{{ijk}}} \leqslant r_{{ijk}}^{0},\quad i = \overline {1,n} ,\quad j = \overline {1,p} ,\quad k = \overline {1,K} ,$(1.4)
$\sum\limits_{i = 1}^n {{{r}_{{ijk}}}} \leqslant {{R}_{{jk}}},\quad j = \overline {1,p} ,\quad k = \overline {1,K} .$Распределение ресурсов указывает для каждой работы ${{w}_{i}} \in W$ и каждого момента времени $t \in [0;T]$, какие процессоры ее исполняют. А для каждого интервала Ij, $j = \overline {1,\;p} $, определяет, какие невозобновляемые ресурсы и в каком количестве выделены этой работе. При этом должны быть верны соотношения (1.1)–(1.4). То же определяет и расписание работ W. Поэтому в дальнейшем, говоря о распределении ресурсов, будем иметь в виду также и расписание. Допустимым распределением ресурсов называется такое распределение, при котором каждая работа полностью выполняется в своем директивном интервале. Задача заключается в том, чтобы определить, существует ли допустимое распределение ресурсов, и в случае положительного ответа найти это распределение и определить допустимое распределение ресурсов с минимальной стоимостью их эксплуатации.
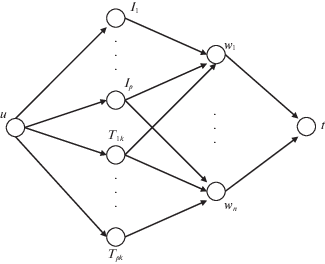
2. Построение сетевой модели. Для решения поставленной задачи построим потоковую сеть ${{G}_{1}} = ({{V}_{1}},\;{{A}_{1}})$ (рис. 1), где ${{V}_{1}} = \{ u,\;t,\;{{I}_{j}},\;{{T}_{{jk}}},\;{{w}_{i}},$ $j = \overline {1,p,} $ $k = \overline {1,K,} $ $i = \overline {1,\;n} \} $ – множество узлов, u – источник, t – сток, ${{A}_{1}} = \{ (u,{{I}_{j}}),\;(u,{{T}_{{jk}}}),\;({{I}_{j}},{{w}_{i}}),\;({{T}_{{jk}}},{{w}_{i}}),$ $({{w}_{i}},\;t)$, $j = \overline {1,p,} $ $k = \overline {1,K,} \;i = \overline {1,n} \} $ – множество ориентированных дуг. Дуги $({{I}_{j}},{{w}_{i}})$ и $({{T}_{{jk}}},\;{{w}_{i}})$ вводятся в сеть ${{G}_{1}}$ только в том случае, когда ${{I}_{j}} \subseteq [{{b}_{i}};\;{{f}_{i}}]$, т.е. если работа ${{w}_{i}}$ может выполняться в интервале Ij. Пропускные способности $U(x,\;y)$ дуг $(x,\;y) \in A{}_{1}$ сети ${{G}_{1}}$ указаны в табл. 1. Их физический смысл следующий. Величина ${{a}_{j}}{\kern 1pt} {{S}_{j}}{{\delta }_{j}}$ равна максимальному объему работы процессоров, доступному в интервале Ij; ${{b}_{{jk}}}{\kern 1pt} {{R}_{{jk}}}$ – максимальный объем работы, который может быть выполнен в интервале Ij с помощью невозобновляемого ресурса k-го типа; ${{b}_{{jk}}}r_{{ijk}}^{0}$ – максимальный объем работы, который может быть предоставлен заданию ${{w}_{i}}$ в интервале Ij с помощью невозобновляемого ресурса k-го типа. Величины $q_{{ij}}^{0}$ и ${{Q}_{i}}$ были определены выше.
Таблица 1.
Пропускные способности дуг сети ${{G}_{1}}$
| Дуга | Пропускная способность |
|---|---|
| $(u,\;{{I}_{j}})$ | ${{a}_{j}}{\kern 1pt} {{S}_{j}}{{\delta }_{j}}$ |
| $(u,\;{{T}_{{jk}}})$ | ${{b}_{{jk}}}{\kern 1pt} {{R}_{{jk}}}$ |
| $({{I}_{j}},{{w}_{i}})$ | $q_{{ij}}^{0}$ |
| $({{T}_{{jk}}},\;{{w}_{i}})$ | ${{b}_{{jk}}}r_{{ijk}}^{0}$ |
| $({{w}_{i}},\;t)$ | ${{Q}_{i}}$ |
Лемма 1. Для существования допустимого распределения ресурсов необходимо и достаточно существование потока g в сети ${{G}_{1}}$, для которого
при всех $i = \overline {1,\;n} $.Доказательство. 1. Необходимость. Предположим, что существует допустимое распределение ресурсов (как было отмечено выше, оно определяет допустимое расписание), которое для каждого задания ${{w}_{i}}$ и каждого интервала Ij указывает, какие процессоры и в какие моменты времени его выполняют и объем невозобновляемого ресурса каждого типа, выделенный ему. Пусть ${{q}_{{ij}}}$ – это суммарный объем работы процессоров при выполнении задания ${{w}_{i}}$ в интервале Ij, а ${{r}_{{ijk}}}$ – величина невозобновляемого ресурса k-го типа, выделенная заданию ${{w}_{i}}$ в интервале Ij. Определим поток g в сети ${{G}_{1}}$ следующим образом:
(2.2)
$g({{I}_{j}},{{w}_{i}}) = {{q}_{{ij}}},\quad g({{T}_{{jk}}},{{w}_{i}}) = {{b}_{{jk}}}{{r}_{{ijk}}},$(2.3)
$g(u,{{I}_{j}}) = \sum\limits_{i = 1}^n {{{q}_{{ij}}}} ,\quad g(u,{{T}_{{jk}}}) = \sum\limits_{i = 1}^n {{{b}_{{jk}}}{{r}_{{ijk}}}} ,$(2.4)
$g({{w}_{i}},t) = \sum\limits_{j = 1}^p {({{q}_{{ij}}} + \sum\limits_{k = 1}^K {{{b}_{{jk}}}{{r}_{{ijk}}}} )} .$Тогда в силу (2.2)–(2.4) в каждом внутреннем узле сети ${{G}_{1}}$ (т.е. в узлах Ij, ${{T}_{{jk}}}$ и ${{w}_{i}}$, $j = \overline {1,p,} $ $k = \overline {1,K,} $ $i = \overline {1,n} $) не нарушается условие сохранения потока. Кроме того, в силу неравенств (1.1)–(1.4) потоки по дугам $(u,{{I}_{j}}),$ $(u,{{T}_{{jk}}}),$ $({{I}_{j}},{{w}_{i}})$ и $({{T}_{{jk}}},{{w}_{i}})$ не превосходят их пропускных способностей. И наконец, поскольку при допустимом распределении ресурсов каждая работа выполняется полностью, то в силу (2.4) $g({{w}_{i}},\;t) = {{Q}_{i}}$ при всех $i = \overline {1,\;n} $, т.е. верно условие (2.1) леммы 1.
2. Достаточность. Предположим теперь, что в сети ${{G}_{1}}$ существует поток g, для которого справедливы равенства (2.1) при всех $i = \overline {1,n} $. Определим ${{q}_{{ij}}} = g({{I}_{j}},{{w}_{i}})$. Тогда верно неравенство (1.1), а в силу сохранения потока в узле Ij выполнены соотношения
Далее, определим ${{r}_{{ijk}}} = {{g({{T}_{{jk}}},\;{{w}_{i}})} \mathord{\left/ {\vphantom {{g({{T}_{{jk}}},\;{{w}_{i}})} {{{b}_{{jk}}}}}} \right. \kern-0em} {{{b}_{{jk}}}}}$. Тогда справедливо неравенство (1.3), а в силу сохранения потока в узле ${{T}_{{jk}}}$ выполнены соотношения
Кроме того, в силу (2.1) и сохранения потока в узле ${{w}_{i}}$ суммарный объем работы по реализации задания ${{w}_{i}}$ равен
Из леммы 1 вытекает следующий алгоритм решения задачи существования и нахождения допустимого распределения ресурсов.
1. Построить сеть ${{G}_{1}}$.
2. Найти в сети ${{G}_{1}}$ максимальный поток g (например, с помощью полиномиального алгоритма А. Карзанова [12]).
3. Если для найденного потока g верны равенства (2.1) при всех $i = \overline {1,\;n} $, то допустимое распределение ресурсов (и допустимое расписание для W) существует и может быть построено в каждом интервале Ij, $j = \overline {1,\;p} $, с помощью леммы 1. Если же условие (2.1) не выполнено хотя бы при одном $i,\;1 \leqslant i \leqslant n$, то допустимого распределения ресурсов (и допустимого расписания) не существует.
Оценим вычислительную сложность каждого шага алгоритма. Шаг 1 – $O({{(Kp + n)}^{2}})$, шаг 2 – $O({{(Kp + n)}^{3}})$, шаг 3 – $O(p(n + K))$. Таким образом, вычислительная сложность предложенного алгоритма составляет $O({{(Kp + n)}^{3}})$, т.е. алгоритм является полиномиальным.
3. Нахождение допустимого распределения ресурсов минимальной стоимости. Для нахождения допустимого распределения ресурсов минимальной стоимости построим сеть ${{G}_{2}}$ с такой же структурой, как у сети ${{G}_{1}}$, и припишем каждой дуге $(x,y) \in {{A}_{1}}$ три параметра: нижнюю границу $L(x,y)$ потока по дуге (x, y), верхнюю границу $U(x,y)$ потока по дуге (x, y) и стоимость $C(x,y)$ единицы потока по дуге (x, y). Значения этих параметров приведены в табл. 2. В этом случае стоимость потока в сети ${{G}_{2}}$ определяется стоимостью потока по дугам $({{I}_{j}},{{w}_{i}})$ и $({{T}_{{jk}}},\;{{w}_{i}})$, $j = \overline {1,p,} $ $k = \overline {1,K,} $ $i = \overline {1,n} $. Поэтому поток минимальной стоимости в сети ${{G}_{2}}$ определяет распределение ресурсов минимальной стоимости, а структура сети и параметры дуг $({{w}_{i}},t)$, $i = \overline {1,\;n} $, таковы, что это распределение является допустимым. Таким образом, с учетом леммы 1 справедливо следующее утверждение.
Таблица 2.
Значения параметров дуг сети ${{G}_{2}}$
| Дуга | L | U | C |
|---|---|---|---|
| $(u,\;{{I}_{j}})$ | 0 | ${{a}_{j}}{\kern 1pt} {{S}_{j}}{{\delta }_{j}}$ | 0 |
| $(u,\;{{T}_{{jk}}})$ | 0 | ${{b}_{{jk}}}{\kern 1pt} {{R}_{{jk}}}$ | 0 |
| $({{I}_{j}},{{w}_{i}})$ | 0 | $q_{{ij}}^{0}$ | ${{c}_{j}}$ |
| $({{T}_{{jk}}},\;{{w}_{i}})$ | 0 | ${{b}_{{jk}}}r_{{ijk}}^{0}$ | ${{d}_{{jk}}}$ |
| $({{w}_{i}},\;t)$ | ${{Q}_{i}}$ | ${{Q}_{i}}$ | 0 |
Лемма 2. 1. Для существования допустимого распределения ресурсов необходимо и достаточно существование потока в сети ${{G}_{2}}$.
2. Поток минимальной стоимости в сети ${{G}_{2}}$ определяет распределение ресурсов минимальной стоимости.
Из леммы 2 вытекает следующий алгоритм решения поставленной задачи.
1. Построить сеть ${{G}_{2}}$.
2. Найти в сети ${{G}_{2}}$ поток g минимальной стоимости (например, с помощью псевдополиномиального алгоритма дефекта [12]).
3. Если поток g в сети ${{G}_{2}}$ существует, то допустимое распределение ресурсов (и допустимое расписание для W) существует, может быть построено в каждом интервале Ij, $j = \overline {1,\;p} $, с помощью леммы 1 и оно будет допустимым распределением ресурсов минимальной стоимости. Если же потока в сети ${{G}_{2}}$ не существует, то допустимого распределения ресурсов (и допустимого расписания) не существует.
Оценим вычислительную сложность каждого шага алгоритма. Шаг 1 – $O({{(Kp + n)}^{2}})$, шаг 2 – $O({{(Kpn)}^{2}}U)$, где U – это максимальная верхняя граница потока по дугам сети ${{G}_{2}}$, шаг 3 – $O(p(n + K))$. Таким образом, вычислительная сложность предложенного алгоритма составляет $O({{(Kpn)}^{2}}U)$, т.е. алгоритм является псевдополиномиальным.
Рассмотрим теперь задачу построения допустимого распределения ресурсов, при котором минимален суммарный объем работы, выполняемой возобновляемыми и невозобновляемыми ресурсами в заданной совокупности интервалов Ij. Для этого определенным образом корректируются некоторые параметры дуг сети ${{G}_{2}}$ и определяется поток минимальной стоимости, с помощью которого можно построить искомое распределение ресурсов, как это указано в лемме 1.
Пусть $J \subseteq \{ 1,\;2,\;...,\;p\} $ и требуется минимизировать суммарный объем работы, выполняемый процессорами в интервалах Ij, $j \in J$. Для этого стоимости единицы потока по дугам сети ${{G}_{2}}$ определим следующим образом: положим $С(u,{{I}_{j}}) = 1$ при всех $j \in J$, $С(x,y) = 0$ для всех остальных дуг сети ${{G}_{2}}$. Значения нижних и верхних границ потока по дугам сети ${{G}_{2}}$ оставим без изменения. Тогда поток минимальной стоимости в сети ${{G}_{2}}$ будет обладать таким свойством, что суммарный поток по дугам $(u,{{I}_{j}})$, $j \in J$, будет минимальным. Следовательно, минимальным будет и суммарный объем работы, выполняемый процессорами в интервалах ${{I}_{j}}$, $j \in J$.
Рассмотрим частный случай, когда $J = \{ {{j}_{0}}\} $ (т.е. множество J состоит из одного элемента ${{j}_{0}}$), все процессоры в интервале ${{I}_{{{{j}_{0}}}}}$ идентичные. Тогда поток минимальной стоимости в сети ${{G}_{2}}$ будет обладать таким свойством, что поток по дуге $(u,{{I}_{{{{j}_{0}}}}})$ будет минимальным. Следовательно, после применения алгоритма упаковки число процессоров, выполняющих задания в интервале ${{I}_{{{{j}_{0}}}}}$, также будет минимальным.
Пусть теперь требуется минимизировать суммарный объем работы, выполняемый невозобновляемыми ресурсами ${{k}_{0}}$-го типа, $1 \leqslant {{k}_{0}} \leqslant K$, в интервалах Ij, $j \in J$. Для этого стоимости единицы потока по дугам сети ${{G}_{2}}$ определим следующим образом: положим $C(u,{{T}_{{j{{k}_{0}}}}}) = 1$ при всех $j \in J$, $С(x,y) = 0$ для всех остальных дуг сети ${{G}_{2}}$. Значения нижних и верхних границ потока по дугам сети ${{G}_{2}}$ оставим без изменения. Тогда поток минимальной стоимости в сети ${{G}_{2}}$ будет обладать таким свойством, что суммарный поток по дугам $(u,{{T}_{{j{{k}_{0}}}}})$, $j \in J$, будет минимальным. Следовательно, минимальным будет и суммарный объем работы, выполняемый невозобновляемыми ресурсами ${{k}_{0}}$-го типа в интервалах Ij, $j \in J$.
Аналогично решается задача построения допустимого распределения ресурсов, при котором суммарный объем работы, выполняемой возобновляемыми и невозобновляемыми ресурсами определенных типов в заданной совокупности интервалов Ij, минимален.
4. Составление допустимого расписания для смешанного набора работ. Предполагается, что помимо основных работ W в каждом интервале Ij требуется выполнить совокупность дополнительных заданий ${{V}_{j}} = \{ {{{v}}_{{j1}}},{{{v}}_{{j2,}}}...,{{{v}}_{{j{{H}_{j}}}}}\} $, $j = \overline {1,p} $. Каждая работа ${{{v}}_{{j{{h}_{j}}}}}$ реализуется с помощью какого-либо одного процессора без прерываний и переключений, не может использовать невозобновляемые ресурсы, а ее объем составляет ${{P}_{{j{{h}_{j}}}}}$, ${{h}_{j}} = \overline {1,{{H}_{j}}} $, $j = \overline {1,p} $. Как и в разд. 2, будем искать допустимое распределение ресурсов. Задачи подобного рода возникают при испытаниях сложных технических объектов (самолеты, ядерные реакторы), когда помимо основных работ W имеются более срочные дополнительные задания ${{V}_{j}}$, $j = \overline {1,p} $, не допускающие прерываний и переключений. Отметим, что эта задача является NP-трудной даже в том случае, когда множество заданий W пусто [13]. Сначала построим допустимое расписание для работ W. Затем в каждом интервале Ij задания ${{V}_{j}}$ распределяются по свободным и не полностью занятым процессорам с использованием, например, точного метода “ветвей и границ” [6], точного псевдополиномиального алгоритма или приближенного “жадного” алгоритма [13].
Расписание для W будем строить таким образом, чтобы для выполнения заданий ${{V}_{j}}$ оставался максимальный объем процессорного времени. Построим сеть ${{G}_{3}}$, имеющую такую же структуру, как и сеть ${{G}_{1}}$, а значения параметров дуг приведены в табл. 3.
Таблица 3.
Значения параметров дуг сети ${{G}_{3}}$
| Дуга | L | U | C |
|---|---|---|---|
| $(u,\;{{I}_{j}})$ | 0 | ${{a}_{j}}{\kern 1pt} {{S}_{j}}{{\delta }_{j}}$ | 0 |
| $(u,\;{{T}_{{jk}}})$ | 0 | ${{b}_{{jk}}}{\kern 1pt} {{R}_{{jk}}}$ | $ - 1$ |
| $({{I}_{j}},{{w}_{i}})$ | 0 | $q_{{ij}}^{0}$ | 0 |
| $({{T}_{{jk}}},\;{{w}_{i}})$ | 0 | ${{b}_{{jk}}}r_{{ijk}}^{0}$ | 0 |
| $({{w}_{i}},\;t)$ | ${{Q}_{i}}$ | ${{Q}_{i}}$ | 0 |
Поскольку стоимость единицы потока по дугам $(u,{{T}_{{jk}}})$ равна минус единице, а для всех остальных дуг – нулю, то стоимость потока в сети ${{G}_{3}}$ определяется только величиной потока по дугам $(u,{{T}_{{jk}}})$, $j = \overline {1,p,} $ $k = \overline {1,K} $. Следовательно, для потока минимальной стоимости в сети ${{G}_{3}}$ суммарный поток по дугам $(u,{{T}_{{jk}}})$, $j = \overline {1,p} ,$ $k = \overline {1,K} $, будет максимальным. Это обеспечит максимальное использование невозобновляемого ресурса при выполнении работ W, и, следовательно, максимальный объем процессорного времени для реализации заданий ${{V}_{j}}$. Расписание работ W строится с помощью найденного потока минимальной стоимости в сети ${{G}_{3}}$ так, как это было описано в разд. 2.
5. Минимизация числа процессоров при жестких временных ограничениях. Допустим, что помимо процессоров (т.е. возобновляемых ресурсов) других ресурсов в системе нет, причем все процессоры идентичные. Каждая работа ${{w}_{i}}$, $i = \overline {1,n} $, полностью выполняется каким-либо одним процессором в течение всего директивного интервала $[{{b}_{i}},{{f}_{i}}]$. После этого процессор может переключиться на другую работу ${{w}_{j}}$. Время, требуемое процессору для такого переключения, равно ${{\sigma }_{{ij}}}$. Каждый процессор одновременно может исполнять не более одной работы. Требуется определить минимальное число процессоров для реализации всей совокупности работ W.
Для решения этой задачи построим потоковую сеть ${{G}_{4}}$ (рис. 2), где ${{V}_{4}} = \{ u,{{w}_{1}},...,{{w}_{n}},{{z}_{1}},...,{{z}_{n}},t\} $ – множество узлов, u – источник, t – сток, узлы ${{w}_{i}}$ и ${{z}_{i}}$ соответствуют заданию ${{w}_{i}}$; A4 = = $\{ (u,{{w}_{i}}),({{z}_{i}},t),({{w}_{i}},{{z}_{j}}),\;i = \overline {1,n} ,\;j = \overline {1,n} \} $ – множество ориентированных дуг. Дуга $({{w}_{i}},{{z}_{j}})$ вводится в сеть ${{G}_{4}}$ в том случае, когда ${{f}_{i}} + {{\sigma }_{{ij}}} \leqslant {{b}_{i}}$, т.е. если процессор после выполнения задания ${{w}_{i}}$ успевает переключиться на работу ${{w}_{j}}$. Пропускные способности всех дуг полагаются равными единице.
Лемма 3. Минимальное число процессоров в сформулированной задаче равно $n - F$, где F – величина максимального потока в сети ${{G}_{4}}$.
Доказательство. Отметим, что поскольку пропускные способности всех дуг сети ${{G}_{4}}$ целочисленные, то, используя алгоритм А. Карзанова [12] для нахождения максимального потока, последний также будет целочисленным. Следовательно, величина потока по каждой дуге $({{w}_{i}},{{z}_{j}})$ равна 0 или 1. Все задания заведомо могут быть выполнены с помощью n процессоров. А каждой единице потока в сети ${{G}_{4}}$ соответствует некоторая дуга $({{w}_{i}},{{z}_{j}})$, поток по которой также равен 1. Это означает возможность выполнить задания ${{w}_{i}}$ и wj одним и тем же процессором, что уменьшает требуемое число процессоров на единицу. Поэтому если величина максимального потока равна F, то минимальное число процессоров, с помощью которых можно выполнить задания W, равно $n - F$.
Заключение. Исследована задача распределения неоднородной и изменяющейся во времени совокупности возобновляемых и невозобновляемых ресурсов при построении допустимого многопроцессорного расписания. Рассмотрены случаи: (1) все процессоры идентичные; (2) процессоры могут различаться своей производительностью; (3) все работы допускают прерывания и переключения с одного процессора на другой; (4) часть работ допускает прерывания и переключения, а часть не допускает. Разработаны алгоритмы минимизации стоимости допустимого распределения ресурсов и числа процессоров при различных ограничениях на параметры задачи. Используемая методика основана на применении теории потоков в сетях.
Список литературы
Филлипс Д., Гарсиа-Диас А. Методы анализа сетей. М.: Мир, 1984.
Давыдов Э.Г. Исследование операций. М.: Высш. шк., 1990.
Танаев В.С., Гордон В.С., Шафранский Я.М. Теория расписаний. Одностадийные системы. М.: Наука, 1984.
Brucker P. Scheduling Algorithms. Heidelberg: Springer, 2007.
Лазарев А.А. Теория расписаний. Оценка абсолютной погрешности и схема приближенного решения задач теории расписаний. М.: МФТИ, 2008.
Мищенко А.В., Сушков Б.Г. Минимизация времени выполнения работ, представленных сетевой моделью, при нефиксированных параметрах сети. М.: ВЦ АН СССР, 1980. С. 3–16.
Малашенко Ю.Е., Новикова Н.М. Анализ многопользовательских сетевых систем с учетом неопределенности // Изв. РАН. ТиСУ. 1998. № 2. С. 134–146.
Mironov A.A., Tsurkov V.I. Network Models with Fixed Parameters at the Communication Nodes. 1 // J. Computer and Systems Sciences International. 1994. V. 32. № 6. P. 1–11.
Mironov A.A., Tsurkov V.I. Network Models with Fixed Parameters at the Communication Nodes. 2 // J. Computer and Systems Sciences International. 1995. V. 33. № 3. P. 107–116.
Mironov A.A., Levkina T.A., Tsurkov V.I. Minimax Estimations of Arc Weights in Integer Networks with Fixed Node Degrees // Applied and Computational Mathematics. 2009. V. 8. № 2. P. 216–226.
Mironov A.A., Tsurkov V.I. Class of Distribution Problems with Minimax Criterion // Doklady Akademii Nauk. 1994. V. 336. № 1. P. 35–38.
Корте Б., Фиген Й. Комбинаторная оптимизация. Теория и алгоритмы. М.: МЦНМО, 2015.
Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления