Известия РАН. Теория и системы управления, 2021, № 6, стр. 158-176

Введение. В статье решается задача приведения космического аппарата (КА) в положение заданной ориентации оптимальным образом. Пространственное движение КА относительно центра масс задается кватернионом [1]. Построение оптимальной программы вращения основано на кватернионных моделях, принципе максимума и универсальных переменных [2].

Вопросы управляемого движения твердого тела вокруг центра масс исследовались многими авторами неоднократно [1–25]. Наиболее детально задача оптимального управления угловым движением КА решена только для плоских вращений КА вокруг одной из главных центральных осей инерции [3] и пространственных вращений сферически-симметричного тела [1]. Для построения программы управления ориентацией КА используются различные методы и алгоритмы (в том числе на основе нечеткой логики [4], концепции обратных задач динамики [5, 6] и др.). Также хорошо известны проблемы оптимального управления движением КА [1, 2, 7–19], в том числе с неограниченным управлением [8, 9] (как с фиксированным [8], так и с нефиксированным временем окончания маневра [9]). Наиболее популярны задачи оптимального по времени разворота [1, 10–16, 18]. Несомненно, практический интерес представляют аналитические решения задачи оптимального разворота, так как они позволяют применять на борту КА готовые законы программного управления и изменения оптимальной траектории движения КА. Некоторые решения получены для осесимметричных КА [14–17]. В частности, авторы работы [17] для решения краевой задачи принципа максимума сделали замену переменных и свели исходную задачу к краевой задаче разворота сферически-симметричного тела. Для КА с произвольным распределением масс при произвольных граничных условиях по угловому положению КА аналитическое решение задачи пространственного разворота не найдено, кроме некоторых особых случаев (например, [1, 18]). Управление ориентацией КА с инерционными исполнительными органами (гиродинами) имеет свои особенности [11, 20–23], и для таких КА ранее был разработан запатентованный метод [26]. Проблема создания высокоэффективных алгоритмов управления ориентацией КА остается актуальной и сегодня.

Ниже исследуется динамическая задача оптимального по времени управления разворотом КА, когда ограничения накладываются как на управляющие функции, так и на фазовые переменные (ограничен не только силовой момент, но и угловая скорость). Найденное решение позволяет разворачивать КА с ограниченной кинетической энергией вращения за минимальное время, что крайне важно для практики космических полетов. Вопросы быстродействия маневров при экономном управлении движением КА остаются до сих пор актуальными, поэтому решаемая в статье задача является практически важной.

1. Уравнения углового движения и постановка задачи управления. Динамика углового движения КА как твердого тела описывается динамическими уравнениями Эйлера [3]:

где J_i, i = $\overline {1,3} $, – главные центральные моменты инерции аппарата, М_i – проекции главного момента М сил на главные центральные оси эллипсоида инерции аппарата, ω_i – проекции вектора ω абсолютной угловой скорости КА на оси связанного базиса E, образованного главными центральными осями эллипсоида инерции аппарата.

Для описания пространственного движения КА воспользуемся математическим аппаратом кватернионов (параметров Родрига–Гамильтона). Движение связанного базиса Е относительно опорного базиса I будем задавать кватернионом Λ [1]. Для определенности базис I считается инерциальным. Поэтому справедливо следующее кинематическое уравнение [1]:

где символ “$ \circ $” – знак умножения кватернионов [1, с. 11–20]. Для удобства кватернион Λ, отражающий текущую ориентацию КА, полагаем нормированным ||Λ|| = 1 [1]. Здесь и далее операция кватернионного умножения на вектор понимается как умножение на кватернион с нулевой скалярной частью; в частности $\Lambda \circ {\mathbf{\omega }} = \Lambda \circ \Omega $, где Ω – кватернион, у которого sqal Ω = 0, vect Ω = ω.

Управление движением КА относительно центра масс осуществляется путем изменения момента сил М. Предположим, что область возможных значений вектора М подобна эллипсоиду инерции КА и описывается неравенством [14]

где u₀ > 0 – некоторая положительная величина, характеризующая мощность исполнительных органов системы ориентации КА. Рассматривается задача разворота с закрепленными левым и правым концами траектории движения, причем начальная и конечная угловые скорости полагаются равными нулю (относительно опорного базиса I); такие задачи встречаются достаточно часто и имеют большое практическое значение. Для исследуемого управления разворотом из положения покоя в положение покоя граничные условия для динамической системы (1.1), (1.2) представляются в виде равенств: где Т – время окончания поворотного маневра. Кватернионы Λ_н и Λ_к, задающие ориентацию связанных с КА осей в начальный и конечный моменты времени, имеют произвольные наперед заданные значения, удовлетворяющие условию ||Λ_н|| = ||Λ_к|| = 1 (считается, что Λ_к ≠ ±Λ_н). Далее полагаем, что для допустимых движений кинетическая энергия вращения КА не должна превышать некоторой положительной величины E_доп. Т.е. управление ограничено условием где E_доп – максимально допустимая кинетическая энергия вращения. Задача оптимального управления пространственным разворотом КА формулируется следующим образом: необходимо перевести КА из состояния (1.4) в состояние (1.5) в соответствии с уравнениями (1.1), (1.2) и ограничениями (1.3), (1.6) за минимальное время Т. Оптимальное решение М(t) ищется в классе кусочно-непрерывных функций.

Сформулированная динамическая задача управления КА отличается от рассматриваемых ранее задач максимального быстродействия тем, что оптимальная траектория вращения определяется при наличии ограничений не только на управляющий момент, но и на фазовые переменные (на угловую скорость КА), в этом состоит ее принципиальное отличие. Поскольку время окончания маневра Т не задано, разворот КА из состояния (1.4) в состояние (1.5) всегда можно осуществить (решение М(t) задачи (1.1)–(1.6) существует для любых сочетаний значений Λ_н, Λ_к, J₁, J₂, J₃, и₀). Оптимальное управление пространственной переориентацией КА обладает важными полезными свойствами. В частности, для управления, ограниченного условием (1.6), остановка вращения (при необходимости прекращения маневра в критической или нештатной ситуации) занимает время, не превышающее заранее известной величины.

2. Решение задачи оптимального управления разворотом. Поставленная задача управления (1.1)–(1.6) есть динамическая задача оптимального разворота твердого тела [1], в которой управляющими переменными являются моменты М_i, $i = \overline {1,3} $. Будем решать указанную задачу, используя принцип максимума Л.С. Понтрягина [27]. Пусть φ_i – сопряженные переменные, соответствующие переменным ${{\omega }_{i}}$, i = $\overline {1,3} $. Вместо сопряженных переменных ψ_j, соответствующих компонентам λ_j кватерниона Λ, $j = \overline {0,\;3} $, используем универсальные переменные r_i, i = $\overline {1,3} $ [2], поскольку критерий оптимальности не включает позиционных координат (элементов кватерниона ориентации Λ). Ограничение на фазовые переменные λ _j (и соответственно Λ) несущественно, так как оно выполняется при любых движениях КА вокруг центра масс; ||Λ(t)|| = const в силу уравнения (1.2) [1]; мы полагали ||Λ(0)|| = ||Λ_н|| = 1, поэтому ||Λ(t)|| = 1 в любой момент времени t ∈ [0, T ].

2.1. Функция Гамильтона и сопряженная система уравнений. Для динамической задачи оптимального управления (1.1)–(1.6) гамильтониан Н равен [2]

где

Оптимальные функции r_i как компоненты вектора r и вектор r удовлетворяют уравнениям [2]

где символ × обозначает операцию векторного произведения векторов. Уравнения для сопряженных функций φ_i имеют вид [27] или в развернутой форме:

Гамильтониан Н составлен без учета ограничения ||Λ|| = 1 в силу равенства ||Λ(0)|| = 1, о чем договорились выше. Вектор r неподвижен относительно инерциального базиса I и |r| = const ≠ 0 (постоянство модуля |r| следует из свойств уравнений (2.1)). Решение r(t) системы (2.1) определяется начальным Λ_н и конечным Λ_к положениями КА. Оптимальная функция r(t) вычисляется через кватернион Λ(t) [1, 2]:

(составляющие вектора c_E – проекции вектора r на оси инерциального базиса I); $\tilde {\Lambda }$ – кватернион, сопряженный кватерниону Λ [1, с. 11–20]. Считается, что r(0) ≠ 0 (в противном случае r₁ = = r₂ = r₃ ≡ 0 и дальнейшее решение задачи теряет смысл). Направление вектора c_E зависит от начального и конечного положений КА. Для того, чтобы КА имел требуемую ориентацию на правом конце Λ(T) = Λ_к, необходимо определить вектор c_E (или значение вектора r в начальный момент времени) исходя из получающихся при этом решений системы (1.2).

2.2. Условия максимума гамильтониана и структура оптимального решения. Определим условия максимума для функции Н. Перепишем гамильтониан в следующем виде:

где H_inv не зависит явно от управляющих функций M_i, $i = \overline {1,3} $. Введем вспомогательные переменные

После замены переменных гамильтониан H принимает вид H = ${{g}_{1}}{{u}_{1}} + {{g}_{2}}{{u}_{2}} + {{g}_{3}}{{u}_{3}}$ + H_inv, а ограничение (1.3) запишется так: $u_{1}^{2} + u_{2}^{2} + u_{3}^{2} \leqslant u_{0}^{2}$. Функция H максимальна, когда

Нетрудно видеть, что в случае, когда $\varphi _{1}^{2} + \varphi _{2}^{2} + \varphi _{3}^{2}$ ≠ 0, максимум функции Н для управлений М_i(t) при ограничении (1.3) достигается, если

Обозначим

В начале и в конце разворота ограничение (1.6) несущественно, оно переходит в строгое неравенство, так как угловые скорости в начальный и конечный моменты времени равны нулю: ω(0) = ω(T) = 0. Поэтому в интервалах движения, когда E(t) < E_доп, оптимальное решение определяется замкнутой системой уравнений (1.1), (1.2), (2.1)–(2.3) с учетом требований (1.4), (1.5). Системе (1.1), (2.1)–(2.3) удовлетворяют функции φ_i, пропорциональные r_i. С учетом условий разворота ω(0) = ω(Т) = 0 система уравнений (1.1), (2.1)–(2.3) имеет единственное решение, в котором φ_i и угловые скорости ω_i связаны с переменными r_i выражениями

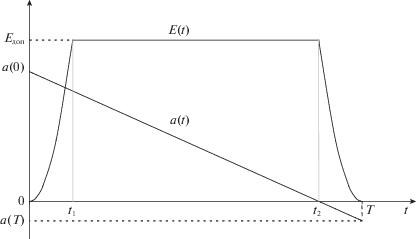
где a(t), b(t) – скалярные функции времени. Подстановка равенств (2.4), (2.5) в систему (2.2) с учетом уравнений (1.1), (2.1), (2.3) превращает все три уравнения (2.2) в тождества, если $\dot {a}$ = –1, что доказывает истинность решения (2.4), (2.5). Оптимальная функция a(t) описывается зависимостью a(t) = a(0) – t. Значение a(0) определяется временными параметрами разворота. Значение r(0) такое, чтобы в результате интегрирования уравнений (1.1), (1.2), (2.1), (2.5) с начальными условиями Λ(0) = Λ_н для траектории движения Λ(t) выполнялось равенство Λ(Т) = Λ_к.

Разворот КА совершается максимально быстро, если в каждый момент времени t угловая скорость максимальна, насколько это позволяют ограничения (1.3) и (1.6). Выше было показано, что если E(t) < E_доп, то оптимальным является управление (2.3) и М ≠ 0, если φ ≠ 0 (компонентами вектора φ являются сопряженные переменные φ_i, а u_i – компоненты вектора u). При условии E(t) = const = E_доп область возможных значений u сокращается из шара |u| ≤ u₀ до плоского круга, ограниченного окружностью, образованной пересечением сферы с плоскостью, перпендикулярной вектору, компонентами которого являются ${{\omega }_{i}}\sqrt {{{J}_{i}}} $ (так как для выполнения E(t) = const = E_доп должно быть $\dot {E} = 0$ и, следовательно, М ⋅ ω = 0); знак умножения “⋅” означает скалярное произведение векторов. Оптимальный момент М обязан находиться внутри сечения эллипсоида (1.3) плоскостью, перпендикулярной угловой скорости ω с тем, чтобы $\dot {E} = 0$, пока не наступит момент начала остановки вращения (а он существует, поскольку ω(T) = 0).

На участке разгона (начиная с момента t = 0), когда E(t) < E_доп и кинетическая энергия вращения E(t) возрастает, оптимальным является М ≠ 0 и a(t) > 0, и как следствие

(заметим, что управляющий момент (2.6) делает раскрутку максимально быстрой [24] и значение E(t) = E_доп достигается за минимальное время при ограничении (1.3)). На участке торможения (в интервале времени слева от момента t = T), когда E(t) < E_доп и кинетическая энергия вращения E(t) уменьшается, оптимальным является М ≠ 0 и a(t) < 0, чтобы $\dot {E} < 0$, и поэтому (слева от момента t = T управляющий момент М и кинетический момент L имеют противоположные направления и длительность остановки вращения минимальна [24]). На участках разгона и торможения, когда E(t) < E_доп, кинетическая энергия вращения изменяется в соответствии с уравнением $\dot {E} = \pm {{u}_{0}}\sqrt {2E} $ (“+” соответствует разгону, “–” – торможению). Поэтому для участка разгона E(t) = $u_{0}^{2}{{t}^{2}}{\text{/}}2$, а для участка торможения E(t) = $u_{0}^{2}$(T – t)²/2. Поскольку в момент окончания разгона и в момент начала торможения кинетическая энергия одна и та же, то длительности разгона и торможения одинаковы и равны τ = t_р = $\sqrt {2{{E}_{{\max }}}} {\text{/}}{{u}_{0}}$, где E_max = E(T/2) – максимальная энергия вращения.

В зависимости от условий разворота (сочетания значений Λ_н, Λ_к и J₁, J₂, J₃, u₀) в оптимальном движении из начального положения Λ_н в конечное положение Λ_к максимальная кинетическая энергия вращения может быть меньше E_доп, а может возникнуть необходимость вращения какое-то время с выполнением равенства E(t) = const = E_доп. Сформулируем условия, когда оптимальное управление исключает наличие моментов времени, в которые КА вращается с постоянной кинетической энергией. Для того, чтобы $\dot {E} \ne 0$ на всем отрезке времени t ∈ [0, T], время разворота T должно быть меньше, чем $2\sqrt {2{{E}_{{{\text{доп}}}}}} {\text{/}}{{u}_{0}}$. Чтобы рассчитать время оптимального разворота T, воспользуемся понятием “функционал пути” [19]:

который не зависит от характера изменения скалярной функции b(t), если движение КА удовлетворяет уравнениям (2.1), (2.5) [19]. Исходя из соотношений $T\sqrt {2{{E}_{{\max }}}} = 2S$, E_max = $u_{0}^{2}{{\tau }^{2}}{\text{/}}2$ и T = 2τ, получаем T = $2\sqrt {S{\text{/}}{{u}_{0}}} $ = T_fast – минимально возможное время разворота в условиях ограничения (1.3) даже без учета требования (1.6) к кинетической энергии вращения. Значение T_fast соответствует развороту, во время которого отсутствует участок движения с E(t) = const. Для оптимального управления с одной точкой переключения в момент времени t = T/2 необходимо выполнение условия T_fast ≤ $2\sqrt {2{{E}_{{{\text{доп}}}}}} {\text{/}}{{u}_{0}}$. Если и₀S ≤ 2E_доп, то во время максимально быстрого разворота вращение КА в режиме E(t) = const невозможно.

Если и₀S > 2E_доп, то неизбежно вращение КА с постоянной кинетической энергией вращения (при этом a(t) ≥ 0). Разница S – 2E_доп/и₀ определяет продолжительность участка движения, когда E(t) = const = E_доп. Найдем, каким должно быть оптимальное управление М, чтобы удовлетворялось условие $\dot {E} = 0$ с одновременной максимизацией гамильтониана H.

При выполнении соотношений (2.4), (2.5) гамильтониан H равен

В интервале вращения с постоянной кинетической энергией E(t) = E_доп выполняется условие

Для решения (2.4), (2.5) при условии E(t) = const = E_доп имеем φ₁М₁/J₁ + φ₂М₂/J₂ + φ₃М₃/J₃ = = а(t)(М₁ω₁ + М₂ω₂ + М₃ω₃)/b(t) = 0 и поэтому

(очевидно, b(t) ≠ 0 в интервале времени, когда E(t) = E_доп). Угловые скорости ω_i, при которых достигается максимум гамильтониана H (с учетом E(t) = E_доп), будут следующими:

Подставив указанные зависимости для оптимальных угловых скоростей ω_i в динамические уравнения (1.1) с учетом уравнений (2.1) для оптимальных функций r_i, получим оптимальный силовой момент М = 0 для моментов времени, когда E(t) = const = E_доп (на участке между разгоном и торможением). Найдем производную $\dot {H}$ с учетом условия E(t) = const :

так как на этапе разгона оптимальный момент М и вектор φ имеют одинаковое направление и в момент окончания разгона r_i = J_iω_i/b. Покажем, что $r_{1}^{2}{\text{/}}{{J}_{1}} + r_{2}^{2}{\text{/}}{{J}_{2}} + r_{3}^{2}{\text{/}}{{J}_{3}} = {\text{const}}$. Возьмем производную от левой части указанного равенства с учетом (2.5):

Поскольку |r| ≠ 0 и H = const внутри отрезка времени, на котором E(t) = const = E_доп (так как $\dot {H}$ = 0), то b = const = $(1 + H){\text{/}}(r_{1}^{2}{\text{/}}{{J}_{1}} + r_{2}^{2}{\text{/}}{{J}_{2}} + r_{3}^{2}{\text{/}}{{J}_{3}})$. Это означает, что в оптимальном развороте в интервале времени, когда E(t) = const = E_доп, будет |L| = const. Этот факт только подтверждает вывод об оптимальности значения М = 0 в моменты времени, когда E(t) = const. Вращение по инерции есть частный случай закономерности (2.5) с учетом (2.1). На момент достижения равенства E(t) = E_доп направления оптимального вектора φ и кинетического момента L совпадают, поэтому единственным решением системы (1.1), (2.1), (2.2) в интервале времени, когда E(t) = const, являются зависимости (2.4), в которых $\dot {a}$ = –1. Из свойства непрерывности функции a(t) следует, что a(t) = a(0) – t  для любого момента времени t, пока a(t) ≥ 0. Как только a(t) < 0, так управление (2.3) становится оптимальным, потому что φ ≠ 0 и силовой момент (2.3) (а значит, и (2.7)) не нарушает требования (1.6), поскольку при таком управлении будет М ⋅ L < 0 и $\dot {E} < 0$. Следовательно, решение (2.4), (2.5), в котором a(t) = a(0) – t, справедливо для всего интервала времени t ∈ [0, T] (в оптимальном решении a(0) > 0, a(T) < 0).

Таким образом, в зависимости от значения “функционала пути” (2.8), вычисленного для движения в соответствии с уравнениями (2.1), (2.5), реализуется один из двух вариантов оптимального управления: если и₀S ≤ 2E_доп, то оптимальным является релейное управление с одной точкой переключения, при котором a(Т) = –a(0), а если и₀S > 2E_доп, то оптимальным является релейное управление с двумя точками переключения, при котором a(0) > –a(T). Рисунок 1 отражает второй вариант оптимального управления, при котором существует отрезок времени с E(t) = const (при выполнении условия S > 2E_доп/и₀ для значения (2.8)); t₁ – ближайший к началу разворота момент достижения равенства E(t) = E_доп; t₂ – момент смены знака скалярной функции a(t) (начиная с момента времени t = t₂ для функции a(t) верно условие a(t) < 0). На временах t > t₂ имеем a(t) < 0 и оптимальным является управление (2.3), потому что при таком силовом моменте будет М ⋅ ω = $\dot {E}$ < 0 и ограничение (1.6) становится несущественным (его можно не учитывать при дальнейшем приближении к t = T). В интервалах t < t₁ и t > t₂ оптимальным управлением является (2.3), при котором соответственно будет |M| = const = u₀/C. Здесь обозначено C = = $\sqrt {p_{1}^{2}{\text{/}}{{J}_{1}} + p_{2}^{2}{\text{/}}{{J}_{2}} + p_{3}^{2}{\text{/}}{{J}_{3}}} $ = const, p_i = r_i/r₀, r₀ = const = |r| ≠ 0.

На участке вращения с максимально допустимой кинетической энергией оптимальный момент М определяется из трех условий: ограничения (1.3), требования (2.9) и условия, что в каждый текущий момент времени t, пока E(t) = const = E_доп, гамильтониан H принимает максимальное значение. Учитывая структуру гамильтониана (2.10), приходим к выводу, что во время вращения КА с постоянной максимально допустимой кинетической энергией оптимальным является такое управление М, при котором в каждый текущий момент времени t, пока E(t) = const = E_доп, угловая скорость ω удовлетворяет соотношениям (2.11). Требование (2.9) привело к структуре (2.10), при которой гамильтониан H не зависит явным образом от силового момента М. Справедливость утверждения, что движение с угловой скоростью (2.11) соответствует максимуму гамильтониана H, легко доказать после замены переменных

записав с учетом равенств ${{J}_{1}}\omega _{1}^{2} + {{J}_{2}}\omega _{2}^{2} + {{J}_{3}}\omega _{3}^{2}$ = 2E_доп, $y_{1}^{2} + y_{2}^{2} + y_{3}^{2}$ = 2E_доп для угловой скорости ω. Оптимальное значение момента М вычисляем путем подстановки оптимальных угловых скоростей (2.11) в динамические уравнения (1.1) с учетом зависимостей (2.1) для универсальных переменных r_i и проверки выполнения условий (1.3), (2.9) (т.е. чтобы управляющий момент М находился внутри области допустимых значений). В результате получили М = 0. Очевидно, что найденное управление М удовлетворяет неравенству (1.3) и равенству (2.9).

Таким образом, структура оптимального управления полностью определена:

Заметим, что вращение по инерции полностью соответствует решению (2.4), (2.5) (угловые скорости (2.11) есть частный случай (2.5) и не противоречат соотношениям (2.4)). Поэтому найденное оптимальное решение (2.4), (2.5) справедливо на всем интервале управления t ∈ [0, T].

Краевая задача принципа максимума заключается в определении такого значения вектора r(0), при котором решение системы дифференциальных уравнений (1.1), (1.2), (2.1), (2.2) с одновременным выполнением условия (2.3), если φ ⋅ r < 0 или E(t) < E_доп, или М = 0, если φ ⋅ r > 0 и E(t) = E_доп, удовлетворяло условиям разворота (1.4), (1.5). Константа r₀ определяется из уравнения H(Т) = 0 (так как время окончания оптимального процесса не фиксировано). Вычислим H(Т) с учетом зависимостей (2.4):

(угловые скорости в конечный момент t = T равны нулю); $С = \sqrt {p_{{10}}^{2}{\text{/}}{{J}_{1}} + p_{{20}}^{2}{\text{/}}{{J}_{2}} + p_{{30}}^{2}{\text{/}}{{J}_{3}}} $, где p₁₀, p₂₀, p₃₀ – компоненты вектора p₀ = p(0) (p = r/|r| – орт вектора r). Значение a(Т) оптимальной функции a(t) в конечный момент времени равно a(Т) = –1/(u₀r₀C). При любом типе оптимального управления (с одной или двумя точками переключения) a(Т) = –τ (напомним, τ – длительность разгона и торможения). Поэтому r₀ = 1/(u₀τC). Отсюда оптимальное значение r₀ равно r₀ = = ${1 \mathord{\left/ {\vphantom {1 {(C\sqrt {2{{E}_{{{\text{доп}}}}}} )}}} \right. \kern-0em} {(C\sqrt {2{{E}_{{{\text{доп}}}}}} )}}$, если присутствует участок вращения с постоянной максимально допустимой кинетической энергией E_доп (так как a(Т) = $ - {{{{\sqrt {2{{E}_{{{\text{доп}}}}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{E}_{{{\text{доп}}}}}} } u}} \right. \kern-0em} u}}_{0}}$). Для оптимального управления с одной точкой переключения a(Т) = –Т/2 = $ - \sqrt {S{\text{/}}{{u}_{0}}} $, поэтому r₀ = ${1 \mathord{\left/ {\vphantom {1 {(C\sqrt {{{u}_{{\text{0}}}}S} )}}} \right. \kern-0em} {(C\sqrt {{{u}_{{\text{0}}}}S} )}}$. В результате

Время оптимального разворота T рассчитывается на основании “функционала пути” (2.8). Поскольку оптимальное движение КА удовлетворяет уравнениям (2.1), (2.5), то значение S не зависит от характера изменения скалярной функции b(t) и является минимально возможным [19]. Если и₀S > 2E_доп, то имеет место участок вращения КА с E(t) = const и длительность оптимального разворота T вычисляется по формуле

При этом время разгона τ составляет

а длительность неуправляемого вращения будет

Если и₀S ≤ 2E_доп, то в оптимальном движении не существует моментов времени, когда E(t) = = const (t_св = 0) и длительность оптимального разворота T равна T = $2\sqrt {S{\text{/}}{{u}_{0}}} $ = T_fast.

С учетом того, что уравнения (2.1), (2.5) удовлетворяются на всем интервале управления t ∈[0, T ], оптимальное движение определяют зависимости:

где p_i – компоненты вектора p, t_р – время окончания разгона, t_т – момент начала торможения,

Закон вращения (2.14) удовлетворяет граничным условиям ω(0) = 0 и ω(T) = 0, так как t_р + t_т = Т, и выражение в скобках обнуляется при t = 0 и t = Т. Зависимости (2.1), (2.13), (2.14) с учетом равенств r_i = r₀р_i – единственное решение задачи оптимального управления (1.1)–(1.6). Из (2.1), (2.13) и соотношений r_i = r₀р_i явно видно, что при оптимальном управлении момент сил М действует вдоль прямой, неподвижной в инерциальной системе координат. Уравнения (2.14) отчетливо показывают, что в геометрическом представлении вектор р интерпретируется как орт оптимального кинетического момента КА L в связанной с КА системе координат. Оптимальным (в смысле минимума времени Т) будет разворот КА, при котором направление кинетического момента остается неизменным относительно инерциальной системы координат (векторы М и L коллинеарны). Еще одним основным свойством оптимального разворота КА является тот факт, что во все время движения (на всем отрезке времени [0, T ]) отношение кинетической энергии вращения Е к квадрату модуля кинетического момента КА постоянно:

Для вращений в соответствии с (2.1), (2.5) значение “функционала пути” (2.8) минимально.

2.3. Обоснование единственности оптимального решения. Покажем, что найденное решение (2.4), (2.5) – единственное решение системы уравнений (1.1), (2.1)–(2.3). Введем единичный вектор q для вектора φ, такой, что q(0) ⋅ φ(0) > 0 и φ = χq, где χ – скалярная функция c начальным значением χ(0) > 0; |q| = 1. Тогда оптимальный момент М будет равен

Так как χ(0) > 0, то в окрестности точки t = 0 имеем М = hq и М || L, L = Kq, где h – скалярная величина (на участке разгона h > 0); L = J_КАω – кинетический момент КА; J_КА = diag {J₁, J₂, J₃} – тензор инерции КА. Подставим формулы (2.3) с учетом зависимости φ = χ (t) q в уравнения (1.1) при наличии равенств J_iω_i = Kq_i:

Сумма $K{\mathbf{\dot {q}}} + \omega \times {\mathbf{q}}K$ ортогональна орту q или равна нулю (всегда q ⋅ ${\mathbf{\dot {q}}}$ = 0, так как |q| = 1). Поэтому уравнение (2.15) выполняется в единственном случае, если $\dot {K} = h$ и ${\mathbf{\dot {q}}} = - \omega \times {\mathbf{q}}$ (т.е. когда направление вектора q остается неизменным относительно инерциального базиса I). Теперь подставим равенства φ_i = χq_i и ω_i = Kq_i/J_i в уравнения (2.2), которые представим в виде

Левая часть уравнения (2.16) для вектора сопряженных переменных равна

(уравнения (1.1), (2.2) должны выполняться одновременно, поэтому свойство ${\mathbf{\dot {q}}} = - \omega \times {\mathbf{q}}$ взято из (2.15)). Правая часть уравнения (2.16) будет такой:

Приравнивая левую и правую части уравнения (2.16), получим уравнение для вектора q:

Отсюда следует необходимое условие оптимальности r = –$\dot {\chi }$q, из которого неизбежны равенства (2.4), в которых а (0) > 0, так как $\dot {a}$(t) = –1, причем $\dot {\chi }$ = const и q = r/|r|, откуда имеем следующие свойства: $\dot {\chi }$ = –r₀, χ(t) = r₀а(t), К = |L| = r₀b(t), где r₀ = const = |r(0)| (так как χ(0) > 0 и χ(T) < 0, а поэтому $\dot {\chi }$ < 0). В итоге заключаем, что если в какой-нибудь момент времени t кинетический момент L и вектор φ коллинеарны, то они коллинеарны на всем интервале времени 0 < t < T. В силу наличия граничных условий ω(0) = 0 и ω(T) = 0 векторы L и φ коллинеарны как минимум 2 раза – в самом начале разворота (L = htq при t → 0) и в самом конце маневра (L = h(t – T)q при t → T); во время остановки вращения h < 0.

На участке разгона существует как минимум один момент времени, когда векторы L и φ коллинеарны, и на участке торможения существует как минимум один момент времени, когда векторы L и φ коллинеарны, а между разгоном и торможением (если существует интервал движения с E(t) = const) оптимальным является вращение по инерции и уравнения (2.1), (2.5) выполняются, из-за чего единственным решением уравнений (2.2) будет (2.4). Следовательно, на всем интервале управления t ∈[0, T ] зависимости (2.4), (2.5) – единственное решение, удовлетворяющее необходимым условиям оптимальности. Значит, никакое отличное от (2.13), (2.14) движение не может быть оптимальным, так как оно не будет удовлетворять необходимым условиям оптимальности.

На участке разгона (когда E(t) < E_доп и $\dot {E}$ > 0) L(t) = |L|$\tilde {\Lambda } \circ $ Λ_н $ \circ $ p(0) $ \circ \,{{\tilde {\Lambda }}_{{\text{н}}}}$ $ \circ $ Λ, на участке вращения с E(t) = const = E_доп будет Λ $ \circ $ L(t) $ \circ \,\tilde {\Lambda }$ = const, а на участке торможения (когда E(t) < E_доп и $\dot {E}$ < 0) L(t) = |L|$\tilde {\Lambda } \circ $ Λ_к $ \circ $ p(T) $ \circ \,{{\tilde {\Lambda }}_{{\text{к}}}}$ $ \circ $ Λ. Поэтому для характерных моментов времени имеем:

Подставив L(t_т) в соотношение Λ(t_т) $ \circ $ L(t_т) $ \circ \,\tilde {\Lambda }({{t}_{{\text{т}}}})$ = |L(t_т)|Λ_к $ \circ $ p(T) $ \circ \,{{\tilde {\Lambda }}_{{\text{к}}}}$, получим

Установлено, что все три участка движения принадлежат одной траектории, определяемой системой уравнений (1.2), (2.1), (2.5); при этом b(t) – кусочно-линейная функция времени с точками излома t_р и t_т, у которой $\dot {b}$ > 0 для t ≤ t_р, $\dot {b}$ = 0 для t_р < t ≤ t_т и $\dot {b}$ < 0 для t > t_т, а b(0) = b(T) = 0. Кроме того, |$\dot {b}$| = const = u₀ /(r₀C), если t ≤ t_р и t > t_т; и в моменты перехода с одного участка траектории на другой участок выполняются соотношения:

Функции Λ(t), ω(t), p(t) непрерывны внутри всего отрезка времени t ∈[0, T] и Λ $ \circ $ p(t) $ \circ \,\tilde {\Lambda }$ = const.

На участке разгона Λ $ \circ $ l(t) $ \circ \,\tilde {\Lambda }$ = const и l(t) = $\tilde {\Lambda } \circ $ Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ $ \circ $ Λ, между разгоном и торможением КА вращается по инерции и Λ $ \circ $ l(t) $ \circ \tilde {\Lambda }$ = const = Λ(t_р) $ \circ $ l(t_р) $ \circ $ $\tilde {\Lambda }({{t}_{{\text{р}}}})$ = Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ (так как l(t_р) = $\tilde {\Lambda }({{t}_{{\text{р}}}}) \circ $ Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ $ \circ $ Λ(t_р)), а l(t) = $\tilde {\Lambda } \circ $ Λ(t_р) $ \circ $ l(t_р) $ \circ $ $\tilde {\Lambda }({{t}_{{\text{р}}}}) \circ $ Λ = $\tilde {\Lambda } \circ $ Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ $ \circ $ Λ; на участке торможения Λ $ \circ $ l(t) $ \circ \tilde {\Lambda }$ = const = Λ(t_т) $ \circ $ l(t_т) $ \circ \tilde {\Lambda }({{t}_{{\text{т}}}})$ = Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ (так как l(t_т) = $\tilde {\Lambda }({{t}_{{\text{т}}}}) \circ $ Λ_н $ \circ $ p(0) $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ $ \circ $ $ \circ $ Λ(t_т)) и l(t) = $\tilde {\Lambda } \circ $ Λ_к $ \circ $ p(T) $ \circ {{\tilde {\Lambda }}_{{\text{к}}}}$ $ \circ $ Λ, откуда l(t) = p(t) на всем отрезке времени t ∈ [0, T], где l = L/|L| – орт кинетического момента КА.

Для функций a(t), b(t) оптимального решения справедливы следующие соотношения:

Время разворота T и оптимальное значение r₀ равны:

Максимальная энергия вращения за время оптимального разворота E_max = min(u₀S/2, E_доп). Максимальный модуль кинетического момента L_max = ${{\sqrt {\min ({{u}_{0}}S,2{{E}_{{{\text{доп}}}}})} } \mathord{\left/ {\vphantom {{\sqrt {\min ({{u}_{0}}S,2{{E}_{{{\text{доп}}}}})} } С}} \right. \kern-0em} С}$.

Покажем, что найденное управление (2.13) действительно оптимально (ему соответствует значение T, определяемое первой формулой (2.17), которое обозначим T_opt). Рассмотрим функцию ${{f}_{0}} = \sqrt {2E(t)} $. Соответственно ${{f}_{{\max }}} = \sqrt {2{{E}_{{{\text{max}}}}}} $. При ограничении (1.3) максимально быстрая раскрутка КА происходит при управлении (2.6) [24], при котором $\ddot {E} = u_{0}^{2}$, а силовой момент M и кинетический момент L одинаково направлены (причем |M| = const и ${\mathbf{\dot {M}}} = - {\mathbf{\omega }} \times {\mathbf{M}}$), что соответствует управлению (2.13). Для наискорейшей остановки вращения при ограничении (1.3) необходимо управление (2.7), при котором управляющий момент M и кинетический момент L имеют противоположные направления, |M| = const и ${\mathbf{\dot {M}}} = - {\mathbf{\omega }} \times {\mathbf{M}}$, что находится в рамках управления (2.13). Если u₀ → ∞, то время разгона и торможения τ → 0 и в течение всего разворота E(t) = const = E_доп. Для любого управления, удовлетворяющего ограничению (1.3), выполняются два условия: f₀(t) ≤ u₀t, если t ≤ T/2, и f₀(t) ≤ u₀(T – t), если t > T/2 (так как ω(0) = ω(T) = 0). При одном и том же значении “функционала пути” S величина T минимальна, если интервал времени, когда E_к(t) = const = E_max, является максимально длительным, а интервалы времени, когда E_к(t) < E_max, максимально короткие. Управление (2.13) удовлетворяет обоим требованиям. Кроме того, для движения (2.13), (2.14) значение S минимально возможное, из-за чего T_opt – абсолютно минимальное время разворота при наличии ограничений (1.3) и (1.6).

Если u₀S ≤ 2E_доп, то в законах (2.13), (2.14) t_т = t_р = T/2 = $\sqrt {S{\text{/}}{{u}_{0}}} $ (оптимальным является релейное управление с одной точкой переключения); при этом E_max = u₀S/2 и ограничение (1.6) несущественно. Время оптимального разворота составляет T_opt = $2\sqrt {S{\text{/}}{{u}_{0}}} $.

Если u₀S > 2E_доп, то t_т > t_р (t_р = τ, t_т = T – τ), в оптимальном по времени развороте имеется участок вращения с постоянной кинетической энергией (реализуется релейное управление с двумя точками переключения). В этом случае при оптимальном управлении (2.13) время разворота T_opt равно (2.12). Каким бы ни было движение, удовлетворяющее условиям разворота (1.4), (1.5) и ограничениям (1.3), (1.6), время разворота T удовлетворяет неравенству

Правая часть указанного неравенства – монотонно убывающая функция аргумента Е_max на всем отрезке [0, u₀S/2] (E_max не может быть больше u₀S/2, так как значение E_max = u₀S/2 соответствует релейному управлению с одной точкой переключения, когда участок вращения КА по инерции отсутствует). При прочих равных условиях время разворота минимально, если “функционал пути” S имеет минимальное значение. Поскольку для всех интересующих нас управлений E_max ≤ E_доп, то правая часть неравенства (2.18) не может быть меньше (2.12), так как для управления (2.13) “функционал пути” S принимает минимальное значение. В результате всегда время разворота T ≥ T_opt. Следовательно, T_opt – действительно минимально возможное время разворота при условии E(t) ≤ E_доп и ограничении (1.3).

3. Построение типовой программы оптимального разворота КА. Выше было продемонстрировано, что функции М_i(t), р_i(t), ω_i(t) будут оптимальными тогда и только тогда, когда они удовлетворяют уравнениям (2.1), (2.13), (2.14) (с учетом равенств r_i = r₀  p_i) и краевым условиям (1.4), (1.5) для решения Λ(t) уравнения (1.2). Задача построения оптимального управления М(t) состоит главным образом в нахождении такого вектора р₀ = р(0) (и значения S), чтобы в результате движения в соответствии с уравнениями (1.2), (2.1), (2.14) и начальными условиями (1.4) выполнялись равенства Λ(Т) = Λ_к и ω(Т) = 0. Для получения функциональной зависимости управлений от фазовых координат необходимо вычислить оптимальное значение r₀ и решить уравнения (2.1). Если J₁, J₂, J₃, и₀, E_доп не меняются, то для всех сочетаний Λ_н, Λ_к с одинаковым кватернионом Λ_р = = ${{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$ решение r(t), М(t), ω(t) будет одним и тем же.

Так как оптимальное решение описывается уравнениями (2.1), (2.5), а для любых движений, удовлетворяющих зависимостям (2.1), (2.5) значение р₀ и интеграл (2.8) не зависят от характера изменения скалярной функции b(t), то при поиске расчетных значений р₀ и S, удовлетворяющих заданным условиям разворота, принимаем b(t) = const > 0 (такой прием применяется для упрощения решения краевой задачи принципа максимума). В этом случае (когда b(t) = const) система уравнений (2.1), (2.5) преобразуется в уравнения

Отметим, что значения р₀ и S определяют время разворота Т, наличие или отсутствие интервала вращения по инерции, максимальный управляющий момент, который равен

а также длительности разгона и торможения, участка неуправляемого движения и максимальную энергию вращения E_max (и максимальную величину кинетического момента L_max).

Управляющие переменные рассчитываются в соответствии с законом (2.13), для реализации которого необходимо в каждый момент времени t знать все три переменные р₁, р₂, р₃. Общее решение системы уравнений (1.2), (2.1), (2.14) (с учетом равенств r_i = r₀p_i) получить практически невозможно; трудность заключается в определении граничных значений p(0) и p(T), которые связаны между собой выражением

где ${{\Lambda }_{{\text{р}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$ – кватернион разворота.

Указанная система имеет аналитическое решение только для динамически симметричного и сферического тел. Для сферически-симметричного КА (J₁ = J₂ = J₃) система (2.1), (2.14) принимает вид ${{\dot {p}}_{i}} = 0$, и решение системы уравнений (1.2), (1.4), (1.5), (2.1), (2.13), (2.14) такое:

где ${{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}$ – компоненты векторной части кватерниона разворота Λ_р; ${{m}_{0}} = {{u}_{0}}\sqrt {{{J}_{1}}} $; Т = t_р + t_т; t_р = = $\min (\sqrt {S{\text{/}}{{u}_{0}}} ,{{\sqrt {2{{E}_{{{\text{доп}}}}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{E}_{{{\text{доп}}}}}} } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}})$, t_т = $\max (\sqrt {S{\text{/}}{{u}_{0}}} ,{S \mathord{\left/ {\vphantom {S {\sqrt {2{{E}_{{{\text{доп}}}}}} }}} \right. \kern-0em} {\sqrt {2{{E}_{{{\text{доп}}}}}} }})$, в которых S = 2J₁Carccos(sqalΛ_р).

Оптимальные развороты вокруг оси, неподвижной относительно инерциальной системы координат, подробно рассмотрены в [1].

Для динамически-симметричного КА (например, когда J₂ = J₃) задача оптимального управления разворотом решается до конца (не умаляя общности рассуждений, за ось симметрии принята ось ОХ КА). Оптимальное движение в этом частном, но достаточно распространенном случае представляет собой одновременное вращение КА как твердого тела вокруг своей продольной оси ОХ и вокруг некоторого направления η, неподвижного в инерциальном пространстве и составляющего с продольной осью КА определенный постоянный угол ϑ. Угловые скорости относительно осей ОХ и η изменяются пропорционально с постоянным коэффициентом пропорциональности, и поэтому справедливо соотношение [14]

где вектор в показателе степени кватернионной экспоненты понимается как кватернион с нулевой скалярной частью; р₀ = р(0); е₁ – орт продольной оси КА; α, β – углы поворота КА вокруг продольной оси ОХ и вокруг вектора р соответственно (считается |α| ≤ π, 0 ≤ β ≤ π). Решение p(t) системы уравнений (1.1), (2.1), (2.14) представим в следующей форме: где p_{i 0} = р_i(0); J = J₂ = J₃; продольная угловая скорость ω₁(t) вычисляется из равенств (2.14) с учетом р₁ = const = р₁₀. Зависимость p_{i 0}, α, β от Λ_н и Λ_к определяется уравнениями где ${{\nu }_{0}},{{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}$ – компоненты кватерниона разворота Λ_р; –π ≤ α ≤ π, 0 ≤ β ≤ π. Существование решения системы (3.3) для любых значений кватерниона разворота Λ_р доказано в [14]. Оптимальное значение управляющего момента М удовлетворяет соотношениям (2.13). Программные значения функций ω_i (проекции требуемой угловой скорости ω* на связанные оси) рассчитываются по формулам (2.14) и (3.2). В явном виде оптимальное решение M_i(t), ω_i(t) запишем следующим образом: где t_р = $\min (\sqrt {{{J}_{2}}\beta {\text{/}}{{m}_{0}}} ,{{\sqrt {2{{E}_{{{\text{доп}}}}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{E}_{{{\text{доп}}}}}} } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}})$; t_т = $\max (\sqrt {{{J}_{2}}\beta {\text{/}}{{m}_{0}}} ,{{{{J}_{2}}\beta C} \mathord{\left/ {\vphantom {{{{J}_{2}}\beta C} {\sqrt {2{{E}_{{{\text{доп}}}}}} }}} \right. \kern-0em} {\sqrt {2{{E}_{{{\text{доп}}}}}} }})$; $\gamma = \arcsin ({{p}_{{20}}}{\text{/}}\sqrt {1 - p_{{10}}^{2}} )$, если р₃₀ ≥ 0, или $\gamma = \pi - \arcsin ({{p}_{{20}}}{\text{/}}\sqrt {1 - p_{{10}}^{2}} )$, если р₃₀ < 0 (|р₁₀| ≠ 1; а случай |р₁₀| = 1 не рассматривается, так как он соответствует плоскому вращению вокруг продольной оси ОХ); Т = t₁ + t₂. В любой текущий момент времени t кватернион ориентации Λ описывается функцией где $\rho = (J - {{J}_{1}}){{p}_{{10}}}\theta {\text{/}}{{J}_{1}}$; значение вектора p₀ определяется из системы (3.3); угол θ равен

Для несимметричного КА (${{J}_{1}} \ne {{J}_{2}} \ne {{J}_{3}}$) решение системы уравнений (1.2), (2.1), (2.14) в квадратурах не представляется возможным и находится исключительно численными методами (например, методом последовательных приближений). Определение вектора p₀ производится путем решения краевой задачи Λ(0) = Λ_н, Λ(Т) = Λ_к с учетом накладываемых на движение связей (1.2), (3.1) и нахождения начальной угловой скорости ω(0) для вращения по инерции.

Для построения оптимального управления при развороте КА необходимо знать не только программу изменения координат р_i(t), но и величину максимального момента m₀, определяющего темп приближения к требуемому конечному состоянию (1.5), а также моменты выключения и включения управления t_р и t_т. Конкретные значения параметров m₀, t_р, t_т, r₀ = |r| и длительность разворота Т зависят от вектора р₀ и характеристики S. Для динамически симметричного КА значение S вычисляется значительно проще (расчет величин r₀, t_р, t_т и E_max также упрощается). В этом частном случае |L| = J₂${{\dot {\beta }}}$ и S = J₂βC, где J₂ – момент инерции относительно поперечной оси (J₂ = J₃); ${{\dot {\beta }}}$ – скорость вращения вокруг кинетического момента L; β – угол поворота КА вокруг кинетического момента L (из физического смысла β ≥ 0). Значения r₀, t_р, t_т, Т, E_max, L_max зависят от угла β поворота КА вокруг кинетического момента L. Чтобы время Т было минимальным, необходимо выполнить условие β ≤ π, при котором S минимально (именно поэтому система (3.3) включает неравенство 0 ≤ β ≤ π).

Решение задачи оптимального по времени разворота с ограничением на фазовые переменные (1.6) подчиняется уравнениям (2.1), (2.4), (2.5), а управляющие переменные М_i и угловые скорости ω_i изменяются в соответствии с законами (2.13), (2.14). Решение (2.13), (2.14) оптимально, потому что оно – единственное; только оно одно (и никакое другое) удовлетворяет необходимым условиям оптимальности. Любое отличное от (2.13), (2.14) движение будет заведомо хуже (в смысле минимума времени разворота T при ограничениях (1.3), (1.6)), поскольку не будет удовлетворять необходимым условиям оптимальности. Значение m₀ в законах движения (2.13), (2.14) определяет максимальную величину управляющего момента, максимальный модуль кинетического момента и длительность участка свободного вращения. Оптимальный вектор р₀ рассчитывается в результате решения краевой задачи принципа максимума. Константы S, С, m₀ полностью определяют программу движения при оптимальном законе управления пространственным разворотом КА. Программное изменение силового момента М описывается зависимостью

где c_p = const = Λ_н$ \circ $ р₀ $ \circ {{\tilde {\Lambda }}_{{\text{н}}}}$ . Для оптимальной программы управления М(t) движение КА относительно центра масс обладает следующими оригинальными свойствами и соотношениями:

Раскрутка КА в начале разворота продолжается до тех пор, пока его кинетический момент L не станет равен заданному значению L_pr, который рассчитывается по формуле

Гашение кинетического момента в конце оптимального разворота осуществляется по закону (2.7). В момент времени t = T, когда ω = 0, управление выключается и M = 0, разворот завершен. Если 2E_доп ≪ u₀S, то торможение КА можем начать с момента выполнения равенства

где δ_j – компоненты кватерниона рассогласования $\tilde {\Lambda }(t) \circ {{\Lambda }_{{\text{к}}}}$, j = $\overline {0,\;3} $; К = |J_КАω| – величина кинетического момента КА. Указанное условие позволяет повысить точность приведения КА в требуемое конечное состояние Λ(Т) = Λ_к, ω(Т) = 0 за счет возможности в бортовой системе управления формировать сигнал на гашение кинетического момента по информации о текущей ориентации КА и измерениям его угловой скорости.

4. Результаты математического моделирования. Приведем численный пример решения задачи управления КА во время программного разворота и построения оптимальной программы вращения. Рассмотрим разворот КА на 180° из начального положения Λ_н, при котором оси КА совмещены (совпадают по направлению) с осями опорного базиса I, в заданное конечное положение Λ_к = Λ_зад. При этом считается, что начальная и конечная угловые скорости нулевые: ω(0) = = ω(Т) = 0. Значения элементов кватерниона Λ_зад, характеризующего требуемое угловое положение КА, были равны: λ₀ = 0; λ₁ = 0.707; λ₂ = 0.39; λ₃ = 0.59. Будем полагать, что инерционные характеристики КА имеют следующие значения, кг ⋅ м² : J₁ = 25 603, J₂ = 91 495, J₃ = 80 662, а мощность исполнительных органов характеризуется величиной u₀ = 0.07077 Н ⋅ кг^–1/2. Во время разворота кинетическая энергия вращения не должна быть больше E_доп = 5 Дж.

Нахождение расчетного значения вектора p₀ начинаем с решения той же краевой задачи для динамически-симметричного КА с моментами инерции J₁ и J, где J – момент инерции относительно поперечной оси, принимаемый равным

В предположении динамической симметричности КА решение p₀ определяется системой (3.3) (для симметричного твердого тела искомое значение следующее: ${\mathbf{p}}_{0}^{{(0)}}$ = {0.4652435; –0.3714789; 0.8034625}). Полученный из уравнений (3.3) вектор p₀ и угол β являются начальным приближением к истинному решению. Они уточняются до тех пор, пока не будут удовлетворять системе уравнений (1.2), (3.1) с учетом накладываемых на движение КА ограничений Λ(0) = Λ_н, Λ(t_пр) = Λ_к, а начальные угловые скорости ω_iн определяются по формулам:

где Т – время разворота (при уточнении вектора p₀ было принято значение Т = 300 с). Прогнозирование “свободного” движения осуществляется интегрированием системы уравнений (1.1), (1.2), описывающих вращение КА, при начальных условиях Λ(0) = Λ_н, ω(0) = ω_н и с учетом того, что M = 0. Степень приближения найденного значения р₀ к искомому решению характеризуется мерой ε = sqal (${{\tilde {\Lambda }}_{{{\text{пр}}}}} \circ {{\Lambda }_{{\text{к}}}}$), где Λ_пр – наиболее близкое к Λ_к положение, полученное в ходе моделирования движения КА около центра масс (согласно уравнениям (1.2), (1.1), в которых M_i = 0). Вектор р₀ уточняется до тех пор, пока ε < ε_пор (ε_пор – некоторое близкое к единице пороговое значение, отражающее точность найденного решения). Как только условие ε ≥ ε_пор достигнуто (прогнозируемая ошибка соответствует требуемой точности), истинное значение p₀, удовлетворяющее граничным условиям Λ(0) = Λ_н, Λ(t_пр) = Λ_к, будет найдено и краевая задача решена. Вектор p₀ уточняется с помощью следующего рекуррентного соотношения: где $\Lambda _{{\text{p}}}^{{(k)}}$ – значение кватерниона разворота на k-й итерации, используемое в системе (3.3). На каждом k-м шаге итераций обновляются элементы кватерниона разворота $\Lambda _{{\text{p}}}^{{(k)}}$ (правые части системы (3.3)), и из уравнений (3.3) мы получаем p₀ и β, а также соответствующую начальную угловую скорость ω_н (в соответствии с (4.1)) и прогноз Λ_пр. Если ε < ε_пор, то вычисляется кватернион разворота $\Lambda _{{\text{p}}}^{{(k + 1)}}$ для следующего (k + 1)-го шага итераций и процесс уточнения вектора p₀ повторяется. За начальное приближение в правых частях системы (3.3) берутся элементы кватерниона $\Lambda _{{\text{р}}}^{{{\text{(0)}}}} = {{\tilde {\Lambda }}_{{\text{н}}}} \circ {{\Lambda }_{{\text{к}}}}$. Итерационный процесс прекращается, когда ε ≥ ε_пор.

Принятая схема итераций аналогична итерационному методу решения уравнения вида x = f(x) для скалярной функции f(x) скалярного (одномерного) аргумента x. В нашем случае аргумент – гиперкомплексное число (кватернион) Λ_р. Функцией является кватернионная величина ${{\Lambda }_{{\text{р}}}} \circ {{\tilde {\Lambda }}_{{\text{к}}}} \circ {{\Lambda }_{{{\text{пр}}}}}$, где Λ_к – постоянный (не зависящий от аргумента Λ_р) кватернион; Λ_пр зависит от аргумента Λ_р через систему уравнений (3.3), (4.1) посредством модели движения (1.1), (1.2) (в уравнениях (1.1) принимается М_i = 0). Изменяя Λ_р, изменяются вектор p₀ (в соответствии с (3.3)) и угловые скорости ω_iн, а значит, изменится и значение Λ_пр, что вызовет изменение функции ${{\Lambda }_{{\text{р}}}} \circ {{\tilde {\Lambda }}_{{\text{к}}}} \circ {{\Lambda }_{{{\text{пр}}}}}$. Как только sqal(${{\tilde {\Lambda }}_{{{\text{пр}}}}} \circ {{\Lambda }_{{\text{к}}}}$) ≥ ε_пор, итерационный процесс прекращается, а решение p₀ считается найденным. Так как |vect (${{\tilde {\Lambda }}_{{\text{к}}}} \circ \Lambda _{{{\text{пр}}}}^{{(k)}}$)| < |vect$\Lambda _{{\text{р}}}^{{(k)}}$| для всех k, то итерационный процесс приближения p₀ к искомому решению сходится. Аналогичный метод определения значения р₀ в решении краевой задачи принципа максимума использовался в предыдущих работах [8, 18]. Заметим, что это лишь один из возможных (но далеко не единственный) итерационных алгоритмов поиска оптимального вектора р₀.

В результате решения краевой задачи разворота из положения Λ(0) = Λ_н в положение Λ(Т) = Λ_к получили расчетное значение вектора р(0) = {0.4552153; –0.3475442; 0.8197513} и “функционал пути” S = 665 м ⋅ кг^1/2. Исходя из найденного значения р₀ получили максимальную величину управляющего момента m₀ = 16.8 Н ⋅ м. Так как и₀S > 2E_доп, то оптимальное управление имеет две точки переключения и между набором и гашением кинетической энергии КА вращается по инерции. Время достижения максимально допустимой кинетической энергии E_доп равно t_р = = ${{\sqrt {2{{E}_{{{\text{доп}}}}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{E}_{{{\text{доп}}}}}} } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}}$ = 44.7 с, а момент начала торможения t_т = ${S \mathord{\left/ {\vphantom {S {\sqrt {2{{E}_{{{\text{доп}}}}}} }}} \right. \kern-0em} {\sqrt {2{{E}_{{{\text{доп}}}}}} }}$ = 210.3 с. Время разворота оказалось равным Т = 255 с. Основные константы оптимального движения такие:

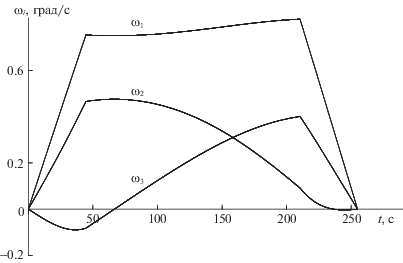
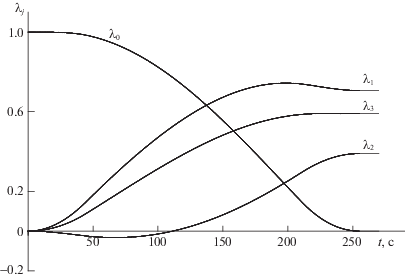
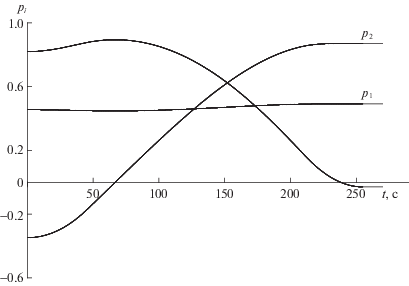
Результаты математического моделирования динамики оптимального по быстродействию разворота представлены рис. 2–5. На рис. 2 изображены графики изменения угловых скоростей в связанной с КА системе координат ω₁(t), ω₂(t), ω₃(t) по времени. Максимальная величина кинетического момента составила L_max = 750.7 Н ⋅ м ⋅ с. Из соотношения моментов инерции J₁, J₂, J₃ следует, что ОХ – продольная ось КА. Отмечаем, что угловая скорость ω₁, соответствующая продольной оси КА, – знакопостоянна. На рис. 3 отображены графики изменения компонент кватерниона Λ(t), определяющего текущую ориентацию КА в процессе совершаемого поворотного маневра: λ₀(t), λ₁(t), λ₂(t), λ₃(t). Оптимальная траектория движения Λ(t) получается из решения уравнений (1.1) с учетом начальных условий Λ(0) = Λ_н и закона изменения угловой скорости ω(t), отраженного на рис. 2. Динамика изменения составляющих p₁(t), p₂(t), p₃(t) орта р по времени приведена на рис. 4. Характерным является незначительное изменение проекции p₁ (угловая скорость ω₁ относительно продольной оси КА на участке между разгоном и торможением также меняется гораздо меньше, чем угловые скорости ω₂ и ω₃ относительно поперечных осей КА). При оптимальном управлении в отличие от переменных ω_i переменные p_i и λ_j – гладкие функции времени. Наконец, рисунок 5 демонстрирует изменение сопряженных переменных φ_i во время оптимального по быстродействию разворота.

Заключение. Рассмотрена и решена динамическая задача оптимального по времени управления пространственным разворотом твердого тела (в частности, КА) из произвольного начального в требуемое конечное угловое положение с учетом ограничений на управляющий момент и кинетическую энергию вращения. Ограниченность максимальной кинетической энергии вращения позволяет в экстренных случаях погасить угловую скорость за время, не превышающее заданного значения (в том числе в нештатной ситуации, когда требуется срочно прекратить маневр и максимально быстро стабилизировать КА). Постановка задачи имеет традиционную форму, в которой управление считается кусочно-непрерывной функцией времени. Нахождение оптимальной по быстродействию программы переориентации КА с кинетической энергией вращения, не превышающей допустимого уровня, весьма актуально.

Представлено аналитическое решение предложенной задачи оптимального разворота и получены формализованные уравнения и расчетные выражения для построения оптимальной программы переориентации КА. Определен тип траектории и изучены ключевые свойства оптимального движения. Найдены условия оптимальности и обоснована структура оптимального управления. Доказано, что в процессе всего разворота отношение кинетической энергии вращения к квадрату модуля кинетического момента КА есть величина постоянная. Для решения сформулированной задачи управления применялся принцип максимума, основываясь на универсальных переменных r_i [2]. Использование кватернионов значительно упрощает расчетные процедуры и снижает вычислительные затраты алгоритма управления, делая его наиболее удобным для бортовой реализации. Задача оптимального управления разворотом решается до конца; даны выражения для расчета ключевых характеристик маневра переориентации.

Показано, что на всем интервале переориентации момент сил действует вдоль прямой, неподвижной в инерциальной системе координат. В общем случае оптимальным является релейное управление с двумя точками переключения, при котором весь разворот делится на раскрутку КА с максимально возможным управляющим моментом, вращение по инерции и торможение с максимально возможным управляющим моментом, противоположно направленным кинетическому моменту КА. Модуль управляющего момента при разгоне и торможении не меняется. Длительности участков разгона и торможения одинаковы (так как начальная и конечная угловые скорости равны нулю) и зависят от мощности исполнительных органов u₀, максимально допустимой кинетической энергии вращения, взаимной ориентации начального и конечного положений КА и его моментов инерции. В случае неограниченного управления (когда u₀ → ∞) времена разгона и торможения бесконечно малы, и практически на всем интервале движения КА вращается с постоянным относительно инерциальной системы координат кинетическим моментом. Другим предельным случаем является управление с одной точкой переключения, при котором участок неуправляемого движения отсутствует (длительность разгона и торможения максимальна и составляет половину времени разворота).

Важность и значение выполненных исследований состоят в том, что в отличие от предыдущих публикаций искомое управление и соответствующее ему движение ограничено максимально допустимой энергией вращения (задача оптимального разворота включает ограничения на силовой момент и угловую скорость КА). В статье приведена процедура реализации оптимального управления переориентацией КА. Момент начала торможения определяется по фактическим параметрам движения (кватерниону рассогласования и кинетическому моменту), исходя из принципов терминального управления (используются информация об угловом положении КА и измерения угловой скорости). Структура построенного управления сравнительно проста, и оно легко может быть реализовано существующими бортовыми системами управления движением КА. Дается описание конструктивной схемы решения краевой задачи принципа максимума для произвольных условий разворота и моментов инерции КА. Для динамически-симметричного КА представлено законченное решение задачи переориентации в замкнутой форме, что придает практическую значимость проведенным исследованиям, поскольку реальные КА во многих случаях близки к телам с осевой симметрией. Записанная в аналитическом виде система уравнений (3.3) позволяет непосредственно найти решение краевой задачи принципа максимума и вычислить необходимые константы оптимального закона управления; при этом искомые значения параметров закона управления могут быть определены известным устройством [28]. Приводятся результаты математического моделирования, иллюстрирующие характер движения КА во время оптимального разворота.

В отличие от работ [8, 9], где рассматривается неограниченное управление (в тех задачах отсутствуют какие-либо ограничения, кроме краевых условий), мы оптимизируем ограниченное управление, когда ограничены не только управляющие функции (силовой момент М), но и фазовые переменные (ограничена угловая скорость КА); это существенное отличие. Кроме того, в [8] оптимальным является непрерывное управление, когда все управляющие функции – непрерывные гладкие функции времени и на всем интервале управления [0, T] (кроме единственного момента времени t = Т/2) управляющий момент М отличен от нуля, а в приведенном решении оптимально релейное управление (с одной или с двумя точками переключения) и может существовать отрезок времени ненулевой продолжительности, на котором М = 0 и КА вращается по инерции. Кроме того, в оптимальном решении, представленном в [8], отсутствуют участки с постоянным модулем управляющего момента.

Принципиальным отличием предложенной динамической задачи оптимального управления относительно известных работ является наличие ограничений как на управляющие функции, так и на фазовые переменные, что придает полученному решению существенную новизну. Наличие готовых формул для синтеза программы оптимального движения во время маневра переориентации делает выполненное исследование практически значимым и пригодным для непосредственного применения в практике космических полетов.