Известия РАН. Теория и системы управления, 2021, № 6, стр. 13-23

ФОРМИРОВАНИЕ СВОЙСТВ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ ЗА СЧЕТ УПРАВЛЕНИЯ РЕАКЦИЯМИ ГОЛОНОМНЫХ КВАЗИИДЕАЛЬНЫХ СВЯЗЕЙ

Е. С. Брискин^a, b, *, В. В. Павловский^d, В. Е. Павловский^c, Л. Д. Смирная^a, b

^a Волгоградский государственный технический ун-т
Волгоград, Россия

^b Центр технологий компонентов робототехники и мехатроники, Университет Иннополис
Иннополис, Россия

^c ФИЦ ИПМ им. М.В. Келдыша РАН
Москва, Россия

^d Российский экономический ун-т им. Г.В. Плеханова
Москва, Россия

^* E-mail: dtm@vstu.ru

Поступила в редакцию 29.10.2020
После доработки 15.12.2020
Принята к публикации 29.03.2021

DOI: 10.31857/S0002338821060068

Полный текст (PDF)

Аннотация

Предлагается метод исследования динамики движения управляемых механических систем. Метод основан на введении управляющих воздействий как функций реакций голономных неидеальных связей. Физический смысл введенных функций – силы, виртуальная работа которых на возможных перемещениях исходной механической системы равна нулю. Введение таких сил позволяет составлять дифференциальные уравнения движения в традиционной форме уравнений Лагранжа с неопределенными множителями, а определение оптимального управления по тому или иному критерию сводится к определению экстремума функции многих переменных, в простейшем случае к установлению коэффициентов линейного преобразования реакций связей. Приведены примеры модельных задач.

0. Введение. Как известно, в случае выбора избыточных координат уравнения движения механической системы, на которые накладываются голономные связи, можно получить из общего уравнения динамики [1, 2]. В обобщенных координатах q_j, i = $\overline {1,S} $, эти уравнения имеют вид

(0.1)

$\frac{d}{{dt}}\left( {\frac{{\partial {\rm T}}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial {\rm T}}}{{\partial {{q}_{j}}}} = {{Q}_{j}} + {{R}_{j}},\quad j = \overline {1,S} .$

В (0.1) T – кинетическая энергия системы, Q_j – обобщенные силы, обусловленные известными активными силами, в общем случае зависящими от обобщенных координат q_j, включая и избыточные, скоростей ${{\dot {q}}_{j}}$ и времени, R_j – обобщенные реакции дополнительных голономных связей, описываемых следующим образом:

(0.2)

${{f}_{n}}({{q}_{1}}, \ldots ,{{q}_{S}},t) = 0,\quad n = \overline {1,N} \quad (N < S).$

При составлении уравнений (0.1) используется принцип освобождаемости от связей, в соответствии с которым связи (0.2) отбрасываются, а их действие заменяется реакциями R_j.

Таким образом, S уравнений (0.1) в совокупности с N уравнениями (0.2) содержат 2S неизвестных q_j и R_j. Поэтому для решения поставленной задачи привлекаются дополнительные уравнения. Обычно эти уравнения получают на основе постулирования идеальности связей:

(0.3)

$\sum\limits_{j = 1}^S {{{R}_{j}}\delta {{q}_{j}}} = 0.$

Варьируя уравнения связей (0.2)

(0.4)

$\sum\limits_{j = 1}^S {\frac{{\partial {{f}_{n}}}}{{\partial {{q}_{j}}}}\delta {{q}_{j}} = 0} ,$

домножая их затем на неопределенные множители Лагранжа λ_n и складывая с (0.3), получают

(0.5)

${{R}_{j}} = \sum\limits_{n = 1}^N {{{\lambda }_{n}}} \frac{{\partial {{f}_{n}}}}{{\partial {{q}_{j}}}}.$

Подставляя затем (0.5) в (0.1) и учитывая (0.2) находят замкнутую систему уравнений, содержащую S + N уравнений с S + N неизвестными q₁, …, q_s, λ₁, …, λ_n:

(0.6)

$\left\{ \begin{gathered} \frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial T}}{{\partial {{q}_{j}}}} = {{Q}_{j}} + \sum\limits_{n = 1}^N {{{\lambda }_{n}}} \frac{{\partial {{f}_{n}}}}{{\partial {{q}_{j}}}} \hfill \\ {{f}_{n}}({{q}_{1}}, \ldots ,{{q}_{S}},t) \hfill \\ \end{gathered} \right..$

1. Постановка задачи. Реакции связей R_j можно рассматривать как управляющие воздействия, реализующие программу движения (0.2) [3]. Условие (0.3) выражает требование минимальности затрат энергии на реализацию такой программы. Действительно, в этом случае сумма элементарных работ всех сил реакций связей равна нулю на любом возможном перемещении. Однако могут быть и другие условия, накладываемые на реакции R_j. В частности, вместо (0.3) можно потребовать, чтобы

(1.1)

$\sum\limits_{j = 1}^S {{{\Psi }_{j}}({{R}_{j}}, \ldots ,{{R}_{S}})} \delta {{q}_{j}} = 0.$

В (1.1) Ψ_j можно определить как “квазиобобщенные” реакции связей, а уравнение (1.1) – как преобразование обобщенных реакций связей и определение “квазиидеальных связей”. Такие связи могут рассматриваться как управляющие воздействия на механическую систему, а метод их учета отличается от учета реакций сервосвязей [4–9] тем, что сохраняются исходные виртуальные перемещения, но реакции изменяются в соответствии с (1.1) таким образом, что виртуальная работа по-прежнему равна нулю. При этом изучение управляемых систем остается в рамках традиционного описания механических систем со связями.

Закон преобразования реакций связей может быть различным и, в частности, линейным:

(1.2)

${{\Psi }_{j}} = \sum\limits_{k = 1}^S {{{R}_{k}}{{a}_{{jk}}}} .$

Тогда вместо (1.1) имеет место уравнение

(1.3)

$\sum\limits_{j = 1}^S {\left[ {\sum\limits_{k = 1}^S {{{R}_{k}}{{a}_{{jk}}}} } \right]} \,\delta {{q}_{j}} = 0.$

Ставится задача составления уравнений движения, позволяющих формировать управляющие воздействия на механическую голономную систему с S степенями свободы, на которую накладываются голономные связи типа (0.2) и требуется определение оптимальных режимов перемещения механических систем по тому или иному критерию, например роботов, за счет целенаправленного выбора управляющих воздействий R_k, входящих в уравнения (1.1).

2. Метод решения. Как и при выводе уравнений Лагранжа 1-го рода за основу берется общее уравнение динамики в обобщенных координатах, отбрасываются дополнительные связи типа (0.2), а их действие заменяется реакциями R_j. В результате, как и ранее, получаются уравнения типа (0.1), которые теперь дополняются не уравнениями (0.3), а уравнениями типа (1.1). Тогда реакции R_k определяются из решения системы алгебраических уравнений:

(2.1)

$\sum\limits_{j = 1}^S {{{a}_{{jk}}}{{R}_{k}}} = \sum\limits_{n = 1}^N {{{\lambda }_{n}}\frac{{\partial {{f}_{n}}}}{{\partial {{q}_{j}}}}} ,\quad k = 1, \ldots ,S.$

Отсюда

(2.2)

${{R}_{k}} = \sum\limits_{j = 1}^S {{{c}_{{jk}}}} \sum\limits_{n = 1}^N {{{\lambda }_{n}}\frac{{\partial {{f}_{n}}}}{{\partial {{q}_{j}}}}} ,$

где c_jk – элементы матрицы, обратной матрице с элементами a_kj.

Если в (2.2) поменять местами индексы j и k и подставить значение R_j в дифференциальные уравнения движения в (0.1), то оно будет иметь вид

(2.3)

$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial T}}{{\partial {{q}_{j}}}} = {{Q}_{j}} + \sum\limits_{n = 1}^N {{{\lambda }_{n}}} \sum\limits_{k = 1}^S {{{c}_{{jk}}}\frac{{\partial {{f}_{n}}}}{{\partial {{q}_{k}}}}} .$

При c_jk = δ_jk, где δ_jk – символы Кронекера, уравнения (2.3) совпадают с уравнениями Лагранжа 1-го рода.

Совместное решение (2.3) и (0.2) позволяет однозначно определить уравнения движения q_j(t) и неопределенные множители Лагранжа λ_n. Что касается реакций R_j, то, в отличие от уравнений Лагранжа 1 рода, они, в общем случае, зависят не только от элементов программного движения (0.2) и действующих активных сил Q_j, но и от вида задаваемой функции Ψ_j (R₁,…,R_S) (1.1), а в рассматриваемом случае – от элементов матрицы a_jk. Это предоставляет дополнительные возможности для формирования управляющих воздействий за счет целенаправленного выбора элементов матрицы a_jk.

3. Модельные задачи. 3.1. Прямолинейное движение материальной точки. Рассматривается задача формирования управляющих воздействий R_x, R_y (рис. 1), действующих на механическую систему, которая моделируется материальной точкой массы m с программным движением по прямолинейной траектории, лежащей в плоскости XOY:

(3.1)

$y = b - kx.$

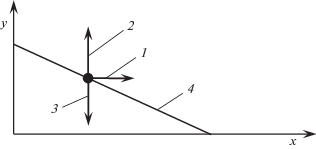
Рис. 1.

Прямолинейное движение материальной точки: 1, 2 – реакции R_x и R_y соответственно, 3 – внешняя активная сила G, 4 – траектория движения

Дифференциальные уравнения движения имеют вид

(3.2)

$\left\{ \begin{gathered} m\ddot {x} = {{R}_{x}}, \hfill \\ m\ddot {y} = - {\kern 1pt} {\kern 1pt} G + {{R}_{y}}, \hfill \\ \end{gathered} \right.$

где G – внешняя активная сила, например сила тяжести.

Эти уравнения решаются совместно с уравнениями (3.1). Для реакций R_x и R_y в соответствии с (2.1) имеют место уравнения

(3.3)

$\left\{ \begin{gathered} {{a}_{{11}}}{{R}_{x}} + {{a}_{{12}}}{{R}_{y}} = \lambda k, \hfill \\ {{a}_{{21}}}{{R}_{x}} + {{a}_{{22}}}{{R}_{y}} = \lambda {\kern 1pt} {\kern 1pt} . \hfill \\ \end{gathered} \right.$

Матрица $\left\| {{{a}_{{jk}}}} \right\|$ задается в форме

(3.4)

$\left\| {{{a}_{{jk}}}} \right\| = \left( {\begin{array}{*{20}{c}} 1&\alpha \\ \beta &1 \end{array}} \right).$

Такая форма (3.4) соответствует понятию “квазиидеальности” относительно преобразованных обобщенных сил, которые фактически являются неидеальными (не выполнено условие (0.3)), а при α = β = 0 это соответствует обычным идеальным связям.

Решением являются

(3.5)

$\begin{gathered} \lambda = G\frac{{1 - \alpha \beta }}{{{{k}^{2}} + 1 - k(\alpha + \beta )}}, \\ {{R}_{x}} = G\frac{{(k - \alpha )}}{{1 + {{k}^{2}} - k(\alpha + \beta )}}, \\ {{R}_{y}} = G\frac{{1 - \beta k}}{{1 + {{k}^{2}} - k(\alpha + \beta )}}. \\ \end{gathered} $

Теперь из (3.2) можно найти ускорения точки a_x, a_y:

(3.6)

$\begin{gathered} {{a}_{x}} = \ddot {x} = \frac{G}{m}\frac{{(k - \alpha )}}{{1 + {{k}^{2}} - k(\alpha + \beta )}}, \\ {{a}_{y}} = \ddot {y} = \frac{G}{m}\frac{{k(\alpha - k)}}{{1 + {{k}^{2}} - k(\alpha + \beta )}}, \\ a = \sqrt {a_{x}^{2} + a_{y}^{2}} = \frac{{G\left| {k - \alpha } \right|}}{{m[1 + {{k}^{2}} - k(\alpha + \beta )]}}\sqrt {1 + {{k}^{2}}} . \\ \end{gathered} $

Уровень тепловых потерь W за время τ в приводных двигателях, генерирующих управляющие силы (реакции связей) R_x, R_y, определяется из выражений [10]

(3.7)

$W = {{\mu }_{x}}\int\limits_0^\tau {R_{x}^{2}dt + \,} {{\mu }_{y}}\int\limits_0^\tau {R_{y}^{2}dt} = {{\mu }_{x}}\frac{{{{G}^{2}}{{{(k - \alpha )}}^{2}}\tau }}{{{{{[1 + {{k}^{2}} - k(\alpha + \beta )]}}^{2}}}} + {{\mu }_{y}}\frac{{{{G}^{2}}{{{(1 - \beta k)}}^{2}}\tau }}{{{{{[1 + {{k}^{2}} - k(\alpha + \beta )]}}^{2}}}},$

где µ_x, µ_y – параметры двигателей горизонтального и вертикального перемещения (для двигателей постоянного тока эти параметры зависят от активного сопротивления обмотки). Механическая работа A реакций связей (управляющих сил) R_x, R_y равна

(3.8)

$A = \int\limits_0^l {{{R}_{x}}dx + } \int\limits_b^{b - k{\kern 1pt} l} {{{R}_{y}}dy} = \frac{{l(\beta k - \alpha )}}{{1 + {{k}^{2}} - k(\alpha + \beta )}},$

где l – расстояние, пройденное материальной точкой вдоль оси X.

Как и следовало ожидать, при α = β = 0 (случай идеальных связей) полная работа равна нулю.

В отличие от уравнений Лагранжа 1-го рода результаты (3.5)–(3.8) позволяют осуществлять многокритериальную оптимизацию [11, 12] по показателям: величина управляющих сил R_x, R_y; ускорение точки a_x, a_y, a; уровень тепловых потерь в приводах; полная работа управляющих сил и др. Это возможно за счет целенаправленного варьирования параметров α и β.

На рис. 2, 3 представлены некоторые зависимости показателей движения.

Рис. 2.

Зависимости реакций R_x (а), R_y (б) от α: 1 – β=2, 2 – β = 0, 3 – β = –2

Рис. 3.

Работа реакций связей (а) и тепловые потери в двигателе (б): 1 – β = 2, 2 – β = 0, 3 – β = –2

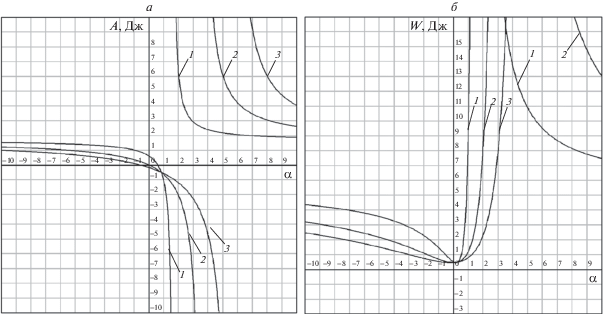
Анализ графиков подтверждает, что при α = β = 0 все анализируемые характеристики движения совпадают с характеристиками, соответствующими идеальным связям, а дополнительные возможности управления описываемой системой обеспечивают введенные “квазиидеальные” связи. Геометрический смысл “квазиидеальных” связей можно установить из условия того, что, как и для идеальных связей, равнодействующая активных сил и реакций связей F коллинеарна прямой, задаваемой уравнением связи (3.1).

Полученные результаты позволяют также определять необходимые оптимальные управляющие воздействия для обеспечения экстремума комплексного критерия качества:

(3.9)

$I = I({{R}_{x}},{{R}_{y}},a,{{a}_{x}},{{a}_{y}},W,A).$

Такая возможность обусловлена зависимостью всех показателей, входящих в (3.9) от элементов α, β матрицы управляющих воздействий.

На графиках рис. 4 представлена зависимость комплексного показателя от элемента α матрицы управляющих воздействий при β = –2, 0 ,2:

(3.10)

$I = \left| A \right| + \chi W,$

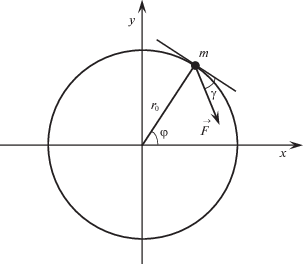
где χ – весовой коэффициент, в расчетах χ = 1.

Рис. 4.

Комплексный показатель I: 1 – β = 2, 2 – β = 0, 3 – β = –2

3.2. Движение материальной точки по окружности. Рассматривается задача формирования управляющих воздействий R_r, R_φ (рис. 5), которые действуют на механическую систему, моделируемую материальной точкой массы m с программным движением по окружности радиуса r₀. На материальную точку действует внешняя активная сила $\vec {F}$, направленная под углом γ к касательной в каждой точке траектории движения.

Рис. 5.

Движение материальной точки по окружности

В полярной системе координат r, φ дифференциальные уравнения движения и уравнение связи имеют вид

(3.11)

$\left\{ \begin{gathered} m\ddot {r} - mr{{{\dot {\varphi }}}^{2}} = - F\sin \gamma + {{R}_{r}}, \hfill \\ m{{r}^{2}}\ddot {\varphi } + 2m\dot {r}\dot {\varphi } = - Fr\cos \gamma + {{R}_{\varphi }}, \hfill \\ f(r,\varphi ) = r - {{r}_{0}} = 0. \hfill \\ \end{gathered} \right.$

Как и в предыдущем случае, матрица ||a_jk|| задается в форме (3.4). Тогда для реакций связи имеют место уравнения

(3.12)

${{R}_{r}} = \frac{\lambda }{{1 - \alpha \beta }};\quad {{R}_{\varphi }} = - \frac{{\beta \lambda }}{{1 - \alpha \beta }}.$

Следует иметь в виду, что в рассматриваемой задаче α, β – размерные коэффициенты: [α] = м^–1; [β] = м.

Дифференциальное уравнение, описывающее движение точки по окружности, имеет вид уравнения Риккати с постоянной правой частью [13]:

(3.13)

$\frac{{d\omega }}{{dt}}\; - \;A{{\omega }^{2}}\; = \;B,$

где

(3.14)

$\omega = \frac{{d\varphi }}{{dt}},\quad А = \frac{\beta }{{{{r}_{0}}}},\quad B = \frac{{F\sin \gamma }}{{m{{r}_{0}}^{2}}}\beta + \frac{{F\cos \gamma }}{{m{{r}_{0}}}}.$

В зависимости от знака величины B/A его решение может быть записано в одном из следующих четырех видов:

1) при B/A > 0

(3.15)

$\omega = \sqrt {\frac{B}{A}} {\text{tg}}(\sqrt {AB} \,t + C),$

2) при B/A = 0 (B = 0)

(3.16)

$\omega = - \frac{1}{{At + C}},$

3) при B/A < 0

(3.17)

$\omega = \sqrt { - \frac{B}{A}} \frac{{1 - C{{e}^{{2\sqrt { - ABt} }}}}}{{1 + C{{e}^{{2\sqrt { - ABt} }}}}} = - \sqrt { - \frac{B}{A}} \,{\text{th}}(\sqrt { - AB} \,t + C),$

4) при A = 0 (специальный случай)

$\frac{{d\omega }}{{dt}} = B,\quad \omega = Bt + C,\quad \varphi = B\frac{{{{t}^{2}}}}{2} + Ct + {{C}_{1}}.$

Во всех случаях С, С₁ – произвольные постоянные.

В случае 1) ω за конечное время “уходит на бесконечность”, следовательно, имеет место так называемый “режим с обострением”. Для такого режима необходима “подкачка энергии” в систему, очевидно, она осуществляется силами реакций дополнительных “квазиидеальных” связей. В случае 3) угловая скорость ω по формуле (3.15) при $t \to \infty $ стремится к постоянному значению, как это следует из соответствующего свойства гиперболического тангенса.

Графики полученных решений представлены на рис. 6. Они построены для следующих значений параметров системы: m = 1, F = 2, r₀ = 2, γ = π/4. Все зависимости построены для C = C₁ = 0, что означает ω(0) = 0, φ(0) = 0 (кроме случая 2)).

Рис. 6.

Зависимость скорости изменения угла φ от времени ω(t): 1 – β = –1, 2 – β = 0, 3 – β = 1, 4 – β = 2, 5 – β = 3

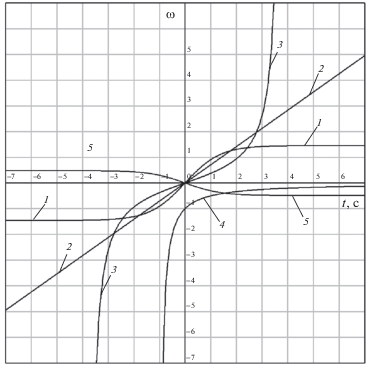
Параметры, определяющие выбор случая из числа приведенных выше, даны в таблице 1.

Таблица 1.

Параметры, определяющие вид решения уравнения Риккати (3.13)

β	A = β/r₀	B = (1 – A)/$\sqrt 2 $	B/A	Случай
–1	–0.5	1.5/$\sqrt 2 $ ≈ 1.06	–2.18	3
0	0	1/$\sqrt 2 $ ≈ 0.7	–	4
1	0.5	0.5/$\sqrt 2 $ ≈ 0.35	0.7	1
2	1	0	0	2
3	1.5	–0.5/$\sqrt 2 $ ≈ –0.35	–0.236	3

Зная решение уравнения (3.11) из уравнений (3.9) с учетом (3.10) можно определить R_r и R_φ:

(3.18)

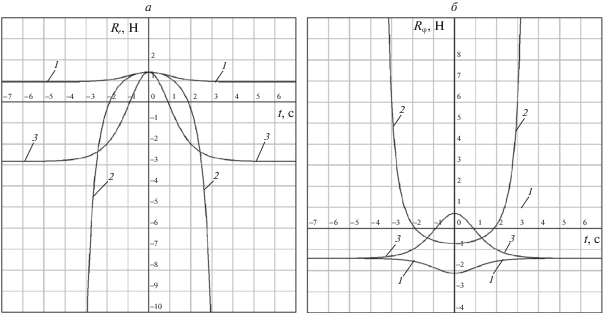
$\left\{ \begin{gathered} {{R}_{r}} = F\sin \gamma - m{{r}_{0}}{{{\dot {\varphi }}}^{2}}, \hfill \\ {{R}_{\varphi }} = m{{r}_{0}}\ddot {\varphi } - F\cos \gamma . \hfill \\ \end{gathered} \right.$

На графиках рис. 7 представлены зависимости R_r = R_r(β, t) и R_φ = R_φ(β, t).

Рис. 7.

Радиальные R_r (а) и трансверсальные R_φ (б) реакции: 1 – β = 3, 2 – β = 1, 3 – β = –1

Уровень тепловых потерь A за время t в приводных двигателях радиального и трансверсального перемещений определяется из выражений, аналогичных (3.7), и графически представлен на графиках (рис. 8) в зависимости от β.

Рис. 8.

Работа дополнительных реакций связей (а), тепловые потери в двигателе (б): 1 – β = 3, 2 – β = 1, 3 – β = –1

Особенность рассматриваемой задачи состоит в том, что на проведение многокритериальной оптимизации влияет только один элемент β из элементов матрицы управляющих воздействий ||a_jk||.

3.3. Плоское движение тела при наложении голономной связи. Рассматривается задача формирования управляющих воздействий на твердое тело, совершающее плоское движение под действием постоянной следящей силы $\vec {F}$, на одну из точек которого накладывается голономная связь (рис. 9):

(3.19)

${{y}_{A}} = H.$

Рис. 9.

Расчетная схема плоского движения твердого тела под действием следящей силы F: С – центр масс тела, ${{x}_{C}}$, ${{y}_{C}}$, $\varphi $ – обобщенные координаты, NL – отрезок прямой, являющейся голономной (геометрической) связью, накладываемой на движение точки A твердого тела

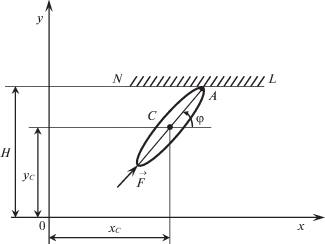
Положение твердого тела описывается координатами центра масс ${{x}_{C}}$, ${{y}_{C}}$ и углом φ, образованным отрезком CA с горизонтальной осью OX.

В обобщенных координатах ${{x}_{C}}$, ${{y}_{C}}$, $\varphi $ уравнение связи имеет вид

(3.20)

$f\left( {{{x}_{C}},{{y}_{C}},\varphi } \right) = {{y}_{C}} + l\sin \varphi = 0,$

где l – длина отрезка CA.

Как и в предыдущих примерах, при линейном преобразовании реакций связей (1.2) уравнения (2.1) имеют вид

(3.21)

$\left\{ \begin{gathered} {{R}_{1}} + \alpha {{R}_{2}} = \lambda \frac{{\partial f}}{{\partial {{x}_{C}}}} = 0, \hfill \\ \beta {{R}_{1}} + {{R}_{2}} = \lambda \frac{{\partial f}}{{\partial {{y}_{C}}}} = \lambda , \hfill \\ {{R}_{3}} = \lambda \frac{{\partial f}}{{\partial \varphi }} = \lambda l\cos \varphi . \hfill \\ \end{gathered} \right.$

Тогда уравнения движения рассматриваемой механической системы можно представить в форме

(3.22)

$\left\{ \begin{gathered} M{{{\ddot {x}}}_{C}} = F\cos \varphi - \frac{{\alpha \lambda }}{{1 - \alpha \beta }}, \hfill \\ M{{{\ddot {y}}}_{C}} = F\sin \varphi - \frac{\lambda }{{1 - \alpha \beta }}, \hfill \\ J\ddot {\varphi } = \lambda l\cos \varphi . \hfill \\ \end{gathered} \right.$

Дифференциальные уравнения (3.22) дополняются дважды продифференцированными уравнениями связей

(3.23)

${{\ddot {y}}_{C}} + l\ddot {\varphi }\cos \varphi = l{{\dot {\varphi }}^{2}}\sin \varphi .$

Совместное решение (3.22) и (3.23) позволяет найти неопределенный множитель λ и получить дифференциальное уравнение относительно φ = φ(t):

(3.24)

$\left\{ \begin{gathered} \lambda = \frac{{\left( {1 - \alpha \beta } \right)J[l{{{\dot {\varphi }}}^{2}}M\cos \varphi \sin \varphi - F\sin \varphi ]}}{{J + M\left( {1 - \alpha \beta } \right){{l}^{2}}\cos \varphi \sin \varphi }}, \hfill \\ J\ddot {\varphi } = \frac{{\left( {1 - \alpha \beta } \right)J[Ml{{{\dot {\varphi }}}^{2}}\cos \varphi \sin \varphi - F\sin \varphi ]}}{{J + M\left( {1 - \alpha \beta } \right){{l}^{2}}\cos \varphi \sin \varphi }}. \hfill \\ \end{gathered} \right.$

Особенность второго уравнения (3.24) состоит в том, что оно позволяет исследовать устойчивость программного движения φ = 0. Действительно, соответствующее уравнение в вариациях имеет вид

(3.25)

$J\delta \ddot {\varphi } + \left( {1 - \alpha \beta } \right)Fl\delta \varphi = 0.$

Если связи идеальные (α = β = 0), то устойчивый режим обеспечивается только в случае “толкающего” режима воздействия внешней силы F на твердое тело (F > 0). Однако в случае учета управляющих “квазиидеальных” связей, таких, что

(3.26)

$1 - \alpha \beta < 0,$

и “тянущий” режим воздействия внешней силы F (F < 0) также оказывается устойчивым. Такая особенность является положительным фактором при проектировании движителей мобильных роботов, работающих в “тянущем” режиме [14], а использование понятия “квазиидеальных” связей служит удобным инструментом для исследования устойчивости движения.

Заключение. Предложено определение “квазиидеальных” связей, отличающихся от идеальных тем, что их реакциями являются “квазиобобщенные” силы, но виртуальная работа которых, так же, как и для реакций идеальных связей, равна нулю. Получены уравнения Лагранжа для механической системы с избыточными координатами и с дополнительными уравнениями голономных “квазиидеальных” связей. Рассмотренный метод составления уравнений движения представляет дополнительные возможности для построения оптимального программного движения по критерию, состоящего из различных показателей. Применение “квазиидеальных” связей в системе управления расширяет возможности обеспечения устойчивости движения механических систем.

Список литературы

Маркеев А.П. Теоретическая механика. Москва–Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2007. 592 с.
Голубев Ю.Ф. Основы теоретической механики. М.: Изд-во МГУ, 2000. 720 с.
Добронравов В.В. Основы аналитической механики. М.: Выс. шк., 1976. 263 с.
Бёген А. Теоретическое исследование гироскопических компасов Аншютца и Сперри: Диссертация защищена в ноябре 1922 г. перед Факультетом наук в Париже. Париж, 1922.
Козлов В.В. Динамика систем с сервосвязями. I // Нелинейная динамика. 2015. Т. 11. № 2. С. 353–376.
Козлов В.В. Динамика систем с сервосвязями. II // Нелинейная динамика. 2015. Т. 11. № 3. С. 579–611.
Голубев Ю.Ф. Динамика систем с сервосвязями // Препринт № 19. М.: ИПМ им. М.В. Келдыша, 2000. 28 с.
Голубев Ю.Ф. Механические системы с сервосвязями // ПММ. 2001. Т. 65. Вып. 2. С. 211–224.
Вондрухов А.С., Голубев Ю.Ф. Оптимальные траектории в задаче о брахистохроне с разгоняющей силой // Изв. РАН. ТиСУ. 2015. № 4. С. 13–23.
Брискин Е.С., Калинин Я.В. Об энергетически эффективных алгоритмах движения шагающих машин с цикловыми движителями // Изв. РАН. ТиСУ. 2011. № 2. С. 170–176.
Малолетов А.В., Брискин Е.С. Оптимизация структуры, параметров и режимов движения шагающих машин со сдвоенными движителями: монография. Волгоград: ВолгГТУ, 2015. 174 с.
Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями: учеб. пособие для вузов. М.: Дрофа, 2006. 175 с.
Степанов В.В. Курс дифференциальных уравнений. Изд. 11-е. испр. М.: Изд-во ДКИ, 2016. 512 с.
Брискин Е.С., Артемьев К.С., Вершинина И.П., Малолетов А.В. Об устойчивости плоского движения мобильных роботов // Изв. Волгоградск. гос. тех. ун-та. 2020. № 9 (244). С. 11–16.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал