Известия РАН. Теория и системы управления, 2021, № 6, стр. 24-34
Идентификация нестационарных аэродинамических характеристик самолета по полетным данным
В. Н. Овчаренко a, *, Б. К. Поплавский b
a МАИ (национальный исследовательский ун-т)
Москва, Россия
b ЛИИ, МАИ
МО, г. Жуковский, Россия
* E-mail: owcharenko.v@yandex.ru
Поступила в редакцию 14.01.2021
После доработки 23.07.2021
Принята к публикации 26.07.2021
Аннотация
Рассматривается проблема описания нестационарных аэродинамических коэффициентов самолета. Предложен подход, основанный на параметризации и последующей идентификации аэродинамических переходных функций частотно-временным методом. Эффективность подхода показана на примере идентификации коэффициента подъемной силы ближнемагистрального самолета по полетным данным.
Введение. В эксплуатационных диапазонах изменения кинематических переменных аэродинамические силы и моменты, действующие на ЛА, определяются мгновенными значениями аэродинамических углов, угловых скоростей и положением аэродинамических органов управления. Эта зависимость аэродинамических характеристик может выражаться линейными или нелинейными функциями от переменных движения.
При энергичном маневрировании или при интенсивных внешних воздействиях (например, при попадании в сильный порыв ветра в полете в неблагоприятных погодных условиях) условия установившегося полета нарушаются и значения кинематических переменных могут выйти за пределы допустимых эксплуатационных ограничений. На больших углах атаки или на больших угловых скоростях возникают нелинейные аэродинамические эффекты, обусловленные отрывом набегающего потока от несущих поверхностей и разрушением системы вихрей. Любой из этих случаев приводит к нестационарным аэродинамическим нагрузкам [1]. Поэтому исследование вопросов безопасности полета, отработка навыков пилотирования в этих условиях приобретают чрезвычайную важность. Эти факторы приводят к необходимости разработки адекватных математических моделей аэродинамических характеристик, которые можно было бы применить как при решении задач динамики полета, так и в программном обеспечении пилотажных стендов и тренажеров.
Можно выделить два основных подхода к построению математических моделей для моделирования нестационарных аэродинамических характеристик самолетов.
Первый подход (в хронологическом порядке) был предложен в работе [2] и основан на использовании аэродинамических переходных функций. В дальнейшем этот подход получил развитие в публикациях [3, 4]. Неопределенность в задании аэродинамических переходных функций для конкретного самолета на заданном маневре составляет основную трудность применения этого подхода.
Второй подход предложен в [5, 6] и основан на знании координаты точки отрыва потока и разрушении вихревой системы на аэродинамическом профиле, которая в летном эксперименте не наблюдается. Применительно к нестационарным аэродинамическим характеристикам самолета этот подход рассмотрен в [7, 8]. По существу в этом случае самолет отождествляется с некоторым аэродинамическим профилем с эквивалентными аэродинамическими характеристиками.
В настоящее время получил развитие метод искусственных нейронных сетей для моделирования динамических эффектов, обусловленных отрывом и разрушением вихрей [9]. В этом случае понятия аэродинамических переходных функций и точки отрыва потока не применяются. Кроме того, рассматриваются и другие подходы к описанию динамики самолета на больших углах атаки [10].
В предлагаемой статье аэродинамические переходные функции аппроксимируются линейным дифференциальным уравнением первого порядка и полиномиальным входным сигналом по углу атаки и угловой скорости тангажа с неизвестными коэффициентами. Значения этих коэффициентов определяются в процессе решения задачи идентификации по полетным данным, полученным в натурном летном эксперименте.
1. Математическая модель нестационарных аэродинамических характеристик самолета. Рассмотрим математическую модель только коэффициента подъемной силы летательного аппарата в целом в условиях нестационарного обтекания. Пусть выполнены следующие предположения:
• аэродинамические характеристики самолета в установившемся движении известны с высокой точностью;
• на интервале обработки полетных данных конфигурация самолета остается постоянной;
• аппроксимация нестационарных аэродинамических коэффициентов зависит от постоянных параметров, значения которых можно уточнить по полетным данным;
• для описания нестационарных аэродинамических коэффициентов можно применить метод аэродинамических переходных функций [3].
Пусть зависимость коэффициента подъемной силы самолета ${{c}_{y}}$ от параметров полета (угла атаки α, числа M, угловой скорости тангажа ${{\omega }_{z}}$) и параметров конфигурации на неустановившемся режиме полета может быть представлена в виде
В силу предположения а) следует ожидать, что поправка $\Delta {{c}_{y}}(t,\alpha ,M,{{\delta }_{{{\text{конф}}}}};\dot {\alpha },{{\dot {\omega }}_{z}})$ мала по абсолютному значению и может быть представлена в виде
Поправку $\Delta {{c}_{{y\infty }}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ удобно представить в виде суммы некоторых функций от наиболее значимых переменных с неизвестными коэффициентами:
(1.1)
$\Delta {{c}_{{y\infty }}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}}) = \sum\limits_{i = 1}^{{{N}_{g}}} \,{{c}_{i}}{{g}_{i}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}}),$Для определения поправки $\Delta {{c}_{{y\;{\text{дин}}}}}(t,\dot {\alpha },{{\dot {\omega }}_{z}})$ применим метод аэродинамических переходных функций. Рассмотрим $\Delta {{c}_{{y\,{\text{дин}}}}}$ вида
(1.2)
$\begin{gathered} \Delta {{c}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },{{{\dot {\omega }}}_{z}}) = \frac{{{{b}_{a}}}}{V}\int\limits_0^t \,{{h}_{\alpha }}(t - \tau ;\alpha (\tau ),{{\omega }_{z}}(\tau ))\frac{{d\alpha }}{{d\tau }}d\tau + \\ + \frac{{{{b}_{a}}}}{V}\int\limits_0^t \,{{h}_{{{{\omega }_{z}}}}}(t - \tau ;\alpha (\tau ),{{\omega }_{z}}(\tau ))\frac{{d{{\omega }_{z}}}}{{d\tau }}d\tau , \\ \end{gathered} $Выражение (1.2) в уравнения динамики продольного движения самолета впервые введено в работе [2] и является результатом эвристических рассуждений о структуре аэродинамических коэффициентов как функционалов от угла атаки $\alpha $ и угловой скорости тангажа ${{\omega }_{z}}$. Однако ни из теории нестационарного обтекания, ни из аэродинамического эксперимента не ясно как задавать аэродинамические переходные функции в аналитическом виде на конкретном маневре самолета. Поэтому для выявления вида аэродинамических переходных функций и накопления статистической информации необходимо идентифицировать ${{h}_{\alpha }},{{h}_{{{{\omega }_{z}}}}}$ вместе с другими аэродинамическими поправками на различных тестовых маневрах в натурном эксперименте. В такой постановке задача идентификации нестационарных аэродинамических характеристик остается все еще сложной. Однако, учитывая достаточно общий характер структуры уравнения (1.2), заменим его выражением
(1.3)
$\Delta {{c}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },{{\dot {\omega }}_{z}}) = \frac{{{{b}_{a}}}}{V}\int\limits_0^t \,{{h}_{\alpha }}(t - \tau ;\alpha (\tau ))\frac{{d\alpha }}{{d\tau }}d\tau + \frac{{{{b}_{a}}}}{V}\int\limits_0^t {{h}_{{{{\omega }_{z}}}}}(t - \tau ;{{\omega }_{z}}(\tau ))\frac{{d{{\omega }_{z}}}}{{d\tau }}d\tau .$Интегралы в (1.3) имеют одинаковую структуру и могут быть изучены как один интеграл с переменным верхним пределом
где $u(\tau ) = (\alpha (\tau )\;{\text{или}}\;{{\omega }_{z}}(\tau ))$.Продифференцируем $\Delta C(t)$ по t, получим
(1.5)
$\frac{d}{{dt}}\Delta C(t) = \int\limits_0^t \,\frac{{\partial h(t - \tau ;u(\tau ))}}{{\partial t}}\dot {u}(\tau )d\tau + h(0;u(t))\frac{{du}}{{dt}}.$Выберем переходную функцию такой, что
(1.6)
$\frac{{\partial h(t - \tau ;u(\tau ))}}{{\partial t}} = ah(t - \tau ;u(\tau )),\quad \tau \leqslant t,$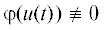 на интервале наблюдений. По условиям устойчивости решений уравнения (1.7) рассматриваются только отрицательные значения параметра a < 0.
на интервале наблюдений. По условиям устойчивости решений уравнения (1.7) рассматриваются только отрицательные значения параметра a < 0.
Решая уравнение (1.7) с нулевым начальным условием и входным сигналом $\phi (u(\tau ))\dot {u}(\tau )$, получим
Функция $\varphi (u(\tau ))$ является неизвестной. Предположим, что на интервале $[0,T]$ функция $\varphi (u(t))$ допускает аппроксимацию ее полиномом по $u(t)$ с неизвестными коэффициентами:
где $K_{m}^{{(u)}}$ – неизвестные коэффициенты полинома; M – наивысшая степень полинома, задается исследователем в процессе решения задачи идентификации.Подстановка функции $\varphi (u(t))$ в (1.8) приводит к выражению
(1.9)
$\Delta C(t) = \sum\limits_{m = 0}^M \,K_{m}^{{(u)}}\int\limits_0^t \,{{e}^{{a(t - \tau )}}}{{u}^{m}}(\tau )\dot {u}(\tau )d\tau .$Вычислим интеграл в (1.9) по частям, получим
(1.10)
$\Delta C(t) = \sum\limits_{m = 0}^M \frac{{K_{m}^{{(u)}}}}{{m + 1}}[{{u}^{{m + 1}}}(t) - {{u}^{{m + 1}}}(0){{e}^{{at}}}] + a\Delta C{\text{*}}(t),$В отличие от (1.9) выражение (1.10) не содержит производной процесса $u(t)$, которая либо не наблюдается в натурном эксперименте, либо вычисляется с большими погрешностями. Поэтому выражение (1.10) является предпочтительным для получения различных расчетных соотношений.
Выполняя в (1.10) замену переменной $u(t)$ на $\alpha (t)$ и ${{\omega }_{z}}(t)$, получим систему выражений, описывающих динамические поправки (1.2) коэффициента аэродинамической подъемной силы:
(1.11)
$\begin{gathered} \Delta {{c}_{{y{\text{дин}}}}}(t,\dot {\alpha },\mathop {\dot {\omega }}\nolimits_z ) = \frac{{{{b}_{a}}}}{V}\left[ {\Delta {{c}_{{y1}}}(t,\dot {\alpha }) + \Delta {{c}_{{y2}}}(t,{{\omega }_{z}})} \right]; \\ \Delta {{c}_{{y1}}}(t,\dot {\alpha }) = \sum\limits_{m = 0}^{{{M}_{\alpha }}} \frac{{K_{m}^{{(\alpha )}}}}{{m + 1}}[{{\alpha }^{{m + 1}}}(t) - {{\alpha }^{{m + 1}}}(0){{e}^{{{{a}_{\alpha }}t}}}] + {{a}_{\alpha }}\Delta c_{{y1}}^{ * }(t); \\ \Delta {{c}_{{y2}}}(t,{{\omega }_{z}}) = \sum\limits_{m = 0}^{{{M}_{\omega }}} \frac{{K_{m}^{{(\omega )}}}}{{m + 1}}[\omega _{z}^{{m + 1}}(t) - \omega _{z}^{{m + 1}}(0){{e}^{{{{a}_{\omega }}t}}}] + {{a}_{\omega }}\Delta c_{{y2}}^{ * }(t); \\ \frac{d}{{dt}}\Delta c_{{y1}}^{ * }(t) = {{a}_{\alpha }}\Delta c_{{y1}}^{ * }(t) + {{{v}}_{\alpha }}(t),\quad \Delta c_{{y1}}^{ * }(0) = 0; \\ \frac{d}{{dt}}\Delta c_{{y2}}^{ * }(t) = {{a}_{\omega }}\Delta c_{{y2}}^{ * }(t) + {{{v}}_{\omega }}(t),_{4}^{{}}\Delta c_{{y2}}^{ * }(0) = 0, \\ \end{gathered} $Совокупность выражений (1.1) и (1.11) образует замкнутую систему уравнений и определяет все поправки коэффициента аэродинамической подъемной силы на произвольном неустановившемся режиме полета. Уравнения зависят только от наблюдаемых в полете переменных и не содержат скрытых переменных. Ниже на примере обработки тестовых полетов магистрального самолета показано, что математическая модель (1.11) справедлива как в стационарных, так и в нестационарных условиях полета.
Для определения неизвестных параметров в выражениях (1.1) и (1.11) по полетным данным применим частотно-временной метод [8] (см. Приложение). Вычислим на множестве частот $\Omega $ финитные преобразования Фурье FT (с учетом обозначений, указанных ниже) всех составляющих поправок коэффициента аэродинамической подъемной силы:
Таким образом, вектор неизвестных параметров $\theta $ имеет вид
Множество допустимых значений параметров определяется условиями устойчивости решений дифференциальных уравнений ${{a}_{\alpha }} < 0,\;{\kern 1pt} {{a}_{\omega }} < 0$, остальные параметры могут принимать любые значения. В зависимости от полетной конфигурации некоторые параметры могут отсутствовать.
Сформируем невязку и критерий метода наименьших квадратов (МНК) в частотной области
Задача идентификации неизвестных параметров сводится к задаче минимизации критерия МНК:
которая решается методами нелинейного математического программирования (например, программой fmincon математического пакета MATLAB).На множестве частот $\Omega $ финитное преобразование Фурье постоянных, которые могут входить в составляющие коэффициента подъемной силы в установившемся движении самолета, равны нулю (см. ПРИЛОЖЕНИЕ). Поэтому для полной оценки всех постоянных дополнительно необходимо решить задачу идентификации во временной области на уже вычисленных оценках поправок $\Delta {{\hat {c}}_{{y\infty }}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ и $\Delta {{\hat {c}}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },{{\dot {\omega }}_{z}})$.
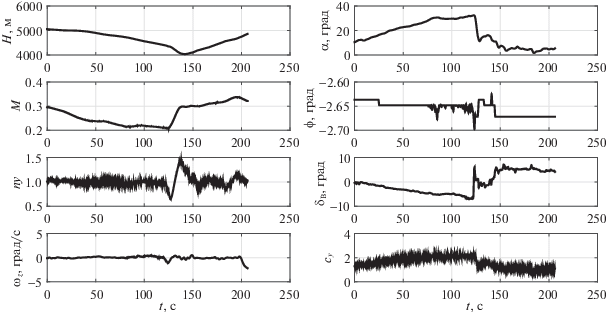
2. Идентификация коэффициента подъемной силы ближнемагистрального самолета. Рассмотрим идентификацию коэффициента подъемной силы ближнемагистрального самолета по полетным данным. Тестовые полеты проводились по программе исследований устойчивости и управляемости самолета в процессе его выхода на большие углы атаки в различных полетных конфигурациях. Тестовый маневр заключался в выводе самолета на большие углы атаки при сохранении балансировки по моменту тангажа, т.е. ${{\dot {\omega }}_{z}} \sim 0$. Балансировка нарушалась только на коротких временных интервалах, когда самолет возвращался к условиям полета на малых углах атаки. Все тестовые маневры выполнялись на высотах примерно H = 5000 м и числах $M = 0.3 \cdots 0.4$. На рис. 1 показан пример полетных данных во взлетной конфигурации ${{\delta }_{{{\text{пр}}}}}$ = 24°; ${{\delta }_{{{\text{закр}}}}}$ = 16°. Далее рассмотрим определение математической модели только динамической поправки $\Delta {{c}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },{{\dot {\omega }}_{z}})$. Измерялись все переменные движения и параметры полетной конфигурации. Полетный коэффициент подъемной силы $c_{y}^{ * }(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ (без учета тяги двигателя) вычислялся по формуле
(2.1)
$c_{y}^{ * }(\alpha ,M,{{\delta }_{{{\text{конф}}}}}) = {{c}_{y}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}}) + {{c}_{P}}sin(\alpha + {{\varphi }_{P}}) = \frac{{mg{{n}_{y}}}}{{qS}},$Рис. 1.
Полетные данные во взлетной конфигурации ${{\delta }_{{{\text{пр}}}}}$ = 24°; ${{\delta }_{{{\text{закр}}}}}$ = 16° (${{\omega }_{z}}$ – угловая скорость тангажа; $\alpha $ – угол атаки; $\varphi $ – угол установки горизонтального оперения; ${{\delta }_{{\text{в}}}}$ – угол отклонения руля высоты)
Требуется по измеренным данным, полученным в тестовом полете, уточнить значение коэффициента подъемной силы в установившемся движении и идентифицировать составляющую $\Delta {{c}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },{{\dot {\omega }}_{z}})$, обусловленную нестационарными аэродинамическими эффектами.
Рассматривались следующие полетные конфигурации самолета: крейсерская, взлетная, заход на посадку, посадка. Поправку $\Delta {{c}_{{y\infty }}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ будем искать в виде
В процессе решения задачи идентификации были выбраны следующие порядки полиномов ${{M}_{\alpha }} = {{M}_{\omega }} = 4$; определялись оценки неизвестных параметров $({{c}_{1}}, \ldots ,{{c}_{4}},{{a}_{\alpha }},{{a}_{\omega }})$, коэффициентов полиномов $(K_{0}^{{(\alpha )}}, \ldots ,K_{4}^{{(\alpha )}};K_{0}^{{(\omega )}}, \ldots ,K_{4}^{{(\omega )}})$ и дополнительных параметров $(\Delta {{c}_{{y1}}}(T),\Delta {{c}_{{y2}}}(T))$; все углы и угловые скорости имеют размерности рад и рад/с соответственно.
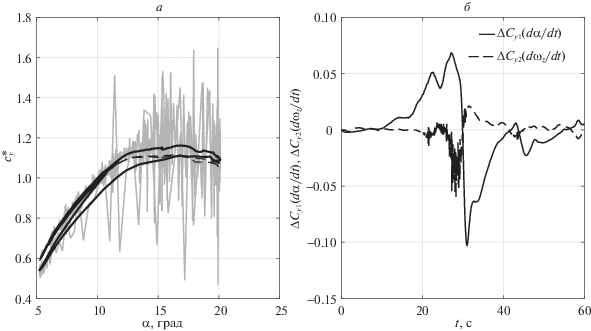
Результаты идентификации коэффициента подъемной силы самолета по полетным данным с учетом конфигурации, статических и динамических поправок показаны на рис. 2–6. На рис. 2, а–6, а помечены следующие данные: полетные данные – сплошная линия светлого оттенка, вычисленная по формуле (2.1); оценка коэффициента подъемной силы в установившемся движении с учетом поправки $\Delta {{\hat {c}}_{{y0}}} + \Delta {{\hat {c}}_{{y\infty }}}(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ – пунктирная линия; оценка коэффициента подъемной силы $\hat {c}_{y}^{*}(\alpha ,M,{{\delta }_{{{\text{конф}}}}})$ в неустановившемся движении – сплошная линия. На рис. 2, б–6, б показаны оценки динамических поправок: сплошная линия – динамическая поправка $\Delta {{\hat {c}}_{{y1}}}(t,\dot {\alpha })$; пунктирная линия – динамическая поправка $\Delta {{\hat {c}}_{{y2}}}(t,{{\dot {\omega }}_{z}})$.
Рис. 2.
Коэффициент подъемной силы (а) и динамические поправки (б) в установившемся полете на малых углах атаки (крейсерская конфигурация)
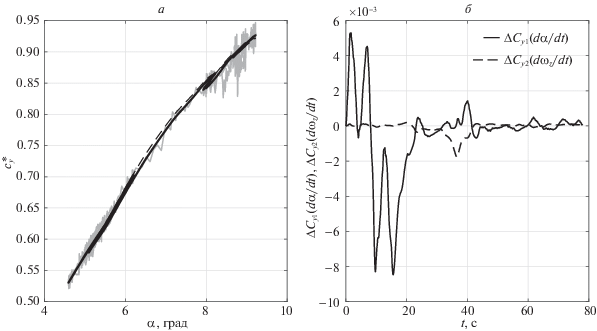
На рис. 2, а представлен коэффициент подъемной силы и его оценки в области малых углов атаки при безотрывном обтекании, полностью совпадающие с аэродинамическими продувками. На рис. 2, б даны оценки динамических поправок. Видно, что динамическая поправка $\Delta {{\hat {c}}_{{y2}}}(t,{{\dot {\omega }}_{z}})$ = 0, а поправка $\Delta {{\hat {c}}_{{y1}}}(t,\dot {\alpha })$ имеет порядок 10–3 и ее влиянием на оценку коэффициента подъемной силы можно пренебречь.
На рис. 3, а–6, а показаны коэффициент подъемной силы и его оценки в диапазоне изменения углов атаки $0 < \alpha \leqslant 35^\circ $ с учетом полетной конфигурации. Разность сплошной и штриховой линий на рис. 3, а–6, а указывает на влияние нестационарных аэродинамических эффектов на аэродинамические характеристики самолета. Возврат самолета на малые углы атаки происходит с потерей подъемной силы. Наблюдается аэродинамический гистерезис (рис. 3, а; 4, а; 6, а). На рис. 5, а показана аэродинамическая нестационарность в виде автоколебаний по коэффициенту подъемной силы при гармоническом изменении угла атаки: автоколебания возникают как на малых, так и на больших углах атаки.
Рис. 4.
Коэффициент подъемной силы (а) и динамические поправки (б), где взлет ${{\delta }_{{{\text{пр}}}}}$ = 24°; ${{\delta }_{{{\text{закр}}}}}$ = 16°
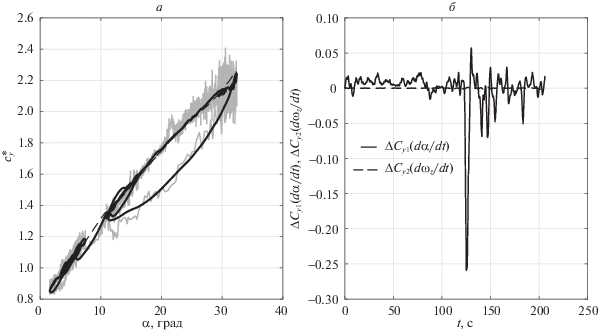
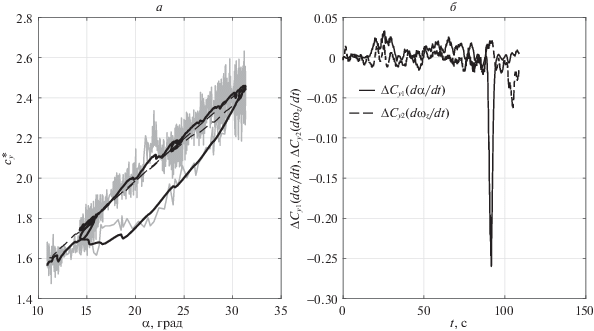
Рис. 5.
Коэффициент подъемной силы (а) и динамические поправки (б), где заход на посадку ${{\delta }_{{{\text{пр}}}}}$ = 24°; ${{\delta }_{{{\text{закр}}}}}$ = 25°
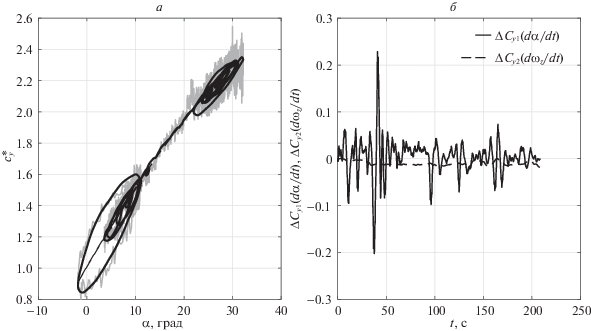
Соизмеримые динамические поправки, обусловленные $\dot {\alpha }$ и ${{\dot {\omega }}_{z}}$ приведены на рис. 3, б. На остальных рассмотренных тестовых режимах полета (см. рис. 4, б–6, б) динамические поправки, обусловленные ${{\dot {\omega }}_{z}}$, практически отсутствуют (т.е. на тестовом режиме самолет сбалансирован в продольном движении). Поэтому динамические поправки оценки коэффициента подъемной силы целиком определяются угловой скоростью угла атаки $\dot {\alpha }$.
В табл. 1 и 2 приведены оценки коэффициентов полиномов по $\alpha (t)$ и ${{\omega }_{z}}(t)$, упорядоченные по возрастанию степени полинома, и коэффициенты поправок, полученные на выбранных тестовых маневрах. Регуляризирущая добавка в критерии МНК имела вид ${{(0.1{{a}_{\alpha }})}^{2}} + {{(0.05{{a}_{\omega }})}^{2}}$.
Таблица 1.
Оценки коэффициентов полиномов
| n/m | Полетная конфигурация самолета | |||||||
|---|---|---|---|---|---|---|---|---|
| крейсерская | взлетная | заход на посадку | посадка | |||||
| $K_{m}^{{(\alpha )}}$ | $K_{m}^{{(\omega )}}$ | $K_{m}^{{(\alpha )}}$ | $K_{m}^{{(\omega )}}$ | $K_{m}^{{(\alpha )}}$ | $K_{m}^{{(\omega )}}$ | $K_{m}^{{(\alpha )}}$ | $K_{m}^{{(\omega )}}$ | |
| 0 | –50.25 | –84.32 | 207.2 | –1.09 | 453.67 | –123.25 | –127.7 | –35.4 |
| 1 | 297.5 | –43.23 | 125.8 | 1.77 | –245.6 | 1.84 | 680.4 | 1668 |
| 2 | 80.9 | –0.38 | 78.6 | –0.081 | –236.9 | 0.46 | –58.7 | 44.3 |
| 3 | 10.75 | –0.012 | 20.9 | –0.06 | –122.7 | –0.008 | –364.7 | 1.7 |
| 4 | –1.95 | 0.005 | –5.09 | 0 | –60.56 | –0.035 | –353.0 | 0.4 |
Таблица 2.
Оценки коэффициентов поправок
| Параметр | Полетная конфигурация самолета | |||
|---|---|---|---|---|
| крейсерская | взлетная | заход на посадку | посадка | |
| ${{c}_{1}}$ | 2.75 | 1.04 | 0.19 | –1.02 |
| ${{c}_{2}}$ | –5.24 | –1.21 | –1.18 | –0.47 |
| ${{c}_{3}}$ | –0.22 | –1.46 | –1.31 | –1.26 |
| ${{c}_{4}}$ | 0.77 | 13.14 | 7.37 | 7.1 |
| ${{a}_{\alpha }}$ | –0.20 | –4.64 | –8.77 | –2.22 |
| ${{a}_{\omega }}$ | –0.20 | –4.70 | –4.70 | –0.009 |
Коэффициенты первой строки табл. 1 соответствуют динамической поправке $\Delta {{c}_{{y\,{\text{дин}}}}}(t,\dot {\alpha },\mathop {\dot {\omega }}\nolimits_z )$, которая является откликом линейной динамической системы только на входные сигналы $\dot {\alpha }(t)$ и ${{\dot {\omega }}_{z}}(t)$ [2, 3]. Это частный случай описания нестационарных аэродинамических эффектов при безотрывном обтекании [6], соответсвующее выражение имеет вид
Заключение. Предложен новый подход к описанию математической модели нелинейных и нестационарных аэродинамических эффектов, обусловленных интенсивным изменением в полете угла атаки самолета и угловой скорости тангажа в продольном движении. Подход основан на применении аэродинамических переходных функций. Новизна подхода заключается в том, что структура аэродинамических переходных функций фиксируется и подбираются входные сигналы, нелинейные по углу атаки и угловой скорости тангажа. Получена замкнутая система уравнений, зависящая только от наблюдаемых в полете переменных. На примере обработки полетных данных магистрального самолета показано, что система уравнений приемлемо описывает как аэродинамический гистерезис, так и автоколебания по коэффициенту подъемной силы при гармоническом изменении угла атаки. Задача идентификации неизвестных параметров решалась частотно-временным методом.
Представленные численные результаты идентификации нестационарного аэродинамического коэффициента подъемной силы относятся только к рассмотренным данным натурного эксперимента и не могут быть обобщены на все полетные случаи.
Список литературы
Канышев А.В., Корсун О.Н., Овчаренко В.Н., Стуловский А.В. Идентификация аэродинамических коэффициентов продольного движения и оценка погрешностей бортовых измерений на закритических углах атаки. Изв. РАН. ТиСУ. 2018. № 3. С. 33–47.
Tobak M. On The use of the Indicial Function Concept in the Analysis of Unsteady Motions of Wings and Wing-tail Combinations // NACA. Report 1188. 1954.
Tobak M., Schiff L.B. On the Formulation of the Aerodynamic Characteristics in Aircraft Dynamics // NASA. TR R-456. Washington. 1976.
Klein V., Morelli E.A. Aircraft System Identification. Theory and Practice. Education Series. Hampton: AIAA. 2006. C. 499.
Гоман М.Г. Математическое описание аэродинамических сил и моментов на неустановившихся режимах обтекания с неединственной структурой // Тр. ЦАГИ. 1983. Вып. 2195. С. 14–27.
Аэродинамика, устойчивость и управляемость сверхзвуковых самолетов / Под ред. Г.С. Бюшгенса. М.: Наука. Физматлит, 1998.
Jategaonkar R.V. Flight Vehicle System Identification:A Time Domain Methodology. Arlington: AIAA, Inc., Reston., 2006. C. 410.
Овчаренко В.Н. Аэродинамические характеристики летательных аппаратов. Идентификация по полетным данным. М.: ЛЕНАНД, 2019. 236 с.
Игнатьев Д.И., Храбров А.Н. Использование искусственных нейронных сетей для моделирования динамических эффектов аэродинамических коэффициентов трансзвукового самолета // Уч. зап. ЦАГИ. 2011. Т. XLII. № 6. С. 84–91.
Кузьмин П.В., Мелешин Б.А., Шелюхин Ю.Ф., Шуховцов Д В. Инженерная модель нестационарных продольных аэродинамических характеристик на больших углах атаки // Уч. зап. ЦАГИ. 2015. Т. 46. № 4. С. 61–70.
Бахвалов Н.С. Численные методы. М.: Наука, 1973.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления