Известия РАН. Теория и системы управления, 2021, № 6, стр. 43-51

Введение. В современной научной литературе проблеме планирования уделяется большое внимание. При этом разнообразие рассматриваемых задач весьма велико [1–3]. Среди них, конечно, значатся традиционные приложения в планировании производства, где можно выделить, например, планирование для одного прибора и для технологических линий ((flow shop)-планирование) [4–6]. С этим базовым направлением на идейном уровне естественным образом переплетается планирование вычислений как в центрах коллективного пользования [7], так и в системах реального времени (СРВ) [8, 9]. В настоящей работе обсуждается последнее направление, а точнее, планирование вычислений в распределенных СРВ. Под планированием вычислений обычно понимают определение для каждой решаемой задачи из заданного множества временного интервала исполнения на выделенном для нее процессоре. При этом если на одном процессоре оказываются две или более задач, не связанных отношением предшествования, попутно возникает вопрос об очередности их выполнения, которая определяется наилучшим образом с точки зрения заданного критерия. Для систем управления и обработки информации реального времени характерна периодичность процессов управления и обработки. В результате при планировании дополнительно должно учитываться ограничение, вызванное периодичностью процессов и требующее учета производительности процессоров и пропускной способности каналов обмена на периоде. Оптимальное решение проблемы планирования может быть получено переборными алгоритмами, однако все они характеризуются экспоненциальной вычислительной сложностью, и в силу этого их применение в целом ряде приложений оказывается невозможным. По этой причине широкое распространение на практике получили субоптимальные алгоритмы.

Среди известных работ широко представлено направление, посвященное планированию в многоканальных системах обработки информации, отождествляемое с (flow shop)-планированием. При этом если в классической постановке рассматриваемая система представляет собой вычислительный конвейер с линейным графом информационных межпроцессорных связей, то в предыдущих наших работах этот граф – ациклический. По данной теме опубликовано значительное число работ, различающихся, конечно, прежде всего, особенностями предлагаемых алгоритмов, но также и видом критерия, в соответствии с которым формируется план. При этом наиболее часто используется минимум общего времени выполнения плана. Для систем реального времени могут применяться и другие характерные только для них критерии, например минимум потребляемой энергии или минимум джиттера (“дрожание” момента старта или завершения некоторой задачи от периода к периоду). Для многих систем реального времени этот параметр имеет важное значение, когда некоторые задачи системы должны быть “привязаны” к заданным моментам времени. Характерным примером может служить ситуация, когда организуется обмен между двумя системами реального времени, причем, по крайней мере, одна из этих систем является распределенной. Пусть дополнительно требуется, чтобы обмен происходил в пределах заданного и весьма ограниченного интервала времени. На практике одной из систем может быть, например, навигационный комплекс, а другой – потребитель навигационной информации.

Именно данной теме и посвящено основное содержание настоящей статьи, где проблема рассматривается в отношении распределенных (flow shop)-систем в отличие от работы [10], исследующей однопроцессорные системы. При этом в ее фокусе лежит подход, основанный на использовании так называемых разрешимых классов систем – РКС-алгоритм. Показывается, что базовая идея РКС-алгоритма, предложенного для (flow shop)-планирования с минимизацией общей длительности плана или максимального отклонения от заданных директивных сроков, оказывается эффективной и при минимизации джиттера. Далее в настоящей статье будут использованы термины (flow shop)-системы и (flow shop)-планирования, несмотря на то, что имеются в виду приложения, далекие от сферы автоматизированных производств.

1. Предварительные сведения. Опишем постановку задачи (flow shop)-планирования. Рассматривается распределенная вычислительная система, которая включает процессоры, имеющие индивидуальную память для хранения кода программ и обменивающиеся информацией через каналы передачи данных.

Предполагается, что множество задач разбито на независимые группы задач, связанных отношением предшествования (далее задания). В результате планированию подлежат n независимых равноприоритетных заданий $\tau = {\text{\{ }}{{\tau }_{{\text{j}}}}{\text{|}}\;j = \overline {1,n} {\text{\} }}$, обрабатывающих входные данные, которые поступают с периодом T. Каждое j-е задание состоит из m задач ${{\tau }_{{j,i}}}$ длительностью ${{e}_{{j,i}}}$ $i = \overline {1,m} $. Также предполагается, что значения длительностей известно точно. С практической точки зрения это означает, что используются, например, средние значения или верхние границы этих длительностей. Все применяемые процессоры из множества P являются универсальными и имеют одинаковую производительность. Произведенное назначение заданий соответствует случаю (flow shop)-системы. Согласно данной работе, все графы заданий одинаковы и имеется n изоморфизмов ${{\varphi }_{j}}{\text{:}}{{G}_{j}}({{S}_{j}},{{T}_{j}}{\text{)}} \to F(Q,P)\,j = \overline {1,n} $, где ${{G}_{j}}({{S}_{j}},{{T}_{j}}{\text{)}}$ – граф межзадачных связей j-го задания, S_j – множество ребер, T_j – множество вершин (задач), $F(Q,P)$ – граф межпроцессорных связей, $Q$ – множество ребер, $P$ – множество процессоров.

Все введенные графы являются направленными, ациклическими, содержащими в общем случае не один путь между любыми выделенными вершинами. Графы характеризуются выделенным подмножеством входных вершин и одной выходной вершиной. Далее для рассматриваемой системы будем использовать обозначение $C{\text{(}}F,\tau {\text{)}}$.

Предполагается, что при назначении задач на процессоры было выполнено условие, гарантирующее независимость обработки разных порций входной информации. В этом случае исключается образование очередей на процессоры из-за незавершенности обработки предыдущей порции входной информации. Охарактеризуем коротко исследуемый ниже алгоритм (flow shop)-планирования – РКС-алгоритм.

Этот алгоритм основан на использовании понятия разрешимого класса системы, обсуждаемого ниже. Важным следствием принадлежности системы к разрешимому классу является существование для нее оптимального алгоритма (flow shop)-планирования линейной сложности [11]. В рассматриваемой системе каждый входной процессор ${{P}_{i}}$ связан с выходным процессором ${{P}_{o}}$ хотя бы одним вычислительным путем (последовательностью процессоров) $p = {{P}_{i}},\,{{P}_{k}},...,{{P}_{o}}$. Назовем $E({{p}_{j}})$ временем выполнения вычислительного пути $p$ на j-м задании. Определим его как сумму времен ${{e}_{{j,i}}}$ выполнения задач j-го задания процессорами, принадлежащими этому пути. Назовем вычислительный путь $p_{j}^{*}$ критическим для  j-го задания, если время его выполнения на j-м задании является максимальным среди всех остальных путей системы. Очевидно, что для разных заданий, решаемых в одной и той же системе, критические вычислительные пути могут быть различными.

С использованием нумерации процессоров вдоль пути p_j выражение для $E({{p}_{j}})$ можно записать в виде

где m* – число процессоров, принадлежащих пути p_j.

Для определения разрешимых классов предварительно введем на множестве процессоров отношение доминирования “>”.

Определение 1. Процессор ${{P}_{q}}$ доминирует над процессором ${{P}_{r}}$ (${{P}_{q}} > {{P}_{r}}$), если $\mathop {\min }\limits_j {{e}_{{j,q}}} \geqslant \mathop {\max }\limits_j {{e}_{{j,r}}}$, $j = \overline {1,n} $.

Общее свойство рассматриваемых далее разрешимых классов распределенных систем состоит в следующем: для любого задания, реализуемого в системе, критический путь единственен и проходит по одним и тем же процессорам ${{P}_{1}},{{P}_{2}},...,{{P}_{{m*}}}$. Теперь приведем определяющие свойства для каждого из разрешимых классов.

Определение 2 (класс 1). Множество процессоров критического пути представляет собой последовательность ${{P}_{1}} > {{P}_{2}} > ... > {{P}_{{m*}}}$, убывающую по отношению доминирования.

Определение 3 (класс 2). Множество процессоров критического пути представляет собой последовательность ${{P}_{1}} < {{P}_{2}} < ... < {{P}_{{m*}}}$, возрастающую по отношению доминирования.

Определение 4 (класс 3). Множество процессоров критического пути представляет собой пару соединенных последовательностей

первая из которых возрастает, а вторая убывает по отношению доминирования (h* – номер процессора стыковки двух последовательностей).

Определение 5 (класс 4). Множество процессоров критического пути представляют собой пару соединенных последовательностей

первая из которых убывает, а вторая возрастает по отношению доминирования.

Класс 4 не является в полном смысле разрешимым, поскольку для него неизвестно оптимального алгоритма планирования линейной сложности, а известный алгоритм субоптимален.

Известно, что длительности плана $\pi $ для разрешимых классов 1–3 определяются выражениями (1.1)–(1.3) соответственно:

где задачи, длительности которых отмечены звездочками, решаются процессорами критического пути, n – число заданий, m* – число процессоров в критическом пути, h* – номер процессора стыковки. Эти выражения можно получить, если записать для некоторого процессора критического пути сумму времен работы и простоя. Для класса 1 таковым процессором будет первый от входа, для класса 2 – последний, для класса 3 – процессор стыковки.

Для класса 4 в рамках рассматриваемого подхода известно лишь выражение для верхней границы длительности плана:

По отношению к традиционным предлагаемое ниже решение отличается особенностями, заключающимися не только в применении нового критерия, но также и в оперировании фактически интервальными длительностями задач, а именно задача ${{\tau }_{{j,i}}}$ имеет длительность ${{\tilde {e}}_{{j,i}}} = [{{\underline e }_{{j,i}}},{{\bar {e}}_{{j,i}}}]$. При этом величину $\Delta ({{\tau }_{{j,i}}}) = {{\bar {e}}_{{j,i}}} - {{\underline e }_{{j,i}}}$ будем называть джиттером задачи ${{\tau }_{{j,i}}}$.

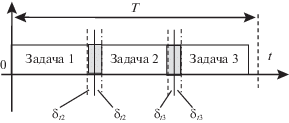
Говорят, что j-я задача привязана к моменту времени t_j с точностью ${{\delta }_{j}}$, если время начала решения этой задачи лежит в интервале $[{{t}_{j}} - {{\delta }_{j}},\;{{t}_{j}} + {{\delta }_{j}}]$. Это понятие поясняется на рис. 1, где представлена временная диаграмма исполнения трех задач ${{\tau }_{1}},{\kern 1pt} {{\tau }_{2}},{\kern 1pt} {{\tau }_{3}}$. Задача ${{\tau }_{1}}$, стоящая первой в цикле обработки, имеет точную временную привязку (${{\delta }_{1}}$= 0) в рамках данной постановки проблемы. Однако уже привязка второй задачи ${{\tau }_{2}}$ характеризуется погрешностью ${{\delta }_{2}}$, равной неопределенности длительности выполнения первой задачи ${{\delta }_{2}} = \Delta ({{\tau }_{1}}) \ne 0$, привязка третьей задачи характеризуется погрешностью ${{\delta }_{3}}$, равной сумме неопределенностей длительностей выполнения первой и второй задач ${{\delta }_{3}} = \Delta ({{\tau }_{1}}) + \Delta ({{\tau }_{2}}) \ne 0$, и т.д.

Приведенные соображения требуют небольшой корректировки традиционного определения отношения доминирования и, как следствие, содержания, но не определений разрешимых классов.

Определение 6. Процессор P_q доминирует над процессором P_r (${{P}_{q}} > {{P}_{r}}$), если $\mathop {\min }\limits_j {{\underline e }_{{j,q}}}$ ≥ ≥ $\mathop {\max }\limits_j {{\bar {e}}_{{j,r}}}$, $(j = \overline {1,n} )$.

Далее будем различать входной и выходной джиттеры задания. В первом случае имеется в виду неточность привязки начала задания, а во втором случае – неточность привязки его конца.

Обсудим выходной джиттер ${{\Delta }_{k}}(\pi )$ для момента окончания плана $\pi $. Запишем выражения для выходных джиттеров планов, представленных через джиттеры задач, в системах из разрешимых классов. Очевидно, что выражения для верхней и нижней границ длительностей планов, а следовательно, и выражение для джиттеров с точностью до обозначений будут совпадать с выражениями (1.1)–(1.4):

Последнее выражение в силу вышесказанного представляет оценку для джиттера плана системы из класса 4.

2. Алгоритмы планирования по критерию минимума среднего по заданиям джиттера в (flow shop)-системах из разрешимых классов. В настоящем разделе предлагаются оптимальные алгоритмы (flow shop)-планирования для определенных в предыдущем разделе разрешимых классов систем при использовании в качестве критерия минимума среднего по заданиям джиттера, характерного для систем реального времени. Подытожим вышесказанное компактной постановкой задачи.

Постановка задачи. Рассматривается распределенная вычислительная (flow shop)-система $C{\text{(}}F,\tau {\text{)}}$, состоящая из m универсальных одинаковых процессоров. Система исполняет n заданий, характеризующихся одинаковыми ациклическими графами предшествования. Требуется найти наилучший план вычислений по критерию минимума среднего по заданиям джиттера, т.е.

Утверждение 1. Минимальное значение среднего по заданиям выходного джиттера ${{\bar {\Delta }}_{1}}(\pi )$ для системы из класса 1 достигается в плане π, в котором задания упорядочены по неубыванию джиттера их первых задач критического пути, т.е.

Доказательство. Запишем с использованием (1.5) выражение для среднего по заданиям выходного джиттера ${{\bar {\Delta }}_{1}}(\pi )$ в случае системы из класса 1:

Поскольку цель заключается в поиске плана, минимизирующего полученное выражение, то второе слагаемое в скобках можно отбросить и перейти к минимизации выражения

Действительно, проанализируем отброшенную двойную сумму. Каждое k-е слагаемое ее внешней суммы представляет собой суммарный джиттер для всех задач, кроме первой (ее джиттер равен нулю), решаемых в k-м задании на критическом пути. Поскольку в сумме присутствует суммарный джиттер всех задач для каждого задания, значение двойной суммы не зависит от упорядоченности заданий, а значит, его можно исключить из рассматриваемого критерия.

Если далее в выражении (2.3) развернуть внутреннюю сумму и привести подобные члены, то приходим к выражению

В этом выражении суммируются почленные произведения двух числовых последовательностей $\{ n - k + 1\} $ и $\{ \Delta (\tau _{{k,1}}^{*})\} ,k = \overline {1,n} $, причем первая из них убывающая. Известно [12], что сумма (2.4) будет иметь минимум, если вторая последовательность будет неубывающей. Отсюда следует, что задания должны упорядочиваться по неубыванию джиттера первых задач критического пути.

Утверждение 2. Минимальное значение среднего по заданиям выходного джиттера ${{\bar {\Delta }}_{2}}(\pi )$ для системы из класса 2 достигается в плане π, для которого выполняется:

1) задания упорядочены по неубыванию джиттера последних задач критического пути, т.е.

2) первое задание плана $\pi $ удовлетворяет условию

Доказательство. Запишем с использованием (1.6) выражение для среднего по заданиям выходного джиттера в системах из класса 2:

Преобразуем первое слагаемое в этом выражении, учитывая, что его внутренняя сумма не зависит от k. Во втором слагаемом развернем внутреннюю сумму и приведем подобные члены. В результате получаем

Отсюда следует, что минимизация первого слагаемого определяется условием (2.6), а минимизация второго слагаемого (по аналогии с доказательством утверждения 1) – условием (2.5).

Утверждение 3. Минимальное значение среднего по заданиям выходного джиттера ${{\bar {\Delta }}_{3}}(\pi )$ для системы из класса 3 достигается в плане π, для которого выполняется:

1) задания упорядочены по неубыванию джиттера задач стыковки критического пути, т.е.

2) первое задание плана π удовлетворяет условию

Доказательство. Запишем с использованием (1.7) выражение для среднего по заданиям выходного джиттера в системах из класса 3:

Как и при анализе систем из класса 1, в этом выражении третье слагаемое в скобках может быть отброшено, как независящее от упорядоченности заданий. В результате можно перейти к минимизации функции:

Оставшиеся слагаемые можно преобразовать в соответствии с использованными в предыдущем утверждении приемами. В результате получаем

Отсюда следует, что минимизация первого слагаемого определяется условием (2.9), а минимизация второго слагаемого – условием (2.8).

Утверждение 4. Минимальное значение оценки ${{\hat {\bar {\Delta }}}_{4}}(\pi )$ среднего по заданиям выходного джиттера ${{\bar {\Delta }}_{4}}(\pi )$ для системы из класса 4 достигается в плане π, для которого выполняется:

1) задания упорядочены по неубыванию суммарного джиттера первых и последних задач критического пути, т.е.

2) первое задание плана π удовлетворяет условию

Доказательство. Запишем с использованием (1.8) выражение для оценки среднего по заданиям выходного джиттера в системах из класса 4:

Как и при анализе систем из класса 1, в этом выражении третье слагаемое может быть отброшено, как независящее от упорядоченности заданий. В результате можно перейти к минимизации функции:

Оставшиеся слагаемые можно преобразовать в соответствии с использованными ранее приемами. В результате получаем

Отсюда следует, что минимизация первого слагаемого определяется условием (2.12), а минимизация второго слагаемого – условием (2.11).

Если в конкретном случае условия в утверждениях 2–4 противоречат друг другу, то лучший из планов может быть определен путем сопоставления двух вариантов. При этом первый план строится в соответствии с первым условием, а второй план получается из первого путем переноса на первую позицию задания, удовлетворяющего второму условию.

Обсудим асимптотическую сложность описанных выше алгоритмов. Для алгоритма класса 1 базовой процедурой является сортировка, сложность которой можно оценить как $O(n\log n)$. Для остальных алгоритмов без учета перебора вариантов добавляется процедура выбора минимальной линейной сложности. Перебор в данном случае также имеет линейную сложность.

3. Алгоритм планирования по критерию минимума джиттера в (flow shop)-системе общего вида. Очевидно, что на практике для распределенной (flow shop)-системы общего вида, описанной в разд. 2 (Постановка задачи), условия ее принадлежности к тому или иному разрешимому классу чаще всего не выполняются. В частности, могут не совпадать критические пути разных заданий, может нарушаться отношение доминирования между процессорами, а если оно и выполняется, то может не быть упорядоченных по этому отношению цепочек процессоров, характерных для разрешимых классов. В результате исчезают гарантии оптимальности приведенных выше алгоритмов. В связи с этим предлагается пусть приближенный, но справедливый для любой из систем итерационный алгоритм планирования, выполняемый за число шагов, не большее, чем число заданий. На каждом шаге итерации определяется некоторый аналог критического пути, называемый псевдокритическим. Далее используется алгоритм планирования (утверждения 1–4), соответствующий тому разрешимому классу, к которому наиболее близка рассматриваемая на данном шаге система $C{\kern 1pt} ' = \{ P,\tau {\kern 1pt} '\} $, где $\tau {\kern 1pt} '$ – множество неразмещенных заданий ($\tau {\kern 1pt} ' \subseteq \tau $). При этом выбранное задание занимает первую позицию из интервала свободных позиций формируемого плана. Заметим, что размещение  j-го задания на l-й позиции плана означает, что на каждом процессоре системы задача из  j-го задания будет находиться на l-й позиции. После размещения это задание исключается из исходного множества и осуществляется переход к следующей итерации, реализуемой уже для оставшегося множества заданий на множестве свободных позиций плана. В  случае  если  достигнутая на k-м шаге достоверность классификации окажется меньше значения достоверности на предыдущем шаге, то планирование завершается с сохранением упорядоченности (k – 1)-го шага. В результате алгоритм последовательно размещает в плане все рассматриваемые задания в направлении от начала плана к его концу.

4. Результаты моделирования. Для исследования эффективности РКС-алгоритма при минимизации джиттера был осуществлен модельный эксперимент, основанный на случайной генерации примеров. При этом использовалась случайная генерация графов заданий, длительностей составляющих их задач, а также джиттеров этих задач. В целях увеличения достоверности результата было сгенерировано порядка 35 тыс. примеров, представленных тремя группами: заданиями, имеющими графы в виде цепочек, деревьев и ациклических графов. Число заданий в примерах варьировалось от 10 до 50 при числе процессоров, равном 20. Длительности задач, измеряемых в условных единицах, задавались интервалами. При этом разность между верхней и нижней границами интервала трактовалась как джиттер. Значения границ формировались как случайные равномерно распределенные величины из интервала [200–1000]. Для каждого примера составлялся план на основе предложенного алгоритма. Для вычисления верхней и нижней границ длительностей плана использовалась алгебра max-plus [13], после чего как разность границ вычислялся джиттер плана. Далее для получения оценки эффективности алгоритма это значение джиттера следовало бы сопоставить с минимальным, полученным в результате полного перебора вариантов плана. Однако известно, что при большом числе заданий поиск оптимального плана путем перебора становится нереализуемым за приемлемое время. По этой причине в модельном эксперименте использовались оценки Тэйларда [14] и их обобщение на случай ациклических графов. Для всех исследованных трех групп примеров средний проигрыш оптимальному результату оказался порядка 8%, при этом наихудшие варианты соответствовали уровню 20%.

Заключение. В статье были рассмотрены вопросы (flow shop)-планирования вычислительного процесса в распределенных СРВ. При планировании в качестве критерия был использован минимум джиттера (“дрожание” старта или завершения некоторой задачи). Особенностью РКС-алгоритма является простота. Моделирование продемонстрировало достаточную эффективность предложенного алгоритма.