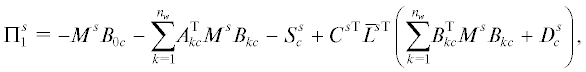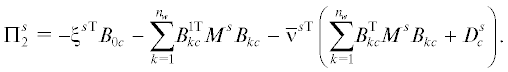Известия РАН. Теория и системы управления, 2021, № 6, стр. 35-42

Введение. На практике часто встречаются достаточно сложные динамические системы, состоящие из нескольких подсистем, для исследования которых требуется точность описания динамики с учетом действия внешних возмущений, ошибок управления и т.д. Одним из вариантов описания таких систем служат так называемые квазилинейные стохастические динамические системы, которые иногда называют системами с мультипликативными возмущениями. По-существу это нелинейные системы, которые доступны эффективному исследованию. В данной статье изучается поведение таких систем на неограниченном интервале времени, что позволяет эффективно решать задачи стабилизации при длительном функционировании.

Кроме того, зачастую передача информации между подсистемами затруднена или не целесообразна. Примером такой задачи является задача синхронизации движения летательных аппаратов (ЛА) при дозаправке в воздухе. Для решения таких прикладных задач стабилизации динамической системы, состоящей из нескольких подсистем, целесообразно использовать не скалярный критерий качества стабилизации, а векторный, оптимизируемый по Нэшу [1]. При таком подходе оказывается достаточно для решения общей задачи стабилизации каждой подсистеме оптимизировать свои затраты на стабилизацию и положение относительно другого объекта.

Исследования основываются на работе [2], где рассматривается проблема равновесия по Нэшу в игровой задаче многих лиц для диффузионных стохастических систем общего вида. Настоящая статья продолжает исследования авторов [1], где получены приведенные в разд. 2 необходимые условия равновесия по Нэшу в квазилинейной стохастической системе, и [3, 4], где получены необходимые условия оптимальности квазилинейных систем, функционирующих на неограниченном интервале времени, в случае скалярного критерия оптимальности.

Примерами применения указанных условий равновесия могут служить задача управления группой ЛА и задача дозаправки в воздухе. Об актуальности таких задач говорит то, что по настоящий день кроме разработки все более совершенных физических систем дозаправки в воздухе [5], также активно разрабатываются и алгоритмы автоматического управления ЛА при дозаправке топливом в воздухе [6–8]. Самые большие перспективы при использовании систем дозаправки открываются перед беспилотными летательными аппаратами (БЛА), которые смогут практически неограниченное время патрулировать воздушное пространство над территорией противника, вести наблюдение и атаковать появляющиеся цели [5].

Процесс дозаправки делится на три этапа [7]:

1) этап сближения ЛА с танкером и стыковки;

2) этап заправки и поддержания относительного положения ЛА и танкера;

3) этап расстыковки и отхода.

В настоящем исследовании в качестве приложения предлагаемой теории рассмотрен второй этап. На примере подробно рассматриваемой задачи стабилизации по высоте движения двух ЛА производится сравнение различных подходов к решению задачи совместной стабилизации. Показано, что предлагаемый метод дает лучшие результаты по сравнению с традиционными.

1. Постановка задачи управления. Пусть управляемый процесс описывается уравнением Ито

Здесь $x(t) \in {{R}^{n}}$ – случайное состояние системы в момент времени $t$; $u(x(t)) \in {{R}^{{{{n}_{u}}}}}$ – вектор-функция управления; $w(t) \in {{R}^{{{{n}_{w}}}}}$ – стандартный винеровский процесс; $t \in [0, + \infty )$ – время функционирования системы; ${{A}_{{kc}}}$, ${{B}_{{kc}}}$, $B_{{kc}}^{1}$, $k = \overline {0,{{n}_{w}}} $, – постоянные матрицы соответствующих размеров. Начальное распределение состояния ${{x}_{0}} = x(0)$ считается заданным и имеет конечную матрицу вторых центральных моментов. Здесь и далее нижний индекс c подчеркивает принадлежность матриц уравнению управляемого процесса (1.1).

Рассматривается неантагонистическая игра q лиц-игроков. Каждый игрок выбирает свою стратегию управления ${{u}^{s}}(x)$, $s = \overline {1,q} $, ${{u}^{s}}(x) = (u_{1}^{s}(x),u_{2}^{s}(x), \ldots ,u_{{{{n}_{{{{u}_{s}}}}}}}^{s}(x{{))}^{{\text{T}}}} \in {{R}^{{{{n}_{{{{u}_{s}}}}}}}}$ так, чтобы минимизировать свой квадратичный критерий:

где ${{f}^{s}}(x,{{u}^{s}}) \geqslant 0$; $Q_{c}^{s}$, $S_{c}^{s}$, $D_{c}^{s} > 0$ – постоянные матрицы соответствующих размеров; а M – операция матожидания.

Чтобы замкнутая стратегией u(x) система (1.1) была квазилинейной, доступной эффективному исследованию, мы вынуждены ограничиться классом линейных по состоянию стратегий.

В общем случае стратегии игроков формируются в условиях неполноты информации о состоянии.

Стратегия s-го игрока ${{u}^{s}}(x)$ задается равенством

где ${{y}^{s}} \in {{R}^{{{{n}_{{{{y}_{s}}}}}}}}$ – выход системы для s-го игрока, ${{L}^{s}}$, ${{\nu }^{s}}$, C^s – матрицы соответствующих размеров, матрица C^s задана. Функцию вида (1.3) будем называть регулятором или стратегией управления s-го игрока.

Общая стратегия $u(x)$ в (1.1) есть совокупность стратегий ${{u}^{s}}(x)$, u(x) = (u^1T(x), u^2T(x), ..., ${{u}^{q}}^{{\text{T}}}(x{{))}^{{\text{T}}}} \in {{R}^{{{{n}_{u}}}}}$, ${{n}_{u}} = {{n}_{{{{u}_{1}}}}} + {{n}_{{{{u}_{2}}}}} + \ldots + {{n}_{{{{u}_{q}}}}}$.

2. Условия оптимальности (равновесия по Нэшу). Для компактности записи введем следующие обозначения:

где $L = ({{L}^{1}}^{{\text{T}}},{{L}^{2}}^{{\text{T}}}, \ldots ,{{L}^{q}}^{{\text{T}}}{{)}^{{\text{T}}}} \in {{R}^{{{{n}_{u}}}}} \times {{R}^{{{{n}_{y}}}}}$, $C = ({{C}^{1}}^{{\text{T}}},{{C}^{2}}^{{\text{T}}}, \ldots ,{{C}^{q}}^{{\text{T}}}{{)}^{{\text{T}}}} \in {{R}^{{{{n}_{y}}}}} \times {{R}^{n}}$, ${{n}_{y}} = {{n}_{{{{y}_{1}}}}} + {{n}_{{{{y}_{2}}}}} + \ldots + {{n}_{{{{y}_{q}}}}}$, ν = = ${{({{\nu }^{1}}^{{\text{T}}},{{\nu }^{2}}^{{\text{T}}}, \ldots ,{{\nu }^{q}}^{{\text{T}}})}^{{\text{T}}}} \in {{R}^{{{{n}_{u}}}}}$.

О п р е д е л е н и е 1. Обозначим через U_a множество стратегий управления u(x), для которых уравнения первого m(t) и второго центрального $\Gamma (t)$ моментов асимптотически устойчивы относительно положения равновесия ${{m}^{\infty }}$, ${{\Gamma }^{\infty }}$, определяемое равенствами:

где матрицы A_k и вектор-столбцы B_k задаются равенствами (2.1). Очевидно, что для стратегий $u(x)$ из U_a решения этих уравнений существуют и система (1.1) устойчива в среднеквадратичном. Стратегии $u( \cdot ) \in {{U}_{a}}$ будем называть допустимыми.

Справедлива следующая теорема [3].

Т е о р е м а 1. Если стратегия управления $u(x)$, т.е. совокупность стратегий ${{u}^{s}}(x)$, $s = \overline {1,q} $, задаваемых равенством (1.3), принадлежит множеству U_a, то для каждого игрока критерий (1.2) для всех распределений начального состояния $x(0) = {{x}_{0}}$ определен и принимает одно и то же значение, которое может быть вычислено по формуле

Здесь симметрическая неотрицательная матрица ${{M}^{s}}$ и вектор ${{\xi }^{s}}$ находятся из уравнений

которые имеют решения, а матрицы ${{A}_{k}}$, ${{B}_{k}}$, ${{Q}^{s}}$, ${{S}^{s}}$, ${{D}^{s}}$ определяются равенствами (2.1), (2.2).

Следствие из теоремы 1. При фиксированных стратегиях всех игроков, кроме $s$-го, критерий ${{J}^{s}}$, значение которого определяется формулой (2.3), является функцией набора параметров ${{\lambda }^{s}} = ({{L}^{s}},{{\nu }^{s}})$, задающих стратегию $s$-го игрока:

где $U_{\alpha }^{s}$ – множество значений ${{\lambda }^{s}}$, таких, что сумарная стратегия $u( \cdot ) \in {{U}_{\alpha }}$.

Совершенно очевидно, что множество $U_{a}^{s}$ зависит от выбора стратегий ${{u}^{k}}(x)$, $k \ne s$, других игроков. Будем иметь это в виду, не вводя эти стратегии в качестве аргументов множества $U_{a}^{s}$ явно.

Задача оптимизации состоит в отыскании, исходя из условий минимума критериев оптимальности (1.2), допустимой стратегии $u( \cdot ) \in {{U}_{a}}$, которая есть совокупность стратегий ${{u}^{s}}(x)$, $s = \overline {1,q} $, обеспечивающей равновесие по Нэшу.

Следуя [9], дадим следующие определения.

О п р е д е л е н и е 2. Допустимая стратегия $\bar {u}( \cdot ) \in {{U}_{a}}$, представляющая собой совокупность стратегий ${{\bar {u}}^{s}}(x)$, $s = \overline {1,q} $, называется приемлемой для s-го игрока, если стратегия s-го игрока ${{\bar {u}}^{s}}(x)$ минимизирует критерий (1.2) на множестве $U_{a}^{s}$ при фиксированных стратегиях других игроков.

О п р е д е л е н и е 3. Допустимая стратегия $\bar {u}( \cdot ) \in {{U}_{a}}$ называется равновесной по Нэшу, если она приемлема для всех игроков.

В результате справедлива следующая теорема.

Теорема 2. Для того, чтобы стратегия $\bar {u}( \cdot ) \in {{U}_{a}}$ была приемлемой для s-го игрока, необходимо и достаточно выполнения условия

при фиксированных стратегиях других игроков.

Доказательство теоремы 2. Теорема 2 представляет собой запись определения 2 с учетом следствия из теоремы 1 (равенство (2.6)).

Условия теоремы 2 необходимы и достаточны, но довольно-таки сложны для использования в связи с тем, что функции ${{F}^{s}}({{\lambda }^{s}})$ содержат матричные переменные ${{M}^{s}}$ и ${{\xi }^{s}}$, зависимость которых от ${{\lambda }^{s}}$ задается неявно уравнениями (2.4), (2.5).

Несколько проще необходимые условия экстремума функций ${{F}^{s}}({{\lambda }^{s}})$ [3, 4], приводящие к необходимым условиям приемлемости.

Теорема 3. Если стратегия управления $\bar {u}(x)$, представляющая собой совокупность стратегий ${{\bar {u}}^{s}}(x) = - {{\bar {L}}^{s}}{{y}^{s}}(x) + {{\bar {\nu }}^{s}}$, $s = \overline {1,q} $, принадлежит множеству U_a и является приемлемой для s-го игрока, то выполнены следующие условия:

где матрица ${{M}^{s}}$ и вектор ${{\xi }^{s}}$ находятся из уравнений (2.4), (2.5),

Оптимальное значение критерия вычисляется по формуле (2.3) при ${{L}^{s}} = {{\bar {L}}^{s}}$, ${{\nu }^{s}} = {{\bar {\nu }}^{s}}$.

Из определений 1, 2 следует, что для поиска оптимальной по Нэшу стратегии нужно применить теорему 2 или 3 для каждого из q игроков при фиксированных стратегиях остальных. Этот факт сформулирован в виде следующей теоремы.

Теорема 4. Для того, чтобы стратегия $\bar {u}( \cdot ) \in {{U}_{a}}$ была равновесной по Нэшу, необходимо и достаточно выполнение условий теоремы 2 и необходимо выполнение условий теоремы 3 для каждого из q игроков.

Как в любых задачах на экстремум, в задаче равновесия по Нэшу возникает проблема существования решения. В общей теории равновесия по Нэшу проблему существования решают с использованием рандомизированных стратегий. Однако если теория применяется к конкретной ситуации, то рандомизированные стратегии неприемлемы. Предложить достаточно содержательные условия существования нерандомизированного решения рассмотренной задачи авторам не удалось вследствие существенной нелинейности функции ${{F}^{s}}({{\lambda }^{s}})$, $s = \overline {1,q} $.

Целесообразно отметить, что в отличие от задачи на экстремум со скалярным критерием необходимые и достаточные условия равновесия по Нэшу допускают наличие нескольких решений с различными значениями критериев игроков.

3. Синхронизация движения двух ЛА по высоте. Рассматривается задача синхронизации движения двух одинаковых ЛА по высоте при дозаправке в воздухе. Пример носит демонстративный характер, поэтому приводится плоская задача: модель учитывает отклонение по высоте ${{H}_{k}}$ k-го ЛА от заданной траектории и вертикальную скорость ${{V}_{k}}$ k-го ЛА, k = 1, 2. Предполагается, что самолет-заправщик и заправляемый самолет движутся в вертикальной плоскости. Считается, что номинальное движение – горизонтальный полет с постоянной скоростью при постоянном расстоянии между самолетами. Будем предполагать, что канал стабилизации скорости ЛА поддерживает с необходимой точностью постоянное расстояние между самолетами вдоль номинальной траектории. В данной задаче рассмотрим канал стабилизации высоты полета и поддержания разности высот ЛА близкой к нулю при действии внешних шумов (ветровых возмущений) и реализации управления с ошибками.

При необходимости практического применения результатов аналогичную задачу можно решить и для канала стабилизации скорости, а также использовать математическую модель, описывающую в том числе и ЛА с различными характеристиками.

Возможны несколько вариантов решения этой задачи. Первый вариант – достаточно жестко стабилизировать вблизи нуля отклонение по высоте ${{H}_{k}}$ и вертикальную скорость ${{V}_{k}}$ независимо для каждого из ЛА, используя квадратичный критерий. Недостатком такого подхода является отсутствие приоритета на стабилизацию взаимного положения ЛА, которое гораздо важнее выдерживать вблизи нуля, чем каждую из переменных. Второй вариант, рекомендованный многими авторами [10, 11], несколько сглаживает недостаток первого варианта. В нем предлагается стабилизировать движение ведущего ЛА (танкера) относительно опорной траектории (как в первом варианте). Затем при фиксированной стратегии ведущего решается задача синхронизации движения за счет ведомого (заправляемого ЛА). И наконец, третий вариант – передавать всю доступную информацию о положении каждого ЛА каждому из участников движения. Недостатком является зачастую переизбыток передаваемой информации, к тому же передача информации между подсистемами может быть затруднена и нецелесообразна.

Нами предлагается вариант взаимной стабилизации с разумным объемом передаваемой и используемой при управлении информации. В этом варианте каждый из двух ЛА оптимизирует свои затраты на стабилизацию и величину ${{({{H}_{1}} - {{H}_{2}})}^{2}}$, характеризующую отклонение по высоте от партнера. Математически это неантагонистическая игра двух лиц – предмет изучаемой здесь теории оптимизации (равновесия) по Нэшу.

Далее произведено сравнение трех подходов к решению поставленной задачи. В задаче 1 реализуется указанный выше последний вариант оптимизации по Нэшу. В задаче 2 стабилизируется движение каждого из двух ЛА по отдельности. В задаче 3 рассматривается второй вариант: ведущий ЛА (танкер) – ведомый.

Для сравнения результатов решения задач 1–3 предложена методика, опирающаяся на разделение критерия оптимальности на сумму составляющих его компонент, отражающих различные характеристики процесса. Такой подход часто встречается в теории дифференциальных игр [12–14]. В нашем случае интересно выделение из критериев каждого из двух ЛА компонент, связанных с отклонением по высоте $({{H}_{1}} - {{H}_{2}})$ и затратами на управление. При этом задача синтеза стратегии управления решается исходя из объединенного критерия качества, на решение которой не влияет подсчет частных критериев, необходимых лишь для сравнения полученных решений. Такой подход, связанный с выделением частных критериев, позволяет отказаться от принципа взвешенного вклада отдельных отклонений и дает мощный инструмент для поиска и анализа компромиссных решений [12].

З а д а ч а 1. Упрощенные линеаризованные уравнения движения двух одинаковых ЛА (k = = 1, 2) имеют вид

где ${{u}_{k}}$ – управление; ${{H}_{k}}$ – отклонение высоты $k$-го ЛА от заданной траектории; ${{V}_{k}}$ – вертикальная скорость k-го ЛА; ${{w}_{{ki}}}$, $i = 1,2$ – независимые стандартные винеровские процессы; $\varepsilon $, c – заданные константы.

В квадратичном критерии учитывается взаимное отклонение по высоте $\Delta H = {{H}_{1}} - {{H}_{2}}$:

где ${{a}_{i}}$, $i = \overline {1,4} $, – заданные константы.

При численных расчетах были выбраны следующие значения констант: ${{a}_{1}} = 0.5$, ${{a}_{2}} = {{a}_{3}} = 1$, ${{a}_{4}} = 20$, $\varepsilon = 0.1$, $c = 1$.

Требуется найти управление в следующем виде:

Применяя полученные выше необходимые условия оптимальности (равновесия) по Нэшу найдем коэффициенты оптимального управления ${{L}_{1}} = 0.696$, ${{L}_{2}} = 3.239$, ${{L}_{3}} = 4.065$ и оптимальные значения критериев ${{\bar {J}}^{k}} = 1.67$, k = 1, 2.

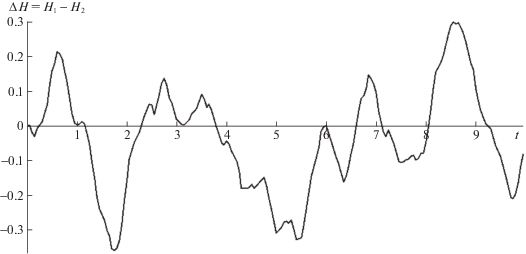
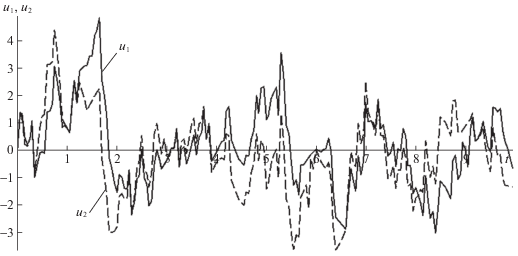
На рис. 1, 2 представлена одна из реализаций взаимного отклонения движения ЛА по высоте $\Delta H = {{H}_{1}} - {{H}_{2}}$ и процессов управления u₁, u₂, полученная в соответствии с предложенной теорией.

Подсчитаем два дополнительных критерия:

которые характеризуют вклад относительного отклонения высоты и расхода энергии на управление в значение критерия соответственно. Верхний индекс в круглых скобках в обозначении критериев (3.2), (3.3) указывает на номер задачи (задача 1). Аналогичные обозначения будут использоваться и для задач 2, 3.

Значения частных критериев (3.2), (3.3) при заданных коэффициентах управления ${{L}_{1}}$, ${{L}_{2}}$, ${{L}_{3}}$ вычисляются достаточно просто с использованием равенств (2.3), (2.4) (${{\xi }^{s}}$ в данном примере равно нулю).

В рассматриваемой задаче значения дополнительных критериев составили $J_{{\Delta H}}^{{(1)}} = 0.018$, $J_{{{{u}_{k}}}}^{{(1)}} = 1.206$, k = 1, 2.

Далее решим задачи 2, 3 и произведем сравнение дополнительных критериев. Задачи 2, 3 решаются с помощью того же изложенного выше математического аппарата, что и задача 1, так как в случае одного игрока условия равновесия по Нэшу совпадают с условиями оптимальности скалярного критерия.

З а д а ч а 2. Рассмотрим алгоритм стабилизации, состоящий в том, что каждый из двух (одинаковых) ЛА независимо стабилизирует свою высоту. Уравнения движения одного из ЛА имеют вид

Управление запишем как

Введем дополнительные критерии

k = 1, 2, которые также характеризуют отклонение ЛА по высоте от заданной траектории и расход энергии.

Желая добиться того же качества стабилизации по высоте движения ЛА в паре, что и в задаче 1, потребуем выполнение условия

Коэффициенты управления ${{L}_{1}}$, ${{L}_{2}}$ подберем так, чтобы при выполнении условия (3.6) затраты на управление $J_{{\Delta {{u}_{k}}}}^{{(2)}}$ были минимальны.

Решая эту задачу, получим коэффициенты управления ${{L}_{1}} = 3.85$, ${{L}_{2}} = 7.42$. При этом расход энергии при индивидуальной стабилизации составляет $J_{{{{u}_{k}}}}^{{(2)}} = 1.488$, $k = 1,2$.

З а д а ч а 3. Первая часть задачи для ведущего ЛА (танкера) аналогична задаче 2. Уравнения движения и вид искомого управления имеют вид, аналогичный (3.4), (3.5) соответственно. Коэффициенты управления ${{L}_{1}} = 3.85$, ${{L}_{2}} = 7.42$ и значения частных критериев $J_{{{{H}_{1}}}}^{{(3)}} = 0.009$, $J_{{{{u}_{1}}}}^{{(3)}}$ = = 1.488.

Затем при фиксированных значениях ${{L}_{1}}$, ${{L}_{2}}$ решим задачу синхронизации движения ведомого ЛА. Уравнения движения имеют вид (3.1), а управление –

Соблюдая выполнение равенства частого критерия

найденного по формуле (3.2), получим коэффициенты управления ${{L}_{3}} = 3.8$, ${{L}_{4}} = 3.8$, ${{L}_{5}} = 2.3$, исходя из минимума частного критерия $J_{{{{u}_{2}}}}^{{(3)}}$, вычисленного для управления u₂ ведомого ЛА. Оптимальное значение этого критерия $\bar {J}_{{{{u}_{2}}}}^{{(3)}} = 1.401$.

Произведем сравнение дополнительных критериев, полученных в задачах 1–3. Найденные решения во всех трех задачах дают одинаковое качество стабилизации по высоте движения ЛА в паре. Сравним частные критерии, характеризующие затраты на управление.

Суммарные затраты на управление двух ЛА следующие: в задаче 1 $J_{u}^{{(1)}} = J_{{{{u}_{1}}}}^{{(1)}} + J_{{{{u}_{2}}}}^{{(1)}} = 2J_{{{{u}_{1}}}}^{{(1)}}$ = = 2.412, в задаче 2 $J_{u}^{{(2)}} = J_{{{{u}_{1}}}}^{{(2)}} + J_{{{{u}_{2}}}}^{{(2)}} = 2J_{{{{u}_{1}}}}^{{(2)}}$ = 2.976, в задаче 3 $J_{u}^{{(3)}} = J_{{{{u}_{1}}}}^{{(3)}} + J_{{{{u}_{2}}}}^{{(3)}} = 1.488 + 1.401$ = 2.881.

Итак,

Таким образом по сравнению с оптимизацией по Нэшу (задача 1) вариант независимой стабилизации ЛА (задача 2) имеет расход энергии на управление больше на 23.4%, а вариант с использованием метода ведущий–ведомый (задача 3) – больше на 19.4%. Настоящие результаты свидетельствуют об эффективности предлагаемого метода.

Заключение. Получены необходимые и одновременно достаточные, а также необходимые первого порядка условия равновесия по Нэшу в игровой задаче q лиц для квазилинейных стохастических систем, функционирующих на неограниченном интервале времени в условиях неполноты информации о состоянии.

Произведено сравнение различных подходов к решению задачи синхронизации движения двух ЛА по высоте в процессе дозаправки. При решении модельного примера применен метод выделения пары частных критериев для каждой компоненты векторного критерия, который представляет собой мощный инструмент для поиска и анализа компромиссных решений в более сложных задачах.