Известия РАН. Теория и системы управления, 2021, № 6, стр. 61-65

Введение. В [1] упоминается о постановках задач об эффективной стрельбе и их связи с классическими задачами транспортного типа. В [2] предлагается метод последовательной модификации коэффициентов целевых функций задач транспортного типа. В настоящей работе, в отличие от последовательного изменения допустимых решений или двойственных переменных, итеративно пересчитываются коэффициенты целевой функции. Строится монотонный по целевой функции процесс, который окончательно приводит к оптимуму, хотя последовательные решения (так называемые псевдорешения) не допустимы к исходным ограничениям. В [3–5] алгоритм применяется к различным задачам транспортного типа. Особым местом является вырождение, когда из промежуточных задач невозможно сформировать исходный оптимум. Это преодолевается для каждого конкретного случая по-разному.

В работе этот подход применяется для так называемой задачи об эффективной стрельбе. Имеется некоторое количество батарей, каждая из которых делает несколько выстрелов по различным целям. Общее количество выстрелов всех батарей равно количеству целей. Для выстрела по каждой цели у каждой батареи имеется коэффициент эффективности стрельбы. Задача состоит в том, чтобы определить такой план стрельбы, при котором достигается максимум суммы эффективностей.

1. Постановка задачи. Формально задача выглядит так:

Здесь индекс $i$ нумерует цели, количество которых $n$. Имеется $m$ батарей, которые производят a_j выстрелов, где  j – номер батареи. Неизвестная величина ${{x}_{{ij}}}$ равна единице, если по цели $i$ производится выстрел из батареи  j, в противном случае эта величина равна нулю. По каждой цели $i$ делается только один выстрел из батареи  j. Задача (1.1)–(1.5) является линейной оптимизационной задачей с булевыми переменными.

2. Алгоритм решения задачи (1.1)–(1.5). Для решения этой задачи построим последовательность ее так называемых псевдорешений [2].

Первое псевдорешение получим следующим образом. Полагаем

и рассмотрим $m$ одномерных задач с ограничениями (1.1), (1.4): а также $n$ одномерных задач с ограничениями (1.3), (1.4):

Для решения одномерной задачи (1.1), (1.4), (2.1) при произвольном $i = i{\kern 1pt} '$ необходимо найти ${{a}_{{i'}}}$ наибольших коэффициентов $c_{{i'j}}^{1}$ из ее целевой функции:

и т.д. Соответственно решением одномерной задачи (1.1), (1.4), (2.1) будет и т.д. Для решения одномерной задачи вида (1.3), (1.4), (2.2) при произвольном $j = j{\kern 1pt} '$ необходимо найти максимальный коэффициент соответствующей целевой функции:

Пусть у всех одномерных задач есть конкретные решения. Объединим эти решения в одно и назовем его псевдорешением исходной задачи. Сумму значений целевых функций одномерных задач будем считать значением целевой функции псевдорешения. Заметим, что эта сумма не меньше значения целевой функции для оптимального решения исходной задачи (1.1)–(1.5). И это верно для любого разбиения каждого c_ij на два слагаемых.

Если псевдорешение задачи об эффективной стрельбе является допустимым решением задачи (1.1)–(1.5), то оно будет и ее оптимальным решением.

Пусть верно обратное: допустимое псевдорешение не является оптимальным решением задачи (1.1)–(1.5). Тогда существует оптимальное решение, отличное от данного, для которого значение целевой функции больше значения целевой функции псевдорешения. Отсюда следует, что хотя бы в одной из одномерных задач, на которые была разбита исходная задача, оптимальное решение дает большее значение целевой функции, чем в псевдорешении, что противоречит определению псевдорешения. Разумеется, первое псевдорешение может оказаться недопустимым в исходной задаче. Для построения последовательности псевдорешений станем циклически решать множество задач с двумя ограничениями.

Рассмотрим первый шаг цикла при i = 1,  j = 1. Решается двумерная задача c ограничениями (1.1), (1.4) при i = 1 и c ограничениями (1.3), (1.4) при j = 1 с общей переменной x₁₁:

Для решения двумерной задачи (2.3)–(2.6) необходимо найти ${{a}_{1}} - 1$ наибольших по величине коэффициентов целевой функции из группы первой суммы $c_{{1j}}^{1}$, $j \ne 1$. Обозначим их индексы $j \in {\text{\{ }}{{j}_{1}},{{j}_{2}}, \ldots ,{{j}_{{{{a}_{1}} - 1}}}{\text{\} }}$. Тогда частью решения будет ${{x}_{{1{{j}_{1}}}}} = $ ${{x}_{{1{{j}_{2}}}}} = $ $ \ldots = $ ${{x}_{{1{{j}_{{{{a}_{1}} - 1}}}}}}$.

Далее возможны два варианта: либо в решение попадут переменные, соответствующие a₁ по величине коэффициентов из группы $c_{{1j}}^{1}$ и максимальному коэффициенту из второй суммы целевой функции $c_{{i1}}^{2}$, либо общая переменная двух ограничений. Обозначим

Возможны три случая соотношения этих коэффициентов.

Первый случай:

Тогда в решение дополнительно войдет ${{x}_{{11}}} = 1$ и двумерная задача (2.3)–(2.6) решена. Рассчитаем новые коэффициенты $c_{{11}}^{1}$ и $c_{{11}}^{2}$ в соответствии с системой:

Это обеспечивает объединение оптимальных решений одномерных задач с ограничениями (2.3), (2.6) и (2.4), (2.6), а значит, совпадение с оптимальным решением задачи (2.3)–(2.6).

Второй случай:

При этом дополнить решение до однозначного невозможно, и если коэффициент $c_{{1j*}}^{1}$ имеется только у ${{x}_{{1j*}}}$, то получаем ограничения

Такое соотношение коэффициентов будем называть вырождением. В общем случае в первом из этих ограничений может быть несколько переменных и правая часть больше единицы. Во втором ограничении тоже может быть несколько переменных, но правая часть при этом остается единицей. Находим новые значения коэффициентов $c_{{11}}^{1} = c_{{1j*}}^{1}$, $c_{{11}}^{2} = c_{{i*1}}^{2}$.

Третий случай:

Тогда в решение войдут дополнительно ${{x}_{{1j*}}} = $ ${{x}_{{i*1}}} = 1$ и двумерная задача (2.3)–(2.6) решена. Новые значения коэффициентов $c_{{11}}^{1}$ и $c_{{11}}^{2}$ с той же целью вычисляем в соответствии с системой:

Заметим, что после пересчета коэффициентов новое значение целевой функции псевдорешения в общем случае уменьшится по сравнению с предыдущим.

На этом первый шаг заканчивается. Далее переходим к шагу i = 1, $j = 2$, затем берем i = 1, $j = 3$ и т.д. до i = 1, $j = n$. Переходим к шагу i = 2, $j = 1$ и т.д. до $i = m$, $j = n$. На этом первый цикл заканчивается, переходим ко второму циклу, где опять начинаем со значений индексов i = 1, $j = 1$.

Циклический процесс останавливается тогда, когда в двух последовательных циклах каждая одномерная задача имеет одинаковые решения или одинаковые ограничения (вырождение). Если вырождения нет, то тем самым получено оптимальное решение задачи (1.1)–(1.5). Наличие вырождения в некоторых ограничениях требует дополнительных процедур.

3. Вырождение. Рассмотрим ситуацию вырождения, которая имеет место по окончании циклического процесса. Отметим важное свойство вырождения (см. второй случай в разд. 2). Если решать задачу с двумя ограничениями с общей переменной ${{x}_{{1j*}}}$, то возникает вырождение, при этом одной из переменных, входящих в первое ограничение, будет x₁₁. Если решать задачу с двумя ограничениями с общей переменной ${{x}_{{i*1}}}$, то и здесь появляется вырождение, а переменная ${{x}_{{11}}}$ участвует во втором ограничении. На этом свойстве и основана процедура определения конкретного решения при вырождении. Если положить общую переменную (x₁₁ в рассмотренном примере) равной единице, то в первом ограничении будет ${{x}_{{1j*}}} = 0$ (или неопределенность уменьшится), а во втором ${{x}_{{i*1}}} = 0$, а также и остальные переменные, у которых коэффициент в целевой функции равен $c_{{i*1}}^{2}$. Переходя далее в другие ограничения, которые дают вырождение, определяем значения других переменных. Если после этого вырождение все еще имеет место, процедура продолжается, начиная с другой переменной, попавшей в ограничения вырождения.

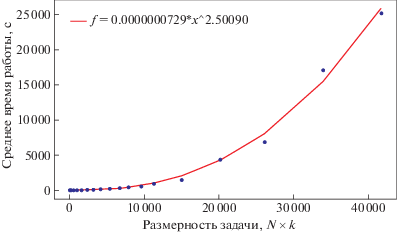
4. Результаты численных расчетов. Размерность задачи равна произведению количества целей на количество батарей. Решалась серия задач, в том числе одинаковой размерности с различными случайными коэффициентами эффективности в заданном диапазоне. Время решения задач одинаковой размерности усреднялось. Времена решения задач при различных размерностях приведены на рисунке. Кривая хорошо аппроксимируется степенной фунцией вида

при значениях $C = 0.0000000729$, $B = 2.50090$.

Заключение. Метод последовательной модификации коэффициентов целевой функции строит точное решение для интересного класса задач об эффективной стрельбе. Дальнейшее рассмотрение может быть направлено на более общий случай трех и более индексов.