Известия РАН. Теория и системы управления, 2022, № 1, стр. 124-144
ВЫБОР ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ РАСПОЛОЖЕНИЯ СИСТЕМЫ ДВИГАТЕЛЕЙ-МАХОВИКОВ ПРИ УПРАВЛЕНИИ ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА
А. И. Игнатов *
МГТУ им. Н.Э. Баумана
Москва, Россия
* E-mail: general_z@mail.ru
Поступила в редакцию 10.11.2020
После доработки 13.09.2021
Принята к публикации 27.09.2021
- EDN: GNFDJT
- DOI: 10.31857/S0002338822010061
Аннотация
Рассмотрены два возможных варианта расположения системы двигателей-маховиков на борту космического аппарата. Первый вариант – система из четырех маховиков, оси вращения которых расположены параллельно боковым ребрам четырехугольной пирамиды. Второй вариант – система из шести маховиков, оси вращения которых расположены параллельно боковым ребрам правильной шестиугольной пирамиды. Каждая система характеризуется геометрическими параметрами, определяющими угловые положения осей вращения маховиков. Построены области возможных значений суммарного кинетического момента, создаваемого системой маховиков, в том числе при отказе одного из них. Приведены параметрические зависимости для выбора наиболее рационального расположения маховиков, обеспечивающие максимально широкие возможности управления угловой скоростью космического аппарата. Рассмотрен режим стабилизации орбитальной ориентации аппарата с учетом воздействия внешних возмущающих моментов. Для этого режима получены зависимости, позволяющие выбрать значения геометрических параметров системы, обеспечивающие минимальную скорость накопления кинетического момента каждым из маховиков. Приведены результаты численного моделирования уравнений движения космического аппарата.
0. Введение. Комплекс электромеханических исполнительных органов (гиросистема), входящий в систему управления космическим аппаратом (КА), предназначен для создания управляющих моментов. Во многих случаях при создании длительно существующих КА использованию гиросистемы в составе системы управления нет альтернативы [1]. В то же время электромеханические исполнительные органы – одни из наиболее массивных и энергопотребляющих устройств, постоянно задействованных в процессе функционирования КА. В связи с этим задачи выбора типа исполнительных органов гиросистемы и оптимизации их характеристик являются актуальными.
Гиросистемы, используемые на КА, могут быть построены на базе трех основных типов электромеханических исполнительных органов:
управляющих двигателей-маховиков (маховиков);
двухстепенных силовых гироскопов (гиродинов);
трехстепенных силовых гироскопов.
В свою очередь силовые гироскопы могут быть реализованы:
с постоянным абсолютным значением кинетического момента;
с изменяемым абсолютным значением кинетического момента.
Для крупногабаритных и тяжелых КА с высокими требованиями к динамике и точности ориентации целесообразность применения гиросистемы на основе силовых гироскопов различного типа во многих случаях очевидна [2]. Для малых КА выбор типа исполнительных органов системы управления, как правило, ограничивается маховиками или гиродинами, что тоже является не тривиальной задачей. Между областями применения перечисленных устройств нельзя провести резких границ. Динамические требования к системе управления КА, включающей в свой состав гиросистему, во многом определяются множеством требуемых значений кинетического момента ${{H}_{T}}$. Множество ${{H}_{T}}$ является областью изменения в связанной с КА системе координат вектора суммарного кинетического момента, создаваемого гиросистемой. Изменение этого вектора в указанной области в соответствии с реализуемыми в системе законами должно обеспечивать требуемое управление параметрами вращательного движения КА. Естественно, что множество ${{H}_{T}}$ должно содержаться внутри множества максимальных значений кинетического момента ${{H}_{C}}$, реализуемых гиросистемой.
Таким образом, для всех вариантов построения гиросистемы должно быть обеспечено выполнение условия:
При этом можно утверждать, что величина суммарного кинетического момента, создаваемого гиросистемой, будет достаточна для обеспечения требуемой угловой скорости вращения КА.
1. Область возможных значений кинетического момента системы маховиков. В работе в качестве электромеханических исполнительных органов рассматривается система управляющих двигателей-маховиков. Область вариации возможных значений суммарного кинетического момента ${{H}_{C}}$, создаваемого системой, зависит от количества маховиков, схемы их расположения относительно жестко связанной с КА системы координат и максимального значения кинетического момента, реализуемого каждым из маховиков.
Вектор ${\mathbf{H}}$ суммарного кинетического момента маховиков выражается формулой
где ${{h}_{k}}$ – алгебраическое значение кинетического момента маховика с номером k, $k = \overline {1,n} $, ${{{\mathbf{g}}}_{k}}$ – орт оси вращения маховика с номером k, $n$ – общее количество маховиков в системе. Здесь и далее считаем, что система всегда состоит из одинаковых маховиков. В этом случае $ - {{h}_{{\max }}}$ ≤ ${{h}_{k}}$ ≤ ${{h}_{{\max }}}$, где ${{h}_{{\max }}}$ – абсолютная величина предельного значения кинетического момента отдельного маховика. Величина ${{h}_{{\max }}}$ – один из параметров системы.Введем связанную с системой маховиков правую декартову систему координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}},$ в которой вектор ${\mathbf{H}}$ представлен своими компонентами ${{H}_{i}}$, $i = 1,2,3.$ Рассмотрим область ${{P}_{n}}$ пространства ${{R}^{3}}\left( {{{H}_{1}},{{H}_{2}},{{H}_{3}}} \right)$, заполняемую концами векторов (1.1) (начала векторов помещены в точку O). Чтобы обеспечить полную ориентацию КА, на нем должно быть установлено не менее трех маховиков [3], орты осей вращения которых линейно независимы. В общем случае область ${{P}_{n}}$ представляет собой многогранник, обладающий центральной симметрией относительно точки O, для которого справедлива теорема Эйлера: В – Р + Г = 2, где $В = n(n - 1) + 2$ – число вершин, $Р = 2n(n - 1)$ – число ребер, $Г = n(n - 1)$ – число граней. Если все маховики в системе одинаковые, то многогранник ${{P}_{n}}$ является выпуклым, а все его грани – ромбы, каждая сторона которых имеет длину $2{{h}_{{\max }}}$ [4]. Стороны каждого ромба параллельны каким-либо из ортов ${{{\mathbf{g}}}_{k}}$ и ${{{\mathbf{g}}}_{j}},$ площадь соответствующего ромба равна $h_{{\max }}^{2}{\text{|}}{{{\mathbf{g}}}_{k}} \times {{{\mathbf{g}}}_{j}}{\text{|}}$, где $k \ne j$, $j,k = \overline {1,n} .$ При построении многогранника ${{P}_{n}}$, не ограничивая общности, будем использовать безразмерные параметры:
(1.2)
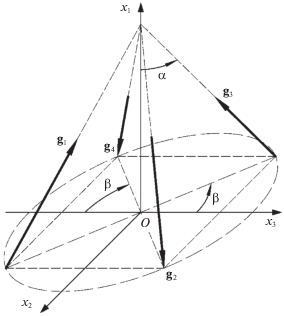
${\mathbf{\tilde {H}}} = \sum\limits_{k = 1}^n {{{{\tilde {h}}}_{k}}{{{\mathbf{g}}}_{k}},\quad {{{\tilde {h}}}_{k}} = \frac{{{{h}_{k}}}}{{{{h}_{{\max }}}}},} $1.1. Схема “четырехугольная пирамида”. Система состоит из четырех маховиков, оси вращения которых расположены параллельно боковым ребрам четырехугольной пирамиды. Высота пирамиды параллельна оси $O{{x}_{1}}$, линии пересечения граней пирамиды с плоскостью $O{{x}_{2}}{{x}_{3}}$ параллельны или перпендикулярны осям $O{{x}_{2}}$, $O{{x}_{3}}$ (рис. 1). Орты ${{{\mathbf{g}}}_{k}}$, $k = \overline {1,4} $, имеют компоненты
(1.3)
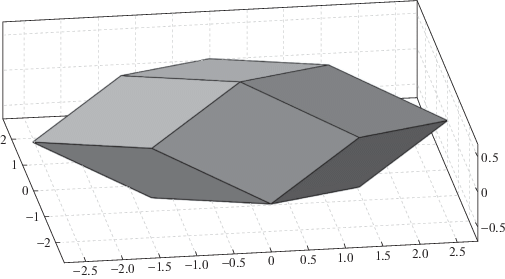
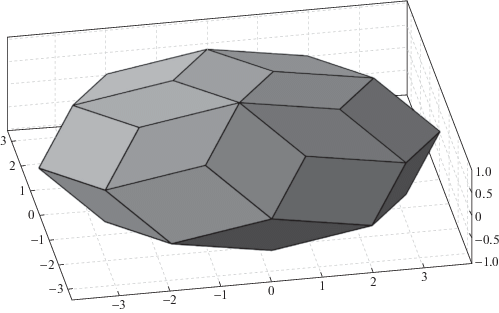
$\begin{gathered} {{{\tilde {H}}}_{1}} = \left( {{{{\tilde {h}}}_{1}} - {{{\tilde {h}}}_{2}} + {{{\tilde {h}}}_{3}} - {{{\tilde {h}}}_{4}}} \right){{d}_{1}},\quad {{{\tilde {H}}}_{2}} = \left( { - {{{\tilde {h}}}_{1}} + {{{\tilde {h}}}_{2}} + {{{\tilde {h}}}_{3}} - {{{\tilde {h}}}_{4}}} \right){{d}_{2}}, \\ {{{\tilde {H}}}_{3}} = \left( {{{{\tilde {h}}}_{1}} + {{{\tilde {h}}}_{2}} - {{{\tilde {h}}}_{3}} - {{{\tilde {h}}}_{4}}} \right){{d}_{3}}. \\ \end{gathered} $Область пространства, заполняемая концами векторов ${\mathbf{\tilde {H}}} = \left\langle {{{{\tilde {h}}}_{1}},{{{\tilde {h}}}_{2}},{{{\tilde {h}}}_{3}},{{{\tilde {h}}}_{4}}} \right\rangle $, представляет собой выпуклый многогранник P4, общий вид которого показан на рис. 2. Предельные значения ${\mathbf{\tilde {H}}} = \left\langle { \pm 1, \pm 1, \pm 1, \pm 1} \right\rangle $ (кроме значений ${\mathbf{\tilde {H}}} = \left\langle { - 1, - 1, - 1, - 1} \right\rangle = {{(0,0,0)}^{{\text{T}}}}$ и ${\mathbf{\tilde {H}}} = \left\langle {1,1,1,1} \right\rangle = $ ${{(0,0,0)}^{{\text{T}}}}$) реализуются в вершинах многогранника P4.
Рассмотрим случай, когда один из маховиков отключен (вышел из строя). Без ограничения общности можно считать, что отключен маховик с осью, параллельной орту g4. Тогда скалярная запись векторного выражения (1.2) имеет вид
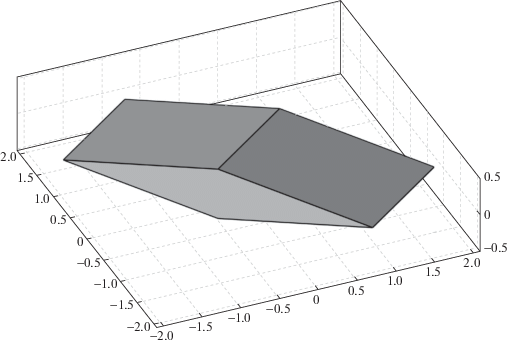
Область пространства, заполняемая концами векторов ${\mathbf{\tilde {H}}} = \left\langle {{{{\tilde {h}}}_{1}},{{{\tilde {h}}}_{2}},{{{\tilde {h}}}_{3}}} \right\rangle $, представляет собой параллелепипед P3, общий вид которого приведен на рис. 3.
Случай, когда отключены два маховика из четырех, в данной работе не рассматривается, поскольку система уже не сможет обеспечить полную ориентацию КА [3].
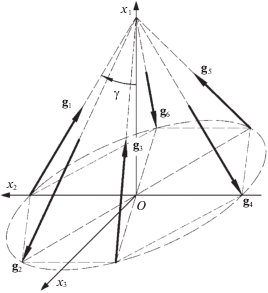
1.2. Схема “шестиугольная пирамида”. Система состоит из шести маховиков, оси вращения которых расположены параллельно боковым ребрам правильной шестиугольной пирамиды. Высота пирамиды параллельна оси $O{{x}_{1}}$, линии пересечения граней пирамиды с плоскостью $O{{x}_{2}}{{x}_{3}}$ образуют правильный шестиугольник (рис. 4). Орты gk, $k = \overline {1,6} $, имеют следующие компоненты:
Здесь ${{d}_{4}} = \cos \gamma $, ${{d}_{5}} = \sin \gamma $, $\gamma $ – угол между осью $O{{x}_{1}}$ и каждым из ортов ${{{\mathbf{g}}}_{k}}$, угол $\gamma $ – параметр системы, $0 < \gamma < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. В этом случае скалярная запись векторного выражения (1.2) имеет вид
(1.4)
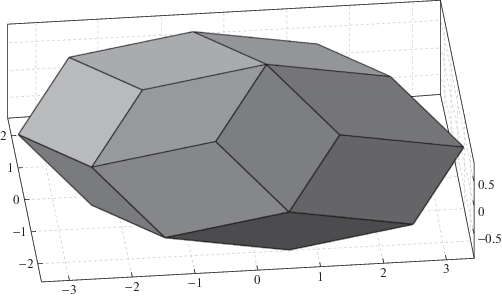
$\begin{gathered} {{{\tilde {H}}}_{1}} = \left( {{{{\tilde {h}}}_{1}} - {{{\tilde {h}}}_{2}} + {{{\tilde {h}}}_{3}} - {{{\tilde {h}}}_{4}} + {{{\tilde {h}}}_{5}} - {{{\tilde {h}}}_{6}}} \right){{d}_{4}},\quad {{{\tilde {H}}}_{2}} = \left( { - 2{{{\tilde {h}}}_{1}} + {{{\tilde {h}}}_{2}} + {{{\tilde {h}}}_{3}} - 2{{{\tilde {h}}}_{4}} + {{{\tilde {h}}}_{5}} + {{{\tilde {h}}}_{6}}} \right)\frac{1}{2}{{d}_{5}}, \\ {{{\tilde {H}}}_{3}} = \left( {{{{\tilde {h}}}_{2}} - {{{\tilde {h}}}_{3}} + {{{\tilde {h}}}_{5}} - {{{\tilde {h}}}_{6}}} \right)\frac{{\sqrt 3 }}{2}{{d}_{5}}. \\ \end{gathered} $Область пространства, заполняемая концами векторов ${\mathbf{\tilde {H}}} = \left\langle {{{{\tilde {h}}}_{1}},{{{\tilde {h}}}_{2}}, \ldots ,{{{\tilde {h}}}_{6}}} \right\rangle $, представляет собой выпуклый многогранник ${{P}_{6}}$, общий вид которого показан на рис. 5. В случае отключения одного из маховиков (к примеру с осью, параллельной орту ${{{\mathbf{g}}}_{6}}$) область пространства, заполняемая концами векторов ${\mathbf{\tilde {H}}} = \left\langle {{{{\tilde {h}}}_{1}},{{{\tilde {h}}}_{2}}, \ldots ,{{{\tilde {h}}}_{5}}} \right\rangle $, представляет собой выпуклый многогранник ${{P}_{5}}$, общий вид которого показан на рис. 6. В этом случае скалярная запись векторного выражения (1.2) имеет вид
Случаи, когда отключены два или три маховика из шести сводятся к рассмотрению систем, описанных в разд. 1.1 для соответствующих ортов ${{{\mathbf{g}}}_{k}}$.
Все необходимые при построении многогранников ${{P}_{3}}$, ${{P}_{4}}$, ${{P}_{5}}$, ${{P}_{6}}$ соотношения для координат вершин, а также параметризация граней будут приведены ниже.
2. Область требуемых значений кинетического момента системы маховиков. Перейдем к рассмотрению области множества требуемых значений кинетического момента ${{H}_{T}}$. Введем связанную с КА правую декартову систему координат $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$, образованную его главными центральными осями инерции. Базисные орты этой системы обозначим ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}},$ ${{{\mathbf{e}}}_{3}}.$ Ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Полный кинетический момент КА можно представить в виде ${\mathbf{K}} = \hat {I}{\mathbf{\omega }} + {\mathbf{H}}$, где $\hat {I} = {\text{diag}}({{I}_{1}},{{I}_{2}},{{I}_{3}})$ – тензор инерции КА, ${\mathbf{\omega }} = {{({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}})}^{{\text{T}}}}$ – абсолютная угловая скорость КА, ${\mathbf{H}} = {{({{H}_{1}},{{H}_{2}},{{H}_{3}})}^{{\text{T}}}}$ – суммарный кинетический момент, создаваемый системой маховиков. В качестве примера будем рассматривать конечный поворот КА вокруг оси конечного вращения (поворот Эйлера), так как с помощью такого поворота может быть задано любое вращательное движение КА. При построении множества HT, необходимого для реализации конечного поворота КА, считаем, что ${\mathbf{\omega }}(0) = 0$ и ${\mathbf{H}}(0) = 0$, а также пренебрегаем накоплением кинетического момента от внешних сил за время поворота КА. Тогда при любом допустимом направлении оси конечного вращения мы имеем, что H = = $ - \hat {I}{\text{|}}{{{\mathbf{\omega }}}_{{{\text{пр}}}}}{\text{|}}{\mathbf{e}},$ или в матричном виде $\left\| {{{H}_{i}}} \right\|_{{i = 1}}^{3} = - \left\| {{{I}_{i}}{{\omega }_{{{\text{пр}}}}}{{e}_{i}}} \right\|_{{i = 1}}^{3}$. Здесь ${\mathbf{e}} = {{({{e}_{1}},{{e}_{2}},{{e}_{3}})}^{{\text{T}}}}$ – орт оси конечного вращения, ${{\omega }_{{{\text{пр}}}}} = {\text{|}}{{{\mathbf{\omega }}}_{{{\text{пр}}}}}{\text{|}}$ – модуль требуемой (программной) угловой скорости конечного поворота КА относительно орта ${\mathbf{e}}$. Откуда следует, что фигура множества ${{H}_{T}}$ представляет собой эллипсоид:
(2.1)
${{\left( {\frac{{{{H}_{1}}}}{{{{I}_{1}}}}} \right)}^{2}} + {{\left( {\frac{{{{H}_{2}}}}{{{{I}_{2}}}}} \right)}^{2}} + {{\left( {\frac{{{{H}_{3}}}}{{{{I}_{3}}}}} \right)}^{2}} \leqslant \omega _{{{\text{пр}}}}^{2}.$Как было сказано выше, чтобы система маховиков обеспечивала требования к динамике КА, должно выполняться условие (0.1). Проще всего проверить выполнение условия (0.1) можно, построив области ${{H}_{T}}$ и ${{H}_{C}}$ в одной системе координат и в едином масштабе, как будет показано далее.
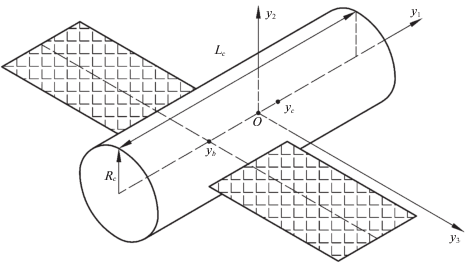
3. Расположение маховиков на КА. Рассмотрим КА – гиростат, форма которого аппроксимируется прямым круговым цилиндром (рис. 7) радиуса ${{R}_{c}}$ и высотой ${{L}_{c}}$, с двумя прикрепленными к нему одинаковыми прямоугольными пластинами – солнечными батареями суммарной площади ${{S}_{b}}$. Панели солнечных батарей неподвижны относительно цилиндра. Ось цилиндра совпадает с осью $O{{y}_{1}}$. Солнечные батареи расположены в плоскости $O{{y}_{1}}{{y}_{3}}$ симметрично относительно оси $O{{y}_{1}}$, стороны батарей параллельны осям $O{{y}_{1}}$ и $O{{y}_{3}}$, ось $O{{y}_{2}}$ перпендикулярна плоскости солнечных батарей. Координаты геометрических центров цилиндра и пластин солнечных батарей обозначим $({{y}_{c}},0,0)$ и $({{y}_{b}},0,0)$ соответственно. Далее, в расчетах используются следующие параметры КА: $m = $ 6440 кг, ${{I}_{1}} = $ 2600 кг ∙ м2, ${{I}_{2}} = $ 11 100 кг ∙ м2, ${{I}_{3}} = $ 10 900 кг ∙ м2, ${{R}_{c}}$ = 1.3 м, ${{L}_{c}}$ = 5.0 м, ${{S}_{b}}$ = 33 м2, ${{y}_{b}}$ = –1 м, ${{y}_{c}}$ = 0.3 м. Указанные параметры приближенно соответствуют спутникам Фотон-М № 4, Бион-М № 1. Полагаем, что на КА используется система одинаковых маховиков, для каждого из которых значение ${{h}_{{\max }}} = $ 18 Н ∙ м ∙ с.
Поскольку система управления ориентацией КА должна быть достаточно универсальной, естественно потребовать, чтобы максимальные абсолютные значения реализуемых ею угловых скоростей вращения КА ${{\omega }_{{i\;\max }}}$ вокруг каждой из осей $O{{y}_{i}},$ $i = 1,2,3,$ были одинаковы. Предположим, что K = 0, тогда справедливо соотношение
где ${{H}_{{i\;\max }}}$ – максимальные абсолютные значения кинетического момента, реализуемого системой маховиков по каждой из осей $O{{y}_{i}},$ $i = 1,2,3,$ здесь и далее полагаем ${{H}_{{i\;\max }}} > 0$.Совместим начала систем координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ в центре масс КА (начало системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ можно поместить в любое место, важно лишь угловое положение осей $O{{x}_{i}}$ относительно осей $O{{y}_{i}}$). Матрицу перехода от $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим U. Поскольку для моментов инерции КА выполняются соотношения ${{I}_{1}} < {{I}_{3}} < {{I}_{2}}$ и ${{I}_{2}} \approx {{I}_{3}}$, то наиболее рационально будет расположить “пирамиду” из четырех или шести маховиков таким образом, чтобы ее вершина лежала на оси $O{{y}_{1}}$ (или $ - O{{y}_{1}}$). Не ограничивая общности, будем считать, что направления осей систем $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ совпадают, $U = E$, где $E$ – единичная матрица порядка 3. Тогда, для системы четырех маховиков, расположенных по схеме “четырехугольная пирамида”, значения ${{H}_{{i\;\max }}}$ определяются соотношениями (1.3):
Исходя из условия ${{\omega }_{{1\;\max }}} = {{\omega }_{{2\;\max }}} = {{\omega }_{{3\;\max }}}$ и с учетом (3.1) зависимости, определяющие значения углов $\alpha $ и $\beta $, имеют вид
Тогда заданным величинам моментов инерции КА соответствуют углы $\alpha = 80.5^\circ $ и $\beta = 45.5^\circ $.
Для системы шести маховиков, расположенных по схеме “шестиугольная пирамида”, значения ${{H}_{{i\;\max }}}$ определяются соотношениями (1.4):
При условии ${{\omega }_{{1\;\max }}} = {{\omega }_{{2\;\max }}} = {{\omega }_{{3\;\max }}}$ зависимость, определяющая значение угла $\gamma $, имеет вид
Для заданных величин моментов инерции КА угол $\gamma = 81.1^\circ $.
Если по какой-либо оси $O{{y}_{i}},$ i = 1, 2, 3 реализуется отвечающее ей максимальное значение угловой скорости ${{\omega }_{{i\;\max }}}$, то компоненты угловой скорости по двум другим осям равны нулю. Значения ${{\omega }_{{i\;\max }}}$, i = 1, 2, 3 характеризуют предельные возможности каждой из рассматриваемых схем расположения маховиков для поворотов КА вокруг его главных центральных осей инерции. При произвольном выборе направления вектора угловой скорости в системе $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ максимальное значение модуля этого вектора будет меньше. Область допустимых значений угловой скорости КА, реализуемой системой маховиков, представляет собой многогранник, получающийся из многогранника ${{P}_{n}}$ преобразованием подобия, задаваемым формулами (3.1). Предельные значения угловых скоростей ${{\omega }_{{i\;\max }}}$, i = 1, 2, 3 реализуются в вершинах этого многогранника.
Еще одним из возможных критериев выбора расположения маховиков на КА является условие максимально возможного объема многогранника ${{P}_{n}}$. Как показано в работе [5], чтобы объем ${{P}_{n}}$ был максимальным, оси вращения всех маховиков системы должны быть расположены по боковым ребрам правильной n-угольной пирамиды, угол между боковым ребром и высотой которой не зависит от числа маховиков $n$ и равен ${\text{arctg}}(\sqrt 2 ) \approx 54.7^\circ $.
4. Анализ динамических возможностей системы маховиков. Как было написано выше, для того, чтобы система маховиков обеспечивала требования к динамике КА, должно выполняться условие (0.1). Условие (0.1) можно проверить, построив области ${{H}_{T}}$ и ${{H}_{C}}$ в одной системе координат и в едином масштабе. Чтобы соответствующим образом отобразить эллипсоид ${{H}_{T}}$ в системе координат $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$, необходимо уравнение (2.1) представить в безразмерном виде:
(4.1)
$\frac{{y_{1}^{2}}}{{l_{1}^{2}}} + \frac{{y_{2}^{2}}}{{l_{2}^{2}}} + \frac{{y_{3}^{2}}}{{l_{3}^{2}}} = 1,\quad {{l}_{i}} = \frac{{{{I}_{i}}{{\omega }_{{\max }}}}}{{{{h}_{{\max }}}}},$Примем значения параметров ${{h}_{{\max }}}$, $\alpha $, $\beta $, $\gamma $ как в разд. 3. Для схемы расположения маховиков “четырехугольная пирамида” на рис. 8 (вверху) показан соответствующий многогранник ${{P}_{4}}$, несколько граней которого изображены прозрачными. На этом же рисунке при значении ${{\omega }_{{\max }}} = $ = 0.184 град/c показан эллипсоид ${{H}_{T}}$, касательный к некоторым граням многогранника ${{P}_{4}}$, что соответствует выполнению условия (0.1). В качестве примера на рис. 8 (внизу) изображены многогранник ${{P}_{4}}$ и эллипсоид ${{H}_{T}}$ для значения ${{\omega }_{{\max }}} = $ 0.190 град/c, при котором эллипсоид выходит за грани многогранника. В случае отказа одного любого из маховиков выполнению условия (0.1) будет соответствовать значение ${{\omega }_{{\max }}} = $ 0.092 град/c.
Рис. 8.
Общий вид многогранника ${{P}_{4}}$ и эллипсоида ${{H}_{T}}$ (вверху при ${{\omega }_{{\max }}} = $ 0.184 град/c, внизу при ${{\omega }_{{\max }}} = $ = 0.190 град/c)
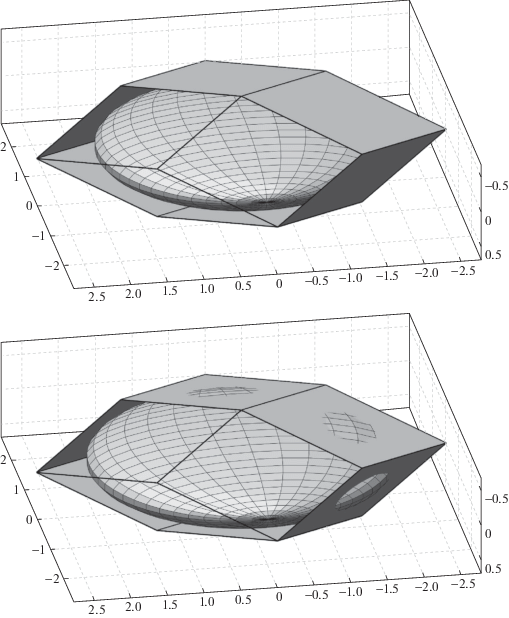
Для схемы расположения маховиков “шестиугольная пирамида” условие (0.1) будет выполнено при ${{\omega }_{{\max }}} = $ 0.292 град/c, а в случае отказа одного из маховиков – при ${{\omega }_{{\max }}} = $ 0.184 град/c. Схема из шести маховиков более устойчива к отказу, поскольку в этом случае реализуемое значение ωmax уменьшится в 1.6 раза, а для схемы из четырех маховиков в аналогичной ситуации значение ωmax уменьшится в 2 раза. Следует отметить, что для заданных значений моментов инерции КА, четыре маховика, используемые в схеме “четырехугольная пирамида”, благодаря более рациональному расположению, позволяют реализовать такое же значение ωmax, что и любые пять из шести маховиков, используемые в схеме “шестиугольная пирамида”.
Аналогичным способом формулу (4.1) можно применить чтобы определить максимальное значение реализуемого углового ускорения программных поворотов КА ${{\varepsilon }_{{\max }}}$ относительно произвольной выбранной оси. Для этого необходимо построить эллипсоид с полуосями li = = ${{I}_{i}}{{\varepsilon }_{{\max }}}{\text{/}}{{m}_{{\max }}}$, i = 1, 2, 3, где ${{m}_{{\max }}}$ – абсолютная величина предельного значения механического момента отдельного маховика. Найденные указанным способом значения ωmax и ${{\varepsilon }_{{\max }}}$ являются оценочными, поскольку не учитывают воздействие на КА внешних возмущающих моментов и физических характеристик самих маховиков.
5. Суммарный кинетический момент системы маховиков. Полагаем, что система состоит из $n \geqslant 3$ маховиков. Запишем орты ${{{\mathbf{g}}}_{k}}$, $k = \overline {1,n} $, осей вращения маховиков в виде матрицы $D = \left\| {{{{\mathbf{g}}}_{1}}, \ldots ,{{{\mathbf{g}}}_{n}}} \right\|$, тогда выражение (1.1) можно представить как
где $U$ – матрица перехода от $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$, $D$ – прямоугольная матрица размерности $3 \times n$, ${\mathbf{G}} = {{({{h}_{1}}, \ldots ,{{h}_{n}})}^{T}}$. В случае $n > 3$ соотношение (5.1) нельзя единственным образом разрешить относительно величин hk, $k = \overline {1,n} $. Для достижения единственности, потребуем, чтобы решение системы (5.1) относительно hk имело минимальную евклидову норму: Тогда где ${{D}^{ + }} = {{D}^{T}}{{(D{{D}^{T}})}^{{ - 1}}}$ – матрица, псевдообратная для матрицы $D$ [6]. Матрица D+ существует при условии, что в системе есть любые три маховика, у которых орты ${{{\mathbf{g}}}_{k}},$ $k = \overline {1,n} $, осей вращения линейно независимы. В случае n = 3 соотношения (5.1) разрешаются относительно ${{h}_{k}}$ единственным образом, при этом в выражении (5.2) матрица ${{D}^{ + }} = {{D}^{{ - 1}}}$ также при условии, что все три орта ${{{\mathbf{g}}}_{k}}$ линейно независимы. Для варианта расположения маховиков по схеме “четырехугольная пирамида” матрицы $D$ и ${{D}^{ + }}$ имеют видДля варианта “шестиугольная пирамида” матрицы $D$ и ${{D}^{ + }}$ имеют вид
Еще одним из способов достижения единственности решения системы (5.1) относительно ${{h}_{k}}$ является требование минимума нормы
Применение метода минимальной нормы ${{l}_{\infty }}$ позволяет системе маховиков наиболее эффективно использовать весь возможный объем области ${{H}_{C}}$ создаваемого кинетического момента [7]. Однако в отличие от решения с минимальной евклидовой нормой ${{l}_{2}}$, метод минимальной нормы ${{l}_{\infty }}$ в общем случае представлен не в виде конечных формул, а как некоторый алгоритм поиска решения. Примеры реализации указанных алгоритмов при использовании систем из четырех или шести маховиков приведены в работах [7–9].
6. Оценка накопленного кинетического момента маховиков. При использовании системы маховиков одним из критериев эффективности ее функционирования является скорость накопления собственного кинетического момента. Эта скорость определяет промежутки времени между разгрузками системы маховиков и должна быть достаточно малой, чтобы обеспечить продолжительные отрезки невозмущенного полета КА.
Введем правую декартову орбитальную систему координат $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$. Точка $O$ – центр масс КА, ось $O{{z}_{3}}$ направлена вдоль геоцентрического радиус-вектора точки $O,$ ось $O{{z}_{2}}$ – вдоль вектора кинетического момента орбитального движения КА. Базисные орты этой системы обозначим через ${{{\mathbf{E}}}_{1}}$, ${{{\mathbf{E}}}_{2}}$, ${{{\mathbf{E}}}_{3}}$. Матрицу перехода от системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ к системе $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$ запишем как $A = \left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$, где ${{a}_{{ij}}} = {{{\mathbf{E}}}_{i}} \cdot {{{\mathbf{e}}}_{j}}$ – косинусы углов, которые образуют ось $O{{y}_{j}}$ с осью $O{{z}_{i}}.$ Матрицу A параметризируем углами $\psi $, $\vartheta $ и $\varphi $, которые введем следующим образом. Система $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ может быть получена из системы $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$ тремя последовательными поворотами: 1) на угол $\vartheta + \pi {\text{/}}2$ вокруг оси $O{{z}_{2}}$, 2) на угол $\varphi $ вокруг новой оси $O{{z}_{3}}$, 3) на угол $\psi $ вокруг оси $O{{z}_{1}},$ полученной после первых двух поворотов и совпадающей с осью $O{{y}_{1}}$. Элементы матрицы $A$ выражаются через эти углы с помощью формул:
Оценим возможности системы маховиков при стабилизации КА в орбитальной системе координат $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$ [10, 11]. При поддержании неизменной ориентации КА в системе $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$ кинетический момент маховиков должен изменяться в соответствии с уравнениями
(6.1)
$\frac{{\tilde {d}{\mathbf{K}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{K}} = {\mathbf{M}},\quad {\mathbf{K}} = \hat {I}{\mathbf{\omega }} + {\mathbf{H}}.$Здесь ${\mathbf{M}} = {{({{M}_{1}},{{M}_{2}},{{M}_{3}})}^{{\text{T}}}}$ – главный момент внешних сил, приложенных к КА, символом $\tilde {d}{\text{/}}dt$ обозначена локальная производная вектора, определяющая его изменение в системе $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Из внешних моментов будем учитывать только гравитационный и восстанавливающий аэродинамический. Гравитационный момент задается формулой [12]
(6.2)
${{{\mathbf{M}}}_{g}} = 3\frac{{{{\mu }_{E}}}}{{{{r}^{5}}}}({\mathbf{r}} \times \hat {I}{\mathbf{r}}),\quad r = {\text{|}}{\mathbf{r}}{\text{|,}}$(6.3)
${{{\mathbf{M}}}_{a}} = p({\mathbf{v}} \times {{{\mathbf{e}}}_{1}}),\quad p = {{\rho }_{a}}(\pi R_{c}^{2}{{y}_{c}}{\text{|}}{{{v}}_{1}}{\text{|}} + {{S}_{b}}{{y}_{b}}{\text{|}}{{{v}}_{2}}{\text{|}} + 2{{R}_{c}}{{L}_{c}}{{y}_{c}}\sqrt {{v}_{2}^{2} + {v}_{3}^{2}} ),$При оценке накопленного кинетического момента маховиков будем считать, что орбита КА круговая радиуса r и неизменна в абсолютном пространстве. Влияние атмосферы учитываем в предположении, что скорость набегающего потока направлена по касательной к орбите КА. Тогда ${\mathbf{\omega }} = {{\omega }_{0}}{{{\mathbf{E}}}_{2}}$, ${\mathbf{r}} = r\,{{{\mathbf{E}}}_{3}}$, ${\mathbf{v}} = {v}{{{\mathbf{E}}}_{1}}$, где ${v} = {\text{|}}{\mathbf{v}}{\text{|}} = {{\omega }_{0}}r$, ${{\omega }_{0}} = \sqrt {{{\mu }_{E}}{\text{/}}{{r}^{3}}} $ – среднее движение КА (орбитальная частота). С учетом указанных допущений уравнение, описывающее изменение кинетического момента системы маховиков, можно представить в виде
(6.4)
$\frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {{\omega }_{0}}{{{\mathbf{E}}}_{2}} \times {\mathbf{H}} = - \hat {I}\frac{{d{\mathbf{\omega }}}}{{dt}} - \omega _{0}^{2}({{{\mathbf{E}}}_{2}} \times \hat {I}{{{\mathbf{E}}}_{2}}) + 3\omega _{0}^{2}({{{\mathbf{E}}}_{3}} \times \hat {I}{{{\mathbf{E}}}_{3}}) + p{v}({{{\mathbf{E}}}_{1}} \times {{{\mathbf{e}}}_{1}}).$Так как мы рассматриваем именно стабилизацию КА, то первым слагаемым в правой части уравнения (6.4) можно пренебречь. Тогда уравнение (6.4) запишем как
(6.5)
$\frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {{\omega }_{0}}{{{\mathbf{E}}}_{2}} \times {\mathbf{H}} = \omega _{0}^{2}[3({{{\mathbf{E}}}_{3}} \times \hat {I}{{{\mathbf{E}}}_{3}}) - ({{{\mathbf{E}}}_{2}} \times \hat {I}{{{\mathbf{E}}}_{2}})] + p{v}({{{\mathbf{E}}}_{1}} \times {{{\mathbf{e}}}_{1}}).$Рассмотрим режим стабилизации КА относительно орбитальной системы координат, при котором ${\mathbf{\omega }} = {{\omega }_{0}}{{{\mathbf{E}}}_{2}}$, а орты ${{{\mathbf{e}}}_{i}}$ совпадают с ортами $ \pm {{{\mathbf{E}}}_{j}}$, $i,j = 1,2,3$. Такую ориентацию КА будем называть орбитальной [10] и в данном случае с учетом принятых допущений она соответствует одному из положений равновесия (покоя) КА в орбитальной системе координат. Для определенности будем рассматривать стабилизацию КА в окрестности положения
(6.6)
${{{\mathbf{e}}}_{1}} = {{{\mathbf{E}}}_{1}},\quad {{{\mathbf{e}}}_{2}} = {{{\mathbf{E}}}_{3}},\quad {{{\mathbf{e}}}_{3}} = - {{{\mathbf{E}}}_{2}}.$При выполнении неравенств ${{I}_{1}} < {{I}_{3}} < {{I}_{2}}$ положение равновесия (6.6) является неустойчивым [12]. Линеаризуем уравнение (6.5) в окрестности положения (6.6), которому соответствуют значения углов $\psi = - \vartheta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, φ = 0. В проекциях на оси системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ с учетом соотношений ${{{\mathbf{E}}}_{i}} = ({{a}_{{i1}}},{{a}_{{i2}}},{{a}_{{i3}}})$, $i = 1,2,3,$ уравнение (6.5) примет вид
(6.7)
$\begin{gathered} {{{\dot {H}}}_{1}} + {{\omega }_{0}}{{H}_{2}} = {{M}_{1}},\quad {{{\dot {H}}}_{2}} - {{\omega }_{0}}{{H}_{1}} = {{M}_{2}},\quad {{{\dot {H}}}_{3}} = {{M}_{3}}, \\ {{M}_{1}} = 4\omega _{0}^{2}({{I}_{2}} - {{I}_{3}})\tilde {\psi },\quad {{M}_{2}} = (\omega _{0}^{2}({{I}_{1}} - {{I}_{3}}) + \pi R_{c}^{2}{{y}_{c}}{{\rho }_{a}}{{{v}}^{2}})\varphi , \\ {{M}_{3}} = (3\omega _{0}^{2}({{I}_{1}} - {{I}_{2}}) - \pi R_{c}^{2}{{y}_{c}}{{\rho }_{a}}{{{v}}^{2}})\tilde {\vartheta },\quad \tilde {\vartheta } = \vartheta + \pi {\text{/}}2,\quad \tilde {\psi } = \psi - \pi {\text{/}}2. \\ \end{gathered} $При фиксированных значениях углов $\psi $, $\vartheta $, $\varphi $ внешние моменты ${{M}_{i}} = {\text{const}}$, и уравнения (6.7) легко проинтегрировать. Их решение с нулевыми начальными условиями запишем как
(6.8)
$\begin{gathered} {{H}_{1}} = \frac{1}{{{{\omega }_{0}}}}\left[ {{{M}_{1}}\sin {{\omega }_{0}}t - {{M}_{2}}(1 - \cos {{\omega }_{0}}t)} \right],\quad {{H}_{2}} = \frac{1}{{{{\omega }_{0}}}}\left[ {{{M}_{1}}(1 - \cos {{\omega }_{0}}t) + {{M}_{2}}\sin {{\omega }_{0}}t} \right], \\ {{H}_{3}} = {{M}_{3}}t. \\ \end{gathered} $Отсюда получаем
В данном случае значения $\tilde {\psi }$, $\tilde {\vartheta }$, $\varphi $ фактически представляют собой точности стабилизации КА относительно положения (6.6) в соответствующем канале управления.
Из уравнений (6.8) следует, что накопление составляющих ${{H}_{1}}$, ${{H}_{2}}$ кинетического момента системы маховиков носит циклический характер, сами составляющие ${{H}_{1}}$, ${{H}_{2}}$ связаны соотношением
При этом составляющая H3 неограниченно возрастает с течением времени.
Приведенные выше соотношения позволяют определить требования к системе маховиков, обеспечивающие реализацию режима стабилизации КА в орбитальной системе координат в окрестности положения (6.6). Необходимость их точного определения возникает, как правило, только при отсутствии в программе функционирования КА режимов программных поворотов, имеющих более высокие требования к множеству возможных значений суммарного кинетического момента, создаваемого маховиками.
Обеспечить стабилизацию КА относительно положения (6.6) можно с помощью системы из четырех или шести маховиков, которые расположены вершиной соответствующей “пирамиды” по оси $O{{y}_{1}}$ (или $ - O{{y}_{1}}$) и при значениях углов $\alpha $, $\beta $ и $\gamma $, приведенных в разд. 3. Но если основным режимом функционирования КА является его орбитальная ориентация в окрестности положения (6.6), то можно выбрать более оптимальные значения углов $\alpha $, $\beta $ и $\gamma $.
Рассмотрим систему четырех маховиков, расположенных по схеме “четырехугольная пирамида” и представим компоненты вектора ${\mathbf{G}},$ определяемого уравнением (5.2), в виде функций ${{h}_{k}}(\alpha ,\beta )$, $k = \overline {1,4} $. В области $0 < \alpha < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, $0 < \beta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ найдем значения углов $\alpha $ и $\beta $, при которых функция
будет иметь минимум. В указанной области функция (6.9) является непрерывно дифференцируемой. Положим, что ${{H}_{i}} = {{H}_{{i\;\max }}} = {\text{const}}\;{\text{ > }}\;{\text{0}}$, $i = 1,2,3,$ тогда минимум функции (6.9) достигается при(6.10)
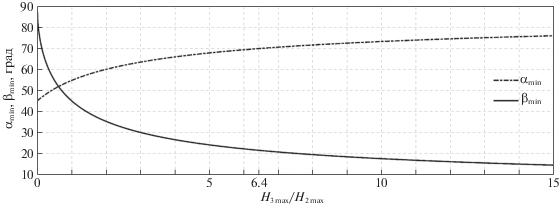
$\begin{gathered} {{\alpha }_{{\min }}} = {\text{arctg}}\left( {\sqrt[4]{{{{{\left( {\frac{{{{H}_{{2\;\max }}}}}{{{{H}_{{1\;\max }}}\sin {{\beta }_{{\min }}}}}} \right)}}^{2}} + {{{\left( {\frac{{{{H}_{{3\;\max }}}}}{{{{H}_{{1\;\max }}}\cos {{\beta }_{{\min }}}}}} \right)}}^{2}}}}} \right) = {\text{arctg}}\left( {\sqrt {\frac{{{{H}_{{2\;\max }}} + {{H}_{{3\;\max }}}}}{{{{H}_{{1\;\max }}}}}} } \right), \\ {{\beta }_{{\min }}} = {\text{arctg}}\left( {\sqrt {\frac{{{{H}_{{2\;\max }}}}}{{{{H}_{{3\;\max }}}}}} } \right). \\ \end{gathered} $На рис. 9 приведен график зависимости углов ${{\alpha }_{{\min }}}$ и ${{\beta }_{{\min }}}$ от ${{{{H}_{{3\;\max }}}} \mathord{\left/ {\vphantom {{{{H}_{{3\;\max }}}} {{{H}_{{2\;\max }}}}}} \right. \kern-0em} {{{H}_{{2\;\max }}}}}$ при условии, что H1 max = ${{H}_{{2\;\max }}}.$
Рис. 9.
Зависимость величин ${{\alpha }_{{\min }}}$, ${{\beta }_{{\min }}}$ от ${{{{H}_{{3\;\max }}}} \mathord{\left/ {\vphantom {{{{H}_{{3\;\max }}}} {{{H}_{{2\;\max }}}}}} \right. \kern-0em} {{{H}_{{2\;\max }}}}}$, при ${{H}_{{1\;\max }}} = {{H}_{{2\;\max }}}$
Аналогичным способом можно выбрать значение угла $\gamma $ при использовании системы шести маховиков, расположенных по схеме “шестиугольная пирамида”. В этом случае минимум функции
на интервале $0 < \gamma < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ достигается при(6.11)
${{\gamma }_{{\min }}} = {\text{arctg}}\left( {\sqrt[4]{{\frac{{2H_{{2\,\max }}^{2} + 2H_{{3\,\max }}^{2}}}{{H_{{1\,\max }}^{2}}}}}} \right).$Соотношение (6.11) верно для систем с любым количеством маховиков, расположенных по боковым ребрам правильной $n$-угольной пирамиды, у которой ${{\gamma }_{{\min }}}$ – угол между боковым ребром и высотой. В случае, когда ${{H}_{{1\;\max }}} = {{H}_{{2\;\max }}} = {{H}_{{3\;\max }}}$, значение угла ${{\gamma }_{{\min }}} = {\text{arctg}}(\sqrt 2 ) \approx 54.7^\circ $, при котором соответствующий многогранник Pn системы маховиков будет иметь максимальный объем.
Используя формулы (6.8), можно получить лишь весьма приблизительную оценку величины накапливаемого собственного кинетического момента системы маховиков. Более точные значения ${{H}_{{i\;\max }}}$, используемые для расчета значений углов ${{\alpha }_{{\min }}}$, ${{\beta }_{{\min }}}$, ${{\gamma }_{{\min }}}$, можно получить в результате численного моделирования уравнений движения КА.
7. Численное моделирование уравнений движения КА. Более точно определить величину накапливаемого кинетического момента системы маховиков, а также рассчитать значения параметров $\alpha ,$ $\beta $ и $\gamma $ можно по результатам численного моделирования полной системы уравнений движения КА. В качестве примера рассмотрим стабилизацию КА в орбитальной системе координат в окрестности положения (6.6). Для стабилизации КА используется система из четырех маховиков, расположенных по схеме “четырехугольная пирамида”.
Введем правую декартову гринвичскую систему координат ${{O}_{E}}{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$. Ее начало находится в центре Земли, плоскость ${{O}_{E}}{{Y}_{1}}{{Y}_{2}}$ совпадает с плоскостью экватора, ось ${{O}_{E}}{{Y}_{1}}$ пересекает гринвичский меридиан, ось ${{O}_{E}}{{Y}_{3}}$ направлена к Северному полюсу. Матрицу перехода от системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ к системе ${{O}_{E}}{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ обозначим $B = \left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$, где bij – косинус угла между осями ${{O}_{E}}{{Y}_{i}}$ и $O{{y}_{j}}$. Матрицу перехода от орбитальной системы к гринвичской системе обозначим $C = \left\| {{{c}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$, где cij – косинус угла между осями ${{O}_{E}}{{Y}_{i}}$ и $O{{z}_{j}}$. Элементы этой матрицы выражаются через координаты и компоненты скорости центра масс КА в гринвичской системе. Справедливо соотношение $B = CA$.
Уравнения движения КА состоят из двух подсистем. Одна подсистема описывает движение центра масс КА, другая – движение относительно центра масс (вращательное движение). Первая подсистема записывается в гринвичской системе координат. Ее переменными служат компоненты векторов ${\mathbf{r}}$ и ${\mathbf{v}}$ [14]. В ней учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16,16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается в соответствии с моделью ГОСТ Р 25645.166-2004. Баллистический коэффициент КА и параметры атмосферы считаются неизменными на всем интервале интегрирования уравнений движения.
Подсистема уравнений вращательного движения КА состоит из уравнений (6.1), где M = = ${{{\mathbf{M}}}_{a}} + {{{\mathbf{M}}}_{g}}$, и уравнений
(7.1)
$\frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{H}} = - {{{\mathbf{M}}}_{c}},\quad \frac{{\tilde {d}{{{\mathbf{b}}}_{1}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{1}} = {{\omega }_{E}}{{{\mathbf{b}}}_{2}},\quad \frac{{\tilde {d}{{{\mathbf{b}}}_{2}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{2}} = - {{\omega }_{E}}{{{\mathbf{b}}}_{1}},$(7.2)
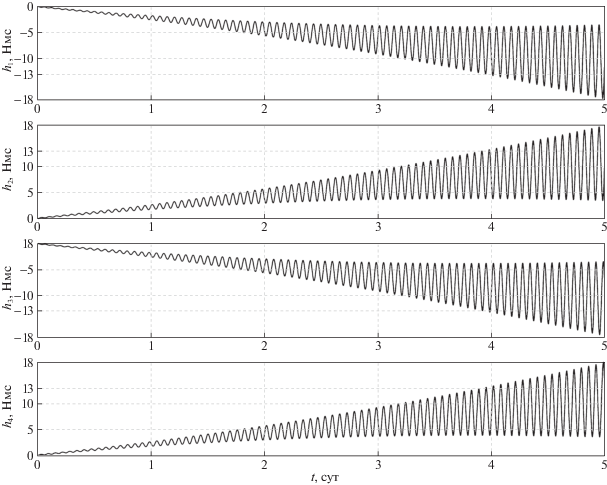
${{{\mathbf{M}}}_{c}} = {{\xi }^{2}}\hat {I}({{{\mathbf{e}}}_{2}} \times {{{\mathbf{E}}}_{3}} + {{{\mathbf{E}}}_{2}} \times {{{\mathbf{e}}}_{3}}) - 2\xi \hat {I}({\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}),$Моделирование режима орбитальной ориентации КА в окрестности положения (6.6) сводилось к численному интегрированию системы (6.1), (7.1), (7.2) с использованием соотношений (5.1), (5.2). Начальные условия движения центра масс КА задавались в восходящем узле орбиты в момент 09:10:34 UTC 21.09.2007. Начальные элементы орбиты: высота в апогее 450 км, высота в перигее 400 км, наклонение 63.0°, аргумент широты перигея 53.5°, долгота восходящего узла (отсчитывается от точки среднего весеннего равноденствия эпохи даты) 164.0°. Параметры модели атмосферы: ${{F}_{{10.7}}} = {{F}_{{81}}} = $ 150, ${{A}_{p}} = $ 12. Начальные условия системы (6.1), (7.1), (7.2): $\psi (0) = - \vartheta (0)$ = π/2, $\varphi (0) = 0$, ${{\omega }_{1}}(0) = {{\omega }_{2}}(0) = 0$, ${{\omega }_{3}}(0) = - {{\omega }_{0}},$ ${\mathbf{H}}(0) = 0$. Они задавались в тот же момент времени, что и начальные условия орбитального движения. Этот момент служит началом отсчета времени – точкой $t = 0$. Параметры КА приведены в разд. 3, значения $\xi = 0.0025$ c–1, ${{\omega }_{0}} = 0.001125$ c–1. Результаты расчетов движения КА, полученные в рамках принятой модели на интервале времени 5 сут, приведены на рис. 10–13. На рис. 10 представлены графики зависимости от времени углов ориентации КА, из которых видно, что закон управления (7.2) обеспечивает стабилизацию КА в окрестности положения (6.6) с погрешностями по углам $\psi ,$ $\theta $, $\varphi $ не более ±0.005°, ±0.5°, ±0.05° соответственно. Амплитуды установившихся колебаний компонентов вектора абсолютной угловой скорости КА ограничены значениями:
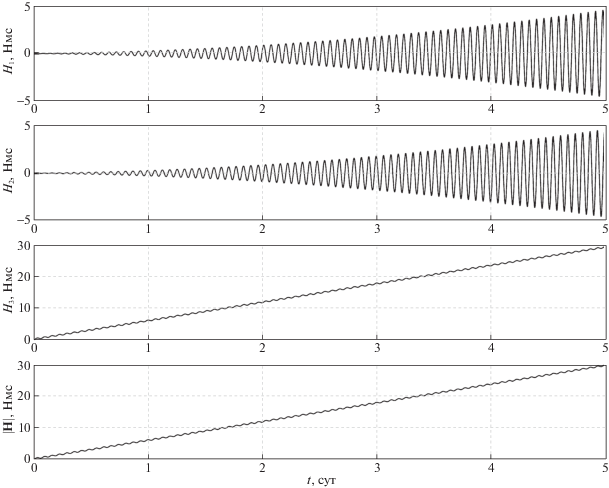
На рис. 11 представлены графики зависимости от времени компонентов вектора собственного кинетического момента системы маховиков Hi, i = 1, 2, 3, которые на момент окончания моделирования достигли значений
(7.3)
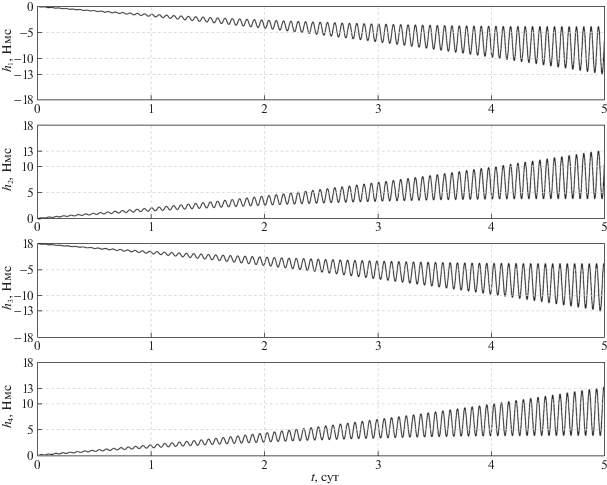
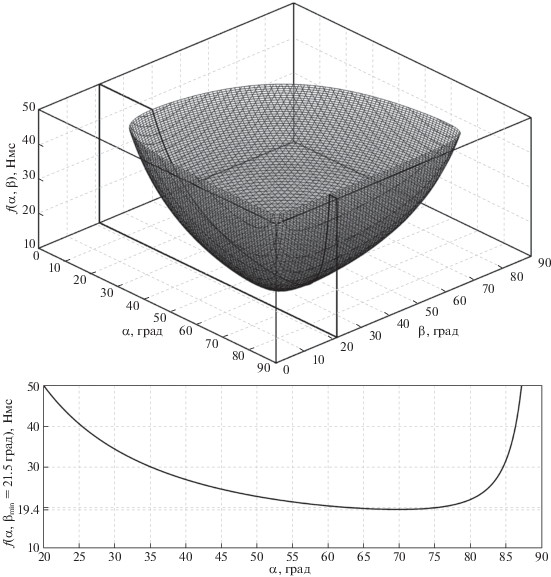
${{H}_{{1\max }}} = {{H}_{{2\max }}} = 4.6\,\,{\text{H}} \cdot {\text{м}} \cdot {\text{c}},\quad {{H}_{{3\max }}} = 29.6\,\,{\text{H}} \cdot {\text{м}} \cdot {\text{c}}.$Величина H3 возрастает на всем интервале времени моделирования, что соответствует третьему уравнению (6.8). На графиках величин ${{H}_{1}}$, ${{H}_{2}}$ видно медленное (по сравнению с возрастанием H3), но постоянное увеличение амплитуд их колебаний относительно средних значений ${{H}_{1}} = 0$ и ${{H}_{2}} = 0$ соответственно. Это вызвано в первую очередь влиянием атмосферы, которое при моделировании движения КА учитывается более точно, чем в случае уравнений (6.7). Частота колебаний значений углов $\psi ,$ $\theta $, $\varphi ,$ компонентов угловой скорости и ${{H}_{i}}$, i = 1, 2, 3, равна ${{\omega }_{0}}$. На рис. 12 представлены графики зависимости от времени собственных кинетических моментов маховиков ${{h}_{k}}$, $k = \overline {1,4} $, в случае, когда значения углов $\alpha = 80.5^\circ $ и $\beta = 45.5^\circ $ (см. разд. 3). На представленных графиках видно, что на момент окончания моделирования кинетический момент каждого из маховиков практически достиг своего предельного значения ${{h}_{{\max }}} = $ 18 Н ∙ м ∙ с, после превышения которого маховик утратит возможность создавать необходимый управляющий момент для поддержания заданной ориентации КА. Воспользуемся уравнением (6.10), использовав полученные значения (7.3), и вычислим значения углов ${{\alpha }_{{\min }}} = $ 70.0° и ${{\beta }_{{\min }}} = $ 21.5°. Поскольку в данном случае ${{H}_{{1\;\max }}} = {{H}_{{2\;\max }}}$, то значения углов ${{\alpha }_{{\min }}}$, ${{\beta }_{{\min }}}$ представлены на графике рис. 9 при ${{{{H}_{{3\;\max }}}} \mathord{\left/ {\vphantom {{{{H}_{{3\;\max }}}} {{{H}_{{2\;\max }}}}}} \right. \kern-0em} {{{H}_{{2\;\max }}}}} \approx $ 6.4. На рис. 13 приведены графики зависимости от времени величин hk, $k = \overline {1,4} $, при значении углов $\alpha = {{\alpha }_{{\min }}} = $ 70.0° и $\beta = {{\beta }_{{\min }}} = $ $21.5^\circ $. На представленных графиках видно, что использование значений $\alpha = {{\alpha }_{{\min }}}$, $\beta = {{\beta }_{{\min }}}$ позволило уменьшить амплитуду колебаний величин hk, $k = \overline {1,4} $, на момент окончания моделирования примерно в 1.4 раза по сравнению с аналогичными графиками на рис. 12. Это дает возможность увеличить продолжительность стабилизации КА относительно положения (6.6) до момента насыщения какого-либо из маховиков примерно на 31 ч. Кроме того, уменьшение амплитуды колебаний величин hk снижает потребление электроэнергии двигателем привода каждого маховика за счет уменьшения величины создаваемого им механического момента. На рис. 14 для значений (7.3) приведен график функции (6.9), его сечение плоскостью $\beta = {{\beta }_{{\min }}} = $ 21.5° и показано значение $f({{\alpha }_{{\min }}},{{\beta }_{{\min }}}) = $19.4 Н · м · с.
В разд. 4 был предложен способ оценки максимальных значений реализуемой угловой скорости ${{\omega }_{{\max }}}$ и углового ускорения ${{\varepsilon }_{{\max }}}$ конечного поворота КА относительно произвольной выбранной оси при условии отсутствия внешних возмущающих моментов. Более точные значения ${{\omega }_{{\max }}}$ и ${{\varepsilon }_{{\max }}}$, реализуемые при конечном повороте, также можно получить путем численного моделирования уравнений движения КА с учетом физических характеристик маховиков, всех действующих внешних возмущающих моментов и выбранного закона управления вращательным движением КА. Но эта задача может послужить темой для отдельного исследования и в данной работе не рассматривалась.
8. Построение областей возможных значений кинетического момента системы маховиков. Обозначим вершины и грани многогранника ${{P}_{n}}$ как ${{V}_{i}}$, $V_{i}^{'}$, $i = \overline {1,{{n(n - 1)} \mathord{\left/ {\vphantom {{n(n - 1)} 2}} \right. \kern-0em} 2} + 1} ,$ и ${{F}_{i}}$, $F_{i}^{'}$, $i = \overline {1,{{n(n - 1)} \mathord{\left/ {\vphantom {{n(n - 1)} 2}} \right. \kern-0em} 2}} ,$ соответственно. Вершины ${{V}_{i}}$, $V_{i}^{'}$ будем задавать своими координатами в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ таким образом, чтобы для координат выполнялось соотношение $V_{i}^{'} = - {{V}_{i}}$. Грани ${{F}_{i}}$ будем задавать списком принадлежащих им вершин ${{V}_{i}}$, $V_{i}^{'}$, при этом $F_{i}^{'}$ будет расположена симметрично ${{F}_{i}}$ относительно точки $O$.
8.1. Схема “четырехугольная пирамида”. Положение вершин ${{V}_{i}},$ $i = \overline {1,7} ,$ многогранника P4 характеризуется следующими соотношениями:
Грани ${{F}_{i}}$, $F_{i}^{'}$, $i = \overline {1,6} ,$ многогранника P4 зададим как
В случае отключения маховика с осью, параллельной орту ${{{\mathbf{g}}}_{4}}$, многогранник P4 трансформируется в параллелепипед P3. Положение вершин ${{V}_{i}}$, $i = \overline {1,4} ,$ параллелепипеда характеризуется соотношениями:
Как всякий параллелепипед, P3 имеет шесть граней, которые зададим в виде
8.2. Схема “шестиугольная пирамида”. Положение вершин Vi, $i = \overline {1,16} ,$ многогранника ${{P}_{6}}$ характеризуется как
Грани ${{F}_{i}}$, $i = \overline {1,15} ,$ многогранника ${{P}_{6}}$ представим как
В случае отключения маховика с осью, параллельной орту ${{{\mathbf{g}}}_{6}}$, многогранник ${{P}_{6}}$ трансформируется в многогранник ${{P}_{5}}$. Положение вершин ${{V}_{i}}$, $i = \overline {1,11} ,$ многогранника ${{P}_{5}}$ характеризуется соотношениями:
Грани ${{F}_{i}}$, $i = \overline {1,10} ,$ многогранника ${{P}_{5}}$ зададим как
Приведенные выше соотношения для координат вершин ${{V}_{i}}$, $V_{i}^{'}$, а также параметризация граней ${{F}_{i}}$, $F_{i}^{'}$ использовались при построении многогранников ${{P}_{4}}$, ${{P}_{3}}$, ${{P}_{6}},$ ${{P}_{5}}$, приведенных на рис. 2, 3, 5, 6 соответственно.
Заключение. В работе исследованы два варианта системы маховиков, расположенной на КА для управления его вращательным движением. Для каждого из вариантов построены области реализуемых системой значений суммарного кинетического момента, в том числе при отказе одного из маховиков.
Для режима программных поворотов КА построена область требуемых значений суммарного кинетического момента системы маховиков. Предложенный в работе способ сравнения областей требуемого и реализуемого кинетического момента и полученные аналитические зависимости позволяют выбрать необходимые параметры системы, обеспечивающие реализацию вектора требуемой угловой скорости вращения КА.
Для режима стабилизации орбитальной ориентации КА приведены зависимости, позволяющие выбрать значения геометрических параметров расположения системы маховиков. Выбранные значения обеспечивают минимальную скорость накопления кинетического момента каждым из маховиков системы. Приведены результаты математического моделирования системы уравнений движения КА, подтверждающие правильность выбранных значений указанных параметров.
Полученные в работе результаты могут быть использованы при предварительном проектировании систем управления ориентацией КА, применяющих в качестве исполнительных органов двигатели-маховики.
Список литературы
Раушенбах Б.В., Токарь Е.Н. Управление ориентацией космических аппаратов. М.: Наука, 1974.
Сорокин А.В., Башкеев Н.И., Яременко В.В. и др. Гиросиловая система ориентации космического аппарата “Ресурс-ДК” // Тр. IX Санкт-Петербургской Междунар. конф. по интегрированным навигационным системам. СПб.: ЦНИИ “Электроприбор”, 2002. С. 268–274.
Васильев В.Н. Системы ориентации космических аппаратов. М.: ФГУП “НПП ВНИИЭМ”, 2009.
Игнатов А.И., Давыдов А.А., Сазонов В.В. Анализ динамических возможностей систем управления малым космическим аппаратом, построенных на базе двигателей-маховиков. Препринт № 47. М.: ИПМ им. М.В. Келдыша РАН, 2005.
Карпачев Ю.А., Павловский М.А. Управление ориентацией космических аппаратов с произвольно-избыточной структурой одноосных электромаховичных двигателей // Космич. исслед. 1987. Т. XXV. № 4. С. 530–536.
Гантмахер Ф.Р. Теория матриц. 4-е изд. М.: Наука. Физматлит, 1988.
Markley F.L., Reynolds R.G., Liu F.X. Maximum Torque and Momentum Envelopes for Reaction-wheel Arrays // J. of Guidance, Control, and Dynamics. 2010. V. 33. № 5. P. 1606–1614.
Yoon H., Seo H.H., Choi H.-T. Optimal Uses of Reaction Wheels in the Pyramid Configuration Using a New Minimum Infinity-norm Solution // Aerospace Science and Technology. 2014. V. 39. P. 109–119.
Yoon H., Seo H. H., Park Y.-W., Choi H.-T. A New Minimum Infinity-Norm Solution: with Application to Capacity Analysis of Spacecraft Reaction Wheels // American Control Conf. (ACC). Chicago, IL. 2015. P. 1241–1245.
Игнатов А.И., Сазонов В.В. Реализация режима орбитальной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы // Изв. РАН. ТиСУ. 2020. № 1. С. 129–142.
Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Стабилизация орбитальной ориентации космического аппарата с одновременной разгрузкой кинетического момента инерционных исполнительных органов // Изв. РАН. ТиСУ. 2015. № 4. С. 124–131.
Белецкий В.В. Движение искусственного КА относительно центра масс. М.: Наука, 1965.
Белецкий В.В., Яншин А.М. Влияние аэродинамических сил на вращательное движение искусственных спутников. Киев: Наук. думка, 1984.
Бажинов И.К., Гаврилов В.П., Ястребов В.Д. и др. Навигационное обеспечение полета орбитального комплекса “Салют-6”–“Союз”–“Прогресс”. М.: Наука, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления