Известия РАН. Теория и системы управления, 2022, № 1, стр. 105-123
ОПТИМИЗАЦИЯ ПРОЦЕССА СОВЕРШЕНСТВОВАНИЯ АВИАЦИОННЫХ КОМПЛЕКСОВ НА БАЗЕ КОНЦЕПЦИИ ФУНКЦИОНАЛЬНОГО ПРОЕКТИРОВАНИЯ
К. С. Анисимов a, В. Н. Евдокименков b, *, М. Н. Красильщиков b, К. И. Сыпало a, Н. Б. Топоров a, c
a ЦАГИ им. проф. Н.Е. Жуковского
Москва, Россия
b МАИ (национальный исследовательский ун-т)
Москва, Россия
c НИЦ им. Н.Е. Жуковского
Москва, Россия
* E-mail: evdokimenkovvn@mai.ru
Поступила в редакцию 17.08.2021
После доработки 27.08.2021
Принята к публикации 27.09.2021
- EDN: MQHLSR
- DOI: 10.31857/S0002338822010036
Аннотация
Развивается концепция функционального проектирования авиационных комплексов – этапа, предшествующего традиционным этапам структурного, компоновочного и обликового проектирования. Показано, что развиваемая концепция функционального проектирования оптимизирует существующий процесс путем сокращения временных и материальных затрат на создание перспективных образцов авиационной техники вследствие исключения из дальнейшего углубленного анализа заведомо неприемлемых вариантов облика перспективного летательного аппарата. Описаны предложенные на основе аппарата оптимизации методы и алгоритмы решения задач, возникающих на этапе функционального проектирования.
Эффективность разработанных методов и алгоритмов иллюстрируется примером формирования облика перспективного самолета транспортной категории на основе развитой концепции.
Введение. Последние десятилетия характеризуются стремительным развитием авиакосмических технологий, что создает необходимые условия для дальнейшего совершенствования авиационной техники. Вместе с тем свойства упомянутых технологий, потенциально способных радикально изменить характеристики авиационных комплексов, таковы, что общепризнанный в настоящее время подход к формированию облика перспективных образцов таких комплексов, состоящий в масштабировании на основе новых технологий характеристик некоторого наилучшего в принятом смысле варианта на предварительно сформированном множестве альтернатив, не приводит к достижению требуемого эффекта с точки зрения принятых критериев. Выход в данном случае, по мнению авторов, состоит в использовании развиваемой концепции так называемого функционального проектирования, заключающейся в генерации комбинаций возможных с точки зрения функциональных требований к проектируемому образцу технических решений. Каждой такой комбинации соответствует альтернативный вариант проектируемого образца авиационной техники (АТ). Количество таких комбинаций ограничивается направленностью процедуры их формирования с учетом перечня задач, для решения которых предполагается использовать проектируемый образец АТ, приоритетными направлениями развития вида АТ, которому принадлежит разрабатываемый образец, а также составом существующих и перспективных технологий реализации функциональных требований к АТ.
Таким образом, в рамках сформулированной выше концепции основные задачи функционального состоят в:
определении предпочтительного с точки зрения решаемой целевой задачи типа перспективного летательного аппарата (ЛА) в зависимости от реализуемого принципа полета;
формировании вариантов облика перспективного ЛА выбранного типа с учетом накопленного научно-технологического задела;
формировании облика проектируемого ЛА с учетом перспективных научно-технических решений (в случае невозможности создания ЛА, удовлетворяющего заданным требованиям, на текущем уровне научно-технологического развития).
В следующих разделах приведено описание возможной формализации перечисленных выше задач.
1. Определение предпочтительного типа перспективного ЛА на основе многокритериального экспертно-статистического метода. Процесс функционального проектирования начинается с определения набора базовых функций, которыми должен обладать проектируемый ЛА, чтобы обеспечить выполнение возложенной на него целевой задачи.
Примерами подобных базовых функций могут служить:
весовая эффективность, выражаемая обычно весовой отдачей перспективного ЛА, характеризующая его способность к перемещению полезной нагрузки;
энергетическая эффективность, характеризующая перспективный ЛА с точки зрения баланса между производимой и потребляемой бортовыми системами электроэнергией;
динамическая эффективность, под которой понимается способность проектируемого ЛА обеспечить требуемые для выполнения целевой задачи динамические характеристики;
уровень безопасности проектируемого ЛА, т.е. его способность обеспечить требования по надeжности критически важных систем, а также запасам устойчивости и управляемости;
экологическая эффективность, характеризующая проектируемый ЛА с точки зрения экологических требований;
экономическая эффективность, выражающая способность проектируемого ЛА обеспечить выполнение требований по затратам на создание, эксплуатацию и утилизацию.
Далее введем в рассмотрение интегральные показатели ${{I}_{j}},j = \overline {1,N} $, количественно оценивающие способность проектируемого ЛА обеспечить реализацию возложенных на него функций. В рамках подобного представления будем полагать, что проектируемый ЛА отвечает требованиям к базовым функциям, если выполняется совокупность условий:
(1.1)
$\left\{ \begin{gathered} {{I}_{{1~{\text{min}}}}} \leqslant {{I}_{1}} \leqslant {{I}_{{1~{\text{max\;}}}}}, \hfill \\ {{I}_{{2~{\text{min}}}}} \leqslant {{I}_{2}} \leqslant {{I}_{{2~{\text{max\;}}}}}, \hfill \\ {{I}_{{3~{\text{min}}}}} \leqslant {{I}_{3}} \leqslant {{I}_{{3~{\text{max}}}}}, \hfill \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots . \hfill \\ ~{{I}_{{N~{\text{min}}}}} \leqslant {{I}_{N}} \leqslant {{I}_{{N~{\text{max\;}}}}}. \hfill \\ \end{gathered} \right.$Предельные значения показателей ${{I}_{{j~{\text{min}}}}},{{I}_{{j~{\text{max}}}}}$ устанавливает специалист, исходя из заданных требований к перспективному ЛА, сформулированных в техническом задании.
Как уже указывалось, первая задача, которая должна быть решена в рамках развиваемой концепции функционального проектирования, заключается в определении конкретного типа (класса) ЛА в зависимости от используемого принципа полета, способного обеспечить выполнение требований (1.1), предъявляемых к его базовым функциям.
Как известно, принцип полета определяется тем, каким образом и за счет чего создается подъемная сила [1]. Учитывая существующее разнообразие классов ЛА, потенциально пригодных для достижения поставленной цели, тип ЛА, способного обеспечить требования к базовым функциям, определяется выбором из следующего набора альтернатив: ${{a}_{1}}$ – бездвигательный ЛА аэростатического типа (свободный или привязной аэростат, стратостат); ${{a}_{2}}$ – дирижабль; ${{a}_{3}}~$ – аэродинамический ЛА самолетного типа; ${{a}_{4}}~$ – аэродинамический ЛА вертолетного типа; ${{a}_{5}}~$ – ЛА баллистического типа; ${{a}_{6}}~$ – ракетодинамический ЛА.
Решение задачи выбора предпочтительного, с точки зрения возможности обеспечения предъявленных требований, типа ЛА на этапе функционального проектирования осложняется существенным влиянием факторов неопределенности, присутствие которых не позволяет применять методы принятия решений, основанные на математических моделях и формализованных критериях. Учитывая это, для выбора предпочтительного (с точки зрения требований к базовым функциям) типа перспективного ЛА предлагается использовать экспертно-статистический подход к многокритериальному принятию решений, развивающий известный метод многокритериальной оценки качества продукции [2], адаптированный для целей функционального проектирования.
Данный метод в наименьшей степени подвержен влиянию субъективных факторов, обусловленных квалификацией экспертов, на достоверность принимаемых решений за счет введения функций ценности показателей, опирающихся на технические характеристики обсуждаемых образцов.
Его реализация опирается на структуру данных, представленную в табл. 1. Строки этой таблицы представляют собой альтернативные типы (классы) ЛА, которые потенциально могут быть задействованы для обеспечения требований, предъявляемых к базовым функциям проектируемого ЛА.
Таблица 1.
Структура данных в экспертно-статистическом методе многокритериального определения предпочтительного (с точки зрения обеспечения требований к базовым функциям) типа перспективного ЛА
| Тип (класс) ЛА | Интегральные показатели, выражающие требования к базовым функциям проектируемого ЛА | |||||
|---|---|---|---|---|---|---|
| ${{I}_{1}}$ ↓ |
${{I}_{2}}$ ↓ |
${{I}_{3}}$ ↓ |
${{I}_{4}}$ ↓ |
…. | ${{I}_{N}}$ ↑ |
|
| Вес показателей | ||||||
| ${{\omega }_{1}}$ | ${{\omega }_{2}}$ | ${{\omega }_{3}}$ | ${{\omega }_{4}}$ | …. | ${{\omega }_{N}}$ | |
| Привлекательность (ценность) альтернативных типов ЛА по отдельным показателям | ||||||
| a1 | ${{U}_{1}}\left( {{{a}_{1}}} \right)$ | ${{U}_{2}}\left( {{{a}_{1}}} \right)$ | ${{U}_{3}}\left( {{{a}_{1}}} \right)$ | ${{U}_{4}}\left( {{{a}_{1}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{1}}} \right)$ |
| a2 | ${{U}_{1}}\left( {{{a}_{2}}} \right)$ | ${{U}_{2}}\left( {{{a}_{2}}} \right)$ | ${{U}_{3}}\left( {{{a}_{2}}} \right)$ | ${{U}_{4}}\left( {{{a}_{2}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{2}}} \right)$ |
| a3 | ${{U}_{1}}\left( {{{a}_{3}}} \right)$ | ${{U}_{2}}\left( {{{a}_{3}}} \right)$ | ${{U}_{3}}\left( {{{a}_{3}}} \right)$ | ${{U}_{4}}\left( {{{a}_{3}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{3}}} \right)$ |
| a4 | ${{U}_{1}}\left( {{{a}_{4}}} \right)$ | ${{U}_{2}}\left( {{{a}_{4}}} \right)$ | ${{U}_{3}}\left( {{{a}_{4}}} \right)$ | ${{U}_{4}}\left( {{{a}_{4}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{4}}} \right)$ |
| a5 | ${{U}_{1}}\left( {{{a}_{5}}} \right)$ | ${{U}_{2}}\left( {{{a}_{5}}} \right)$ | ${{U}_{3}}\left( {{{a}_{5}}} \right)$ | ${{U}_{4}}\left( {{{a}_{5}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{5}}} \right)$ |
| a6 | ${{U}_{1}}\left( {{{a}_{6}}} \right)$ | ${{U}_{2}}\left( {{{a}_{6}}} \right)$ | ${{U}_{3}}\left( {{{a}_{6}}} \right)$ | ${{U}_{4}}\left( {{{a}_{6}}} \right)$ | …. | ${{U}_{N}}\left( {{{a}_{6}}} \right)$ |
Столбцами таблицы выступают перечисленные выше интегральные показатели ${{I}_{j}},j = \overline {1,N} $, выражающие требования к базовым функциям проектируемого ЛА. Каждый интегральный показатель помечен либо символом стрелка вниз (↓), либо символом стрелка вверх $( \uparrow )$. Наличие символа $ \downarrow $ для некоторого интегрального показателя предполагает, что наиболее привлекательным с точки зрения этого показателя является тип (класс) ЛА, обеспечивающий его наименьшее значение. Если некоторый показатель помечен символом $ \uparrow $, то наиболее привлекательным с точки зрения этого показателя будет тип (класс) ЛА, обеспечивающий его наибольшее значение.
Полагаем, что априори заданы:
1) веса (важности) ${{\omega }_{{j~}}} \geqslant 0,j = \overline {1,N} $, каждого из интегральных показателей с точки зрения необходимости их учета при выборе типа (класса) перспективного ЛА, которые подчиняются условию нормировки:
2) оценки ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right),i = \overline {1,6} $, выражающие привлекательность (ценность) каждого из альтернативных классов ЛА по отдельным интегральным показателям.
Тогда предпочтительность каждого альтернативного типа (класса) перспективного ЛА по комплексу интегральных показателей оценивается величиной
В результате решение принимается в пользу того класса ЛА, для которого наблюдается максимум величины $U\left( {{{a}_{{i~}}}} \right)$.
Очевидно, что достоверность решения относительно предпочтительности того или иного класса ЛА с точки зрения его способности обеспечить выполнение требований к базовым функциям перспективного авиационного комплекса определяющим образом зависит от того, насколько достоверно выбраны веса ${{\omega }_{j}}$ и оценки ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$, выражающие привлекательность (ценность) каждого из альтернативных классов ЛА по отдельным интегральным показателям.
Возможны различные способы определения этих величин.
Первый способ является традиционным для экспертных систем и опирается на опыт и знания специалистов-экспертов. При этом для обеспечения максимальной объективности оценок ωj, $j = \overline {1,N} ,$ и ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right),i = \overline {1,6} ,$ учитывается коллективное мнение группы специалистов-экспертов. Предположим, что в процессе получения интересующих нас величин участвует группа из $L$ специалистов. Каждый эксперт, исходя из того, насколько жестко, по его мнению, должны учитываться требования к каждой из базовых функций при определении облика перспективного ЛА, назначает весовые коэффициенты $\omega _{j}^{l},~l = \overline {1,L} $. Эти оценки, полученные от экспертов, усредняются, в результате чего получаются значения весов ${{\omega }_{{j~}}}$, выражающие их коллективное мнение:
Аналогичным образом, опираясь на собственный опыт и знания, а также привлекая доступную справочную информацию, эксперты определяют значения $U_{j}^{l}\left( {{{a}_{{i~}}}} \right),\;i = \overline {1,6} ;\;j = \overline {1,N} ;\;l = \overline {1,L} $, характеризующие ценность каждого типа (класса) ЛА с точки зрения его способности обеспечить требуемые значения интегральных показателей.
В результате рассчитываются усредненные оценки ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$, выражающие коллективное мнение экспертов:
(1.4)
${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right) = \frac{1}{L}\mathop \sum \limits_{l = 1}^L U_{j}^{l}\left( {{{a}_{{i~}}}} \right).$Несмотря на очевидную простоту описанной выше экспертной процедуры определения предпочтительного (с точки зрения возможности обеспечения требований к базовым функциям) типа перспективного ЛА, еe практическое использование сталкивается с рядом трудностей.
Первая трудность связана с фундаментальной проблемой систем поддержки принятий решений, основанных на экспертных знаниях. Известно, что результаты коллективного мнения группы специалистов экспертов являются достаточно достоверными лишь в том случае, когда специалисты, привлекаемые в экспертную группу, обладают сопоставимыми знаниями в данной предметной области. Иными словами, в состав экспертной группы включаются специалисты, индивидуальные оценки которых в необходимой степени согласованы. Чаще всего для оценки согласованности экспертных мнений используется коэффициент конкордации, позволяющий подтвердить, насколько удачно подобрана экспертная группа. Тем не менее, подбор специалистов, обладающих сопоставимыми знаниями, может стать проблемой на пути реализации описанной процедуры.
Вторая трудность связана с надежностью экспертных оценок $U_{j}^{l}\left( {{{a}_{{i~}}}} \right)$, выражающих ценность каждого типа (класса) ЛА с точки зрения его способности обеспечить требуемые значения интегральных показателей. Получение таких оценок, обладающих необходимой достоверностью, требует участия специалистов, демонстрирующих одинаково глубокие знания в области проектирования ЛА всех обсуждаемых классов. Очевидно, что подобрать специалистов, обладающих подобными энциклопедическими знаниями, чрезвычайно сложно.
Учитывая это, предлагается экспертно-статистический подход для определения предпочтительного типа перспективного ЛА. Информационной основой развиваемого экспертно-статистического подхода является база данных (БД), обобщающая накопленный опыт создания ЛА различных классов и содержащая конкретные значения интегральных показателей, полученные в реализованных проектах. Указанная БД имеет вид электронной таблицы формата, представленного в табл. 2. Строки этой таблицы соответствуют анализируемым типам (классам) ЛА ${{a}_{{i~}}},i = \overline {1,6} $, которые потенциально могут использоваться для обеспечения требований предъявляемых к перспективному авиационному комплексу. Предполагается, что для каждого типа (класса) ЛА ai доступна информация по ранее реализованным проектам $q = \overline {1,{{M}_{i}}} $. Таким образом, данные, приведенные в табл. 2, в совокупности объединяют реализации $I_{j}^{q}\left( {{{a}_{{i~}}}} \right),i = \overline {1,6} $; $j = \overline {1,N} ;q = \overline {1,{{M}_{i}}} $, значений интегральных показателей, достигнутые в ранее реализованных проектах с участием анализируемых типов (классов) ЛА.
Таблица 2.
Значения интегральных показателей, выражающих требования к базовым функциям ЛА, накопленные в ходе реализации предшествующих проектов
| Тип (класс) ЛА | Ранее реализован-ные проекты | ${{I}_{1}}\left( {{{a}_{i}}} \right)$ | ${{I}_{2}}\left( {{{a}_{i}}} \right)$ | ${{I}_{3}}\left( {{{a}_{i}}} \right)$ | ${{I}_{4}}\left( {{{a}_{i}}} \right)$ | ……. | ${{I}_{N}}\left( {{{a}_{i}}} \right)$ |
|---|---|---|---|---|---|---|---|
| a1 | 1 | $I_{1}^{1}\left( {{{a}_{1}}} \right)$ | $I_{2}^{1}\left( {{{a}_{1}}} \right)$ | $I_{3}^{1}\left( {{{a}_{1}}} \right)$ | $I_{4}^{1}\left( {{{a}_{1}}} \right)$ | ……. | $I_{N}^{1}\left( {{{a}_{1}}} \right)$ |
| a1 | 2 | $I_{1}^{2}\left( {{{a}_{1}}} \right)$ | $I_{2}^{2}\left( {{{a}_{1}}} \right)$ | $I_{3}^{2}\left( {{{a}_{1}}} \right)$ | $I_{4}^{2}\left( {{{a}_{1}}} \right)$ | ……. | $I_{N}^{2}\left( {{{a}_{1}}} \right)$ |
| ……. | ……. | ……. | ……. | ……. | ……. | ……. | ……. |
| a1 | M1 | $I_{1}^{{{{M}_{1}}}}\left( {{{a}_{1}}} \right)$ | $I_{2}^{{{{M}_{1}}}}\left( {{{a}_{1}}} \right)$ | $I_{3}^{{{{M}_{1}}}}\left( {{{a}_{1}}} \right)$ | $I_{4}^{{{{M}_{1}}}}\left( {{{a}_{1}}} \right)$ | ……. | $I_{N}^{{{{M}_{1}}}}\left( {{{a}_{1}}} \right)$ |
| a2 | 1 | $I_{1}^{1}\left( {{{a}_{2}}} \right)$ | $I_{2}^{1}\left( {{{a}_{2}}} \right)$ | $I_{3}^{1}\left( {{{a}_{2}}} \right)$ | $I_{4}^{1}\left( {{{a}_{2}}} \right)$ | ……. | $I_{N}^{1}\left( {{{a}_{2}}} \right)$ |
| a2 | 2 | $I_{1}^{2}\left( {{{a}_{2}}} \right)$ | $I_{2}^{2}\left( {{{a}_{2}}} \right)$ | $I_{3}^{2}\left( {{{a}_{2}}} \right)$ | $I_{4}^{2}\left( {{{a}_{2}}} \right)$ | ……. | $I_{N}^{2}\left( {{{a}_{2}}} \right)$ |
| ……. | ……. | ……. | ……. | ……. | ……. | ……. | ……. |
| a2 | M2 | $I_{1}^{{{{M}_{2}}}}\left( {{{a}_{2}}} \right)$ | $I_{2}^{{{{M}_{2}}}}\left( {{{a}_{2}}} \right)$ | $I_{3}^{{{{M}_{2}}}}\left( {{{a}_{2}}} \right)$ | $I_{4}^{{{{M}_{2}}}}\left( {{{a}_{2}}} \right)$ | ……. | $I_{N}^{{{{M}_{2}}}}\left( {{{a}_{2}}} \right)$ |
| ……. | ……. | ……. | ……. | ……. | ……. | ……. | ……. |
| a6 | 1 | $I_{1}^{1}\left( {{{a}_{6}}} \right)$ | $I_{2}^{1}\left( {{{a}_{6}}} \right)$ | $I_{3}^{1}\left( {{{a}_{6}}} \right)$ | $I_{4}^{1}\left( {{{a}_{6}}} \right)$ | ……. | $I_{N}^{1}\left( {{{a}_{6}}} \right)$ |
| a6 | 2 | $I_{1}^{2}\left( {{{a}_{6}}} \right)$ | $I_{2}^{2}\left( {{{a}_{6}}} \right)$ | $I_{3}^{2}\left( {{{a}_{6}}} \right)$ | $I_{4}^{2}\left( {{{a}_{6}}} \right)$ | ……. | $I_{N}^{2}\left( {{{a}_{6}}} \right)$ |
| ……. | ……. | ……. | ……. | ……. | ……. | ……. | ……. |
| a6 | M6 | $I_{1}^{{{{M}_{6}}}}\left( {{{a}_{6}}} \right)$ | $I_{2}^{{{{M}_{6}}}}\left( {{{a}_{6}}} \right)$ | $I_{3}^{{{{M}_{6}}}}\left( {{{a}_{6}}} \right)$ | $I_{4}^{{{{M}_{6}}}}\left( {{{a}_{6}}} \right)$ | ……. | $I_{N}^{{{{M}_{6}}}}\left( {{{a}_{6}}} \right)$ |
Реализации $I_{j}^{q}\left( {{{a}_{{i~}}}} \right)$, представленные в табл. 2, в дальнейшем используются для расчета значений ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$. Каждый показатель ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$ выражает ценность типа (класса) ЛА ai с точки зрения его способности обеспечить требуемое значение интегрального показателя Ij. Для этого по аналогии с [2] применяются линейные функции ценности ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$. Эти функции конструируются по следующим простым правилам.
Если некоторый интегральный показатель Ij в табл. 1 помечен символом $ \downarrow $, наиболее привлекательным с точки зрения этого показателя является тип (класс) ЛА ai, обеспечивающий его наименьшее значение. В этом случае линейная функция ценности ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$ задается совокупностью условий:
(1.5)
${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right) = \left\{ \begin{gathered} 1,~\quad {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) < {{I}_{{j~{\text{min}}~}}}, \hfill \\ \frac{{{{I}_{{j~{\text{max}}}}} - {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right)}}{{{{I}_{{j~{\text{max}}}}} - {{I}_{{j~{\text{min}}~}}}}},\quad {{I}_{{j~{\text{min}}~}}} \leqslant {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) \leqslant {{I}_{{j~{\text{max}}~}}}, \hfill \\ 0,~\quad {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) > {{I}_{{j~{\text{max}}~}}}, \hfill \\ \end{gathered} \right.$Если некоторый интегральный показатель Ij в табл. 1 помечен символом ↑, предпочтительным является тип (класс) ЛА ai, обеспечивающий его наибольшее значение, а линейная функция ценности ${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right)$ приобретает вид
(1.6)
${{U}_{{j~}}}\left( {{{a}_{{i~}}}} \right) = \left\{ \begin{gathered} 0,~\quad {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) < {{I}_{{j~{\text{min}}~}}}, \hfill \\ \frac{{{{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) - {{I}_{{j~{\text{min}}}}}}}{{{{I}_{{j~{\text{max}}}}} - {{I}_{{j~{\text{min}}~}}}}},\quad {{I}_{{j~{\text{min}}~}}} \leqslant {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) \leqslant {{I}_{{j~{\text{max}}~}}}, \hfill \\ 1,~\quad {{I}_{{j~}}}\left( {{{a}_{{i~}}}} \right) > {{I}_{{j~{\text{max}}~}}}. \hfill \\ \end{gathered} \right.$Таким образом, на основе БД выполненных ранее проектов (табл. 2) можно реализовать экспертно-статистический метод многокритериального выбора предпочтительного (с точки зрения возможности обеспечения требований к базовым функциям) типа перспективного ЛА путем выполнения следующих процедур.
1. На основе мнения группы экспертов относительно того, насколько жестко должны учитываться требования к каждой из базовых функций при определении облика перспективного ЛА, назначаются весовые коэффициенты $\omega _{j}^{l},~\;j = \overline {1,N} ;\;l = \overline {1,L} $.
2. Рассчитываются усредненные значения весов ${{\bar {\omega }}_{{j~}}}$, выражающие коллективное мнение экспертов:
3. Используя реализации $I_{j}^{q}\left( {{{a}_{{i~}}}} \right),i = \overline {1,6} ;j = \overline {1,N} ;q = \overline {1,{{M}_{i}}} $, представленные в табл. 2, рассчитываются значения $U_{j}^{q}\left( {{{a}_{{i~}}}} \right)$ функций ценности с помощью (1.5) или (1.6) в зависимости от того, какое значение интегрального показателя является наилучшим, т.е. помечен ли он в табл. 1 символом ↑ или символом ↓.
4. На основе полученных значений функций ценности $U_{j}^{q}\left( {{{a}_{{i~}}}} \right)$ рассчитываются выборочные оценки их математических ожиданий:
(1.8)
${{\bar {U}}_{j}}\left( {{{a}_{i}}} \right) = \frac{1}{{{{M}_{i}}}}~\mathop \sum \limits_{q = 1}^{{{M}_{i}}} U_{j}^{q}\left( {{{a}_{{i~}}}} \right).~$5. Оцениваются предпочтительности каждого типа (класса) ЛА по комплексу интегральных показателей, выражающих требования к базовым функциям перспективного ЛА:
(1.9)
$\bar {U}\left( {{{a}_{{i~}}}} \right) = \mathop \sum \limits_{j = 1}^N {{\bar {\omega }}_{{j~}}}{{\bar {U}}_{{j~}}}\left( {{{a}_{{i~}}}} \right),\quad i = \overline {1,6} .$Полученные таким образом оценки $\bar {U}\left( {{{a}_{{i~}}}} \right),i = \overline {1,6} ,$ отображаются лицу, принимающему решение (ЛПР), для последующего выбора предпочтительного типа (класса) перспективного ЛА в зависимости от реализуемого им принципа полета. Решение принимается в пользу того типа ЛА ${{a}_{{k~}}}$, которому соответствует максимум величины $\bar {U}\left( {{{a}_{{i~}}}} \right)$:
(1.10)
$\bar {U}\left( {{{a}_{{k~}}}} \right) = \mathop {\max }\limits_{i = \overline {1,6} } \bar {U}\left( {{{a}_{{i~}}}} \right).$Структура описанного алгоритма, реализующего экспертно-статистическую процедуру, приведена на рис. 1.
Рис. 1.
Структура алгоритма, реализующего экспертно-статистическую процедуру определения предпочтительного (с точки зрения возможности обеспечения требований к базовым функциям) типа перспективного ЛА
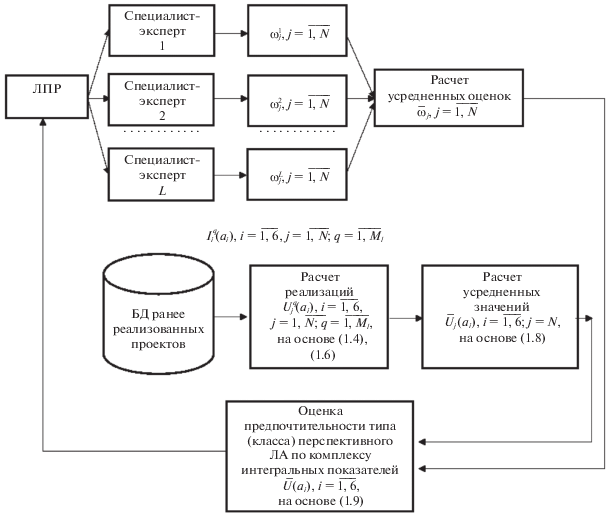
Основное преимущество описанного экспертно-статистического метода определения предпочтительного типа ЛА заключается в том, что наиболее сложный этап, связанный с выбором адекватных оценок $U_{j}^{l}\left( {{{a}_{{i~}}}} \right),$ выражающих ценность каждого типа (класса) ЛА с точки зрения его способности обеспечить требуемые значения интегральных показателей, опирается на использование объективной информации, аккумулирующей накопленный опыт проектирования. Заметим, что число обсуждаемых классов может быть расширено за счет учета в пределах каждого класса некоторого числа подклассов. При этом описанные выше процедуры никак не изменятся.
Таблица 3.
Значение компонент вектора ЛТХ, получененые в процессе случайного поиска
| Итерация | Взлетная масса, кг | Степень двухконтурности двигателя | Коэффициент лобового сопротивления на крейсерском режиме | Расход топлива на крейсерском режиме, кг/кгс в час | Длина разбега, м | Длина пробега, м | Крейсерская скорость, км/ч | Масса топлива, кг | Весовая отдача | Относительный вес конструкции |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 200 000 | 11.0 | 0.010 | 0.58 | 1652 | 1369 | 942 | 26 352 | 0.4 | 0.57 |
| 2 | 200 000 | 9.0 | 0.010 | 0.59 | 1652 | 1362 | 942 | 27 224 | 0.4 | 0.56 |
| 3 | 200 000 | 4.5 | 0.010 | 0.66 | 1652 | 1337 | 942 | 30 347 | 0.5 | 0.55 |
| 4 | 200 000 | 11.0 | 0.015 | 0.55 | 1652 | 1308 | 851 | 34 074 | 0.5 | 0.53 |
| 5 | 200 000 | 9.0 | 0.015 | 0.57 | 1652 | 1299 | 851 | 35 257 | 0.5 | 0.52 |
| 6 | 200 000 | 4.5 | 0.015 | 0.64 | 1652 | 1265 | 851 | 39 489 | 0.5 | 0.50 |
| 7 | 200 000 | 11.0 | 0.020 | 0.53 | 1652 | 1254 | 792 | 40 953 | 0.5 | 0.50 |
| 8 | 200 000 | 9.0 | 0.020 | 0.55 | 1652 | 1242 | 792 | 42 420 | 0.5 | 0.49 |
| 9 | 160 000 | 11.0 | 0.010 | 0.55 | 1031 | 1085 | 842 | 22 382 | 0.5 | 0.49 |
| 10 | 160 000 | 9.0 | 0.010 | 0.57 | 1031 | 1079 | 842 | 23 162 | 0.5 | 0.48 |
| 11 | 160 000 | 4.5 | 0.010 | 0.63 | 1031 | 1057 | 842 | 25 955 | 0.5 | 0.46 |
| 12 | 200 000 | 4.5 | 0.020 | 0.62 | 1652 | 1201 | 792 | 47 672 | 0.5 | 0.46 |
| 13 | 160 000 | 11.0 | 0.015 | 0.52 | 1031 | 1032 | 761 | 29 022 | 0.6 | 0.44 |
| 14 | 160 000 | 9.0 | 0.015 | 0.54 | 1031 | 1024 | 761 | 30 080 | 0.6 | 0.44 |
| 15 | 160 000 | 4.5 | 0.015 | 0.61 | 1031 | 994 | 761 | 33 865 | 0.6 | 0.41 |
| 16 | 160 000 | 11.0 | 0.020 | 0.51 | 1031 | 986 | 708 | 34 950 | 0.6 | 0.41 |
| 17 | 160 000 | 9.0 | 0.020 | 0.53 | 1031 | 975 | 708 | 36 262 | 0.6 | 0.40 |
| 18 | 160 000 | 4.5 | 0.020 | 0.59 | 1031 | 938 | 708 | 40 959 | 0.6 | 0.37 |
| 19 | 120 000 | 11.0 | 0.010 | 0.51 | 566 | 802 | 729 | 18 216 | 0.7 | 0.35 |
| 20 | 120 000 | 9.0 | 0.010 | 0.53 | 566 | 797 | 729 | 18 892 | 0.7 | 0.34 |
| 21 | 120 000 | 4.5 | 0.010 | 0.60 | 566 | 778 | 729 | 21 310 | 0.7 | 0.32 |
| 22 | 120 000 | 11.0 | 0.015 | 0.49 | 566 | 759 | 659 | 23 704 | 0.7 | 0.30 |
| 23 | 120 000 | 9.0 | 0.015 | 0.51 | 566 | 752 | 659 | 24 620 | 0.7 | 0.29 |
| 24 | 120 000 | 4.5 | 0.015 | 0.58 | 566 | 726 | 659 | 27 898 | 0.7 | 0.27 |
| 25 | 120 000 | 11.0 | 0.020 | 0.48 | 566 | 721 | 613 | 28 616 | 0.7 | 0.26 |
| 26 | 120 000 | 9.0 | 0.020 | 0.50 | 566 | 712 | 613 | 29 753 | 0.7 | 0.25 |
| 27 | 120 000 | 4.5 | 0.020 | 0.57 | 566 | 680 | 613 | 33 820 | 0.8 | 0.22 |
2. Формирование облика перспективного ЛА с учетом накопленного научно-технологического задела на основе решения задачи математического программирования. Рассмотренный выше экспертно-статистический подход позволяет выбрать тип (класс) перспективного ЛА в зависимости от реализуемого принципа полета, использование которого способно обеспечить выполнение комплекса многодисциплинарных требований, предъявляемых к проектируемому ЛА.
Следующая задача, возникающая на этапе функционального проектирования, заключается в определении предварительного облика перспективного ЛА на основе анализа ограниченного набора потенциально приемлемых вариантов реализации ЛА выбранного типа.
В рамках развиваемой концепции функционального проектирования приемлемым полагается облик перспективного ЛА, описываемый вектором проектных параметров r, при котором обеспечивается одновременное выполнение комплекса многодисциплинарных требований. Формальный учет этих требований базируется на использовании интегральных показателей ${{I}_{j}}\left( r \right),j = \overline {1,N} $:
(2.1)
$\left\{ \begin{gathered} {{I}_{{1~{\text{min}}}}} \leqslant {{I}_{1}}\left( r \right) \leqslant {{I}_{{1~{\text{max\;}}}}}, \hfill \\ {{I}_{{2~{\text{min}}}}} \leqslant {{I}_{2}}\left( r \right) \leqslant {{I}_{{2~{\text{max\;}}}}}, \hfill \\ {{I}_{{3~{\text{min}}}}} \leqslant {{I}_{3}}\left( r \right) \leqslant {{I}_{{3~{\text{max}}}}}, \hfill \\ ... \ldots \ldots \ldots \ldots \ldots \ldots \ldots .. \hfill \\ {{I}_{{N~{\text{min}}}}} \leqslant {{I}_{N}}\left( r \right) \leqslant {{I}_{{N~{\text{max\;}}}}}. \hfill \\ \end{gathered} \right.$Предельные значения показателей ${{I}_{{j~{\text{min}}}}},{{I}_{{j~{\text{max}}}}}$ устанавливает специалист, исходя из заданных требований к перспективному ЛА. Заметим, что система неравенств (2.1) позволяет в наиболее общем виде учесть требования к базовым функциям перспективного ЛА. Действительно, специалист может задать только максимальное значение некоторого интегрального показателя ${{I}_{j}}\left( r \right)$. В этом случае, допустимым полагается его любое значение, удовлетворяющее условию:
Если специалист, исходя из требований, предъявляемых к некоторой базовой функции, задает минимально допустимое значение соответствующего интегрального показателя, приемлемым полагается любое его значение, удовлетворяющее неравенству:
Наконец, требование к некоторой базовой функции может выражаться конкретным значением соответствующего интегрального показателя. В этом случае специалист в рамках (2.1) выбирает равные предельные значения, что приводит к условию
Конкретный набор интегральных показателей в (2.1) определяется пользователем в рамках выбранного типа (класса) проектируемого ЛА с учетом требований, предъявляемых к его базовым функциям.
Вектор $r = {{\left( {{{r}_{1}},{{r}_{2}}, \ldots ,{{r}_{n}}} \right)}^{{\text{T}}}}$ в (2.1) представляет собой n-мерный вектор, компоненты которого ${{r}_{i}},i = \overline {1,n} $, в совокупности объединяют летно-технические характеристики (ЛТХ), участвующие в вычислении интегральных показателей ${{I}_{j}}\left( r \right),j = \overline {1,N} $. Конкретный набор компонент вектора r и зависимостей $~{{I}_{j}}\left( r \right)$, связывающих интегральные показатели Ij с ЛТХ (компонентами вектора r), будут разными в зависимости от выбранного типа (класса) проектируемого ЛА.
Вследствие различного уровня априорной информированности о значениях ЛТХ, участвующих в описании интегральных показателей $~{{I}_{j}}\left( r \right)$, компоненты ${{r}_{i}},i = \overline {1,n,} ~$ вектора r могут интерпретироваться как:
1) детерминированные, если их значения точно известны и не подвержены вариациям (в качестве допустимого ${{r}_{i}}$ задается единственное значение соответствующей компоненты):
2) неопределенные, если для них достоверно известны лишь диапазоны допустимых значений:
(специалист задает предельные значения ${{r}_{{i~{\text{min}}}}},{{r}_{{i~{\text{max}}}}}$ соответствующей компоненты);3) случайные, информация о которых ограничена лишь их статистическими характеристиками. В подобной ситуации в качестве интервала допустимых значений $\left[ {{{r}_{{i~{\text{min}}}}},{{r}_{{i~{\text{max}}}}}} \right]~$ компоненты ri выступает доверительный интервал, которому с заданной вероятностью, близкой к единице, принадлежат значения ri. Универсальный алгоритм, пригодный для вычисления границ доверительного интервала $\left[ {{{r}_{{i~{\text{min}}}}},{{r}_{{i~{\text{max}}}}}} \right]~$ в ситуациях, когда распределение случайной величины ${{r}_{i}}$ является произвольным, описан в работе [3].
Таким образом, компоненты вектора ЛТХ $r$ объединяют данные различной физической природы (детерминированные, неопределенные, случайные). Учитывая это, с целью унифицированного описания допустимых значений компонент вектора r, в качестве множества его допустимых значений будем использовать n-мерный параллелепипед ${{W}_{r}}$, задаваемый, совокупностью условий:
(2.7)
${{W}_{r}} = \{ r:{{r}_{{i~{\text{min}}}}} \leqslant {{r}_{i}} \leqslant {{r}_{{i~{\text{max}}}}},i = \overline {1,n} \} .$В рамках подобного формального описания задача определения предварительного облика перспективного ЛА сводится к отысканию множества ${{\Omega }} \subset {{W}_{r}}~$ комбинаций значений компонент вектора ЛТХ $r \in {{W}_{r}}$, при которых выполняется совокупность условий:
(2.8)
$\left\{ \begin{gathered} {{I}_{{1~{\text{min}}}}} \leqslant {{I}_{1}}\left( r \right) \leqslant {{I}_{{1~{\text{max\;}},}}} \hfill \\ {{I}_{{2~{\text{min}}}}} \leqslant {{I}_{2}}\left( r \right) \leqslant {{I}_{{2~{\text{max\;}},}}} \hfill \\ {{I}_{{3~{\text{min}}}}} \leqslant {{I}_{3}}\left( r \right) \leqslant {{I}_{{3~{\text{max}}}}}~, \hfill \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots .. \hfill \\ {{I}_{{N~{\text{min}}}}} \leqslant {{I}_{N}}\left( r \right) \leqslant {{I}_{{N~{\text{max\;}}.}}} \hfill \\ \end{gathered} \right.$Численные методы поиска множества значений вектора ЛТХ ${{\Omega }} \subset {{W}_{r}}$, удовлетворяющих системе неравенств (2.8), обсуждаются ниже.
Наиболее простой метод предполагает представление множества допустимых значений ЛТХ Wr в виде дискретного набора реализаций ${{r}^{t}},t = \overline {1,T} ~$. Для этого на отрезках $[{{r}_{{i~{\text{min}}}}},{{r}_{{i~{\text{max}}}}}]$, $i = \overline {1,n} $, определяющих допустимые значения компонент вектора ЛТХ, выделяются q точек $r_{i}^{1} = {{r}_{{i{\text{min}}}}},\;r_{i}^{2},\;r_{i}^{3}$, ..., $r_{i}^{q} = {{r}_{{i{\text{max}}}}},\;i = \overline {1,n} $. Очевидно, что общее число реализаций ${{r}^{t}},t = \overline {1,T,} ~$ вектора ЛТХ в этом случае равно $T = {{q}^{n}}$.
В результате перебора реализаций ${{r}^{t}},t = \overline {1,T,} $ находится множество ${{{{\Omega }}}_{1}} \subset {{W}_{r}}$, при котором выполняется первое из условий (2.8):
(2.9)
${{{{\Omega }}}_{1}} = \{ {{r}^{t}}:~{{I}_{{1~{\text{min}}}}} \leqslant {{I}_{1}}({{r}^{t}}) \leqslant {{I}_{{1~{\text{max}}}}},~t = \overline {1,T} \} .$Аналогичным образом определяются множества ${{{{\Omega }}}_{2}} \subset {{W}_{r}},{{{{\Omega }}}_{3}} \subset {{W}_{r}}, \ldots ,~{{{{\Omega }}}_{N}} \subset {{W}_{r}}$, при которых выполняются второе, третье и последующие из условий (2.8):
(2.10)
$ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots $В итоге получаем множество значений вектора ЛТХ ${{\Omega }} \subset {{W}_{r}}$, удовлетворяющее системе неравенств (2.8), как пересечение полученных таким образом множеств ${{{{\Omega }}}_{1}} \subset {{W}_{r}}$, ${{{{\Omega }}}_{2}} \subset {{W}_{r}}$, ..., ${{{{\Omega }}}_{N}} \subset {{W}_{r}}{\text{:}}$
(2.11)
${{\Omega }} = \{ {{r}^{t}}:{{{{\Omega }}}_{1}} \cap {{{{\Omega }}}_{2}} \cap \ldots \cap {{{{\Omega }}}_{N}},~t = \overline {1,T} \} \,.$Главный недостаток подобной процедуры определения предварительного облика перспективного ЛА путем перебора допустимых значений ЛТХ заключается в том, что она требует проведения большого числа вычислений, объем которых лавинообразно увеличивается с ростом размерности вектора $r.$ Учитывая это, рассмотрим численный метод определения множества ${{\Omega }}$, основанный на решении задачи математического программирования.
Введем в рассмотрение скалярные функции ${{\varphi }_{j}}\left( r \right),j = \overline {1,N} $, количественно выражающие для любого фиксированного вектора ЛТХ r степень выполнения каждого из условий (2.8). Эти функции определим следующим образом:
(2.12)
${{\varphi }_{j}}(r) = \left\{ \begin{gathered} {{I}_{j}}(r) - {{I}_{{j~{\text{min}}}}},~\quad {{I}_{j}}(r) < {{I}_{{j~{\text{min}}}}}, \hfill \\ 0,\quad {{I}_{{j~{\text{min}}}}} \leqslant {{I}_{j}}(r) \leqslant {{I}_{{j~{\text{max}}}}}, \hfill \\ {{I}_{j}}(r) - {{I}_{{j~{\text{max}}}}},\quad {{I}_{j}}(r) > {{I}_{{j~{\text{max}}}}}. \hfill \\ \end{gathered} \right.$Выражение (2.12) задает способ определения функций ${{\varphi }_{j}}\left( r \right)$ для наиболее общего случая, когда для каждого интегрального показателя ${{I}_{j}}\left( r \right)$, выражающего требования к базовым функциям перспективного ЛА, заданы минимально допустимое и максимально допустимое значения.
Если специалист задает только максимальное значение некоторого интегрального показателя ${{I}_{j}}\left( r \right),~$ приемлемым полагается его любое значение, удовлетворяющее условию:
В этом случае выражение для соответствующей функции ${{\varphi }_{j}}\left( r \right)$ несколько упрощается и принимает вид
(2.13)
${{\varphi }_{j}}\left( r \right) = \left\{ \begin{gathered} 0,~\quad {{I}_{j}}(r) \leqslant {{I}_{{j~{\text{max}}}}}, \hfill \\ {{I}_{j}}(r) - {{I}_{{j~{\text{max}}}}},\quad {{I}_{j}}(r) > {{I}_{{j~{\text{max}}}}}. \hfill \\ \end{gathered} \right.$Если же специалист, исходя из требований, предъявляемых к некоторой базовой функции, задает только минимально допустимое значение соответствующего интегрального показателя, приемлемым полагается любое его значение, удовлетворяющее неравенству:
В подобной ситуации выражение для функции ${{\varphi }_{j}}\left( r \right)$ примет вид
(2.14)
${{\varphi }_{j}}\left( r \right) = \left\{ \begin{gathered} {{I}_{j}}\left( r \right) - {{I}_{{j~{\text{min}}}}},~\quad {{I}_{j}}\left( r \right) < {{I}_{{j~{\text{min}}}}}, \hfill \\ 0,{{I}_{{j~{\text{min}}}}} \leqslant {{I}_{j}}\left( r \right). \hfill \\ \end{gathered} \right.$Наконец, если требование к некоторой базовой функции выражается определенным, конкретным значением соответствующего интегрального показателя
то выражение для функции ${{\varphi }_{j}}\left( r \right)$ запишется как(2.15)
${{\varphi }_{j}}\left( r \right) = \left\{ \begin{gathered} {{I}_{j}}\left( r \right) - I_{j}^{*},~\quad {{I}_{j}}\left( r \right) \ne I_{j}^{*}, \hfill \\ 0,\quad {{I}_{j}}\left( r \right) = I_{j}^{*}. \hfill \\ \end{gathered} \right.$Далее определим скалярную функцию ${{\Phi }}\left( r \right)$, количественно выражающую для любого фиксированного вектора ЛТХ r степень выполнения всей совокупности условий (2.8):
(2.16)
${{\Phi }}\left( r \right) = \mathop \sum \limits_{j = 1}^N \varphi _{j}^{2}\left( r \right).$В рамках подобного представления задача сводится к отысканию такого вектора ЛТХ r*, при котором достигается минимум скалярной функции ${{\Phi }}\left( r \right)$:
(2.17)
${{\Phi }}\left( {r{\text{*}}} \right) = \mathop {\min }\limits_{r \in {{W}_{r}}} {{\Phi }}\left( r \right).$Если при этом ${{\Phi }}\left( {r{\text{*}}} \right) = 0$, облик перспективного ЛА, описываемый вектором ЛТХ r*, является приемлемым с точки зрения выполнения совокупности требований (2.8).
Задача минимизации вида (2.17) есть ни что иное как задача условной оптимизации [4]. Для ее решения можно использовать метод случайного поиска [5] с проверкой принадлежности решения множеству допустимых значений. В результате выполнения случайного поиска находится вектор ЛТХ r*, при котором достигается минимум скалярной функции ${{\Phi }}\left( r \right)$. При этом возможны следующие ситуации.
1. ${{\Phi }}\left( {r{\text{*}}} \right) = 0$. Выполнение этого равенства означает, что облик проектируемого ЛА, описываемый вектором ЛТХ $r{\text{*}} \in {{W}_{r}}$, удовлетворяет требованиям (2.8), предъявляемым к базовым функциям.
Множество Wr в (2.8) определяет допустимые значения ЛТХ, которые могут быть достигнуты с учетом текущего уровня развития авиационных технологий и накопленного опыта проектирования. Следовательно, вектор ЛТХ r* задает облик перспективного ЛА, удовлетворяющего требованиям к базовым функциям, который может быть реализован на существующем уровне развития технологий.
2. ${{\Phi }}\left( {r{\text{*}}} \right) \ne 0$. Полученный результат указывает на невозможность создания перспективного ЛА, удовлетворяющего всей совокупности требований к базовым функциям, на современном уровне развития авиационных технологий. Возникает следующая задача, связанная с формированием облика перспективного ЛА с учетом внедрения перспективных научно-технологических решений и оценки возможности выполнения заданных требований к базовым функциям перспективного ЛА на основе этих решений. Формализация этой задачи и возможный способ ее решения рассматриваются ниже. Очевидно, что подобная задача возникает в случае, когда накопленный научно-технологический задел не позволяет сформировать ЛА, удовлетворяющий комплексу многодисциплинарных требований к базовым функциям перспективного ЛА выбранного типа.
3. Формирование облика проектируемого ЛА с учетом перспективных научно-технических решений на основе решения обобщенной задачи минимизации. Как указывалось выше, подобная задача возникает тогда, когда накопленный научно-технологический задел не позволяет сформировать ЛА, удовлетворяющий комплексу многодисциплинарных требований к базовым функциям перспективного ЛА выбранного типа. Формализованным признаком подобной ситуации является неравенство
(3.1)
${{\Phi }}\left( {r{\text{*}}} \right) = \mathop {\min }\limits_{r \in {{W}_{r}}} {{\Phi }}\left( r \right) \ne 0,$Заметим, что в процессе решения задачи оптимизации (3.1) будет найден оптимальный вектор ЛТХ r*, описывающий облик будущего ЛА, и соответствующие этому вектору функции φj(r*), $j = \overline {1,N} $, количественно выражающие степень выполнения каждого из требований, предъявляемых к базовым функциям перспективного ЛА, на текущем уровне научно-технологического развития.
Объектом исследования являются отличные от нуля функции ${{\varphi }_{j}}\left( {r{\text{*}}} \right) \ne 0$, конкретизирующие те отдельные требования к базовым функциям, которые не могут быть удовлетворены на текущем уровне развития технологий. Список этих базовых функций отображается специалистам для их последующего анализа. Каждая из функций, для которой имеет место неравенство ${{\varphi }_{j}}\left( {r{\text{*}}} \right) \ne 0$, в соответствии с (2.12)–(2.15) имеет знак, указывающий на то, что именно стало причиной нарушения заданных требований.
1. Если ${{\varphi }_{j}}\left( {r{\text{*}}} \right) < 0$, значение соответствующего интегрального показателя ${{I}_{j}}\left( {r{\text{*}}} \right)$, которое может быть достигнуто на современном уровне научно-технологического развития, меньше минимально допустимого значения ${{I}_{{j~{\text{min}}}}}$, заданного специалистом с учетом требований к соответствующей базовой функции. Фактически рассматриваемая ситуация означает следующее: на современном уровне научно-технологического развития невозможно создание ЛА, обеспечивающего минимально допустимое значение интегрального показателя ${{I}_{{j~{\text{min}}}}}$. Oднако возможно создание перспективного ЛА, если несколько ослабить предъявленное требование, приняв в качестве минимально допустимого значения ${{I}_{{j~{\text{min}}}}} = {{I}_{j}}\left( {r{\text{*}}} \right)$.
2. При ${{\varphi }_{j}}\left( {r{\text{*}}} \right) > 0$ значение соответствующего интегрального показателя ${{I}_{j}}\left( {r{\text{*}}} \right)$, которое может быть обеспечено на современном уровне научно-технологического развития, больше максимально допустимого значения ${{I}_{{j~{\text{max}}}}}$. В этом случае можно говорить о возможности создания перспективного ЛА, если несколько ослабить предъявленное требование, приняв в качестве максимально допустимого значения ${{I}_{{j~{\text{max}}}}} = {{I}_{j}}\left( {r{\text{*}}} \right)$.
3. Наконец, если требование к некоторой базовой функции выражается конкретным значением соответствующего интегрального показателя, тогда в соответствии с (2.15) неравенство ${{\varphi }_{j}}\left( {r{\text{*}}} \right) \ne 0$ указывает на невозможность обеспечения значения этого показателя на современном уровне научно-технологического развития. В этом случае в качестве достижимого (с учетом накопленного опыта проектирования) принимается значение $I_{j}^{*} = {{I}_{j}}\left( {r{\text{*}}} \right)$.
Таким образом, специалист, если это допустимо, имеет возможность несколько изменить исходные требования, предъявляемые к базовым функциям перспективного ЛА, путем соответствующей коррекции предельных значений интегральных показателей. Это касается показателей, для которых невозможно обеспечить выполнение исходных требований на существующем уровне научно-технологического развития. При этом специалист получает количественную оценку того, насколько должны быть расширены их предельные значения.
В некоторых ситуациях подобная корректировка исходных требований может оказаться вполне приемлемой и не приведет к значительным потерям функциональных возможностей проектируемого ЛА.
Однако чаще всего требуется жесткое выполнение исходных требований, предъявляемых к базовым функциям перспективного ЛА. В этом случае единственным способом выполнения исходных требований является использование перспективных научно-технологических решений, внедрение которых возможно в обозримой перспективе. Вопрос в том, какие именно перспективные научно-технологические решения являются наиболее приоритетными с точки зрения необходимости выполнения заданных требований к базовым функциям перспективного ЛА.
Влияние перспективных научно-технологических решений проявляется изменениями формы и размеров множества допустимых значений ЛТХ Wr. Таким образом, в задаче определения облика проектируемого ЛА с учетом перспективных решений множество Wr становится дополнительным параметром оптимизации, что приводит к задаче вида
(3.2)
${{\Phi }}(W_{r}^{*},r{\text{*}}) = \mathop {\min }\limits_{{{W}_{r}} \in {{\Xi }}} \mathop {\min }\limits_{r \in {{W}_{r}}} {{\Phi }}\left( r \right) = 0,$В результате решения задачи оптимизации (3.2) будут рассчитаны:
1) $W_{r}^{*}$ – оптимальное (с учетом внедрения перспективных научно-технологических решений) множество допустимых значений ЛТХ, при котором обеспечивается выполнение заданных требований к базовым функциям проектируемого ЛА;
2) r* – оптимальный вектор ЛТХ, определяющий возможный (с учетом внедрения перспективных научно-технологических решений) облик проектируемого ЛА, при котором обеспечивается выполнение заданных требований к базовым функциям проектируемого ЛА.
Задачи оптимизации, подобные (3.2), достаточно глубоко исследованы в рамках обобщенного минимаксного подхода [6–9], где предложены различные численные процедуры оптимизации доверительных множеств. С точки зрения возможности практического использования наибольший интерес представляет алгоритм получения оптимального множества $W_{r}^{*}$, основанный на последовательной деформации начального параллелепипеда Wr. Рассмотрим основные шаги этого алгоритма более подробно с учетом его адаптации к особенностям рассматриваемой задачи.
Ш а г 1. Формируется начальное приближение $W_{r}^{0}$ для множества допустимых значений ЛТХ. Как указывалось ранее, в качестве начального приближения $W_{r}^{0}$ используется n-мерный параллелепипед, задаваемый совокупностью условий:
(3.3)
$W_{r}^{0} = \{ r:r_{{i~{\text{min}}}}^{0} \leqslant {{r}_{i}} \leqslant r_{{i~{\text{max}}}}^{0},i = \overline {1,n} \} ,$Шаг 2. Последовательно варьируется значение ${{r}_{{1~{\text{min}}}}}$ в сторону уменьшения:
(3.4)
$r_{{1~{\text{min}}}}^{k} = r_{{1~{\text{min}}}}^{0} - k\delta {{r}_{1}},\quad k = 1.2,3 \ldots ,$(3.5)
$W_{r}^{k} = \{ r:r_{{1~{\text{min}}}}^{k} \leqslant {{r}_{1}} \leqslant r_{{1~{\text{max}}}}^{0},~r_{{j~{\text{min}}}}^{0} \leqslant {{r}_{j}} \leqslant r_{{j~{\text{max}}}}^{0},~j = \overline {2,n} ~\} .$Сформированное таким образом множество $W_{r}^{k} \in {{\Xi }}$ в дальнейшем используется для решения задачи оптимизации (3.1), в результате чего находится вектор ${{\hat {r}}^{k}}$, удовлетворяющий условию
(3.6)
${{\Phi }}({{\hat {r}}^{k}}) = \mathop {\min }\limits_{r \in W_{r}^{k}} {{\Phi }}\left( r \right).$Шаг 3. В результате перебора значений $r_{{1~{\text{min}}}}^{k},k = 1,2,3 \ldots $ находится, во-первых, граница $r_{{1~{\text{min}}}}^{*}$, во-вторых, соответствующее этой границе множество $W_{r}^{*} \in {{\Xi }}$, определяемое условиями (3.5), а также вектор ЛТХ r*, при которых достигается минимум критериальной функции ${{\Phi }}\left( r \right)$.
Шаг 4. Проверяется условие
Если это равенство выполняется, процесс уточнения множества допустимых (с учетом внедрения перспективных научно-технических решений) значений ЛТХ может быть завершен. При этом приоритет имеют те перспективные технологии, которые направлены на расширение нижней границы параметра ${{r}_{1}}$.
На практике обычно строгое выполнение условия (3.7) не требуется, т.е. приемлемым полагается вектор ЛТХ, для которого справедливо неравенство:
где ε – малая положительная константа, задаваемая специалистом.Если же приведенное выше равенство (3.7) не обеспечивается, значение ${{r}_{{1~{\text{min}}}}}$ фиксируется ${{r}_{{1~{\text{min}}}}} = r_{{1~{\text{min}}}}^{*}$ и аналогичным образом сначала варьируются максимально допустимые значения $r_{{1~{\text{max}}}}^{k} = r_{{1~{\text{max}}}}^{0} + k\delta {{r}_{1}},k = 1,2,3 \ldots ,$ с повторением шагов 1–4. В результате возможны два исхода:
последовательное увеличение значения ${{r}_{{1~{\text{max}}}}}$ приводит к (3.7), описанная выше процедура завершается;
за счет роста значения ${{r}_{{1~{\text{max}}}}}$ не удается добиться справедливости равенства (3.7). В этом случае продолжается реализация описанной процедуры для предельных значений компонент ${{r}_{2}},{{r}_{3}}~$ и т.д.
Таким образом, в результате выполнения шагов 1–4 находится (рис. 2):
Рис. 2.
Иллюстрация процедуры оптимизации множества допустимых значений ЛТХ с учетом перспективных научно-технологических решений
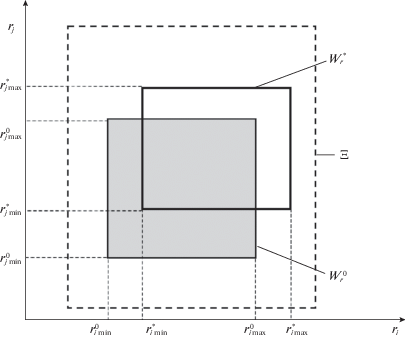
– оптимальное множество допустимых значений ЛТХ $W_{r}^{*}$ с конкретизацией тех приоритетных научно-технических решений, внедрение которых обеспечит создание ЛА, отвечающего заданным требованиям к базовым функциям;
– вектор ЛТХ r*, определяющий возможный облик проектируемого ЛА.
Следующий раздел статьи иллюстрирует работу алгоритмов, описанных в разд. 2, 3, на примере формирования предварительного облика перспективного самолета транспортной категории в рамках развитой концепции функционального проектирования.
4. Пример функционального проектирования перспективного самолета транспортной категории. Допустим, что целью функционального проектирования является формирование предварительного облика перспективного самолета транспортной категории, отвечающего следующим требованиям:
1) вес перевозимой целевой нагрузки – ${{G}_{{{\text{ц}}{\text{.н}}}}} = 60~$ т,
2) дальность полета при полной загрузке ${{L}_{{{\text{п}}{\text{.з}}}}} = 5000~$ км,
3) перегоночная дальность полета (без загрузки) ${{L}_{{{\text{б}}{\text{.з}}}}}~$ = 12 000 км,
4) способность взлетать и совершать посадку на аэродромы с длиной взлетно-посадочной полосы (ВПП) не более 1300 м.
При формировании облика перспективного ЛА ограничимся только требованиями весовой и динамической эффективности. Это допущение никак не повлияет на существо развиваемой концепции функционального проектирования, но обеспечит более наглядное представление результатов.
Прежде всего определим зависимости ${{I}_{j}}\left( r \right),j = \overline {1,N} $, составляющие основу развиваемой концепции функционального проектирования.
Интегральной характеристикой весовой эффективности проектируемого ЛА выступает его весовая отдача – безразмерная величина, равная отношению массы полезной нагрузки ЛА ${{m}_{{{\text{п}}{\text{.н}}}}}$ к его взлетной массе m0:
(4.1)
${{I}_{1}} = {{I}_{1}}\left( r \right) = {{\bar {m}}_{{{\text{п}}{\text{.н}}}}} = \frac{{{{m}_{{{\text{п}}{\text{.н}}}}}}}{{{{m}_{0}}}}.$На величину весовой отдачи накладывается дополнительное ограничение, которое непосредственно следует из уравнения существования самолета:
(4.2)
${{\bar {m}}_{{{\text{пн}}}}} + {{\bar {m}}_{{{\text{кон}}}}} + {{\bar {m}}_{{{\text{с}}{\text{.у}}}}} + {{\bar {m}}_{{{\text{о}}{\text{.у}}}}} + {{\bar {m}}_{{\text{т}}}} = 1,$В итоге, требование к весовой эффективности ЛА может быть выражено условием
(4.3)
${{I}_{{1~{\text{min}}}}} \leqslant {{I}_{1}}\left( r \right) = 1 - \left( {{{{\bar {m}}}_{{{\text{кон}}}}} + {{{\bar {m}}}_{{{\text{с}}{\text{.у}}}}} + {{{\bar {m}}}_{{{\text{о}}{\text{.у}}}}} + {{{\bar {m}}}_{{\text{т}}}}} \right) \leqslant ~{{I}_{{1~{\text{max}}}}}.$Из (4.3) непосредственно следует набор ЛТХ (компонент вектора r), участвующих в расчете показателя весовой эффективности: ${{r}_{1}} = {{m}_{0}}$; $~{{r}_{2}} = {{\bar {m}}_{{{\text{кон}}}}}$; ${{r}_{3}} = {{\bar {m}}_{{{\text{с}}{\text{.у}}}}}$; ${{r}_{4}} = {{\bar {m}}_{{{\text{о}}{\text{.у}}}}}$; ${{r}_{5}} = {{\bar {m}}_{{\text{т}}}}~$.
Существенно сложнее оценить динамическую эффективность ЛА, которая, как правило, характеризуется комплексом показателей. Набор этих показателей может быть разным для ЛА различных классов и возлагаемых на них целевых задач. Введем некоторые базовые понятия, используемые в дальнейшем для оценки динамической эффективности на этапе функционального проектирования.
Режим полета ЛА – этап или участок управляемого движения ЛА, характеризующийся конкретной целью (взлет, посадка, крейсерский полет и др.).
Расчетный случай – совокупность условий для выбранного режима полета, подлежащих обязательному учету (расчету) в процессе функционального проектирования, которые определяются тактико-техническими требованиями на проектируемое изделие и действующими нормами летной годности.
В частности, для оценки динамической эффективности самолетов транспортной категории используются следующие расчетные случаи.
1. Полет на дальность. Типичная постановка задачи: определить относительный вес топлива, достаточный для полета на заданную дальность при заданных значениях скорости и высоты полета.
2. Взлет. Предполагается определение допустимых значений проектных параметров (прежде всего потребная тяговооруженность), при которых обеспечивается взлет с ВПП заданной длины при соблюдении требований норм летной годности по высоте и скорости взлета. Безопасной высотой по международным нормам считается высота 10.7 м [10]. Безопасной скоростью является скорость, на которой самолет обладает устойчивостью и управляемостью и может перейти к следующему этапу – начальному набору высоты.
3. Продолженный взлет – взлет многодвигательного самолeта с отказом двигателя в процессе взлета. Он протекает как нормальный полет до момента отказа двигателя, после чего взлет продолжается и завершается с отказавшим двигателем. В этом случае необходимо определить допустимые значения проектных параметров, при которых возможно продолжение взлета с неработающим двигателем по траектории наиболее крутого набора высоты и соблюдение норм летной годности самолетов соответствующей категории к градиенту (углу) набора высоты.
4. Крейсерский полет. Отыскание допустимых значений проектных параметров, при которых обеспечивается крейсерский полет на режиме минимального удельного расхода топлива при заданных значениях крейсерской скорости и крейсерской высоты.
5. Посадка. Определение допустимых проектных параметров, при которых обеспечивается посадка на ВПП требуемой длины с соблюдением норм летной годности по скорости захода на посадку.
Основная идея предлагаемого метода оценки динамической эффективности заключается в следующем: для каждого расчетного случая используются функциональные зависимости $\begin{array}{*{20}{c}} {{{I}_{2}}\left( r \right) - {{I}_{6}}} \end{array}\left( r \right)$, описывающие влияние проектных параметров ЛА на тактико-технические требования и требования норм летной годности, которые основаны на базовых соотношениях теории полета ЛА как материальной точки.
Для самолетов транспортной категории эти зависимости имеют слeдующий вид [11, 12]:
(4.4)
$\left\{ \begin{gathered} {{I}_{2}}\left( r \right) = {{r}_{6}} - \frac{{{{r}_{7}}{{r}_{8}}}}{{{{r}_{9}}}}{\text{ln}}\frac{1}{{1 - {{r}_{5}}}} = 0, \hfill \\ {{I}_{3}}\left( r \right) = {{r}_{{10}}} - \frac{{1.656}}{{g{{\rho }_{0}}{{r}_{{11}}}}}\frac{{{{r}_{{12}}}}}{{{{r}_{{13}}}{{r}_{{14}}}}} = 0, \hfill \\ {{I}_{4}}\left( r \right) = {{r}_{{14}}} - \frac{{{{r}_{{15}}}}}{{{{r}_{{15}}} - 1}}\frac{1}{{{{r}_{{16}}}}}\left( {\frac{1}{{{{r}_{{17}}}}} + {{r}_{{18}}}} \right) \geqslant 0, \hfill \\ {{I}_{5}}\left( r \right) = {{r}_{{14}}} - \frac{1}{{{{r}_{{19}}}{{r}_{{20}}}{{r}_{7}}}} \geqslant 0, \hfill \\ {{I}_{6}}\left( r \right) = {{r}_{{12}}} - \frac{{{{r}_{{21}}}{{r}_{{22}}}{{r}_{{10}}}}}{{30.2\left( {1 - {{r}_{5}}} \right)}} \leqslant 0, \hfill \\ \end{gathered} \right.$Конкретные значения компонент вектора r могут быть заданы тактико-техническими требованиями или определяться на основе накопленного опыта проектирования.
Полученные таким образом зависимости $\begin{array}{*{20}{c}} {{{I}_{1}}\left( r \right) - {{I}_{6}}} \end{array}\left( r \right)$, описывающие требования к базовым функциям проектируемого ЛА, в дальнейшем используются для определения его предварительного облика.
Решение задачи формирования облика перспективного самолета транспортной категории, удовлетворяющего комплексу требований (4.3), (4.4), начинается с решения задачи оптимизации (2.17), в которой множество допустимых значений ЛТХ представляет собой параллелепипед, задаваемый совокупностью условий:
(4.5)
${{W}_{r}} = \left\{ {r:{{r}_{{i~{\text{min}}}}} \leqslant {{r}_{i}} \leqslant {{r}_{{i~{\text{max}}}}},i = \overline {1,22} } \right\}.$Предельные значения ЛТХ ${{r}_{{i~{\text{min}}}}},{{r}_{{i~{\text{max}}}}},i = \overline {1,22} $, в этих условиях определялись на основе обобщения накопленного опыта проектирования самолетов транспортной категории.
Для решения задачи оптимизации (2.17) использовался метод случайного поиска, реализуемый в виде итерационной процедуры последовательного уточнения значений ЛТХ, присутствующих в описании условий (4.3), (4.4).
В табл. 3 приведены наиболее значимые ЛТХ, полученные в процессе решения задачи оптимизации (2.17) на основе итерационной процедуры случайного поиска.
Варианты обликов ЛА, представленные в первых 16 строках табл. 3, являются абсолютно неприемлемыми с точки зрения сформулированных требований и должны быть исключены из процесса дальнейшего анализа как заведомо неприемлемые.
Варианты обликов, расположенные в следующих 11 строках, могут представлять потенциальный интерес, демонстрируя близкие к нулю значения критериальной функции (0 < ${{\Phi }}(r{\text{*}}) \leqslant 49.6)$. Наилучшим решением, с точки зрения задачи (2.17), при котором выполняется условие ${{\Phi }}\left( {r{\text{*}}} \right) = 0$, является облик, перспективного ЛА, описываемый комбинацией значений ЛТХ, представленных в последней строке табл. 3. Именно этот вариант и должен стать объектом последующего углубленного анализа на этапах структурного, компоновочного и обликового проектирования.
Мы рассмотрели пример, в котором возможно формирование облика ЛА, допускающего реализацию на современном уровне научно-технологического развития авиастроения.
Ужесточим требования, предъявляемые к перспективному ЛА, увеличив перегоночную дальность полета (без загрузки) до величины ${{L}_{{{\text{б}}{\text{.з}}}}} = 17000$ км.
Варианты обликов ЛА, полученные в процессе решения задачи (2.17) приведены в табл. 4.
Таблица 4.
Варианты обликов ЛА
| Итерация | Взлетная масса, кг | Степень двухконтурности двигателя | Коэффициент лобового сопротивления на крейсерском режиме | Расход топлива на крейсерском режиме, кг/кгс в час | Длина разбега, м | Длина пробега, м | Крейсерская скорость, км/ч | Масса топлива, кг | Весовая отдача | Относительный вес конструкции |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 120 000 | 4.5 | 0.015 | 0.58 | 566 | 418 | 659 | 66 956 | 0.0 | –0.06 |
| 2 | 120 000 | 11.0 | 0.020 | 0.48 | 566 | 405 | 613 | 68 679 | 0.0 | –0.07 |
| 3 | 120 000 | 9.0 | 0.020 | 0.50 | 566 | 383 | 613 | 71 406 | 0.0 | –0.10 |
| 4 | 120 000 | 4.5 | 0.020 | 0.57 | 566 | 306 | 613 | 81 169 | 0.0 | –0.18 |
| 5 | 200 000 | 11.0 | 0.010 | 0.58 | 1652 | 1078 | 942 | 63 245 | 0.6 | 0.38 |
| 6 | 200 000 | 9.0 | 0.010 | 0.59 | 1652 | 1062 | 942 | 65 339 | 0.6 | 0.37 |
| 7 | 200 000 | 4.5 | 0.010 | 0.66 | 1652 | 1002 | 942 | 72 833 | 0.7 | 0.34 |
| 8 | 200 000 | 11.0 | 0.015 | 0.55 | 1652 | 932 | 851 | 81 778 | 0.7 | 0.29 |
| 9 | 160 000 | 11.0 | 0.010 | 0.55 | 1031 | 838 | 842 | 53 718 | 0.7 | 0.29 |
| 10 | 160 000 | 9.0 | 0.010 | 0.57 | 1031 | 823 | 842 | 55 590 | 0.7 | 0.28 |
| 11 | 200 000 | 9.0 | 0.015 | 0.57 | 1652 | 910 | 851 | 84 616 | 0.7 | 0.28 |
| 12 | 160 000 | 4.5 | 0.010 | 0.63 | 1031 | 770 | 842 | 62 293 | 0.8 | 0.24 |
| 13 | 200 000 | 4.5 | 0.015 | 0.64 | 1652 | 830 | 851 | 94 773 | 0.8 | 0.23 |
| 14 | 200 000 | 11.0 | 0.020 | 0.53 | 1652 | 802 | 792 | 98 288 | 0.8 | 0.21 |
| 15 | 200 000 | 9.0 | 0.020 | 0.55 | 1652 | 774 | 792 | 101 808 | 0.8 | 0.19 |
| 16 | 160 000 | 11.0 | 0.015 | 0.52 | 1031 | 712 | 761 | 69 654 | 0.8 | 0.19 |
| 17 | 160 000 | 9.0 | 0.015 | 0.54 | 1031 | 692 | 761 | 72 191 | 0.8 | 0.17 |
| 18 | 120 000 | 11.0 | 0.010 | 0.51 | 566 | 602 | 729 | 43 719 | 0.9 | 0.14 |
| 19 | 200 000 | 4.5 | 0.020 | 0.62 | 1652 | 675 | 792 | 114 412 | 0.9 | 0.13 |
| 20 | 120 000 | 9.0 | 0.010 | 0.53 | 566 | 589 | 729 | 45 340 | 0.9 | 0.12 |
| 21 | 160 000 | 4.5 | 0.015 | 0.61 | 1031 | 621 | 761 | 81 276 | 0.9 | 0.12 |
| 22 | 160 000 | 11.0 | 0.020 | 0.51 | 1031 | 600 | 708 | 83 880 | 0.9 | 0.10 |
| 23 | 160 000 | 9.0 | 0.020 | 0.53 | 1031 | 575 | 708 | 87 029 | 0.9 | 0.08 |
| 24 | 120 000 | 4.5 | 0.010 | 0.60 | 566 | 543 | 729 | 51 145 | 0.9 | 0.07 |
| 25 | 120 000 | 11.0 | 0.015 | 0.49 | 566 | 498 | 659 | 56 890 | 1.0 | 0.03 |
| 26 | 160 000 | 4.5 | 0.020 | 0.59 | 1031 | 487 | 708 | 98 301 | 1.0 | 0.01 |
| 27 | 120 000 | 9.0 | 0.015 | 0.51 | 566 | 480 | 659 | 59 088 | 1.0 | 0.01 |
Заметим, что ни один из представленных в табл. 4 вариантов облика перспективного ЛА не обеспечивает выполнения условия ${{\Phi }}\left( {r{\text{*}}} \right) = 0$. Это значит, что создание ЛА, удовлетворяющего сформулированным требованиям, на современном уровне научно-технологического развития невозможно.
В этом случае в рамках функционального проектирования возникает задача, связанная с определением перспективных научно-технических решений, внедрение которых обеспечит создание ЛА, удовлетворяющего предъявленным требованиям. Эта задача интерпретирована нами как обобщенная задача минимизации (3.2), результатом решения которой является оптимальное множество допустимых значений ЛТХ, рассчитанное с учетом перспективных научно-технических решений.
Результаты оптимизации множества допустимых значений ЛТХ и варианты обликов перспективных ЛА, полученные в ходе решения обобщенной задачи минимизации, приведены в табл. 5.
Таблица 5.
Варианты обликов ЛА, полученные с учетом внедрения перспективных научно-технических решений
| Направления деформации множества допустимых значений ЛТХ | Взлетная масса, кг | Степень двухконтурности двигателя | Коэффициент лобового сопротивления на крейсерском режиме | Расход топлива на крейсерском режиме, кг/кгс в час | Длина разбега, м | Длина пробега, м | Крейсерская скорость, км/ч | Масса топлива, кг | Весовая отдача | Относительный вес конструкции |
|---|---|---|---|---|---|---|---|---|---|---|
| Расширение диапазонов значений аэродинамических характеристик | 200 000 | 9.0 | 0.01 | 0.59 | 1652 | 1062 | 942 | 65 339 | 0.6 | 0.37 |
| Расширение диапазонов массовых и энергетических характеристик | 220 000 | 9.0 | 0.02 | 0.56 | 1412 | 875 | 830 | 10 8963 | 0.8 | 0.23 |
| Улучшение расходных показателей | 200 000 | 11.0 | 0.02 | 0.53 | 1652 | 802 | 792 | 98 288 | 0.8 | 0.21 |
| Базовый вариант | 200 000 | 9.0 | 0.02 | 0.55 | 1652 | 774 | 792 | 101 808 | 0.8 | 0.19 |
Анализ полученных результатов показывает, что наибольшего эффекта можно ожидать от расширения диапазонов значений аэродинамических характеристик (максимальные значения коэффициентов подъемной силы) и, в несколько меньшей степени, за счет улучшения расходных показателей (расход топлива на крейсерском режиме), что и определяет приоритетные направления дальнейших исследований. Заметим, что реализация этих мер обеспечивает решение задачи (3.2), а значит, делает возможным создание перспективного ЛА, удовлетворяющего заявленным требованиям.
Заключение. Таким образом, развитая концепция функционального проектирования позволяет оптимизировать процесс предварительного проектирования, предшествующего этапам структурного, компоновочного и обликового проектирования, путем:
1) сокращения временных и материальных затрат на создание перспективных образцов ЛА вследствие исключения из процесса последующего углубленного анализа вариантов облика, которые являются заведомо неприемлемыми с точки зрения предъявленных требований;
2) определения предварительного облика перспективного ЛА, обеспечивающего требования к его базовым функциям и реализуемого на существующем научно-технологическом уровне развития авиастроения, с целью его последующего уточнения на этапах структурного, компоновочного и обликового проектирования;
3) определения перспективных научно-технических решений, внедрение которых обеспечит создание перспективного ЛА, отвечающего всем заявленным требованиям, сформулированным в техническом задании.
Список литературы
Егер С.М., Матвеенко А.М., Шаталов И.А. Основы авиационной техники: учебник / Под ред. И.А. Шаталова. М.: Изд-во МАИ, 1999.
Семенов С.С., Щербинин В.В. Оценка технического уровня систем наведения управляемых авиационных бомб. М.: Машиностроениe, 2015.
Евдокименков В.Н., Карлов В.И., Красильщиков М.Н. Оценка вероятностных показателей качества, близких к единице, на основе методов планирования эксперимента // Изв. АН СССР. Техн. кибернетика. 1989. № 4.
Стрекаловский А.С. Введение в выпуклый анализ: учеб. пособие. Иркутск: Иркут. ун-т, 2009.
Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1980.
Кибзун А.И., Лебедев А.А., Малышев В.В. О сведении задачи с вероятностными ограничениями к эквивалентной ей минимаксной // Изв. АН СССР. Техн. кибернетика. 1984. № 4.
Малышев В.В. Методы оптимизации ЛА при действии случайных и неопределенных факторов. М.: Изд-во МАИ, 1987.
Малышев В.В., Красильщиков М.Н., Карлов В.И. Оптимизация наблюдения и управления летательных аппаратов. М.: Машиностроение, 1989.
Евдокименков В.Н., Динеев В.Г., Карп К.А. Инженерные методы вероятностного анализа авиационных и космических систем. М.: Физматлит, 2010.
Авиационные правила. Часть 25. Нормы летной годности самолетов транспортной категории. М.: Авиаиздат, 2015.
Чепурных И.В. Динамика полeта самолeтов: учеб. пособие. Комсомольск-на-Амуре: ФГБОУ ВПО “КнАГТУ”, 2014.
Бюшгенс Г.С., Студнев Р.В. Динамика самолета. Пространственное движение. М.: Машиностроение, 1983
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


