Известия РАН. Теория и системы управления, 2022, № 1, стр. 67-75
ВИРТУАЛЬНЫЕ ДАТЧИКИ В ЗАДАЧЕ ФУНКЦИОНАЛЬНОГО ДИАГНОСТИРОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
А. Н. Жирабок a, b, *, Ким Чхун Ир a
a Дальневосточный федеральный ун-т
Владивосток, Россия
b Институт проблем морских технологий ДВО РАН
Владивосток, Россия
* E-mail: zhirabok@mail.ru
Поступила в редакцию 04.07.2021
После доработки 20.08.2021
Принята к публикации 27.09.2021
- EDN: MOJDZG
- DOI: 10.31857/S0002338822010139
Аннотация
Рассматривается задача построения виртуальных датчиков в технических системах, описываемых нелинейными моделями, для решения задач функционального диагностирования. Приводятся соотношения, позволяющие построить датчик минимальной сложности, оценивающий заданную компоненту вектора состояния. Теоретические результаты иллюстрируются примером.
Введение. Проблема функционального диагностирования (ФД) к настоящему времени уже достаточно хорошо изучена, задачи обнаружения, поиска и идентификации дефектов решены для широкого класса динамических систем [1–4]. Одним из препятствий на пути реализации методов ФД может быть недостаточное число датчиков, которыми оснащена диагностируемая система. Введение дополнительных датчиков приводит к дополнительным затратам и не всегда реализуемо на практике. Более перспективным является использование так называемых виртуальных датчиков [3, 4], которые строятся на основе наблюдателей Люенбергера и в работах [3, 4] имеют размерность, совпадающую с размерностью исходной системы. В статье ставится и решается задача построения виртуальных датчиков минимальной размерности, оценивающих заданные компоненты вектора состояния нелинейной системы.
Для решения этой задачи предлагается использовать так называемый логико-динамический (ЛД) подход, который был успешно применен как для решения задачи ФД [5], так и анализа наблюдаемости и управляемости нелинейных систем [6]. ЛД-подход характерен тем, что он не гарантирует достижения оптимального решения задачи в смысле размерности получаемых в результате решения систем, но оперирует только линейными методами даже для систем с недифференцируемыми нелинейностями.
1. Основные модели. Рассмотрим стационарную систему, описанную нелинейной моделью
(1.1)
$\begin{gathered} \dot {x}(t) = Fx(t) + Gu(t) + C\Psi (x(t),\;u(t)) + L\rho (t), \\ y(t) = Hx(t), \\ \end{gathered} $Требуется построить виртуальный датчик, оценивающий переменную ${{y}_{v}}(t) = {{H}_{v}}x(t)$ с известной матрицей ${{H}_{v}}$. Способ ее нахождения определяется рассматриваемой задачей диагностирования. В частности, наиболее благоприятной для реализации процедуры ФД является ситуация, когда все компоненты вектора состояния системы могут быть измерены. В этом случае матрица ${{H}_{v}}$ должна удовлетворять условию
В дальнейшем для простоты будем предполагать, что ${{H}_{v}}$ – матрица-строка. Если эта матрица содержит более одной строки, предлагаемое решение распространяется и на этот случай. Другие варианты задания матрицы ${{H}_{v}}$ приведены в [7], где было получено решение задачи в линейном случае.
Решение рассматриваемой задачи состоит в построении нелинейного наблюдателя, оценивающего переменную ${{y}_{v}}(t)$ и, таким образом, выполняющего функцию виртуального датчика. Уравнение искомого наблюдателя имеет вид
(1.2)
$\begin{gathered} {{{\dot {x}}}_{v}}(t) = {{F}_{*}}{{x}_{v}}(t) + {{J}_{*}}{{y}_{0}}(t) + {{G}_{*}}u(t) + {{C}_{*}}\Psi ({{x}_{v}}(t),\;{\kern 1pt} {{y}_{0}}(t),\;{\kern 1pt} u(t)) + {{J}_{v}}r(t), \\ {{y}_{*}}(t) = {{H}_{*}}{{x}_{v}}(t), \\ {{y}_{v}}(t) = {{H}_{{*v}}}{{x}_{v}}(t) + Qy(t), \\ r(t) = {{R}_{*}}y(t) - {{y}_{*}}(t), \\ \end{gathered} $Отметим, что переменная ${{y}_{*}}(t)$ в (1.2) необходима для формирования невязки r(t), используемой в цепи обратной связи для обеспечения устойчивости наблюдателя.
В соответствии с ЛД-подходом решение задачи осуществляется в три этапа. На первом этапе строится линейная модель, не чувствительная к возмущениям:
(1.3)
$\begin{gathered} {{{\dot {x}}}_{v}}(t) = {{F}_{*}}{{x}_{v}}(t) + {{J}_{*}}{{y}_{0}}(t) + {{G}_{*}}u(t), \\ {{y}_{*}}(t) = {{H}_{*}}{{x}_{v}}(t). \\ \end{gathered} $Далее проверяется возможность введения в нее нелинейной составляющей ${{C}_{*}}\Psi ({{x}_{v}},{{y}_{0}},u)$ и возможность оценки переменной ${{y}_{v}}(t)$ на основе условия
На последнем этапе ищется матрица ${{J}_{{v}}}$, обеспечивающая устойчивость наблюдателя.
2. Построение модели. Для получения решения на первом этапе матрицы ${{F}_{*}}$ и ${{H}_{*}}$ ищутся в каноническом виде:
(2.1)
${{F}_{*}} = \left( {\begin{array}{*{20}{c}} 0&1&0& \cdots &0 \\ 0&0&1& \cdots &0 \\ 0&0&0& \cdots &0 \\ \cdots & \cdots & \cdots & \ddots & \cdots \\ 0&0&0& \cdots &0 \end{array}} \right),\quad {{H}_{*}} = (\begin{array}{*{20}{c}} 1&0&0& \cdots &0 \end{array}).$Предполагается, что после окончания переходного процесса векторы x(t) и ${{x}_{{v}}}(t)$ связаны матрицей Φ:
Известно, что матрицы, описывающие модель, удовлетворяют следующим уравнениям [5, 6]:
(2.2)
${{R}_{*}}H = {{H}_{*}}\Phi ,\quad \Phi F = {{F}_{*}}\Phi + {{J}_{*}}{{H}_{0}},\quad {{G}_{*}} = \Phi G,$(2.3)
${{C}_{*}} = \Phi C,\quad A{\kern 1pt} ' = {{A}_{*}}\left( {\begin{array}{*{20}{c}} \Phi \\ {{{H}_{0}}} \end{array}} \right).$Последнее соотношение эквивалентно ранговому равенству
(2.4)
${\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ {{{H}_{0}}} \end{array}} \right) = {\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ {{{H}_{0}}} \\ {A'} \end{array}} \right),$Решение задачи на первом этапе осуществляется на основе уравнения [5, 6]
(2.5)
$(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}& \ldots &{ - {{J}_{{*k}}}} \end{array})({{V}^{{(k)}}}{\text{ }}{{L}^{{(k)}}}) = 0,$Для построения модели из (2.6) определяется минимальное k и из (2.5) – строка $(\begin{array}{*{20}{c}} {{{R}_{*}}}&{ - {{J}_{{*1}}}}& \ldots &{ - {{J}_{{*k}}}} \end{array})$, затем на основе соотношений
Для реализации второго этапа представим уравнение (1.4) в виде
откуда следует(2.7)
${{H}_{{v}}} = {{H}_{{*{v}}}}\Phi + QH = (\begin{array}{*{20}{c}} {{{H}_{{*{v}}}}}&Q \end{array})\left( {\begin{array}{*{20}{c}} \Phi \\ H \end{array}} \right),$(2.8)
${\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ H \end{array}} \right) = {\text{rank}}\left( {\begin{array}{*{20}{c}} \Phi \\ H \\ {{{H}_{{v}}}} \end{array}} \right).$Выполнение условия (2.8) означает, что матрица-строка ${{H}_{{v}}}$ может быть выражена через матрицу ${{({{\Phi }^{{\text{T}}}}{\text{ }}{{H}^{{\text{T}}}})}^{{\text{T}}}}$ и построенная линейная модель будет оценивать заданную компоненту ${{y}_{v}} = {{H}_{v}}x$; матрицы ${{H}_{{*{v}}}}$ и Q определяются из алгебраического уравнения (2.7).
Для проверки возможности преобразования построенной линейной модели в нелинейную рассчитывается матрица ${{C}_{*}} = \Phi C$, определяются номера ${{j}_{1}},{{j}_{2}},...,{{j}_{d}}$ ненулевых ее столбцов и по описанному выше правилу строится матрица $A{\kern 1pt} '$. Далее проверяется условие (2.4) и при его выполнении строится нелинейная составляющая:
Если хотя бы одно из условий (2.4) и (2.8) не верно, нужно найти другое решение уравнения (2.5) при прежней или увеличенной размерности k.
Полагая, что условия (2.4) и (2.8) выполняются, примем ${{G}_{*}} = \Phi G$, на чем заканчивается процедура построения нелинейной модели (второй этап).
Соотношение (2.7) предлагается использовать для получения критерия возможности построения виртуального датчика, не чувствительного к возмущениям. Для этого введем матрицу максимального ранга ${{L}_{*}}$, такую, что ${{L}_{*}}L = 0$. Тогда $\Phi = K{{L}_{*}}$ для некоторой матрицы K. Заменим в (2.7) $\Phi $ на $K{{L}_{*}}$ и преобразуем полученное выражение:
Из последнего уравнения ясно, что оно имеет решение в том случае, когда
(2.9)
${\text{rank}}\left( {\begin{array}{*{20}{c}} {{{L}_{*}}} \\ H \end{array}} \right) = {\text{rank}}\left( {\begin{array}{*{20}{c}} {{{L}_{*}}} \\ H \\ {{{H}_{{v}}}} \end{array}} \right).$Приведенное ранговое равенство и является искомым критерием: если оно выполняется, виртуальный датчик может быть построен, в противном случае решение не существует. Отметим, что условие (2.9) дополняет условия существования решения, не чувствительного к возмущениям, найденные в [5].
3. Обеспечение устойчивости. На третьем этапе для определения матрицы ${{J}_{v}}$, обеспечивающей устойчивость наблюдателя, введем ошибку по состоянию $e(t) = \Phi x(t) - {{x}_{{v}}}(t)$ и с учетом (1.1), (1.2) и (2.2) запишем и преобразуем уравнение для $\dot {e}(t)$:
Рассмотрим два подхода к выбору матрицы ${{J}_{v}}$. В первом из них предполагается, что функция $\Psi (x,u)$ удовлетворяет условию Липшица по аргументу $x$, т.е.
(3.1)
$\left\| {\Psi (x,u) - \Psi (x{\kern 1pt} ',u)} \right\| \leqslant N\left\| {x - x{\kern 1pt} '} \right\|,$Известно, что если пара $({{F}_{*}},{{H}_{*}})$ наблюдаема, то существует такая матрица ${{J}_{{v}}}$, что ${{F}_{{**}}} = ({{F}_{*}} - {{J}_{{v}}}{{H}_{*}})$ устойчива. Из канонической формы (2.1) с очевидностью следует наблюдаемость пары $({{F}_{*}},{{H}_{*}})$ и, следовательно, существование матрицы ${{J}_{{v}}}$, обеспечивающей устойчивость матрицы ${{F}_{{**}}}$. Из устойчивости этой матрицы также вытекает, что существуют симметрические положительно-определенные матрицы P и W, такие, что
Рассмотрим функцию Ляпунова $V(t) = {{e}^{{\text{T}}}}(t)Pe(t)$ и найдем ее производную с учетом (3.1) и (3.2):
Будем искать ${{J}_{v}}$ в виде ${{J}_{v}} = {{(\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}& \ldots &{{{a}_{k}}} \end{array})}^{{\text{T}}}}$. Тогда
Коэффициенты ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$ связаны с собственными числами ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ матрицы ${{F}_{*}} - {{J}_{v}}{{H}_{*}}$ известными соотношениями:
Исходя из заданных требований к качеству переходного процесса, можно выбрать собственные числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ и определить коэффициенты ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$.
Отметим, что из-за наличия слагаемого ${{J}_{*}}{{y}_{0}}(t)$ в модели (1.2) может появиться обратная связь по переменной ${{y}_{v}}(t) = {{H}_{{*{v}}}}{{x}_{{v}}}(t) + Qy(t),$ что приведет к матрице ${{F}_{*}}$, отличной от канонического вида (2.1). В этом случае выбор коэффициентов ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$ должен быть осуществлен так, чтобы собственные числа матрицы ${{F}_{*}} - {{J}_{v}}{{H}_{*}}$ удовлетворяли требованию устойчивости. Сделать это можно, если выразить в общем виде собственные числа матрицы ${{F}_{*}} - {{J}_{{v}}}{{H}_{*}}$ через коэффициенты ${{a}_{1}},{{a}_{2}},...,{{a}_{k}}$, выбрав числа ${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{k}}$ и найдя из полученных уравнений искомые коэффициенты.
Рассмотренный подход накладывает довольно жесткие ограничения на класс функций $\Psi (x,u)$, которые диктуются условием (3.4) на константу ${{N}_{*}}$ – как правило, она должна быть меньше единицы. Только при k = 1 из (3.3) следует ${{\lambda }_{{\min }}}(W) = 2P{{J}_{v}}$ и ${{N}_{*}}{\text{ }} < {{J}_{v}}$, т.е. коэффициент ${{J}_{v}}$ всегда может быть выбран так, чтобы соблюсти условие ${{N}_{*}}{\text{ }} < {{J}_{v}}$ для произвольной функции, удовлетворяющей условию Липшица.
Отметим, что условие Липшица (3.1) носит глобальный характер и выполняется далеко не всегда, однако любая дифференцируемая функция локально удовлетворяет этому условию, поскольку верно приближенное равенство
Это положено в основу второго подхода, где предполагается, что функция $\Psi (x,u)$ дифференцируема, ошибка e(t) мала и функция $\Delta \Psi (t)$ может быть разложена в ряд Тейлора относительно текущего значения.
Более детально рассмотрим это вначале для случая, когда система содержит одну нелинейность и $\Psi (x(t),u(t)) = \varphi (Ax(t),u(t))$. Поскольку $A = {{A}_{*}}\left( {\begin{array}{*{20}{c}} \Phi \\ {{{H}_{0}}} \end{array}} \right)$ и $e = \Phi x - {{x}_{v}}$, то
В результате получаем окончательное уравнение для ошибки e(t):
(3.5)
$\dot {e}(t) = \left( {{{F}_{*}} - {{J}_{v}}{{H}_{*}} + \Phi C\frac{{\partial \varphi ({{x}_{{v}}},{{y}_{0}},u)}}{{\partial {{x}_{{v}}}}}A_{*}^{1}} \right)e(t) = {{F}_{e}}({{J}_{{v}}},{{x}_{{v}}},{{y}_{0}},u)e(t),$найти характеристический полином матрицы ${{F}_{e}}({{J}_{{v}}},{{x}_{{v}}},{{y}_{0}},u)$ в виде
составить систему нелинейных уравнений:
При наличии в системе нескольких нелинейностей получаем
На практике рассмотренный метод может быть использован для наблюдателя размерности не более 3–4, поскольку приводит к громоздким выражениям при вычислении определителя $\det ({{F}_{e}}({{J}_{{v}}},{{x}_{{v}}},{{y}_{0}},u) - \lambda E)$. Его преимущество по сравнению с методами, изложенными в [8], состоит в том, что он не приводит к производным в управляющих и выходных сигналах.
4. Пример. Рассмотрим систему управления
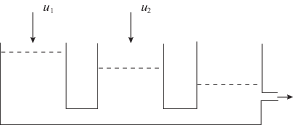
(4.1)
$\begin{gathered} {{{\dot {x}}}_{1}}(t) = {{u}_{1}}(t){\text{/}}{{\vartheta }_{1}} - {{b}_{1}}\sqrt {{{x}_{1}}(t) - {{x}_{2}}(t)} , \\ {{{\dot {x}}}_{2}}(t) = {{u}_{2}}(t){\text{/}}{{\vartheta }_{2}} + {{b}_{1}}\sqrt {{{x}_{1}}(t) - {{x}_{2}}(t)} - {{b}_{2}}\sqrt {{{x}_{2}}(t) - {{x}_{3}}(t)} , \\ {{{\dot {x}}}_{2}}(t) = {{b}_{2}}\sqrt {{{x}_{2}}(t) - {{x}_{3}}(t)} - {{b}_{3}}\sqrt {{{x}_{3}}(t) - {{\vartheta }_{3}}} + \rho (t), \\ {{y}_{1}}(t) = {{x}_{2}}(t),\quad {{y}_{2}}(t) = {{x}_{3}}(t). \\ \end{gathered} $Уравнения (4.1) описывают так называемую трехтанковую систему (см. рисунок), состоящую из трех резервуаров, соединенных между собой трубами. Жидкость поступает в первый и второй танки и выливается из третьего танка. Уровни жидкости в танках обозначены ${{x}_{1}}(t)$, ${{x}_{2}}(t)$ и ${{x}_{3}}(t)$; ${{\vartheta }_{1}}$, ${{\vartheta }_{2}}$, ${{\vartheta }_{3}}$, ${{b}_{1}}$, ${{b}_{2}}$ и ${{b}_{3}}$ – коэффициенты, значения которых определяются геометрическими размерами системы.
Поскольку неизмеряемой является компонента ${{x}_{1}}(t)$, примем ${{y}_{v}}(t) = {{x}_{1}}(t)$, ${{H}_{{v}}} = (1{\text{ }}0{\text{ 0}})$ и построим соответствующий виртуальный наблюдатель. Для простоты зададим ${{\vartheta }_{1}} = {{\vartheta }_{2}} = 1$, ${{\vartheta }_{3}} = 0$, ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = 1$. Поскольку уравнения (4.1) содержат только нелинейные члены, для них F = 0 и решение задачи описанным методом невозможно. Для устранения этого недостатка, согласно ЛД-подходу, добавим в первое уравнение формальный член $ - ({{x}_{1}} - {{x}_{2}}) + ({{x}_{1}} - {{x}_{2}})$, первый элемент которого отнесем к линейной части, второй – к нелинейной. Аналогично во второе уравнение добавим член ${{x}_{1}} - {{x}_{2}} - ({{x}_{2}} - {{x}_{3}}) - ({{x}_{1}} - {{x}_{2}}$ – $({{x}_{2}} - {{x}_{3}}))$, в третье – член $({{x}_{2}} - {{x}_{3}} - {{x}_{3}})$ – (x2 – x3 – x3). В результате получим следующее описание системы:
Нетрудно проверить, что условие (2.6) выполняется при k = 1, однако при этом не верно условие (2.8), поэтому принимаем k = 2. Составная матрица $({{V}^{{(2)}}}{\text{ }}{{L}^{{(2)}}})$ имеет вид
Можно проверить, что с матрицей $({{V}^{{(2)}}}{\text{ }}{{L}^{{(2)}}})$ уравнение (2.5) имеет два решения:
Рассмотрим первое из них. Так как
то ${{j}_{1}} = 2$, ${{j}_{2}} = 1$ иНетрудно видеть, что условие (2.4) выполняется и нелинейная составляющая может быть добавлена в линейную модель. Уравнение (2.3) принимает вид
В результате получаем модель:
Уравнение (3.5) для ошибки e(t) принимает вид
Примем ${{\lambda }_{1}} = {{\lambda }_{2}} = - 1$, тогда
Приведем описание наблюдателя:
Заключение. В работе предложен метод построения виртуальных датчиков в технических системах, описываемых нелинейными моделями. На основе наблюдателей Люенбергера получены соотношения, позволяющие построить датчики минимальной размерности, оценивающие заданные компоненты вектора состояния диагностируемой системы. Синтезированные виртуальные датчики дают возможность в ряде случаев не только уменьшить сложность средств диагностирования и повысить глубину диагностирования, но и рассмотреть задачи, которые без использования таких датчиков не могли быть решены.
Список литературы
Мироновский Л.А. Функциональное диагностирование динамических систем. М.; СПб.: МГУ-ГРИФ, 1998.
Шумский А.Е., Жирабок А.Н., Гаджиев Ч. Диагностирование и отказоустойчивое управление динамическими системами. Монография [электронный ресурс]. Владивосток: ДВФУ, 2016. 178 с. http://elib.dvfu.ru/vital/access/manager/Repository/fefu:4053.
Blanke M., Kinnaert M., Lunze J., Staroswiecki M. Diagnosis and Fault Tolerant Control. Berlin: Springer-Verlag, 2003.
Witczak M. Fault Diagnosis and Fault Tolerant Control Strategies for Nonlinear Systems. Berlin: Springer, 2014.
Жирабок А.Н., Зуев А.В., Шумский А.Е. Метод идентификации дефектов в нелинейных системах на основе скользящих наблюдателей // Изв. РАН. ТиСУ. 2021. № 1. С. 11–23.
Жирабок А.Н. Анализ наблюдаемости и управляемости нелинейных динамических систем линейными методами // Изв. РАН. ТиСУ. 2010. № 1. С. 10–17.
Жирабок А.Н., Ким Чхун Ир. Виртуальные датчики в задаче функционального диагностирования // Мехатроника, автоматизация, управление. 2021. № 6. С. 298–303.
Misawa E.A., Hedrick J.K. Nonlinear Observers – a State of the Art Survey // J. Dynamic Systems, Measurements and Control. 1989. V. 111. P. 344–352.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления