Известия РАН. Теория и системы управления, 2022, № 1, стр. 56-66
Анализ критически опасных повреждений сети связи. IV. Многокритериальные оценки уязвимости кластеров
Ю. Е. Малашенко a, И. А. Назарова a°, *
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 20.04.2021
После доработки 14.07.2021
Принята к публикации 26.07.2021
- EDN: JYGWUB
- DOI: 10.31857/S0002338821060135
Аннотация
На модели многопользовательской системы связи анализируются изменения допустимых информационных потоков внутри кластерных объединений при разрушении фрагментов сети. В ходе вычислительных экспериментов для каждого центрального узла-источника последовательно определяются компоненты вектора исходящего многопродуктового потока во все вершины-приемники. Для оценки последствий каждого повреждения вычисляется разность максимальных значений потоков между всеми парами корреспондентов в исходной и поврежденной сети. На основе агрегированных расчетных показателей строятся итоговые диаграммы и определяются наиболее уязвимые узлы с недоминируемыми многокритеральными оценками ущерба.
Введение. Работа продолжает исследования по построению многокритериальных и гарантированных оценок функциональных характеристик многопользовательской системы связи в случае разрушающих воздействий. При моделировании узлы сети рассматриваются как центры информационных кластеров. Для центрального узла кластера анализируются изменения исходящего многопродуктового потока к остальным вершинам-корреспондентам при удалении фрагментов сети.
Для всех пар узлов вычисляются величины максимальных однопродуктовых потоков, которые используются для оценки предельных функциональных возможностей кластерного объединения в неповрежденной сети. Множество исследуемых критически опасных повреждений, как и в наших предыдущих работах, формируется из специально подобранных минимальных и вершинных разрезов. В поврежденной сети последовательно определяются исходящие максимальные потоки из центра кластера к остальным вершинам-приемникам. Параметрические оценки изменений компонент вектора потока в кластере подсчитываются как разность максимальных значений в исходной и поврежденной сети для пар источник-приемник с учетом направления передачи.
Для всех повреждений на основе агрегированных оценок информационного обмена внутри кластеров строятся диаграммы, позволяющие выделить наиболее уязвимые узлы сети.
1. Математическая модель. Для описания многопользовательской сетевой системы используется математическая запись модели передачи многопродуктового потока [1]. Структура сети $G({\mathbf{d}})$ задается множествами $\langle V,R,U\rangle $: узлов (вершин) сети $V = {\text{\{ }}{{{v}}_{1}},{{{v}}_{2}},...,{{{v}}_{n}},...,{{{v}}_{N}}{\text{\} }}$, неориентированных ребер $R = {\text{\{ }}{{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}{\text{\} }}$ и ориентированных дуг $U = {\text{\{ }}{{u}_{1}},{{u}_{2}},...,$ ${{u}_{k}},...,{{u}_{{2E}}}{\text{\} }}$. Ребро ${{r}_{k}} = ({{{v}}_{{{{n}_{k}}}}},{{{v}}_{{{{j}_{k}}}}})$ соединяет вершины ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$ (инцидентно вершинам ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$), которые для него служат концевыми. Предполагается, что в сети отсутствуют петли и сдвоенные ребра. Ребру rk ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ прямого и обратного направления из множества U. Дуги ${\text{\{ }}{{u}_{k}},{{u}_{{k + E}}}{\text{\} }}$ определяют направление передачи потока по ребру rk между концевыми вершинами ${{{v}}_{{{{n}_{k}}}}}$, ${{{v}}_{{{{j}_{k}}}}}$.
Обозначим через $K({{{v}}_{n}})$ множество номеров ребер, инцидентных вершине $({{{v}}_{n}})$; $S({{{v}}_{n}})$ – множество номеров исходящих дуг, по которым поток покидает узел ${{{v}}_{n}}$; $T({{{v}}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{{v}}_{n}}$. Состав множеств $S({{{v}}_{n}})$, $T({{{v}}_{n}})$ однозначно определяется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами n и j, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{{v}}_{n}},{{{v}}_{j}})$ считается исходящей из вершины ${{{v}}_{n}}$ и ее номер k заносится в множество $S({{{v}}_{n}})$, ориентированная дуга ${{u}_{{k + E}}} = ({{{v}}_{j}},{{{v}}_{n}})$ – входящей для ${{{v}}_{n}}$ и ее номер $k + E$ помещается в список $T({{{v}}_{n}})$. Дуга uk является входящей для ${{{v}}_{j}}$ и ее номер k попадает в $T({{{v}}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ вносится в список исходящих дуг $S({{{v}}_{j}})$.
Предполагается, что в сети между любой парой узлов могут передаваться потоки разных видов. Назовем парой узлов-корреспондентов ${{p}_{m}}$ упорядоченную пару вершин ${{p}_{m}} = ({{{v}}_{{{{s}_{m}}}}},{{{v}}_{{{{t}_{m}}}}})$, где вершина с номером sm является источником, а с номером tm – приемником потока m-го вида. В настоящей работе в сети из N узлов рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных потоков различных видов, которые передаются между всеми парами узлов из множества $P = {\text{\{ }}{{p}_{1}},{{p}_{2}},...,{{p}_{M}}{\text{\} }}$.
Множество пар узлов разбивается на N кластеров по следующему правилу. Некоторый узел ${{{v}}_{n}}$, $n = \overline {1,N} $, рассматривается как центр кластера и является вершиной-источником для исходящих потоков соответствующих видов во все остальные вершины сети, которые считаются вершинами-приемниками указанного n-го кластера.
Обозначим через: ${{z}_{m}}$ величину потока m-го вида, который поступает в сеть в узле с номером ${{s}_{m}}$ и покидает из узла с номером ${{t}_{m}}$; ${{x}_{{mk}}}$ – величину потока m-го вида, который передается по дуге uk в прямом, а ${{x}_{{m(k + E)}}}$ – величину потока m-го вида, который передается по дуге ${{u}_{{k + E}}}$ в обратном направлении, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $. Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$, определяющее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей – ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектором d определяются следующие ограничения на все потоки, передаваемые по ребру rk:
(1.1)
$\sum\limits_{m = 1}^M ({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$Во всех узлах сети ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, для всех видов потоков должны выполняться условия сохранения потоков:
(1.2)
$\begin{gathered} \sum\limits_{i \in S({{{v}}_{n}})}^{} {{{x}_{{mi}}} - } \sum\limits_{i \in T({{{v}}_{n}})}^{} {{{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{s}_{m}}}}}, \hfill \\ - {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{t}_{m}}}}}, \hfill \\ 0\quad {\text{в}}\,{\text{остальных}}\,{\text{случаях,}} \hfill \\ \end{gathered} \right.} \\ n = \overline {1,N} ,\quad m = \overline {1,M} ,\quad {{x}_{{mi}}} \geqslant 0,\quad {{z}_{m}} \geqslant 0. \\ \end{gathered} $Величина zm равна входному потоку m-го вида, который пропускается от источника к стоку пары pm при распределении потоков xmi по дугам сети.
Ограничения (1.1), (1.2) задают множество допустимых значений компонент векторов потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:
(1.3)
$\mathcal{Z}(x,{\mathbf{d}}) = {\text{\{ }}{\mathbf{z}} \geqslant 0|({\mathbf{z}},x)\;{\text{удовлетворяют}}\;(1.1),(1.2){\text{\} }}{\text{.}}$2. Функциональные характеристики узлов. Обозначим через ${{z}_{i}}(j)$ однопродуктовый поток, направленный из центрального узла ${{{v}}_{j}}$ кластера в некоторую вершину-приемник ${{{v}}_{i}}$.
З а д а ч а 1. Найти максимальный однопродуктовый поток из центрального узла ${{{v}}_{j}}$ в узел-приемник ${{{v}}_{i}}$:
Каждому максимальному значению $z_{i}^{0}(j)$ соответствует минимальный разрез — множество ребер
Для некоторого фиксированного центрального узла ${{{v}}_{j}}$ кластера решим задачу 1 для всех ${{{v}}_{i}} \in V,i \ne j$, сформируем все ${{h}_{i}}(j)$ и на основе найденных значений $z_{i}^{0}(j)$ построим вектор
Для узла ${{{v}}_{j}}$ обозначим через D(j) предельно возможную пропускную способность инцидентных дуг для всех исходящих из ${{{v}}_{j}}$ потоков во все остальные узлы сети ${{{v}}_{i}} \in V,i \ne j$:
Величину ${{\theta }^{0}}(j)$ определим как коэффициент передачи вектора потоков z0(j) из узла ${{{v}}_{i}} \in V$:
(2.1)
${{\theta }^{0}}(j) = \frac{{D(j)}}{{\sum\limits_{i \ne j} z_{i}^{0}(j)}}\quad {\text{при}}\;{\text{условии}}\quad \sum\limits_{i \ne j} z_{i}^{0}(j) > 0.$Последовательно рассмотрим каждый узел сети ${{{v}}_{j}} \in V$ в качестве центрального в соответствующем кластере и решим цепочки задач 1. На основе найденных решений построим множество векторов
3. Множество повреждений. Множеству Z(0) поставим в соответствие множество
Для целей дальнейшего анализа формируется множество возможных повреждений сети на основе решения следующей аналогичной задачи о максимальном потоке — минимальном разрезе. В физическом графе сети $G(d)$ пропускная способность всех ребер полагается равной единице, ${{d}_{k}} = 1,k = \overline {1,E} $. Для каждого узла ${{{v}}_{j}}$ сети, который считается центром кластера, на графе с единичными пропускными способностями вычисляется максимальный поток из ${{{v}}_{j}}$ в узел-приемник ${{{v}}_{i}}$.
З а д а ч а 2. Найти $z_{i}^{1}(j) = ma{{x}_{{z \in Z(1)}}}{{z}_{i}}(j),$ где
Величина $z_{i}^{1}(j)$ численно равна числу ребер в минимальном разрезе для максимального целочисленного потока из ${{{v}}_{j}}$ в ${{{v}}_{i}}$.
Обозначим через
Обозначим через u(j) множество номеров ребер, инцидентных узлу ${{{v}}_{j}},{{{v}}_{j}} \in V$, и введем множество U(⋅), элементами которого являются списки номеров ребер, инцидентных каждой вершине ${{{v}}_{j}},j = \overline {1,N} $:
С помощью $H( \cdot ),Q( \cdot ),U( \cdot )$ формируется множество повреждений сети W, которое в дальнейшем используется для оценки уязвимости кластеров. Совпадающим спискам ${{h}_{i}}(j),{{q}_{m}}(n),u(s)$ в множествах $H( \cdot ),Q( \cdot ),U( \cdot )$ поставим в соответствие единственный в множестве W элемент wl — список номеров ребер, входящих в каждый из одинаковых элементов ${{h}_{i}}(j),{{q}_{m}}(n),u(s)$:
Кроме этого, каждому wl поставим в соответствие тройку индикаторов $str({{w}_{l}}) = (a,b,c)$, значения которых определим следующим образом. Положим:
a = 1, если множество wl совпадает с одним или более списком ${{h}_{i}}(j)$ в $H( \cdot )$, a = 0 – в противном случае;
b = 1, если список wl встречается в множестве $Q( \cdot )$ хотя бы один раз, $b = 0$ – в противном случае;
c = 1, если wl идентичен одному или более элементам в $U( \cdot )$, c = 0 – в противном случае.
Всего возможно семь вариантов возможных записей тройки индикаторов $(a,b,c)$, каждая из которых поэлементно характеризует множество повреждений W. Общее число элементов множества W обозначим через L, $W = {\text{\{ }}{{w}_{1}},{{w}_{2}},..,{{w}_{L}}{\text{\} }}$. Совпадение списков дуг, образующих разрезы, указывает на подмножества пересечений $H( \cdot ),Q( \cdot ),U( \cdot )$ и структурную зависимость различных потоков от всех критически опасных повреждений.
4. Оценки характеристик узлов при повреждениях. Рассмотрим последовательно каждый элемент ${{w}_{l}} \in W$ как повреждение физического графа сети $G(d)$. Для каждого ${{w}_{l}} \in W$ определим пропускную способность дуги ${{r}_{k}}$ следующим образом:
Пропускную способность узла ${{{v}}_{j}}$ после повреждения wl обозначим через D(j, l):
Тогда величина характеризует долю сохранившейся пропускной способности при повреждении wl, а усредненный показатель — среднюю величину сохраняющейся пропускной способности узла ${{{v}}_{j}}$ относительно всех повреждений из множества W.Для оценки изменения коэффициентов передачи θ0(j) при повреждении wl последовательно для каждого ${{{v}}_{i}}$ ∈ V решается следующая задача.
З а д а ч а 3. При некоторых фиксированных ${{{v}}_{j}}$, ${{{v}}_{i}}$, wl найти максимальный поток из центрального узла ${{{v}}_{j}}$ в вершину ${{{v}}_{i}}$:
Для полученных решений задачи 3 для каждого центрального узла ${{{v}}_{j}}$ вычисляются
Для узла-центра ${{{v}}_{j}}$ задается среднее изменение коэффициента передачи потока при всех повреждениях ${{w}_{l}} \in W$:
Величина δ(j) показывает, как изменится возможность передачи исходящих потоков из узла-центра ${{{v}}_{j}}$ при усреднении по множеству W.
Рассмотрим изменения максимально возможных информационных потоков между корреспондентами при повреждениях из W. На основе последовательного решения задачи 3 для всех пар узлов ${{{v}}_{j}} \in V,{{{v}}_{i}} \in V,i \ne j$, и повреждения ${{w}_{l}} \in W$ вводится индексный показатель
Сумма
равна числу узлов, связь с которыми из узла ${{{v}}_{j}}$ невозможна, т.е. при повреждении wl ∈ W поток из центра ${{{v}}_{j}}$ в вершины-приемники ${{{v}}_{i}}$ равен нулю. Вычислим среднюю долю ρ(j, W) узлов ${{{v}}_{i}}$, потоки в которые из центра ${{{v}}_{j}}$ равны нулю для всего множества повреждений W:Для всех потоков $z_{i}^{0}(j,l) > 0$ априори задается величина γ – уровень критических повреждений. При заданном значении $\gamma $ рассмотрим индикаторную функцию для исходящего потока из центра ${{{v}}_{j}}$ в узел ${{{v}}_{i}}$ при повреждении ${{w}_{l}} \in W$:
Если ψi(j, l, γ) = 1, то будем говорить, что потери информационного потока из центрального узла ${{{v}}_{j}}$ в ${{{v}}_{i}}$ для кластера при повреждении wl ∈ W превышают допустимый критический уровень γ. Для исходящих потоков из узла ${{{v}}_{j}}$ для всех повреждений из W величина
При оценке изменений функционирования кластера с центром в узле ${{{v}}_{j}}$ величина $\psi (j,\gamma )$ характеризует среднее число узлов ${{{v}}_{i}} \in V,i \ne j$, уменьшение входящих потоков (потери) в которые на всем множестве повреждений W окажутся выше критических.
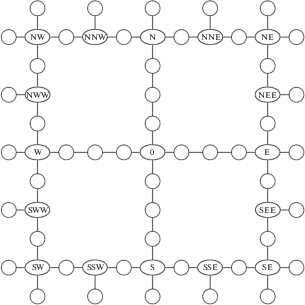
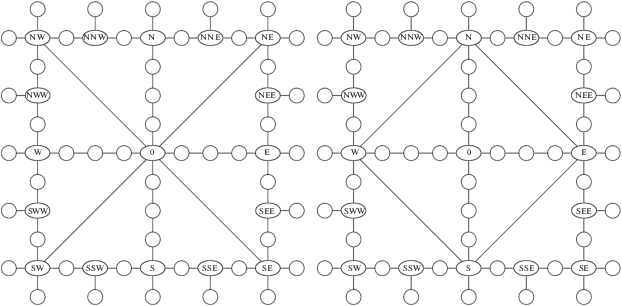
5. Вычислительный эксперимент. Вычислительный эксперимент проводился на моделях сетевых систем, имеющих исходный, базовый граф “крестовина” (рис. 1). Узлы сети обозначены согласно картушке компаса. Базовая сеть “крестовина” состоит из 65 вершин. Пропускные способности дуг указанной сети выбирались случайным образом с равной вероятностью из интервала [900, 999]. Для сетей с графом “звезда” и графом “ромб” (рис. 2) расчеты проводились на том же множестве вершин при сохранении пропускных способностей общих дуг. Пропускная способность каждой из четырех дуг, добавленных в центральной части в сетях “звезда” и “ромб”, была равна 900.
Общее число пар вершин – более 4 × 103. Исходное суммарное число элементов-разрезов в множествах $H( \cdot ),Q( \cdot )$ – более 8 × 103, а в $U( \cdot )$ – 65 по числу узлов сети. Число уникальных элементов в W составило для базовой сети 121, для “звезды” – 119, для “ромба” – 118. Состав множества W приведен в таблице.
Таблица
| $H,Q,U$ | Базовая | “Звезда” | “Ромб” | Cреднее |
|---|---|---|---|---|
| (1, 0, 0) | 28/121 = 23% | 18/119 = 15% | 28/118 = 24% | 21% |
| (0, 1, 0) | 22/121 = 18% | 24/119 = 20% | 19/118 = 16% | 18% |
| (0, 0, 1) | 17/121 = 14% | 17/119 = 14% | 16/118 = 14% | 14% |
| (1, 1, 1) | 30/121 = 25% | 34/119 = 29% | 30/118 = 25% | 26% |
| (1, 1, 0) | 6/121 = 5% | 12/119 = 10% | 6/118 = 5% | 7% |
| (0, 1, 1) | 18/121 = 15% | 14/119 = 12% | 19/118 = 16% | 14% |
| (1, 0, 1) | 0/121 = 0% | 0/119 = 0% | 0/118 = 0% | 0% |
Все элементы множества $U( \cdot )$ вошли в W. В таблице в первом столбце указаны строки-индексы, характеризующие принадлежности (“происхождение”) элементов W к множествам $H( \cdot ),Q( \cdot )$, $U( \cdot )$ и/или их пересечениям.
Например, для базовой сети 17 элементов множества W содержатся только в множестве вершинных разрезов U(⋅), что составляет 26% от общего числа элементов в $U( \cdot )$. Соответствующие цифры для множеств H(⋅) и Q(⋅) составляют доли процента. В множестве W 23% от всех повреждений являются разрезами из множества H(⋅), а число разрезов только из Q(⋅) составляет 18% числа элементов W.
Данные, собранные в таблице, позволяют говорить о (почти) равном представительстве разрезов $H( \cdot ),Q( \cdot )$ в множестве повреждений W. Без учета элементов “крупномасштабных” (“сильных”) повреждений из U(⋅) разрезы из $H( \cdot ),Q( \cdot )$ составляют 86% уникальных повреждений из W. Анализ элементов множества W показывает, насколько важно сформировать его из разрезов всех имеющихся множеств.
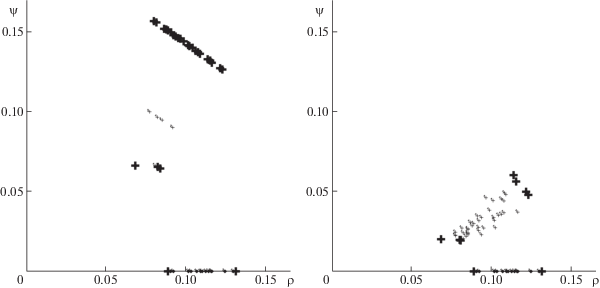
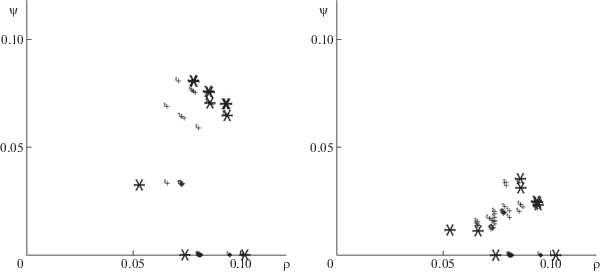
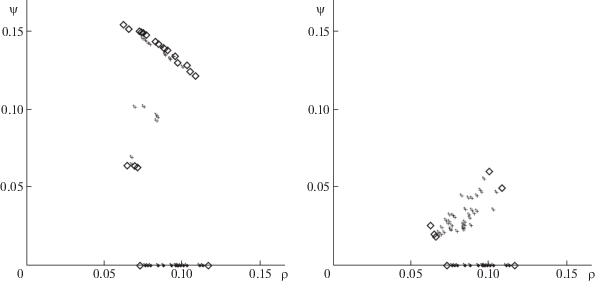
На рис. 3–5 представлены диаграммы для расчетных пар показателей $(\rho (j),\psi (j))$ при значениях $\gamma = 0.4$ (слева) и $\gamma = 0.5$ (справа) для всех сетей (базовой, “звезды” и “ромба”). На каждой из диаграмм недоминируемые значения выделены значками (крестиками, звездочками, ромбиками), которые соответствуют названиям графов.
Детальный анализ результатов расчетов указывает, что вершины-центры объединены в некоторые группы (см. диаграммы потерь $(\rho (j),\psi (j))$ на рис. 4, 5). Точки (значки), находящиеся на северо-восточной границе, являются недоминируемыми по максимальным потерям $(\rho (j),\psi (j))$. Поскольку большое число точек расположено в непосредственной близости от границы, то при анализе использовались все точки с близкими значениями. Аналогично в юго-западном углу, вблизи начала координат, расположены вершины-центры с наименьшими показателями потерь по критериям $(\rho (j),\psi (j))$.
В базовой сети (граф “крестовина”) центральный узел ${{{v}}_{0}}$ является недоминируемым по минимальным значениям для обоих критериев $(\rho (j),\psi (j))$ и $(\delta (j),\delta D(j))$. Узлы ${v}(N)$, ${v}(S)$, ${v}(E)$, ${v}(W)$ входят не во все списки недоминируемых точек, но всегда имеют численные показатели, близкие к предельным. Для сети “звезда” центральный узел ${{{v}}_{0}}$ будет недоминируемым по минимальным значениям для обоих критериев $(\rho (j),\psi (j))$ и $(\delta (j),\delta D(j))$ с большим преимуществом перед остальными вершинами. На объединенной диаграмме недоминируемых точек для всех сетей это становится особенно заметно (рис. 6). Для сети “ромб” центральный узел ${{{v}}_{0}}$ не является недоминируемым и не входит ни в один список вершин с показателями, близкими к предельным. Все списки недоминируемых по минимальным значениям потерь или “близких” (юго-западный угол на диаграмме) возглавляют узлы ${v}(N)$, ${v}(S)$, ${v}(E)$, ${v}(W)$.
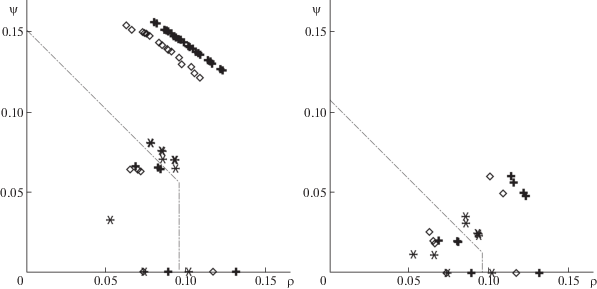
На рис. 6 представлены объединенные диаграммы по критериям $(\rho (j),\psi (j))$ для всех сетей при значениях $\gamma = 0.4$, $\gamma = 0.5$. Штрихпунктирная линия разделяет граничные точки, относящиеся к северо-восточной границе (максимальные потери) и точки из юго-западного угла, для которых потери минимальны. Таким образом указанная линия разделяет недоминируемые по максимуму $(\rho (j),\psi (j))$ вершины-центры кластеров от тех, для которых потери минимальны. Выше штрихпунктирной линии лежат вершины-центры кластеров, для которых потери максимальны среди всех вершин.
Слои недоминируемых вершин-центров строго упорядочены: наибольшие потери наблюдаются в базовой сети “крестовина”, далее – в сети “ромб” и наименьшие – в сети “звезда”. Ниже указанной линии тенденция сохраняется – наименьшие потери в сети “звезда”. Точка, ближайшая к началу координат, соответствует вершине ${{{v}}_{0}}$. Точки, лежащие вблизи разделяющего штрихпунктира, относятся к базовой сети.
Действительно, вершина ${{{v}}_{0}}$ является единственным узлом в базовом графе “крестовина”, которому инцидентны четыре дуги, а в графе “звезда” у ${{{v}}_{0}}$ – восемь инцидентных дуг, что значительно увеличивает количество путей обхода при повреждениях, обуславливает исключительно низкие показатели потерь по критериям $(\rho (j),\psi (j))$ и затрудняет сравнение с другими точками, лежащими в данном случае вдали от границы.
Вершины ${v}(N)$, ${v}(S)$, ${v}(E)$, ${v}(W)$ формально имеют:
четыре инцидентных дуги в базовом графе, но одна из этих дуг ведет в висячую вершину;
шесть инцидентных дуг в графе “ромб”, пять из них позволяют использовать большое число обходных путей при повреждениях;
функциональные показатели, которые значительно уступают ${{{v}}_{0}}$.
Последнее закономерно, поскольку четыре дополнительных дуги в сетях “звезда” и “ромб” значительно увеличивают число обходных путей при повреждениях и уменьшают значения $(\rho (j),\psi (j))$. Размытые оценки для сети “звезда” обусловлены тем, что угловые вершины ${v}(NE)$, ${v}(SE)$, ${v}(NW)$, ${v}(SW)$ хотя и имеют по пять инцидентных дуг, однако две из них ведут в висячие вершины.
Заключение. В последнее время возрос интерес к оценке устойчивости функционирования многопользовательских сетевых систем при повреждениях [2–4]. В рамках предлагаемой модели обеспечение информационного обмена между узлами-корреспондентами рассматривается как основная функция сети связи, а соответствующие величины потоков – как функциональные характеристики системы. В наших предыдущих работах при выборе критериев предполагалось, что неуязвимость системы целесообразно количественно оценивать исходя из того, какие показатели работоспособности сохраняются, а уязвимость – какие возможности по передаче потока утрачиваются при повреждениях.
Анализ уязвимости и вычислительные эксперименты проводились в рамках методологии исследования операций [5–7] с использованием методов оптимизации и потокового программирования [8–10]. Изучение влияния каждого повреждения на информационный обмен внутри кластера позволяет получить агрегированный срез данных о взаимосвязи между жесткой комбинаторно-графовой природой сети и множеством векторов допустимых потоков. Способ формирования множества критически опасных повреждений допускает оценку неуязвимости сети в условиях реально существующей неопределенности о месте и мощности разрушения систем связи, например в случае стихийных бедствий.
Представленный в работе метод выделения узлов, недоминируемых по потерям исходящего многопродуктового потока, можно расценивать как один из вариантов постановки задачи о поиске и определении критических элементов в сети, тогда предложенная агрегированная оценка ущерба будет служить вариантом коэффициента кластеринга для содержательной постановки [2]. Для поиска критически опасных повреждений [3], который сводится к NP-трудной задаче, в качестве эффективных эвристик для метода ветвей-и-границ подойдут изложенные в статье варианты вычисления векторных оценок. Данная работа является одним из возможных подходов к принятию решений в условиях реально существующей неопределенности о месте и цели повреждения систем связи и управления специального назначения.
Список литературы
Assad A.A. Multicommodity Network Flows: a Survey // Networks. 1978. V. 8. № 1. P. 37–91.
Ponton J., Wei P., Sun D. Weighted Clustering Coefficient Maximization for Air Transportation Networks // Control Conference (ECC). Zurich, 2013. P. 866–871.
Kuhnle A., Nguyen N.P., Dinh T.N., Thai M.T. Vulnerability of Clustering under Nodes Failure in Complex Networks // Social Network Analysis and Mining. 2017. V.7. Iss. 1. P. 8–24.
Ramirez-Marquez J.E., Rocco C.M., Barker K. Bi-Objective Vulnerability-Reduction Formulation for a Network under Diverse Attacks // ASCE-ASME J. of Risk and Uncertainty in Engineering Systems. Pt A: Civil Engineering. 2017. V. 3. Iss. 4. P. 04017025-04017041.
Фрэнк Г., Фриш М. Сети, связь и потоки. М.: Связь, 1978.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Данскин Дж.М. Теория максимина и ее приложение к задачам распределения вооружения. М.: Сов. радио, 1970.
Йенсен П., Барнес Д. Потоковое программирование. М.: Радио и связь, 1984.
Ogryczak W., Luss H., Pioro M., Nace D., Tomaszewski A. Fair Optimization and Networks: a survey // J. Appl. Math. 2014. V. 25. P. 1–25.
Chankong V., Haimes Y.Y. Multiobjective Decision Making: Theory and Methodology. Dover: Mineola, NY, 2008.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления