1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 2, 2022

Известия РАН. Теория и системы управления, 2022, № 2, стр. 3-21

СТАБИЛИЗАЦИЯ СИСТЕМЫ НЕУСТОЙЧИВЫХ МАЯТНИКОВ: ДИСКРЕТНЫЙ И НЕПРЕРЫВНЫЙ СЛУЧАЙ

П. А. Мелешенко a, b, В. А. Нестеров c, М. Е. Семенов a, d, e, *, А. М. Соловьев f, К. И. Сыпало g

a Воронежский государственный ун-т
Воронеж, Россия

b Целевая поисковая лаборатория прорывных технологий радиосвязи Фонда перспективных исследований, НИУ МИЭТ
Зеленоград, Москва, Россия

c МАИ (национальный исследовательский ун-т)
Москва, Россия

d ФГБУН Федеральный исследовательский центр “Единая геофизическая служба Российской академии наук”
Обнинск, Россия

e Воронежский государственный технический ун-т
Воронеж, Россия

f ГК Ростех, АО “Концерн “Созвездие”
Воронеж, Россия

g Федеральное государственное унитарное предприятие “Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского”
Жуковский, Россия

* E-mail: mkl150@mail.ru

Поступила в редакцию 04.10.2021
После доработки 30.10.2021
Принята к публикации 29.11.2021

Полный текст (PDF)

Аннотация

Исследуется динамика системы неустойчивых маятников в условиях упругих связей, находящихся под воздействием внешней вынуждающей силы, которая трактуется как управление, т.е. представлена задача управления неустойчивой системой с дефицитом управляющих воздействий. Кроме того, приведен случай нелинейных упругих связей (с кубической нелинейностью). Рассматривается переход от дискретной к непрерывной системе, описывающей материал, который является континуальным аналогом дискретной системы, находящийся в неравновесном, структурно-неустойчивом состоянии. Проводится исследование динамических характеристик неустойчивой системы и материала (в условиях дефицита управляющих воздействий), а также идентифицируются значения параметров, обеспечивающих ее стабилизацию.

Найдены необходимые и достаточные условия стабилизации системы перевернутых упругосвязанных маятников, формализуемые в виде ограничений на коэффициент жесткости упругой связи. Для континуального аналога рассматриваемой системы было доказано, что для стабилизации неустойчивого материала необходимо, чтобы ее параметры принимали значения, удовлетворяющие следующему условию: время прохождения упругой волны от одного конца системы до другого и обратно не должно превышать периода ее собственных колебаний. Приводятся результаты вычислительных экспериментов, иллюстрирующие теоретические построения.

Введение. Одна из важных задач теории управления связана с проблемой стабилизации неустойчивых динамических систем, в частности, с проблемой синтеза управляющего воздействия, обеспечивающего ограниченность фазовых координат системы в окрестности неустойчивого положения равновесия. Еще одна классическая задача математического моделирования исследует динамические режимы систем связанных осцилляторов (отметим, что эта система традиционно используется в качестве простейшей модели твердого тела). В работе рассматривается задача стабилизации системы связанных неустойчивых осцилляторов. Отдельно отметим, что в классической постановке равновесное положение осцилляторов, как правило, предполагается устойчивым. В то же время известны примеры систем, в которых отдельные элементы находятся в структурно неустойчивых состояниях (например, ионизированные атомы в плазме). Указанная проблема становится еще более сложной, если число управляющих воздействий меньше числа степеней свободы системы и ресурсы системы управления ограничены.

После того, как многими авторами в различных постановках был решен целый ряд задач управления однозвенным обратным маятником [1–14], интерес исследователей постепенно перемещается к более сложной проблеме управления системой обратных связанных маятников. При этом исследуемая система может представлять собой как многозвенные перевернутые маятники (двойной и тройной маятник), так и связанные однозвенные обратные маятники.

Значительные трудности вызывают задачи управления подобными системами с дефицитом числа управляющих воздействий, например, в случае многозвенного обратного маятника, когда управляющий момент прикладывается только в одном шарнире. При этом требуется так распорядиться относительным перемещением звеньев, чтобы приложенные силы гравитации вместе с внешним активным управляющим моментом способствовали приведению системы в желаемое положение [15–22]. Ряд публикаций указанной тематики посвящены построению различных контроллеров на основе нечеткого управления и искусственных нейронных сетей, предназначенных для стабилизации систем обратных маятников [23–27]. Отдельно отметим работы [28–31], в которых получены оригинальные и важные результаты в области оптимального по быстродействию управления перевернутым маятником. В частности, в [29] построены оптимальные переходные процессы (с учетом цилиндрической симметрии пространства состояний управляемой системы) для различных значений параметров и ограничений, накладываемых на управляющий момент. Помимо этого, следует отметить важную работу [32], которая посвящена новым методам управления сложными динамическими системами и описывает нелинейные системы управления, обладающие несколькими степенями свободы, а также подверженные неконтролируемым возмущениям и содержащие неопределенные параметры.

Исследования динамических свойств механических систем, в состав которых входят обратные мятники различных конфигураций, можно встретить во многих областях науки от медицины и биологии [33] до робототехники и космических технологий [34]. Данная статья является продолжением работ [8–14], посвященных решению задачи стабилизации обратного маятника для случая жесткого [8] и гибкого стержня [9–11], а также случая двух обратных маятников в условиях упругих связей [12, 13]. В настоящей работе производится обобщение классической системы связанных маятников для произвольного числа n упруго связанных обратных маятников, шарнирно закрепленных на подвижной платформе. При этом сила, приложенная к платформе и вызывающая ее горизонтальные перемещения, трактуется как управление. Кроме того, выполняется предельный переход от дискретной к непрерывной модели, описывающей материал, который находится в неравновесном, структурно-неустойчивом состоянии. Выполнено исследование динамических характеристик указанных систем (в случае управления по принципу обратной связи), а также получены условия, обеспечивающие их стабилизацию.

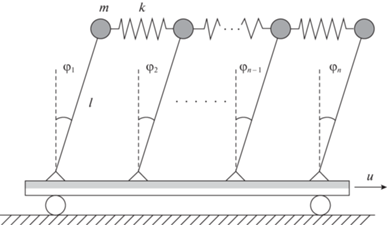
1. Дискретная система. 1.1. Математическая модель. Рассмотрим систему из n перевернутых маятников, каждый из которых имеет массу m и длину стержня l, жестко закрепленных на подвижной тележке и связанных между собой пружинами жесткостью k. При этом пружины находятся в недеформированном состоянии в случае, когда маятники занимают вертикальное положение. Будем считать, что тележка не имеет массы и движется без трения, а управляющее воздействие, приложенное к тележке, сообщает ей ускорение u (рис. 1).

Рис. 1.

Система связанных обратных маятников

Пренебрегая трением, запишем уравнения моментов исследуемой системы (в неинерциальной системе координат, связанной с тележкой):

(1.1)
$\left\{ \begin{gathered} {{I}_{1}}\frac{{d{{{\vec {\omega }}}_{1}}}}{{dt}} = \vec {M}_{1}^{{\left( g \right)}} + \vec {M}_{1}^{{\left( {kr} \right)}} + {{{\vec {M}}}^{{\left( u \right)}}}, \hfill \\ {{I}_{i}}\frac{{d{{{\vec {\omega }}}_{i}}}}{{dt}} = \vec {M}_{i}^{{\left( g \right)}} + \vec {M}_{i}^{{\left( {kr} \right)}} + \vec {M}_{i}^{{\left( {kl} \right)}} + {{{\vec {M}}}^{{\left( u \right)}}}\begin{array}{*{20}{c}} ,&{i = \overline {2,n - 1} } \end{array}, \hfill \\ {{I}_{n}}\frac{{d{{{\vec {\omega }}}_{n}}}}{{dt}} = \vec {M}_{n}^{{\left( g \right)}} + \vec {M}_{n}^{{\left( {kl} \right)}} + {{{\vec {M}}}^{{\left( u \right)}}}. \hfill \\ \end{gathered} \right.$

Здесь I – момент инерции маятника относительно оси шарнира, который соединяет его с тележкой, ω – угловая скорость, M(g) – возвращающий момент силы тяжести, M(kl) и M(кr) – моменты силы упругости пружин, расположенных слева и справа от i-го маятника соответственно, а M(u) – момент управления, равный моменту переносной силы инерции.

Поскольку рассматривается плоское движение, все указанные векторы имеют направления, перпендикулярные плоскости рисунка, что позволяет перейти к уравнениям в скалярной форме. Как следует из рис. 1, положение маятников характеризуется углами их отклонения от вертикальной оси φ. При этом углы отклонения маятников предполагаются малыми. В этом случае удлинение пружины Δx можно приближенно записать как

(1.2)
$\Delta {{x}_{i}} \approx l\left( {{{\varphi }_{{i + 1}}} - {{\varphi }_{i}}} \right).$

Введем собственную частоту колебаний для изолированного маятника:

(1.3)
$\omega = \sqrt {\frac{{mgl}}{I}} .$

Также предположим, что массы являются точечными, сосредоточенными на концах соответствующих стержней, тогда

(1.4)
$I = m{{l}^{2}} \Rightarrow \omega = \sqrt {\frac{g}{l}} .$

Таким образом, учитывая равенства (1.2)–(1.4), система уравнений (1.1) будет иметь вид

(1.5)
$\left\{ \begin{gathered} {{{\ddot {\varphi }}}_{1}} = {{\omega }^{2}}{{\varphi }_{1}} + a\left( {{{\varphi }_{2}} - {{\varphi }_{1}}} \right) - c, \hfill \\ {{{\ddot {\varphi }}}_{i}} = {{\omega }^{2}}{{\varphi }_{i}} + a\left( {{{\varphi }_{{i + 1}}} - 2{{\varphi }_{i}} + {{\varphi }_{{i - 1}}}} \right) - c, \hfill \\ {{{\ddot {\varphi }}}_{n}} = {{\omega }^{2}}{{\varphi }_{n}} - a\left( {{{\varphi }_{n}} - {{\varphi }_{{n - 1}}}} \right) - c, \hfill \\ \end{gathered} \right.$
где $a = {k \mathord{\left/ {\vphantom {k m}} \right. \kern-0em} m}\begin{array}{*{20}{c}} ,&{c = {u \mathord{\left/ {\vphantom {u l}} \right. \kern-0em} l}.} \end{array}$

1.2. Стабилизация системы. Стабилизацию дискретной системы (1.5) будем осуществлять посредством управления, формируемого по принципу обратной связи [8–13]. Найдем суммарное отклонение маятников относительно вертикального положения. С этой целью просуммируем все уравнения системы (1.5):

(1.6)
$\ddot {s} = {{\omega }^{2}}s - nc,\quad s = \sum\limits_{i = 1}^n {{{\varphi }_{i}}} .$

Тогда ускорение (управление), приложенное к тележке (рис. 1), определим следующим соотношением:

(1.7)
$u = A{\text{sign}}\left( {Bs + \dot {s}} \right),$
где A и B – коэффициенты, задающие характер управления.

1.3. Коэффициенты управления. Проведем исследование динамики дискретной системы и найдем значения коэффициентов A и B, приводящие к стабилизации маятников в окрестности неустойчивого вертикального положения.

Заметим, что управление (ускорение) u, как видно из уравнения (1.6), влияет только на суммарное угловое положение маятников в пространстве, а жесткость пружин k – только на их положение относительно друг друга.

Общее решение дифференциального уравнения (1.6) на временном интервале с постоянным управлением имеет следующий вид:

(1.8)
$s\left( t \right) = {{C}_{1}}{{e}^{{\omega t}}} + {{C}_{2}}{{e}^{{ - \omega t}}} + \frac{{nu}}{{{{\omega }^{2}}l}}.$

Пусть начальное значение суммарного отклонения $s(0) = {{s}_{0}}$, а его производная $\dot {s}(0) = {{s}_{1}}$. Тогда решение задачи Коши уравнения (1.6) запишем как

(1.9)
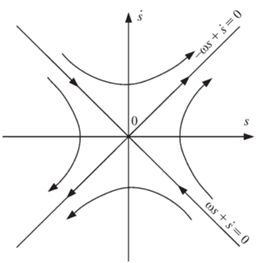
$s\left( t \right) = \frac{1}{2}\left( {{{s}_{0}} + \frac{{{{s}_{1}}}}{\omega } - \frac{{nu}}{{{{\omega }^{2}}l}}} \right){{e}^{{\omega t}}} + \frac{1}{2}\left( {{{s}_{0}} - \frac{{{{s}_{1}}}}{\omega } - \frac{{nu}}{{{{\omega }^{2}}l}}} \right){{e}^{{ - \omega t}}} + \frac{{nu}}{{{{\omega }^{2}}l}}.$

Рассмотрим фазовый портрет исследуемой системы (рис. 2) [13].

Рис. 2.

Фазовый портрет системы

При отсутствии управления, как видно из рисунка, попадая на прямую $\omega s + \dot {s} = 0$, фазовые координаты будут “стремиться” к нулевому положению равновесия. Другими словами, когда управление u способно “довести” суммарное положение маятников до прямой $\omega s + \dot {s} = 0$, система будет стабилизирована [13]. Таким образом, из решения (1.9) следует, что для стабилизации системы необходимо (в начальный момент времени) выполнение условия

(1.10)
${{s}_{0}} + \frac{{{{s}_{1}}}}{\omega } - \frac{{nu}}{{{{\omega }^{2}}l}} = 0 \Rightarrow u = \frac{{\omega {\kern 1pt} l}}{n}\left( {\omega {\kern 1pt} {{s}_{0}} + {{s}_{1}}} \right),$
до тех пор, пока $\omega s + \dot {s}$ сохраняет знак. С учетом (1.10) управление (1.7) можно записать в следующем виде:

(1.11)
$u = \frac{{\omega {\kern 1pt} l}}{n}\left| {\omega {\kern 1pt} {{s}_{0}} + {{s}_{1}}} \right|{\text{sign}}\left( {\omega {\kern 1pt} s + \dot {s}} \right).$

Таким образом, искомые коэффициенты управления (1.7), приводящие к стабилизации системы (1.6), определяются посредством соотношений

(1.12)
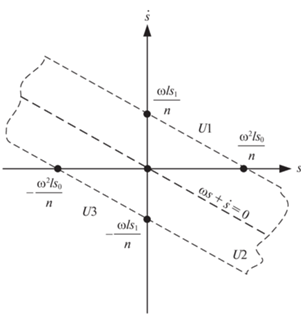
$\left\{ \begin{gathered} A = \frac{{\omega l}}{n}\left| {\omega {{s}_{0}} + {{s}_{1}}} \right|, \hfill \\ B = \omega . \hfill \\ \end{gathered} \right.$

Отметим, что устойчивое положение маятников, к которому приводит выполнение условия (1.12), не является вертикальным, так как в этом случае суммарное отклонение маятников $s \to {{nu} \mathord{\left/ {\vphantom {{nu} {{{\omega }^{2}}l}}} \right. \kern-0em} {{{\omega }^{2}}l}}$, что демонстрирует траектория a фазового пространства (рис. 3), при выполнении условий (1.12). Однако из решения (1.9) также следует, что при

(1.13)
${{s}_{0}} + \frac{{{{s}_{1}}}}{\omega } - \frac{{nu}}{{{{\omega }^{2}}l}} < 0$
управление будет “возвращать” маятники в сторону вертикального положения, что соответствует движению фазовых координат к прямой $\omega s + \dot {s} = 0$ фазового пространства. Попадая же на прямую $\omega s + \dot {s} = 0$, фазовые координаты будут “стремиться” к нулевому положению равновесия, что демонстрирует траектория b фазового пространства (рис. 3), при выполнении условия (1.13). Таким образом, необходимое условие стабилизации системы имеет следующий вид:

(1.14)
$\left\{ \begin{gathered} A \geqslant \frac{{\omega l}}{n}\left| {\omega {{s}_{0}} + {{s}_{1}}} \right|, \hfill \\ B = \omega . \hfill \\ \end{gathered} \right.$
Рис. 3.

Область устойчивости системы

Графически условие (1.14) можно отобразить на фазовой плоскости в форме, представленной на рис. 3.

Области U1 и U3 определяют все возможные начальные состояния системы, при которых маятники невозможно “удержать” в окрестности вертикального положения равновесия, а область U2 является областью устойчивости системы при выполнении условий (1.14), наложенных на управляющее воздействие (1.7).

Отметим, что после воздействия управления суммарный угол отклонения маятников s может изменить знак, вследствие чего на каждой расчетной итерации необходимо переопределять управляющее воздействие. Однако из-за консервативности рассматриваемой системы для успешного управления достаточно переопределить лишь знак величины u исходя из текущих значений $s$ и $\dot {s}$, согласно (1.7), при этом коэффициенты A и B, согласно (1.14), оставив неизменными.

1.4. Параметры системы. Условие (1.14) является необходимым, но не достаточным условием стабилизации системы (1.5). Как уже указывалось ранее, на положение маятников друг относительно друга и, как следствие, на возможность стабилизации системы также влияют ее параметры, а именно коэффициент жесткости пружин k, а также масса грузов m и количество маятников n. Найдем параметры системы, обеспечивающие ее стабилизацию при условии выполнения соотношений (1.14).

Исследуем относительное перемещение маятников. С этой целью найдем попарные разности уравнений системы (1.5):

(1.15)
$\left\{ \begin{gathered} {{{\ddot {d}}}_{1}} = {{\omega }^{2}}{{d}_{1}} + \frac{k}{m}\left( {{{d}_{2}} - 2{{d}_{1}}} \right), \hfill \\ {{{\ddot {d}}}_{i}} = {{\omega }^{2}}{{d}_{i}} + \frac{k}{m}\left( {{{d}_{{i - 1}}} - 2{{d}_{i}} + {{d}_{{i + 1}}}} \right),\quad i = \overline {2,m - 1} . \hfill \\ {{{\ddot {d}}}_{m}} = {{\omega }^{2}}{{d}_{m}} - \frac{k}{m}\left( {{{d}_{{m - 1}}} - 2{{d}_{m}}} \right), \hfill \\ \end{gathered} \right.$
где ${{d}_{i}} = {{\varphi }_{i}} - {{\varphi }_{{i + 1}}}$, а $m = n - 1$. Запишем систему уравнений (1.15) в матричной форме:
(1.16)
$\ddot {D} = A \times D,$
где

(1.17)
${\mathbf{D}} = \left( \begin{gathered} {{d}_{1}} \\ \vdots \\ {{d}_{m}} \\ \end{gathered} \right),\quad {\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{a}_{{1,1}}}}& \cdots &{{{a}_{{1,m}}}} \\ \vdots & \ddots & \vdots \\ {{{a}_{{m,1}}}}& \cdots &{{{a}_{{m,m}}}} \end{array}} \right),\quad \left\{ \begin{gathered} {{a}_{{i,i}}} = {{\omega }^{2}} - \frac{{2k}}{m},\quad i = \overline {1,m} , \hfill \\ {{a}_{{i + 1,i}}} = {{a}_{{i,i + 1}}} = \frac{k}{m},\quad i = \overline {1,m - 1} , \hfill \\ {{a}_{{i,j}}} = 0,\quad i = \overline {1,m - 2} ,\quad j = \overline {i + 2,m} , \hfill \\ {{a}_{{j,i}}} = 0,\quad i = \overline {1,m - 2} ,\quad j = \overline {i + 2,m} . \hfill \\ \end{gathered} \right.$

Параметры системы (k, m, n), обеспечивающие стабилизацию маятников по относительному перемещению, можно определить из условия

(1.18)
$\operatorname{Re} {{\lambda }_{1}} \leqslant 0 \wedge \operatorname{Re} {{\lambda }_{2}} \leqslant 0 \ldots \wedge \operatorname{Re} {{\lambda }_{m}} \leqslant 0,$
где λi – собственные числа матрицы коэффициентов A.

Так, в качестве примера, при n = 6 из условия (1.18) можно найти область значений жесткости пружин k, при которой обеспечивается устойчивость маятников по отношению друг к другу:

(1.19)
$k \geqslant \frac{{{{\omega }^{2}}m}}{{2 - \sqrt 3 }}.$

1.5. Результаты компьютерного моделирования. Проведем компьютерное моделирование динамики исследуемой механической системы. С этой целью найдем решение системы уравнений (1.5), когда

(1.20)
$\begin{gathered} m = 0.1\;{\text{кг,}}\quad l = 1\;{\text{м,}}\quad n = 6, \\ {{\varphi }_{1}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{1}}\left( 0 \right) = 0.1\;{\text{рад/с}}, \\ {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {2,n} . \\ \end{gathered} $

Решение будем искать с помощью одношагового метода Рунге–Кутта 5-го порядка. Построим графики функций s и d, определяемых как

(1.21)
$s = \sum\limits_{i = 1}^n {{{\varphi }_{i}}} ,\quad d = \sum\limits_{j = 1}^{n - 1} {{{d}_{j}}} .$

Здесь s – суммарное отклонение маятников от вертикальной оси, а d – суммарное отклонение маятников друг относительно друга.

На рис. 4 приведены графики функций s и d при выполнении условий (1.14) и (1.18), когда k = = 20 Н/м, A = 0.0722, B = 3.1337, на рис. 5 – в случае невыполнения условия (1.14) и выполнения (1.18) при k = 20 Н/м, A = 0.0322, B = 3.1337, на рис. 6 – при невыполнении условия (1.18) и выполнении (1.14), когда k = 3 Н/м, A = 0.0722, B = 3.1337, а на рис. 7 – фазовые траектории при строгом выполнении условий (1.14) и (1.18).

Рис. 4.

Графики функций s (слева) и d (справа) при выполнении условий (1.14) и (1.18)

Рис. 5.

Графики функций s (слева) и d (справа) при невыполнении условия (1.14) и выполнении условия (1.18)

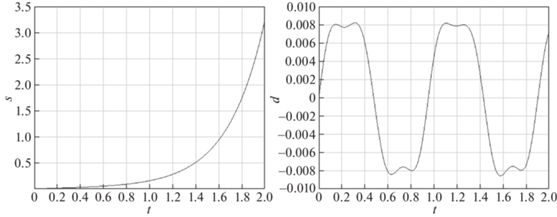
Рис. 6.

Графики функций s (слева) и d (справа) при выполнении условия (1.14) и невыполнении условия (1.18)

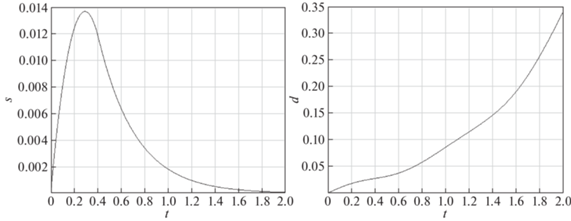
Рис. 7.

Фазовые траектории при строгом выполнении неравенств (1.14), (1.18) и начальных условиях ${{s}_{0}} = 0,$ ${{s}_{1}} = 0.01$ (слева), ${{s}_{0}} = 0,$ ${{s}_{1}} = - 0.01$ (справа)

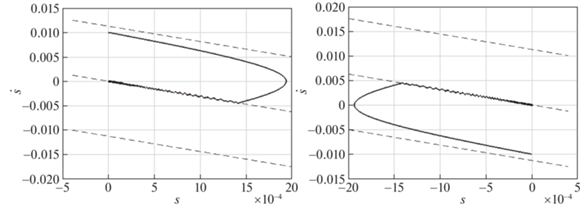
Как видно из результатов компьютерного моделирования, неравенства (1.14), (1.18) являются необходимыми и достаточными условиями стабилизации системы (1.5).

1.6. Упругие волны. Как известно [35], при возбуждении цепочки связанных осцилляторов в условиях упругих связей возникает волновое движение, при котором фазовый волновой фронт перемещается с конечной скоростью, постоянной для однородной среды, перенося энергию колебаний. Это явление называется бегущей волной. Примерами бегущих волн могут служить упругие волны в металлическом стержне, столбе газа или жидкости, электромагнитные волны, распространяющиеся вдоль длинной линии или в волноводе.

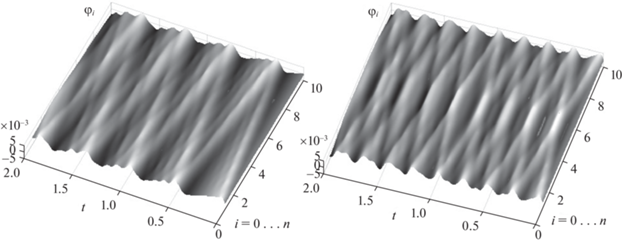
В исследуемой механической системе при определенных начальных условиях в процессе стабилизации также возникают упругие волны, что демонстрируют результаты компьютерного моделирования. Так, на рис. 8 (слева) показана упругая волна, движущаяся от 1-го маятника системы к n-му и в обратном направлении, возникающая при следующих начальных условиях:

(1.22)
$\begin{gathered} {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad i = \overline {1,n} , \\ {{{\dot {\varphi }}}_{1}}\left( 0 \right) = 0.1\;{\text{рад/с}},\quad {{{\dot {\varphi }}}_{j}}\left( 0 \right) = 0\;{\text{рад/с}},\quad j = \overline {2,n} . \\ \end{gathered} $
Рис. 8.

Упругие волны в стабилизированной системе

На рис. 8 (справа) изображены две упругие волны, движущиеся в противоположных направлениях, возникающие при начальных условиях:

(1.23)
$\begin{gathered} {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}}\quad i = \overline {1,n} , \\ {{{\dot {\varphi }}}_{1}}\left( 0 \right) = 0.1\;{\text{рад/с}}\quad {{{\dot {\varphi }}}_{n}}\left( 0 \right) = - 0.1\;{\text{рад/с}}\quad {{{\dot {\varphi }}}_{j}}\left( 0 \right) = 0\;{\text{рад/с}}\quad j = \overline {2,n - 1} . \\ \end{gathered} $

2. Непрерывная система. 2.1. Математическая модель. Произведем формальный переход от дискретной системы, состоящей из n обратных маятников, к непрерывной, описывающей материал, который находится в неравновесном, структурно-неустойчивом состоянии. С этой целью перепишем второе уравнение системы (1.5) следующим образом:

(2.1)
${{\ddot {\varphi }}_{i}} = {{\omega }^{2}}{{\varphi }_{i}} + \frac{{k{{h}^{2}}}}{m}\frac{{\left( {{{\varphi }_{{i + 1}}} - 2{{\varphi }_{i}} + {{\varphi }_{{i - 1}}}} \right)}}{{{{h}^{2}}}} - \frac{u}{l},$
где h – расстояние между маятниками системы (по оси OX). Очевидно, что

(2.2)
$\mathop {\lim }\limits_{h \to 0} \frac{{\left( {{{\varphi }_{{i + 1}}} - 2{{\varphi }_{i}} + {{\varphi }_{{i - 1}}}} \right)}}{{{{h}^{2}}}} = \frac{{{{\partial }^{2}}\varphi (x,t)}}{{\partial {{x}^{2}}}} = \varphi ''(x,t).$

Будем считать, что длина маятников сопоставима с расстоянием между ними, т.е. l = h. Тогда, учитывая (2.2), уравнение (2.1) в предельном случае будет иметь вид

(2.3)
$\ddot {\varphi }(x,t) = {{\omega }^{2}}\varphi (x,t) + \frac{{k{{h}^{2}}}}{m}\varphi ''(x,t) - \frac{{u\left( {\dot {\varphi },\varphi ,t} \right)}}{h}.$

Уравнение (2.3) описывает материал с поперечным сечением S. Механическое напряжение под воздействием приложенной силы F в таком материале можно найти как

(2.4)
$T = \frac{F}{S}.$

С другой стороны, напряжение можно найти из закона Гука:

(2.5)
$T = E\frac{{\Delta x}}{h},$
где E – модуль Юнга.

Исходя из того, что $F = k\Delta x$, из (2.4) и (2.5) можно выразить коэффициент жесткости пружин:

(2.6)
$k = \frac{{ES}}{h}.$

Будем считать, что материал имеет квадратное сечение ($S = {{h}^{2}}$), тогда масса, сосредоточенная в одной его элементарной ячейке

(2.7)
$m = \rho {{h}^{3}}.$

Также, будем считать, что материал имеет массу $M = {{m{\kern 1pt} L} \mathord{\left/ {\vphantom {{m{\kern 1pt} L} h}} \right. \kern-0em} h}$, где L – его длина по оси OX. Следовательно, из (2.7) найдем

(2.8)
$h = \sqrt {\frac{M}{{\rho L}}} .$

Подставляя (2.6)–(2.8) в (2.3), получим

(2.9)
$\ddot {\varphi }\left( {x,t} \right) = {{\omega }^{2}}\varphi \left( {x,t} \right) + \frac{E}{\rho }\varphi {\kern 1pt} '{\kern 1pt} '\left( {x,t} \right) - \sqrt {\frac{{\rho L}}{M}} u\left( {\dot {\varphi },\varphi ,t} \right).$

Рассмотрим первое и последнее уравнение системы (1.5). В предельном случае данные уравнения можно получить из второго уравнения системы (1.5), если выполняются следующие условия:

(2.10)
$\left\{ \begin{gathered} {{\left. {\frac{{\partial \varphi \left( {x,t} \right)}}{{\partial x}}} \right|}_{{x = 0}}} = \varphi {\kern 1pt} '\left( {0,t} \right) = 0, \hfill \\ {{\left. {\frac{{\partial \varphi \left( {x,t} \right)}}{{\partial x}}} \right|}_{{x = L}}} = \varphi {\kern 1pt} '\left( {L,t} \right) = 0. \hfill \\ \end{gathered} \right.$

Таким образом, при учете (2.10) система уравнений, являющаяся континуальным аналогом системы (1.5) и описывающая динамику неустойчивого материала, имеет вид

(2.11)
$\left\{ \begin{gathered} \ddot {\varphi }\left( {x,t} \right) = {{\omega }^{2}}\varphi \left( {x,t} \right) + {{V}^{2}}\varphi {\kern 1pt} '{\kern 1pt} '\left( {x,t} \right) - \alpha u\left( {\dot {\varphi },\varphi ,t} \right), \hfill \\ \varphi '\left( {0,t} \right) = 0, \hfill \\ \varphi '\left( {L,t} \right) = 0, \hfill \\ \varphi \left( {x,0} \right) = f\left( x \right), \hfill \\ \dot {\varphi }\left( {x,0} \right) = g\left( x \right), \hfill \\ \alpha = \sqrt {\frac{{\rho L}}{M}} , \hfill \\ {{\omega }^{2}} = g\alpha , \hfill \\ {{V}^{2}} = \frac{E}{\rho }. \hfill \\ \end{gathered} \right.$

Здесь M – масса материала, ρ – его плотность, L – длина, ω – собственная частота, V – скорость распространения упругой волны, а функции  f (x) и g (x) формализуют начальные условия. Отметим, что выражение ${{\omega }^{2}} = g\alpha $ в (2.11) является следствием равенства l = h и выражения (2.8).

2.2. Стабилизация непрерывной системы. Стабилизацию системы (2.11) будем осуществлять посредством управления, формируемого по принципу обратной связи, аналогично (1.6), (1.7). Переходя к континуальному аналогу, запишем интегральное отклонение элементов материала:

(2.12)
$s\left( t \right) = \int\limits_0^L {\varphi \left( {x,t} \right)dx} .$

Управляющее воздействие, аналогично дискретному случаю (1.7), будет иметь вид

(2.13)
$u = A{\text{sign}}\left( {Bs + \dot {s}} \right).$

2.3. Коэффициенты управления. Найдем значения коэффициентов A и B (2.13), приводящие к стабилизации исследуемого материала. С этой целью проинтегрируем первое уравнение системы (2.11) в интервале [0, L]:

(2.14)
$\ddot {s}\left( t \right) = {{\omega }^{2}}s\left( t \right) + {{V}^{2}}\left[ {\varphi {\kern 1pt} '\left( {L,t} \right) - \varphi {\kern 1pt} '\left( {0,t} \right)} \right] - L\alpha u\left( {\dot {s},s,t} \right).$

Принимая во внимание 2-е и 3-е уравнения системы (2.11), окончательно получим

(2.15)
$\ddot {s}\left( t \right) = {{\omega }^{2}}s\left( t \right) - L\alpha u\left( {\dot {s},s,t} \right).$

Аналогично дискретному случаю (1.8)–(1.11) можно получить необходимое условие стабилизации системы:

(2.16)
${{s}_{0}} + \frac{{{{s}_{1}}}}{\omega } - \frac{{L\alpha u}}{{{{\omega }^{2}}}} = 0 \Rightarrow {{s}_{0}} + \frac{{{{s}_{1}}}}{\omega } - \frac{{Lu}}{g} = 0 \Rightarrow u = \frac{g}{{\omega L}}\left( {\omega {{s}_{0}} + {{s}_{1}}} \right).$

Отсюда по аналогии с (1.14) найдем

(2.17)
$\left\{ \begin{gathered} A \geqslant \frac{g}{{\omega L}}\left| {\omega {{s}_{0}} + {{s}_{1}}} \right|, \hfill \\ B = \omega \,. \hfill \\ \end{gathered} \right.$

2.4. Параметры материала. Как и в случае с дискретной системой, условие (2.17) является необходимым для стабилизации исследуемого материала, но отнюдь не достаточным. На возможность стабилизации материала, помимо коэффициентов управления, влияют также его параметры. Найдем параметры материала, обеспечивающие его стабилизацию в случае выполнения условия (2.17). С этой целью продифференцируем первое уравнение системы (2.11) по переменной x:

(2.18)
$\ddot {\varphi }{\kern 1pt} '\left( {x,t} \right) = {{\omega }^{2}}\varphi {\kern 1pt} '\left( {x,t} \right) + {{V}^{2}}\varphi {\kern 1pt} '{\kern 1pt} '{\kern 1pt} '\left( {x,t} \right).$

Произведем замену переменных $d(x,t) = \varphi {\kern 1pt} '(x,t)$ и с учетом граничных условий из системы (2.11) получим

(2.19)
$\left\{ \begin{gathered} \ddot {d}\left( {x,t} \right) = {{\omega }^{2}}d\left( {x,t} \right) + {{V}^{2}}d{\kern 1pt} '{\kern 1pt} '\left( {x,t} \right), \hfill \\ d\left( {0,t} \right) = 0, \hfill \\ d\left( {L,t} \right) = 0, \hfill \\ \end{gathered} \right.$
где величина d пропорциональна отклонению элементов материала относительно друг друга с течением времени.

Решим систему (2.19) с помощью метода Фурье (разделения переменных). Для этого представим решение первого уравнения системы (2.19) в виде произведения двух функций, каждая из которых зависит только от одной переменной:

(2.20)
$d(x,t) = X(x)T(t).$

Подставим (2.20) в первое уравнение системы (2.19):

(2.21)
$X\ddot {T} = {{\omega }^{2}}XT + {{V}^{2}}X{\kern 1pt} '{\kern 1pt} 'T.$

Перепишем уравнение (2.21) в виде

(2.22)
$\frac{{\ddot {T}}}{{{{\omega }^{2}}T}} = 1 + \frac{{{{V}^{2}}X{\kern 1pt} '{\kern 1pt} '}}{{{{\omega }^{2}}X}}.$

Уравнение (2.22) можно представить в виде системы двух независимых уравнений:

(2.23)
$\left\{ \begin{gathered} \frac{{\ddot {T}}}{{{{\omega }^{2}}T}} = \lambda , \hfill \\ 1 + \frac{{{{V}^{2}}X{\kern 1pt} '{\kern 1pt} '}}{{{{\omega }^{2}}X}} = \lambda , \hfill \\ \end{gathered} \right.$
где λ = const.

Перепишем (2.23) в другом виде и, учитывая граничные условия из (2.19), получим систему

(2.24)
$\left\{ \begin{gathered} {{V}^{2}}X{\kern 1pt} '{\kern 1pt} '\; + {{\omega }^{2}}X\left( {1 - \lambda } \right) = 0, \hfill \\ \ddot {T} - {{\omega }^{2}}T\lambda = 0, \hfill \\ X(0) = 0, \hfill \\ X(L) = 0. \hfill \\ \end{gathered} \right.$

Рассмотрим первое уравнение системы (2.24). С учетом граничных условий решение этого уравнения сводится к классической задаче Штурма–Лиувилля первого рода [36–38]:

(2.25)
$\left\{ \begin{gathered} X{\kern 1pt} '{\kern 1pt} '\; + \beta X = 0, \hfill \\ X(0) = 0, \hfill \\ X(L) = 0, \hfill \\ \end{gathered} \right.$
где

(2.26)
$\beta = {{\left( {\frac{\omega }{V}} \right)}^{2}}\left( {1 - \lambda } \right).$

Решением системы (2.25) является множество нетривиальных решений:

(2.27)
$\left\{ \begin{gathered} {{\beta }_{n}} = {{\left( {\frac{{\pi n}}{L}} \right)}^{2}}, \hfill \\ {{X}_{n}}\left( x \right) = \sin (\sqrt {{{\beta }_{n}}} x), \hfill \\ n \in N. \hfill \\ \end{gathered} \right.$

Произведем обратную замену (2.26) и получим решение первого уравнения системы (2.24):

(2.28)
$\left\{ \begin{gathered} {{\lambda }_{n}} = 1 - {{\left( {\frac{{\pi nV}}{{\omega L}}} \right)}^{2}}, \hfill \\ X\left( x \right) = \sin \left( {\frac{{\pi n}}{L}x} \right), \hfill \\ n \in N. \hfill \\ \end{gathered} \right.$

Рассмотрим второе уравнение системы (2.24). Общее решение этого уравнение имеет вид

(2.29)
${{T}_{n}}(t) = A{{e}^{{\sqrt {{{\lambda }_{n}}} \omega t}}} + B{{e}^{{ - \sqrt {{{\lambda }_{n}}} \omega t}}}.$

Так как решение системы (2.19) ищется в виде (2.20), очевидно, что для устойчивости решения необходима ограниченность функций X(x) и T(t). Функция X(x), согласно (2.28), имеет гармонический характер и является ограниченной. Из (2.29) также очевидно, что для ограниченности функции T(t) необходимо выполнение условия ${{\lambda }_{n}} \leqslant 0.$ В этом случае функция (2.29) также будет иметь гармонический характер или принимать постоянное значение при λn = 0.

Таким образом, условие устойчивости решения системы (2.19) запишется как

(2.30)
$1 - {{\left( {\frac{{\pi nV}}{{\omega L}}} \right)}^{2}} \leqslant 0$
или, что то же самое,

(2.31)
$\frac{{\pi nV}}{{\omega L}} \geqslant 1.$

Так как собственные числа n изменяются в интервале $\left[ {1, + \infty } \right)$, то n = 1 соответствует минимальному значению левой части неравенства (2.31). Учитывая этот факт, перепишем (2.31) следующим образом:

(2.32)
$\frac{V}{L} \geqslant \frac{\omega }{\pi }.$

Введем следующие обозначения:

(2.33)
$\begin{gathered} {{T}_{v}} = \frac{{2L}}{V}, \hfill \\ {{T}_{\omega }} = \frac{{2\pi }}{\omega }, \hfill \\ \end{gathered} $
где ${{T}_{v}}$ – время, за которое упругая волна проходит от одного конца материала до его другого конца и обратно, а Tω – период собственных колебаний материала. Перепишем равенство (2.32) с учетом обозначений (2.33) и получим

(2.34)
${{T}_{v}} \leqslant {{T}_{\omega }}{\kern 1pt} {\kern 1pt} .$

Неравенство (2.34) определяет параметры материала, обеспечивающие его стабилизацию в случае выполнения условия (2.17). Также из неравенства (2.34) следует важный вывод: с физической точки зрения, для стабилизации исследуемого материала (с учетом управления по принципу обратной связи) необходимо, чтобы время прохождения упругих волн от одного конца материала до другого и обратно не превышало периода его собственных колебаний.

Таким образом, (2.17) и (2.34) являются необходимыми и достаточными условиями стабилизации материала, находящегося в неравновесном, структурно-неустойчивом состоянии, динамика которого описывается системой уравнений (2.11).

2.5. Результаты компьютерного моделирования. Проведем компьютерное моделирование динамики исследуемого материала. С этой целью найдем решение системы уравнений (2.11) для случая, когда

(2.35)
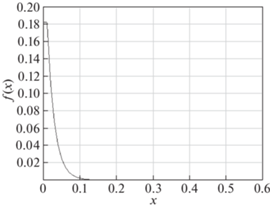
$L = 0.6{\text{ м}},\quad M = 5{\text{ кг}},\quad \rho = 0.2 \times {{10}^{5}}\,\,{\text{кг/}}{{{\text{м}}}^{{\text{3}}}},\quad E = 0.1 \times {{10}^{6}}\,\,{\text{Н/}}{{{\text{м}}}^{2}}.$

Пусть начальные условия из системы (2.11) имеют вид, приведенный на рис. 9 и формализуемый следующим образом:

(2.36)
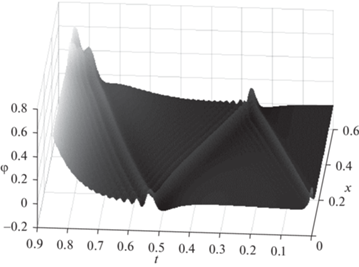
$\left\{ \begin{gathered} f\left( x \right) = 0.3{{e}^{{ - 0.5x}}}, \hfill \\ g\left( x \right) = 0, \hfill \\ \end{gathered} \right.$
а параметры управления:

(2.37)
$A = 0.1055,\quad B = 11.4663.$
Рис. 9.

Распределение отклонений по длине материала при t = 0

Заметим, что параметры системы (2.35) и коэффициенты управления (2.37) удовлетворяют условиям стабилизации (2.17) и (2.34). Численное решение системы (2.11) представлено на рис. 10.

Рис. 10.

Динамика материала при выполнении условий стабилизации

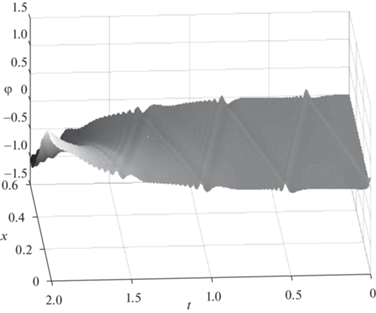
Изменим коэффициент управления (2.37), пусть A = 0.0455, при этом перестанет выполняться условие (2.17). Решение системы (2.11) тогда будет иметь вид, описанный на рис. 11.

Рис. 11.

Динамика материала при невыполнении условия (2.17) и выполнении (2.34)

Вернем коэффициенты управления (2.37) и изменим массу материала (2.35). Пусть M = 3.2 кг, при этом перестанет выполняться условие (2.34). Решение системы (2.11) в этом случае будет иметь вид, приведенный на рис. 12.

Рис. 12.

Динамика материала при выполнении условия (2.17) и невыполнении (2.34)

Как видно из рис. 10–12, численное моделирование подтверждает необходимость выполнения условий стабилизации (2.17) и (2.34), а при невыполнении хотя бы одного из них исследуемый материал с течением времени разбалансируется и теряет устойчивость.

2.6. Упругие волны. Как и в случае дискретной системы обратных связанных маятников в исследуемом материале при определенных начальных условиях в процессе стабилизации также возникают упругие волны, что демонстрируют результаты компьютерного моделирования (рис. 10–12).

Скорость упругих волн в материале, как указывалось ранее, можно определить с помощью равенства

(2.38)
$V = \sqrt {\frac{E}{\rho }} ,$
а время, за которое волна проходит от одного конца материала до его другого конца, равно

(2.39)
${{T}_{v}} = \frac{{2L}}{V}.$

Из параметров (2.35) можно найти V = 2.2361 м/с, Tv = 0.54 c. Это также полностью согласуется с результатом моделирования динамики материала, изображенном на рис. 10.

3. Дискретная система c нелинейными связями. 3.1. Математическая модель. Рассмотрим систему связанных обратных маятников из разд. 1.1. Представленная выше математическая модель предполагает линейный характер связей между обратными маятниками. Проведем исследование аналогичной механической системы с наличием нелинейности. С этой целью опишем модель, в которой сила жесткости, действующая со стороны пружины на каждый маятник системы, имеет нелинейный характер и описывается следующим равенством:

(3.1)
${{F}^{{\left( k \right)}}} = {{k}_{1}}\Delta x + {{k}_{2}}\Delta {{x}^{3}},$
где k1 и k2 – линейный и нелинейный коэффициенты жесткости, а Δx – удлинение пружины.

С учетом (3.1) система уравнений (1.5) будет иметь следующий вид:

(3.2)
$\left\{ \begin{gathered} {{{\ddot {\varphi }}}_{1}} = {{\omega }^{2}}{{\varphi }_{1}} + {{a}_{1}}\left( {{{\varphi }_{2}} - {{\varphi }_{1}}} \right) + {{a}_{2}}{{\left( {{{\varphi }_{2}} - {{\varphi }_{1}}} \right)}^{3}} - c, \hfill \\ {{{\ddot {\varphi }}}_{i}} = {{\omega }^{2}}{{\varphi }_{i}} + {{a}_{1}}\left( {{{\varphi }_{{i + 1}}} - 2{{\varphi }_{i}} + {{\varphi }_{{i - 1}}}} \right) + {{a}_{2}}[{{\left( {{{\varphi }_{{i + 1}}} - {{\varphi }_{i}}} \right)}^{3}} - {{\left( {{{\varphi }_{i}} - {{\varphi }_{{i - 1}}}} \right)}^{3}}] - c, \hfill \\ {{{\ddot {\varphi }}}_{n}} = {{\omega }^{2}}{{\varphi }_{n}} - {{a}_{1}}\left( {{{\varphi }_{n}} - {{\varphi }_{{n - 1}}}} \right) - {{a}_{2}}{{\left( {{{\varphi }_{n}} - {{\varphi }_{{n - 1}}}} \right)}^{3}} - c, \hfill \\ \end{gathered} \right.$
где ${{a}_{1}} = \begin{array}{*{20}{c}} {{{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} m}} \right. \kern-0em} m},}&{{{a}_{2}} = } \end{array}\begin{array}{*{20}{c}} {{{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} m}} \right. \kern-0em} m},}&{c = {u \mathord{\left/ {\vphantom {u l}} \right. \kern-0em} l}.} \end{array}$

Проводя аналогичные разд. 1.2 преобразования, можно показать, что для нелинейной системы (3.2) также справедливо условие стабилизации (1.14) в случае использования управления по принципу обратной связи (1.7). Однако следует отметить, что условие (1.14), описывающее параметры управляющего воздействия, является необходимым, но не достаточным условием стабилизации системы (3.2). Для успешной стабилизации также необходимо дополнительное условие, описывающее параметры непосредственно самой механической системы, аналогичное (1.19). В силу нелинейности системы (3.2) подобное условие получить весьма затруднительно, поэтому с целью упрощения анализа динамики будем считать параметры механической системы подборными на этапе проведения численного эксперимента.

3.2. Результаты компьютерного моделирования. Проведем компьютерное моделирование динамики исследуемой нелинейной механической системы. С этой целью найдем решение системы уравнений (3.2) для случая, когда

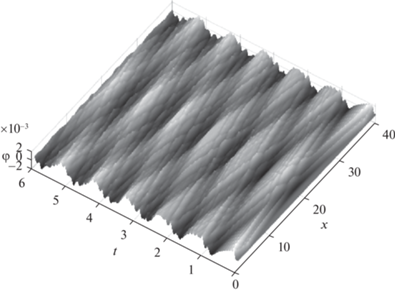
(3.3)
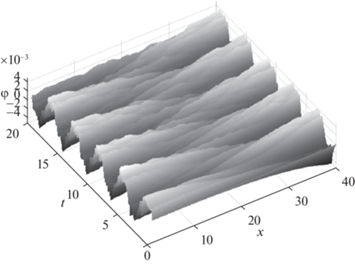
$\begin{gathered} m = 0.1\;{\text{кг}},\quad l = 1\;{\text{м}},\quad n = 40, \\ {{\varphi }_{1}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{1}}\left( 0 \right) = 0.1\;{\text{рад/с}} \\ {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {2,n} , \\ {{k}_{1}} = 200\;{\text{Н/м}},\quad {{k}_{2}} = {{10}^{5}}\;{\text{Н/м}}. \\ \end{gathered} $

Решение будем искать с помощью одношагового метода Рунге–Кутта 5-го порядка. Далее рассмотрим случаи, когда управляющее воздействие удовлетворяет условию стабилизации (1.14). Результат компьютерного моделирования представлен на рис. 13.

Рис. 13.

Динамика системы с параметрами (3.3)

Изменим начальные условия (3.3) следующим образом:

(3.4)
$\begin{gathered} {{\varphi }_{1}}\left( 0 \right) = 0.1\;{\text{рад}},\quad {{{\dot {\varphi }}}_{1}}\left( 0 \right) = 0\;{\text{рад/с}}, \\ {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {2,n} . \\ \end{gathered} $

Динамика системы для (3.4) показана на рис. 14.

Рис. 14.

Динамика системы с параметрами (3.4)

Изменим начальные условия следующим образом:

(3.5)
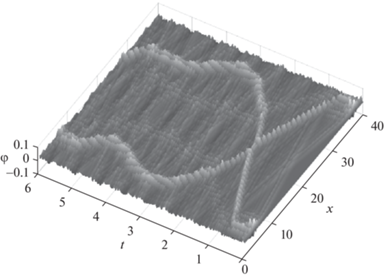
$\begin{gathered} {{{\dot {\varphi }}}_{4}}\left( 0 \right) = 0.1\;{\text{рад}},\quad {{{\dot {\varphi }}}_{{37}}}\left( 0 \right) = 0.1\;{\text{рад/с}}, \\ {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {1,n} \wedge i \ne 4 \wedge i \ne 37. \\ \end{gathered} $

Динамика системы для (3.5) представлена на рис. 15.

Рис. 15.

Динамика системы с параметрами (3.5)

Изменим начальные условия следующим образом:

(3.6)
$\begin{gathered} {{\varphi }_{4}}\left( 0 \right) = 0.1\;{\text{рад}},\quad {{\varphi }_{{37}}}\left( 0 \right) = 0.1\;{\text{рад/с}}, \\ {{\varphi }_{i}}\left( 0 \right) = 0\;{\text{рад}},\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {1,n} \wedge i \ne 4 \wedge i \ne 37. \\ \end{gathered} $

Динамика системы для случая (3.6) описана на рис. 16.

Рис. 16.

Динамика системы с параметрами (3.6)

Изменим начальные условия следующим образом:

(3.7)
$\begin{gathered} {{{\dot {\varphi }}}_{{26}}}\left( 0 \right) = 0.1\;{\text{рад}},\quad {{{\dot {\varphi }}}_{{27}}}\left( 0 \right) = - 0.1\;{\text{рад/с}}, \\ {{\varphi }_{i}}\left( 0 \right) = 0,\quad {{{\dot {\varphi }}}_{i}}\left( 0 \right) = 0\;{\text{рад/с}},\quad i = \overline {1,n} \wedge i \ne 26 \wedge i \ne 27. \\ \end{gathered} $

Динамика системы для (3.5) показана на рис. 17.

Рис. 17.

Динамика системы с параметрами (3.7)

Таким образом, как видно из результатов компьютерного моделирования динамики системы (3.2), при ненулевом начальном отклонении и нулевой начальной скорости одного или нескольких маятников помимо линейных упругих волн имеют место также нелинейные колебания. В случае же нулевого начального отклонения и ненулевой начальной скорости система демонстрирует нелинейное поведение, характеризующееся появлением нелинейных локальных возмущений, имеющих динамику, сходную с динамикой уединенных нелинейных волн (солитонов) [39, 40]. Отметим также, что характер динамики таких солитоноподобных волн крайне чувствителен к малым изменениям параметров системы и, как следствие, к погрешностям вычислений, что в свою очередь приводит к зависимости от выбранного численного метода решения.

Заключение. Проведено обобщение системы связанных маятников для произвольного числа упругосвязанных перевернутых маятников, а также выполнен переход от дискретной к непрерывной системе, описывающей материал, который находится в неравновесном, структурно-неустойчивом состоянии. Исследованы динамическиe характеристики указанных систем в случае управления, формируемого по принципу обратной связи, найдены необходимые и достаточные условия их стабилизации. В частности, установлено условие устойчивости материала, являющегося континуальным аналогом системы из n обратных связанных маятников, которое заключается в следующем: необходимо, чтобы время прохождения упругих волн от одного конца материала до другого и обратно не превышало периода его собственных колебаний. Проведено компьютерное моделирование динамики изучаемых систем, результаты которого иллюстрируют теоретические построения. Также выполнено исследование динамики системы перевернутых связанных маятников с нелинейными связями. В результате было показано, что представленная система при определенных параметрах и начальных условиях демонстрирует нелинейное поведение, характеризующееся появлением локальных возмущений, которые имеют динамику, сходную с динамикой солитонов.

Список литературы

  1. Boubaker O. The Inverted Pendulum: a Fundamental Benchmark in Control Theory and Robotics // Intern. Conf. on Education and e-Learning Innovations (ICEELI 2012). Sousse, Tunisia, 2012. P. 1–6.

  2. Chang L.H., Lee A.C. Design of Nonlinear Controller for Bi-axial Inverted Pendulum System // IET Control Theory Appl. 2007. V. 1. P. 979–986.

  3. Dadios E.P., Fernandez P.S., Williams D.J. Genetic Algorithm on Line Controller for the Flexible Inverted Pendulum Problem // J. Adv. Comput. Intell. Intell. Inform. 2006. V. 10. P. 155–160.

  4. Li G., Liu X. Dynamic Characteristic Prediction of Inverted Pendulum Under the Reduced-gravity Space Environments // Acta Astronaut. 2010. V. 67. P. 596–604.

  5. Lozano R., Fantoni I., Block D.J. Stabilization of the Inverted Pendulum Around its Homoclinic Orbit // Syst. Control Lett. 2000. V. 40. P. 197–204.

  6. Tang J., Ren G. Modeling and Simulation of a Flexible Inverted Pendulum System // Tsinghua Sci. Technol. 2009. V. 14 (Suppl. 2). P. 22–26 .

  7. Wang J.J. Simulation Studies of Inverted Pendulum Based on PID Controllers // Simul. Model. Pract. Theory. 2011. V. 19. P. 440–449.

  8. Semenov M.E., Abbas Z.H., Ishchuk I.N., Kanishcheva O.I., Meleshenko P.A. State-feedback Control Principles for Inverted Pendulum with Hysteresis in Suspension // J. Siberian Federal University. Mathematics and Physics. 2016. № 4 (9). P. 498–509. https://doi.org/10.17516/1997-1397-2016-9-4-498-509

  9. Semenov M.E., Solovyov A.M., Meleshenko P.A. Elastic Inverted Pendulum with Backlash in Suspension: Stabilization Problem // Nonlinear Dyn. 2015. V. 82. P. 677. https://doi.org/10.1007/s11071-015-2186-y

  10. Semenov M.E., Solovyov A.M., Meleshenko P.A., Kanishcheva O.I. Stabilization of a Flexible Inverted Pendulum via Hysteresis Control: the Bouc-Wen approach // Vibration Engineering and Technology of Machinery: Proceedings of VETOMAC XV 2019. Springer International Publishing, 2021. P. 267–279.

  11. Медведский А.Л., Мелешенко П.А., Нестеров В.А., Решетова О.О., Семенов М.Е., Соловьев А.М. Неустойчивые колебательные системы с гистерезисом: задачи стабилизации и управления // Изв. РАН. ТиСУ. 2020. № 4. 58–82. https://doi.org/10.31857/S0002338820030099

  12. Semenov M.E., Solovyov A.M., Meleshenko P.A. Stabilization of Coupled Inverted Pendula: From Discrete to Continuous Case // J. Vibration and Control. 2021. V. 27. № 1–2. P. 43–56.

  13. Semenov M.E., Solovyov A.M., Popov M.A., Meleshenko P.A. Coupled Inverted Pendulums: Stabilization Problem // J. Archive of Applied Mechanics. 2018. V. 88. № 4. P. 517–524. https://doi.org/10.1007/s00419-017-1323-0

  14. Meleshenko P.A., Semenov M.E., Klinskikh A.F. Conservative Chaos in a Simple Oscillatory System with Non-smooth Nonlinearity // Nonlinear Dynamics. 2020. V. 101. № 4. P. 2523–2540.

  15. Bortoff S., Spong M.W. Pseudolinearization of the Acrobot Using Spline Functions // Proc. IEEE Conf. on Decision and Control. Tucson, 1992. P. 593–598.

  16. Spong M.W. The Swing up Control Problem for the Acrobot // IEEE Control Systems Magazine. 1995. V. 15. № 1. P. 49–55.

  17. Olfati-Saber R. Control of Underactuated Mechanical Systems with two Degrees of Freedom and Symmetry // Proc. American Control Conf. Chicago, 2000. V. 6. P. 4092–4096.

  18. Olfati-Saber R. Normal Forms for Underactuated Mechanical Systems with Symmetry // IEEE Trans. on Automat. Control. 2002. V. 47. № 2. P. 305–308.

  19. Решмин С.А. Метод декомпозиции в задаче управления перевернутым двойным маятником с использованием одного управляющего момента // Изв. РАН. ТиСУ. 2005. № 6. С. 28–45.

  20. Решмин С.А., Черноусько Ф.Л. Синтез управления в нелинейной динамической системе на основе декомпозиции // ПММ. 1998. Т. 62. Вып. 1. С. 121–128.

  21. Черноусько Ф.Л. Декомпозиция и субоптимальное управление в динамических системах // ПММ. 1990. Т. 54. Вып. 6. С. 883–893.

  22. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.

  23. Wai R.J., Kuo M.A., Lee J.D. Design of Cascade Adaptive Fuzzy Sliding-mode Control for Nonlinear Two-axis Inverted-pendulum Servomechanism // IEEE Transactions on Fuzzy Systems. 2008. V. 16. № 5. P. 1232–1244. https://doi.org/10.1109/TFUZZ.2008.924277

  24. Wei H., Qian Q., Qiang H. Optimization of Sliding Mode Controller for Double Inverted Pendulum Based on Genetic Algorithm // 2008 2nd Intern. Sympos. on Systems and Control in Aerospace and Astronautics. Shenzhen, China, 2008. https://doi.org/10.1109/ISSCAA.2008.4776281

  25. Chaoui H., Sicard P. Motion and Balance Neural Control of Inverted Pendulums with Nonlinear Friction and Disturbance // 2011 24th Canadian Conf. on Electrical and Computer Engineering (CCECE). Niagara Falls, Ontario, Canada, 2011. https://doi.org/10.1109/CCECE.2011.6030657.

  26. Haibo He, Zhen Ni, Jian Fu. A Three-network Architecture for On-line Learning and Optimization Based on Adaptive Dynamic Programming // Neurocomputing. 2012. V. 78. № 1. P. 3–13. https://doi.org/10.1016/j.neucom.2011.05.031

  27. Zhong W., Rock H. Energy and Passivity Based Control of the Double Inverted Pendulum on a Cart // Control Applications. (CCA '01). Proceedings of the IEEE Intern. Conf. Mexico City, Mexico, 2001 https://doi.org/10.1109/CCA.2001.973983.

  28. Chernous’ko F.L., Reshmin, S.A. Time-optimal Swing-up Feedback Control of a Pendulum // Nonlinear Dynamics. 2007. V. 47. P. 65–73. https://doi.org/10.1007/s11071-006-9059-3

  29. Решмин С.А., Черноусько Ф.Л. Оптимальный по быстродействию синтез управления нелинейным маятником // Изв. РАН. ТиСУ. 2007. № 1. С. 13–22.

  30. Reshmin S.A., Chernous’ko F.L. Properties of the Time-optimal Feedback Control for a Pendulum-like System // J. Optimization Theory and Applications. 2014. V. 163. № 1. P. 230–252. https://doi.org/10.1007/s10957-013-0480-8

  31. Решмин С.А. Пороговая абсолютная величина релейного управления при наискорейшем приведении спутника в желаемое угловое положение // Изв. РАН. ТиСУ. 2018. № 5. С. 30–41. https://doi.org/10.31857/S000233880002843-6

  32. Reshmin S.A., Chernous’ko F.L., Ananievski I.M. Control of Nonlinear Dynamical Systems. Berlin, Heidelberg: Springer, 2008. 408 p.

  33. Ivanenko Y.P., Dominici N., Cappellini G., Dan B., Cheron G., Lacquaniti F. Development of Pendulum Mechanism and Kinematic Coordination from the First Unsupported Steps in Toddlers // J. Experimental Biology. 2004. V. 207. P. 3797–3810. https://doi.org/10.1242/jeb.01214

  34. Losurdo G. An Inverted Pendulum Preisolator Stage for the VIRGO Suspension System // Review of Scientific Instruments. 1999. V. 70. № 5. P. 2507–2515. https://doi.org/10.1063/1.114978

  35. Scott A., Sørensen M.P., Christiansen P.L. Nonlinear Science: Emergence and Dynamics of Coherent Structures. Oxford University Press, 1999. 474 p.

  36. Al-Gwaiz M. Sturm-Liouville Theory and its Applications. London: Springer-Verlag, 2008. 264 p. https://doi.org/10.1007/978-1-84628-972-9

  37. Zettl A. Sturm-Liouville Theory // Mathematical Surveys and Monographs. 2005. V. 121. https://doi.org/10.1090/surv/121

  38. Amrein W.O., Hinz A.M., Pearson D.B. Sturm-Liouville Theory: Past and Present. Basel: Birkhäuser, 2005. 336 p. https://doi.org/10.1007/3-7643-7359-8

  39. Semenov M.E., Reshetova O.O., Tolkachev A.V., Solovyov A.M., Meleshenko P.A. Oscillations Under Hysteretic Conditions: From Simple Oscillator to Discrete Sine-Gordon Model // Topics in Nonlinear Mechanics and Physics. Singapore: Springer, 2019. P. 229–253.

  40. Tolkachev A.V., Semenov M.E., Meleshenko P.A., Reshetova O.O., Klinskikh A.F., Karpov E.A. Sine-Gordon System with Hysteretic Links // J. Physics: Conference Series. V. 1096. № 1. P. 012072.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал