Известия РАН. Теория и системы управления, 2022, № 2, стр. 62-79
ОПТИМИЗАЦИЯ ПЛАНИРОВАНИЯ НАБЛЮДЕНИЯ КАТАЛОГА ОБЪЕКТОВ ПОДВИЖНЫМ НАБЛЮДАТЕЛЕМ С УЧЕТОМ НАКЛАДЫВАЕМЫХ ОГРАНИЧЕНИЙ
Д. Н. Рулев *
ПАО “РКК “Энергия” им. С.П. Королёва”
Королёв, Моск. обл., Россия
* E-mail: dmitry.rulev@rsce.ru
Поступила в редакцию 02.09.2020
После доработки 14.10.2021
Принята к публикации 29.11.2021
- EDN: GHWPRO
- DOI: 10.31857/S0002338822020135
Аннотация
Задача планирования наблюдений заданного каталога объектов подвижным наблюдателем с учетом наложения ограничений на моменты выполнения наблюдений и затраты на перемещение наблюдателя между его задаваемыми “граничными” положениями рассмотрена как задача выбора маршрута. Предложен алгоритм решения задачи как задачи минимальной размерности, равной сумме количества объектов наблюдения и сегментов маршрута (числа наблюдателей). При этом контроль выполнения остальных условий и ограничений осуществляется без увеличения размерности решаемой задачи путем проверки данных ограничений на каждом шаге итерационного процесса решения задачи. Приведены примеры построения программ наблюдений наземных и астрономических объектов с летательного/космического аппарата при решении ряда практических задач в области сельского хозяйства и космических исследований, показывающие эффективность использования предложенного подхода.
Введение. Рассматривается задача планирования наблюдений заданного перечня объектов подвижным наблюдателем. Требуется выбрать последовательность наблюдений так, чтобы затраты на переход от наблюдения одного объекта к следующему были минимальны [1–5]. В качестве затрат может выступать, например, длительность перемещения/переориентации наблюдателя между наблюдениями или расход требуемых для этого ресурсов.
Задача сводится к выбору маршрута: из начальной точки маршрута (начального положения наблюдателя) после однократного просмотра всех объектов требуется перейти в конечную точку маршрута (конечное положение наблюдателя), при этом искомый маршрут должен удовлетворять накладываемым на него ограничениям.
Наблюдатель имеет ограниченный запас необходимых ресурсов, который может восполняться в задаваемых точках. Если затраты на наблюдение объектов превышают предельный запас ресурсов, то искомый маршрут должен состоять из отрезков (называем их сегментами), начинающихся и заканчивающихся в точках восполнения ресурсов, и затраты на реализацию каждого из которых не превышают предельный запас ресурсов наблюдателя. Кроме этого возможно требование выполнения наблюдений объектов (прохождения точек маршрута) в заданные интервалы времени.
1. Формализация и метод решения задачи. Рассматриваем полный ориентированный граф $G = \left( {V,A} \right)$:
$V = N \cup K$ – множество вершин, включающее подмножество $N~ = ~\{ \overline {1,n} \} $ внутренних вершин сегментов маршрута (наблюдаемые объекты) и подмножество $K~ = ~\{ \overline {1,\left| K \right|} \} $ граничных вершин сегментов маршрута;
$A = \left\{ {\left( {i,j} \right) \in V \times V:i \ne j,\left( {i,j} \right) \notin K \times K} \right\}$ – множество дуг; длина cij дуги (i, j) составляет затраты на переход от вершины i к вершине j (для $i = j \in N$ и $\left( {i,j} \right) \in K \times K$ значения cij можно доопределить как ∞), tij – время, необходимое для перехода от вершины i к вершине j.
Требуется найти в графе (V, A) кратчайший замкнутый маршрут (цикл), проходящий через все вершины, каждую не более одного раза. Для формализации задачи используем булевские переменные xij, $x_{{ij}}^{k}$:
(1.1)
$\mathop \sum \limits_{k \in K} x_{{ij}}^{k}~ = ~{{x}_{{ij}}},\quad \forall \left( {i,j} \right) \in A,{\text{\;}}$(1.2)
$x_{{ij}}^{k} \in \left\{ {0,1} \right\},\quad \forall \left( {i,j} \right) \in A,~\quad \forall k \in K,{\text{\;}}$(1.3)
${{x}_{{ij}}} \in \left\{ {0,1} \right\},\quad \forall \left( {i,j} \right) \in A.~{\text{\;}}$Требуется минимизировать целевую функцию затрат (длину маршрута):
при выполнении (1.1)–(1.3) и следующих условий.В каждой внутренней вершине заканчивается и начинается по одной дуге одного и того же сегмента маршрута:
(1.5)
$\mathop \sum \limits_{i \in V,~i \ne l} {{x}_{{il}}} = 1,~\quad \mathop \sum \limits_{j \in V,j \ne l} {{x}_{{lj}}} = 1,\quad \forall l \in N,~$(1.6)
$\mathop \sum \limits_{i \in V,~i \ne l} x_{{il}}^{k} \leqslant \mathop \sum \limits_{j \in V,~j \ne l} x_{{lj}}^{k},\quad \forall l \in N,\quad \forall k \in K.~$В каждой граничной вершине начинается дуга с окончанием во внутнней вершине и заканчивается дуга с началом во внутренней вершине:
(1.7)
$\mathop \sum \limits_{i \in N} {{x}_{{il}}}~ = ~1,\quad \mathop \sum \limits_{j \in N} {{x}_{{lj}}}~ = ~1,\quad \forall l \in K.~~$Запрещены циклические последовательности внутренних вершин:
(1.8)
$\mathop \sum \limits_{i~ = ~1}^{p - 1} {{x}_{{{{j}_{i}}{{j}_{{i + 1}}}}}} + {{x}_{{{{j}_{p}}{{j}_{1}}}}} < p,\quad p~ = ~\{ \overline {2,n - \left| K \right|} \} ,\quad {{j}_{1}}{{j}_{2}} \ldots {{j}_{p}} \subseteq P(n,\left| K \right|),~~~$Вершины подмножества K разбивают искомый маршрут на сегменты, каждый из которых начинается вершиной подмножества K, оканчивается вершиной подмножества K, содержит как минимум одну вершину подмножества N и не содержит других вершин подмножества K. Длина каждого сегмента не превышает заданного значения ${{C}_{0}}$:
(1.9)
$\mathop \sum \limits_{(i,j) \in A} x_{{ij}}^{k}{{c}_{{ij}}} \leqslant {{C}_{0}},\quad \forall k \in K.~$Обозначаем через ti время начала прохождения вершины $i \in V$; $t_{l}^{*}$ – время вхождения в вершину $l \in K$ по окончании сегмента маршрута.
Каждая вершина $i \in V$ должна быть пройдена в течение интервалов времени $[t_{{im}}^{ - },t_{{im}}^{ + }],~\;m~\; = ~\;\overline {1,{{M}_{i}}} ,$ при длительности нахождения в вершине не менее Δi:
для $\forall i \in V$ существует m, такое, что
для $\forall l \in K$ существует m, такое, что(1.11)
$t_{{lm}}^{ - } \leqslant t_{l}^{*},~\quad t_{l}^{*} + {{\Delta }_{l}} \leqslant t_{{lm}}^{ + }.~$Если соединяющая внутреннюю или граничную вершину $l \in V$ и внутреннюю вершину $j \in N$ дуга $(l,j)$ входит в маршрут, то вершину j проходят через требуемое время после вершины l:
Если соединяющая внутреннюю вершину $i \in N$ и граничную вершину $l \in K$ дуга (i, l) входит в маршрут, то вход в граничную вершину l выполняется через требуемое время после прохождения внутренней вершины i:
При последовательном прохождении сегментов маршрута для всех граничных вершин $l \in K$ кроме вершины начала/окончания маршрута l*
При параллельном прохождении сегментов маршрута несколькими наблюдателями условия (1.14) отсутствуют.
В постановках транспортных задач Vehicle Routing Problem (VRP) [6–8] и др. множество вершин $V~ = ~\{ 0\} \cup N$ содержит одну граничную вершину {0}, а формализация требований/ограничений (1.1), (1.5)–(1.7), (1.9), связанных с наличием нескольких сегментов маршрута, реализуется использованием множества $K~ = ~\{ \overline {1,\left| K \right|} \} $ транспортных средств (наблюдателей) с формулировкой условий по прохождению всех сегментов маршрута через данную одну вершину:
(1.16)
$\mathop \sum \limits_{\left( {i,j} \right) \in {{\delta }^{ + }}\left( S \right)} {{x}_{{ij}}} \geqslant r(S),\quad \forall S \subseteq N,~$Задача c условиями на интервалы времени прохождения вершин известна как Vehicle Routing Problem with Time Windows (VRPTW) [9–13] и др. При ее решении, в частности, ограничения (1.10)–(1.14) формализуются условиями вида
(1.17)
$\mathop \sum \limits_{\left( {i,j} \right) \in A\left( p \right)}^L {{x}_{{ij}}} \leqslant {\text{|}}A(p){\text{|}} - 1,\quad \forall p \in P,~~$Задача (1.4) при условиях (1.1)–(1.3), (1.5)–(1.14) и/или соответствующих эквивалентных условиях (1.15)–(1.17) является частично целочисленной задачей линейного программирования и решается методами линейного и целочисленного программирования [14, 15].
Например, данными методами в [16] задача планирования наблюдений с космического аппарата (КА) каталога наземных объектов решается как задача построения программы маневров КА при минимизации затрат энергетических ресурсов КА и максимизации информативности наблюдений с учетом заданных ограничений, в том числе на моменты выполнения наблюдений. Задачи планирования астрономических наблюдений с КА при ограничениях на моменты времени выполнения наблюдений, включая моменты переориентации оси визирования аппаратуры наблюдения, рассмотрены и решаются указанными методами в [1, 2, 5, 17].
Особенностью сформулированной задачи является существенное количество и сложность ограничений (1.1), (1.6), (1.8)–(1.14).
2. Алгоритм решения задачи. В настоящей работе задачу (1.4) решаем как задачу минимальной размерности – при условиях (1.3), (1.5), (1.7) (т.е. размерность решаемой задачи равна сумме количества объектов и сегментов маршрута $n + \left| K \right|$), а контроль остальных условий и ограничений осуществляем без увеличения размерности решаемой задачи путем проверки выполнения данных ограничений на каждом шаге итерационного процесса решения задачи.
Задача (1.4) решается как задача минимальной размерности, например по алгоритму Литтла [18], использующему идею метода “ветвей и границ”. Алгоритм основан на разделении числа перебираемых вариантов на классы (ветви) с расчетом оценок (границ) для этих классов так, чтобы иметь возможность прерывать ветви, которые не приведут к оптимальному решению. При этом учет ограничений (1.1), (1.6) и (1.8)–(1.14) выполняем путем исключения из дальнейшего рассмотрения тех комбинаций вершин, которые не удовлетворяют данным ограничениям. Алгоритм решения задачи можно представить в следующем виде.
Называем: решение – набор присутствующих и запрещенных в маршруте дуг; запрет дуги – замена стоимости дуги на ∞; оценка (О) – нижняя граница стоимости решения; главный список (ГС) – набор решений, подлежащих рассмотрению; рекорд – стоимость кратчайшего из найденных циклов; приведение матрицы – операция, согласно которой вычитаем последовательно из каждой строки и каждого столбца матрицы их минимальные элементы, которые называем приводящими константами.
Шаг 1. Текущее решение R и ГС пусты. Приводим матрицу затрат и вычисляем O(R) как сумму приводящих констант (СПК): ${\text{O}}\left( R \right) = СПК\left( R \right)$.
Шаг 2. Элементом ветвления $(k,l)$ решения R выбираем нулевой элемент приведенной матрицы с максимальным штрафом (штраф вычисляем как сумму наименьших ненулевых элементов строки k и столбца l). Формируем решение ${{R}^{ + }}$ как $R$ с присутствием дуги (k, l). Если оно не удовлетворяет условиям (1.1), (1.6), (1.9)–(1.14), то исключаем его из дальнейших операций, иначе в ${{R}^{ + }}$ запрещаем дуги, присутствие которых приведет к возникновению “внутреннего” цикла (контролируем выполнение условий (1.8)), и вычисляем ${\text{O}}({{R}^{ + }}) = {\text{O}}\left( R \right) + {\text{СПК}}({{R}^{ + }})$. Формируем решение ${{R}^{ - }}$ как $R$ с запрещением дуги $(k,l)$ и вычисляем ${\text{O}}({{R}^{ - }}) = {\text{O}}\left( R \right) + {\text{СПК}}({{R}^{ - }})$.
Шаг 3. Если ГС, ${{R}^{ + }}$ и ${{R}^{ - }}$ пусты, то на шаг 5, иначе берем из ГС решение ${{R}^{{ГС}}}$ с минимальной оценкой и определяем ${{{\text{O}}}^{{{\text{min}}}}} = {\text{min}}\{ {\text{O}}({{R}^{ + }}),{\text{O}}({{R}^{ - }}),{\text{O}}({{R}^{{ГС}}})\} $. Решение с ${{{\text{O}}}^{{{\text{min}}}}}$ назначаем новым решением R, ${\text{O}}(R) = {{{\text{O}}}^{{{\text{min}}}}}$, оставшиеся из решений ${{R}^{ + }}$, ${{R}^{ - }}$ и ${{R}^{{ГС}}}$ добавляем/возвращаем в ГС. Если R – цикл, то на шаг 4, иначе – на шаг 2.
Шаг 4. Если рекорд пуст или ${{{\text{O}}}^{{{\text{min}}}}}$ < рекорд, то рекорд = ${{{\text{O}}}^{{{\text{min}}}}}$ и удаляем из ГС решения c оценкой меньше, чем рекорд. Если ГС пуст, то на шаг 5, иначе – берем из ГС решение ${{R}^{{ГС}}}$ с минимальной оценкой как новое решение R, ${\text{O}}(R) = {\text{O}}({{R}^{{ГС}}})$ и идем на шаг 2.
Шаг 5. Текущий рекорд оптимален (если рекорд пуст, то задача не имеет решения).
Рассмотрим примеры построения программ наблюдений наземных и астрономических объектов с летательного/космического аппарата (ЛА/КА) при решении ряда практических задач. Примеры, представленные в разд. 3, иллюстрируют учет ограничений на моменты времени выполнения наблюдений, в разд. 4 – ограничений на затраты на перемещение наблюдателя. В обоих разделах представлен учет наличия нескольких сегментов маршрута (нескольких наблюдателей) и требований к граничным положениям наблюдателя.
3. Построение последовательностей наблюдения объектов с ЛА/КА, движущегося па заданной траектории/орбите. 3.1. Наблюдение астрономических объектов. Рассмотрим планирование наблюдений с орбитального КА каталога астрономических объектов – например, 13 наиболее ярких звезд из созвездий Близнецов, Возничего, Малого и Большого Пса, Ориона, Тельца: 1) Бета Ориона (Ригель), 2) Альфа Возничего (Капелла), 3) Гамма Ориона (Беллатрикс), 4) Бета Тельца (Эльнат), 5) Дзета 1 Ориона (Альнитак), 6) Альфа Ориона (Бетельгейзе), 7) Бета Возничего (Менкалинан), 8) Гамма Близнецов (Альхена), 9) Альфа Большого Пса (Сириус), 10) Эпсилон Большого Пса (Адара), 11) Бета Большого Пса (Мирцам), 12) Альфа Близнецов (Кастор), 13) Альфа Малого Пса (Процион). На теневых участках орбиты необходимо выполнить наблюдение всех объектов, при этом исходная и конечная ориентации КА совпадают с ориентацией для наблюдения объектов. Затраты на переориентацию КА от наблюдения одного объекта к другому характеризуем угловым расстоянием между объектами. Требуется построить программу наблюдений так, чтобы сумма затрат на переориентацию КА была минимальна [3, 5].
Наблюдения выполняем с орбитальной космической станции с параметрами орбиты: высота околокруговой орбиты ≈410 км, на момент прохождения восходящего узла орбиты 01.02.2017 23:57:52.42 (ДМВ – декретное московское время) долгота восходящего узла орбиты в инерциальной системе координат Ω = 352.9°, наклонение орбиты составляет 51.64°. Возможные интервалы $[t_{{im}}^{ - },t_{{im}}^{ + }]$, $m = \overline {1,{{M}_{i}}} $, времени выполнения наблюдений определяются зонами видимости объектов на теневой части витков орбиты КА. Значение требуемой длительности наблюдения объектов $\Delta t$ (считаем ее одинаковой для всех объектов) выбираем с учетом длительности T теневых участков орбиты на рассматриваемом интервале полета. Например, в интервале 07.09 … 25.10.2017 величина T составляет 22 … 36 мин, что соответствует максимальным значениям $\Delta t$ 1.7 … 2.8 мин (Δt < T/N, N = 13). Рассмотрим планирование наблюдений для вариантов значений $\Delta t$ = 1.5 и 2 мин; длительности tij перехода от объекта к объекту определяем как отношение углового расстояния между объектами к скорости поворота оси визирования аппаратуры наблюдения в инерциальном пространстве, принимаемой равной 180 град/мин.
В табл. 1 и на рис. 1 представлены полученные кратчайшие маршруты, S, град – длины маршрутов.
Таблица 1.
Длины кратчайших маршрутов наблюдения объектов с КА
| Дата | Ω, град | T, мин | S, град, $\Delta t$ = 1.5 мин | S, град, $\Delta t$ = 2 мин |
|---|---|---|---|---|
| 07.09.2017 | 349.3 | 36.0 | 178.23 (рис. 1, а) | 198.00 |
| 10.09.2017 | 333.3 | 35.6 | 185.82 | $\overline \exists $ |
| 13.09.2017 | 317.2 | 34.5 | 185.82 | $\overline \exists $ |
| 16.09.2017 | 301.2 | 32.4 | 185.69 | $\overline \exists $ |
| 20.09.2017 | 285.2 | 30.0 | 180.22 | $\overline \exists $ |
| 23.09.2017 | 269.1 | 29.1 | 174.51 | 180.22 |
| 26.09.2017 | 253.1 | 31.1 | 174.51 | 174.51 |
| 29.09.2017 | 237.1 | 33.5 | 174.51 | 174.51 |
| 06.10.2017 | 205.0 | 35.9 | 174.51 | 174.51 |
| 12.10.2017 | 173.0 | 34.9 | 178.23 | 178.23 |
| 15.10.2017 | 156.9 | 32.8 | 188.31 (рис. 1, б) | 188.63 |
| 19.10.2017 | 140.9 | 28.6 | 192.71 | $\overline \exists $ |
| 22.10.2017 | 124.9 | 22.3 | 177.30 (рис. 1, в) | $\overline \exists $ |
| 25.10.2017 | 108.8 | 22.1 | 174.51 | $\overline \exists $ |
Рис. 1.
Кратчайшие маршруты наблюдения объектов с КА: а – $\Delta t$ = 1.5 мин, S = 178.2 град (07.09.2017); б – $\Delta t$ = 1.5 мин, S = 188.3 град (15.10.2017); в – $\Delta t$ = 1.5 мин, S = 177.3 град (22.10.2017)
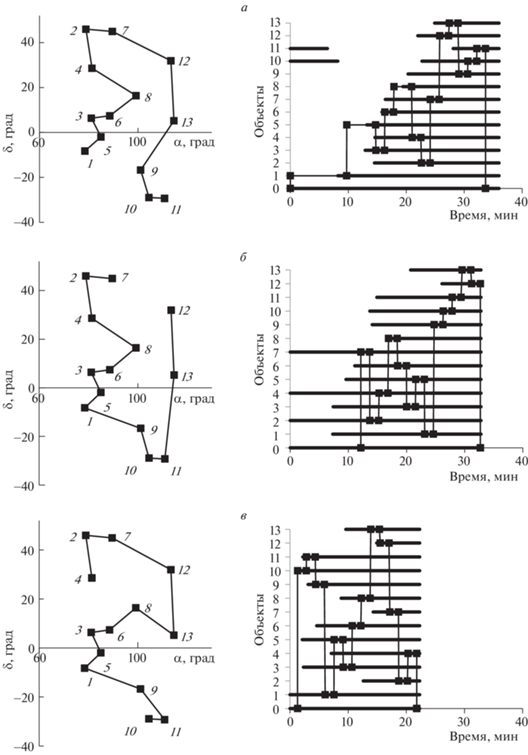
На рис. 1 в левой части рисунков на карте звездного неба приведены маршруты наблюдения объектов с указанием даты, $\Delta t$ и длины S, в правой части рисунков по вертикальной оси – номера объектов/вершин (0 – граничная вершина). По горизонтальной оси отображена шкала времени от начала теневого участка, относительно которой показаны интервалы видимости объектов и последовательность переориентаций КА из исходной ориентации КА (граничная вершина под номером 0), через ориентацию КА для наблюдения каждого из объектов (внутренние вершины под номерами объектов 1–13) в конечную ориентацию КА (возврат в граничную вершину под номером 0).
Представленные результаты показывают, что для рассмотренного примера длина кратчайшего маршрута изменяется в зависимости от даты полета в пределах ~10% от минимально возможной. При этом на каждом витке можно реализовать последовательное наблюдение всех объектов с длительностью наблюдения объекта не менее $\Delta t$ = 1.5 мин, в то время как при $\Delta t$ = 2 мин в определенные даты такой возможности не существует: при T < 26 мин – из-за недостаточности данной продолжительности теневого участка для наблюдения 13 объектов; при T > 26 мин – из-за “неудачного” относительного расположения зон видимости объектов. Отметим, что на более широком интервале дат может также не существовать как возможности наблюдения по крайней мере одного из объектов (видимость объекта на теневом участке орбиты <$\Delta t$), так и самого теневого участка (“солнечная” орбита).
3.2. Наблюдение наземных объектов. Рассмотрим планирование наблюдений наземных объектов с ЛА/КА, движущегося па заданной траектории/орбите. Направление оси визирования аппаратуры наблюдения задаем следующими углами: γ – угол от направления в надир до проекции оси визирования на плоскость орбиты (положительный отсчет в сторону полета); β – угол от направления в надир до проекции оси визирования на плоскость, перпендикулярную вектору скорости ЛА/КА (положительный отсчет в сторону вектора кинетического момента орбитального движения ЛА/КА). Считаем, что техническими характеристиками аппаратуры наблюдения определены максимальные абсолютные значения $\omega _{*}^{\gamma },\omega _{*}^{\beta }$ угловой скорости поворота оси визирования по данным углам.
Требуется построить программу наблюдений так, чтобы минимизировать суммарное время на переориентацию оси визирования от наблюдения очередного объекта к последующему.
На каждом шаге итерационного процесса решения задачи проверяем выполнение условий (1.10)–(1.14), которые определяют возможность наблюдений, используя следующую расчетную схему:
(3.2)
$\vec {r}\left( {{{t}_{i}}} \right) + \vec {l}\left( {{{t}_{i}},{{\gamma }_{i}},{{\beta }_{i}}} \right) = {{\vec {\rho }}_{i}},\quad \vec {r}\left( {{{t}_{i}} + {{\Delta }_{i}}} \right) + \vec {l}({{t}_{i}} + {{\Delta }_{i}},{{\gamma }_{i}},\beta _{i}^{\Delta }) = {{\vec {\rho }}_{i}},~~$Здесь ${{p}_{j}}$ ≥ 0 – время от окончания поворота оси визирования в положение для наблюдения объекта ϳ до начала выполнения наблюдения (на данном интервале ось визирования фиксирована в положении ${{\gamma }_{j}},{{\beta }_{j}}$); tij – длительность поворота оси визирования от наблюдения объекта $i$ в положение для наблюдения объекта ϳ:
(3.4)
${{t}_{{ij}}}~ = ~\max \left\{ {\frac{{\left| {{{\gamma }_{j}} - {{\gamma }_{i}}} \right|}}{{\omega _{*}^{\gamma }}},\frac{{\left| {{{\beta }_{j}} - \beta _{i}^{\Delta }} \right|}}{{\omega _{*}^{\beta }}}} \right\},~$Здесь ${{\gamma }_{i}}$ – угол γ на интервале наблюдения объекта i, βi, $\beta _{i}^{\Delta }$ – угол β на моменты начала и окончания наблюдения объекта $i$, $\omega _{{ij}}^{\gamma }$, $\omega _{{ij}}^{\beta }$ – угловые скорости поворота оси визирования от наблюдения объекта i в положение для наблюдения объекта ϳ по углам γ и β, $\omega _{j}^{\beta }$ – угловая скорость поворота оси визирования по углу β в процессе наблюдения объекта ϳ , $\vec {r}\left( t \right)$ – радиус-вектор ЛА/КА в момент t , $\vec {l}\left( {t,\gamma ,\beta } \right)$ – вектор от ЛА/КА до земной поверхности вдоль направления оси визирования, заданного углами γ и β, в момент t , ${{\vec {\rho }}_{i}}$ – радиус-вектор объекта $i$.
Для круговой орбиты ЛА/КА и сферической Земли (3.2) принимает вид
Здесь $({{x}_{j}},{{y}_{j}})$ – координаты объекта ϳ относительно трассы полета ЛА/КА: расстояние $x$ вдоль трассы полета от точки t = 0 и расстояние $y$ от трассы полета (положительный отсчет в сторону вектора кинетического момента орбитального движения), $\nu = 2\pi \,{{R}_{e}}{\text{/}}{{T}_{{orb}}}$ – линейная скорость перемещения подспутниковой точки вдоль трассы полета, ${{T}_{{orb}}}$ – период обращения ЛА/КА вокруг Земли, ${{R}_{e}}$ – радиус Земли; ${{H}_{{orb}}}$ – высота полета ЛА/КА над поверхностью Земли.
Коэффициентами матрицы затрат являются длительности поворота оси визирования между наблюдениями объектов, точные значения которых задаются (3.4) и в рассматриваемой формулировке задачи не могут быть определены заранее – до получения точных значений углов ${{\gamma }_{i}}$, βi, $\beta _{i}^{\Delta }$.
Поэтому для составления целевой функции используем условные ожидаемые значения длительности поворота, соответствующие наблюдению объектов на минимальном удалении от ЛА/КА. Коэффициенты матрицы затрат рассчитываем как длительности переориентации оси визирования после завершения наблюдения объекта i в момент $t_{i}^{{\min }}$ минимального удаления ЛА/КА от объекта i в положение для наблюдения объекта ϳ в момент, максимально близкий к моменту $t_{j}^{{\min }}$ минимального удаления ЛА/КА до объекта ϳ:
(3.5)
${{c}_{{ij}}} = \left\{ \begin{gathered} \frac{{{\text{|}}{{\gamma }_{j}} - {{\gamma }_{i}}{\text{|}}}}{{\omega _{*}^{\gamma }}}\quad {\text{при}}\quad {{x}_{i}} - {{x}_{j}} + \frac{{\nu {\text{|}}{{\gamma }_{j}} - {{\gamma }_{i}}{\text{|}}}}{{\omega _{*}^{\gamma }}} \leqslant 0, \hfill \\ \max \left\{ {\frac{{{\text{|}}{{\gamma }_{j}} - {{\gamma }_{i}}{\text{|}}}}{{\omega _{*}^{\gamma }}},\frac{{{\text{|}}\beta _{j}^{*}{\text{|}}}}{{\omega _{*}^{\beta }}}} \right\}\quad {\text{при}}\quad 0 < {{x}_{i}} - {{x}_{j}} + \nu \frac{{{\text{|}}{{\gamma }_{j}} - {{\gamma }_{i}}{\text{|}}}}{{\omega _{*}^{\gamma }}} < \nu (d{{t}_{j}} + d{{t}_{i}} - {{\Delta }_{i}} - {{\Delta }_{j}}), \hfill \\ \infty \quad {\text{при}}\quad \nu (d{{t}_{j}} + d{{t}_{i}} - {{\Delta }_{i}} - {{\Delta }_{j}}) \leqslant {{x}_{i}} - {{x}_{j}} + \nu \frac{{{\text{|}}{{\gamma }_{j}} - {{\gamma }_{i}}{\text{|}}}}{{\omega _{*}^{\gamma }}}, \hfill \\ \end{gathered} \right.$(3.6)
${\text{tg}}\beta _{j}^{*} = \frac{{\sin (({{x}_{j}} - {{x}_{i}} - \nu \left| {{{\gamma }_{j}} - {{\gamma }_{i}}} \right|{\text{/}}\omega _{*}^{\gamma }){\text{/}}{{R}_{e}})}}{{1 + \frac{{{{H}_{{orb}}}}}{{{{R}_{e}}}} - \cos \frac{{{{x}_{j}} - {{x}_{i}} - \nu \left| {{{\gamma }_{j}} - {{\gamma }_{i}}} \right|{\text{/}}\omega _{*}^{\gamma }}}{{{{R}_{e}}}}}}.~~~$В (3.5) первое и второе условия определяют длительности поворота оси визирования после наблюдения объекта $i$ в момент минимального удаления ЛА/КА от объекта ($\beta _{i}^{\Delta }$ = 0) в положение для наблюдения объекта ϳ в момент минимального удаления ЛА/КА до объекта (${{\beta }_{j}} = 0$) (первое условие) и в положение для наблюдения объекта ϳ максимально близко ко времени минимального удаления ЛА/КА до объекта (${{\beta }_{j}} = \beta _{j}^{*}$ задается соотношением (3.6)) (второе условие); третье условие описывает случай, когда после объекта i наблюдение объекта ϳ невозможно.
При проверке выполнения условий (3.1) в процессе решения задачи моменты наблюдения (3.3) определяем их самыми ранними значениями:
По окончании решения осуществляем перерасчет моментов наблюдения для получения их итоговых значений, максимально близких к моментам ${{T}_{{{\text{min}}}}} = ~\{ t_{i}^{{{\text{min}}}}\} $ минимального удаления ЛА/КА от объектов наблюдений (пересчет осуществляется последовательно в обратном порядке – от следующего объекта наблюдения к предыдущему):
(3.7)
$\left| {{{t}_{i}} - t_{i}^{{{\text{min}}}}} \right| = \left| {{{t}_{j}} - {{\Delta }_{i}} - {{t}_{{ij}}} - {{p}_{j}} - t_{i}^{{{\text{min}}}}} \right| = > {\text{min}},{\text{\;}}$Поскольку решение оптимизационной задачи будет получено минимизацией целевой функции (1.4) не с точными (3.4), а с условными значениями (3.5) длительности переориентации оси визирования, то найденное таким образом решение в общем случае превышает истинное кратчайшее решение исходной задачи. Поэтому в дальнейшем при анализе качества получаемых решений будем называть решения задачи (1.4) с (3.5), (3.7) не оптимальными, а оптимизированными.
В качестве примера рассмотрим наблюдение случайных каталогов наземных объектов с ЛА (самолета) с высотой полета 2 км и с КА с высотой орбиты 400, 500 и 600 км. Ограничение на угловые скорости переориентации оси визирования аппаратуры наблюдения, установленной на самолете, составляет 30 град/с, на КА – 3 град/с, угол поля зрения аппаратуры наблюдения от надира – 45° для наблюдений с самолета и 30° – с КА.
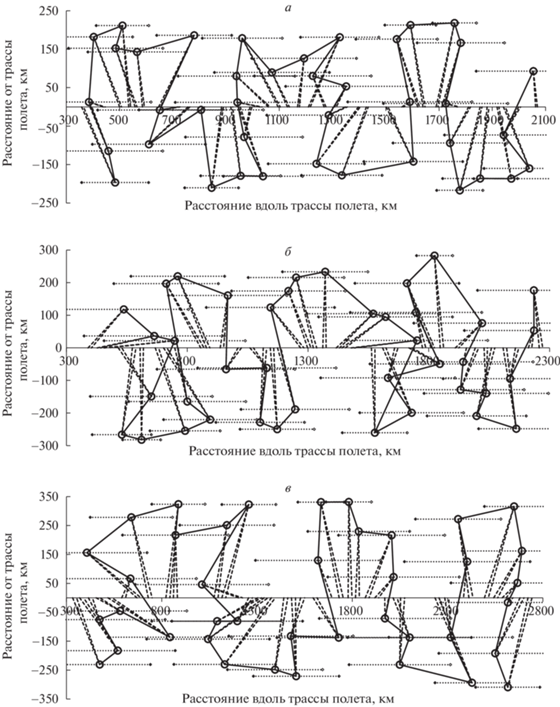
На рис. 2 и 3 представлены примеры оптимизированных решений для n = 40 объектов: в системе координат, связанной с трассой полета, пунктирном показаны направления от ЛА/КА на наблюдаемый объект в моменты начала и окончания наблюдения, точечными линиями – отрезки, проекция которых на трассу полета составляет интервал местоположений ЛА/КА, когда соответствующий объект доступен наблюдению. Для наблюдений с самолета представлены оптимизированные решения с 1, 2 и 3 сегментами маршрута, которые соответствуют наличию на ЛА/КА нескольких наблюдателей (комплектов аппаратуры наблюдения). Данные решения, в частности, иллюстрируют возможность увеличения длительности наблюдения объектов ${{\Delta }_{i}}$ за счет использования дополнительных наблюдателей.
Рис. 2.
Оптимизированные последовательности наблюдения объектов с ЛА с высотой полета 2 км: а – Δ = 2 с, K = 1, S = 37 с; б – Δ = 5 с, K = 2, S = 38 с; в – Δ = 7 с, K = 3, S = 35 с

Рис. 3.
Оптимизированные последовательности наблюдения объектов с КА: а – ${{H}_{{orb}}}$ = 400 км, Δ = 1 с, K = 1, S = 197 с; б – ${{H}_{{orb}}}$ = 500 км, Δ = 2 с, K = 1, S = 190; в – ${{H}_{{orb}}}$ = 600 км, Δ = 3 с, K = 1, S = 181 с
На рис. 4 приведено изменение углов γ, β и порядок наблюдения объектов по номерам, присвоенным по порядку моментов времени начала зон видимости объектов, в оптимизированном решении наблюдения объектов с ЛА (рис. 2, а) K = 1 (в длину маршрута S входит время переориентации оси визирования аппаратуры между наблюдениями без времени поворота оси визирования по углу β в процессе наблюдения).
Рис. 4.
Изменение углов γ, β и порядок наблюденния объектов в оптимизированном решении, представленном на рис. 2, а
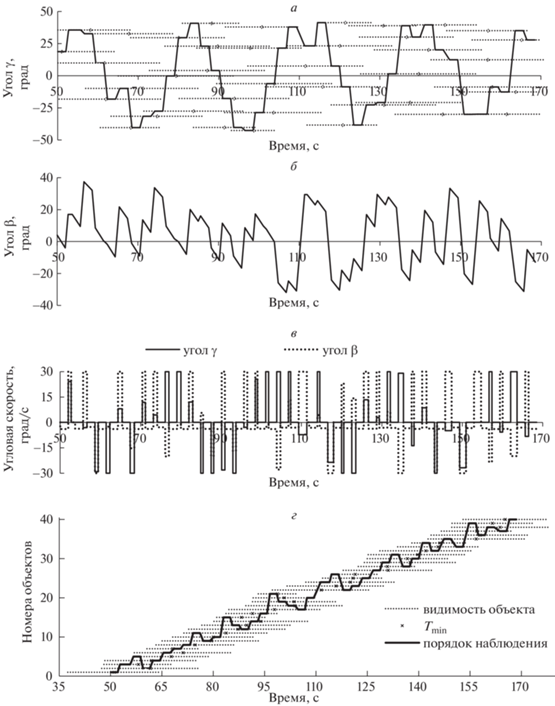
Для анализа эффективности решений выполнено моделирование, включающее получение для 100 случайных каталогов объектов оптимизированных решений, точных кратчайших решений методом перебора и простых решений (в случаях, когда они существуют) в виде упорядоченных последовательностей объектов по порядку времени минимального удаления объекта от трассы (решение простое 1) или по порядку начала зоны видимости объекта с ЛА/КА (решение простое 2). Простым решением считаем лучшее из имеющихся в наличии данных двух решений.
Длительность интервала полета, в течение которого на подстилающей поверхности вдоль трассы полета (в области, доступной наблюдению с ЛА/КА) появляются n случайных объектов, составляет
На рис. 5 представлены результаты моделирования по 100 случайным каталогам для рассмотренных четырех вариантов высоты полета ЛА/КА при q = 1; 1.25; 1.5; 1.75; 2 (данные значения реализуют случаи от максимальной при q = 1 до двукратно уменьшенной при q = 2 частоты появления объектов на подстилающей поверхности вдоль трассы полета).
Рис. 5.
Результаты моделирования для q = 1, 1.25, 1.5, 1.75, 2: а – среднее отличие оптимизированных (опт) решений (в процентах) от простых (прост) и кратчайших (кратч); б – объем вычислений (среднее количество решенных задач ${{N}_{{{\text{зад}}}}}$ и среднее число переменных в задаче ${{N}_{{{\text{пер}}}}}$); в – процент наличия простых решений; г – среднее отличие оптимизированных решений (в процентах) с n* = 5 – 15 от решения с n* = 16
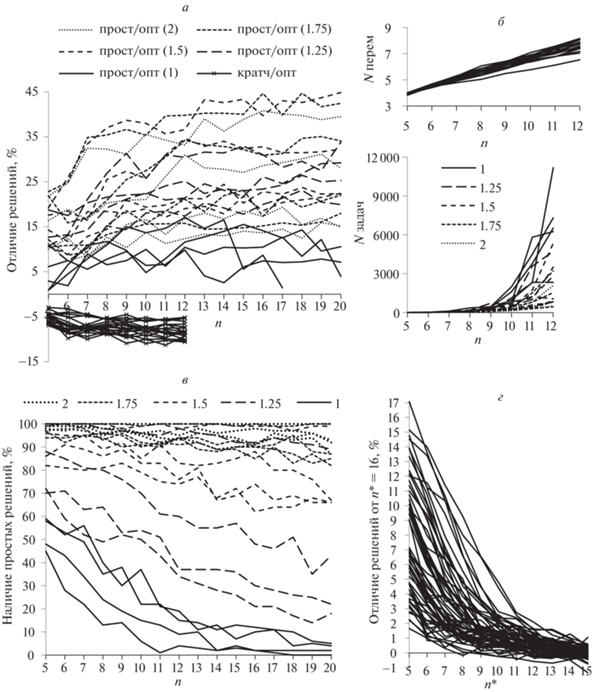
На рис. 5, а приведено среднее отличие оптимизированных решений от простых и кратчайших для n = 5 – 12 объектов при одном наблюдателе и при значениях коэффициента q = 1; 1.25; 1.5; 1.75; 2. Графики рис. 5, а показывают, что получаемые оптимизированные решения превышают кратчайшие на 5–10% и улучшают простые решения (при их наличии) до 35%.
На рис. 5, б представлен объем вычислений для получения оптимизированных решений, характеризуемый средним числом выполненных итераций (количеством решенных задач – на каждой итерации выполняется операция приведения матрицы затрат и вычисляется сумма приводящих констант) и средним числом переменных в решенных задачах. На рис. 5, в показан процент наличия простых решений.
Отличие значений простых решений от оптимизированных, объем вычислений и наличие простых решений существенно зависят от указанной частоты появления объектов и количества объектов n. Максимальной частоте появления объектов (q = 1) соответствует минимальное отличие значений простых решений от оптимизированных, максимальный объем вычислений для получения оптимизированного решения, минимальное наличие простых решений. С уменьшением данной частоты (с увеличением q) объем вычислений (число выполненных итераций) существенно сокращается, а наличие простых решений увеличивается (вплоть до 100%). С ростом количества объектов n объем вычислений (число выполненных итераций) существенно возрастает, наличие простых решений сокращается (вплоть до исчезновения), а отличие значений простых решений от оптимизированных остается примерно на одном и том же уровне. Среднее число переменных в решенных задачах с ростом количества объектов n монотонно увеличивается с коэффициентом ~1/2.
Спецификой рассматриваемой задачи является то, что возможность выполнения наблюдений объектов возникает последовательно по мере пролета ЛА/КА над подстилающей поверхностью. При этом на оптимальный выбор следующего объекта для выполнения наблюдений влияние оказывает только некоторое ограниченное количество n* предшествующих наблюдений. Их количество можно определить термином глубина планирования. Поэтому задачу поиска оптимального решения целесообразно разбивать на решение последовательных подзадач, каждая из которых охватывает данное количество наблюдений.
На рис. 5, г приведены результаты моделирования для рассмотренных четырех вариантов высоты полета ЛА/КА по 100 случайным каталогам объектов для каждого n = 30, 50, 70 при значениях коэффициента q = 1; 1.25; 1.5; 1.75 – среднее отличие оптимизированных решений, полученных с n* = 5 – 15, от решения, найденного с n* = 16. Графики на рис. 5, г показывают, что для рассмотренных вариантов ЛА/КА глубину планирования можно определить значениями n* ~10–12 объектов. Оптимизированные решения для любого количества объектов наблюдения могут быть получены последовательным решением оптимизационных задач для n = n* объектов, в которые входят n – 1 последних объекта из решения предшествующей оптимизационной задачи и один новый объект – следующий объект из упорядоченной последовательности объектов наблюдений. Данное упорядочивание объектов можно выполнять как по временам минимального удаления объектов от трассы (как в решении простое 1), так и по началу зоны видимости объекта с ЛА/КА (как в решении простое 2). Учитывая, что решение простое 1 реализуется до 20% чаще, чем решение простое 2, можно для определенности применять этот вариант упорядочивания. Таким образом, описанная методика обеспечивает возможность решения задач планирования практически без ограничений на количество объектов наблюдений.
4. Примеры построения маршрутов наблюдения наземных объектов с беспилотного летательного аппарата (БЛА). Рассмотрим планирование наблюдений каталога наземных объектов с БЛА, например при мониторинге проблемных участков посевов [4]. Нахождение кратчайшего маршрута наблюдения объектов позволит обеспечить эффективный расход ресурсов БЛА, а также решить задачу максимальной синхронизации съемки данного района земной поверхности с КА с подспутниковыми наблюдениями, выполняемыми с БЛА.
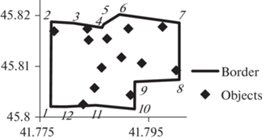
На рис. 6 на карте земной поверхности отображены 13 объектов (точек) наблюдения и замкнутая ломаная линия из 12 отрезков границы поля, которая рассматривается как возможная область начала/окончания движения БЛА (вершины/отрезки линии границы поля отсчитываем по часовой стрелке начиная с/от левой нижней вершины). В зависимости от особенностей эксплуатации БЛА можно сформулировать, например, следующие варианты искомых маршрутов.
1. Маршрут, начинающийся и заканчивающийся в точке граничной области, положение которой определяется исходя из требования минимизации длины маршрута. Задача решается в два этапа: а) находим кратчайший цикл (без условий на начало/окончание маршрута: $K = \emptyset $); б) определяем точку граничной области, расстояние от которой до двух соседних вершин кратчайшего цикла минимально. Искомый маршрут получаем введением в кратчайший цикл между данными двумя вершинами найденной точки граничной области. На рис. 7 отображен кратчайший цикл длиной 6.925 км и кратчайший замкнутый маршрут длиной 6.946 км для граничной области, заданной отрезком 7 линии границы поля.
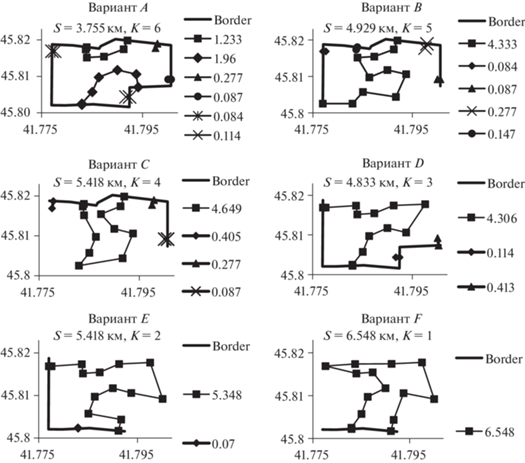
2. Кратчайшие маршруты наблюдения объектов для различных вариантов граничной области, на которой могут располагаться граничные вершины сегментов маршрута. Варианты граничной области задаем наборами отрезков линии границы поля. Задачу решаем последовательно для различного количества $K = 1,2,...$ граничных вершин, останавливая вычисления, когда длина маршрута перестанет уменьшаться. В табл. 2 и на рис. 8 представлены варианты A – F граничной области и полученные кратчайшие маршруты с указанием длины маршрута S (км) и количества сегментов K. На рис. 8 в легенде рядом с типом линии/маркера сегмента маршрута указана длина сегмента (км).
Таблица 2.
Кратчайшие маршруты для различных вариантов граничной области
| Варианты граничной области | Длина S, км | K |
|---|---|---|
| A (отрезки 1–12 линии границы поля) | 3.755 | 6 |
| B (отрезки 1–7 линии границы поля) | 4.928 | 5 |
| C (отрезки 2–7 линии границы поля) | 5.418 | 4 |
| D (отрезки 1, 8–12 линии границы поля) | 4.832 | 3 |
| E (отрезки 1, 10–12 линии границы поля) | 5.417 | 2 |
| F (отрезки 10–12 линии границы поля) | 6.548 | 1 |
3. Кратчайшие маршруты наблюдения для случая, когда точки начала/окончания сегментов маршрутов выбираются из заданного перечня фиксированных точек. Рассмотрим различные ограничения на длины сегментов и требования к связности маршрутов (связным маршрутом называем маршрут, в котором следующий сегмент начинается в точке окончания предшествующего сегмента). Граничную область представляем четырьмя точками – вершинами 1, 4, 7, 9 линии границы поля (нумерация вершин приведена на рис. 6). В табл. 3 и на рис. 9 рассмотрены варианты ограничений на длины сегментов и кратчайшие маршруты, которые в общем случае не являются связными (рис. 9, а), произвольные связные маршруты (рис. 9, б) и маршруты, все сегменты которых замкнуты в одну вершину (рис. 9, в). Требуемую связность сегментов маршрута достигаем путем решения задачи для всех соответствующих приведенному требованию связности вариантов местоположения граничных вершин, каждая из которых содержит окончание одного и начало другого сегмента маршрута.
Таблица 3.
Кратчайшие маршруты, сегменты которых могут начинаться и заканчиваться в вершинах 1, 4, 7, 9 линии границы поля
| Ограничение на длину сегментов | Маршруты без требования связности (рис. 9, а) | Связные маршруты (рис. 9, б) | Сегменты маршрута замкнуты в одну вершину (рис. 9, в) | |||
|---|---|---|---|---|---|---|
| S, км | K | S, км | K | S, км | K | |
| Нет | 6.249 | 2 | 6.362 | 1 | 6.925 | 1 |
| Не более 6 км | 6.249 | 2 | 6.616 | 2 | 7.243 | 2 |
| Не более 5 км | 6.249 | 2 | 6.616 | 2 | 7.838 | 2 |
| Не более 4 км | 6.249 | 2 | 6.749 | 3 | 8.843 | 3 |
| Не более 3 км | 6.696 | 3 | 7.000 | 3 | $\overline \exists $ | |
Рис. 9.
Кратчайшие маршруты для граничной области, заданной точками: а – маршруты без требования связности; б – связные маршруты; в – маршруты, все сегменты которых замкнуты в одну вершину
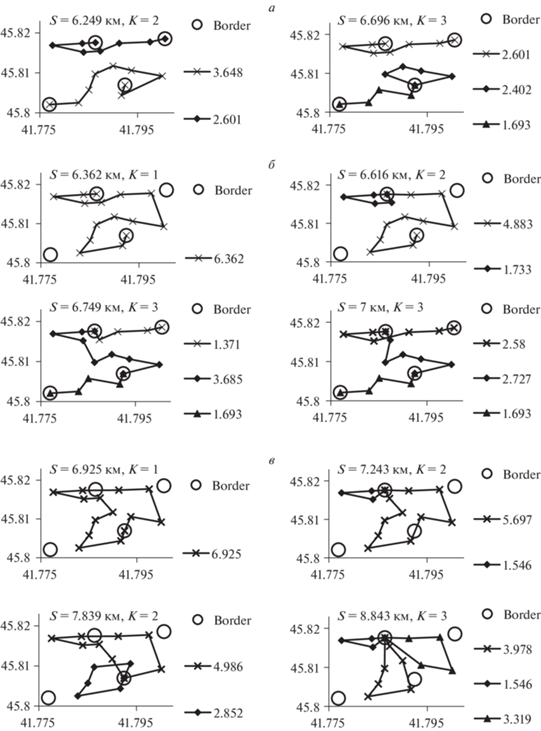
Представленные результаты, в частности, показывают, что для описанного примера длина кратчайшего маршрута изменяется: в зависимости от вариантов граничных областей (табл. 2) – в пределах ~80% от минимально возможной; в зависимости от ограничений на длины сегментов и требований связности искомых маршрутов (табл. 3) – в пределах ~40% от минимально возможной.
Заключение. Задача оптимизации планирования наблюдения каталога объектов подвижным наблюдателем с учетом ограничений на моменты выполнения наблюдений и затраты на перемещение наблюдателя между возможными/требуемыми граничными положениями рассмотрена как задача выбора маршрута.
Сформулированную задачу выбора маршрута решаем как задачу минимальной размерности, равной сумме количества объектов наблюдения и сегментов маршрута (числа наблюдателей). При этом контроль выполнения условий и ограничений на моменты времени выполнения наблюдений и на затраты на перемещение наблюдателя между возможными/требуемыми граничными положениями осуществляем без увеличения размерности решаемой задачи путем проверки выполнения данных ограничений на каждом шаге итерационного процесса решения задачи.
Учет наличия нескольких наблюдателей (или нескольких сегментов маршрута, замыкающихся в одни и те же граничные положения наблюдателя) реализуем путем дополнения графа задачи соответствующим количеством граничных вершин, что позволяет формализовать и решать рассматриваемую задачу как задачу определения кратчайшего цикла с использованием соответствующего простого алгоритма ее решения.
Представленные примеры иллюстрируют применение предложенного подхода при решении ряда практических задач.
Список литературы
Бырков Б.П., Силов В.В. К вопросу об оптимизации расписания функционирования перспективных космических станций // Тр. XVI чтений, посвященных разработке научного наследия и развитию идей К.Э. Циолковского. Секция “Проблемы ракетной и космической техники”. М.: ИИЕТ, 1982. С. 37–44.
Garton D., Frank H. ROSAT Mission Planning and its Perspectives for Planning Future Scientific Missions // AIAA Pap. 1990. № 5092. 6 p.
Беляев М.Ю., Легостаев В.П., Рулев Д.Н. Экономия энергетических затрат при планировании последовательности наблюдения с космического аппарата астрономических объектов // Изв. РАН. Энергетика. 2013. № 1. С. 15–23.
Федоренко В.Ф., Воронков И.В., Рулев Д.Н., Рулев Н.Д. Оптимизация маршрутов технических средств мониторинга и обработки посевов // Техника и оборудование для села. 2017. № 10 (244). С. 10–15.
Рулев Д.Н., Рулев Н.Д. Планирование наблюдений астрономических объектов с космического аппарата с учетом ограничений на моменты выполнения наблюдений // Космическая техника и технологии. 2019. № 1 (24). С. 110–119.
Christofides N., Mingozzi A., Toth P. The Vehicle Routing Problem // Combinatorial Optimization / Eds N. Christofides, A. Mingozzi, P. Toth, and C. Sandi. Chichester, UK. 1979. Ch. 11. P. 315–338.
Laporte G., Nobert Y., Desrochers M. Optimal Routing under Capacity and Distance Restrictions // Operations Research. 1985. V. 33. № 5. P. 1050–1073.
Toth P., Vigo D. An Overview of Vehicle Routing Problems // The Vehicle Routing Problem / Eds P. Toth and D. Vigo. SIAM, Philadelphia. 2002. Ch. 1. P. 1–26.
Solomon M.M. Algorithms for the Vehicle Routing and Scheduling Problem with Time Window Constraints // Operations Research. 1987. V. 35. № 2. P. 254–265.
Cordeau J.-F., Desaulniers G., Desrosiers J., Solomon M.M., Soumis F. VRP with Time Windows // The Vehicle Routing Problem / Eds P. Toth and D. Vigo. SIAM, Philadelphia. 2002. Ch. 7. P. 157–193.
Bard J., Kontoravdis G., Yu G. A Branch-and-Cut Procedure for the Vehicle Routing Problem with Time Windows // Transportation Science. 2002. V. 36. № 2. P. 250– 269.
Kallehauge B. Formulations and Exact Algorithms for the Vehicle Routing Problem with Time Windows // Computers & Operations Research. 2008. V. 35. P. 2307–2330.
Baldacci R., Mingozzi A., Roberti R. Recent Exact Algorithms for Solving the Vehicle Routing Problem under Capacity and Time Window Constraints // Europ. Operational Research. 2012. V. 218. P. 1–6.
Моудер Дж., Элмаграби С. Исследование операций. Методологические основы и математические методы. М.: Мир, 1981. 704 с.
Муртаф Б. Современное линейное программирование. М.: Мир, 1984. 224 с.
Беляев М.Ю., Рулев Д.Н. Повышение информативности наблюдений наземных объектов с ИСЗ // Космич. исслед. 1990. Т. 28. № 1. С. 56–68.
Ryumin V.V., Solovyov V.A., Belyaev M.Yu., Rulev D.N., Teslenko V.P. Optimization of Control of Space Investigations in “Gamma” project // 11th IFAC World Congress on Automatic Control. Tallinn, Estonia, USSR, 1990, 1.1-CS control in aerospace. Preprints. V. 1. P. 96–100.
Литтл Дж. и др. Алгоритм решения задачи о коммивояжере // Экономика и мат. методы. 1965. Т. 1. № 1. С. 94–107.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления