Известия РАН. Теория и системы управления, 2022, № 3, стр. 81-96
НЕОДНОРОДНОСТЬ РАСПРЕДЕЛЕНИЯ ПОТОКОВ ПРИ ПРЕДЕЛЬНОЙ ЗАГРУЗКЕ МНОГОПОЛЬЗОВАТЕЛЬСКОЙ СЕТИ
Ю. Е. Малашенко a, И. А. Назарова a, *
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 25.06.2021
После доработки 09.11.2021
Принята к публикации 29.11.2021
- EDN: XLRYTE
- DOI: 10.31857/S000233882202010X
Аннотация
В рамках многопродуктовой сетевой модели изучаются решения многокритериальных оптимизационных задач поиска недискриминирующих распределений равноправных, невзаимозаменяемых потоков различных видов, передаваемых между всеми узлами одновременно. Для оценки функциональных возможностей системы используется вектор предельных значений совместно допустимых межузловых потоков при максимальной загрузке всех ребер сети. Рассматриваются уравнительная и равнодолевая стратегии распределения потоков. Анализ результатов вычислительных экспериментов на сетях различной конфигурации показал, что для небольшого числа пар узлов-корреспондентов выделяемые системные ресурсы и результирующие значения межузловых потоков намного превышают соответствующие показатели для остальных.
Введение. В настоящее время для анализа проблем создания, развития и эксплуатации оптоволоконных и беспроводных систем часто используется математическая модель передачи многопродуктового потока, в рамках которой решаются многокритериальные оптимизационные задачи. Например, в [1] проводится анализ сетей управления воздушным сообщением с помощью взаимодействия радаров, компьютеров и телекоммуникационных систем. В [2] многопродуктовые модели применяются для анализа уязвимости и живучести многопользовательских систем связи. В [3, 4] предлагаются алгоритмы проектирования многопродуктовой сетевой системы, позволяющей передавать потоки, согласно требованиям ее пользователей.
В [5] описан детерминированный алгоритм маршрутизации при больших требованиях на передачу многопродуктовых потоков в режиме онлайн. В ряде работ анализируется проблема наличия нескольких маршрутов для передачи каждого вида потока в многопродуктовой сети [6–8]. Для случая передачи заданного многопродуктового потока в [9, 10] исследуется распределение ресурсов, а в [11, 12] – решается задача поиска минимальной стоимости. Разнообразные подходы к решению специальных задач диспетчеризации и выполнения требований пользователей предлагаются в [13]. В [14] рассматриваются стохастические сети с многокритериальной оценкой распределения потоков в многопользовательской многопродуктовой сети.
В рамках методологии исследования операций изучаются справедливые распределения потоков при заданных требованиях [15–17]. Для решения оптимизационных многопродуктовых задач предлагаются различные методы [18–20], в том числе специально разработанные алгоритмы [21]. Для многокритериальных моделей требуется большое число вычислительных экспериментов, с приемлемой погрешностью позволяющих проводить оценку решений [21, 22]. Большая размерность и специальные ограничения порождают приближенные алгоритмы [23]. Обзор “точных” алгоритмов решения многопродуктовых задач с дискретной функцией стоимости изложен в [24].
Данная работа продолжает исследование проблемы распределения ресурсов и межузловых потоков в территориально распределенных многопользовательских системах связи. Как и в нашей предыдущей статье, математическая запись модели передачи многопродуктового потока в явном виде учитывает ресурсы сети. Рассматривается модель, в которой межузловые потоки различных видов передаются между всеми парами узлов-корреспондентов одновременно. Множества векторов совместно допустимых межузловых потоков предлагается использовать в качестве многокритериальных оценок предельных функциональных возможностей сети. В рамках вычислительных экспериментов сравниваются две многокритериальные стратегии распределения потоков и пропускной способности ребер. Цель управления при уравнительной стратегии состоит в получении равных значений межузловых потоков между всеми парами узлов-корреспондентов. При равнодолевом распределении предполагается, что каждый конкретный межузловой поток должен быть прямо пропорционален максимально возможному для соответствующей пары вершин источник-приемник. Для вычислительных экспериментов использовалась итерационная процедура решения последовательности однопродуктовых задач поиска максимального потока для выделенной пары узлов при фиксированных нулевых значениях для всех остальных. Разработанный нами в предыдущей статье метод позволяет за конечное число шагов найти финальное распределение совместно допустимых межузловых потоков, такое, что предельная загрузка достигается для всех ребер сети. Указанный вектор значений многопродуктового потока является аппроксимирующим решением при использовании лексикографической процедуры получения справедливого максиминного распределения.
В настоящей работе сравнение равнодолевой и уравнительной стратегий проводится на основе оценки удельных затрат на передачу единичного потока для каждой пары корреспондентов. Анализ полученных результатов показал, что пары узлов-корреспондентов можно разделить на два непересекающихся подмножества, для которых принципиально отличаются как распределения межузловых потоков, так и доли выделяемой пропускной способности. Распределение в соответствии с заложенными принципами доступно только для части пар источник–сток, для остальных финальные значения не отвечают критериям равноправности. При этом корреспонденты, связанные напрямую одним ребром, находятся в более привилегированном положении, чем использующие транзитные вершины. Для реальной многопользовательской сети результаты, полученные в ходе эксперимента, могут указывать на неэффективное применение пропускных способностей или о несоответствии структуры сети требованиям корреспондентов.
1. Математическая модель. Многопользовательские сетевые системы связи описываются следующей математической моделью передачи многопродуктового потока. Сеть $G$ задается множествами $\langle V,\;R,\;U,P\rangle $: узлов (вершин) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $. Ребро ${{r}_{k}}$ соединяет концевые вершины ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Предполагается, что в сети отсутствуют петли и сдвоенные ребра. Каждому ребру ${{r}_{k}}$ ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ из множества ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют прямое и обратное направления передачи потока по ребру ${{r}_{k}}$ между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. По определению, каждой паре узлов-корреспондентов ${{p}_{m}}$ из множества $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $ отвечают: вершина-источник с номером ${{s}_{m}}$, из которой входной поток m-го вида поступает в сеть; вершина-приемник с номером ${{t}_{m}}$, из которой поток m-го вида покидает сеть. В многопользовательской сети $G$ рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных межузловых потоков различных видов.
Обозначим через ${{z}_{m}}$ величину межузлового потока m-го вида, поступающего в сеть из узла с номером ${{s}_{m}}$ и покидающего из узла с номером ${{t}_{m}}$; ${{x}_{{mk}}}$, ${{x}_{{m(k + E)}}}$ – величину потока m-го вида, ${{x}_{{mk}}}$ передающегося по дуге ${{u}_{k}}$ и ${{x}_{{m(k + E)}}}$ – по дуге ${{u}_{{k + E}}}$, согласно направлению передачи, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $; $S({{v}_{n}})$ – множество номеров исходящих дуг, по которым поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{v}_{n}}$. Состав множеств $S({{v}_{n}})$, $T({{v}_{n}})$ однозначно определяется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами $n$ и $j$, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$, направленная из вершины ${{v}_{n}}$ в ${{v}_{j}}$, считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, а дуга ${{u}_{{k + E}}}$, направленная из ${{{v}}_{j}}$ в ${{{v}}_{n}}$, – входящей для ${{{v}}_{n}}$ и ее номер $k + E$ помещается в список $T({{{v}}_{n}})$. Дуга ${{u}_{k}}$ является входящей для ${{{v}}_{j}}$ и ее номер k попадает в $T({{{v}}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ вносится в список исходящих дуг $S({{{v}}_{j}})$.
Во всех узлах сети ${{{v}}_{n}} \in V$, $n = \overline {1,N} $, для каждого вида потока должны выполняться условия сохранения потоков:
(1.1)
$\begin{gathered} \sum\limits_{i \in S({{{v}}_{n}})} {{x}_{{mi}}} - \sum\limits_{i \in T({{{v}}_{n}})} {{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{s}_{m}}}}}, \hfill \\ - {{z}_{m}},\quad {\text{если}}\quad {{{v}}_{n}} = {{{v}}_{{{{t}_{m}}}}}, \hfill \\ 0\quad {\text{в остальных случаях,}} \hfill \\ \end{gathered} \right. \\ n = \overline {1,N} ,\quad m = \overline {1,M} ,\quad {{x}_{{mi}}} \geqslant 0,\quad {{z}_{m}} \geqslant 0. \\ \end{gathered} $Величина ${{z}_{m}}$ равна входному межузловому потоку $m$-го вида от источника к приемнику пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.
Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$ – суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектором d определяются следующие ограничения на сумму потоков всех видов, передаваемых по ребру ${{r}_{k}}$ одновременно:
(1.2)
$\sum\limits_{m = 1}^M ({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$В рамках данной модели пропускная способность ребер сети – вектор d, трактуется как ресурсное ограничение, а сумма дуговых потоков рассматривается как показатель использования ресурсов сети при передаче межузловых потоков.
Для ${{z}_{m}}$, ${{x}_{{mi}}}$, удовлетворяющих условиям (1.1), (1.2), вычисляются суммарные потоки по ребрам сети:
Суммарный поток ${{y}_{m}}$ характеризует нагрузку на сеть при передаче межузлового потока величины ${{z}_{m}}$ из узла-источника ${{s}_{m}}$ в узел-приемник ${{t}_{m}}$. Величина ${{y}_{m}}$ показывает, какая суммарная пропускная способность сети используется для передачи межузлового потока ${{z}_{m}}$, а отношение
можно трактовать как удельные затраты ресурсов для передачи единичного потока m-го вида между узлами ${{s}_{m}}$ и ${{t}_{m}}$ при соответствующих дуговых потоках ${{x}_{{mi}}}$.Ограничения (1.1)–(1.2) задают множество допустимых значений компонент вектора межузловых потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:
(1.4)
$\mathcal{Z}({\mathbf{d}}) = \{ {\mathbf{z}} \geqslant 0\,|\,\exists \;{\mathbf{x}} \geqslant 0:\;({\mathbf{z}},{\mathbf{x}})\;{\text{удовлетворяют}}\;(1.1){\kern 1pt} - {\kern 1pt} (1.2)\} .$Допустимые распределения реберных потоков принадлежат подмножеству
(1.5)
$Y({\mathbf{d}}) = \{ {\mathbf{y}} \geqslant 0\,|\,({\mathbf{z}},{\mathbf{x}},{\mathbf{y}})\;{\text{удовлетворяют}}\;(1.1){\kern 1pt} - {\kern 1pt} (1.3)\} .$2. Монопольный режим передачи потока. В рамках модельного описания по определению монопольным режимом называется способ управления, при котором все ресурсы сети используются для передачи потока одной выделенной пары узлов-корреспондентов ${{p}_{a}} \in P$, а потоки для всех остальных пар при этом полагаются равными нулю. Предельно допустимый поток, проходящий между фиксированной парой узлов-корреспондентов в монопольном режиме, является решением стандартной задачи о максимальном однопродуктовом потоке [25].
Задача 1. Найти $z_{a}^{0}(1) = \mathop {\max }\limits_{\mathbf{z}} {{z}_{a}}$
Решение задачи 1 $z_{a}^{0}(1)$ – поток, передаваемый в сети в монопольном режиме, максимальный (МРМ-поток) однопродуктовый межузловой для пары pa. Обозначим через $(x_{{ai}}^{0}(1),x_{{a(i + E)}}^{0}(1))$, i = = $\overline {1,E} $, потоки по дугам, соответствующие решению $z_{a}^{0}(1)$. Вектор ${\mathbf{z}}_{a}^{0}(1) = (0,0,...,z_{a}^{0}(1),...,0,0)$ задает координаты угловой точки множества $\mathcal{Z}({\mathbf{d}})$, лежащей на пересечении границы $\mathcal{Z}({\mathbf{d}})$ с координатной осью za.
Для пары pa подсчитываются величина суммарного потока по ребрам сети $y_{a}^{0}(1)$ и удельные затраты ресурсов $w_{a}^{0}(1)$, требуемые для передачи одной единицы потока $z_{a}^{0}(1)$:
Задача 1 решается последовательно для всех ${{p}_{m}} \in P$, вычисляются значения $z_{m}^{0}(1)$, $m = \overline {1,M} $, на их основе формируются: вектор межузловых МРМ-потоков ${{{\mathbf{z}}}^{0}}(1) = (z_{1}^{0}(1),z_{2}^{0}(1),...$, $z_{m}^{0}(1)$, …, $z_{M}^{0}(1))$; вектор дуговых потоков ${{{\mathbf{x}}}^{0}}(1) = (x_{{mi}}^{0}(1),$ $x_{{m(i + E)}}^{0}(1))$, $m = \overline {1,M} $, $i = \overline {1,E} $; вектор y0(1) = = $(y_{1}^{0}(1),y_{2}^{0}(1),...,y_{m}^{0}(1),...,y_{M}^{0}(1))$ суммарных потоков по ребрам сети для всех пар ${{p}_{m}} \in P$.
В нашей предыдущей статье была предложена итерационная PLD-процедура вычисления межузловых потоков, при одновременной передаче которых полностью используется пропускная способность всех ребер сети. Аббревиатура PLD – от английского peak load distribution – распределение (потоков) при предельной загрузке (сети). Выполнение каждого шага PLD-процедур разбивается на несколько этапов. На предварительном этапе первого шага для всех пар источник–приемник ${{p}_{a}},a = \overline {1,M} $, с помощью решения задачи 1 определяются МРМ-потоки. Для всех пар вычисляется предельно допустимое совместное распределение межузловых потоков и находятся ребра с полностью использованной пропускной способностью. Для остальных ребер подсчитывается остаточная (неиспользованная) пропускная способность. На последующих итерациях значения МРМ-потоков рассчитываются в сети для значений остаточных пропускных способностей, найденных на предыдущих шагах. Снова находится предельно допустимое совместное распределение потоков, а также ребра с не полностью исчерпанной пропускной способностью. Таким образом, за конечное число итераций, не превосходящее общего числа ребер сети, определяется финальное распределение, при котором сумма реберных потоков всех видов оказывается равна сумме пропускных способностей.
При реализации PLD-процедуры допускается использование различных правил распределения межузловых потоков. В разд. 3, 4 приводится детализированное изложение схемы применения PLD-процедуры для вычисления равнодолевого и уравнительного распределений потоков при предельной загрузке сети.
3. Равнодолевое распределение при предельной загрузке сети. При использовании равнодолевой стратегии на каждой итерации парам узлов-корреспондентов на передачу потока выделяются различные квоты, прямо пропорциональные соответствующим текущим значениям МРМ-потоков.
При реализации PLD-процедуры на первом этапе первого шага ($t = 1$) последовательно для всех ${{p}_{m}} \in P$ решается цепочка задач 1 и определяются МРМ-вектор z0(1) = $(z_{1}^{0}(1),z_{2}^{0}(1),...,z_{m}^{0}(1),...,z_{M}^{0}(1))$, а также вектор дуговых потоков ${{{\mathbf{x}}}^{0}}(1) = (x_{{mk}}^{0}(1),x_{{m(k + E)}}^{0}(1))$, $m = \overline {1,M} $, $k = \overline {1,E} $. На следующем этапе первого шага найденные значения ${{{\mathbf{z}}}^{0}}(1)$, ${{{\mathbf{x}}}^{0}}(1)$ используются при поиске совместно допустимого распределения потоков, при котором достигается предельно возможная загрузка одного или нескольких ребер.
Задача 2. Найти $\theta {\kern 1pt} *{\kern 1pt} *(1) = \mathop {\max }\limits_\theta \theta $
Решение задачи 2 θ**(1) – максимальная доля МРМ-потока, равная для всех ${{p}_{m}} \in P$. На основе θ**(1) вычисляются допустимые значения $z_{m}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)z_{m}^{0}(1),$ $m = \overline {1,M} $, равнодолевых квот на одновременную передачу потоков для всех пар источник–приемник ${{p}_{m}} \in P$. В рамках рассматриваемой модели отношение $z_{m}^{{**}}(1){\text{/}}z_{m}^{0}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)$ показывает, какую долю от МРМ-потока составляет выделенная квота $z_{m}^{{**}}(1)$. Поскольку по построению единственное оптимальное значение θ**(1) одинаково для всех пар ${{p}_{m}} \in P$, то указанное распределение называется равнодолевым распределением квот при одновременной передаче межузловых потоков.
Вычисляются: дуговые потоки $x_{{mi}}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)x_{{mi}}^{0}(1)$, $x_{{m(i + E)}}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)x_{{m(i + E)}}^{0}(1)$, $m = \overline {1,M} $, $i = \overline {1,E} $; суммарный поток по ребрам сети для $m$-й пары:
В множестве P выделяется подмножество $P({{R}_{ + }})$ смежных узлов-корреспондентов, расположенных в концевых вершинах ребра ${{r}_{k}}$, $k = \overline {1,E} $. Остальные пары относятся к множеству $P({{R}_{ - }})$:
По завершении первой итерации для проведения постанализа формируются массивы расчетных данных по следующему правилу:
если ${{p}_{m}} \in P({{R}_{ + }})$, то значения $z_{m}^{{**}}(1),\;y_{m}^{{**}}(1),\;w_{m}^{{**}}(1)$ помещаются в массивы ${\mathbf{Z}}_{ + }^{{**}}(1)$, ${\mathbf{Y}}_{ + }^{{**}}(1)$, ${\mathbf{W}}_{ + }^{{**}}(1)$;
если ${{p}_{m}} \in P({{R}_{ - }})$, то значения $z_{m}^{{**}}(1),\;y_{m}^{{**}}(1),\;w_{m}^{{**}}(1)$ попадают в ${\mathbf{Z}}_{ - }^{{**}}(1)$, ${\mathbf{Y}}_{ - }^{{**}}(1)$, ${\mathbf{W}}_{ - }^{{**}}(1)$;
производится переход на следующий шаг, t = 2.
На первом этапе каждого последующего шага $t$ ($t \geqslant 2$, $t \leqslant E$) для вектора ${\mathbf{d}}{\kern 1pt} *{\kern 1pt} *(t - 1)$ последовательно для каждого ${{p}_{m}} \in P$ решается цепочка задач поиска МРМ-потока.
Задача 3. Для некоторой пары узлов pa найти
при дополнительных условиях ${\mathbf{z}} \in \mathcal{Z}({\mathbf{d}}{\kern 1pt} *{\kern 1pt} *(t - 1));$ ${{z}_{m}} = 0,$ $m \ne a,$ $m = \overline {1,M} .$
Оптимальному решению задачи 3 (текущему МРМ-потоку $z_{a}^{0}(t)$) соответствует распределение потоков по дугам сети $(x_{{ai}}^{0}(t),x_{{a(i + E)}}^{0}(t))$, ${{p}_{a}} \in P$, $i = \overline {1,E} $. Исходя из решения задачи 3 для всех ${{p}_{m}} \in P$ вычисляются коэффициенты
На втором этапе текущего шага t для определения максимально допустимого равнодолевого распределения квот формулируется задача поиска “узкого места” в сети с заданными остаточными пропускными способностями $d_{i}^{{**}}(t - 1),$ $i = \overline {1,E} $.
Задача 4. Найти $\theta {\kern 1pt} *{\kern 1pt} *(t) = \mathop {\max }\limits_\theta \theta $
На основании решения задачи 4 θ**(t) определяются результирующие межузловые и дуговые потоки:
На заключительном этапе текущего шага $t$ ($t \geqslant 2$) для всех ребер сети вычисляется остаточная пропускная способность
После завершения очередного шага $t$ PLD-процедуры осуществляется проверка условий:
1) если окажется, что хотя бы для одного ${{r}_{i}} \in R$ величина остаточной пропускной способности $d_{i}^{{**}}(t) > 0$, то:
значения $z_{m}^{{**}}(t),\;y_{m}^{{**}}(t),\;w_{m}^{{**}}(t)$ помещаются в ${\mathbf{Z}}_{ + }^{{**}}(t)$, ${\mathbf{Y}}_{ + }^{{**}}(t)$, ${\mathbf{W}}_{ + }^{{**}}(t)$ для ${{p}_{m}} \in P({{R}_{ + }})$,
значения $z_{m}^{{**}}(t),\;y_{m}^{{**}}(t),\;w_{m}^{{**}}(t)$ попадают в ${\mathbf{Z}}_{ - }^{{**}}(t)$, ${\mathbf{Y}}_{ - }^{{**}}(t)$, ${\mathbf{W}}_{ - }^{{**}}(t)$ для ${{p}_{m}} \in P({{R}_{ - }})$,
выполняется очередная итерация $t + 1$;
2) если же $d_{i}^{{**}}(t) = 0$ для всех $i = \overline {1,E} $, то происходит останов, поскольку все пропускные способности всех ребер исчерпаны, и достигнута предельная загрузка сети. Последняя итерация обозначается номером $t: = T.$
Финальный вектор распределения межузловых потоков z**(T), полученный в ходе выполнения PLD-процедуры при равнодолевом распределении квот на каждом шаге, называется PLES-потоком (от английского peak load equal share – предельная загрузка (сети) при равнодолевом распределении). Сформированные массивы данных используются при составлении таблиц и диаграмм, представленных в разд. 5.
4. Уравнительное распределение потоков. При уравнительной стратегии распределения с помощью PLD-процедуры на каждой итерации вычисляются равные квоты на предельно допустимые потоки для передачи по сети одновременно для всех пар-корреспондентов ${{p}_{m}} \in P$.
На первом этапе первого шага ($t = 1$) для всех ${{p}_{m}} \in P$ решается цепочка задач 1 и определяются: дуговые потоки ${{{\mathbf{x}}}^{0}}(1) = (x_{{mi}}^{0}(1),x_{{m(i + E)}}^{0}(1))$, $m = \overline {1,M} $, $i = \overline {1,E} $; компоненты МРМ-вектора ${{{\mathbf{z}}}^{0}}(1) = (z_{1}^{0}(1),z_{2}^{0}(1),...,z_{m}^{0}(1),...,z_{M}^{0}(1))$ и коэффициенты для задачи 5 (приведенной ниже):
На втором этапе первого шага формулируется задача поиска равных предельных квот на передачу потоков между всеми парами ${{p}_{m}} \in P$ и “узкого места” – ребер, пропускная способность которых при соответствующем распределении окажется полностью исчерпана.
Задача 5. Найти $\alpha {\text{*}}(1) = \mathop {\max }\limits_\alpha \alpha $
Обозначим через $z_{m}^{*}(1) = \alpha {\kern 1pt} {\text{*}}(1)$ предельно допустимое значение межузловых потоков для передачи одновременно между всеми парами узлов-корреспондентов ${{p}_{m}},\;m = \overline {1,M} $. При этом компоненты вектора дуговых потоков x*(1) равны $x_{{mi}}^{*}(1) = \alpha {\kern 1pt} {\text{*}}(1)\omega _{m}^{0}(1)x_{{mi}}^{0}(1)$, $x_{{m(i + E)}}^{*}(1)$ = $\alpha {\kern 1pt} {\text{*}}(1)\omega _{m}^{0}(1)x_{{m(i + E)}}^{0}(1)$, $m = \overline {1,M} $, $i = \overline {1,E} ,$ и определяют допустимое уравнительное распределение дуговых потоков по ребрам сети.
Для каждого $z_{m}^{*}(1)$ вычисляются суммарный поток по ребрам сети:
Для всех ребер сети рассчитывается остаточная пропускная способность:
Как и в разд. 3, после завершения первой итерации PLD-процедуры производится разделение данных на массивы по следующему правилу:
если ${{p}_{m}} \in P({{R}_{ + }})$, то значения $z_{m}^{*}(1),\;y_{m}^{*}(1),\;w_{m}^{*}(1)$ помещаются в массивы ${\mathbf{Z}}_{ + }^{*}(1)$, ${\mathbf{Y}}_{ + }^{*}(1)$, ${\mathbf{W}}_{ + }^{*}(1)$;
если ${{p}_{m}} \in P({{R}_{ - }})$, то значения $z_{m}^{*}(1),\;y_{m}^{*}(1),\;w_{m}^{*}(1)$ попадают в ${\mathbf{Z}}_{ - }^{*}(1)$, ${\mathbf{Y}}_{ - }^{*}(1)$, ${\mathbf{W}}_{ - }^{*}(1)$.
На первом этапе шага $t$ ($t \geqslant 2$, $t \leqslant E$) для полученных значений остаточных пропускных способностей $d_{i}^{*}(t - 1)$ последовательно решается цепочка следующих задач, аналогичных задаче 1.
Задача 6. Для некоторой пары узлов pa найти
Оптимальному решению задачи 6 (МРМ-потоку $z_{a}^{0}(t)$) соответствует распределение потоков по дугам сети $(x_{{ai}}^{0}(t),x_{{a(i + E)}}^{0}(t))$, $i = \overline {1,E} $.
После решения цепочки задач 6 для всех ${{p}_{m}},\;m = \overline {1,M} $, вычисляются коэффициенты
На втором этапе текущего шага t ($t \geqslant 2$) формулируется задача поиска “узкого места” в сети с заданными остаточными пропускными способностями $d_{i}^{*}(t - 1)$: определение максимальных равных квот на совместную одновременную передачу предельно допустимых потоков между всеми парами узлов-корреспондентов.
Задача 7. Найти $\alpha {\kern 1pt} *(t) = \mathop {\max }\limits_\alpha \alpha $
На основании решения задачи 7 на шаге $t$ ($t \geqslant 2$) подсчитываются
результирующие межузловые потоки для всех пар ${{p}_{m}} \in P$:
На заключительном этапе текущего шага $t$ ($t \geqslant 2$) для всех ребер сети вычисляется остаточная пропускная способность
если после завершения очередного шага t окажется, что хотя бы для одного ребра ${{r}_{i}} \in R$ величина остаточной пропускной способности $d_{i}^{*}(t) > 0$, то производится переход к следующему $t: = t + 1$ и разделение полученных значений $z_{m}^{*}(t),\;y_{m}^{*}(t),\;w_{m}^{*}(t)$ на массивы ${\mathbf{Z}}_{ + }^{*}(t)$, ${\mathbf{Y}}_{ + }^{*}(t)$, ${\mathbf{W}}_{ + }^{*}(t)$, ${\mathbf{Z}}_{ - }^{*}(t)$, ${\mathbf{Y}}_{ - }^{*}(t)$, ${\mathbf{W}}_{ - }^{*}(t)$;
если же $d_{i}^{*}(t) = 0$ для всех $i = \overline {1,E} $, то происходит останов, поскольку все пропускные способности ребер исчерпаны и сеть полностью загружена. Финальная итерация обозначается $t: = T$ и формируются массивы ${\mathbf{Z}}_{ + }^{*}(T)$, ${\mathbf{Y}}_{ + }^{*}(T)$, ${\mathbf{W}}_{ + }^{*}(T)$, ${\mathbf{Z}}_{ - }^{*}(T)$, ${\mathbf{Y}}_{ - }^{*}(T)$, ${\mathbf{W}}_{ - }^{*}(T)$, которые характеризуют финальное распределение потоков при предельной загрузке сети.
Указанное распределение называется PLED-потоком (от английского peak load equalitarian distribution – предельная загрузка (сети) при уравнительном распределении).
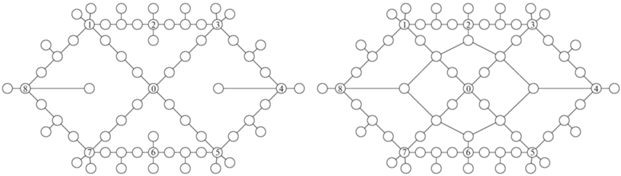
5. Вычислительный эксперимент. Описанные ниже результаты вычислительных экспериментов являются продолжением исследований нашей предыдущей статьи. Эксперименты с использованием PLD-процедуры проводились на моделях сетевых систем, представленных на рис. 1 (слева – базовая сеть, справа – кольцевая). В каждой сети 69 узлов. Пропускные способности ребер dk выбирались случайным образом из отрезка [900, 999] и совпадают для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900.
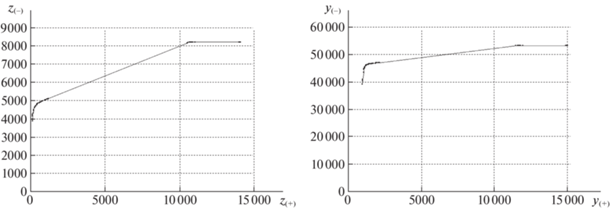
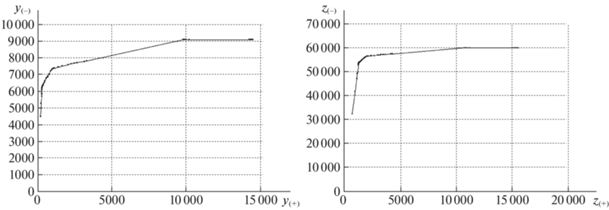
На рис. 2–5 и в табл. 1, 2 приведены данные о распределении потоков в базовой и кольцевой сетях, полученные в ходе выполнения PLD-процедуры. На диаграммах рис. 2–5 слева указаны суммарные значения межузловых потоков в сети на каждой итерации, а справа – соответствующие реберные потоки. По горизонтальной оси откладываются суммарные значения межузловых потоков между смежными парами узлов, а по вертикальной – для корреспондентов из множества $P({{R}_{ - }})$. Точки на графике относятся к очередной итерации и следуют снизу вверх и слева направо, согласно порядку их выполнения. Финальным значениям отвечает крайняя точка в северо-восточной части графика. На диаграммах справа указан ход изменения суммарных реберных потоков для пар из множеств $P({{R}_{ - }})$ и $P({{R}_{ + }})$. Из табл. 1, 2 и рис. 2–5 следует, что за несколько промежуточных итераций резко меняются доли суммарных потоков, которые распределяются между корреспондентами из групп $P({{R}_{ - }})$ и $P({{R}_{ + }})$.
Таблица 1.
Базовая сеть
| Распределение потоков | Равнодолевое | Уравнительное | |
|---|---|---|---|
| Подмножества пар | $P({{R}_{ - }}):P({{R}_{ + }})$ | $P({{R}_{ - }}):P({{R}_{ + }})$ | |
| Пары–корреспонденты | Общее число | 4500: 150 | 4500: 150 |
| Соотношение | 30 : 1 | 30 : 1 | |
| В процентах | 97 : 3% | 97 : 3% | |
| Межузловые потоки меж- | Суммарные ${{z}_{{( \cdot )}}}(t{\text{*}})$ | 5100: 1200 | 5760: 1600 |
| ду 40-й и 50-й итерациями | Соотношение | 4.25 : 1 | 3.6 : 1 |
| Межузловые потоки при | Суммарные ${{z}_{{( \cdot )}}}(T)$ | 8200 : 14 100 | 8500 : 13 100 |
| предельной загрузке | Соотношение | 1 : 1.7 | 1: 1.5 |
| Реберные потоки между | Суммарные ${{y}_{{( \cdot )}}}(t{\text{*}})$ | 47 000 : 2100 | 49 000 :2300 |
| 40-й и 50-й итерациями | Соотношение | 22.4 : 1 | 21.5: 1 |
| В процентах | 70 : 3% | 72 : 3% | |
| Реберные потоки при | Суммарные ${{y}_{{( \cdot )}}}(T)$ | 53 250 : 15 000 | 54 500: 13 750 |
| предельной загрузке | Соотношение | 3.55 : 1 | 4 : 1 |
| В процентах | 78 : 22% | 80 : 20% | |
| Усредненные удельные затраты между | |||
| 40-й и 50-й итерациями ${{w}_{{( \cdot )}}}(t{\text{*}})$ | 9.04 : 1.75 | 8.5 : 1.44 | |
| Усредненные удельные затраты | |||
| при предельной загрузке ${{w}_{{( \cdot )}}}(T)$ | 6.5 : 1.06 | 6.4 : 1.05 | |
| Суммарная пропускная способность сети D* | 68 250 | 68 250 | |
Таблица 2.
Кольцевая сеть
| Распределение потоков | Равнодолевое | Уравнительное | |
|---|---|---|---|
| Подмножества пар | $P({{R}_{ - }}):P({{R}_{ + }})$ | $P({{R}_{ - }}):P({{R}_{ + }})$ | |
| Пары–корреспонденты | Общее число | 4500: 150 | 4500: 150 |
| Соотношение | 30 : 1 | 30 : 1 | |
| В процентах | 97 : 3% | 97 : 3% | |
| Межузловые потоки меж- | Суммарные ${{z}_{{( \cdot )}}}(t{\text{*}})$ | 7050 : 760 | 7000 : 600 |
| ду 40-й и 50-й итерациями | Соотношение | 9.3 : 1 | 11.7 : 1 |
| Межузловые потоки при | Суммарные ${{z}_{{( \cdot )}}}(T)$ | 9100 : 14 500 | 9540 : 13140 |
| предельной загрузке | Соотношение | 1 : 1.6 | 1: 1.4 |
| Реберные потоки между | Суммарные ${{y}_{{( \cdot )}}}(t{\text{*}})$ | 55 600 : 1760 | 60 000 :1310 |
| 40-й и 50-й итерациями | Соотношение | 31.5 : 1 | 45: 1 |
| В процентах | 74 : 2.5% | 80 : 1.7% | |
| Реберные потоки при | Суммарные ${{y}_{{( \cdot )}}}(T)$ | 59 700 : 15 750 | 61 600: 13 850 |
| предельной загрузке | Соотношение | 3.8 : 1 | 4.5 : 1 |
| В процентах | 79 : 21% | 82 : 18% | |
| Усредненные удельные затраты между | |||
| 40-й и 50-й итерациями ${{w}_{{( \cdot )}}}(t{\text{*}})$ | 7.9 : 2.32 | 8.6 : 2.18 | |
| Усредненные удельные затраты | |||
| при предельной загрузке ${{w}_{{( \cdot )}}}(T)$ | 6.6 : 1.09 | 6.5 : 1.05 | |
| Суммарная пропускная способность сети D* | 75 455 | 75 455 | |
На начальных итерациях суммарные потоки согласовываются как с числом корреспондентов в каждой группе, так и с правилом распределения на каждом шаге: график поднимается почти вертикально. После 40-й итерации сеть начинает распадаться на отдельные фрагменты, поскольку остаточная пропускная способность некоторых ребер становится равной нулю. В результате для многих пар-корреспондентов не существует путей соединения, и потоки фиксируются на достигнутом уровне. После 50-й итерации около 20–25% остаточной суммарной пропускной способности распределяется только между смежными узлами по инцидентным ребрам.
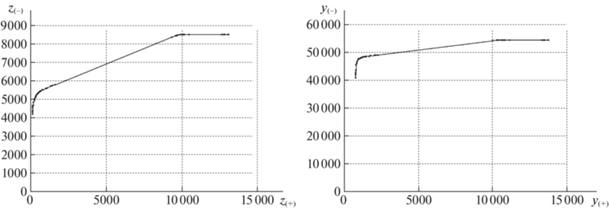
Для примера рассмотрим табл. 1 и диаграмму на рис. 3, относящиеся к базовой сети при уравнительном распределении на каждом этапе выполнения PLD-процедуры. В ней суммарная пропускная способность
а соотношение числа пар, входящих в подмножества $P({{R}_{ - }})$ и $P({{R}_{ + }})$,На диаграмме рис. 3 слева по вертикальной и горизонтальной осям откладываются соответственно суммарные значения межузловых потоков из массивов расчетных данных ${\mathbf{Z}}_{ - }^{*}(t)$ и ${\mathbf{Z}}_{ + }^{*}(t)$:
Излом графика на диаграмме происходит между 40-й и 50-й итерациями, и верны следующие соотношения для суммарных потоков и долей реберных потоков:
При этом используется почти 75% суммарной пропускной способности всех ребер сети. Однако для финальных суммарных значений верно ${{Z}_{ - }}(T):{{Z}_{ + }}(T) = 1:1.5$. Таким образом для 150 смежных пар узлов финальные межузловые потоки превышают в 1.5 раза суммарный поток для 4500 оставшихся корреспондентов. Финальные реберные потоки – использование ресурсов сети, для 3% смежных пар-корреспондентов составляет 20% от пропускной способности D*.
Значения усредненных удельных затрат ${{\overline w }_{ + }}(T)$ для смежных корреспондентов при предельной загрузке сети равны
Таким образом на последних итерациях при распределении остаточной пропускной способности парам узлов из множества $P({{R}_{ + }})$ выделяются бóльшие квоты на поток по инцидентным ребрам, что приводит к уменьшению удельных затрат. Усредненные значения удельных затрат указаны в табл. 1, 2:
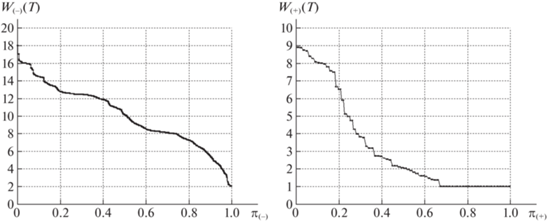
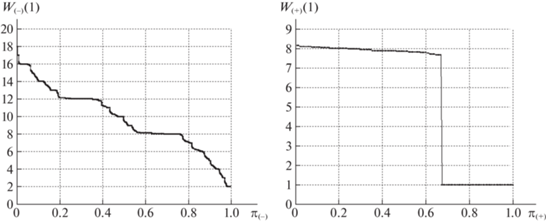
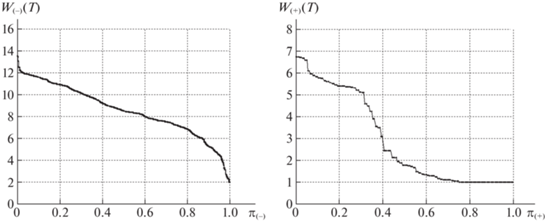
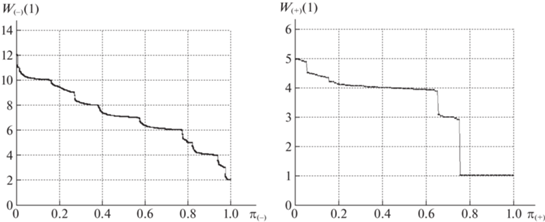
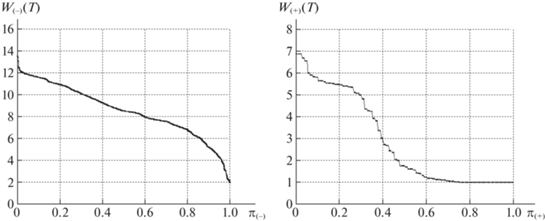
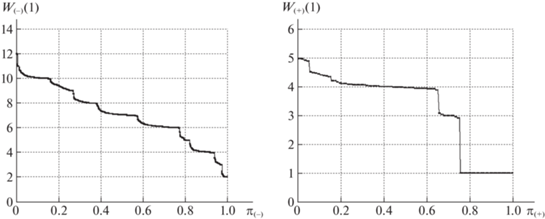
На рис. 6–13 представлены диаграммы удельных затрат при передаче межузловых потоков. На всех диаграммах слева указаны удельные затраты для пар узлов из $P({{R}_{ - }})$, справа – для смежных пар ${{p}_{k}} \in P({{R}_{ + }})$. Все полученные значения ${{w}_{m}}( \cdot )$ из массивов ${{W}_{ - }}( \cdot )$, ${{W}_{ + }}( \cdot )$ упорядочиваются по величине от большего к меньшему (по невозрастанию). По горизонтальной оси указываются относительные порядковые номера корреспондентов в упорядоченных последовательностях:
Для базовой сети на рис. 6, 7 представлены диаграммы расчетных значений затрат из массивов данных ${\mathbf{W}}_{ - }^{*}(T)$, ${\mathbf{W}}_{ + }^{*}(T)$, ${\mathbf{W}}_{ - }^{*}(1)$, ${\mathbf{W}}_{ + }^{*}(1)$, полученные при выполнении PLD-процедуры. На рис. 7 указаны значения $w_{m}^{*}(1)$ после завершения первой итерации PLD-процедуры, на рис. 6 – финальные значения $w_{m}^{*}(T)$ при достижении предельной загрузки сети. Кривая $w_{m}^{*}(T)$, ${{p}_{m}} \in P({{R}_{ - }})$, расположена строго выше кривой $w_{m}^{*}(1)$. Таким образом, удельные затраты на передачу межузловых потоков для ${{p}_{m}} \in P({{R}_{ - }})$ увеличиваются, поскольку используются маршруты с бóльшим числом ребер.
Диаграммы на рис. 6, 7 справа относятся к смежным парам ${{p}_{k}} \in P({{R}_{ + }})$. На диаграмме рис. 7 справа представлены удельные затраты после выполнения первой итерации. Значения из ${\mathbf{W}}_{ + }^{*}(1)$ и ${\mathbf{W}}_{ + }^{*}(T)$ равны 1 более чем для 30% смежных пар. Последнее означает, что более 30% смежных узлов имеют единственный маршрут соединения – по инцидентному ребру. Для остальных пар ${{p}_{k}} \in P({{R}_{ + }})$ в исходной сети существует несколько маршрутов передачи потока, проходящих через минимальные разрезы. Для 20% смежных пар узлов удельные финальные затраты больше исходных значений, т.е. $w_{ + }^{*}(T) \geqslant w_{ + }^{*}(1)$, что свидетельствует об увеличении числа ребер в обходных путях для таких пар. Однако более чем для 40% смежных пар финальные удельные затраты меньше значений на первой итерации ($w_{ + }^{*}(1) \geqslant w_{ + }^{*}(T)$). Дело в том, что в ходе выполнения PLD-процедуры при увеличении числа ребер с нулевой остаточной пропускной способностью для смежных пар чаще остается единственный путь по инцидентному ребру. На последних итерациях суммарная остаточная пропускная способность составляет 20–25% от исходной и распределяется в основном между смежными парами, связанными ребром в оставшихся фрагментах сети. Финальным значениям $z_{k}^{*}(T)$ из массива ${\mathbf{Z}}_{ + }^{*}(T)$ для 40% ${{p}_{k}} \in P({{R}_{ + }})$ соответствует поток $y_{k}^{*}(T)$ по инцидентному ребру rk, что приводит к значительному уменьшению удельных затрат и резкому росту $z_{k}^{*}(T)$. Указанная особенность распределения при предельной загрузке наблюдается в случае использования обеих стратегий. Из табл. 1, 2 следует, что усредненные значения удельных затрат для смежных пар узлов отличаются незначительно и лежат в диапазоне $1.09 \geqslant w_{ + }^{*}(T) \geqslant 1.05$ для обеих сетей.
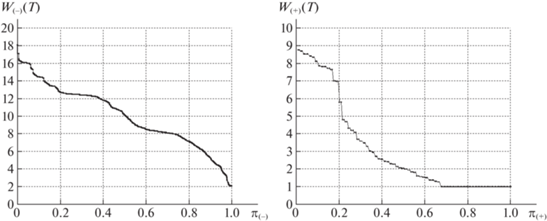
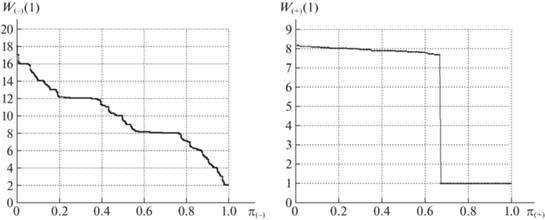
На рис. 8, 9 для базовой сети представлены диаграммы удельных затрат при уравнительном способе распределения потоков. Для кольцевой сети на рис. 10, 11 размещены диаграммы при равнодолевом, а на рис. 12, 13 – при уравнительном способе распределения на каждой итерации PLD-процедуры. Суммарная пропускная способность в кольцевой сети на 11% больше, чем в базовой. Численные значения на всех приведенных диаграммах различаются на 5–10%, однако все графики наглядно демонстрируют указанные выше закономерности и основные особенности распределения потоков при предельной загрузке всех ребер сети.
Заключение. Описанные в разд. 5 вычислительные эксперименты проводились для оценки предельных возможностей многопользовательской сети и сравнения различных принципов распределения межузловых потоков. Для исследования модели требовалось многократное решение оптимизационных задач с векторным функционалом. При разработке вычислительной процедуры для определения угловых и граничных точек множества допустимых потоков использовался метод последовательного поиска лексикографического максимина. Предложенная алгоритмическая процедура и способ представления результатов эксперимента позволили выявить особенности в распределении межузловых потоков при предельной загрузке сети.
При реализации итерационной схемы на каждом шаге применялись недискриминирующие правила распределения невзаимозаменяемых межузловых потоков различных видов. Таким образом соблюдались требования равноправности корреспондентов – условие, формализованное в рамках исходной многокритериальной модели многопользовательской сети. Однако в ходе анализа решений с содержательной точки зрения возник целый ряд вопросов.
Прежде всего только для 80% корреспондентов удается поддерживать распределение в соответствии с заложенными принципами, а для 20% финальные значения межузловых потоков не отвечают критериям и могут отличаться на два порядка для пар узлов из разных подмножеств.
Из результатов следует, что корреспонденты, расположенные в смежных узлах, имеют привилегированный доступ к ресурсам сети: около 4% таких корреспондентов получают от 20 до 25% всех ресурсов сети. Весьма существенно отличаются функциональные показатели: для 5% смежных корреспондентов сумма финальных значений межузловых потоков больше, чем для 95% оставшихся пар узлов.
Для реальной сетевой многопользовательской системы указанные особенности финальных распределений могут свидетельствовать, например, о неэффективном использовании ресурсов, об ошибках проектирования и/или указывать на необходимость введения нормативных ограничений на рабочие режимы диспетчеризации при предельной загрузке сети.
Список литературы
Ahmed W., Hasan O., Pervez U. et al. Reliability Modeling and Analysis of Communication Networks // J. Netw. Comput. Applcations. 2017. V. 78. P. 191–215.
Kabadurmus O., Smith A.E. Multicommodity k-Splittable Survivable Network Design Problems with Relays // Telecommun. Syst. 2016. V. 62. Iss. 1. P. 123–133.
Agarwal Y.K. Design of Capacitated Multicommodity Networks with Multiple Facilities // Oper. Res. 2002. V. 50. Iss. 2. P. 333–344.
Balakrishnan A., Li G., Mirchandani P. Optimal Network Design with End-to-End Service Requirements // Oper. Res. 2017. V. 65. Iss. 3. P. 729–750.
Even G., Medina M. Online Multicommodity Flow with High Demands // Int. Workshop on Approximation and Online Algorithms. Berlin: Springer, 2012. P. 16–29.
Baier G., Kohler E., Skutella M. The k-Splittable Flow Problem // Algorithmica. 2005. V. 42. Iss. 3–4. P. 231–248.
Brandt S., Foerster K.-T., Wattenhofer R. Augmenting Flows for the Consistent Migration of Multicommodity Single-destination Flows in SDNS // Pervasive Mobile Comput. 2017. V. 36. P. 134–150.
Bialon P. A Randomized Rounding Approach to a k-Splittable Multicommodity Flow Problem with Lower Path Flow Bounds Affording Solution Quality Guarantees // Telecommun. Syst. 2017. V. 64. Iss. 3. P. 525–542.
Liu L., Cao X., Cheng Y. Energy-Aware Optimal Resource Allocation in MR-MC Wireless Networks // IEEE Global Communications Conf. (GLOBECOM-2013). Atlanta: IEEE-Press, 2013. P. 4865–4870.
Liu L., Cao X., Cheng Y. et al. Energy-Efficient Capacity Optimization in Wireless Networks // IEEE Conf. on Computer Communications. Toronto: IEEE-Press, 2013. P. 1384–1392.
Ding S. Uncertain Minimum Cost Multicommodity Flow Problem // Soft Comput. 2017. V. 21. Iss. 1. P. 223–231.
Fortz B., Gouveia L., Joyce-Moniz M. Models for the Piecewise Linear Unsplittable Multicommodity Flow Problems // Eur. J. Oper. Res. 2017. V. 261. Iss. 1. P. 30–42.
Chekuri C., Khanna S., Shepherd F.B. The All-or-Nothing Multicommodity Flow Problem // SIAM J. Comput. 2013. V. 42. Iss. 4. P. 1467–1493.
Robinson A.R., Chan Y., Dietz D.C. Detecting a Security Disturbance in Multicommodity Stochastic Networks // Telecommun. Syst. 2006. V. 31. Iss. 1. P. 11–27.
Nace D., Doan L.N., Klopfenstein O. et al. Max-min Fairness in Multicommodity Flows // Comput. Oper. Res. 2008. V. 35. Iss. 2. P. 557–573.
Radunovic B., Le Boudec J.-Y. A Unified Framework for Max-Min and Min-Max Fairness With Applications // IEEE/ACM Transactions on Networking. 2007. V. 15. Iss. 5. P. 1073–1083.
Georgiadis L., Georgatsos P., Floros K. et al. Lexicographically Optimal Balanced Networks // Proc. IEEE INFOCOM 2001 Conf. on Comput. Communications. Anchorage: IEEE-Press, 2001. P. 689–698.
Velichko A., Gribova V., Fedori L. Simulation Software for Multicommodity Flows Model of Interregional Trade // 3rd Russian-Pacific conf. on Computer Technology and Applications (RPC). Vladivostok: IEEE-Press, 2018. P. 1–5.
Ouorou A., Mahey P., Vial J.-P. A Survey of Algorithms for Convex Multicommodity Flow Problems // Manag. Sci. 1997. V. 46. Iss. 1. P. 126–147.
Ogryczak W., Luss H., Pioro M. et al. Fair Optimization and Networks: A Survey // J. Appl. Math. 2014. V. 3. P. 1–25.
Masri H., Krichen S., Guitouni A. Metaheuristics for Solving the Bi-objective Single-Path Multicommodity Communication Flow Problem // Int. Trans. Oper. Res. 2019. V. 26. Iss. 2. P. 589–614.
Masri H., Krichen S., Guitouni A. A Multi-start Variable Neighborhood Search for Solving the Single Path Multicommodity Flow Problem // Appl. Math. Comput. 2015. V. 251. P. 132–142.
Leighton T., Makedon F., Plotkin S. et al. Fast Approximation Algorithms for Multicommodity Flow Problems // J. Comput. Syst. Sci. 1995. V. 50. Iss. 2. P. 228–243.
Minoux M. Discrete Cost Multicommodity Network Optimization Problems and Exact Solution Methods // Ann. Oper. Res. 2001. V. 106. Iss. 1–4. P. 19–46.
Йенсен П., Барнес Д. Потоковое программирование. М.: Радио и связь, 1984.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления