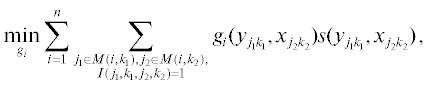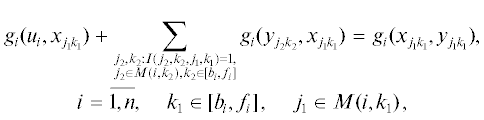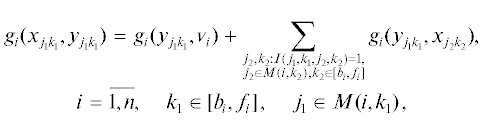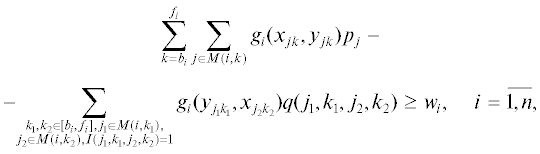Известия РАН. Теория и системы управления, 2022, № 3, стр. 97-103
Оптимизация структуры многопроцессорной системы реального времени
М. Г. Фуругян *
Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
* E-mail: rtsccas@yandex.ru
Поступила в редакцию 29.11.2021
После доработки 13.12.2021
Принята к публикации 31.01.2022
- EDN: ZKTDWD
- DOI: 10.31857/S0002338822030064
Аннотация
Рассматривается задача оптимизации структуры многопроцессорной вычислительной системы реального времени, где под структурой понимается набор связей между процессорами, который может изменяться во времени при определенных условиях. Эти условия, во-первых, связаны с физической возможностью или невозможностью установления связи между каждой парой процессоров в определенные моменты времени и, во-вторых, должны гарантировать существование допустимого расписания для заданного множества заданий с известными характеристиками (директивные интервалы, объемы работ, привязка к определенным процессорам и требуемые объемы памяти). Установление подобных связей дает возможность переключать выполнение работ с одного процессора на другой и требует некоторых затрат. Ставится задача определения структуры с минимальными затратами. Она сведена к многопродуктовой потоковой задаче в сети специального вида, для которой получены необходимые и достаточные условия существования решения в виде системы линейных булевых соотношений для исходных параметров.
Введение. В настоящее время вычислительные системы реального времени востребованы во многих отраслях производства. Они применяются в гражданском и военном строительстве, при разработке газовых и нефтяных месторождений, при испытаниях самолетов, ракет и других технических объектов, в конвейерных производствах, транспортных системах, при разработке систем противовоздушной и противоракетной обороны, обработке больших массивов информации технического, экономического и экологического характера в реальном масштабе времени. Так, при проведении летных испытаний данные, поступающие с борта самолета с высокой частотой, должны успевать обрабатываться в темпе поступления с тем, чтобы передавать на борт корректирующие команды. С использованием вычислительных сетей, многопроцессорной и многоядерной техники возникли новые математические и прикладные задачи, как, например, оптимизация структуры вычислительной системы реального времени. В [1–3] такая задача для многоядерной вычислительной системы реального времени решается с использованием обобщенных конечных автоматов и построенной на их основе имитационной модели. С помощью этой модели строится временная диаграмма, описывающая функционирование системы и позволяющая осуществить непосредственную проверку того, что каждая работа выполняется в заданном директивном интервале. Публикации [4–6] посвящены исследованию изменений работоспособности многопользовательской информационной сети в результате повреждений. Данный анализ проводится с использованием теории потоков в сетях. Для оценки ущерба строится двухкритериальная модель, с помощью которой определяется влияние различных повреждений на функционирование информационных направлений. Проводится анализ устойчивости характеристик многопродуктовой потоковой сети к различным разрушениям. В [7] рассматривается аппаратно-программный комплекс вычислительной системы реального времени и решается задача минимизации затрат при его проектировании с заданными требованиями на производительность и надежность функционирования. Разработана методика сведения указанной задачи к задаче однокритериальной условной оптимизации, для решения которой используются эволюционные алгоритмы. В ряде случаев задачи сетевой оптимизации и составления графиков выполнения работ сводятся к поиску минимакса [8–11]. В [12] определяются производительности процессоров, при которых многопроцессорная система реального времени способна выполнять требуемые вычисления в заданном темпе. Исследованы постановки с фиксированными и нефиксированными параметрами, с возобновляемыми и невозобновляемыми ресурсами. Показано, что исходная задача сводится к нахождению допустимых решений в системе линейных неравенств. Разработан алгоритм нахождения парето-оптимальных решений. В [13] рассмотрена задача оптимизации выполнения комплекса работ с нефиксированными длительностями, для решения которой применяется метод ветвей и границ.
В статье приводится задача оптимизации структуры многопроцессорной вычислительной системы реального времени. Устанавливаются допустимые и минимальные по стоимости связи между процессорами, которые при определенных условиях и ограничениях в разные моменты времени можно переопределять. Эти ограничения указывают физическую возможность (или невозможность) установления связи между каждой парой процессоров в фиксированный момент времени и, кроме того, требуют существования допустимого расписания для множества заданий с известными характеристиками (директивные интервалы, объемы требуемой работы, привязка к определенным процессорам и необходимые объемы памяти). Установление подобных связей дает возможность в определенные моменты времени переключать выполнение заданий с одного процессора на другой, но требует определенных затрат. Необходимо найти структуру связей между процессорами с минимальными затратами. Эта задача сводится к сетевой многопродуктовой потоковой задаче и для ее решения получены необходимые и достаточные условия существования решения в виде системы линейных булевых соотношений. В отличие от [14] в настоящей работе помимо поиска допустимого расписания решается задача построения допустимой структуры вычислительной системы и минимизации ее стоимости, а также рассматриваются дополнительные ограничения на выполнение заданий (ограничения по памяти, привязке к процессорам и др.).
1. Постановка задачи. Имеется m процессоров, занумерованных от 1 до m, из которых требуется спроектировать вычислительную систему реального времени, и комплекс работ (заданий) N = {$\overline {1,n} $}, занумерованных от 1 до n, который необходимо выполнить с помощью этой системы. Горизонтом планирования является отрезок [0, T], который разделен на T временных отрезков единичной длины Δk = [tk – 1, tk] k = $\overline {1,T} $ t0 = 0, tT = T. Каждая работа не может одновременно выполняться несколькими процессорами, а один процессор не может одновременно исполнять несколько работ. Производительность j-го процессора (или произведенный в единицу времени объем работы) составляет pj, а объем его оперативной памяти, доступной в интервале Δk, равен Bjk. Каждое задание i ∈ N характеризуется директивным временным интервалом [bi, fi] (внутри которого допускается его реализация; bi, fi ∈ {t0, t1, …, tT}), объемом требуемой работы процессоров wi и необходимым объемом оперативной памяти ci. Внутри каждого интервала Δk ⊆ [bi, fi], k = = $\overline {1,T} $, не допускаются прерывания и переключения задания i ∈ N с одного процессора на другой. Если в этом случае исполнителем является процессор j, то объем сделанной им работы составляет pj.
Имеются следующие ограничения, связанные с исполнением работ.
Ограничения на использование процессоров: в интервале Δk задание i может выполняться только одним из процессоров из заданного множества M(i, k) ⊆ {$\overline {1,m} $}.
Ограничения на переключения между процессорами: задан четырехмерный массив I, каждый элемент I(j1, k1, j2, k2) которого равен 1, если можно установить связь между процессорами j1 и j2, позволяющую после выполнения задания в интервале ${{\Delta }_{{{{k}_{1}}}}}$ процессором j1 переключить его на процессор j2 в интервале ${{\Delta }_{{{{k}_{2}}}}}$, и равен 0, если указанная связь невозможна, j1 ∈ M(i, k1), j2 ∈ ∈ M(i, k2), i ∈ N, k1, k2 = $\overline {1,T} $, k1 < k2. Суммарный объем работы процессоров j1 и j2, необходимый для такого переключения, составляет q(j1, k1, j2, k2).
Ограничения по памяти: объем памяти, требуемой для выполнения работы, не должен превосходить доступного в соответствующем интервале объема оперативной памяти процессора, исполняющего ее.
Массив I определяет возможность или невозможность установления связи между процессорами в различные моменты времени. Так, если I(j1, k1, j2, k2) = 1, то при проектировании вычислительной системы возможно установление связи, обеспечивающей переключение задания с процессора j1 в момент времени ${{t}_{{{{k}_{1}}}}}$ на процессор j2 в момент времени ${{t}_{{{{k}_{2}} - 1}}}$. При этом стоимость установления такой связи составляет s(j1, k1, j2, k2). Допустимая структура Σ вычислительной системы задается установлением указанных связей между процессорами, не противоречащих массиву I. Иными словами, Σ = {(j1, k1, j2, k2) : I(j1, k1, j2, k2) = 1}. Таким образом, связь между процессорами может быть непостоянной во времени, что имеет место, например, в транспьютерных системах. Стоимость S(Σ) допустимой структуры Σ – это суммарная стоимость по каждой установленной связи, т.е.
Допустимым расписанием R(Σ) для комплекса N при выбранной допустимой структуре Σ является такое расписание, при котором каждое задание i ∈ N начинает выполняться не ранее момента времени bi и завершается не позднее момента времени fi, суммарный объем работы процессоров при его исполнении равен wi. Все переключения с одного процессора на другой осуществляются в соответствии со структурой Σ. Кроме того, выполнены ограничения, накладываемые на объем памяти процессоров и их привязке к заданиям. Допустимым решением задачи будем называть пару (Σ, R(Σ)), где Σ – допустимая структура вычислительной системы, R(Σ) – допустимое расписание при структуре Σ, а стоимостью этого решения будет стоимость структуры Σ.
Требуется определить, существует ли в поставленной задаче допустимое решение (Σ, R(Σ)), и в случае положительного ответа найти допустимое решение минимальной стоимости.
Данная задача является NP-трудной. Действительно, используя схему доказательства, аналогичную той, которая применена в [14], можно показать, что известная NP-трудная задача о разбиении [15] полиномиально сводится к рассматриваемой задаче.
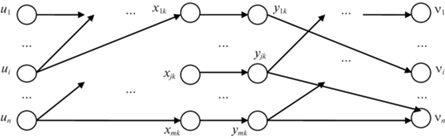
2. Решение задачи с помощью сетевого моделирования. Будем рассматривать n-продуктовую потоковую сеть G1 = (V1, A1), где V1 = {ui, ${{{v}}_{i}}$, xjk, yjk, i = $\overline {1,n} $, j = $\overline {1,m} $, k = $\overline {1,T} $} – множество узлов (ui и ${{{v}}_{i}}$ – источник и сток i-го продукта соответственно), A1 = {(ui, xjk), i = $\overline {1,n} $, k ∈ [bi, fi], j ∈ M(i, k); (yjk, ${{{v}}_{i}}$), i = $\overline {1,n} $, k ∈ [bi, fi], j ∈ M(i, k); (xjk, yjk), i = $\overline {1,n} $, j = $\overline {1,m} $, k = $\overline {1,T} $; (${{y}_{{{{j}_{1}}{{k}_{1}}}}}$, ${{y}_{{{{j}_{2}}{{k}_{2}}}}}$), j1, j2 = $\overline {1,m} $, k1, k2 = = $\overline {1,T} $, k1 < k2, I(j1, k1, j2, k2) = 1} – множество дуг. Узлы xjk и yjk обозначают процессор j и соответственно начало временного отрезка Δk и его окончание. Фрагмент сети G1 изображен на рис. 1.
В сети G1 будем искать n-продуктовый поток gi(a, b), i = $\overline {1,n} $, (a, b) ∈ A1, принимающий значения 0 или 1, такой, что ровно одна единица потока i-го продукта доставляется из источника ui в сток ${{{v}}_{i}}$. Смысловое значение единицы потока gi по дугам сети G1 указано в таблице.
Если по дуге (xjk, yjk) проходит единица потока gi, то это означает, что в интервале Δk задание i выполняется процессором j, объем работы которого составляет pj, и эту величину следует прибавить к суммарному объему работы процессоров по исполнению задания i. Если единица потока gi проходит по дуге (${{y}_{{{{j}_{1}}{{k}_{1}}}}}$, ${{x}_{{{{j}_{2}}{{k}_{2}}}}}$), то это означает, что, во-первых, данная дуга должна быть включена в структуру вычислительной системы и, во-вторых, из суммарного объема работы процессоров по выполнению задания i следует вычесть величину q(j1, k1, j2, k2). Таким образом, каждому n-продуктовому потоку gi(a, b) в сети G1 соответствует некоторая допустимая структура Σ вычислительной системы и некоторое расписание R(Σ) выполнения множества заданий N. Будем искать такой n-продуктовый поток, для которого стоимость структуры Σ минимальна, а соответствующее расписание R(Σ) является допустимым.
3. Необходимые и достаточные условия существования допустимого решения. Задачу построения допустимой структуры минимальной стоимости и поиска допустимого расписания сведем к задаче булева линейного программирования. Запишем условия, накладываемые на поток gi(a, b) и сформулированные в разд. 2, в виде минимизации линейного функционала и линейных ограничений с булевыми переменными gi(a, b), i = $\overline {1,n} $, (a, b) ∈ A1:
(3.2)
$\sum\limits_{k = {{b}_{i}}}^{{{f}_{i}}} {\sum\limits_{j \in M(i,k)}^{} {{{g}_{i}}({{u}_{i}},{{x}_{{jk}}}) = 1,\quad i = \overline {1,n} ,} } $(3.3)
$\sum\limits_{k = {{b}_{i}}}^{{{f}_{i}}} {\sum\limits_{j \in M(i,k)}^{} {{{g}_{i}}({{y}_{{jk}}},{{{v}}_{i}}) = 1,\quad i = \overline {1,n} ,} } $(3.4)
$\sum\limits_{i = 1}^n {{{g}_{i}}({{x}_{{jk}}},{{y}_{{jk}}}) \leqslant 1,\quad j = \overline {1,m} ,\quad } k = \overline {1,T} ,$(3.8)
$\sum\limits_{i = 1}^n {{{g}_{i}}({{x}_{{jk}}},{{y}_{{jk}}}){{c}_{i}} \leqslant {{B}_{{jk}}},\quad j = \overline {1,m} {\kern 1pt} } ,\quad k = \overline {1,T} ,$Данная система содержит O(n(mT)2) булевых переменных и O(nmT) линейных ограничений.
Поясним физический смысл выражений (3.1)–(3.9). Равенства (3.2), (3.3) означают, что суммарная величина i-го продукта, исходящего из источника ui и соответственно входящего в сток ${{{v}}_{i}}$, i = = $\overline {1,n} $, равна единице. В силу (3.4) суммарная величина потока по каждой дуге (xjk, yjk), j = $\overline {1,m} $, k = $\overline {1,T} $, не превосходит единицы. Равенства (3.5), (3.6) гарантируют сохранение потока i-го продукта во внутренних узлах xjk и yjk соответственно, i = $\overline {1,n} $, j = $\overline {1,m} $, k = $\overline {1,T} $. Согласно неравенства (3.7), суммарный объем работы процессоров при выполнении задания i не меньше wi, i = $\overline {1,n} $. Величина, стоящая в левой части соотношения (3.8), равна объему памяти, требуемой для работы, выполняемой j-м процессором в интервале Δk, j = $\overline {1,m} $, k = $\overline {1,T} $. Это значение не должнo превосходить доступного объема оперативной памяти j-го процессора в интервале Δk, т.е. величины Bjk. Согласно (3.9), в сети G1 будут найдены такие n непересекающихся путей, что величина потока i-го продукта по i-му пути равна единице. Минимизация выражения (3.1) обеспечивает построение структуры вычислительной системы минимальной стоимости.
Л е м м а 1. Для существования допустимого решения (Σ, R(Σ)) минимальной стоимости в исходной задаче необходимо и достаточно наличия решения в задаче булева линейного программирования (3.1)–(3.9).
Д о к а з а т е л ь с т в о. 1. Необходимость. Если в исходной задаче существует допустимое решение (Σ, R(Σ)), то при структуре Σ для каждого i = $\overline {1,n} $ расписание исполнения i-й работы описывает путь из ui в ${{{v}}_{i}}$ в сети G1, по которому можно пропустить единицу потока i-го продукта, причем все эти n путей не пересекаются. Все работы полностью завершаются в своих директивных интервалах и, кроме того, не нарушаются ограничения по требуемой памяти. Это обеспечивает выполнение условий (3.2)–(3.9). Поскольку структура Σ имеет минимальную стоимость, то верно условие (3.1).
2. Достаточность. В силу соотношений (3.2)–(3.6), (3.9) в сети G1 существуют n непересекающихся путей из ui в ${{{v}}_{i}}$, i = $\overline {1,n} $, таких, что вдоль i-го из них протекает единица i-го продукта, благодаря чему существует некоторое расписание для комплекса заданий N, согласно которому каждая работа выполняется в своем директивном интервале. Согласно (3.7), каждое задание исполняется полностью, а из (3.8) следует, что не нарушаются ограничения по памяти. Таким образом, это расписание является допустимым. Дуги (yjk, xjk), по которым поток равен единице, образуют искомую структуру Σ. Поскольку верно условие (3.1), то стоимость этой структуры минимальна. Лемма доказана.
При выполнении условий (3.1)–(3.9) решение (Σ, R(Σ)) исходной задачи строится следующим образом. Если gi(${{y}_{{{{j}_{1}}{{k}_{1}}}}}$, ${{x}_{{{{j}_{2}}{{k}_{2}}}}}$) = 1 при некотором i = $\overline {1,n} $, то в проектируемую структуру Σ системы необходимо включить связь, обеспечивающую возможность переключения задания i с процессора j1 в момент времени ${{t}_{{{{k}_{1}}}}}$ на процессор j2 в момент времени ${{t}_{{{{k}_{2}} - 1}}}$. Равенство gi(xjk, yjk) = 1 означает, что, согласно допустимому расписанию R(Σ), в интервале Δk работа i исполняется процессором j.
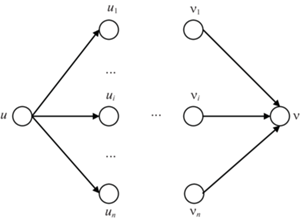
4. Упрощенный вид необходимых условий существования допустимого решения. В этом разделе предполагается, что память, требуемая для выполнения каждого задания, не превосходит объема памяти любого процессора. В таком случае неравенства (3.8) верны и их можно опустить. Для данного частного случая сформулируем упрощенный вид необходимых условий существования допустимого решения. Для этого построим однопродуктовую потоковую сеть G2 = (V2, A2) следующим образом. Добавим к сети G1 два узла (источник u и сток ${v}$) и дуги (u, ui) и (${{{v}}_{i}}$, ${v}$), i = $\overline {1,n} $. Таким образом, V2 = V1 ∪ {u, ${v}$}, A2 = A1 ∪ {(u, ui), (${{{v}}_{i}}$, ${v}$), i = $\overline {1,n} $}. Фрагмент сети G2 изображен на рис. 2. Дуги (a, b) ∈ A2 сети G2 имеют три параметра: нижнюю и верхнюю границы потока (соответственно L(a, b) и U(a, b)), а также стоимость C(a, b) единицы потока. Значения этих параметров определим следующим образом: L(a, b) = 0, U(a, b) = 1 при всех (a, b) ∈ A2; C(xjk, yjk) = pj, C(${{y}_{{{{j}_{1}}{{k}_{1}}}}}$, ${{x}_{{{{j}_{2}}{{k}_{2}}}}}$) = –q(j1, k1, j2, k2), C(a, b) = 0 для всех остальных дуг (a, b) ∈ A2. Пусть h(a, b), (a, b) ∈ ∈ A2 – некоторый однопродуктовый поток в сети G2, а величина
– его стоимость.Л е м м а 2. Для существования допустимого решения (Σ, R(Σ)) в рассматриваемом частном случае исходной задачи необходимо наличие однопродуктового потока h в сети G2, для которого справедливо неравенство
Д о к а з а т е л ь с т в о. Если существует допустимое решение (Σ, R(Σ)), то в силу леммы 1 для некоторого n-продуктового потока g в сети G1 верны соотношения (3.2)–(3.7), (3.9). Определим однопродуктовый поток h в сети G2 следующим образом:
Из (3.2)–(3.6) и (3.9) следует, что h является потоком в сети G2, т.е. удовлетворяет ограничениям сверху и снизу по каждой дуге, а также условию сохранения в каждом внутреннем узле сети G2. Кроме того, из (3.7) следует (4.1). Лемма доказана.
Для проверки выполнения условия леммы 2 можно воспользоваться известным алгоритмом нахождения потока минимальной стоимости в сети следующим образом [15]. Заменим знаки определенных выше стоимостей потоков по дугам на противоположные. В сети G2 найдем однопродуктовый поток $\bar {h}$ минимальной стоимости и пусть C($\bar {h}$) – его стоимость. Тогда если
то условие леммы 2 и необходимые условия существования допустимого решения верны. В противном случае условие леммы 2 и необходимые условия существования допустимого решения не выполнены.Поскольку поиск однопродуктового потока минимальной стоимости в сети G2 существенно проще решения задачи булева линейного программирования (3.1)–(3.9), то решение исходной задачи можно проводить по следующей схеме. Сначала проверить выполнение условия леммы 2. И только в случае положительного результата перейти к проверке условий леммы 1.
Заключение. Решена задача оптимизации структуры многопроцессорной вычислительной системы реального времени и построения допустимого расписания комплекса работ для найденной структуры. Предполагается, что заданы ограничения на связи между процессорами, на их привязку к заданиям, на объемы оперативной памяти, а также на временные ограничения, определяемые директивными интервалами. Получены необходимые и достаточные условия существования допустимой структуры минимальной стоимости и допустимого расписания работ в виде системы булевых линейных соотношений. Методика решения основана на сведении исходной задачи к многопродуктовой потоковой задаче в сети.
Таблица 1.
Смысловое значение единицы потока gi по дугам сети G1
| Дуга (a, b)∈ A1 | Смысловое значение единицы потока gi(a, b) |
| (ui, xjk) | Начало выполнения работы i процессором j в момент времени tk– 1 |
| (xjk, yjk) | Выполнение работы i процессором j в интервале Δk |
| (${{y}_{{{{j}_{1}}{{k}_{1}}}}}$, ${{x}_{{{{j}_{2}}{{k}_{2}}}}}$) | Переключение работы i с процессора j1 в момент времени ${{t}_{{{{k}_{1}}}}}$ на процессор j2 в момент времени ${{t}_{{{{k}_{2}} - 1}}}$ |
| (yjk, ${{{v}}_{i}}$) | Завершение выполнения работы i процессором j в момент времени tk |
Список литературы
Глонина А.Б., Балашов В.В. О корректности моделирования модульных вычислительных систем реального времени с помощью сетей временных автоматов // Моделирование и анализ информационных систем. 2018. Т. 25. № 2. С. 174–192.
Глонина А.Б. Обобщенная модель функционирования модульных вычислительных систем реального времени для проверки допустимости конфигураций таких систем // Вестник ЮУрГУ. Сер. Вычисл. математика и информатика. 2017. Т. 6. № 4. С. 43–59.
Глонина А.Б. Инструментальная система проверки выполнения ограничений реального времени для конфигураций модульных вычислительных систем // Вестн. МГУ. Сер. 15. Вычисл. математика и кибернетика. 2020. № 3. С. 16–29.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Один подход к анализу возможных структурных повреждений в многопродуктовых сетевых системах // ЖВМ и МФ. 2019. Т. 59. № 9. С. 1626–1638.
Малашенко Ю.Е., Назарова И.А., Новикова Н.М. Анализ кластерных повреждений в сетевых системах // Изв. РАН. ТиСУ. 2020. Т. 60. № 2. С. 338–348.
Малашенко Ю.Е., Новикова Н.М. Анализ многопользовательских сетевых систем с учетом неопределенности // Изв. РАН. ТиСУ. 1998. № 2. С. 134–146.
Ефимов С.Н., Терсков В.А., Ярков К.В., Серикова О.Ю. Оптимизация затрат при проектировании аппаратно-программного комплекса системы реального времени // Научно-технический вестник Поволжья. 2021. № 4. С. 35–37.
Mironov A.A., Tsurkov V.I. Network Models with Fixed Parameters at the Communication Nodes. 1 // J. Computer and Systems Sciences International. 1994. V. 32. № 6. P. 1–11.
Mironov A.A., Tsurkov V.I. Network Models with Fixed Parameters at the Communication Nodes. 2 // J. Computer and Systems Sciences International. 1995. V. 33. № 3. P. 107–116.
Mironov A.A., Levkina T.A., Tsurkov V.I. Minimax Estimations of Arc Weights in Integer Networks with Fixed Node Degrees // Applied and Computational Mathematics. 2009. V. 8. № 2. P. 216–226.
Mironov A.A., Tsurkov V.I. Class of Distribution Problems with Minimax Criterion // Doklady Akademii Nauk. 1994. V. 336. № 1. P. 35–38.
Фуругян М.Г. Некоторые алгоритмы анализа и синтеза многопроцессорных вычислительных систем реального времени // Программирование. 2014. № 1. С. 36–44.
Мищенко А.В., Кошелев П.С. Оптимизация управления работами логистического проекта в условиях неопределенности // Изв. РАН. ТиСУ. 2021. № 4. С. 86–101.
Фуругян М.Г. Планирование вычислений в многопроцессорных АСУ реального времени с дополнительным ресурсом // АиТ. 2015. № 3. С. 144–150.
Корте Б., Фиген Й. Комбинаторная оптимизация. Теория и алгоритмы. М.: МЦНМО, 2015.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления