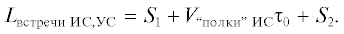Известия РАН. Теория и системы управления, 2022, № 3, стр. 104-115
КОНСТРУИРОВАНИЕ ТРАЕКТОРИЙ ВСТРЕЧИ В БАЗАХ ЗНАНИЙ БОРТОВЫХ ОПЕРАТИВНО-СОВЕТУЮЩИХ ЭКСПЕРТНЫХ СИСТЕМАХ ЭТАПА ПОЛЕТА
С. К. Галиханов a, *, Б. Е. Федунов a, b, **, М. А. Шигина a, ***
a МАИ (Национальный исследовательский ун-т)
Москва, Россия
b ГНЦ ФГУП ГосНИИАС
Москва, Россия
* E-mail: galikbwat@gmail.com
** E-mail: boris_fed@gosniias.ru
*** E-mail: shiginamarina@yandex.ru
Поступила в редакцию 15.10.2021
После доработки 16.11.2021
Принята к публикации 31.01.2022
- EDN: APTGSX
- DOI: 10.31857/S0002338822030076
Аннотация
Предлагается новый алгоритм конструирования траектории встречи самолета с другим летательным аппаратом, летящим по прямолинейной траектории с меньшей скоростью. Траектория формируется для профиля полета “набор высоты–полет на заданной высоте (полка)–снижение на точку встречи”. Необходимые характеристики этапов “набор высоты”, “полка” и “снижение” для конструирования траектории до момента встречи определяются в результате обработки летного эксперимента.
Введение. В базе знаний некоторых бортовых оперативно-советующих экспертных систем (БОСЭС) — этапа полета требуется сконструировать траекторию встречи истребителя (ИС) с ударным самолетом (УС), летящим на постоянной высоте с постоянным вектором скорости [1].
Траекторию встречи следует определять в классе траекторий со следующими характеристиками:
траектория имеет профиль — “набор заданной высоты (высота “полки”)–полет на “полке”–снижение на высоту полета УС”;
начальная и конечная высота ИС равна высоте УС;
проекция траектории ИС на горизонтальную плоскость является прямой линией.
Приводятся процедуры конструирования названных типов траекторий и результаты математического моделирования имитационного моделирования работы фрагмента базы знаний БОСЭС, который реализован в программно-математическом комплексе (ПМК).
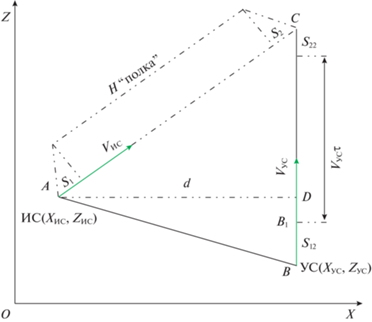
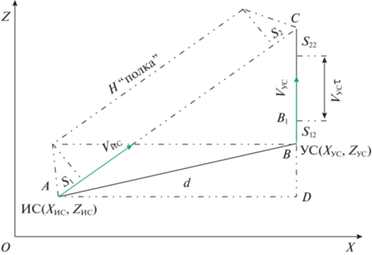
1. Постановка задачи конструирования траекторий встречи. Введем прямоугольную систему координат на горизонтальной плоскости полета УС (рис. 1). Вертикальная ось ОZ направлена параллельно траектории УС, горизонтальная ось ОХ – от ИС, находящегося слева от УС, в сторону УС. Начало координат выбрано слева от ИС и ниже его. Отметим начальное расположение ИС (находится в точке А) и УС (находится в точке В).
Спроектируем на горизонтальную плоскость траекторию ИС (отрезок АС) и отметим:
в начале этой проекции проекцию участка траектории набора ИС высоты “полки”, обозначив его S1, и зафиксируем для него время набора высоты ∆t1;
в конце этой проекции проекцию участка траектории снижения ИС с высоты “полки” на высоту УС, обозначив его S2, и зафиксируем для этого участка полета время снижения ∆t2.
Найдем соответствующие длины траекторий УС: S12 = VУС∆t1 и S22 = VУС∆t2, отложив в начале траектории УС отрезок S12 (на рис. 1 отрезок ВВ1) и в конце траектории УС в окрестности точки встречи – отрезок S22 (отрезок С1С).
Определение длины проекции на горизонтальную плоскость участка траектории полета ИС на “полке” (искомое время полета ИС на “полке” обозначим через $\tau $) и длины соответствующего ему участка В1С1 траектории УС проведем, используя прямоугольный треугольник ACD, полученный при проектировании точки А на траекторию УС.
Использование прямоугольного треугольника (“треугольника $\tau $”) для определения длин упомянутых отрезков зависит от взаимного начального расположения ИС и УС и расположения точек В1 и D.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}}$, находим:
(1.1)
$\begin{array}{*{20}{c}} {AC = \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{V}_{{{\text{ИС}}}}}\tau ,} \\ {AD = {{X}_{{{\text{УС}}}}} - {{X}_{{{\text{ИС}}}}} = d,} \\ {DC = {{S}_{{22}}} + {{V}_{{{\text{УС}}}}}\tau + {{B}_{1}}D.} \end{array}$В таком случае время полета ИС на “полке” $\tau $ определим из решения соответствующего квадратного уравнения $a{{\tau }^{2}} + b\tau + c = 0$ полученного из $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}}$ и с учетом системы (1.1). Далее вычисляются корни квадратного уравнения ${{\tau }_{{1,2}}}$ и выбирается наименьший положительный.
Причем координаты точки встречи ИС с УС соответственно равны:
(1.2)
$\begin{array}{*{20}{c}} {{{X}_{{{\text{т}}{\text{.в}}}}} = {{X}_{{{\text{УС}}}}};} \\ {{{Z}_{{{\text{т}}{\text{.в}}}}} = {{Z}_{{{\text{УС}}}}} + {{S}_{{12}}} + {{V}_{{{\text{УС}}}}}\tau + {{S}_{{22}}}.} \end{array}$Время полета ИС до встречи с УС соответствует сумме времени выхода ИС на заданную “полку” ∆t1, времени полета на “полке” τ, времени ∆t2 снижения ИС на высоту УС. Заметим, что в описанных вычислениях не используется математическая модель ИС на этапах “набор высоты” и “спуск”. Необходимые для расчетов проекции длины участков S1, S2 и минимального времени ИС для прохождения этих этапов ∆t1 могут быть получены на основании результатов летных испытаний.
2. Формирование исходных данных для конструирования траекторий ИС. Пусть заданы экспериментальные зависимости траектории ИС типа “набор заданной высоты – полет на заданной высоте – снижение”: изменение высоты полета по времени полета и изменение скорости полета по этой траектории по времени полета (зависимости взяты из [2]).
На рис. 2 представлены графики зависимости скорости и высоты полета от времени для траектории самолета, проекция которой на горизонтальную плоскость X, Z – прямая линия, а проекция траектории на вертикальную плоскость состоит из участков: полет на начальной высоте Н0, набор заданной высоты (высота “полки”), полет на заданной высоте с постоянной скоростью (полет на “полке”), спуск на начальную высоту Н0.
Рис. 2.
Зависимости скорости и высоты от времени для траектории встречи ИС с УС (зависимости взяты из [2])

Для конструирования в базах знаний БОСЭС-этапов полета таких траекторий удобно аппроксимировать экспериментальные траектории следующим образом: участки набора и спуска представлять временем выполнения участков и проекцией их длины на горизонтальную плоскость, участок полета на “полке” считать выполняемым с постоянной вертикальной скоростью, время участка снижения совпадает с экспериментальным.
Разобьем временную ось экспериментальных зависимостей на отрезки, на которых вертикальная скорость самолета Vy не изменяется (нулевая или постоянная с любым знаком), а скорость по траектории V или не изменяется, или изменяется по линейному закону.
На каждом таком временном участке определим проекцию скорости самолета Vxz на горизонтальную плоскость и рассчитаем: (1) длину горизонтальной проекции траектории самолета, соответствующей этому временному участку, и (2) время прохождения самолетом этого участка.
Суммируя длины и продолжительности всех временных участков на наборе высоты, получим необходимые в базе знаний бортовой интеллектуальной системы (БИС) полетного задания длину проекции траектории набора высоты на горизонтальную плоскость и время набора. Аналогично определим эти величины и для траектории спуска.
Этап “Набор высоты” состоит из нескольких участков.
Участок 1, $t \in \left[ {{{t}_{1}},{{t}_{2}}} \right]$:
Участок 2, $t \in \left[ {{{t}_{2}},{{t}_{3}}} \right]$:
Участок 3, $t \in \left[ {{{t}_{{3.2}}},{{t}_{4}}} \right]$:
Участок 4, $t \in \left[ {{{t}_{4}},{{t}_{5}}} \right]$:
Участок 5, $t \in \left[ {{{t}_{5}},{{t}_{6}}} \right]$:
Итог по этапу “Набор высоты”:
Этап “Полка”, $t \in \left[ {{{t}_{6}},{{t}_{7}}} \right]$:
Этап “Снижение” состоит из двух участков.
Участок 1:
Участок 2:
Итог по этапу “Снижение”:
Таким образом на этапе “Набор высоты” истребитель за 255 с преодолевает 107025.6 м, при этом его высота полета меняется с 4000 до 16 000 м. В то время как на этапе “Снижение” за 130 с преодолевает 68 606 м, при этом его высота полета меняется с 16 100 до 4000 м.
3. Решение конструирования траекторий ИС типа “набор высоты–полет на заданной высоте (высота “полки”)–снижение”, обеспечивающих встречу ИС с УС.
3.1. Определение “треугольника τ” при начальной ZИС больше начальной ZУС. Здесь возможны три случая использования прямоугольного треугольника для определения времени полета ИС на “полке”.
Случай I. Точка В1 находится выше точки D (рис. 3).
Получим следующие начальные положения: ZИС > ZУС и (ZУС + S12) > ZИС.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}}$, находим:
(3.1)
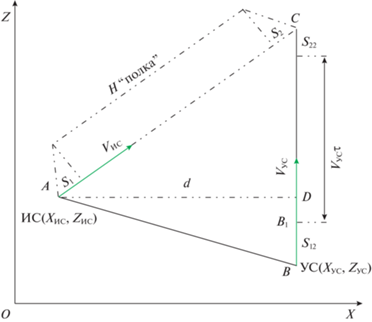
$\begin{array}{*{20}{c}} {AC = \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{V}_{{{\text{ИС}}}}}\tau ,} \\ {AD = {{X}_{{{\text{УС}}}}} - {{X}_{{{\text{ИС}}}}} = d,} \\ {DC = {{S}_{{22}}} + {{V}_{{УС}}}\tau + {{В}_{1}}D = {{S}_{{22}}} + {{V}_{{{\text{УС}}}}}\tau + {{Z}_{{УС}}} + {{S}_{{12}}}--{{Z}_{{{\text{ИС}}}}} = {{\Sigma }_{2}} + {{V}_{{{\text{УС}}}}}\tau ,} \\ {{\text{где}}\quad ~{{\Sigma }_{2}} = {{S}_{{22}}} + {{Z}_{{{\text{УС}}}}} + {{S}_{{12}}}--{{Z}_{{{\text{ИС}}}}}.} \end{array}~$Случай II. Точка В1 находится ниже точки D (рис. 4).
Получим следующие начальные положения: ZИС > ZУС и (ZУС+S12) < ZИС.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}},$ находим:
(3.2)
$\begin{array}{*{20}{c}} {AC = \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{V}_{{{\text{ИС}}}}}\tau ,} \\ {AD = {{X}_{{{\text{УС}}}}} - {{X}_{{{\text{ИС}}}}} = d,} \\ {DC = {{S}_{{22}}} + {{V}_{{{\text{УС}}}}}\tau - {{В}_{1}}D = {{S}_{{22}}} + {{V}_{{{\text{УС}}}}}\tau --\left[ {{{Z}_{{{\text{ИС}}}}}--{{S}_{{12}}}--{{Z}_{{УС}}}} \right]~.} \end{array}$Случай III. Точка В1 совпадает с точкой D.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}},$ находим:
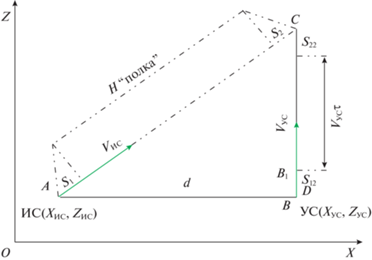
3.2. Определение “треугольника $\tau $” при начальной ZИС, равной начальной ZУС. Геометрическое представление задачи показано на рис. 5.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}}$, находим:
(3.3)
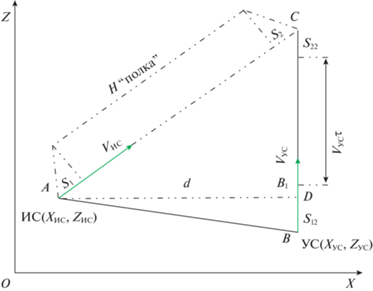
$\begin{array}{*{20}{c}} {AC = \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{V}_{{{\text{ИС}}}}}\tau ,} \\ {AD = {{X}_{{{\text{УС}}}}} - {{X}_{{{\text{ИС}}}}} = d,} \\ {DC = {{S}_{{12}}} + {{V}_{{{\text{УС}}}}}\tau + {{S}_{{22}}}.} \end{array}$3.3. Определение “треугольника $\tau $” при начальной ZИС, меньшей начальной ZУС. Геометрическое представление задачи показано на рис. 6.
Из прямоугольного треугольника АСD, учитывая $A{{C}^{2}} = A{{D}^{2}} + D{{C}^{2}}$, находим:
(3.4)
$\begin{array}{*{20}{c}} {AC = \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{V}_{{{\text{ИС}}}}}\tau ,} \\ {AD = {{X}_{{{\text{УС}}}}} - {{X}_{{{\text{ИС}}}}} = d,} \\ {DC = {{S}_{{12}}} + {{V}_{{{\text{УС}}}}}\tau + {{S}_{{22}}} + {{Z}_{{{\text{УС}}}}}--{{Z}_{{{\text{ИС}}}}}.} \end{array}$3.4. Определение времени полета ИС на заданной “полке”. Для всех вариантов “треугольника $\tau $” справедливы единые формулы расчета коэффициентов соответствующего квадратного уравнения $a{{\tau }^{2}} + b\tau + c = 0$:
коэффициент при $\tau $2: $[V_{{{\text{ИС}}}}^{2} - V_{{{\text{УС}}}}^{2}]$,
коэффициент при $\tau $1: $\left[ {2\left( {{{S}_{1}} + {{S}_{2}}} \right){{V}_{{{\text{ИС}}}}}--2\left[ {{{S}_{{11}}} + {{S}_{{12}}} + {{Z}_{{{\text{УС}}}}} - {{Z}_{{{\text{ИС}}}}}} \right]{{V}_{{{\text{УС}}}}}} \right]$,
коэффициент при τ0: $[{{\left( {{{S}_{1}} + {{S}_{2}}} \right)}^{2}} - {{\left[ {{{S}_{{11}}} + {{S}_{{12}}} + {{Z}_{{{\text{УС}}}}} - {{Z}_{{{\text{ИС}}}}}} \right]}^{2}} - {{\left[ {{{X}_{{УС}}} - {{X}_{{{\text{ИС}}}}}} \right]}^{2}}]$.
Напомним, что в зависимостях (3.1)–(3.4), VИС – скорость полета ИС на заданной “полке”, а наименьший положительный корень квадратного уравнения τ0 определяет время полета ИС на “полке”.
Тогда время полета ИС до встречи с УС
координаты точки встречи ИС с УС(3.6)
$\begin{array}{*{20}{c}} {{{X}_{{{\text{т}}{\text{.в}}}}} = {{X}_{{{\text{УС}}}}},} \\ {{{Z}_{{{\text{т}}{\text{.в}}}}} = {{Z}_{{{\text{УС}}}}} + {{V}_{{{\text{УС}}}}}{{T}_{{{\text{встречи}}}}},} \end{array}$4. Результаты имитационного моделирования решения задачи конструирования траектории встречи для базы знаний БОСЭС – “Возврат в строй”. В качестве основного инструмента отработки предложенного алгоритма было выбрано имитационное моделирование [3]. В рамках этого подхода был разработан ПМК, где ключевое место в решении задачи конструирования траектории отводится фрагменту десктопного приложения “Конструирование траектории встречи” для базы знаний БОСЭС – “Возврат в строй $\tau $”.
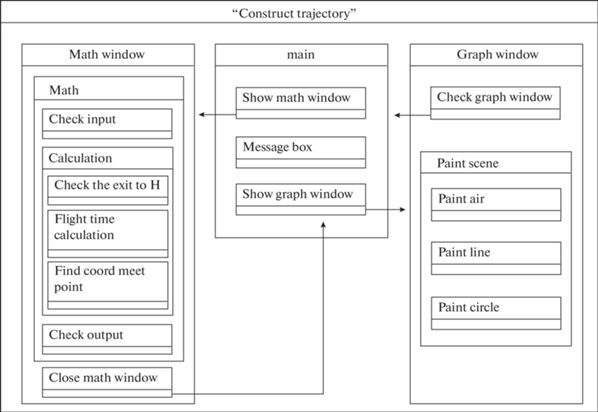
Десктопное приложение11 реализовано на языке программирования C++ (стандарт 2014 г.) с использованием кроссплатформенной библиотеки Qt. На рис. 6 приведена диаграмма взаимодействия основных объектов десктопного приложения. На рис. 7 “Math window” – компонент интерфейса, обеспечивающий работу с входными данными и расчет выходных параметров, “Graph window” – компонент интерфейса, обеспечивающий построение “Профиля полета” и “Маршрута полета”, согласно полученным в “Math window” параметрам, “main” – компонент, связывающий работу “Math window” и “Graph window” в параллели и независимо друг от друга, “Calculation” – класс, отвечающий за выполнение расчетов по приведенному в разд. 1–3 алгоритму; “Check the exit to H” – блок проверки возможности выхода ИС на “полку”; “Flight time calculation” – блок расчета времени полета ИС на “полке”; “Find coord meet point” – блок расчета координат точки встречи; “Check input” – блок проверки возможности выхода ИС на “полку”; “Check output” – блок проверки возможности выхода ИС на “полку”; “Paint scene” – класс-компоновщик объектов, входящих в графики “Профиля полета” и “Маршрута полета”; “Paint air” – блок, формирующий объект сцены “самолет” с заданными координатами и передающий сформированный объект на компоновку; “Paint line” – блок, формирующий объект сцены и передающий сформированный объект на компоновку; прямая, соединяющая две точки с заданными координатами; “Paint circle” – блок, формирующий объект сцены “точка” с заданными координатами и передающий сформированный объект на компоновку; “Message box” – класс, формирующий информационное послание пользователю о выполнении выбранного действия.
Исходя из построенной диаграммы взаимодействий выделено три основных блока математики фрагмента “Конструирование траектории встречи”:
1) “Проверка возможности выхода на заданную H“полки” ИС”;
2) “Расчет времени полета ИС на заданной “полке””;
3) “Расчет координат точки встречи и длина проекции траектории ИС на горизонтальную плоскость”.
В блоке 1 конструируется траектория встречи ИС с УС без выхода ИС на “полку”: полет ИС на высоте УС со скоростью на заданной “полке” V “полки” ИС. Определяется длина траектории истребителя сопровождения Lбез “полки” ИС:
в формулах разд. 3.4 обнуляются ${{S}_{1}} + {{S}_{2}} = 0,~~{{S}_{{21}}} + {{S}_{{22}}} = 0$,
из квадратного уравнения определяется время ${{\tau }_{0}}$ полета ИС,
находится длина 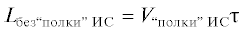 .
.
Строить траекторию ИС с заданной полкой возможно, если 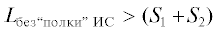 . В этом случае переходим на следующий блок программы. В противном же случае выдается
сообщение, сигнализирующее о невозможности выхода на “полку”.
. В этом случае переходим на следующий блок программы. В противном же случае выдается
сообщение, сигнализирующее о невозможности выхода на “полку”.
В блоках 2 и 3 реализованы расчеты по приведенным в разд. 3.4 зависимостям.
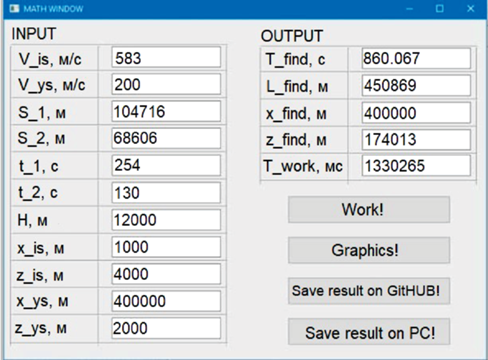
Для конструирования траектории требуются следующие исходные данные:
расположение ИС и УС: координаты XИС, ZИС, XУС, ZУС в описанной выше системе координат,
высота ИС и высота УС и его скорость VУС,
заданная высота “полки” H“полки” ИС и скорость V“полки” ИС,
полученная с летного эксперимента характеристика этапа набора ИС высоты H“полки” ИС: S1, ∆t1,
найденная с летного эксперимента характеристика этапа снижения ИС с высоты H“полки” ИС до высоты полета УС: S2, ∆t2.
Результатами работы десктопного приложения являются:
время полета ИС до встречи с УС ${{T}_{{{\text{встречи}}}}}$,
координаты точки встречи Xт.в, Zт.в,
длина проекции траектории ИС на горизонтальную плоскость ${{L}_{{{\text{встречи\;ИС,\;УС}}}}}$.
Эксперимент проводился на персональном компьютере с техническими характеристиками: оперативное запоминающее устройство: 12 Гб; центральный процессор: Intel® Core™ i5-7200U CPU @ 2.50GHz × 4; графический процессор: Mesa Intel® HD Graphics 620 (KBL GT2).
Пример конструирования траектории встречи ИС с УС с “полкой” на $H = 12~$ км приведен в табл. 1 и 2.
Таблица 1.
Характеристики набора ИС высоты “полки” $H = 12~$ км и снижения (данные п. 1)
| Этап полета ИС | $S,~$ м | ∆t, с |
|---|---|---|
| Набор высоты c H = HУС | S1 = 104 716 | ∆t1 = 255 |
| Расстояние, преодолеваемое УC за время набора ИС высоты H = HУС | S21 = VУС∆t1 | ∆t1 |
| Снижение на высоту H = HУС | S2 = 68 606 | ∆t2 = 130 |
| Расстояние, преодолеваемое УC за время снижения ИС на высоту H = HУС | S21 = VУС∆t2 | ∆t2 |
Таблица 2.
Варианты различного расположения начального положения УС относительного одного и того же начального положения ИС (различные “треугольники τ”)
| Вариант | Самолет | $X$ | $Z$ | $V$ | $V$ |
|---|---|---|---|---|---|
| м | м/с | ||||
| I | ИС | 1000 | 4000 | 583 | – |
| I | УС | 400 000 | 2000 | – | 200 |
| II | ИС | 1000 | 4000 | 583 | – |
| II | УС | 400 000 | 4000 | – | 200 |
| III | ИС | 1000 | 4000 | 583 | – |
| III | УС | 400 000 | 7000 | – | 200 |
Результаты расчета вариантов начального расположения ИС и УС с помощью сформированного десктоп приложения представлены в табл. 3.
Таблица 3.
Результаты расчета вариантов начального расположения ИС и УС, указанных в табл. 2
| Вариант | Время полета ИС до встречи с УС Tвстречи, с | Координаты точки встречи xт.в, м, zт.в, м | Длина проекции траектории ИС на горизонтальную плоскость Lвстречи ИС, УС, м | Время расчета, мс |
|---|---|---|---|---|
| I | 860.067 | x = 400 000, | 450 869 | ~0.84 |
| z = 174 013 | ||||
| II | 861.852 | x = 400 000, | 451 910 | ~0.68 |
| z = 176 370 | ||||
| III | 864.547 | x = 400 000, | 453 481 | ~0.16 |
| z = 179 909 |
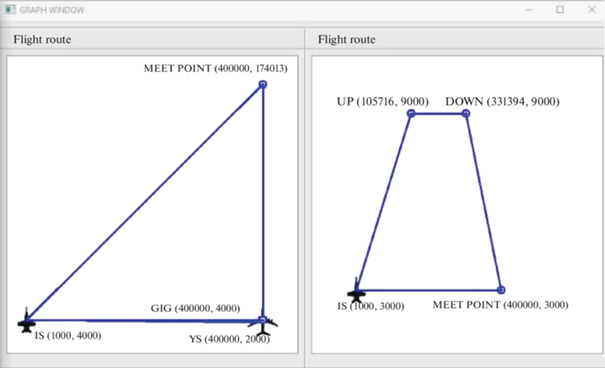
На рис. 8 представлены исходные данные для расчета траектории встречи (рис. 9). Заметим, что изображенные на рис. 9 траектории встречи и профили полета сохраняют горизонтальный и вертикальный масштабы независимо друг от друга.
Заключение. Разработан новый алгоритм “Конструирования траектории встречи” в базе знаний бортовой
оперативно-советующей экспертной системы этапа полета, обеспечивающий расчет траектории
до момента встречи носителя БОСЭС с прямолинейно летящим самолетом, скорость которого
меньше скорости полета носителя БОСЭС. Данный алгоритм отличается от существующих
отсутствием итерационной процедуры определения момента “схода с “полки”” и не содержит
аналитической модели носителя БОСЭС на этапах “подъем” и “спуск”, что значительно
упрощает его реализацию. Вместо аналитической модели носителя в базу знаний БОСЭС
включается специальная база данных (S, ∆t) конкретного носителя этой БОСЭС, определенные для характерных для него значений
 и различных наборов условий начала участка набора (V, H) и условий окончания участка спуска (V, H).
и различных наборов условий начала участка набора (V, H) и условий окончания участка спуска (V, H).
Создан ПМК моделирования, на котором получены характеристики траекторий встречи (время полета до момента встречи, координаты точки встречи; длина проекции траектории на горизонтальную плоскость), подтверждающие работоспособность во всех возможных вариантах расположения УС и ИС и обосновывающие возможность применения предложенного алгоритма.
Список литературы
Федунов Б.Е. Бортовые интеллектуальные системы тактического уровня для антропоцентрических объектов (примеры для пилотируемых летательных аппаратов). М.: ДеЛибри, 2018. 246 с.
Гревцов Н.М., Перчиц С.Н., Федунов Б.Е., Юневич Н.Д. Интеллектуальная поддержка командира группы истребителей сопровождения при решении им задачи возврата части группы, отразившей атаку истребителей противника // Изв. РАН. ТиСУ. 2018. № 4. С. 139–152.
ГОСТ Р 58048-2017 “Трансфер технологий. Методические указания по оценке уровня зрелости технологий”. Введ. 2018-06-01. М.: Стандартинформ, 2018. 42 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления