1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 3, 2022

Известия РАН. Теория и системы управления, 2022, № 3, стр. 157-164

ПРЕДОТВРАЩЕНИЕ НЕЛИНЕЙНЫХ КОЛЕБАНИЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ С ИНТЕГРАЛЬНЫМИ АЛГОРИТМАМИ УПРАВЛЕНИЯ МЕТОДОМ НЕЛИНЕЙНОЙ КОРРЕКЦИИ

Ю. С. Зайцева a, b

a ИПМаш РАН, СПбГУ
Санкт-Петербург, Россия

b ЛУТ
Финляндия, Лаппеенранта

Поступила в редакцию 20.02.2021
После доработки 20.01.2022
Принята к публикации 31.01.2022

Полный текст (PDF)

Аннотация

Инженерные системы содержат исполнительные приводы, которые имеют ограничение на тяговые усилия, поэтому наличие нелинейностей в виде насыщения их скорости и уровня сигнала часто встречаются в системах управления. Широко применяют пропорционально-интегрально-дифференциальный регулятор, в котором возможен так называемый эффект возбуждения интегратора, или виндап, возникающий при выходе регулятора на неустойчивые состояния. Предотвращение возбуждения интегратора осуществляют путем синтеза регулятора с обратной связью, полученной с помощью вычитания входного и выходного сигналов нелинейности. Однако конструктивно такой алгоритм возможно реализовать не на всех объектах, также при синтезе существуют вычислительные трудности. Предлагается применить метод нелинейной коррекции систем. Введение в контур управления нелинейного корректирующего устройства позволяет формировать амплитудную и фазовую частотные характеристики гармонически линеаризованной системы независимо друг от друга. Работа полученной скорректированной системы проиллюстрирована на примере системы управления летательным аппаратом в боковом угловом направлении. Изложен сравнительный анализ статического антивиндап-регулятора и нелинейной коррекции в частотно-временной области. Вычислены обобщенные функции чувствительности для линейной и нелинейной систем для различных законов управления. Нелинейная коррекция при интегральном законе управления допускает более широкий диапазон амплитуд входных сигналов.

Введение. Несмотря на то, что в инженерной практике системы нелинейные, линейные модели описывают их поведение с достаточной точностью для анализа в окрестности рабочей точки. Физические исполнительные приводы по своей природе имеют ограничения на величину амплитуды, скорости сигнала или мощности. Из-за внезапных внешних возмущений или изменения режима работы, например, при пуске ошибка управления может значительно увеличиться. Тогда выходной сигнал регулятора становится больше, чем сигнал, приводящий систему в действие, т.е. происходит насыщение исполнительного механизма [1, 2]. При интегральных алгоритмах управления с насыщением по входу переходные процессы могут протекать дольше и со значительным перерегулированием. Поскольку при насыщении изменения входного сигнала системы не влияют на вход, обратная связь прерывается и в регуляторе могут развиваться как устойчивые, так и неустойчивые режимы. В результате в системе могут появиться нежелательные колебательные процессы, вплоть до потери устойчивости [3–5]. Это явление называют возбуждением интегратора или виндапом (от англ. wind up) [6, 7]. Возбуждение интегратора можно избежать путем увеличения мощности исполнительных приводов, но это решение всегда связано с компромиссом между стоимостью и технологическими требованиями и подходит не для всех систем. Например, в аэрокосмической технике налагаются ограничения на массу и размеры исполнительных механизмов, при этом они зачастую работают на максимальном уровне своей мощности. Для решения данной проблемы разработаны алгоритмические средства подавления возбуждения интегратора на основе теории автоматического регулирования. Распространенным подходом является введение обратной связи по разности сигналов между входом и выходом нелинейности с коэффициентом усиления, который может представлять собой либо статический, либо динамический фильтр [7, 8]. Основной метод синтеза – решение линейно-матричных неравенств с накладываемыми ограничениями на область устойчивости. Известны работы, в которых синтез реализуется при условии обладания системой свойства конвергенции [9–11].

Однако технически реализовать антивиндап-регулятор достаточно сложно и возможно не на всех системах, при этом при синтезе динамического антивиндап-регулятора существуют вычислительные трудности, связанные с нелинейной зависимостью выхода регулятора от его вектора состояния. В связи с чем в настоящей статье предлагается предотвратить возбуждение интегратора с помощью метода последовательной нелинейной коррекции, которая хорошо себя зарекомендовала при решении близкой задачи – предотвращения колебаний, вызванных летчиком, показанной в работах [1, 4, 12–14].

1. Метод нелинейной коррекции. Как известно, наличие нелинейностей в системе может существенно ухудшить качество регулирования, поэтому при проектировании таких систем для улучшения показателей качества их работы широко применяют линейные и нелинейные корректирующие устройства [15, 16]. Включение корректирующих устройств в контур системы управления позволяет сформировать заданные динамические качества системы, в том числе скомпенсировать влияние нелинейной статической характеристики, подавить автоколебания, уменьшить инерционность системы и обеспечить в ней необходимые запасы устойчивости.

В современных системах управления чаще применяют нелинейные корректирующие устройства (НКУ), так как линейные корректирующие устройства имеют ограниченные возможности для получения высоких показателей качества, а также меньшую помехозащищенность и надежность действия систем [4, 12, 15]. Среди НКУ выделяют класс псевдолинейных корректирующих устройств, которые позволяют формировать эквивалентные амплитудные и фазовые характеристики независимо друг от друга, что важно для нелинейных систем, в которых динамика зависит не только от частоты, но и амплитуды входного сигнала.

Свойством независимости фазовой характеристики от амплитудной обладает нелинейный фильтр с фазовым опережением, описываемый следующими уравнениями [15, 16]:

(1.1)
$\begin{gathered} y\left( t \right) = \left| {ku\left( t \right)} \right|{\text{sign}}~x\left( t \right), \\ X\left( s \right) = {{W}_{p}}\left( s \right)U\left( s \right),~ \\ \end{gathered} $
где t – время, u, y – вход и выход фильтра, k – постоянный коэффициент, $X\left( s \right),U\left( s \right)$ – изображения по Лапласу функций $x\left( t \right),u\left( t \right)$, s – комплексная переменная, x – сигнал на выходе фазоопережающего фильтра ${{W}_{p}}\left( s \right)$, имеющего передаточную функцию:
(1.2)
${{W}_{p}}(s) = \frac{{{{T}_{2}}s + 1}}{{{{T}_{1}}s + 1}},$
где $0 < {{{\text{T}}}_{1}} < {{{\text{T}}}_{2}}$ – постоянные времени фильтра. Этот фильтр позволяет получить фазовое опережение без изменения амплитуды. В случае если помимо изменения фазы требуется изменить амплитуду, то в амплитудную ветвь фильтра (1.1) вводят фильтр низких частот с передаточной функцией:
(1.3)
${{W}_{a}}(s) = \frac{1}{{{{T}_{s}} + 1}},$
где T – постоянная времени.

С помощью метода гармонической линеаризации из уравнений (1.1) получают эквивалентную частотную характеристику в виде коэффициентов, зависящих только от частоты, которые имеют следующий вид [15, 17, 18]:

(1.4)
$\begin{gathered} a(\omega ) = \frac{k}{\pi }(\pi - 2\phi + \sin 2\phi ), \\ b(\omega ) = \frac{k}{\pi }(1 - \cos 2\phi ), \\ \end{gathered} $
где ϕ(ω) – фазовый сдвиг, $\phi \left( \omega \right) = \arctan \left( {\omega {{{\text{T}}}_{2}}} \right) - \arctan \left( {\omega {{{\text{T}}}_{1}}} \right) > 0$ для $~\forall \omega > 0$, величина которого регулируется параметрами ${{{\text{T}}}_{1}},{{{\text{T}}}_{2}}$. Тогда для (1.1) с учетом (1.4) эквивалентная амплитудная характеристика будет описываться как $q = a{{\left( \omega \right)}^{2}} + b{{\left( \omega \right)}^{2}},$ а эквивалентная фазовая характеристика выражается как $\mu = \arctan (b\left( \omega \right){\text{/}}a\left( \omega \right)).$ Для корректирующего устройства, содержащего фильтр ${{W}_{a}}(s),$ выражения (1.4) имеют более громоздкий вид и приведены в [19].

Положительный эффект введения НКУ в пилотируемые системы управления полетом описан в следующих работах. В [4] показано, что колебания, вызванные пилотом по причине ограничения управляющей поверхности самолета, подавляются путем введения в контур управления нелинейного фильтра с фазовым опережением (1.1). Наличие скрытых колебаний и предельных циклов в асимптотически устойчивой линейной системе управления самолетом в продольном направлении показано в [13, 20]. Появление этих нежелательных колебательных процессов также предотвращают с помощью фильтра (1.1). В [12, 21] нелинейные колебания углового движения дистанционно управляемого беспилотного летательного аппарата (ЛА) подавляют с помощью фильтра с раздельными каналами для амплитуды и фазы, содержащего (1.2), (1.3).

2. Применение нелинейной коррекции для подавления эффекта возбуждения интегратора для случая управления углом рыскания ЛА. Рассмотрим линеаризованную модель бокового углового движения ЛА, описываемого следующими уравнениями [22, 23]:

(2.1)
$\left\{ \begin{gathered} \dot {\beta }(t) = \alpha _{z}^{\beta }\beta (t) + \cos \alpha {\text{*}}{{\omega }_{y}}(t) + \alpha _{z}^{{{{\delta }_{r}}}}{{\delta }_{r}}(t), \hfill \\ {{{\dot {\omega }}}_{y}}(t) = \alpha _{{{{m}_{y}}}}^{\beta }(t) + \alpha _{{{{m}_{y}}}}^{{{{\omega }_{y}}}}(t) + \alpha _{{{{m}_{y}}}}^{{{{\delta }_{r}}}}{{\delta }_{r}}(t), \hfill \\ \dot {\psi }(t) = {{\omega }_{y}}(t), \hfill \\ \end{gathered} \right.$
где β(t) – угол скольжения ЛА, $\psi (t),~{{\omega }_{y}}(t)$ – угол и угловая скорость рыскания, α* – угол атаки, ${{\alpha }}_{z}^{{{\beta }}},$ ${{\alpha }}_{z}^{{{{{{\delta }}}_{r}}}},$ ${{\alpha }}_{{{{m}_{y}}}}^{{{\beta }}},$ ${{\alpha }}_{{{{m}_{y}}}}^{{{{{{\omega }}}_{y}}}},$ ${{\alpha }}_{{{{m}_{y}}}}^{{{{{{\delta }}}_{r}}}}$ – коэффициенты линеаризованной модели ЛА. Численные значения коэффициентов модели (2.1): ${{\alpha }}_{z}^{{{\beta }}} = - 0.152,$ ${{\alpha }}_{z}^{{{{{{\delta }}}_{r}}}} = - 0.032,$ ${{\alpha }}_{{{{m}_{y}}}}^{{{{{{\omega }}}_{y}}}} = - 0.136,$ ${{\alpha }}_{{{{m}_{y}}}}^{{{{{{\delta }}}_{r}}}} = - 1.46,$ ${{\alpha }} = 0.4363$ рад.

Сервопривод руля направления описывается следующими уравнениями второго порядка [4, 14]:

$\left\{ \begin{gathered} {{{\dot {\delta }}}_{r}}\left( t \right) = {{\omega }_{r}}\left( t \right),~ \hfill \\ {{{\dot {\omega }}}_{r}}\left( t \right) = {{k}_{{{\sigma }}}}\left( {{{\sigma }_{r}}\left( t \right) - {{\delta }_{r}}\left( t \right)} \right) - {{k}_{2}}{{\omega }_{r}}\left( t \right), \hfill \\ \end{gathered} \right.$
где ${{\delta }_{r}}(t),~{{\omega }_{r}}(t)$ – угол и угловая скорость отклонения руля, ${{k}_{{{\sigma }}}},{{k}_{2}}$ – коэффициенты передачи, ${{k}_{{{\sigma }}}} = 67.2$ с–2, ${{k}_{2}} = 11.5$ с–1. Таким образом, передаточная функция от сигнала управления ${{\sigma }_{r}}\left( t \right)$ к углу рыскания $\psi \left( t \right)$ имеет вид [10]

(2.2)
$W_{\psi }^{{{{\sigma }_{r}}}}\left( s \right) = \frac{{ - 98.2\left( {s + 0.113} \right)}}{{s({{s}^{2}} + 0.288s + 1.61)({{s}^{2}} + 11.5s + 67.2)}}.$

Для системы (2.2) без учета насыщения проведен синтез пропорционально-интегрально-дифференцирующего (ПИД) регулятора с параметрами kp = 0.37, ${{k}_{{\text{I}}}} = 0.46$ с–1, ${{k}_{{\text{D}}}} = 1.8$ с [10].

Положим, что характеристика функции насыщения описывается следующими уравнениями [24]:

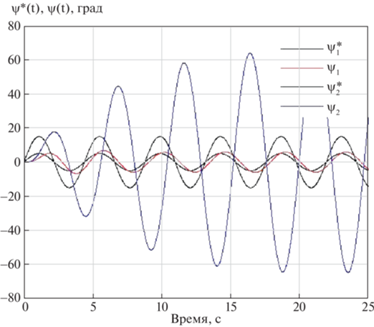
$sa{{t}_{{\bar {\dot {\delta }}}}} = \left\{ \begin{gathered} {{{\dot {\delta }}}_{e}}\quad {\text{при}}\quad {\text{|}}{{{\dot {\delta }}}_{e}}{\text{|}} \leqslant {{{\dot {\delta }}}_{e}}, \hfill \\ {\text{иначе}}\,\,\,\dot {\delta } \cdot {\text{sign}}({{{\dot {\delta }}}_{e}}), \hfill \\ \end{gathered} \right.$
где $\overline {\dot {\delta }} - $ усредненная величина насыщения скорости привода.

Учтем влияние насыщения скорости привода входного сигнала, лежащее в пределах от –20 до 20 град/с, ограничение уровня сигнала составляет от –25 до 25°. Как отмечено выше, при некоторых видах входного воздействия наличие насыщения может привести к ухудшению качества управления и нежелательным колебательным процессам. Проиллюстрируем этот факт на рис. 1, где изображены переходные процессы при гармоническом входном воздействии с амплитудами 5°; 15°, частотой 0.025 с–1.

Рис. 1.

Временные процессы по углу рыскания

Из рис. 1 видно, что при амплитуде входного сигнала $\psi _{1}^{*}(t) = 5$ град, выходной сигнал ${{\psi }_{1}}\left( t \right)$ устойчив, при увеличении амплитуды $\psi _{2}^{*}\left( t \right) = 15$ град наблюдается выходной сигнал ${{\psi }_{2}}\left( t \right)$ с амплитудой, превышающий входную амплитуду в 4 раза.

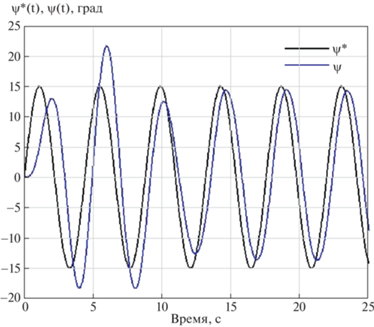
Введем в контур управления НКУ, описываемое (1.1) с параметрами фильтром ${{{\text{T}}}_{1}} = 0.001$ с, ${{{\text{T}}}_{2}}$ = 10 с так, что его вход соединяется с выходом ПИД-регулятора. В результате моделирования переходный процесс по углу рыскания имеет вид, представленный на рис. 2, где ψ*(t) = $15{\text{sin}}(0.025t)$ – входной сигнал, $\psi \left( t \right)$ – выход системы. Из рисунка видно, что переходный процесс устойчивый.

Рис. 2.

Временные процессы по углу рыскания скорректированной системы

В подавляющем большинстве работ под проблемой антивиндап-коррекции понимается обеспечение глобальной асимптотической устойчивости состояния равновесия автономной системы с насыщением и ограничение траекторий неавтономной системы малым коэффициентом передачи ${{\mathcal{L}}_{2}}$ [7, 8, 25]. Недостаточность требования глобальной асимптотической устойчивости показана в работах [26, 27] и привела к использованию другого подхода, основанного на свойстве конвергенции системы [11, 28], позволяющего проводить синтез регулятора независимо от начальных условий и вида входного сигнала.

Выполним теперь сравнительный анализ системы с нелинейной коррекцией, описанной выше, и статическим антивиндап-регулятором, представленным в [10], на основе свойства конвергенции системы для всего диапазона рабочих амплитуд и частот с помощью вычисления обобщенной функции чувствительности. Для неавтономной равномерно конвергентной системы в форме Лурье

(2.3)
$\begin{array}{*{20}{c}} {{\mathbf{\dot {x}}}\left( t \right) = f\left( {{\mathbf{x}},r} \right),} \\ {{\mathbf{y}}\left( t \right) = h\left( {{\mathbf{x}},r} \right),} \end{array}$
где ${\mathbf{x}}\left( t \right) \in {{\mathbb{R}}^{m}}$ – вектор пространства состояния, ${\mathbf{y}}\left( t \right) \in \mathbb{R}$ – выход системы, $r\left( t \right)$ – входной сигнал, $r\left( t \right) = a \cdot {\text{sin}}\left( {\omega t} \right)$, ${\mathbf{\varepsilon }}\left( t \right)$ – рассогласование, такое, что ${\mathbf{\varepsilon }}\left( t \right) = r\left( t \right) - {\mathbf{y}}\left( t \right)$, существует периодическое решение $~\bar {x}\left( t \right)$ с соответствующим выходом $\bar {y}\left( t \right)$ и $\bar {\varepsilon }\left( t \right) = r\left( t \right) - \bar {y}\left( t \right)$.

Тогда, обобщенная функция чувствительности для системы (2.3) имеет следующий вид [18, 29, 30]:

(2.4)
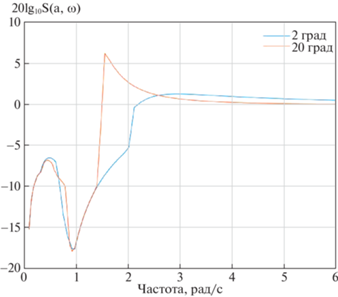
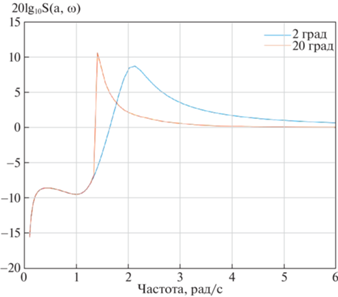
$\mathbb{S}(a,\omega ) = \frac{{{\text{||}}\bar {\varepsilon }{\text{|}}{{{\text{|}}}_{2}}}}{{{\text{||}}r{\text{|}}{{{\text{|}}}_{2}}}},$
где

${\text{||}}z{\text{|}}{{{\text{|}}}_{2}} = {{\left( {\frac{\omega }{{2\pi }}\int\limits_0^{2\pi {\text{/}}\omega } {{{z}^{2}}(\tau )d\tau } } \right)}^{{1/2}}}.$

Согласно (2.4), на рис. 3 изображены функции чувствительности для системы с НКУ для малой и большой амплитуд входного сигнала. Аналогичная иллюстрация представлена на рис. 4 для системы с антивиндап-регулятором.

Рис. 3.

Функция чувствительности для скорректированной системы

Рис. 4.

Функция чувствительности для системы с антивиндап-регулятором

Сравнительный анализ рис. 3, 4 показывает, что величина функции чувствительности в диапазоне 1.5–3 рад/с для системы с антивиндап-регулятором приблизительно в 2 раза выше при больших амплитудах, чем для системы с НКУ. Для малых амплитуд величина функции чувствительности стремится к нулю для системы с НКУ, тогда как для системы с антивиндап-регулятором она составляет около восьми. Заметим, что при уменьшении ${{{\text{k}}}_{{\text{A}}}}$ величина функции чувствительности резко возрастает.

На рис. 5 изображены обобщенные функции чувствительности, вычисленные для исследуемой системы при амплитуде входного сигнала 15°, с различными законами управления: 1 – линейная система с ПИД-регулятором, 2 – система с ПИД-регулятором и ограничением скорости привода, 3 – система с ПИД-регулятором и НКУ, 4 – система с антивиндап-коррекцией.

Рис. 5.

Функция чувствительности для системы с различными законами управления

Из рис. 5 видно негативное влияние нелинейности при интегральном законе управления, а также наименьшее влияние на ошибку управления в области частот 1–3 рад/с при законе управления, содержащем ПИД-регулятор и НКУ.

Заключение. Проведена нелинейная коррекция системы с интегральным законом управления. В качестве объекта управления представлена модель ЛА, описывающая его боковое угловоe движение. При ограничении скорости привода руля направления и больших амплитудах входного сигнала ошибка управления не парируется регулятором, что приводит к нежелательным колебательным процессам. Для решения этой проблемы в контур управления введено нелинейное корректирующее устройство. В результате моделирования было показано, что диапазон амплитуд входного сигнала достигает 20$^\circ $ при насыщении сигнала, равным 20 град/с. По сравнению с работой статического антивиндап-регулятора нелинейная коррекция позволяет расширить диапазон рабочих сигналов. Помимо этого, конструктивно нелинейную коррекцию проще реализовать.

Список литературы

  1. Андриевский Б.Р., Кузнецов Н.В., Леонов Г.А. Методы подавления нелинейных колебаний в астатических системах автопилотирования летательных аппаратов // Изв. РАН. ТиСУ. 2017. № 3. С. 118–134. https://doi.org/10.7868/S0002338817030040

  2. Andrievsky B., Arseniev D., Kuznetsov N., Zaitceva I. Pilot-Induced Oscillations and Their Prevention // Cyber-Physical Systems and Control. Lecture Notes in Networks and Systems. Cham: Springer, 2020. V. 95. P. 108–123. https://doi.org/10.1007/978-3-030-34983-7_11

  3. Андриевский Б.Р., Кузнецов Н.В., Кузнецова О.А., Леонов Г.А., Мокаев Т.Н. Локализация скрытых колебаний в системах управления полетом // Тр. СПИИРАН. 2016. Т. 6. № 49. С. 5–31. https://doi.org/10.15622/sp.49.1

  4. Andrievsky B., Kravchuk K., Kuznetsov N.V., Kuznetsova O.A., Leonov G.A. Hidden Oscillations in the Closed-loop Aircraft-pilot System and Their Prevention // Proc. 6th IFAC Workshop on Periodic Control Systems. 2016. V. 49. P. 30–35. https://doi.org/10.1016/j.ifacol.2016.07.970.

  5. Andrievsky B., Kudryashova E., Kuznetsov N., Kuznetsova O.A., Mokaev T.N. Hidden Oscillations in an Active Flutter Suppression System and Flight of a Manned Aircraft // Mathematics in Engineering, Science and Aerospace. 2019. V. 10. P. 357–371. Available at: http://nonlinearstudies.com/index.php/mesa/article/view/2002.

  6. Hippe P. Windup in Control: Its Effects and Their Prevention. N. Y.: Springer-Verlag, 2006. 315 p.

  7. Hussain M., Rehan M., Ahmed S., Abbas T., Tufail M. A Novel Approach for Static Anti-Windup Compensation of One-sided Lipschitz Systems Under Input Saturation // Applied Mathematics and Computation. 2020. V. 380. P. 125229. https://doi.org/10.1016/j.amc.2020.125229

  8. Tarbouriech S., Queinnec I., Prieur C. Nonstandard Use of Anti-Windup Loop for Systems with Input Backlash // IFAC J. of Systems and Control. 2018. V. 6. P. 33–42. https://doi.org/10.1016/j.ifacsc.2018.10.003

  9. Andrievsky B., Kuznetsov N., Leonov G. Convergence-based Analysis of Robustness to Delay in Anti-windup Loop of Aircraft Autopilot // Proc. IFAC Workshop on Advanced Control and Navigation for Autonomous Aeroespace Vehicles. IFAC Proceedings Volumes (IFAC-PapersOnline). Seville, Spain: IFAC, 2015. V. 48. № 9. P. 144–149. https://doi.org/10.1016/j.ifacol.2015.08.074.

  10. Леонов Г.А., Андриевский Б.Р., Кузнецов Н.В., Погромский А.Ю. Управление летательными аппаратами AW-коррекцией // Дифференциальные уравнения и процессы управления. 2012. № 3. 36 с. Available at: https://diffjournal.spbu.ru/RU/numbers/2012.3/article.1.1.html.

  11. Turner M. C., Sofrony J., Prempain E. Anti-windup for Model-reference Adaptive Control Schemes with Rate-limits // Systems and Control Letters. 2020. V. 137. P. 1–9. [104630]. https://doi.org/10.1016/j.sysconle.2020.104630

  12. aitceva I. Nonlinear Oscillations Prevention in Unmanned Aerial Vehicle // Proc. of 11 Majorov Intern. Conf. on Software Engineering and Computer Systems. V. 2590. St-Petersburg, Russia, 2019. 8 p. Available at: http://ceur-ws.org/Vol-2590/short3.pdf

  13. Andrievsky B., Kuznetsov N., Kuznetsova O., Leonov G., Seledzhi S. Nonlinear Phase Shift Compensator for Pilot-induced Oscillations Prevention // Proc. IEEE Europ. Modelling Sympos. on Computer Modelling and Simulation. Madrid, Spain, 2016. P. 225–231. https://doi.org/10.1109/EMS.2015.43.

  14. Андриевский Б.Р., Зайцева Ю.С., Кудряшова Е.В., Кузнецов Н.В., Кузнецова О.А. Обзор методов предотвращения раскачки самолета летчиком // Дифференциальные уравнения и процессы управления. 2020. № 2. С. 131–172. https://diffjournal.spbu.ru/RU/numbers/2020.2/article.1.8.html.

  15. Очиров В.В., Скороспешкин М.В. Псевдолинейный ПИД-регулятор для системы второго порядка // Сб. тр. 13-й Междунар. научно-практической конф. студентов, аспирантов и молодых ученых. Т. 1. Томск, 2016. С. 181–182. http://earchive.tpu.ru/handle/11683/17128.

  16. Зельченко В.Я., Шаров С.Н. Нелинейная коррекция автоматических систем. Л.: Судостроение, 1981. 167 с.

  17. Chechurin L., Chechurin S. Physical fundamentals of oscillations. Frequency Analysis of Periodic Motion Stability. Springer, 2019. 264 p.

  18. Андриевский Б.Р., Фрадков А.Л., Бобцов А.А. Методы анализа и синтеза нелинейных систем управления. СПб.: Институт компьютерных исследований, 2018. 336 с.

  19. Нелинейные корректирующие устройства в системах автоматического управления / Под ред. Е.П. Попова. М.: Машиностроение, 1971. 466 с.

  20. Кузнецов Н.В. Теория скрытых колебаний и устойчивость систем управления // Изв. РАН. ТиСУ. 2020. № 5. С. 5–27. https://doi.org/10.31857/S0002338820050091

  21. Зайцева Ю.С. Подавление автоколебаний при дистанционном управлении БПЛА // Тр. 11-й общероссийской молодежной научно-практической конф. “Молодежь. Техника. Космос”. Т. 1. СПб.: 2019. С. 245–249. https://www.voenmeh.ru/images/docs/science/MTK_2019_trudi_tom1.pdf.

  22. Бюшгенс Г.С., Студнев Р.В. Аэродинамика самолета: динамика продольного и бокового движения. М.: Машиностроение, 1979. 352 с.

  23. Stengel R. Lecture Notes in Aircraft Flight Dynamics. Princeton, USA. Princeton University, 2018. http://www.stengel.mycpanel.princeton.edu/MAE331Lecture15.pdf.

  24. Zaitceva I., Chechurin L. The Estimation of Aircraft Control System Stability Boundaries by the Describing Function Method // Cybernetics and Physics. 2020. V. 9. № 2. P. 117–122. https://doi.org/10.35470/2226-4116-2020-9-2-117-122

  25. Buratti N., Invernizzi D., Lovera M. Experimental Validation of LMI-based Anti-Windup Compensators for Attitude Control in Multirotor UAVs // Proc. 21st IFAC Sympos. on Automatic Control in Aerospace. Cranfield, UK, 2019. V. 52. № 12. P. 164–169. https://doi.org/10.1016/j.ifacol.2019.11.191.

  26. Pogromsky A., Van den Berg R. Frequency Domain Performance Analysis of Lur’e Systems // IEEE Transaction on Control Systems Technology. 2014. V. 22. № 5. P. 1949–1955. https://doi.org/10.1109/TCST.2013.2296097

  27. Van den Berg R., Pogromsky A.Y., Leonov G.A., Rooda J.E. Design of Convergent Switched Systems // Group Coordination and Cooperative Control. Lecture Notes in Control and Information Sciences. V. 336. Springer, 2006. P. 291–311. https://doi.org/10.1007/11505532_17

  28. Pavlov A., Van den Wouw N. Convergent Systems: Nonlinear Simplicity // Nonlinear Systems. Lecture Notes in Control and Information Sciences. V. 470. Springer, 2017. P. 51–77. https://doi.org/10.1007/978-3-319-30357-4_3

  29. Andrievsky B., Pogromsky A.Y., Rooda J. Observer-based Production Control of Manufacturing Machines // Proc. 13th IFAC Sympos. on Information Control Problems in Manufacturing. Moscow, 2009. P. 264–269. https://doi.org/10.3182/20090603-3-RU-2001.0088.

  30. Andrievsky B., Kudryashova E., Kuznetsov N., Kuznetsova O. Aircraft Wing Rock Oscillations Suppression by Simple Adaptive Control // Aerospace Science and Technology. 2020. V. 105. P. 106049. https://doi.org/10.1016/j.ast.2020.106049

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал