Известия РАН. Теория и системы управления, 2022, № 3, стр. 21-30

Введение. Одной из задач функционального диагностирования является задача идентификация дефектов [1]. В последние годы для ее реализации активно применяется подход, основанный на наблюдателях, которые работают в скользящем режиме и используют особенности этого режима [2]. Далее наблюдатель со скользящим режимом работы будем называть скользящим наблюдателем.

Настоящая публикация является логическим продолжением статей [3, 4], посвященных разработке методов построения скользящих наблюдателей для решения задачи идентификации дефектов. Указанные наблюдатели описываются дифференциальным уравнением с разрывной правой частью и обеспечивают возникновение в системе скользящего режима при соблюдении определенных условий.

Скользящие наблюдатели применяются для решения задачи идентификации дефектов в линейных [3, 5–7] и нелинейных [4, 8, 9] системах, для обеспечения отказоустойчивого управления [10], в ряде практических приложений [11–13]. Во всех таких работах на исходную систему накладывается ряд ограничений, в частности, требуется, чтобы выполнялось так называемое условие согласования и система была минимально фазовой.

Для ослабления условия согласования были предложены методы, использующие скользящие наблюдатели высокого порядка [14, 15] и каскадное соединение наблюдателей [16], но при этом система должна быть минимально фазовой. В [17] последнее условие ослаблено ценой того, что в выражение для оценки дефекта входит производная величины дефекта, в [18] для этого вводится предположение об ограниченности ошибки оценивания. В [19, 20] требование минимальной фазовости системы ослаблено до условия детектируемости.

Отметим, что в известных работах скользящие наблюдатели строятся на основе исходной системы и, следовательно, имеют размерность, совпадающую с размерностью этой системы. В настоящей статье предложен метод, позволяющий осуществить дальнейшее ослабление указанных условий. В его основе лежит идея использования редуцированной (имеющей меньшую размерность) модели исходной системы, что и позволяет ослабить эти условия. Кроме того, это дает возможность уменьшить размерность скользящих наблюдателей.

1. Построение редуцированной модели. Рассмотрим стационарную систему, описанную нелинейным уравнением состояния и линейной функцией выхода:

Здесь x(t) ∈ Rⁿ, u(t) ∈ R^m, y(t) ∈ R^l – векторы состояния, управления и выхода; F ∈ R^{n ×n}, G ∈ ∈ R^n × m, D ∈ R^{n ×q}, L ∈ R^{n ×p} и H ∈ R^{l ×n} – известные постоянные матрицы; d(t) ∈ R – функция, описывающая дефекты: при их отсутствии d(t) = 0, при появлении дефекта d(t) становится неизвестной функцией времени; ρ(t) ∈ R^p – неизвестная функция времени, описывающая действующие на систему возмущения, Ψ(x, u) – нелинейная составляющая:

A₁, …, A_s – матрицы-строки; φ₁, …, φ_s – нелинейные (возможно, недифференцируемые) функции, удовлетворяющие условию Липшица по аргументу x, откуда следует, что функция Ψ(x, u) также удовлетворяет условию Липшица, т.е. N ≥ 0 – некоторая константа. Предполагается, что известны, и ограничены нормы |d(t)| и ||ρ(t)|| функций d(t) и ρ(t).

Для решения задачи идентификации функции d(t) в [8] предполагается, что система (1.1) удовлетворяет следующим условиям: 1) rank(H[L, D]) = rank([L, D]) (условие согласования), 2) все инвариантные нули тройки (F, [L, D], H) лежат в левой полуплоскости (минимальная фазовость). В [19, 20] эти условия ослаблены – требуется, чтобы линейная часть системы (1.1) была детектируемой, т.е. ненаблюдаемая часть системы устойчива.

Целью работы является дальнейшее ослабление этих условий за счет построения скользящих наблюдателей на основе модели исходной системы пониженной размерности, что дополнительно приводит к понижению размерности наблюдателя. Эффект ослабления условий достигается за счет того, что модель пониженной размерности может не иметь тех свойств, которые присутствуют в исходной системе и препятствуют возможности построения для нее скользящего наблюдателя.

Предполагается, что линейная часть системы (1.1) недетектируема, т.е. Ker(V⁽ⁿ⁾) ≠ $\emptyset $, где

и ненаблюдаемая подсистема линейной части неустойчива.

Д о п у щ е н и е 1. Линейное подпространство Im(D) $ \not\subset $ Ker(V⁽ⁿ⁾).

Здесь Im(D) означает линейное подпространство, индуцированное столбцами матрицы D, Ker(V⁽ⁿ⁾) – линейное подпространство, такое, что из z ∈ Ker(V⁽ⁿ⁾) следует V⁽ⁿ⁾z = 0. Обозначим через r_d минимальную сравнительную степень вектора y по отношению к функции d(t), ${{y}_{*}}$ – компоненту вектора y, соответствующую r_d, и ${{R}_{*}}$ – матрицу-строку, такую, что ${{R}_{*}}$y(t) = ${{y}_{*}}$(t). Из допущения 1 следует, что r_d < ∞ и матрица ${{R}_{*}}$ существует. Напомним, что сравнительная степень вектора y по отношению к функции d(t) – это минимальное целое k, такое, что HF^{k – 1}D ≠ 0.

Предположим вначале, что возмущение ρ(t) отсутствует, и построим модель системы (1.1) минимальной размерности с выходом ${{y}_{*}}$(t), которая описывается уравнением

где ${{x}_{*}}$ ∈ R^k – вектор состояния меньшей размерности k < n, ${{F}_{*}}$, ${{G}_{*}}$, ${{J}_{*}}$, ${{H}_{*}}$ и ${{D}_{*}}$ – матрицы, подлежащие определению, функция ${{C}_{*}}$Ψ(${{x}_{*}}$, y, u) имеет вид ${{C}_{*}}$, ${{A}_{{*1{{i}_{1}}}}}$, ${{A}_{{*2{{i}_{1}}}}}$, …, ${{A}_{{*1{{i}_{p}}}}}$, ${{A}_{{*2{{i}_{p}}}}}$ – матрицы, подлежащие определению. Как обычно [3, 7], предполагается, что при отсутствии дефектов и возмущений выполняются равенства для некоторых матриц Φ и ${{R}_{*}}$. Известно [4], что эти матрицы удовлетворяют условиям ${{C}_{*}}$ – матрица, получаемая из произведения ΦC путем удаления нулевых столбцов, i₁, …, i_p – номера ненулевых столбцов в ΦC.

Д о п у щ е н и е 2. Пара (${{F}_{*}}$, ${{H}_{*}}$) наблюдаема.

Из допущения 2 следует, что матрицы ${{F}_{*}}$ и ${{H}_{*}}$ могут быть представлены в каноническом виде:

Такой вид матриц позволяет получить следующие уравнения для строк матриц Φ и ${{J}_{*}}$:

В [3, 21] показано, что эти уравнения могут быть свернуты в одно:

Запишем его в виде

где и найдем решение уравнения (1.6) при минимальном k ≥ r_d. Далее из (1.5) определяются строки матрицы Φ, находится матрица ${{C}_{*}}$ и проверяется условие

Если оно выполняется, то принимается ${{G}_{*}}$ = ΦG и ${{D}_{*}}$ = ΦD; матрицы ${{A}_{{*1i}}}$ и ${{A}_{{*2i}}}$, i = $\overline {{{i}_{1}},{{i}_{p}}} $, определяются из (1.4). При невыполнении условия (1.7) ищется другое решение уравнения (1.6) при прежней или увеличенной размерности k. Предполагается, что ${{D}_{*}}$ ≠ 0.

2. Преобразование редуцированной модели. Дальнейшие построения осуществляются по аналогии с [20] с тем отличием, что предложенные там действия применяются в настоящей работе не к исходной системе, а модели (1.3) с учетом канонической формы матриц ${{F}_{*}}$ и ${{H}_{*}}$. Для этого представим описывающие ее матрицы в следующем виде:

где остальные матрицы в (2.1) имеют соответствующие размеры.

Введем преобразование координат z = T${{x}_{*}}$ с матрицей T = $\left( {\begin{array}{*{20}{c}} {{{I}_{{k - 1}}}}&Q \\ 0&1 \end{array}} \right)$, где I_{k – 1} ∈ R^{(k– 1) × (k– 1)} – единичная матрица, матрица-столбец Q = (q₁q₂ … q_{k – 1})^T ∈ R^{(k– 1)} выбирается так, чтобы сделать матрицу ${{\bar {F}}_{1}}$ = F₁ + QF₃  устойчивой. Поскольку пара (F₁, F₃) с очевидность наблюдаема, такая матрица существует. В результате модель (1.3) принимает вид

где

Отметим, что ключевую роль в модели (2.2) играет тот факт, что матрица ${{\bar {F}}_{1}}$ устойчива. В [8] это следует из того, что все инвариантные нули тройки (F, [L D], H) лежат в левой полуплоскости, в [19, 20] – из детектируемости системы (1.1), в нашей работе – из канонического вида матриц ${{F}_{*}}$ и ${{H}_{*}}$.

3. Построение скользящего наблюдателя. Поскольку матрица ${{\bar {F}}_{1}}$ устойчива, существуют симметрические положительно-определенные матрицы P и W, такие, что $\bar {F}_{1}^{{\text{T}}}$P + P${{\bar {F}}_{1}}$ = –W. По аналогии с [20] скользящий наблюдатель строится в виде

где e₂(t) = ${{y}_{*}}$(t) – ${{\hat {y}}_{*}}$(t), ${v}$(t) = sign(e₂(t)), ${{\bar {K}}_{1}}$ = P^–1$\bar {F}_{3}^{T}$k₁, k₁, k₂, k₃ – положительные числа, e₁(t) = z₁(t) – – ${{\hat {z}}_{1}}$(t).

Из (2.2) и (3.1) получаем

где ΔΨ = Ψ(z₁, ${{y}_{*}}$, y, u) – Ψ(${{\hat {z}}_{1}}$, ${{y}_{*}}$, y, u). Будем полагать, что функция Ψ(x, u) удовлетворяет условию Липшица (1.2), а тогда Ψ(z₁, ${{y}_{*}}$, y, u) также удовлетворяет этому условию по z₁: для некоторого ${{N}_{*}}$ > 0.

Т е о р е м а. Пусть выполняется условие $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } $(W) ≥ 2||P${{\bar {C}}_{{*1}}}$||${{N}_{*}}$. Тогда если ${{\bar {D}}_{{*1}}}$ = 0, то наблюдатель (3.1) оценивает функцию d(t) в виде

в противном случае как где $D_{{*1}}^{ + }$ = ${{(\bar {D}_{{*1}}^{T}\bar {D}_{{*1}}^{{}})}^{{ - 1}}}\bar {D}_{{*1}}^{{}}$ и $D_{{*2}}^{ + }$ = ${{(\bar {D}_{{*2}}^{T}\bar {D}_{{*2}}^{{}})}^{{ - 1}}}\bar {D}_{{*2}}^{{}}$, ${{{v}}_{{{\text{eq}}}}}(t)$ – сигнал, представляющий разрывную функцию ${v}(t)$. Согласно [8], в качестве ${{{v}}_{{{\text{eq}}}}}(t)$ может быть принята непрерывная функция где ε – малое положительное число.

Д о к а з а т е л ь с т в о. По аналогии с [20] докажем, во-первых, что ||e₁|| ≤ δ = max{δ₁, δ₂}, где

β > ||d(t)||, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } $(P) и $\bar {\lambda }$(P) – минимальное и максимальное собственные числа матрицы P соответственно. Рассмотрим функцию Ляпунова V₁ = $e_{1}^{{\text{T}}}$Pe₁ и найдем ее производную по времени с учетом (3.2) и (3.3):

Используя известное неравенство

получим

Остальная часть доказательства с учетом того, что $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } $(W) ≥ 2||P${{\bar {C}}_{{*1}}}$||${{N}_{*}}$, совпадает с [20].

Покажем, во-вторых, что при соответствующем выборе коэффициентов усиления наблюдателя e₂ = 0 за конечное время, т.е. достигается скользящий режим. Рассмотрим функцию Ляпунова V₂ = $e_{2}^{2}$ и найдем ее производную по времени с учетом (3.2) и (3.3):

Поскольку ${v}$ = sign(e₂), то 2e₂k₃${v}$ = 2k₃|e₂| и Если k₃ удовлетворяет условию и k₂ > 0, то ${{\dot {V}}_{2}}$ ≤ 0. По аналогии с [20] можно показать, что ${{\dot {V}}_{2}}$ ≤ –c₂$\sqrt {{{V}_{2}}} $ для некоторого c₂ > 0, т.е. за конечное время возникает скользящий режим с e₂ = ${{\dot {e}}_{2}}$ = 0.

В-третьих, для доказательства того, что при соответствующем выборе коэффициентов усиления наблюдателя e₁ = 0 за конечное время, рассмотрим функцию Ляпунова V₁ = $e_{1}^{{\text{T}}}$Pe₁ и ее производную (3.7). Из второго уравнения в (3.2) и скользящего режима, когда e₂ = ${{\dot {e}}_{2}}$ = 0, следует ${{\bar {F}}_{3}}$e₁ = k₃${v}$ – ${{\bar {C}}_{{*2}}}$ΔΨ – ${{\bar {D}}_{{*2}}}$d. Так как ${{\bar {K}}_{1}}$ = P^–1$\bar {F}_{3}^{{\text{T}}}$k₁, из (3.7) вытекает

Так как ||e₁|| ≤ δ, получаем

Если k₃ и k₁ выбрать соответственно как

то ${{\dot {V}}_{1}}$ ≤ 0 и по аналогии с [20] можно показать, что ${{\dot {V}}_{1}}$ ≤ –c₁$\sqrt {{{V}_{1}}} $ для некоторого c₁ > 0, т.е. за конечное время возникает скользящий режим с e₁ = ${{\dot {e}}_{1}}$ = 0. Исходя из (3.8) и (3.9), коэффициент k₃ следует выбирать из условия Теорема доказана.

Поскольку в скользящем режиме e₁ = ${{\dot {e}}_{1}}$ = 0 и e₂ = ${{\dot {e}}_{2}}$ = 0, то при ${{\bar {D}}_{{*1}}}$ = 0 функция d(t) может быть оценена из второго уравнения в (3.2) в виде (3.4); в противном случае нужно использовать первое уравнение в (3.2), что дает оценку (3.5).

4. Идентификация в присутствии возмущений. Условие ΦL = 0 нечувствительности к возмущению имеет вид (1 – ${{J}_{{*k}}}$ … –${{J}_{{*1}}}$)L^(k) = 0 [3, 4], где

Последнее уравнение и (1.6) дают уравнение

решение которого ищется при минимальном k ≥ r_d; дальнейшие действия аналогичны описанным выше. Если при всех k < n уравнение (4.1) не имеет решения, модель, не чувствительная к возмущению, не существует. В этом случае необходимо обратиться к робастным методам, описанным в [3], которые позволят найти приближенное решение.

5. Пример. Рассмотрим систему управления:

Приведем матрицы и нелинейности, описывающие систему:

Так как rank(H[L D]) = 1 ≠ rank([L D]) = 2, то условие согласования не выполняется. Нетрудно видеть, что

откуда Ker(V⁽³⁾) = (0 0 1 0)^T, а так как F(3, 3) = 1, ненаблюдаемая часть системы неустойчива, т.е. система недетектируема. Ясно, что Im(D) $ \not\subset $ Ker(V⁽³⁾), r_d = 2, ${{y}_{*}}$ = y₁ и ${{R}_{*}}$ = (1 0). Матрицы W⁽²⁾ и L⁽²⁾ принимают вид

Нетрудно видеть, что уравнение (4.1) имеет решение с матрицами ${{J}_{{*1}}}$ = (–1, 1), ${{J}_{{*2}}}$ = (–2, 0), тогда Φ₁ = (1 1 0 0), Φ₂ = (1 0 0 0) и ${{D}_{*}}$ = (0 1)^T, ${{G}_{*}}$ = (1 1)^T, ${{C}_{*}}$ = $\left( {\begin{array}{*{20}{c}} 1&0 \\ 1&0 \end{array}} \right)$, ${{C}_{*}}$Ψ(${{x}_{*}}$, y, u) = sin(${{x}_{{*1}}}$ – y₁). В результате модель (1.3) принимает следующий вид:

где ${{x}_{{*1}}}$ = x₁+ x₂, ${{x}_{{*2}}}$ = x₁. Принимая Q = –1 и T = $\left( {\begin{array}{*{20}{c}} 1&{ - 1} \\ 0&1 \end{array}} \right)$, получаем модель (2.2): где z₁ = ${{x}_{{*1}}}$ – ${{x}_{{*2}}}$, z₂ = ${{x}_{{*2}}}$. Из вида модели следует, что ${{\bar {F}}_{3}}$ = 1, ${{\bar {D}}_{{*1}}}$ = 1, ${{\bar {D}}_{{*2}}}$ = 0, ${{\bar {C}}_{{*1}}}$ = 0, ${{\bar {C}}_{{*2}}}$ = 1, ${{N}_{*}}$ = 1; так как ${{\bar {F}}_{1}}$ = –1, можно принять P := 1, откуда W = 2. Ясно, что условие теоремы выполняется.

Скользящий наблюдатель описывается уравнениями

где e₂(t) = ${{y}_{*}}$(y) – ${{\hat {y}}_{*}}$(t), ${v}$(t) = sign(e₂(t)), ${{\bar {K}}_{1}}$ = P^–1${{\bar {F}}_{3}}$k₁ = k₁, k₂ > 0, β > ||d(t)||, δ = max{2(β + k₁), |e₁(0)|}. Коэффициенты k₁ и k₃ определяются условиями (3.9) и (3.10), на основе которых можно принять k₁ = β, k₃ = 2δ. Так как ${{\bar {D}}_{{*1}}}$ ≠ 0, функция d(t) может быть оценена в виде где ${{{v}}_{{{\text{eq}}}}}(t)$ дается выражением (3.6).

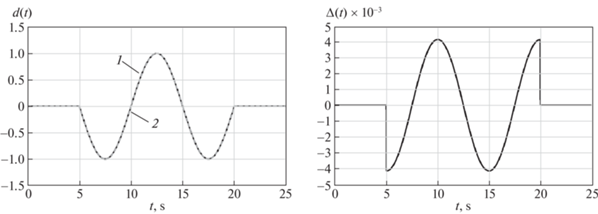
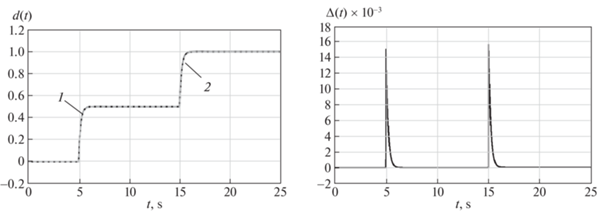
Для моделирования рассмотрим систему (5.1) и наблюдатель (5.2) с u(t) = sin(t), β = 1.5, k₁ = 1.5, k₂ = 0.01, k₃ = 6, |e₁(0)| = 0. Результаты моделирования приведены на рис. 1 и 2, где показано поведение функции d(t), ее оценки $\hat {d}$(t) и ошибки оценивания Δ(t) = $\hat {d}$(t) – d(t) для двух типов функции d(t) – синусоидальной и ступенчатой соответственно.

Заключение. Рассмотрена задача идентификации дефектов в системах, описываемых нелинейными дифференциальными уравнениями, в присутствии возмущений на основе наблюдателей, работающих в скользящем режиме. Скользящий наблюдатель строится на базе редуцированной (имеющей меньшую размерность) модели исходной системы, обладающей избирательной чувствительностью по отношению к дефектам и возмущению. За счет введения такой модели удалось ослабить условия существования скользящих наблюдателей по сравнению с известными работами. Эффект ослабления указанных условий возник за счет того, что модель пониженной размерности может не иметь тех свойств, которые присутствуют в исходной системе и препятствуют возможности построения для нее скользящего наблюдателя. Результаты моделирования подтвердили работоспособность предложенного метода.