Известия РАН. Теория и системы управления, 2022, № 3, стр. 31-40

Введение. Сложная экологическая ситуация заставляет людей искать различные возобновляемые источники энергии. Кроме того, использование таких источников позволяет обеспечить электропитание в местах, куда невозможно провести стационарные линии электропередачи. В частности, подобные системы могут быть весьма полезны при освоении других планет. Одним из основных источников возобновляемой энергии является ветер. Для преобразования его энергии в электричество, как правило, используют ветротурбины разных типов (с горизонтальной или вертикальной осью вращения). Однако в последние два десятилетия активно изучается возможность создания ветроэнергетических установок (малых и миниатюрных), в которых рабочий элемент не вращается в потоке ветра, а совершает колебания.

Эти колебания могут быть вызваны различными эффектами, такими, как флаттер, галопирование, сход вихрей и т.д. Так, в публикациях [1–4] изучается динамика ветроэнергетических установок, в которых рабочий элемент представляет собой тонкое крыло и совершает колебания типа флаттера. Рассматриваются разные конфигурации таких устройств. Электричество генерируется пьезоэлементами, которые деформируются в процессе колебаний крыла.

Возможность использования галопирования, т.е. поступательных колебаний плохообтекаемого тела, которые совершаются в направлении поперек набегающего потока, анализируется в [5]. В [6] даны оценки влияния электрической нагрузки на мощность, вырабатываемую ветроэнергетической установкой, рабочий элемент которой совершает такие колебания. Ряд публикаций, в частности, [7, 8], посвящены изучению влияния формы тела на эффективность отбора энергии потока за счет галопирования.

В [9] анализируется возможность выработки энергии за счет колебаний кругового цилиндра, индуцированных сходящими вихрями. В [10] исследуется влияние числа Рейнольдса на характеристики подобных колебаний (включая выходную мощность). Автор [11] показывает, что система типа динамического гасителя колебаний при надлежащем подборе параметров позволяет увеличить мощность, вырабатываемую за счет колебаний, индуцированных вихрями.

В [12, 13] рассматриваются вызванные потоком колебания двойного аэродинамического маятника и показано, что этот объект также может применяться в качестве рабочего элемента колебательных ветроэнергетических установок.

Можно выделить два основных способа генерации электроэнергии, которые могут быть реализованы в ветроэнергетических установках колебательного типа. Преимуществом этих способов является отсутствие необходимости преобразования колебательного движения во вращение. Первый – это применение пьезоэлементов, о чем упоминалось выше, второй – использование линейных генераторов на постоянном магните. В [14, 15] показано, что такие генераторы также могут быть достаточно эффективны в ветроустановках рассматриваемого типа.

В целом, задача поиска наиболее эффективной конфигурации ветроэнергетических установок колебательного типа в настоящее время остается открытой.

Необходимо отметить, что отдельной проблемой в динамике ветроэнергетических установок является необходимость их торможения, когда скорость потока становится слишком большой (во избежание поломки), и разгона, когда эта скорость возвращается в допустимые пределы. Поэтому целесообразно предусмотреть возможность управления в этих системах. Одним из способов управления является регулирование нагрузки (для автономных малых ветроэнергетических установок с вертикальной осью вращения такое управление описано, в частности, в [16, 17]). Кроме того, в ряде работ (например, [11, 18]) описывается пассивное управление ветроэнергетическими установками, осуществляемое за счет перемещения внутренних масс и направленное на повышение производительности.

В статье рассматривается электромеханическая система, представляющая собой аэродинамический маятник с упруго закрепленной точкой подвеса, соединенный с линейным электрогенератором. Изучаются области устойчивости “флюгерного” положения равновесия в пространстве параметров. Анализируется возможность его стабилизации/дестабилизации путем изменения радиуса инерции маятника и коэффициента, характеризующего демпфирование и нагрузку в электрической цепи. С помощью численного моделирования исследуются периодические режимы, возникающие в этой системе, и влияние указанных параметров на область существования этих режимов.

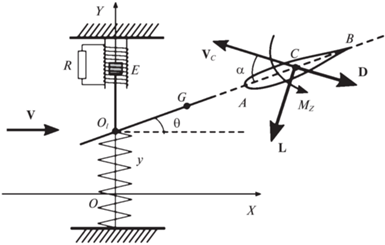
1. Описание системы и постановка задачи. Рассмотрим электромеханическую систему, состоящую из аэродинамического маятника, соединенного с линейным электрогенератором (рис. 1). Маятник представляет собой крыло с симметричным профилем, закрепленное на державке ${{O}_{1}}B$ (твердом стержне) таким образом, что хорда $AB$ крыла расположена на этом стержне. Ось вращения маятника ${{O}_{1}}$ вертикальна и закреплена на ползуне ${{O}_{1}}E$, который может двигаться вдоль неподвижной горизонтальной оси $OY$. Таким образом, маятник может совершать колебания в горизонтальной плоскости. Ползун с помощью цилиндрической пружины прикреплен к неподвижной точке O.

В точке E ползуна находится постоянный магнит. Этот магнит представляет собой сердечник линейного электрогенератора. При его возвратно-поступательном движении в обмотке генератора (катушке индуктивности) возникает электродвижущая сила (ЭДС). К обмотке генератора подключена внешняя полезная нагрузка, которая моделируется активным сопротивлением $R$.

Система помещена в поток среды, скорость которого на бесконечности постоянна, горизонтальна и перпендикулярна оси $OY$. Будем считать, что поток воздействует только на крыло и воспользуемся для описания этого воздействия квазистатическим подходом. Предположим, что аэродинамические силы (подъемная сила ${\mathbf{L}}$ и сила лобового сопротивления ${\mathbf{D}}$) приложены в середине хорды $C$, причем вектор ${\mathbf{D}}$ направлен против воздушной скорости ${{{\mathbf{V}}}_{C}}$ этой точки (т.е. ее скорости относительно набегающего потока), а ${\mathbf{L}}$ – перпендикулярно ему. Кроме того, на маятник действует аэродинамический момент ${{M}_{z}}$.

Описание аэродинамического воздействия на рабочий элемент ветроэнергетической установки представляет собой достаточно сложную задачу. Следуя [19, 20], воспользуемся квазистатическим подходом. С одной стороны, он позволяет описать поведение объекта с помощью системы обыкновенных дифференциальных уравнений. С другой стороны, он во многих случаях обеспечивает достаточно хорошую точность при моделировании. В рамках этого подхода аэродинамические силы и момент имеют следующую структуру:

Здесь $\rho $ – плотность среды, $b$ – длина хорды крыла, $S$ – площадь крыла, ${{C}_{l}}\left( \alpha \right)$, ${{C}_{d}}\left( \alpha \right)$, ${{C}_{m}}\left( \alpha \right)$ – безразмерные коэффициенты подъемной силы, лобового сопротивления и аэродинамического момента соответственно. Будем считать, что они зависят только от мгновенного угла атаки $\alpha $, под которым понимается угол между вектором ${{{\mathbf{V}}}_{C}}$ и хордой крыла. Величины ${{V}_{C}}$ и $\alpha $ удовлетворяют следующим кинематическим соотношениям:

Здесь V – скорость потока на бесконечности, $r$ – расстояние от точки подвеса до середины C хорды.

Введем неподвижную систему координат $OXY$ и будем использовать в качестве обобщенных координат величины ординату $y$ оси вращения маятника и угол $\theta $ между державкой и осью абсцисс. Будем считать без потери общности, что пружина крепления не напряжена, когда y = 0. Кроме того, предположим, что пружина имеет нелинейную жесткость: $K = k + {{k}_{3}}{{y}^{2}}$.

Для описания электромеханического взаимодействия между механической и электрической частями системы воспользуемся подходом, примененным, в частности, в [16]. Составим уравнения динамики:

Здесь $m$ – масса системы, $\xi $ – расстояние от оси вращения до центра масс $G$, ${{r}_{0}}$ – радиус инерции относительно центра масс, $h$ – коэффициент демпфирования пружины, $I$ – ток в обмотках генератора и на внешнем сопротивлении $R$, ${{L}_{c}}$ и ${{R}_{c}}$ – индуктивность и сопротивление обмоток генератора соответственно, c – коэффициент электро-механического взаимодействия.

Уравнения (1.3) вместе с соотношениями (1.2) образуют замкнутую систему.

Чтобы несколько упростить последующий анализ, обезразмерим нашу систему. Для этого введем безразмерное время $\tau = t\sqrt {k{\text{/}}m} $ и следующие безразмерные величины:

Тогда уравнения движения и кинематические соотношения примут вид:

Точка здесь обозначает производную по безразмерному времени. В дальнейшем для сокращения будем опускать черточки над безразмерными переменными.

Считаем, что индуктивность обмоток генератора достаточно мала, так что ${{\bar {L}}_{c}} \ll 1$ – малый параметр. Это означает, что электрические процессы происходят существенно быстрее, чем механические. Нетрудно показать, что условия теоремы Тихонова для системы (1.5) выполнены. Рассмотрим вырожденную систему:

Здесь $\chi = h + \varsigma {{\left( {1 + R} \right)}^{{ - 1}}}$. Этот параметр отражает суммарное влияние демпфирования в пружине и нагрузки в электрической цепи.

Исследуем положения равновесия и периодические режимы этой системы и обсудим возможность управления за счет изменения параметров.

2. Положение равновесия “вдоль потока” и его стабилизация. Для симметричного профиля ${{C}_{l}}\left( \alpha \right)$ и ${{C}_{m}}\left( \alpha \right)$ – нечетные 2π-периодические функции, а ${{C}_{d}}\left( \alpha \right)$ – четная π-периодическая функция. При этом ${{C}_{l}}\left( \pi \right) = {{C}_{m}}\left( \pi \right) = 0$ и ${{C}_{d}}\left( \alpha \right) > 0$ для всех $\alpha $.

Как видно из (1.6), величины угла отклонения державки в неподвижных точках определяются уравнением

Здесь ${{C}_{n}}\left( \theta \right)$ – так называемый коэффициент нормальной силы. Известно, что для симметричных профилей функция ${{C}_{n}}\left( \theta \right)$ обращается в нуль только при $\theta = \pi n$ ($n \in \mathbb{Z}$), а величина ${{C}_{m}}\left( \theta \right){\text{/}}{{C}_{n}}\left( \theta \right)$ ограничена. Поэтому если длина державки достаточно велика, то знак выражения ${{C}_{m}}(\theta )\, - \,r{{C}_{n}}(\theta )$ будет при всех значениях угла атаки совпадать со знаком ${{C}_{n}}\left( \theta \right)$. Соответственно уравнение (2.1) имеет только решения вида $\theta = \pi n$ ($n \in \mathbb{Z}$), и в нашей электромеханической системе (при условии, что ${{k}_{3}} > 0$) существует лишь два различных положения равновесия: $\theta = y = I \equiv 0$ и $\theta \equiv \pi ,y = I \equiv 0$. Нетрудно показать, что второе равновесие статически неустойчиво, если скорость потока не равна нулю.

Проанализируем подробнее первое равновесие, в котором маятник ориентирован вдоль потока (далее для краткости будем называть это положение “флюгерным”). Напомним, что с точки зрения преобразования энергии потока необходимо, чтобы маятник совершал колебания. Это означает, что рассматриваемое положение равновесия должно быть неустойчивым или, по крайней мере, иметь сравнительно маленькую область притяжения. С другой стороны, когда скорость потока становится относительно большой, необходимо “гасить” колебания, чтобы избежать поломки устройства. Это значит, что положение равновесия должно быть асимптотически устойчивым (или иметь достаточно большую область притяжения).

Эти требования, очевидно, противоречат друг другу. Следовательно, в системе требуется управление. Его можно обеспечить с помощью привода в шарнире, но тогда управляющий момент должен будет “парировать” аэродинамическую нагрузку, которая быстро растет с увеличением скорости потока, и питание привода может оказаться достаточно серьезной проблемой, особенно с учетом того, что установка должна работать в автономном режиме. Поэтому представляется целесообразным исследовать возможность параметрического управления. Ограничимся анализом влияния двух параметров: суммарного коэффициента демпфирования $\chi $ и радиуса инерции ${{r}_{0}}$. С технической точки зрения, первый из них можно регулировать, изменяя сопротивление во внешней цепи. Второй параметр можно изменять, например, перемещая две точечные массы таким образом, чтобы они все время были расположены симметрично относительно главной центральной оси инерции маятника, перпендикулярной плоскости движения. При этом величины всех остальных параметров системы останутся неизменными.

Запишем характеристический полином системы (1.6), линеаризованной вблизи тривиального равновесия:

Здесь использованы следующие обозначения:

Предположим, что центр масс расположен достаточно близко к точке подвеса маятника, так что

Тогда все коэффициенты полинома (2.2) положительны, и характер устойчивости определяется третьим минором матрицы Гурвица для этого полинома. Обозначим этот минор через H₃.

Нетрудно показать, что H₃ представляет собой кубический полином по $\chi $. Коэффициент при старшей степени имеет вид $r{{\zeta }^{2}}{{V}^{3}}{{\mu }^{2}}(r_{0}^{2} + {{\xi }^{2}}) > 0$, следовательно, если значение эффективного коэффициента демпфирования $\chi $ будет больше некоторого критического значения, то будет иметь место асимптотическая устойчивость. Это критическое значение, вообще говоря, зависит от скорости потока. Заметим, что, поскольку коэффициент при старшей степени $\chi $ не обращается в нуль при $V > 0$, область неустойчивости на плоскости $(V,\chi )$ не уходит на бесконечность ни при каких конечных значениях скорости потока.

Легко показать, что H₃ представляет собой биквадратный трехчлен относительно ${{r}_{0}}$, причем с учетом неравенств (2.3) свободный член всегда положителен, а коэффициент при старшей степени имеет вид

Соответственно при $V \geqslant {{V}_{1}} = \sqrt {{r \mathord{\left/ {\vphantom {r {\mu C_{l}^{\alpha }}}} \right. \kern-0em} {\mu C_{l}^{\alpha }}}} $ уравнение ${{H}_{3}} = 0$ имеет ровно один положительный корень, причем в одной из полуокрестностей точки $V = {{V}_{1}}$ один из корней стремится к $ + \infty $. В области $V \gg 1$ граница области устойчивости принимает следующий вид:

Рассмотрим случай, когда демпфирование и нагрузка отсутствуют: $\chi = 0$. Тогда уравнение ${{H}_{3}} = 0$ запишем как

Из (2.4) следует, что при $0 \leqslant V < {{V}_{1}}$ уравнение (2.4) имеет два положительных корня, причем один из этих корней стремится к $ + \infty $ при $V \to {{V}_{1}} - 0$. Учет малого $\chi $ не приводит к качественному изменению этой ситуации, по крайней мере вне области $V \ll \chi $.

Рассмотрим случай малой скорости потока: $V \ll \chi \ll 1$. Тогда знак H₃ определяется выражением $\mu \zeta r\chi V(r_{0}^{2} + {{\xi }^{2}}) > 0$. Таким образом, введение даже малого демпфирования обеспечивает стабилизацию равновесия в области малых скоростей потока. Соответственно существует такое значение ${{V}_{2}} \leqslant {{V}_{1}}$, что при ${{V}_{2}} < V \leqslant {{V}_{1}}$ уравнение ${{H}_{3}} = 0$ имеет два положительных корня, а при $0 \leqslant V < {{V}_{2}}$ – ни одного.

Из вышесказанного следует, что существует такое значение ${{r}_{{0\min }}} > 0$, что при ${{r}_{0}} < {{r}_{{0\min }}}$ равновесие асимптотически устойчиво при всех $V > 0$, а при ${{r}_{0}} > {{r}_{{0\min }}}$ на луче $V > 0$ существует ровно один интервал, внутри которого имеет место неустойчивость, а вне него – асимптотическая устойчивость.

Отметим также, что в области $V \geqslant {{V}_{1}}$ можно добиться стабилизации равновесия за счет уменьшения ${{r}_{0}}$. В то же время в области ${{V}_{2}} < V \leqslant {{V}_{1}}$ уменьшение ${{r}_{0}}$ в некоторых случаях, напротив, приводит к дестабилизации.

Чтобы проиллюстрировать зависимость области неустойчивости от параметров, построим ее численно. Примем следующие значения для безразмерных параметров:

Для зависимости аэродинамических коэффициентов от угла атаки воспользуемся экспериментальными данными для стандартного профиля NACA0012, приведенными в работе [21]. На рис. 2 изображены границы области неустойчивости флюгерного равновесия на плоскостях параметров $(V,\chi )$ и $(V,{{r}_{0}})$.

Области неустойчивости на плоскости $(V,\chi )$ расположены ниже соответствующих сплошных кривых, а области неустойчивости на плоскости $(V,{{r}_{0}})$ – между изображенными ветвями.

3. Периодические режимы и управление ими. Для исследования периодических режимов, возникающих в системе, проведем численное моделирование. Примем для безразмерных параметров значения (2.5).

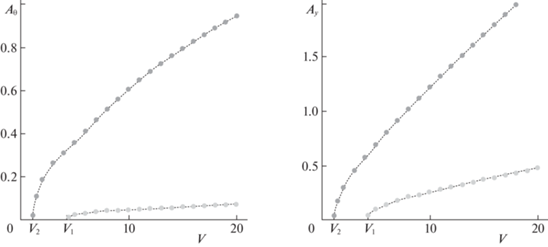
В случае, когда $\chi = 0.1$ и ${{r}_{0}} = 1$, флюгерное положение неустойчиво в диапазоне скоростей от ${{V}_{2}} \approx 1.13$ до ${{V}_{1}} \approx 4.24$. Амплитуды циклов, существующих в системе при различных значениях скорости потока, представлены на рис. 3, где ${{A}_{\theta }}$ – амплитуда по углу $\theta $, а ${{A}_{y}}$ – по перемещению $y$ точки подвеса. Притягивающие циклы отмечены черными кружками, отталкивающие – серыми. Отметим, что бифуркации Андронова–Хопфа, происходящие на границах интервала $({{V}_{2}},{{V}_{1}})$, имеют различный характер: на левой границе существует суперкритическая бифуркация, на правой – субкритическая. Численное моделирование показывает, что такая картина наблюдается в достаточно широком диапазоне значений параметров системы.

Как было отмечено выше, одной из основных целей управления является приведение маятника в положение, близкое к положению равновесия, при больших скоростях потока. Наличие отталкивающего цикла показывает, что для этого может оказаться недостаточным просто стабилизировать положение равновесия. Чтобы гарантировать гашение колебаний, желательно изменить параметры таким образом, чтобы притягивающий и отталкивающий циклы исчезли.

Изменить положение центра масс и радиус инерции можно, например, за счет перемещения внутренних точечных масс, связанных с маятником. При этом изменение $\xi $ обязательно влечет за собой изменение ${{r}_{0}}$ (учитывая, что масса неизменяемых частей маятника не равна нулю). Поэтому при анализе динамики маятника с таким управлением необходимо задаться конкретной схемой перемещения внутренних масс. Рассмотрение различных вариантов таких схем остается вне рамок настоящей работы. В то же время, радиус инерции можно изменять независимо от других параметров (например, перемещая две одинаковые точечные массы таким образом, чтобы их центр масс был неподвижен относительно державки).

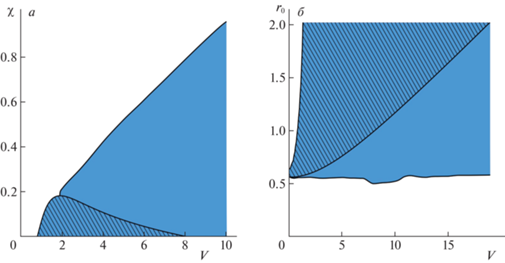
Рассмотрим влияние параметров $\chi $ и ${{r}_{0}}$ на область существования притягивающего колебательного режима. Построим область существования притягивающего цикла на плоскости $(V,\chi )$, используя метод продолжения по параметру. Значение радиуса инерции примем фиксированным: ${{r}_{0}} = 1$. Результаты расчетов приведены на рис. 4, а. Штриховкой изображена область, в которой флюгерное равновесие неустойчиво, а сплошной заливкой – область, в которой существует притягивающий колебательный режим.

Видно, что есть область значений параметров, в которой положение равновесия асимптотически устойчиво, но при этом существует притягивающий цикл. Таким образом, для гарантированного гашения колебаний при фиксированной скорости потока V (а не просто обеспечения асимптотической устойчивости равновесия) требуется достаточно сильно увеличить нагрузку: $\chi > {{\chi }_{{cr}}}(V)$. Заметим, что в диапазоне скоростей $V > 2$ критическая величина ${{\chi }_{{cr}}}$ почти линейно растет с ростом $V$. В то же время, возможности изменения величины $\chi $ за счет внешнего сопротивления ограничены, поскольку $\chi \leqslant h + \varsigma $ при любых значениях $R$.

Теперь рассмотрим влияние радиуса инерции на область существования притягивающего колебательного режима. Расчеты будем проводить при $\chi = 0$, поскольку случай, когда демпфирование в пружине и нагрузки отсутствуют, по-видимому, представляет собой “наихудший” вариант с точки зрения стабилизации положения равновесия.

Результаты численного моделирования проиллюстрированы на рис. 4, б. Область неустойчивости на плоскости $(V,{{r}_{0}})$ выделена пунктиром, а область существования притягивающего колебательного режима – сплошной заливкой. Видно, что при радиусе инерции ${{r}_{0}} \leqslant 0.5$ притягивающий предельный цикл отсутствует при всех рассмотренных значениях скорости потока. Соответственно уменьшение момента инерции не только стабилизирует флюгерное положение равновесия, но и обеспечивает для него достаточно большую область притяжения.

Таким образом, алгоритм управления может выглядеть следующим образом: в случае увеличения скорости ветра сверх критического значения радиус инерции уменьшается до величины порядка 0.5. Притягивающий цикл исчезает, и маятник приходит в асимптотически устойчивое флюгерное положение равновесия. При уменьшении скорости ветра до безопасного значения радиус инерции увеличивается, принимая “рабочее” значение. При этом флюгерное положение дестабилизируется, и маятник выходит на притягивающий колебательный режим.

Вообще говоря, для некоторого ускорения переходных процессов можно регулировать нагрузку: увеличивать ее до максимума ($\chi = h + \varsigma $, внешняя электрическая цепь замкнута накоротко) при торможении и уменьшать ее до минимального возможного значения ($\chi = h$, электрическая цепь разомкнута) при разгоне.

Проведем численное моделирование поведения маятника в случае, когда скорость потока представляет собой кусочно-постоянную функцию:

Будем считать, что управление радиусом инерции осуществляется следующим образом:

Пусть целевая величина нагрузки составляет $\chi = {{\chi }_{0}} = 0.1$. Рассмотрим два варианта управления нагрузкой: без управления и с управлением в соответствии со следующим алгоритмом:

Здесь ${{\tau }_{2}}$ – момент, когда скорость потока становится меньше порогового значения ${{V}_{*}}$, а $T$ – длительность задержки до возврата к целевому значению нагрузки.

Примем следующие значения параметров управления:

Пусть ${{V}_{1}} = 2$, ${{V}_{2}} = 10$, ${{\tau }_{1}} = 50$, ${{\tau }_{2}} = 100$. Для остальных параметров будем использовать те же значения, что и ранее. Кроме того, проведем моделирование без управления как радиусом инерции, так и нагрузкой.

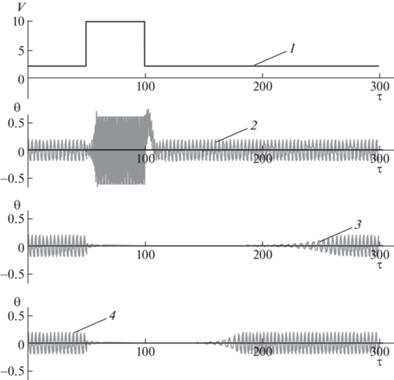
Результаты расчетов представлены на рис. 5. Видно, что в случае, когда управление отсутствует, увеличение скорости потока приводит к существенному росту амплитуды и частоты колебаний. В то же время предложенный алгоритм управления обеспечивает торможение установки при увеличении скорости потока. Следует отметить, что выход на режим после возвращения скорости к нормальному значению происходит достаточно медленно. Однако управление нагрузкой позволяет заметно ускорить этот процесс.

Заключение. Рассмотрена динамика ветроэнергетической установки колебательного типа, представляющей собой аэродинамический маятник с упруго закрепленной точкой подвеса, сопряженный с линейным электрическим генератором на постоянном магните. Исследовано влияние параметра, характеризующего нагрузку в электрической цепи, и радиуса инерции маятника на устойчивость флюгерного положения равновесия. Показано, в частности, что уменьшение радиуса инерции маятника обеспечивает стабилизацию этого положения. Проанализировано влияние указанных параметров на область существования притягивающего колебательного режима в системе. Предложена стратегия управления радиусом инерции, обеспечивающая гашение колебаний в случае, когда скорость потока оказывается слишком большой.