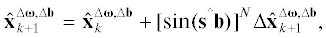Известия РАН. Теория и системы управления, 2022, № 4, стр. 143-159
ИССЛЕДОВАНИЕ АЛГОРИТМОВ ОПРЕДЕЛЕНИЯ УГЛОВОГО ДВИЖЕНИЯ НАНОСПУТНИКА НА ЛАБОРАТОРНОМ СТЕНДЕ
А. А. Болотских a, Р. Н. Жарких a, Д. С. Иванов b, *, С. В. Лебедев a, С. С. Ткачев b
a ООО Спутникс
Москва, Россия
b ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: danilivanovs@gmail.com
Поступила в редакцию 24.01.2022
После доработки 01.02.2022
Принята к публикации 28.03.2022
- EDN: NUTNXH
- DOI: 10.31857/S0002338822040023
Аннотация
Рассматриваются алгоритмы определения углового движения наноспутника на основе расширенного фильтра Калмана с использованием измерений бортовых солнечных датчиков, магнитометра и датчика угловой скорости. Эксперименты выполняются на стенде с аэродинамическим подвесом. Проводится лабораторное исследование влияния наиболее значимых параметров алгоритма на качество его работы – точность получаемых оценок и времени сходимости. Для алгоритма определения с помощью измерений магнитометра и солнечных датчиков ключевым фактором является зависимость точности оценок от угла между векторами направления на Солнце и локальным геомагнитным полем. Предложены и протестированы модификации алгоритмов определения углового движения, уменьшающих это влияние.
Введение. Перед запуском космических аппаратов проводится серия наземных тестов и лабораторных испытаний всех бортовых систем. Для тестирования и отладки алгоритмов определения и управления углового движения часто применяются лабораторные стенды, позволяющие в некоторой степени имитировать условия космического полета с точки зрения динамики и внешней среды. Это обеспечивает корректную работу исполнительных органов и бортовых датчиков. Одним из наиболее распространенных стендов является стенд с использованием аэродинамического подвеса. Благодаря подаваемому сжатому воздуху между двумя вложенными полусферами образуется небольшой зазор – воздушная подушка, обеспечивающая угловое движение плавающей полусферы практически без трения. К полусфере крепится платформа, на которую устанавливается либо макет системы ориентации космического аппарата, либо весь аппарат в сборе. Платформа имеет три угловые степени свободы, однако неограниченное движение возможно только относительно вертикальной оси; по двум другим осям аппарат может совершать только ограниченные повороты [1, 2]. Аэродинамический подвес обычно помещается в имитатор геомагнитного поля на основе колец Геймгольца, что позволяет создавать изменяющееся в соотвествии с движением аппарата по орбите магнитное поле. Для тестирования алгоритмов определения углового движения с использованием измерений солнечных датчиков к стенду добавляют имитатор Солнца. Подобные стенды с аэродинамическим подвесом достаточно широко распространены в зарубежных и отечественных университетах и исследовательских центрах [3–10].
Угловое движение спутника в космическом пространстве и макета на аэродинамическом подвесе описывается одними и теми же уравнениями движения, но различаются внешние возмущения, действующие на тело. Основное возмущение, обуславливающее движение макета, вызвано действием момента гравитационной силы вследствие отличия “точки подвеса” (неподвижной точки) и центра масс системы. Влияние этого доминирующего момента на динамику углового движения можно уменьшить с помощью процедуры балансировки [11–14], однако полностью исключить не удается. На практике это приводит к некоторому отличию результатов моделирования работы алгоритмов определения углового движения, предназначенных для работы в условиях орбитального полета, и результатов лабораторных экспериментов. Несмотря на отличия моделей углового движения макета наноспутника на аэродинамическом подвесе и спутника на орбите, на стенде удается проверить работоспособность бортовых алгоритмов управления ориентацией и оценки углового движения. Благодаря имитации внешней среды орбитального полета с помощью имитатора геомагнитного поля и имитатора Солнца, а также системе независимых измерений углового движения представляется возможным исследовать характеристики работы алгоритмов определения на основе измерения магнитометра, солнечного датчика, датчика угловой скорости (ДУС) и звездного датчика. Особый интерес для наноспутников представляют достижимые точности, которые можно получить без звездного датчика на освещенной и теневой стороне низкой околоземной орбиты. В работе приводятся результаты лабораторных исследований бортовых алгоритмов оценки углового движения наноспутника типа 3U CubeSat. Алгоритмы основаны на расширенном фильтре Калмана, в вектор состояния включены кватернион ориентации, вектор угловой скорости, а также смещение нуля измерений магнитометра, вызванное переменными бортовыми магнитными полями аппарата, и смещение ноля измерений ДУС. На освещенной части орбиты точность оценки углового положения зависит от угла между вектором геомагнитной индукции и направлением на Солнце, при коллинеарности этих направлений наблюдается резкое увеличение ошибок. В статье предложен подход, который позволяет уменьшить эти ошибки оценки вектора состояния.
1. Стенд для имитации углового движения микроспутников. В работе используется стенд для испытаний алгоритмов управления угловым движением макетов наноспутников, разработанный компанией СПУТНИКС [15]. В состав стенда входят имитатор магнитного поля, имитатор Солнца, макет системы ориентации микроспутника и аэродинамический подвес. Фото стенда представлено на рис. 1, а, платформа с установленным на ней наноспутником формата 3U CubeSat изображена на рис. 1, б. Платформа благодаря воздушной подушке способна совершать трeхосное угловое движение относительно точки подвеса.
Рис. 1.
Стенд с аэродинамическим подвесом (а), платформа с установленным наноспутником формата 3U CubeSat на аэродинамическом подвесе (б)

В общем случае вследствие произвольного распределения массы в аппарате положение точки подвеса не совпадает с центром масс системы и возникает момент силы тяжести, который влияет на угловое движение системы. Чтобы уменьшить влияние этого момента, на макете установлена система балансировки, состоящая из набора грузов, которые перемещаются вдоль осей системы координат, связанной с платформой. Однако установить положение центра масс относительно точки подвеса возможно с точностью около 10 мкм [14], что делает момент силы тяжести самым значительным возмущением, действующим на платформу с аппаратом.
Для определения углового движения платформы с наноспутником используется система независимых измерений на основе оптических измерений. Она с помощью обработки изображений, получаемых с камеры, неподвижно установленной на имитаторе геомагнитного поля, определяет по специальным меткам на платформе угловое положение макета относительно неподвижной лабораторной системы координат. Среднеквадратическая ошибка определения углового положения макета с помощью системы оптических измерений составляет ${{\sigma }_{{{\text{изм}}}}} = 0.2^\circ $, частота поступающих измерений – около 5 Гц.
Для имитации геомагнитного поля в составе стенда используется система из трех пар установленных взаимно перпендикулярно квадратных катушек, называемых кольцами Гельмгольца (рис. 1). Стороны квадратов пар катушек имеют размеры 2; 1.9; 1.8 м. Данная система способна создавать практически однородное магнитное поле до 200 мТл в заданной области, которая представляет собой шар с диаметром 650 мм.
Имитатор Солнца создает постоянный параллельный световой поток на расстоянии до 1.5 м мощностью не менее 80 000 лк. В качестве имитатора Солнца используется прожектор PAR-64 с лампой Philips 1000W230V.
Для проведения экспериментов использовалась модель наноспутника 3U CubeSat, имеющего размеры 10 × 10 × 30 см. Масса аппарата составляет 3.5 кг. Тензор инерции наноспутника вместе с платформой, записанный в строительных осях, которые направлены вдоль граней параллелепипеда с началом в геометрическом центре аппарата, согласно расчетам в SolidWorks, имеет следующий вид:
На модели наноспутника установлен набор магнитных катушек и блок маховиков для управления угловым движением. Для определения углового движения используются измерения солнечных датчиков, магнитометра и ДУС. Цель статьи заключается в лабораторном исследовании характеристик работы алгоритмов определения углового движения с применением этого набора датчиков.
2. Модель движения и модель измерений. Движение платформы с наноспутником описывается с помощью динамических уравнений Эйлера. Используемые переменные можно разделить на две группы. Первую группу составляют компоненты ${{\omega }_{1}},\,\,{{\omega }_{2}},\,\,{{\omega }_{3}}$ абсолютной угловой скорости спутника ${\mathbf{\omega }}$, записанные в осях связанной с телом системы координат. Для описания ориентации применяется кватернион $\left( {{\mathbf{q}},\,\,{{q}_{0}}} \right)$, где ${\mathbf{q}}$ – векторная, ${{q}_{0}}$ – скалярная часть кватерниона [16]. Динамические уравнения Эйлера движения твердого тела относительно неподвижной точки имеют вид
В случае движения наноспутника на стенде в качестве возмущающего момента рассматривается момент силы тяжести, который записывается в связанной с макетом системе координат в точке подвеса следующим образом:
Динамические уравнения дополняются кинематическими уравнениями. При использовании кватерниона $\left( {{\mathbf{q}},\,\,{{q}_{0}}} \right)$ – это векторное уравнение следующего вида:
Рассмотрим модели измерений бортовых датчиков – солнечных датчиков, магнитометра и ДУС. В модель измерений магнитометра и ДУС включены смещения нулей измерений, которые на практике являются непостоянными, что усложняет возможность их нахождения с помощью наземной калибровки. Измерения магнитометра ${{{\mathbf{b}}}_{{{\text{изм}}}}}$, солнечных датчиков ${{{\mathbf{s}}}_{{{\text{изм}}}}}$ и ДУС ${{{\mathbf{\omega }}}_{{{\text{изм}}}}}$ описываются следующими моделями:
3. Алгоритмы оценки углового движения. Для определения углового движения наноспутника рассматриваются два типа алгоритмов: локальный алгоритм TRIAD и алгоритм на основе расширенного фильтра Калмана.
Локальный алгоритм TRIAD не использует модель ошибок измерений и является более грубым способом оценки ориентации, но не требующим больших вычислительных затрат [17]. С помощью измерений солнечных датчиков и магнитометра можно вычислить единичные векторы направления на центр диска Солнца ${{{\mathbf{s}}}_{{{\text{изм}}}}}$ и направление локального магнитного поля ${{{\mathbf{b}}}_{{{\text{изм}}}}}$ в связанной с наноспутником системе координат. Для известного положения центра масс аппарата, согласно моделям направления на Солнце и геомагнитного поля Земли, эти же векторы ${\mathbf{s}}$ и ${\mathbf{b}}$ вычисляются в системе координат, связанной с Землей. Переход из инерциальной системы координат в связанную задается матрицей ориентации ${\mathbf{A}}$ и определяется соотношением
По двум непараллельным векторам можно построить ортонормированные базисы в связанной с телом и инерциальной системах координат:
Ортогональная матрица ${\mathbf{A}}$, удовлетворяющая уравнениям
выражается следующей формулой:Эта матрица перехода и является оценкой ориентации аппарата, согласно алгоритму TRIAD.
Определение углового движения наноспутников можно выполнить на основе постполетной реконструкции движения, как в работах [18, 19], или на борту аппарата в режиме реального времени [20]. Фильтр Калмана, несмотря на ограничения по бортовым вычислительным мощностям, широко используется на малогабаритных космических аппаратах. Фильтр Калмана разработан для линейных динамических систем и дает наилучшую оценку вектора состояния по среднеквадратическому критерию [21–23]. Однако расширенный фильтр Калмана применяется для нелинейных моделей как динамической системы, так и измерений:
Для построения фильтра функции ${\mathbf{f}}({\mathbf{x}},t)\,\,{\text{и}}\,\,{\mathbf{h}}({\mathbf{x}},t)$ представляются в виде разложения в ряд Тейлора в окрестности оценки текущего вектора состояния. После этого удерживаются только линейные члены разложения. Матрица динамики системы и матрица модели измерений вычисляются как
Для расширенного фильтра Калмана при дискретно поступающих измерениях вектор состояния на этапе прогноза вычисляется путем интегрирования нелинейных уравнений движения и на этапе коррекции используется нелинейная модель измерений. Пусть в некоторый момент ${{t}_{{k - 1}}}$ известна оценка вектора состояния ${\mathbf{\hat {x}}}_{{k - 1}}^{ + }$ с ковариационной матрицей ${\mathbf{P}}_{{k - 1}}^{ + }$. Работа расширенного дискретного фильтра Калмана описывается с помощью следующих двух этапов.
Этап прогноза:
Этап коррекции:
Вектор состояния фильтра Калмана состоит из векторной части кватерниона ориентации, вектора угловой скорости, а также смещения нулей измерений магнитометра и ДУС:
После линеаризации уравнений движения матрица динамики имеет следующий вид:
Здесь ${{[{\mathbf{a}}]}_{ \times }}$ обозначает кососимметрическую матрицу, заполненную заданными компонентами вектора ${\mathbf{a}} = {{\left[ {\begin{array}{*{20}{c}} {{{а}_{1}}}&{{{а}_{2}}}&{{{а}_{3}}} \end{array}} \right]}^{T}}$:
Матрица измерений зависит от набора применяемых датчиков. Для случая использования измерений всех трех датчиков она имеет следующий вид:
Точность оценок фильтра Калмана зависит от весовой матрицы ${\mathbf{K}}$. Элементы этой матрицы сложным образом зависят от начального значения матрицы ошибок ${\mathbf{P}}(0) = M[\Delta {\mathbf{x}}\left( {{{t}_{0}}} \right)\Delta {{{\mathbf{x}}}^{{\text{T}}}}\left( {{{t}_{0}}} \right)]$, где $\Delta {\mathbf{x}}\left( {{{t}_{0}}} \right)$ – вектор ошибок априорного вектора состояния в начальный момент времени ${{t}_{0}}$, от задания матрицы ошибки модели движения Q и матрицы шума измерений ${\mathbf{R}}$. Матрицы ${\mathbf{P}}(0)$, Q, ${\mathbf{R}}$ выбираются в соответствии с параметрами системы. Однако зачастую реальные параметры системы известны неточно и отличаются от предполагаемых значений, используемых в фильтре Калмана. Поэтому возникает задача нахождения таких параметров фильтра Калмана, при которых оценка будет наилучшей при заданных неучтенных шумах модели и измерений, которые имеют ненулевое математическое ожидание. Эта процедура называется настройкой фильтра Калмана.
Точность оценок фильтров Калмана, основанных на измерениях магнитометра и солнечного датчика, зависит от угла между вектором направления на Солнце и вектором геомагнитного поля. При движении по орбите могут возникать такие ситуации, когда эти векторы становятся близкими к коллинеарным. В этом случае оценки вектора состояния ухудшаются до уровня, если бы использовались измерения только одного позиционного датчика. В настоящей работе на этапе коррекции вектора состояния весовую матрицу ${\mathbf{K}}$ предлагается умножить на некоторый коэффициент меньше 1, зависящий от угла между ${\mathbf{s}}$ и ${\mathbf{b}}$. При таком подходе после сходимости оценки фильтра Калмана будут больше опираться на результат интегрирования уравнений движения, чем на корректировку оценок при получении измерений, и при уменьшении угла между ${\mathbf{s}}$ и ${\mathbf{b}}$ не произойдет значительного ухудшения точности. Однако некоторое ухудшение точности все же неизбежно, так как неучтенные в фильтре Калмана возмущения приведут к ошибкам в интегрировании уравнений движения. Как показали результаты численных исследований, ухудшение точности происходило в основном за счет неправильной оценки смещений нулей датчиков в ситуации, когда ${\mathbf{s}}$ и ${\mathbf{b}}$ почти коллинеарны. Поэтому вышеприведенная формула для коррекции смещений нуля датчиков была преобразована к виду
где k – номер итерации, ${\mathbf{\hat {x}}}_{{}}^{{\Delta {\mathbf{\omega }},\Delta {\mathbf{b}}}}$ – часть вектора состояния, содержащая оценки смещений нулей магнитометра и ДУС,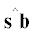 – угол между векторами на Солнце и магнитного поля, $\Delta {\mathbf{\hat {x}}}_{k}^{{\Delta {\mathbf{\omega }},\Delta {\mathbf{b}}}}$ – величина коррекции смещения нулей датчиков, $N$ – настроечный параметр.
– угол между векторами на Солнце и магнитного поля, $\Delta {\mathbf{\hat {x}}}_{k}^{{\Delta {\mathbf{\omega }},\Delta {\mathbf{b}}}}$ – величина коррекции смещения нулей датчиков, $N$ – настроечный параметр.
4. Лабораторные исследования алгоритмов определения углового движения. Процесс настройки и исследования работы фильтров Калмана происходит в два этапа: численное моделирование орбитального углового движения и проведение экспериментов на лабораторном стенде. Моделирование позволяет найти параметры фильтров и оценить точность определения углового движения с учетом выбранных наиболее существенных возмущающих моментов, действующих на аппарат. При проведении лабораторных экспериментов на аппарат действует неучтенный в модели движения момент силы гравитации. На оценки точности работы алгоритмов в лабораторных условиях влияют неточности имитатора Солнца, имеющего угол расхождения, неравномерность создания магнитного поля катушками Геймгольца, а также неточность определения ориентации системой независимых измерений. Совокупность перечисленных факторов приводит к ситуации, в которой наилучшие настройки алгоритмов при математическом моделировании и при проведении эксперимента отличаются. Альтернативой является использование грубых коэффициентов, не приводящих к существенному ухудшению точности ни в одном из видов моделирования работы системы определения углового движения.
В таблице 1 приведены параметры фильтра Калмана для моделирования и проведения экспериментов на стенде. При математическом моделировании рассматривалась солнечно-синхронная орбита наклонением 97.2° и высотой 470 км.
Таблица 1.
Параметры фильтра Калмана
| Название | Величина |
|---|---|
| Среднеквадратичное отклонение (солнечные датчики, магнитометр, датчик угловой скорости) | $\sigma _{s}^{{}} = 0.01^\circ $, $\sigma _{b}^{{}} = 100\,\,{\text{нТл}}$, $\sigma _{\omega }^{{}} = 0.05\,{\text{град/c}}$ |
| Начальные значения диагональных элементов матрицы ${\mathbf{P}}$ | $\sigma _{{\mathbf{q}}}^{2} = {{10}^{{ - 2}}}$, $\sigma _{{\mathbf{\omega }}}^{2} = {{10}^{{ - 2}}}{{{\text{с}}}^{{ - 2}}}$, $\sigma _{{\Delta {\mathbf{\omega }}}}^{2} = {{10}^{{ - 6}}}{{{\text{с}}}^{{ - 2}}}$, $\sigma _{{\Delta {\mathbf{b}}}}^{2} = 1$ |
| Диагональные элементы матрицы ${\mathbf{D}}$ для освещенного участка орбиты | $\sigma _{{\mathbf{d}}}^{2} = {{10}^{{ - 10}}}{{{\text{н}}}^{2}} \cdot {{{\text{м}}}^{2}}$, $\sigma _{{\Delta {\mathbf{\omega }}}}^{2} = {{10}^{{ - 8}}}{{{\text{с}}}^{{ - 2}}}$, $\sigma _{{\Delta {\mathbf{b}}}}^{2} = {{10}^{{ - 9}}}$ |
| Диагональные элементы матрицы ${\mathbf{D}}$ для теневого участка орбиты | $\sigma _{d}^{2} = {{10}^{{ - 9}}}{{{\text{н}}}^{2}} \cdot {{{\text{м}}}^{2}}$, $\sigma _{{\Delta {\mathbf{\omega }}}}^{2} = {{10}^{{ - 14}}}{{{\text{с}}}^{{ - 2}}}$, $\sigma _{{{{\Delta }}{\mathbf{b}}}}^{2} = {{10}^{{ - 10}}}$ |
4.1. Результаты моделирования работы алгоритмов на освещенном участке орбиты. Для тестирования работы расширенного фильтра Калмана на освещенной части орбиты задается режим движения с переориентацией. На рис. 2 представлены суммарный угол рассогласования текущей и требуемой ориентации и угол между направлением вектора локального геомагнитного поля и направлением на Солнце. Большие углы рассогласования на интервале от начала до 100 с объясняются переходными процессами при стабилизации в орбитальной системе координат. Скачок в рассогласовании в момент 200 с обусловлен маневром переориентации. На графике угла между векторами ${\mathbf{s}}$ и ${\mathbf{b}}$ можно наблюдать интервалы, когда векторы становятся близкими к коллинеарным, а именно на интервале 800–1000 с. На рис. 3 приведены результаты оценки смещений нулей магнитометра и ДУС. Благодаря предложенной модификации алгоритма при приближении угла к критическому значению коррекция смещений нулей не происходит, что положительно сказывается на общей точности оценок фильтра. Эмпирическим путем было выбрано значение настроечного параметра N = 4.
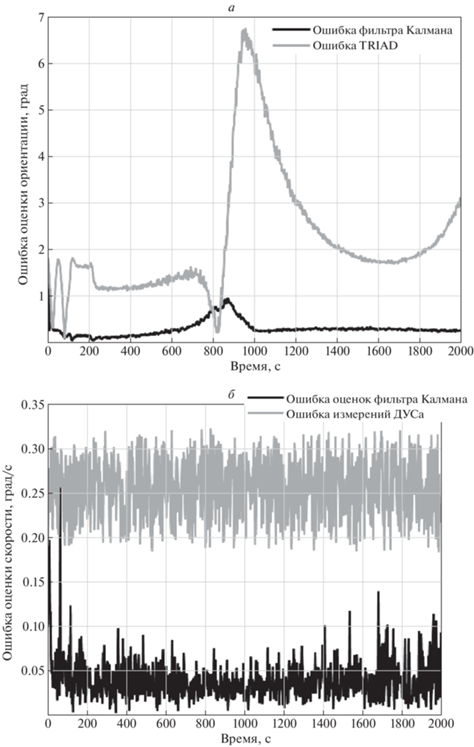
Сравнивая результаты работы алгоритма TRIAD и фильтра Калмана, на рис. 4, а можно увидеть, что на интервале 800–1000 с ошибка оценки локального алгоритма превышает 6°, в то время как ошибка фильтра находится в пределах 1.5°. Вне критического интервала угла между ${\mathbf{s}}$ и ${\mathbf{b}}$ точность TRIAD составляет около 1.5°, фильтра Калмана – 0.5°. На рис. 4, б представлена ошибка оценки угловой скорости, полученной с помощью фильтра Калмана, и ошибка измерений ДУС, которая имеет значительно большее значение за счет смещения нуля измерений.
4.2. Результаты лабораторных экспериментов при работе алгоритмов на освещенном участке орбиты. Магнитное поле на стенде моделируется в соответствии с орбитальным движением спутника, идентичным рассмотренному выше случаю. Однако положение имитатора Солнца на стенде отличается от направления на Солнце при математическом моделировании. Поэтому угол между ${\mathbf{s}}$ и ${\mathbf{b}}$ отличается от результатов моделирования (рис. 5). Критический интервал с неблагоприятными углами между ${\mathbf{s}}$ и ${\mathbf{b}}$ наблюдается на участке между 500–700 с. Во время эксперимента система стабилизации удерживает требуемое угловое положение в лабораторной системе координат.
Рис. 5.
Точность алгоритмов определения ориентации от времени (а), изменение угла между ${\mathbf{s}}$ и ${\mathbf{b}}$ от времени (б)
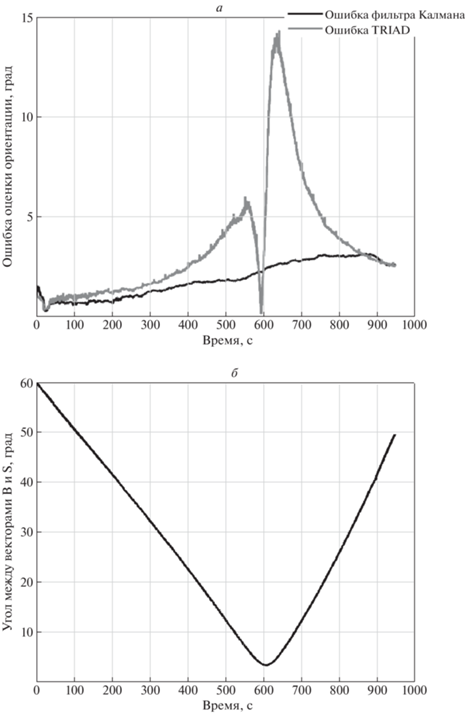
Точность алгоритмов оценивалась с использованием системы независимых измерений. С течением времени изменялся угол между вектором магнитного поля и направлением на Солнце, что приводило к резкому снижению точности алгоритма TRIAD. На рис. 5, а приведена разность оценок углового положения, полученных с помощью алгоритмов определения ориентации и системой независимых измерений. На графике для алгоритма TRIAD виден резкий скачок ошибки до 15° около момента времени 630 с. При этом ошибка фильтра Калмана также ухудшается, однако подобного скачка не имеет. Сопоставив эти графики с углом между ${\mathbf{s}}$ и ${\mathbf{b}}$ (рис. 5, б), заметим, что ухудшение точности происходит синхронно с приближением угла между ${\mathbf{s}}$ и ${\mathbf{b}}$ к нулевому значению. Отметим, что наблюдаемые в лабораторном эксперименте ошибки алгоритмов отличаются от результатов моделирования. Это обусловлено отличием максимального приближения к коллинeарности векторов ${\mathbf{s}}$ и ${\mathbf{b}}$ и влиянием неучтенного в уравнениях движения момента силы тяжести, воздействующего на движение платформы с наноспутником.
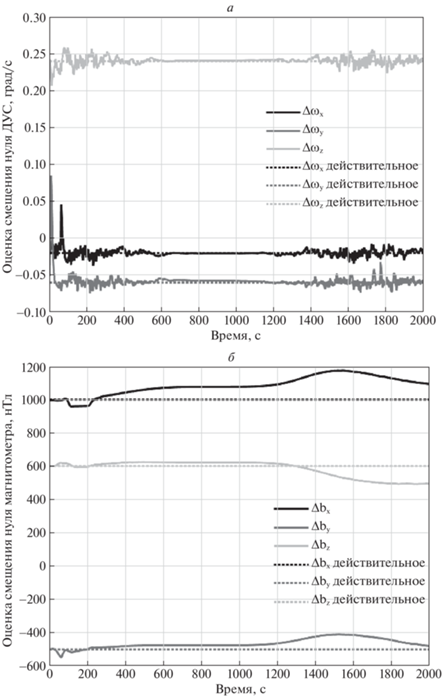
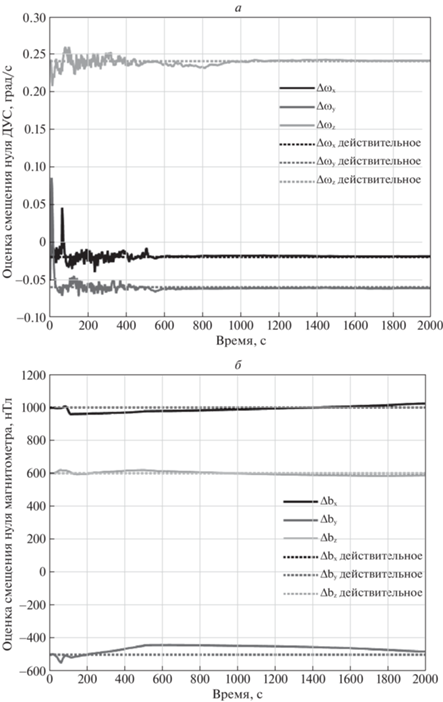
На рис. 6 представлено изменение оценки смещений нулей датчиков от времени. Соотнеся их с графиком изменения угла между ${\mathbf{s}}$ и ${\mathbf{b}}$, можно заметить, что коррекция этих параметров происходит более активно при отдалении от критического значения угла между ${\mathbf{s}}$ и ${\mathbf{b}}$, а при его приближении к коллинеарности векторов – фиксируется.
4.3. Результаты моделирования работы алгоритма на теневом участке орбиты. На рис. 7 и 8 можно увидеть результаты моделирования для ситуации потери измерений датчиков Солнца, которое может происходить на теневом участке орбиты. Заметим, что в момент потери телеметрии солнечных датчиков в точке 500 с выключается алгоритм TRIAD, а фильтр Калмана на основе измерений солнечного датчика, магнитометра и ДУС переключается на режим работы с использованием только магнитометра и ДУС. График оценки точности алгоритма TRIAD после выключения солнечных датчиков показывает разность последнего значения алгоритма и текущей ориентации, что на теневой стороне орбиты является неадекватным значением. В момент выключения солнечных датчиков наблюдается ухудшение точности фильтра Калмана. На приведенных далее графиках оценок смещений нулей датчиков видно, что коррекция значений практически не выполняется за счет задания другого набора параметров фильтра Калмана, представленных в таблице.
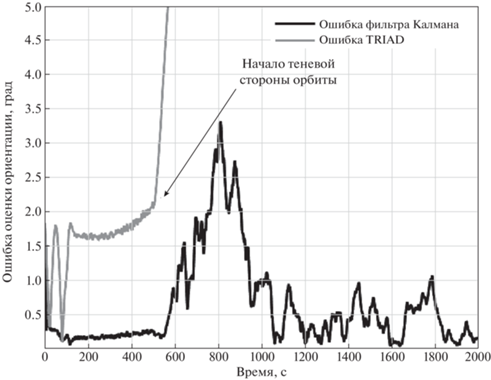
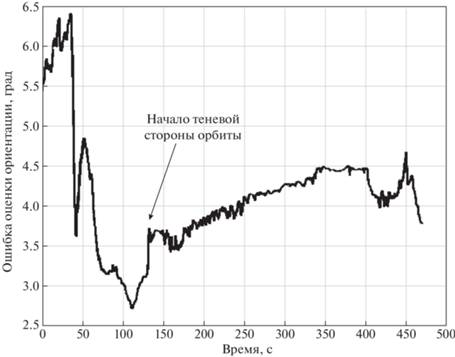
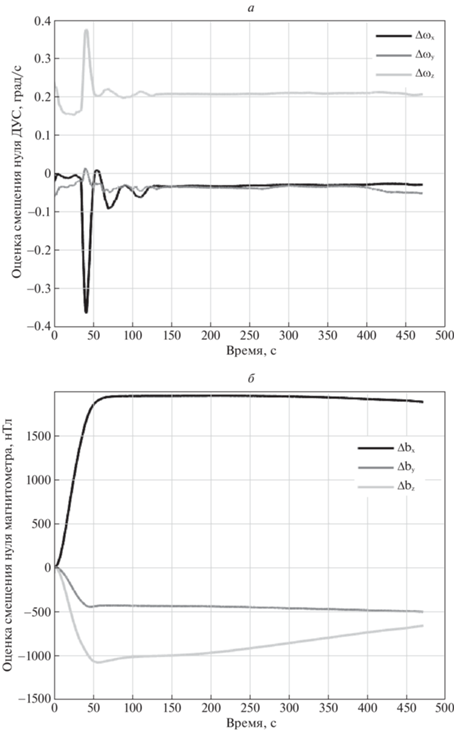
4.4. Результаты экспериментов при работе алгоритма на теневом участке орбиты. На рис. 9 и 10 можно увидеть результаты эксперимента на стенде. На первом графике приведено отклонение оценок ориентации фильтра Калмана от оценок системы независимых измерений. Рисунок 10 демонстрирует изменение оценки смещений нулей датчиков. До момента выключения имитатора Солнца в момент около 130 с наблюдается процесс сходимости оценок фильтра Калмана, в момент выключения ошибка определения ориентации составила около 3°. После выключения имитатора Солнца точность ухудшилась, но не превышала ошибки в 4.5° на протяжении более 300 с. На рис. 10 также наблюдается процесс сходимости оценок смещения нулей. После выключения имитатора Солнца значения оценок смещений нулей датчиков остаются на прежнем уровне. С течением времени наблюдается плавное изменение этих значений, вызванное влиянием неучтенного момента силы тяжести.
Рис. 10.
Оценка смещения нуля датчика угловой скорости (а) и магнитометра с помощью фильтра Калмана (б)
Заключение. Приведены результаты исследования алгоритмов определения углового движения с использованием математического моделирования их работы и с помощью полунатурного стенда, позволяющего имитировать угловое движение наноспутника и создавать внешние условия, необходимые для измерений бортовых датчиков. Вследствие влияния неучтенного в модели движения момента силы тяжести, возникающего из-за смещения центра масс системы относительно точки подвеса, ошибки оценок алгоритмов на основе расширенного фильтра Калмана несколько отличаются от результатов математического моделирования. Однако алгоритмы имеют похожее качественное поведение ошибок в зависимости от угла между направлением локального геомагнитного поля и направления на Солнце. Предложенная модификация расширенного фильтра Калмана, позволяющая уменьшить коррекцию оценок смещения нулей магнитометра и ДУС при приближении векторов к коллинеарности, приводит к уменьшению ошибки оценки ориентации.
Список литературы
Ovchinnikov M., Ivanov D., Ivlev N. et al. Development, Integrated Investigation, Laboratory and In-Flight Testing of Chibis-M Microsatellite ADCS // Acta Astronautica. 2014. V. 93. P. 23–33.
Иванов Д.С., Карпенко С.О., Овчинников М.Ю. и др. Испытания алгоритмов управления ориентацией микроспутника “Чибис-М” на лабораторном стенде // Изв. РАН. ТиСУ. 2012. № 1. С. 118–137.
Haeussermann W., Kennel H. A Satellite Motion Simulator // Automatica. 1960. V. 5. № 12. P. 22–25; 90–91.
Peck M., Miller L., Cavender A. et al. An Airbearing-Based Testbed for Momentum Control Systems and Spacecraft Line of Sight // Advances in the Astronautical Sciences. 2003. V. 114. P. AAS 03-127.
Cordova S.S.F., DeBra D.B. Mass Center Estimation of a Drag-Free Satellite // Proc. of the 6th Triennial World Congr. of the IFAC. Boston, 1975.
Prado J., Bisiacchi G., Reyes L. et al. Three-axis Air-bearing Based Platform for Small Satellite Attitude Determination and Control Simulation // J. Applied Research and Technology. 2005. V. 3. № 3. P. 222–237.
Post M.A., Li J., Lee R. Design and Construction of a Magnetic Field Simulator for CubeSat Attitude Control Testing // J. Instrumentation, Automation and Systems. 2014. V. 1. № 1. P. 1–9.
Prinkey M., Miller D., Bauer P. et al. CubeSat Attitude Control Testbed Design: Merritt 4-Coil per Axis Helmholtz Cage and Spherical Air Bearing // AIAA Guidance, Navigation, and Control (GNC) Conf. Reston, Virginia, 2013.
Silva R., Ishioka I., Cappelletti C. et al. Helmholtz Cage Design and Validation for Nanosatellites HWIL Testing // IEEE Transactions on Aerospace and Electronic Systems. 2019. V. 55. № 6. P. 3050–3061.
Pastena M., Sorrentino L., Grassi M. Design and Validation of the University of Naples Space Magnetic Field Simulator (SMAFIS) // J. IEST. Institute of Environmental Sciences & Technology. 2001. V. 44. № 1. P. 33–42.
Kim J.J., Agrawal B.N. Automatic Mass Balancing of Air-Bearing-Based Three-Axis Rotational Spacecraft Simulator // J. Guidance, Control, and Dynamics. 2009. V. 32. № 3. P. 1005–1017.
Wang S., Ma J., Gao S. Balancing Methods on the Three-Axis Air-Bearing Platform // Asia Simulation Conf. Shaghai: Springer, 2012. P. 117–125.
Chesi S., Gong Q., Pellegrini V. et al. Automatic Mass Balancing of a Spacecraft Three-Axis Simulator: Analysis and Experimentation // J. Guidance, Control, and Dynamics. 2014. V. 37. № 1. P. 197–206.
Иванов Д.С., Иванова Т.А., Ивлев Н.А. и др. Оценка тензора инерции и автоматическая балансировка макета микроспутника на аэродинамическом подвесе // Изв. РАН. ТиСУ. 2021. № 2. С. 138–155.
СПУТНИКС – Испытательные стенды [электронный ресурс]. URL: https://sputnix.ru/ru/oborudovanie/ispytatelnye-stendy/ (дата доступа: 12.02.2021).
Бранец В.Н. Лекции по теории бесплатформенных инерциальных навигационных систем управления. М.: МФТИ, 2009. 304 p.
Иванов Д.С., Ивлев Н.А., Карпенко С.О. и др. Результаты летных испытаний системы ориентации микроспутника Чибис-М // Космич. исслед. 2014. Т. 52. № 3. С. 218–228.
Kramlikh A.V., Lomaka I.A. Nanosatellite’s Rotational Motion Parameters Determination Using Light Sensor and Angular Velocity Sensor Measurements // 25th Saint Petersbg. Int. Conf. Integr. Navig. Syst. (ICINS 2018). Saint Petersbg. Proc. Institute of Electrical and Electronics Engineers Inc., 2018. P. 1–3.
Белоконов И.В., Крамлих А.В., Ломака И.А. и др. Восстановление углового движения космического аппарата по данным о токосъеме с панелей солнечных батарей // Изв. РАН. ТиСУ. 2019. № 2. С. 133–144.
Ivanov D., Roldugin D., Tkachev S. et al. Attitude Motion and Sensor Bias Estimation Onboard the SiriusSat-1 Nanosatellite Using Magnetometer Only // Acta Astronautica 2021. V. 188. P. 295–307.
Kalman R.E. A New Approach to Linear Filtering and Prediction Problems // Trans. ASME, Ser. D, J. Basic Eng. 1960. V. 82. P. 35–45.
Степанов О.А. Фильтр Калмана: история и современность (к 80-летию Рудольфа Калмана) // Гироскопия и навигация. 2010. № 2. С. 107–121.
Голован А.А., Парусников Н.А. Математические основы навигационных систем. Ч. I. Математические модели инерциальной навигации. 2-е изд. М.: Изд-во МГУ, 2010. 126 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления