Известия РАН. Теория и системы управления, 2022, № 4, стр. 160-176

Введение. В настоящее время имеется много проектов полезного применения группировок космических аппаратов (КА) для различных целей (навигация, связь, наблюдение, измерения и т.д.). Важное место при этом занимают проекты использования тросовых группировок космических аппаратов (ТГКА), имеющих дополнительные механические связи между КА, что помогает при определенных условиях сохранять их геометрическую конфигурацию с минимальными затратами энергии. Среди наиболее известных конфигураций ТГКА можно отметить линейные структуры [1–5], когда КА располагаются на одной прямой чаще всего вдоль местной вертикали в режиме гравитационной стабилизации. Более сложные структуры ТГКА в отличие от линейных обычно стабилизированы вращением с некоторой заданной угловой скоростью относительно своего центра масс системы. Здесь можно отметить структуры в виде “кольца” [1, 6–11] и лучевые “звездные” конфигурации(“Hub-Spoke”) [12–17]. Если “кольца” не имеют центрального КА и управление их движением распределяется по всем КА, то в лучевых “звездных” структурах все управляющие функции, как правило, принадлежат центральному КА, в частности, с помощью специальных механизмов осуществляется управление выпуском тросов. Наряду с плоскими ТГКА представляют интерес пространственные системы, которые, например, можно использовать для многоточечных 3D-измерений в околоземном пространстве. Это пирамидальные структуры [1, 18, 19], которые вращаются вокруг вертикали, проходящей через их центр масс.

Из-за сложной динамики рассматриваемых многоэлементных тросовых систем методы их управления движением требуют дальнейшего развития. Наиболее сложным с этой точки зрения является этап формирования ТГКА, который (особенно для систем со сложной нелинейной структурой) еще недостаточно изучен. Второе направление исследований – это совершенствование математических моделей движения ТГКА. Здесь следует отметить, что рассмотрение ТГКА как системы с распределенными параметрами позволяет осуществлять контроль над формой тросов в процессе их развертывания и при дальнейшем функционировании ТГКА на орбите. Важным также представляется учет углового движения КА, входящих в состав ТГКА, относительно своих центров масс. Здесь следует отметить, что в подавляющем числе работ, посвященных динамике ТГКА, КА рассматриваются как материальные точки, что во многих случаях является недопустимым упрощением, в частности, если имеются ограничения на угловые положения КА относительно направления тросов [20] в процессе управления системой.

В работе предлагается и исследуется способ управления при формировании ТГКА треугольной лучевой конфигурации, вращающейся в плоскости орбиты ее центра масс. После развертывания ТГКА имеет симметричную структуру, в центре которой находится КА достаточно большой массы. При этом концевые малые КА (далее просто спутники) прикреплены к нему тросами, которые составляют между собой угол 120°. Особенностью предлагаемого комбинированного подхода при управлении процессом формирования вращающейся ТГКА является совместное применение электромагнитных сил, действующих на проводящие ток тросы в магнитном поле Земли, и механизмов выпуска тросов, расположенных на центральном КА. Электромагнитные силы, которые на каждом элементарном участке троса ему ортогональны, представляют собой распределенную по длине тросов нагрузку, равнодействующая которой создает вращающий момент, в конечном итоге обеспечивающий заданную угловую скорость вращения системы после ее формирования. Технология использования проводящих ток тросов в космосе активно разрабатывается. Достаточно сказать, что до настоящего времени различными странами проведено более 10 реальных тросовых экспериментов на орбите [21, 22].

Механизмы, обеспечивающие выпуск тросов, предназначены для регулирования силы натяжения тросов в соответствии с заданной номинальной программой их развертывания. Регулирование осуществляется по измерениям скорости и длины тросов в момент их выпуска из механизмов управления. Аналогичное регулирование при выпуске троса использовалось при проведении тросового эксперимента на орбите YES2 [23]. Основная цель регулирования – это обеспечить выполнение заданных ограничений на силу натяжения тросов (тросы должны быть натянуты) и на скорость выпуска тросов (механизмы работают только на их торможение), которая при достижении заданной длины тросов должна быть равна нулю.

Применяется классическая схема управления с обратной связью по отклонениям переменных состояния системы от номинальных значений. Для выбора номинальной программы формирования ТГКА осуществляется построение упрощенной модели движения системы с помощью уравнений Лагранжа. Упрощенная модель движения ТГКА служит для обоснованного выбора параметров номинальной программы ее развертывания, которая строится таким образом, чтобы обеспечить асимптотическую устойчивость конечного состояния системы после окончания выпуска тросов. Понятно, что в этом случае свойство асимптотической устойчивости имеет место в силу упрощенной модели движения системы. В процессе развертывания ТГКА величина тока в тросах постоянна и его выключение происходит уже после окончания выпуска тросов при достижении требуемой угловой скорости вращения системы относительно центра масс.

Проверка возможности реализации предлагаемой номинальной программы формирования ТГКА производится с использованием более полной модели движения системы, учитывающей растяжимость и односторонность механических связей между КА (тросов), работу системы регулирования с учетом инерционности механизмов управления, изгибные колебания тросов под действием распределенной нагрузки от электромагнитных сил, возможный пространственный характер движения ТГКА при наличии возмущений, связанных с начальными условиями движения (включая ошибки при разделении КА и влияние наклонения орбиты). В более полной модели движения ТГКА центральный КА рассматривается как твердое тело для возможности контроля его углового движения. Контроль углового движения центрального КА необходим для согласования его вращения с вращением тросов, которые в идеальном случае должны иметь ту же угловую скорость, что и центральный КА, в процессе развертывания системы. Для оценки изменения формы тросов в процессе развертывания системы они в более полной модели движения ТГКА описываются множеством материальных точек, связанных между собой растяжимыми односторонними связями.

Здесь можно отметить, что принципиально существует альтернативный способ создания вращательного момента, обеспечивающего заданную угловую скорость вращения системы вокруг центра масс в процессе формирования ТГКА, который связан с использованием двигателей малой тяги, расположенных на концевых спутниках. Например, такой способ был рассмотрен в работе [24] для тросовой системы, состоящей из двух КА. Однако такой подход имеет недостаток, связанный с необходимостью обеспечения заданной ориентации векторов тяги относительно направлений тросов, что ведет к необходимости стабилизации движения спутников вокруг своих центров масс, т.е. разработке дополнительной системы управления. Если концевые тела представляют собой малоразмерные спутники малой массы, то использование двигателей малой тяги становится проблематичным.

Для оценки возможности применения предлагаемой схемы управления процессом формирования ТГКА приводятся характерные примеры численного моделирования движения системы в плоском и пространственном случаях с учетом действующих возмущений с помощью более полной модели движения. Показано, что после окончания формирования ТГКА тросы практически прямолинейны и совершают малые колебания с почти постоянной амплитудой относительно своих номинальных значений. С учетом этого предлагается дополнительный алгоритм стабилизации движений тросов, основанный на регулировании величины тока в тросах.

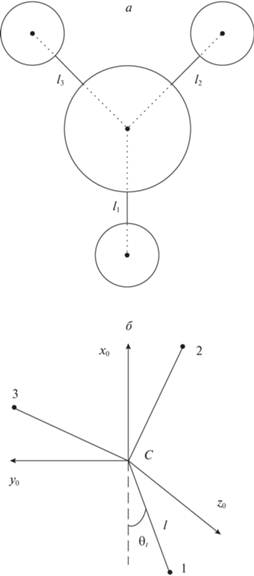
1. Постановка задачи. Необходимо разработать программу управления для формирования вращающейся ТГКА треугольной лучевой конфигурации разомкнутого типа, которая характеризуется тем, что концевые спутники не соединены между собой тросами. В начальном положении КА и спутники жестко связаны между собой, т.е. представляют собой симметричное твердое тело (рис. 1, а), которое по своей структуре повторяет геометричную конфигурацию системы в конечном состоянии после ее формирования. В номинальном случае (без учета возмущений) до разделения КА и спутников твердое тело вращается в плоскости орбиты с некоторой угловой скоростью ${{{{\omega }}}_{0}}.$ Отделение спутников от КА происходит с некоторыми относительными скоростями, причем их векторы в идеальном случае составляют между собой угол 120° и имеют равные модули. Все управляющие функции возлагаются на центральный КА, на котором имеются специальные механизмы для регулирования процесса выпуска тросов и бортовые источники энергии для обеспечения заданной величины тока в тросах. Применяется традиционная схема электродинамической тросовой системы в режиме генерации тяги для изолированного троса [1, 25], когда формируется контур электрической цепи, который замыкается через ионосферу. Используя описанные органы управления процессом формирования ТГКА, необходимо перевести систему в заданное конечное состояние. В конечном состоянии ТГКА имеет симметричную структуру, приведенную выше, и вращается с угловой скоростью ${{{{\omega }}}_{{end}}}$, которая зависит от момента выключения тока. По окончании развертывания тросов необходимо обеспечить плавное их торможение, а именно, чтобы при $l = {{l}_{{end}}}$ выполнялось $dl{\text{/}}dt = {{d}^{2}}l{\text{/}}d{{t}^{2}} = 0$.

2. Простая модель движения и номинальная программа формирования ТГКА. Для построения номинальной программы развертывания тросов и закона изменения тока применяются достаточно простые уравнения плоского движения системы относительно центра масс, соответствующие идеальному случаю, когда в процессе формирования ТГКА сохраняется ее полная симметрия. Основные допущения: центральный КА и спутники рассматриваются как материальные точки, тросы нерастяжимы, невесомы и прямолинейны, влиянием гравитационных сил на движение системы относительно центра масс и вращением орбитальной подвижной системы координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ (рис. 1, б) пренебрегается, вектор магнитной индукции определяется в центре масс системы (C) и постоянен, нагрузка от сил Ампера равномерно распределена по длине каждого троса, центр масс системы совпадает с центром масс центрального КА и движется по невозмущенной круговой орбите. Для орбитальной прямоугольной правой системы координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ направление оси $C{{x}_{o}}$ совпадает с направлением геоцентрического радиус-вектора центра масс системы, ось $C{{y}_{o}}$ лежит в плоскости орбиты и направлена в сторону движения.

Уравнения Лагранжа имеют вид

где $q = {{\left( {l,{{{{\theta }}}_{t}}} \right)}^{{\text{T}}}}$ и $\dot {q}$ – вектор обобщенных координат (рис. 1, б) и соответствующий вектор обобщенных скоростей, ${{{{\theta }}}_{t}}$ – угол отклонения первого троса от вертикали (рис. 1, б) в плоскости орбиты центра масс системы, ${{T}_{c}}$ – кинетическая энергия системы, $Q = {{\left( {{{Q}_{l}},{{Q}_{{{{{{\theta }}}_{t}}}}}} \right)}^{{\text{T}}}}$ – вектор обобщенных сил.

Координаты спутников определяются в плоском случае в орбитальной системе координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ (рис. 1, б):

где ${{{{\theta }}}_{{ok}}} = 2\left( {k - 1} \right)\pi {\text{/}}3,$ $k = \overline {1,\,3} $.

Кинетическая энергия системы

где m – масса спутников, ${{T}_{{c0}}} = {\text{const}}$ – кинетическая энергия центрального КА.

Учитывая выражения (2.2)–(2.3) и проводя дифференцирование, уравнения (2.1) представим как

Обобщенные силы определяются через возможные перемещения и имеют вид

где $F = {{B}_{o}}lI$ – сила Ампера, I – величина тока, ${{B}_{o}} = {{{{\mu }}}_{m}}{\text{/}}R_{c}^{3}$ – модуль вектора магнитной индукции на экваторе, ${{{{\mu }}}_{m}}$ – магнитный момент земного диполя, ${{R}_{c}}$ – модуль радиус-вектора центра масс системы на круговой орбите, $T$ – силы натяжения тросов, которые в данной постановке (тросы невесомы) равны силам их торможения в механизмах управления. Здесь и далее в качестве модели магнитного поля Земли рассматривается прямой диполь [1].

Для обеспечения условий асимптотической устойчивости решения системы (2.4), соответствующего конечному положению тросов $l = {{l}_{{end}}}$, силу натяжения необходимо задать в виде

где ${{k}_{{v}}},\;{{k}_{l}}$ – коэффициенты (аналогичные коэффициентам обратной связи), выбором которых можно обеспечить заданные свойства конечного состояния тросов.

Подстановка выражения (2.6) во второе уравнение системы (2.4) дает

В этом случае решение уравнения для l (2.7) не зависит от решения первого уравнения системы (2.4). С другой стороны, решения первого уравнения системы (2.4) зависят от решения уравнения для l. Корни характеристического уравнения, соответствующие (2.7) и записанного через отклонения $\Delta l = l - {{l}_{{end}}}$, имеют вид

Таким образом, если ${{k}_{{v}}},{{k}_{l}} > 0$ и $k_{v}^{2}{\text{/}}4 - {{k}_{l}} > 0$, то конечное состояние тросов будет асимптотически устойчиво в силу системы (2.4), причем переходный процесс будет апериодическим ($\dot {l} > 0$). Последнее обстоятельство является важным, так как предполагается, что механизмы выпуска тросов, расположенные на центральном КА, работают только на торможение.

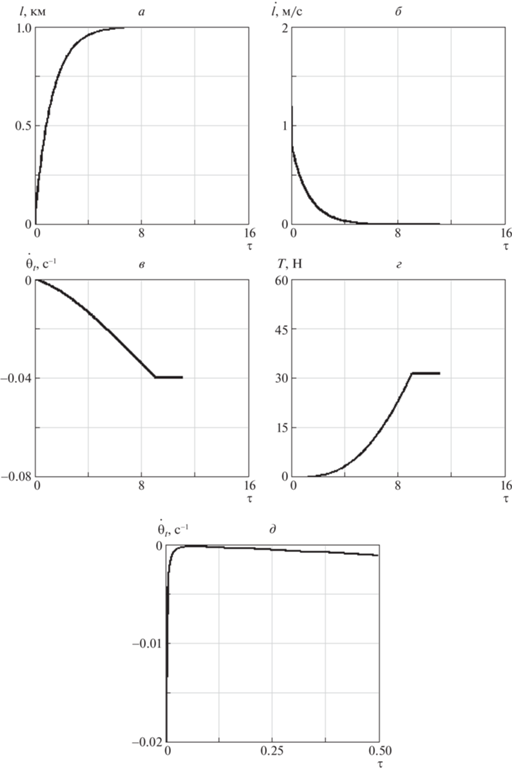
На рис. 2 приводятся основные характеристики номинальной программы формирования ТГКА в зависимости от безразмерного времени ${{\tau }} = {{\omega }}t$, где ${{\omega }}$ – угловая скорость центра масс системы по круговой орбите. Исходные данные и параметры выбранной номинальной программы формирования ТГКА: масса центрального КА – 500 кг, массы спутников – 20 кг, высота круговой экваториальной орбиты – 500 км, конечная длина тросов – 1 км, величина тока $I = - 10\,{\text{A}}$, начальная угловая скорость вращения системы в плоскости орбиты до разделения ${{{{\omega }}}_{0}} = 0.1$ с^–1, относительная скорость разделения центрального КА и спутников ${{V}_{r}} = 1.6$ м/с, коэффициенты ${{k}_{{v}}} = 0.6$ кг/с, ${{k}_{l}} = 0.5 \times {{10}^{{ - 3}}}$ кг/с². Здесь за положительное направление тока принимается направление от спутников к центральному КА, а угловая скорость ${{{{\omega }}}_{0}}$ направлена противоположно направлению отчета угла ${{{{\theta }}}_{t}}$ (рис. 1, б), т.е. ее проекция на ось $C{{z}_{o}}$ орбитальной системы координат отрицательна:  ${{{{\omega }}}_{{z0}}} = - 0.1$ с^–1. Приведенные численные результаты подтверждают асимптотическую устойчивость конечного состояния ТГКА по переменным $l,\;\dot {l}$ (рис. 2, а, б), при этом ${{d}^{2}}l{\text{/}}d{{t}^{2}} \approx 0$. После окончания выпуска тросов их длина фиксируется, однако ток выключается только тогда, когда угловая скорость ${{{{\dot {\theta }}}}_{t}}$ достигает заданного значения. В данном случае ${{{{\dot {\theta }}}}_{t}} = - 0.04$ с^–1 (рис. 2, в). После выключения тока угловая скорость вращения системы и силы натяжения тросов постоянны (рис. 2, г). Особенностью изменения угловой скорости ${{{{\dot {\theta }}}}_{t}}$ является быстрое ее уменьшение (точнее, ее модуля) почти до нуля (рис. 2, д) сразу после разделения центрального КА и спутников. Это объясняется быстрым увеличением момента инерции системы при увеличении длин тросов на этом начальном участке формирования ТГКА. Однако затем в результате действия вращающего момента от сил Ампера угловая скорость вращения системы монотонно увеличивается (по модулю) и в некоторый момент достигает заданного значения (рис. 2, в).

Далее приведенная номинальная программа используется в более полной модели движения ТГКА для оценки возможности ее реализации при действии достаточно широкой совокупности действующих возмущений.

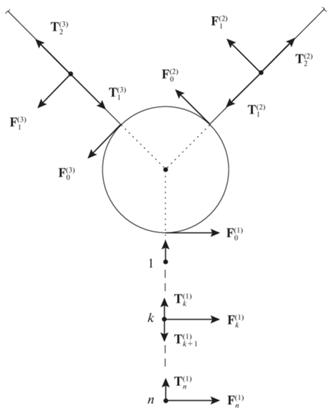
3. Математическая модель движения в геоцентрической неподвижной системе координат. Более полные уравнения движения ТГКА записываются в неподвижной геоцентрической системе координат $OXYZ$, в которой основная плоскость совпадает с плоскостью экватора, ось OZ направлена по оси вращения Земли на север, ось $OX$ – в точку весеннего равноденствия. Уравнения, описывающие движение центров масс КА, спутников и множества материальных точек, моделирующих движения тросов, имеют вид

где ${{R}_{s}}$, $R_{n}^{{\left( i \right)}},$ $k = \overline {1,n} $, – радиус-векторы центров масс КА и $i$-го спутника, $R_{1}^{{\left( i \right)}},...,R_{{n - 1}}^{{\left( i \right)}},$ $i = \overline {1,3} $, – радиус-векторы материальных точек, на которые разбивается трос, ${{G}_{s}} = - \mu {{m}_{s}}{{R}_{s}}{\text{/}}R_{s}^{3}$, $G_{k}^{{(i)}}\, = \, - {\kern 1pt} \mu mR_{k}^{{(i)}}{\text{/}}{{(R_{k}^{{(i)}})}^{3}}$ – гравитационные силы, ${{\mu }}$ – гравитационная постоянная, $T_{k}^{{\left( i \right)}}$ – сила натяжения троса, приложенная к k-й точке i-го троса и направленная в сторону $k - 1$-й точке, $T_{{n + 1}}^{{\left( i \right)}} = 0$, $F_{k}^{{\left( i \right)}}$ – сила Ампера, приложенная к k-й точке i-го троса, $F_{0}^{{\left( i \right)}}$ – составляющая силы Ампера, приложенной к первому участку $i$-го троса и действующая на центральный КА. В системе (3.1) индекс n соответствуют концевым спутникам, которые в данной модели рассматриваются как материальные точки. Схема сил, действующих на ТГКА, приводится на рис. 3.

Силы натяжения тросов вычисляются следующим образом:

где $\Delta r_{k}^{{\left( i \right)}}\, = R_{{k - 1}}^{{\left( i \right)}} - \Delta R_{k}^{{\left( i \right)}}$ – радиус-векторы, соединяющие точки крепления тросов, $L_{k}^{{\left( i \right)}}$ – нерастянутые длины участков тросов, $R_{0}^{{\left( i \right)}}$ – радиус-векторы точек крепления тросов к центральному КА (центральный КА – твердое тело), $c = ES$, E – модуль Юнга, S – площадь поперечного сечения троса. Выражения (3.2) соответствуют односторонней механической связи между точками троса и точками его крепления к центральному КА, причем для описания растяжения тросов используется закон Гука.

Силы Ампера $F_{k}^{{\left( i \right)}}$, действующие на k-й участок i-го троса, вычисляются как [25]

где $B_{k}^{{\left( i \right)}}$ – вектор магнитной индукции.

Используется модель магнитного поля Земли – прямой диполь [1]:

где ${{B}_{0}} = {{{{\mu }}}_{m}}{\text{/}}r_{c}^{3}$, ${{{{\mu }}}_{m}} = 8 \times {{10}^{6}}$ Тл ⋅ км³ – магнитный момент земного диполя, $e_{k}^{{\left( i \right)}} = r_{k}^{{\left( i \right)}}{\text{/}}r_{k}^{{\left( i \right)}}$, e – единичный вектор оси вращения Земли, $(ee_{k}^{{\left( i \right)}})$ – скалярное произведение. Здесь вектор $B_{k}^{{\left( i \right)}}$ определяется в середине отрезка троса, т.е. $r_{k}^{{\left( i \right)}} = (R_{{k - 1}}^{{\left( i \right)}} + \Delta R_{k}^{{\left( i \right)}}){\text{/}}2$.

Силы $\Delta {{F}_{k}}$ распределяются по точкам следующим образом:

Процесс выпуска тросов моделируется с помощью динамических уравнений [20]

где коэффициент ${{m}_{{in}}}$ учитывает инерционность механизмов управления, U⁽ⁱ⁾ – управляющие силы, $L_{1}^{{\left( i \right)}}$ – недеформированная длина первого участка троса, считая от центрального КА.

Силы торможения в механизмах управления определяются с использованием принципа обратной связи:

где ${{K}_{l}},\,\,{{K}_{{v}}}$ – коэффициенты обратной связи, а номинальные значения ${{l}_{1}},\,\dot {l}$ находятся интегрированием системы уравнений (2.4), причем номинальная длина на первом участке тросов определяется с учетом суммы длин недеформированных участков тросов, выпущенных до этого: $l_{1}^{{\left( i \right)}} = l - l_{{n - 1}}^{{\left( i \right)}}$. Аналогичный принцип управления выпуском троса применялся ранее при проведении реального тросового эксперимента на орбите YES2 [23]. В этом эксперименте управляющие механизмы осуществляли только торможение троса, поэтому если $\dot {L}_{1}^{{\left( i \right)}} \leqslant 0$ или  $T_{1}^{{\left( i \right)}} \leqslant 0$, то выпуск i-го троса прекращается: $\ddot {L}_{1}^{{\left( i \right)}} = \dot {L}_{1}^{{\left( i \right)}} = 0$.

Использование уравнений движения (3.1), (3.6) предполагает применениe некоторого алгоритма введения новых точек тросов, когда недеформированная длина первого участка троса, считая от центрального КА, становится больше ${{l}_{{end}}}{\text{/}}N$, где N – количество отрезков, на которые разбивается полная длина троса (является параметром модели). Здесь применяется алгоритм добавления новой точки, описанный в [26]. Основные принципы этого алгоритма: 1) положение новой точки определяется из условия равенства сил натяжения с обеих сторон, причем величина этих сил натяжения должна быть равна силе натяжения на этом же участке до введения новой точки; 2) по положению новой точки находятся составляющие ее скорости относительно центрального КА по известной относительной скорости второй точки через соответствующие пропорции; 3) проводится коррекция составляющих скоростей центрального КА на основании закона сохранения количества движения системы. Для сохранения вида уравнения движения (3.1), (3.6) номера точек тросов изменяются.

4. Уравнения движения центрального КА относительно центра масс. Для контроля за угловыми движениями центрального КА с целью согласования его вращения с вращением тросов уравнения (3.1), (3.6) дополняются уравнениями движения КА относительно центра масс. Динамические уравнения вращательного движения КА записываются в традиционной форме

где ${{\omega }_{s}}$ и ${{J}_{s}}$ – вектор угловой скорости и тензор инерции центрального КА, ${{M}_{s}}$ – векторная сумма моментов, действующих на КА. Уравнения (4.1) проецируются на оси связанной с КА прямоугольной системы координат $sxyz$, где s – центр масс КА, ось sx проходит через точку крепления первого троса (i = 1), плоскость sxy в невозмущенном случае в момент отделения спутников совпадает с орбитальной плоскостью.

Вектор ${{M}_{s}}$ определяется как

где $r_{s}^{{\left( i \right)}}$ – радиус-векторы точек крепления тросов относительно центра масс КА, ${{M}^{{\left( u \right)}}}$ – управляющий момент системы стабилизации движения КА.

Предполагается, что эллипсоид инерции КА близок к сфере и движение системы рассматривается на достаточно высоких орбитах. Поэтому гравитационные и аэродинамические моменты не учитываются.

Управляющий момент ${{M}^{{\left( u \right)}}}$ системы стабилизации движения КА определяется в соответствии с отклонениями от номинальной программы изменения переменных ${{{{\theta }}}_{t}}{\text{,}}\;{{{{\dot {\theta }}}}_{t}}$, рассчитанной по простым уравнениям движения ТГКА (2.4). Компоненты момента ${{M}^{{\left( u \right)}}}$ в связанной с КА системе координат $sxyz$ имеют вид

где ${{{{\omega }}}_{{x,y,z}}}$ – проекции угловой скорости КА на оси связанной системы координат, ${{k}_{{{\omega }}}},\,\,{{k}_{z}},\,\,{{k}_{{{\theta }}}}$ – коэффициенты обратной связи. При этом угол ${{\theta }}$ определяется интегрированием

Таким образом, предполагается, что система стабилизации КА для своей работы использует стандартные датчики угловых скоростей (ДУС) и интегратор.

Кинематические уравнения записываются в виде уравнений Эйлера–Пуассона

где ${{e}_{{x,y,z}}}$ – орты связанной системы координат $sxyz$.

Проекции единичных векторов ${{e}_{{x,y,z}}}$ на оси неподвижной системы координат $OXYZ$ являются компонентами матрицы перехода от системы координат $OXYZ$ к связанной системе координат $sxyz$. Следовательно, зная координаты точек крепления тросов в системе координат $sxyz$ (проекций векторов $r_{s}^{{\left( i \right)}}$), нетрудно вычислить координаты точек крепления тросов в системе координат $OXYZ$ (векторов $R_{0}^{{\left( i \right)}}$) и определить силы натяжения тросов с учетом углового движения центрального КА. При численном интегрировании уравнений (4.4) осуществляется контроль за выполнением условий ортогональности векторов ${{e}_{{x,y,z}}}$ и $\left| {{{e}_{{x,y,z}}}} \right| = 1$. При необходимости можно использовать оптимальный алгоритм коррекции компонент векторов ${{e}_{{x,y,z}}}$ [27].

Система (3.1), (3.6), (4.1), (4.4) при задании всех коэффициентов обратной связи, входящих в выражения (3.7), (4.3), представляет собой замкнутую систему обыкновенных дифференциальных уравнений, которая может быть проинтегрирована численным методом при заданных начальных условиях.

В системе уравнений (3.1), (3.6), (4.1), (4.4) не имеют места многие допущения, которые были приняты при построении простой модели движения ТГКА, а именно: центральный КА рассматривается как твердое тело конечных размеров; учитывается растяжимость и масса тросов, которые под действием распределенной нагрузки от сил Ампера деформируются (не прямолинейны); центр масс системы перемещается по возмущенной орбите, изменение параметров которой нетрудно вычислить; вектор магнитной индукции определяется в каждой точке троса в соответствии с принятой моделью магнитного поля Земли (3.4); учитывается взаимное влияние движений центрального КА и тросов; рассматривается пространственное движение системы; оценивается влияние ошибок в начальных условиях движения (включая ошибки, возникающие при разделении КА и спутников) на процесс формирования ТГКА; оценивается качество работы системы стабилизации центрального КА и управляющих механизмов выпуска тросов; моделируется процесс формирования ТГКА на орбитах с ненулевым наклонением. В построенной более полной модели движения ТГКА концевые спутники рассматриваются как материальные точки, так как предлагаемая схема управления не накладывает жестких ограничений на угловые движения спутников.

5. Моделирование процесса разделения КА и спутников. Для определения начальных условий движения ТГКА необходимо рассмотреть процесс разделения КА и спутников. Если $V_{r}^{{\left( i \right)}},\,\,i = \overline {1,3} $, – относительные скорости отделения спутников от КА, то, используя закон сохранения импульса, найдем

где ${{V}_{c}}$ – вектор скорости центра масс системы до разделения, ${{V}_{{s0}}},\,\,V_{0}^{{\left( i \right)}}$ – векторы начальных скоростей движения КА и спутников после их разделения.

На основании теоремы об изменении кинетического момента твердого тела при ударном взаимодействии найдем

где ΔK_s – приращение моментов импульса центрального КА, ${{S}^{{\left( i \right)}}} = - m(V_{0}^{{\left( i \right)}} - {{V}_{s}})$ – импульс, действующий на центральный КА при отделении i-го спутника.

По приращению импульса (5.2) определяется изменение вектора угловой скорости КА:

В идеале векторы S⁽ⁱ⁾ проходят через центр масс КА и его угловые скорости не изменяются. В противоположном случае, когда $\Delta {{K}_{s}} \ne 0$, имеют место возмущения при разделении, и угловые скорости вращения КА изменяются.

6. Моделирование возмущенного движения ТГКА при ее развертывании. При моделировании возмущенного движения ТГКА использовалась система уравнений, записанная в геоцентрической неподвижной системе координат (3.1), (3.6), (4.1), (4.4). Были приняты следующие исходные данные (они дополняют данные, принятые для построения номинального движения системы): жесткость и линейная плотность троса $c = 2 \times {{10}^{4}}$ Н и ${{\rho }} = 0.8$ кг/км; количество отрезков, на которые разбиваются тросы в своем конечном состоянии, N = 10; коэффициенты обратной связи ${{K}_{l}} = 0.2$ кг/с², ${{K}_{{v}}} = 7.8$ кг/с, ${{k}_{{{\theta }}}} = - {{10}^{2}}$ Нм, ${{k}_{{{\omega }}}} = - {{10}^{3}}$ кг м²/с, ${{k}_{z}} = - 5 \times {{10}^{3}}$ кг м²/с; диаметр центрального КА (сфера) и его моменты инерции (имеется инерционная асимметрия) ${{D}_{s}} = 2$ м, ${{J}_{x}} = 200$ кг м², ${{J}_{y}} = 210$ кг м²; ${{J}_{z}} = 190$ кг м²; смещения центра масс КА относительно центра сферы (статическая асимметрия) в связанной системе координат $sxyz$ $\Delta {{y}_{s}} = 0.05$ м, $\Delta {{z}_{s}} = - 0.05$ м. Предполагается, что начальные угловые скорости твердого тела до разделения КА и спутников отличны от номинального случая (${{{{\omega }}}_{{x0}}} = {{{{\omega }}}_{{y0}}} = 0,$ ${{{{\omega }}}_{{z0}}} = - 0.1$ с^–1) и равны ${{{{\omega }}}_{{x0}}} = 0.05$ с^–1, ${{{{\omega }}}_{{y0}}}$ = –0.05 с^–1, ${{{{\omega }}}_{{z0}}} = - 0.1$ с^–1. Здесь необходимо отметить, что увеличение числа отрезков, на которые разбиваются тросы, по сравнению с N = 10 практически не приводило к изменению результатов моделирования, что и обусловило такую дискретизацию тросов. Величины коэффициентов обратной связи ${{K}_{l}}$, ${{K}_{{v}}}$ были выбраны исходя из результатов работы [26], где рассматривалась аналогичная задача управления выпуском троса с малым по массе грузом. Правда, тросовая система состояла из двух КА и ее развертывание осуществлялось в вертикальное положение. Остальные коэффициенты обратной связи были выбраны в процессе решения рассматриваемой задачи.

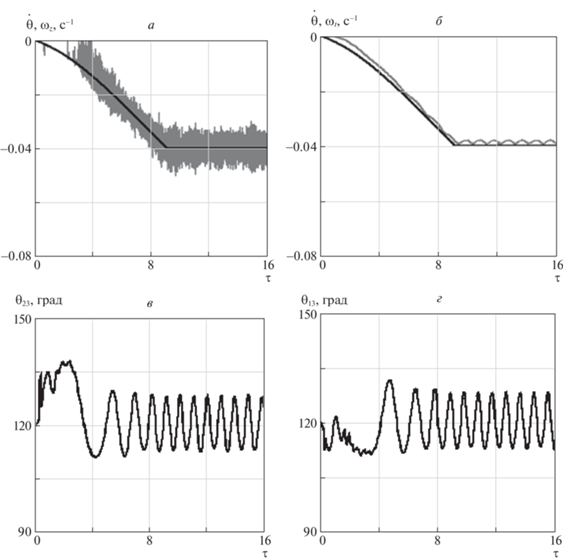
Результаты моделирования движения ТГКА для экваториальной орбиты представлены на рис. 4 и 5. Из них следует, что предлагаемый метод управления при развертывании ТГКА треугольной конфигурации обеспечивает согласованное изменение угловых скоростей вращения в плоскости орбиты центрального КА (${{{{\omega }}}_{z}}$) и тросов (${{{{\omega }}}_{t}}$), которые близки к номинальной угловой скорости (${{{{\dot {\theta }}}}_{t}}$) (на рис. 4, а, б – это жирная линия, на рис. 4, б для примера показана угловая скорость первого троса). При формировании ТГКА в конечном итоге после окончания развертывания системы углы между тросами должны составлять в идеальном случае 120°. На рис. 4, в, г продемонстрировано в качестве примера, как изменяются углы между тросами 2, 3 (${{{{\theta }}}_{{23}}}$) и 1, 3 (${{{{\theta }}}_{{13}}}$) в процессе развертывания системы. После того, как происходит выключение тока (τ = 9) при достижении конечной угловой скорости вращения системы (–0.04  с^–1), углы между тросами колеблются относительно значения 120° с почти постоянной амплитудой (приблизительно 13°). На рис. 5 показано, как изменяется форма тросов в процессе развертывания ТГКА. Если на начальном этапе формирования системы под действием распределенной нагрузки тросы имеют заметный изгиб, то по мере увеличения угловой скорости вращения системы в результате действия центробежных сил инерции они постепенно выпрямляются и в конечном итоге их форма близка к прямой линии (при τ > 9). Здесь можно отметить, что существует некоторая асимметрия при формировании ТГКА с точки зрения направления ее вращения, если движение системы рассматривать в подвижной орбитальной системе координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$. Это связано с влиянием силы Кориолиса. Если сила Кориолиса, действующая на спутники и на любой участок троса, при развертывании системы создает момент, противоположный по знаку с направлением заданного вращения системы, то сразу после разделения КА и спутников (когда относительная скорость выпуска тросов еще велика) тросы могут вращаться в направлении, противоположном заданному (относительно вертикали). Данного эффекта можно избежать, если направление тока будет отрицательным (от КА к спутникам). Тогда знаки моментов от сил Ампера и сил Кориолиса будут совпадать и описанный эффект исчезнет. Поэтому в данном случае знак заданной угловой скорости вращения системы относительно оси $C{{z}_{o}}$ выбран отрицательным ${{{{\omega }}}_{z}} < 0.$

Для уменьшения амплитуды колебаний углов ${{{{\theta }}}_{{13}}},\;{{{{\theta }}}_{{12}}},\;{{{{\theta }}}_{{23}}}$ между тросами предлагается ввести дополнительное управление величиной тока на заключительном этапе развертывания системы, когда ${{l}_{{1,2,3}}}{\text{/}}{{l}_{{end}}} > 0.8$. Управление предлагается осуществлять в соответствии с текущей угловой скоростью тросов, которая определяется по относительному движению крайних точек тросов, фактически по относительному движению центров масс центрального КА и спутников. Оценка угловой скорости тросов происходит следующим образом:

где $\Delta {{r}^{{\left( i \right)}}} = R_{n}^{{\left( i \right)}} - R_{s}^{{\left( i \right)}}$, $\Delta {{V}^{{\left( i \right)}}} = \dot {R}_{n}^{{\left( i \right)}} - \dot {R}_{s}^{{\left( i \right)}}$.

Управляющая добавка к величине тока определяется как

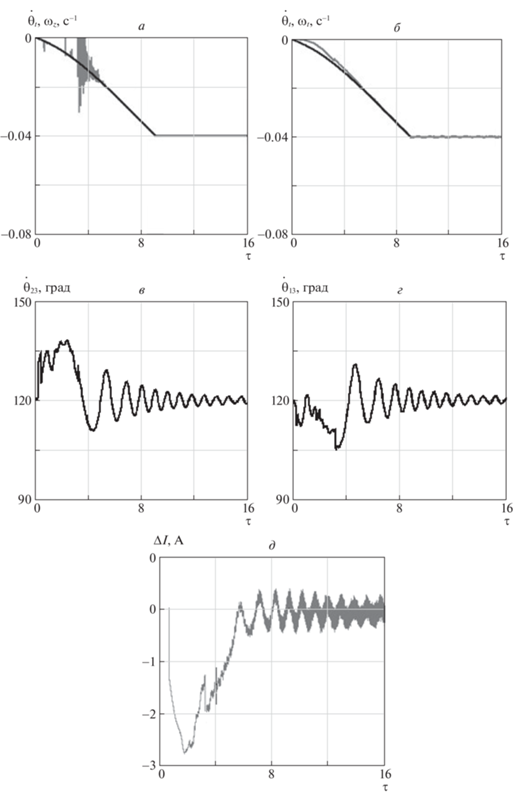
где ${{(\omega _{t}^{{\left( i \right)}})}_{{zo}}}$ – проекции угловых скоростей (6.1) на ось $C{{z}_{o}}$ орбитальной системы координат, ${{K}_{I}}$ – коэффициент обратной связи, ${{{{\dot {\theta }}}}_{t}}$ – номинальное значение угловой скорости вращения тросов.

Результаты моделирования процесса развертывания ТГКА с управлением (6.2) представлены на рис. 6 (${{K}_{I}} = - {{10}^{3}}$ А с). Введение управления величиной тока приводит к уменьшению амплитуды колебаний углов ${{{{\theta }}}_{{13}}},\;{{{{\theta }}}_{{12}}},\;{{{{\theta }}}_{{23}}}$ (рис. 6, в, г), которые приближаются к величине 120°. С другой стороны, существенно уменьшаются в этом случае ошибки регулирования по угловым скоростям ${{{{\omega }}}_{z}},{{{{\omega }}}_{t}}$, что иллюстрируется на рис. 6, а, б. На рис. 6, д для примера показано, как изменяется управление (6.2) для первого троса.

Развертывание ТГКА на экваториальной орбите (или на орбитах с малым наклонением при использовании модели магнитного поля Земли – наклонного диполя) фактически характеризует движение системы, близкое к плоскому. На орбитах с малым наклонением применение электромагнитных сил для управления движением космических систем является наиболее эффективным, так как это приводит к наибольшей величине электромагнитных сил, действующих на проводящий ток трос в магнитном поле Земли [1]. Это связано с тем, что вектор магнитной индукции ортогонален (или почти ортогонален) любому участку троса. Из этого следует, что модуль векторного произведения (3.3), а значит, величина результирующей силы Ампера близка к максимальной.

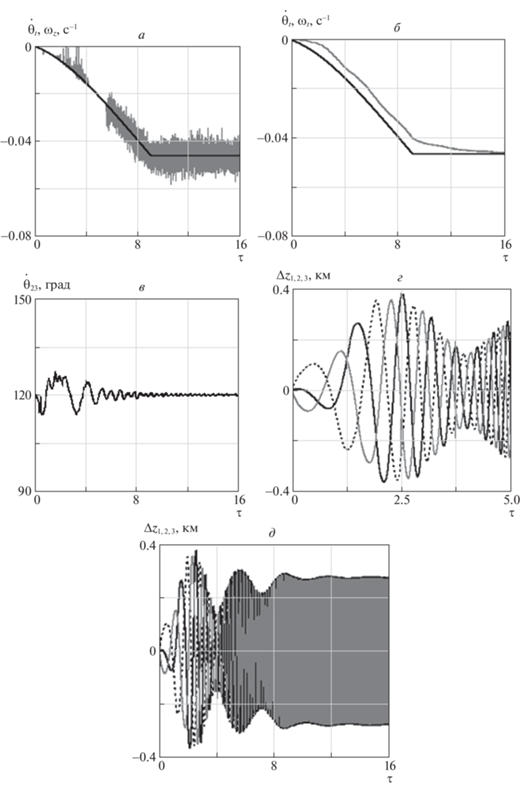
Так как на орбите с ненулевым наклонением сила Ампера (3.3) имеет составляющую, перпендикулярную плоскости орбиты, то при развертывании ТГКА всегда реализуется пространственный случай движения системы, даже когда начальное состояние системы невозмущенное. Известно [1], что для орбит с ненулевым наклонением для сохранения той же эффективности использования сил Ампера необходимо увеличить величину тока приблизительно в $1{\text{/}}\cos {{i}_{0}}$ раз, где ${{i}_{0}}$ – наклонение орбиты. На рис. 7 приводятся зависимости, характеризующие процесс развертывания системы на орбите с наклонением 30°. Номинальная величина тока по модулю увеличилась и составила приблизительно 11.5 А (ранее было 10 А). Такое увеличение величины тока для рассматриваемой задачи оказалось чрезмерным, так как конечная величина угловой скорости вращения системы стала больше (по модулю), около –0.045 с^–1 (ранее было –0.04 с^–1). Алгоритм стабилизации угловой скорости вращения тросов с использованием управления (6.2) сохранил свою эффективность (рис. 7, в). Однако ошибки регулирования по угловым скоростям ${{{{\omega }}}_{z}},\;{{{{\omega }}}_{t}}$ в этом случае увеличились (рис. 7, а, б). Это связано со сложным пространственным характером движения ТГКА, когда тросы совершают также колебания вне плоскости орбиты центра масс системы. На рис. 7, г, д приводятся зависимости от времени отклонений спутников относительно орбитальной плоскости в процессе развертывания системы $\Delta {{z}_{{1,2,3}}}$. Амплитуды этих колебаний одинаковы для всех спутников, а по окончании выпуска тросов почти постоянны (рис. 7, д). Максимальные отклонения спутников от плоскости орбиты составляют приблизительно 0.38 км. Фазы колебаний $\Delta {{z}_{{1,2,3}}}$ различаются, что нетрудно заметить на рис. 7, г.

Заключение. Oценивается возможность использования электромагнитных сил (сил Ампера), возникающих при взаимодействии проводящих ток тросов с магнитным полем Земли, для формирования вращающейся ТГКА треугольной лучевой симметричной конфигурации. Предлагается и обосновывается метод управления, включающий в себя регулирование выпуском тросов с центрального КА и создание момента с помощью сил Ампера, обеспечивающего вращение системы с заданной угловой скоростью после выключения тока. Для обоснования рассматриваемого подхода к формированию ТГКА разработаны и используются две математические модели. Первая сравнительно простая модель, полученная с помощью уравнений Лагранжа, служит для построения номинальных законов или программ управления. Вторая модель применяется для оценки реализуемости построенного программного движения системы. В этой модели тросы представляются как множество материальных точек, связанных между собой упругими односторонними механическими связями. Это позволяет оценить величину изгиба тросов при действии распределенных сил Ампера, а центральный КА рассматривается как твердое тело конечных размеров. Реализация номинального движения системы с использованием более сложной модели ее движения и при действии достаточно полной совокупности возмущений осуществляется с помощью достаточно простых линейных регуляторов. Представленные результаты численного моделирования развертывания ТГКА доказывают принципиальную возможность применения предлагаемой схемы управления. Более детальные вопросы технической реализации данного подхода к формированию конфигурации ТГКА (выбор совокупности средств и погрешности измерений, влияние дискретности управления, ошибки при реализации управляющих воздействий и т.д.) здесь не рассматриваются и требуют дальнейшего изучения.