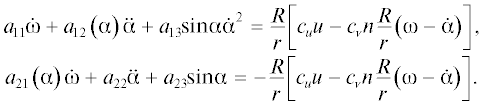Известия РАН. Теория и системы управления, 2022, № 4, стр. 95-108

Введение. В настоящее время в литературе можно найти много работ, посвященных различным конструкциям сферических роботов, вопросам управления ими, теоретическим вопросам динамики, математическому моделированию, экспериментам. В [1] содержится значительное количество опубликованных ранее в разных изданиях работ, касающихся сферических роботов, а также ссылки на многие публикации, связанные с ними. В недавних работах [2, 3], в частности, рассматривается динамика робота-шара, приводимого в движение с использованием омниколес.

Внутренний механизм робота-шара во многих случаях конструируют так, чтобы была возможность отклонить проекцию центра масс всего робота на опорную поверхность от точки (области) контакта сферы с этой поверхностью. Возникающий в этих случаях момент силы тяжести относительно точки контакта стремится повернуть сферу в ту сторону, в которую отклоняется эта проекция центра масс. При этом и происходит качение робота-шара по опорной поверхности. Качение робота может быть организовано также путем вращения расположенных внутри сферы массивных тел.

Робот-шар может применяться для мониторинга окружающей местности, для перемещения грузов и т.д. При мониторинге окружающей местности такой робот должен нести на борту видеокамеру, акустический датчик. Когда робот-шар используется для перемещения тех или иных грузов, эти грузы, естественно, размещаются на его борту. При этом вибрации и перегрузки, появляющиеся в процессе перемещения робота, могут быть нежелательны, и их необходимо предотвращать.

Перемещение робота-шара является, вообще говоря, пространственным. При этом причиной возникновения тех или иных колебаний робота или его частей может быть взаимное влияние продольного и поперечного движений. С этим связаны определенные трудности управления им. Теоретические исследования, проведенные в настоящей работе, показывают, что при плоском продольном движении (в отсутствие поперечного) неудачное управление также может вызвать нежелательные колебания.

Настоящая статья посвящена проблеме синтеза такого управления продольным (плоским) движением сферического робота, при котором в какой-то степени удается предотвратить возникновение колебаний и перегрузок при перемещении робота.

1. Конструкция робота. В НИИ механики МГУ сконструирован робот-шар, фотография которого показана на рис. 1.

Корпус робота представляет собой прозрачную сферу. Внутри сферы находится круглая платформа, диаметр которой меньше диаметра сферы. Своими краями платформа опирается на нижнюю половину внутренней поверхности сферического корпуса и может скользить по ней. В середине платформы сделан круглый вырез, в котором смонтирована вилка. Ось вилки перпендикулярна плоскости платформы. Внутри вилки находится колесо, которое своим ободом опирается на внутреннюю поверхность сферы. Робот оснащен двумя электроприводами. Один из них поворачивает вилку колеса относительно платформы, управляя направлением движения робота. Другой электропривод – маршевый, поворачивает колесо вокруг его оси, заставляя колесо катиться по внутренней поверхности сферы. Управляя электроприводами, можно заставить колесо катиться в том или ином направлении по внутренней поверхности сферы с той или иной скоростью. При этом сама сфера будет катиться по опорной поверхности в желаемом направлении. Робот управляется оператором при помощи джойстика.

Описанный выше внутренний механизм робота, по существу, представляет собой маятник, центр масс которого располагается ниже центра сферы. Перемещая маятник так, чтобы проекция его центра масс на опорную поверхность отклонялась в том или ином направлении от точки контакта сферы с опорой, можно регулировать момент силы тяжести относительно точки контакта и, тем самым, управлять направлением и скоростью движения всего робота. Подобный механизм предложен в патентах [4, 5]. В [6] рассматривается аналогичный механизм, но с некоторыми модификациями.

При проведении теоретических и экспериментальных исследований продольного движения, показанного на рис. 1 робота, наблюдаются угловые колебания платформы, а также колебания скорости перемещения. В сравнительно недавней публикации [7] также указывается на возникновение подобных нежелательных явлений и предлагаются “интуитивные” способы борьбы с ними. Подход к синтезу управления, используемый в настоящей статье, описан в работах [8–10].

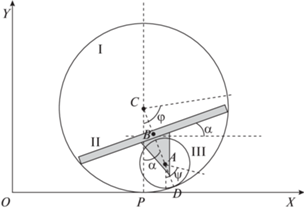
2. Математическая модель продольного движения робота. Ограничимся рассмотрением продольного движения робота по горизонтальной поверхности, при котором центр сферы C и плоскость колеса располагаются все время в одной и той же вертикальной плоскости. На рис. 2 приведена схема робота в его разрезе этой вертикальной плоскостью.

Римскими цифрами I–III на рис. 2 показаны сфера, плоская платформа и колесо соответственно. Буквами B и A обозначены геометрический центр платформы (он же – ее центр масс) и центр колеса, через L – расстояние CB  от центра сферы C до центра масс платформы B. Здесь P и D – точки контакта сферы с опорной поверхностью и колеса со сферой соответственно. Сферу, платформу, вилку колеса и само колесо считаем абсолютно твердыми телами. Будем предполагать, что колесо может без проскальзывания катиться по внутренней поверхности сферы, платформа может без сопротивления скользить по этой поверхности, а сфера может катиться без проскальзывания по опорной поверхности. Буквами $\varphi $, α и $\psi $ на рис. 2 обозначены отсчитываемые против часовой стрелки угол между вертикалью и отмеченным в сфере радиусом, угол между горизонтальной плоскостью и платформой (он же – угол между вертикалью и вилкой колеса) и, наконец, угол между вертикалью и отмеченным в колесе радиусом соответственно. Вилка колеса приводится во вращение вокруг оси BA с помощью привода, статор которого жестко скреплен с платформой, а ротор – с вилкой. Масса платформы существенно больше массы вилки с колесом, поэтому не представляет труда поворачивать вилку относительно сферы на желаемый угол и благодаря этому перемещать (“катить”) сферу в нужном направлении.

В продольном (плоском) движении система имеет две степени свободы. В отсутствие проскальзывания колеса по внутренней поверхности сферы и сферы по опоре существует следующая связь между угловыми скоростями :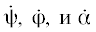

Здесь $R = CD$ – радиус сферы, $r = AD$ – радиус колеса.

Составим уравнения продольного движения системы методом Лагранжа второго рода. Для этого выпишем выражения для кинетической T, потенциальной V  энергии системы и виртуальной работы $\delta W$:

Здесь введены обозначения:

в которых ${{m}_{0}}$ и ${{J}_{0}}$ – масса сферы и ее момент инерции относительно диаметра соответственно, ${{m}_{1}}$ и ${{J}_{1}}$ – масса платформы и ее момент инерции относительно ее диаметра, ${{m}_{2}}$ – масса колеса, ${{J}_{2}} = J_{2}^{'} + {{J}_{{rot}}}{{n}^{2}}$, где $J_{2}^{'}$ – момент инерции колеса относительно его оси вращения, проходящей через его центр А, ${{J}_{{rot}}}$ – момент инерции ротора маршевого двигателя колеса, n – коэффициент редукции маршевого привода. При выписывании выражения для виртуальной работы (2.4), в котором M – момент, развиваемый маршевым приводом, используется кинематическое соотношение (2.1).

Будем считать, что момент M, развиваемый электроприводом, имеет следующую структуру:

В выражении (2.6) u – напряжение, подаваемое на маршевый двигатель, второе слагаемое в этом выражении описывает противоэлектродвижущую силу (противоЭДС), возникающую в обмотке двигателя, c_u и ${{c}_{{v}}}$ – параметры двигателя (постоянные величины). Выражение (2.6) получается, если в уравнении Кирхгофа, описывающем баланс напряжений в обмотке электродвигателя, пренебречь индуктивностью или, другими словами, пренебречь электромагнитной постоянной времени [11–13].

Угол поворота сферы ${{\varphi }}$ является циклической координатой. Введем обозначение для соответствующей угловой скорости ${{\dot {\varphi }}} = {{\omega }}$ и, воспользовавшись соотношениями (2.2)–(2.6), запишем систему уравнений плоского движения:

Здесь в дополнение к (2.5) введены также следующие обозначения:

Будем считать, что напряжение u, подаваемое на двигатель, представляет собой кусочно-непрерывную функцию u(t), ограниченную по абсолютной величине заданным значением u₀:

При $u\left( t \right) \equiv 0$ система (2.7) имеет тривиальное решение:

Наряду с полными нелинейными уравнениями (2.7) продольного движения будем рассматривать также приближенные линейные уравнения, отвечающие малым отклонениям фазовых переменных ${{\omega ,\alpha ,\dot {\alpha }}}$ от значений (2.10):

В уравнениях (2.11) для фазовых переменных используются те же обозначения ${{\omega , \alpha , \dot {\alpha }}}$, что и в полных уравнениях (2.7). В первом из уравнений (2.11) опущен член . Кроме того, в соответствии с обозначениями (2.5) принято, что

Уравнения (2.11) можно преобразовать к виду

где

Если величиной противоЭДС в обмотке электродвигателя пренебречь, то уравнения (2.12) упрощаются и принимают вид

При $u\left( t \right) \equiv 0$ уравнения (2.14) становятся независимыми, а переменные ${{y}_{1}}$, ${{y}_{2}}$ представляют собой не что иное, как нормальные координаты [14]. Из рассмотрения обозначений (2.5), (2.8) следует, что ${{a}_{{11}}} > 0$, ${{a}_{{23}}} > 0$. Кроме того, ${{a}_{{11}}}{{a}_{{22}}} - a_{{12}}^{2}\left( 0 \right) > 0$, поскольку квадратичная форма (2.2), описывающая кинетическую энергию системы, положительно определена. Таким образом, однородная (при $u\left( t \right) \equiv 0$) система (2.14) имеет двукратное нулевое собственное значение и пару чисто мнимых:

Величина $\mu $ представляет собой частоту собственных колебаний переменной ${{y}_{2}}$ (или, другими словами, платформы), а ${{\theta }} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} \mu }} \right. \kern-0em} \mu }$ – период этих колебаний. Уравнения (2.14) перепишем в виде

где

3. Синтез управления, предотвращающего нежелательные колебания. Задаче управления колебательными системами посвящено значительное количество исследований. При этом для борьбы с нежелательными колебаниями механических систем, для их подавления, предотвращения применяются различные методы. В монографии [15] для управления колебаниями используются методы теории оптимального управления. В [16] для колебательных систем предлагается строить квазистационарное финитное управление, в [17] для управления одномерными колебательными системами с распределенными параметрами используется граничное кинематическое управление. В [18] предлагается способ гашения колебаний перемещающейся консоли, в [19] для гашения нежелательных колебаний применяется принцип Гаусса. В работе [20] рассматривается вопрос о гашении остаточных колебаний гибкого манипулятора при перемещении груза. В то время как в большинстве исследований рассматривается вопрос о гашении нежелательных колебаний, в [8–10, 21] предлагаются способы управления механическими системами, при использовании которых удается вообще предотвратить их, причем как в переходном процессе, так и после его окончания. В большинстве описанных в литературе исследований, касающихся борьбы с нежелательными колебаниями, рассматриваются механические системы, содержащие “упругие” объекты. В отличие от них в настоящей работе изучается система, содержащая только абсолютно твердые тела. Однако, как оказывается, методы, описанные в [8–10], могут быть использованы и в подобном случае.

Пусть в начале процесса управления, т.е. при $t = 0$, угловая скорость сферы $\dot {\varphi } = \omega $ равна нулю, угол ${{\alpha }}$ поворота платформы и его угловая скорость ${{\dot {\alpha }}}$ также равны нулю:

Начальные условия (3.1) в переменных ${{\dot {y}}_{1}}$, ${{y}_{2}}$, ${{\dot {y}}_{2}}$, вычисляемые при помощи формул (2.13), имеют аналогичный вид:

Рассмотрим сначала разрывное управление, принимающее при $t \geqslant 0$ максимально возможное (см. неравенство (2.9)) значение ${{u}_{0}}$:

При управлении (3.3) и начальных условиях (3.2) производная ${{\dot {y}}_{1}}$ при $t \geqslant 0$ растет линейно во времени (см. уравнения (2.16)), а переменная ${{y}_{1}}$ – как квадратичная функция:

Что касается переменных ${{y}_{2}}$ и ${{\dot {y}}_{2}}$, то их изменение при управлении (3.3) и начальных условиях (3.2) описывается выражениями

Из (3.5) следует, что при управлении (3.3), изменяющемся в момент t = 0 “скачкообразно”, угол α отклонения маятника от вертикали колеблется около стационарного состояния $ - {{{{b}_{2}}{{u}_{0}}} \mathord{\left/ {\vphantom {{{{b}_{2}}{{u}_{0}}} {{{\mu }^{2}}}}} \right. \kern-0em} {{{\mu }^{2}}}}$ с частотой ${{\mu }}$. Напомним, что формулы (3.4)–(3.6) получены для линеаризованной модели (2.16) и в отсутствие противоЭДС.

Из соотношений (2.13), (3.4), (3.6) получаем, что при управлении (3.3) изменение угловой скорости вращения сферы описывается как

Из выражения (3.7) следует, что угловая скорость $\omega \left( t \right)$ при $t \geqslant 0$ растет “в среднем” линейно во времени, но на ее поведение накладываются незатухающие колебания. На изменение угла поворота сферы ${{\varphi }}$, очевидно, также накладываются колебания с частотой ${{\mu }}$. Амплитуда этих колебаний обратно пропорциональна величине μ². Угловое ускорение сферы

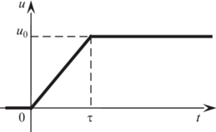
а значит, и ускорение ее центра масс $\ddot {x}\left( t \right) = R{{\dot {\omega }}}\left( t \right)$ претерпевает колебания.

Построим теперь управление системой (2.16), при котором удается предотвратить возникновение указанных выше колебаний. Для этого рассмотрим вместо разрывной (“скачкообразно” изменяющейся) управляющей функции (3.3) непрерывную, полученную “добавлением” к функции (3.3) участка, на котором она возрастает от 0 до величины ${{u}_{0}}$ линейно во времени (см. рис. 3):

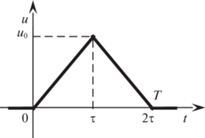
Здесь ${{\tau }}$ – постоянная положительная величина, которая будет выбрана ниже. Непрерывное управление (3.8) в отличие от “скачкообразно” изменяющегося (3.3) можно назвать “плавным” [16].

Решив уравнения (2.16), (3.8) при начальных условиях (3.2), найдем для производной ${{\dot {y}}_{1}}$ выражение

Для переменных ${{y}_{2}}$ и ${{\dot {y}}_{2}}$ запишем следующие соотношения:

Выражения (3.9)–(3.11) найдены путем припасовывания решений уравнений (2.16), (3.8), полученных при $0 \leqslant t < {{\tau }}$, а затем при $t \geqslant {{\tau }}$. Промежуточные выкладки здесь опущены из-за их громоздкости.

Из соотношений (2.13), (3.9) и (3.11) видно, что при управлении (3.8) изменение угловой скорости сферы ${{\omega }}$ при $t \geqslant 0$ описывается как

Соотношения (3.10)–(3.12) показывают, что изменение угла $\alpha $ и угловой скорости $\omega $ при “плавном” управлении (3.8) происходит с колебаниями так же, как и при разрывном управлении (3.3). Однако амплитуды этих колебаний можно уменьшить, увеличив время ${{\tau }}$ “нарастания” управляющего сигнала (3.8). При управлении (3.8) эти амплитуды могут быть сделаны сколь угодно малыми путем выбора достаточно большого значения времени ${{\tau }}$. Таким образом, изменяя в законе управления (3.8) параметр ${{\tau }}$, можно влиять желаемым образом на амплитуду вибраций в системе, причем при любых значениях параметров системы. Не следует забывать, однако, что с увеличением времени ${{\tau }}$ время переходного процесса также увеличивается, что нежелательно. Рассматривая выражения (3.10)–(3.12), удается сделать и другой, более важный, вывод (см. ниже).

Допустим, что время τ кратно периоду собственных колебаний платформы 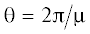с некоторым коэффициентом l, т.е.

где $l = \overline {1,n} $. Тогда формулы (3.10)–(3.12) при $t \geqslant 0$ приобретают следующий вид:

Формулы (3.14)–(3.16) показывают, что при $t \geqslant l{{\theta }}$, когда управляющий сигнал (3.8) становится постоянным, угол ${{\alpha }} = {{y}_{2}}$ остается постоянным (отрицательным), а угловая скорость сферы ${{\omega }}$ растет линейно и монотонно во времени:

При этом каких-либо колебаний по углу ${{\alpha }}$ или по угловой скорости ${{\omega }}$ нет.

Таким образом, если время ${{\tau }}$ кратно периоду собственных колебаний платформы θ, т.е. имеет место условие (3.13), то вибрации в системе на участке постоянства управляющего сигнала (3.8), т.е. при $t \geqslant {{\tau }}$, отсутствуют вообще. Но сформулированное утверждение справедливо, когда противоЭДС пренебрежимо мала. Однако вследствие непрерывной зависимости решения дифференциальных уравнений от параметров при “малой” величине коэффициента ${{c}_{{{\nu }}}}$ амплитуда колебаний на участке постоянства управляющей силы будет “малой”.

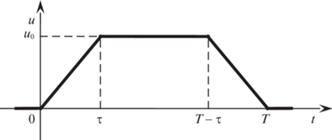
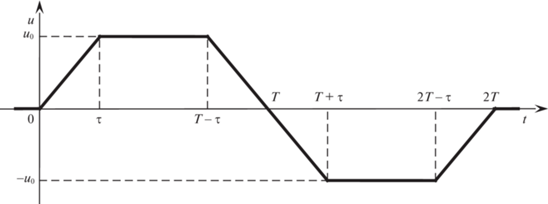
4. Трапецеидальное управление. Рассмотрим управление вида

График функции (4.1), графически изображенный на рис. 4, имеет вид равнобочной трапеции. Если имеет место условие (3.13), то, как нетрудно убедиться, при $t \geqslant T$ угол $\alpha $ при управлении (4.1) остается равным нулю, а угловая скорость сферы $\omega $ остается постоянной величиной, отличной от нуля:

Второе из равенств (4.2) получается при условии $T \geqslant 2l\theta $. Угловая скорость ${{\omega }}\left( t \right)$ при $t \geqslant T$ тем больше, чем больше время T и чем меньше величина l. Если же, например, желаемая скорость вращения сферы ${{{{\omega }}}_{d}} = {{b}_{1}}{{u}_{0}}l\theta $, то, как следует из второго равенства (4.2), должно иметь место соотношение $T = 2l\theta $, и управление (4.1) из “трапецеидального” превращается в “треугольное” (см. рис. 5). Если желаемая скорость ${{{{\omega }}}_{d}} < {{b}_{1}}{{u}_{0}}l\theta $, то у треугольного управления максимальное значение управляющего сигнала u должно быть меньше величины u₀. Такое управление u(t) удовлетворяет строгому неравенству $\left| {u\left( t \right)} \right| < {{u}_{0}}$ вместо нестрогого (2.9). При помощи управлений, показанных на рис. 4, 5, можно организовать движение робота-шара с желаемой скоростью.

Рассмотрим теперь управление, которое графически изображается на рис. 6 в виде двух равнобочных трапеций. Одна из трапеций описывается выражением (4.1) и представлена на рис. 4, а другая симметрична ей относительно точки $\left( {t = T,{\text{ }}u = 0} \right)$.

При $t < 0$ и $t > {\text{2}}T$ управление $u\left( t \right)$, показанное на рис. 6, равно нулю. Момент времени, когда управление становится тождественно равным нулю, здесь обозначен через $2T.$ Если время ${{\tau }}$ удовлетворяет равенству (3.13), то при использовании этого управления на интервалах $\left( {{{\tau }},T - {{\tau }}} \right)$, $\left( {T + {{\tau }},2T - {{\tau }}} \right)$, а также при $t > 2T$, где управляющий сигнал принимает постоянное значение, колебания по углу α и по угловой скорости ${{\omega }}$ отсутствуют; при $t \geqslant 2T$, имеют место тождества ${{\alpha }}\left( t \right) \equiv 0$, ${{\omega }}\left( t \right) \equiv 0$, ${{\varphi }}\left( t \right) \equiv {{\varphi }}\left( {2T} \right) > 0$ (если ${{\varphi }}\left( 0 \right) = 0$). Чем больше время T, тем больше угол поворота сферы ${{\varphi }}\left( {2T} \right)$ и тем больше будет расстояние, на которое она переместится вдоль оси OX (см. рис. 2), поскольку $x\left( {2T} \right) = R\varphi \left( {2T} \right)$. График управляющей функции $u\left( t \right)$ на рис. 6 симметричен относительно точки $\left( {t = T,\;u = 0} \right)$. Поэтому график соответствующей функции ${{\dot {y}}_{1}}\left( t \right)$ симметричен относительно прямой t = T и, кроме того, если ${{\dot {y}}_{1}}\left( 0 \right) = 0$, то ${{\dot {y}}_{1}}\left( t \right) > 0$ при $t \in \left( {0,{\text{2}}{\rm T}} \right)$. В свою очередь график функции ${{y}_{1}}\left( t \right)$ симметричен относительно точки пересечения прямой t = T и кривой ${{y}_{1}} = {{y}_{1}}\left( t \right)$. И, кроме того, если ${{y}_{1}}\left( 0 \right) = 0$, то ${{y}_{1}}\left( t \right) > 0$ при $t \in \left( {0,{\text{2}}{\rm T}} \right)$. При условии (3.13) график функции ${{y}_{2}}\left( t \right) = {{\alpha }}\left( t \right)$ симметричен относительно точки $\left( {t = T,\alpha = 0} \right)$. Из условия симметрии функции ${{y}_{1}}\left( t \right)$ вытекает, что если ${{y}_{1}}\left( 0 \right) = 0$, то

При начальных условиях (3.1), (3.2) (${{y}_{2}}\left( 0 \right) = {{\alpha }}\left( 0 \right) = 0$) и ${{\varphi }}\left( 0 \right) = 0$ из равенства (4.3) следует, что .

Рассмотрим теперь вместо управления, показанного на рис. 6, другое трапецеидальное управление (см. рис. 7).

Управление, изображенное на рис. 7, состоит из двух неравнобочных трапеций. Оно отличается от управления на рис. 6 размером интервала, на котором происходит смена знака управляющего сигнала. На рис. 6 длина этого интервала $\left( {T - {{\tau }},T + {{\tau }}} \right)$ равна $2{{\tau }}$, а на рис. 7 длина соответствующего интервала $\left( {T - {\tau \mathord{\left/ {\vphantom {\tau {2,}}} \right. \kern-0em} {2,}}T + {{{\tau }} \mathord{\left/ {\vphantom {{{\tau }} 2}} \right. \kern-0em} 2}} \right)$ равна ${{\tau }}$, т.е. в 2 раза меньше. Поэтому если имеет место условие (3.13), то и при управлении, представленном на рис. 7, ни угол $\alpha $, ни угловая скорость $\omega $ не совершают колебаний на интервале $\left( {T + {{{\tau }} \mathord{\left/ {\vphantom {{{\tau }} 2}} \right. \kern-0em} 2},2T - {{\tau }}} \right)$ постоянства управляющего сигнала.

Рассмотрим теперь управление, которое находится из управления, показанного на рис. 6, если вторую трапецию, начинающуюся в точке $t = T$, “отодвинуть” направо от первой и положить $u\left( t \right) \equiv 0$ на получившемся между трапециями интервале (см. рис. 8).

Считается, что длина интервала $\left( {2{{\tau }} + \Delta , 2T - 2{{\tau }} - \Delta } \right)$ на рис. 8 не равна нулю, т.е. величина T настолько велика, что $2T - 4{{\tau }} - 2\Delta > 0$. При условии (3.13), на интервале $\left( {2{{\tau }} + \Delta , 2T - 2{{\tau }} - \Delta } \right)$ имеют место тождества:

Таким образом, на этом интервале $\left( {2{{\tau }} + \Delta , 2T - 2{{\tau }} - \Delta } \right)$ робот-шар движется с постоянной скоростью. Второе из равенств (4.4) совпадает со вторым из равенств (4.2), если в (4.4) вместо величины $\Delta $ подставить $T - 2{{\tau }}$. Это естественно, поскольку управление (4.1) (см. рис. 4) на интервале (0, T) совпадает с управлением на интервале $\left( {0,2{{\tau }} + \Delta } \right)$, изображенном на рис. 8. При управлении, приведенном на рис. 8, сфера к моменту времени $2T$ перемещается на бόльшее расстояние, нежели при управлении на рис. 6, если управление на рис. 8 получается из управления на рис. 6 добавлением интервала $\left( {2{{\tau }} + \Delta , 2T - 2{{\tau }} - \Delta } \right)$, на котором сфера движется с постоянной скоростью. Управление, изображенное на рис. 8, может быть использовано, если скорость перемещения сферы по каким-нибудь причинам ограничена. При “длинном” интервале (2τ + Δ, $2T - 2{{\tau }} - \Delta )$ сфера будет “долго” перемещаться с постоянной скоростью.

5. Численные исследования разомкнутой системы. Рассмотрим следующие численные значения параметров сферического робота:

Эти значения соответствуют параметрам прототипа робота-шара, показанного на рис. 1. При значениях (5.1) параметров системы частота собственных колебаний платформы ${{\mu }} \approx 39.9$ с^–1, а период этих колебаний $\theta = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \mu }} \right. \kern-0em} \mu } \approx 0.16$ с.

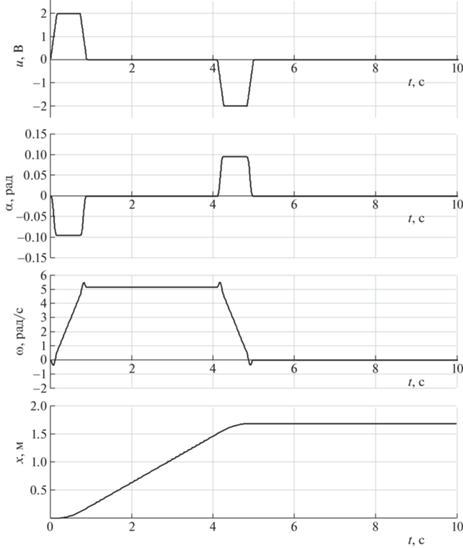
На рис. 9 приведены полученные при решении линейной системы уравнений (2.16), где ${{c}_{{v}}} = 0$, графики изменения во времени трапецеидального управляющего сигнала $u\left( t \right)$, угла ${{\alpha }}\left( t \right)$, угловой скорости ${{\omega }}\left( t \right)$ и расстояния $x\left( t \right) = R{{\varphi }}\left( t \right)$, пройденного центром сферы. При этом считается, что ${{\tau }} = {{\theta }}$ (l = 1), а максимальное напряжение, подаваемое на двигатель, равно 2 В.

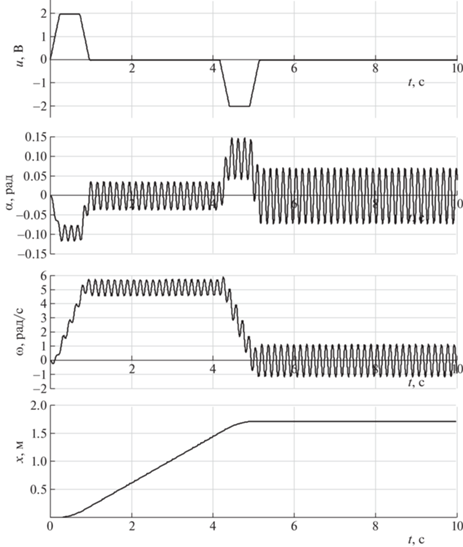
Для сравнения на рис. 10 изображены графики, получающиеся в случае, когда длительность наклонных участков трапеции ${{\tau }} = 1.5 \cdot {{\theta }}$, т.е. не кратна периоду собственных колебаний ${{\theta }}$. Длительность этапа разгона подбирается таким образом, чтобы средняя угловая скорость на следующем этапе (где $u\left( t \right) \equiv 0$) была такой же, как и в случае управления с ${{\tau }} = {{\theta }}$. Из рассмотрения рис. 10 следует, что при указанном управлении наблюдаются заметные колебания величин α и ω.

На рис. 11 графически показаны результаты решения полных нелинейных уравнений движения (2.7) с учетом противоЭДС (${{c}_{{v}}} = 5 \times {{10}^{{ - 5}}}$ Н ⋅ м ⋅ с). При этом длительность этапа торможения уменьшена с тем, чтобы в его конце угловая скорость робота-шара так же, как на рис. 9, обратилась в нуль. Длительность остальных этапов движения осталась такой же, как на рис. 9.

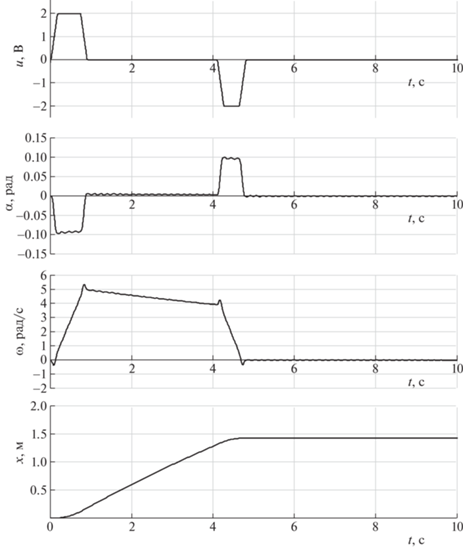
Из рассмотрения рис. 11 следует, что предложенный закон управления позволяет почти полностью предотвратить возникновение колебаний по углу наклона платформы ${{\alpha }}$ и по угловой скорости ${{\omega }}$. Пройденное расстояние, как и следовало ожидать, оказывается несколько меньшим, чем в случае ${{c}_{{v}}} = 0$. Эту разницу можно компенсировать за счет изменения длительности этапов разгона и торможения.

На рис. 9–11 в начале и в конце участков линейного изменения напряжения u(t) видны “небольшие” промежутки времени, на которых угловая скорость ${{\omega }}\left( t \right)$ изменяется немонотонно. Подобное поведение угловой скорости обнаруживается и аналитически. С увеличением коэффициента l, однако, промежутки такого немонотонного изменения скорости ${{\omega }}\left( t \right)$ уменьшаются.

При каждом из управлений, изображенных на рис. 9–11, сфера перемещается на некоторое расстояние и останавливается. Изменяя длительность участков постоянства подаваемого на маршевый привод напряжения, можно изменять расстояние, на которое перемещается робот. Изменить это расстояние можно также, увеличив или уменьшив (после разгона робота) время, в течение которого управляющее напряжение равно нулю. При управлении роботом-шаром в супервизорном режиме (с оператором) имеет место визуальная обратная связь. В этом случае оператор во время движения робота или во время его остановок может вводить ту или иную коррекцию в управление в зависимости от решаемой задачи.

Заключение. Рассматривается продольное движение сферического робота, внутренний механизм которого содержит платформу, опирающуюся своими краями на внутреннюю поверхность сферы. К платформе прикреплена вилка, внутри которой смонтировано колесо, касающееся этой внутренней поверхности. Построено в виде непрерывной функции времени подаваемое на электропривод колеса управляющее напряжение, при котором удается избежать “больших” колебаний по углу наклона платформы и по угловой скорости робота в его продольном движении. Управляющее напряжение состоит из участков постоянства, перемежающихся с участками линейного во времени роста или убывания. Продолжительность участков линейного изменения напряжения выбирается кратной периоду собственных колебаний робота.

Результаты численного моделирования также свидетельствуют об эффективности предложенного алгоритма управления.