Известия РАН. Теория и системы управления, 2022, № 4, стр. 66-94
МИНИМИЗАЦИЯ БИНАРНЫХ ДИАГРАММ РЕШЕНИЙ СИСТЕМ НЕ ПОЛНОСТЬЮ ОПРЕДЕЛЕННЫХ БУЛЕВЫХ ФУНКЦИЙ С ИСПОЛЬЗОВАНИЕМ АЛГЕБРАИЧЕСКИХ РАЗЛОЖЕНИЙ КОФАКТОРОВ
П. Н. Бибило *
Объединенный ин-т проблем информатики НАН Беларусии
Минск, Беларусия
* E-mail: bibilo@newman.bas-net.by
Поступила в редакцию 18.03.2021
После доработки 16.11.2021
Принята к публикации 31.01.2022
- EDN: NBFHUL
- DOI: 10.31857/S0002338822030027
Аннотация
Основным критерием оптимизации при синтезе комбинационных схем из библиотечных логических элементов является число литералов в алгебраических многоуровневых представлениях систем полностью определенных булевых функций. После получения бинарных диаграмм решений исходных систем не полностью определенных (частичных) булевых функций, предлагается выполнять дополнительную логическую оптимизацию на основе поиска алгебраических представлений частичных подфункций (кофакторов) одного уровня бинарной диаграммы решений в виде дизъюнкции либо конъюнкции других подфункций данного уровня бинарной диаграммы решений. Предложенный метод позволяет уменьшать число литералов путем замены формул разложений Шеннона более простыми формулами при переходе к многоуровневому представлению системы полностью определенных функций, по которому осуществляется синтез комбинационной логической схемы.
Введение. Математический аппарат бинарных диаграмм решений (binary decision diagrams (BDD) – бинарные диаграммы решений, диаграммы двоичного выбора) в настоящее время используется в различных областях науки [1, 2], в последнее время он применяется для решения задач выполнимости конъюнктивных нормальных форм булевых функций [3]. BDD используются как структуры данных [4] для представления булевых функций, в [5] были предложены эффективные алгоритмы для сокращения BDD и выполнения логических (двухместных) операций над BDD. Статья [5] оказалась настолько актуальной, что она стала наиболее цитируемой в информатике, “поскольку революционизировала структуры данных, используемые для представления булевых функций” [1, с. 303]. Области применения BDD расширяются, этот аппарат явился вычислительной основой решения задач верификации параллельных систем с конечным числом состояний на основе метода model checking, что позволило “увеличить сложность анализируемых систем в миллионы миллионов раз” [2, c. 295]. В [2] приводится много примеров применения BDD, там же указываются и некоторые из модификаций BDD.
В системах проектирования цифровых сверхбольших интегральных схем (СБИС) графовый аппарат BDD применяется при верификации и тестировании СБИС [6], а также при технологически независимой оптимизации, выполняемой как первый этап синтеза логических схем в различных технологических базисах [7]. BDD представляет собой ациклический граф, задающий булеву функцию либо систему полностью определенных булевых функций. Каждой вершине этого графа соответствует полная либо редуцированная (сокращенная) формула разложения Шеннона. Поэтому при построении BDD стремятся сократить число вершин BDD – сложность функционального описания в виде взаимосвязанных формул разложений Шеннона [8–13].
Схемная реализация (логический синтез) исходных систем частичных булевых функций осуществляется чаще всего в три этапа. На первом этапе происходит логическая оптимизация систем частичных функций и их доопределение до систем полностью определенных функций. Логический синтез для полностью определенных булевых функций составляет содержание следующих двух этапов (логической технологически независимой оптимизации) и технологического отображения в требуемый базис (целевую библиотеку) логических элементов. Однако методы логической оптимизации систем частичных функций, ориентированные на требуемую библиотеку элементов, развиты недостаточно. Чаще всего путем минимизации систем в классе дизъюнктивных нормальных форм (ДНФ) на первом этапе осуществляется переход от систем частичных функций к системам полностью определенных функций, после чего может выполняться минимизация BDD-представлений, позволяющая уменьшать число литералов в многоуровневых представлениях систем функций. При синтезе логических схем из библиотечных элементов уменьшение числа литералов в представлениях систем полностью определенных булевых функций приводит к менее сложным схемам. Поэтому число литералов – это основной критерий минимизации алгебраических представлений функций на первых двух этапах синтеза логических схем [14].
В [15] предложено осуществлять поиск в графе BDD-представлений булевых функций в виде разложений кофакторов на две подфункции с алгебраической выходной функцией, в зарубежной литературе такие разложения называют bi-decomposition (англ.). В системе BDS [15] данный вид оптимизации был дополнен также факторизацией – поиском одинаковых логических подвыражений и поиском подфункций, допускающих простое (с одной промежуточной булевой переменной) функциональное разложение.
Различные виды декомпозиции BDD-представлений систем булевых функций изучены в [7], минимизация BDD-представлений может выполняться с нахождением пар взаимно инверсных кофакторов [16], что дает значительный эффект при синтезе схем. Для дополнительной логической оптимизации в [17] предложен метод, основанный на поиске алгебраических разложений подфункций, входящих в минимизированные BDD-представления. Метод позволяет заменять формулы разложения Шеннона двухоперандными формулами дизъюнкций и конъюнкций и формулами вида gp = gi $ \oplus $ gj, что уменьшает число литералов в результирующих логических формулах, по которым выполняется заключительный этап синтеза схемы. Программная реализация алгоритмов и результаты вычислительных экспериментов, приведенные в [18], показали, что для разложений кофакторов целесообразно использовать только дизъюнктивные и конъюнктивные разложения. Причем кофакторы в таких разложениях могут быть как в инверсной, так и безынверсной форме. Эксперименты показали также, что наиболее эффективной эвристикой в данных алгоритмах, влияющей на сокращение площади схем, является эвристика, ориентированная на нахождение дизъюнктивных и конъюнктивных разложений не для всех кофакторов, а только для тех, которые представлены полными уравнениями разложений Шеннона. Эксперименты были проведены на 59 примерах схем из широко известной библиотеки [19] и 14 примерах схем модулярных сумматоров. Используя после BDD-оптимизации программы поиска алгебраических разложений кофакторов, для 33 схем из [19] было получено 10–15% сокращение площади, при этом площадь уменьшалась преимущественно для схем с достаточно большим числом (10–27) входных переменных. Для девяти (из 14) схем модулярных сумматоров было получено сокращение площади, достигающее 28%.
Для систем частичных функций в [7] была предложена модификация BDD, отличительной особенностью которой является то, что для частичных функций все листовые вершины “–” (неопределенные значения частичных функций) рассматриваются как различные, в отличие от вершин-констант 0, 1. Каждая вершина “–” отдельно доопределяется при оптимизации до 0 либо 1. Для таких BDD-представлений систем частичных функций в [20] были предложены методы, позволяющие доопределить частичные функции до полностью определенных и минимизировать сложность BDD, находя пары взаимно инверсных частичных кофакторов. При решении задач логической оптимизации систем частичных булевых функций поиск рациональных доопределений применяется не только при минимизации BDD-представлений [7, с. 102], но и при совместной минимизации функций в классе ДНФ [20, с. 258], сокращении числа аргументов [20, с. 269], декомпозиции [7, с. 146; 20, с. 287] и при решении других задач, возникающих на этапе технологически независимой оптимизации. По аналогии с минимизацией многоуровневых BDD-представлений систем полностью определенных функций для повышения эффективности логической минимизации BDD-представлений систем частичных функций целесообразно проводить дополнительную логическую минимизацию и находить в таких случаях соответствующие доопределения функций с целью увеличения числа кофакторов, которые будут иметь алгебраические (дизъюнктивные либо конъюнктивные) разложения.
В работе предлагается метод минимизации BDD-представлений систем частичных функций, основанный на поиске алгебраических разложений частичных кофакторов одного уровня BDD в виде дизъюнкции либо конъюнкции других кофакторов того же уровня BDD. При поиске алгебраических разложений частичных кофакторов проводится их доопределение и используются как прямые (безынверсные), так и инверсные формы кофакторов. Суть предлагаемого метода состоит в нахождении алгебраических разложений кофакторов в классе частичных булевых функций, затем частичные функции доопределяются и для полученных многоуровневых представлений функций дополнительно ищутся алгебраические разложения кофакторов в классе полностью определенных булевых функций. Применение предлагаемого метода позволяет уменьшать число литералов в результирующих многоуровневых представлениях систем булевых функций, состоящих из формул разложения Шеннона и формул дизъюнктивного и конъюнктивного разложений. Приведенный в [7, 16–18] подход к оптимизации многоуровневых BDD-представлений систем полностью булевых функций, включающий:
минимизацию сложности BDD-представлений с нахождением взаимно инверсных кофакторов на каждом уровне BDD [16];
алгебраические разложения кофакторов [17];
программную реализацию и выбор эффективных эвристик [18],
распространяется и на случай систем частичных функций. Для BDD-представлений таких систем функций минимизация сложности BDD на первом этапе выполняется на основе сокращения числа пар взаимно инверсных частичных кофакторов [20], а на втором этапе – на базе предлагаемого в данной статье метода их алгебраических разложений. На третьем этапе предполагается программная реализация и проверка эффективности такого подхода к технологически независимой оптимизации при логическом синтезе схем из библиотечных элементов.
1. Основные определения. Булевыми называются двоичные (0, 1) функции f(x) = f(x1, x2, …, xn) двоичных (булевых) переменных x1, x2, …, xn. Пусть Vx – булево пространство, построенное над переменными булева вектора x = (x1, x2, …, xn). Элементами этого пространства являются n-компонентные наборы (векторы) x* нулей и единиц. Булева функция, значения 0, 1 которой определены на всех элементах x* ∈ Vx, называется полностью определенной. Множество $M_{f}^{1}$ элементов x* булева пространства, на которых полностью определенная булева функция принимает значение 1, называется характеристическим множеством функции. Если же на некоторых элементах булева пространства Vx значения функции не определены, то такая функция будет не полностью определенной, или частичной. Частичная булева функция принимает единичное значение на элементах x* подмножества $M_{f}^{1}$ булева пространства Vx и нулевое значение на элементах подмножества $M_{f}^{0}$. На всех остальных элементах пространства Vx, образующих подмножество $M_{f}^{ - }$ пространства Vx, значения частичной функции не определены, подмножество $M_{f}^{ - }$ будем называть также областью неопределенных значений частичной функции. Неопределенное значение функции обозначается символом “–”. Очевидно, что $M_{f}^{1} \cap M_{f}^{0} = \emptyset $, $M_{f}^{1}\, \cap \,M_{f}^{ - }\, = \,\emptyset $, $M_{f}^{0}\, \cap \,M_{f}^{ - }\, = \,\emptyset $, ${{V}^{x}} = M_{f}^{0} \cup M_{f}^{1} \cup M_{f}^{ - }$.
Частичные функции f1(x) и f2(x) равны, если и только если
(1.1)
$M_{{{{f}_{1}}}}^{1} = M_{{{{f}_{2}}}}^{1},\quad M_{{{{f}_{1}}}}^{0} = M_{{{{f}_{2}}}}^{0},\quad M_{{{{f}_{1}}}}^{ - } = M_{{{{f}_{2}}}}^{ - }.$Будем называть частичные функции f1(x) и f2(x) взаимно инверсными (f2 = ${{\bar {f}}_{1}}$, f1 = ${{\bar {f}}_{2}}$), если и только если
(1.2)
$M_{{{{f}_{1}}}}^{1} = M_{{{{f}_{2}}}}^{0},\quad M_{{{{f}_{1}}}}^{0} = M_{{{{f}_{2}}}}^{1},\quad M_{{{{f}_{1}}}}^{ - } = M_{{{{f}_{2}}}}^{ - }.$Согласно (1.2), инверсией частичной функции является частичная функция, при этом взаимно инверсные частичные функции имеют одну и ту же область неопределенных значений.
Частичная функция fi реализуется частичной (либо полностью определенной) функцией fj (обозначается fi $ \prec $ fj), если и только если
(1.3)
$M_{{{{f}_{i}}}}^{1} \subseteq M_{{{{f}_{j}}}}^{1},\quad M_{{{{f}_{i}}}}^{0} \subseteq M_{{{{f}_{j}}}}^{0}.$Функцию fj называют доопределением функции fi. Для пары полностью определенных булевых функций fi, fj отношение реализации является отношением равенства. Под векторной булевой функцией f(x) будем понимать упорядоченную систему частичных булевых функций f(x) = = (f1(x), …, fm(x)), значениями векторных функций на элементах x* булева пространства являются m-компонентные троичные векторы f(x*).
Разложением Шеннона полностью определенной либо частичной булевой функции f = f(x), x = (x1, x2, …, xn), по переменной xi называется представление
Функции f0 = f0(x1, …, xi – 1, 0, xi + 1, …, xn), f1 = f1(x1, …, xi – 1, 1, xi + 1, …, xn) называются кофакторами (cofactors, англ.) разложения по переменной xi либо подфункциями. Они получаются из функции f = f(x1, …, xn) подстановкой вместо переменной xi константы 0 и 1 соответственно. Каждая из подфункций f0 и f1 может быть разложена по одной из переменных из множества {x1, …, xi – 1, xi + 1, …, xn}. Процесс разложения подфункций заканчивается, когда все n переменных будут использованы для разложения либо когда все подфункции выродятся до констант 0, 1, “–” (неопределенное значение). На каждом шаге разложения выполняется сравнение на равенство полученных подфункций и оставляется одна из нескольких попарно равных подфункций.
Под BDD-представлением частичной векторной булевой функции f(x) = (f1(x), …, fm(x)) понимается ориентированный ациклический граф, задающий последовательные разложения Шеннона всех компонентных функций fi(x), $i = \overline {1,m} $, по всем ее переменным x1, …, xn при одном и том же заданном порядке (перестановке) переменных, по которым проводятся разложения [7]. Для упрощения графа листовые вершины обычно дублируются, а ориентация дуг на рисунках графов BDD не показывается, так как всегда принимается, что дуги ориентированы сверху вниз.
Наиболее близкими к графам BDD для частичных векторных функций (назовем такие графы частичными BDD) являются широко известные в литературе сокращенные упорядоченные BDD (англ. reduced ordered BDD, ROBDD) для одной полностью определенной булевой функции, в которых каждой функциональной вершине соответствует одна функция (подфункция разложения Шеннона), при этом функциональные вершины лишь подразумеваются (отождествляются с вершинами-переменными). Подробное описание OBDD (упорядоченных BDD) дано в [12, 13], ROBDD – в [1]. Далее под BDD будут пониматься ROBDD для систем функций (векторных функций).
Будем изображать на рисунках графы BDD, содержащие три вида вершин: функциональные вершины, соответствующие разлагаемым функциям; вершины-переменные; листовые вершины-константы 0, 1 “–” [7, с. 16]. BDD-представлению соответствуют формулы разложения Шеннона, каждой функциональной вершине – своя формула. По BDD-представлению можно найти задание каждой из компонентных функций fi(x) в виде трех ортогонализованных ДНФ: одна из таких ДНФ задает область $M_{{{{f}_{i}}}}^{1}$ единичных значений компонентной функции, другая ДНФ – область $M_{{{{f}_{i}}}}^{0}$ нулевых значений функции, третья ДНФ – область $M_{{{{f}_{i}}}}^{ - }$ неопределенных значений компонентной частичной функции fi(x). BDD является более компактной формой по сравнению с ортогонализованной формой представления булевых функций (такие формы будут рассмотрены далее). Так BDD – это граф, а ортогонализованная форма задает все пути из корневых вершин в листовые в этом графе. Задание графа более компактно, чем перечисление всех путей в нем. Поэтому BDD и нашли широкое применение не только при проектировании логических схем, но и в информатике в целом [1, 2].
З а м е ч а н и е 1. Рисунки и структуры данных классических BDD не содержат функциональных вершин. Функциональные вершины обычно показываются на рисунках для удобства изложения методов минимизации BDD и иллюстрации зависимостей переменных в формулах разложений Шеннона, в компьютерных структурах данных функциональные вершины не указываются [7, с. 177].
2. Алгебраические разложения частичных функций. З а д а ч а 1. Заданы частичные булевы функции φ(x), f1(x), f2(x). Требуется найти, если это возможно, такие доопределения φ*(x), $f_{1}^{*}$(x), $f_{2}^{*}$(x) соответствующих функций (запишем это в виде φ(x) $ \prec $ φ*(x), f1(x) $ \prec $ $f_{1}^{*}$(x), f2(x) $ \prec $ $f_{2}^{*}$(x)), что будет выполняться одно из алгебраических разложений:
Естественно, для каждого из разложений (2.1), (2.2) требуются свои доопределения функций φ(x), f1(x), f2(x). Логические операторы $ \vee $ (дизъюнкция), & (конъюнкция) в формулах (2.1), (2.2) называют также выходными функциями соответствующего разложения. В [7] логические операции над частичными булевыми функциями (троичными переменными) определены следующим образом:
| функция f1 | 0 | 0 | 0 | – | – | – | 1 | 1 | 1 |
| функция f2 | 0 | – | 1 | 0 | – | 1 | 0 | – | 1 |
| отрицание ${{\bar {f}}_{1}}$ | 1 | 1 | 1 | – | – | – | 0 | 0 | 0 |
| дизъюнкция f1 $ \vee $f2 | 0 | – | 1 | – | – | 1 | 1 | 1 | 1 |
| конъюнкция f1 & f2 | 0 | 0 | 0 | 0 | – | – | 0 | – | 1 |
У т в е р ж д е н и е 1. Задача нахождения разложения (2.1) не имеет решения тогда и только тогда, когда выполняется хотя бы одно из условий (2.3)–(2.5):
Условие (2.3) говорит о том, что, если найдется хотя бы один набор значений переменных, на котором обе функции f1(x), f2(x) принимают значение нуль, а функция φ(x) принимает значение единица, то через операцию дизъюнкции функций f1(x), f2(x) нельзя выразить функцию φ(x), так как дизъюнкция двух нулей не может быть равна единице. В случае (2.4) от значения функции f2(x) ничего не зависит, дизъюнкция f1(x) $ \vee $ f2(x) не может принять значение нуль (значение нуль имеет функция φ(x)), так f1(x) принимает значение единица. Аналогично в случае (2.5). Условия (2.3)–(2.5) можно задать в табличном виде (табл. 1). Таблица 2 позволяет проверить возможность доопределения функций φ(x), f1(x), f2(x) для проверки реализации φ*(x) $ \prec $ ($f_{1}^{*}$(x) $ \vee $ $f_{2}^{*}$(x)). Рассмотрим третью строку табл. 2, в которой f1(x) = 0, f2(x) = 0, φ(x) = “–”. Для выполнения дизъюнктивного разложения нужно заменить значение “–” на 0: φ(x) = 0. Аналогично можно доопределять значения “–” и для других строк из табл. 2, не содержащих пометку “Нет решения”.
Таблица 1.
Условия, не позволяющие провести разложение с выходной функцией “$ \vee $”
| Значение функции | |||
|---|---|---|---|
| f1(x) | f2(x) | φ(x) (φ(x) ≠ f1(x) $ \vee $f2(x)) | Условие |
| 0 | 0 | 1 | (2.3) |
| 1 | – | 0 | (2.4) |
| – | 1 | 0 | (2.5) |
Таблица 2.
Доопределения частичных функций f1(x), f2(x), φ(x) для разложения φ*(x) $ \prec $ ($f_{1}^{*}(x) \vee f_{2}^{*}(x)$)
| Значения исходных функций | Значения реализующих функций φ*(x) $ \prec $ ($f_{1}^{*}(x) \vee f_{2}^{*}(x)$ | ||||
|---|---|---|---|---|---|
| f1(x) | f2(x) | φ(x) | $f_{1}^{*}(x)$ | $f_{2}^{*}(x)$ | φ*(x) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | Нет решения | ||
| 0 | 0 | – | 0 | 0 | 0 |
| 0 | 1 | 0 | Нет решения | ||
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | – | 0 | 1 | 1 |
| 0 | – | 0 | 0 | 0 | 0 |
| 0 | – | 1 | 0 | 1 | 1 |
| 0 | – | – | 0 | – | – |
| 1 | 0 | 0 | Нет решения | ||
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | – | 1 | 0 | 1 |
| 1 | 1 | 0 | Нет решения | ||
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | – | 1 | 1 | 1 |
| 1 | – | 0 | Нет решения | ||
| 1 | – | 1 | 1 | – | 1 |
| 1 | – | – | 1 | – | 1 |
| – | 0 | 0 | 0 | 0 | 0 |
| – | 0 | 1 | 1 | 0 | 1 |
| – | 0 | – | – | 0 | – |
| – | 1 | 0 | Нет решения | ||
| – | 1 | 1 | – | 1 | 1 |
| – | 1 | – | – | 1 | 1 |
| – | – | 0 | 0 | 0 | 0 |
| – | – | 1 | 1 | – | 1 |
| – | 1 | 1 | |||
| – | – | – | – | – | – |
У т в е р ж д е н и е 2. Задача нахождения разложения (2.2) не имеет решения тогда и только тогда, когда верно хотя бы одно из условий (2.6)–(2.8):
Условия (2.6)–(2.8) можно задать в табличном виде (табл. 3). Таблица 4 позволяет проверить возможность доопределения функций φ(x), f1(x), f2(x) для проверки реализации φ*(x) $ \prec $ ($f_{1}^{*}$(x) & $f_{2}^{*}$(x)), замены неопределенных значений “–” нулями или единицами в строках, не содержащих пометку “Нет решения”, всегда могут быть выполнены для конъюнктивного разложения.
Таблица 3.
Условия, не позволяющие провести разложение с выходной функцией “&”
| Значение функции | |||
|---|---|---|---|
| f1(x) | f2(x) | φ(x) (φ(x) ≠ f1(x) $\& $f2(x)) | Условие |
| 0 | – | 1 | (2.6) |
| – | 0 | 1 | (2.7) |
| 1 | 1 | 0 | (2.8) |
Таблица 4.
Доопределения частичных функций f1(x), f2(x), φ(x) для разложения φ*(x) $ \prec $ ($f_{1}^{*}(x)\& f_{2}^{*}(x)$)
| Значения исходных функций | Значения реализующих функций φ*(x) $ \prec $ ($f_{1}^{*}(x)\& f_{2}^{*}(x)$) | ||||
|---|---|---|---|---|---|
| f1(x) | f2(x) | φ(x) | $f_{1}^{*}(x)$ | $f_{2}^{*}(x)$ | φ*(x) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | Нет решения | ||
| 0 | 0 | – | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | Нет решения | ||
| 0 | 1 | – | 0 | 1 | 0 |
| 0 | – | 0 | 0 | 0 | 0 |
| 0 | – | 1 | Нет решения | ||
| 0 | – | – | 0 | – | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | Нет решения | ||
| 1 | 0 | – | 1 | 0 | 0 |
| 1 | 1 | 0 | Нет решения | ||
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | – | 1 | 1 | 1 |
| 1 | – | 0 | 1 | 0 | 0 |
| 1 | – | 1 | 1 | 1 | 1 |
| 1 | – | – | 1 | – | – |
| – | 0 | 0 | 0 | 0 | 0 |
| – | 0 | 1 | Нет решения | ||
| – | 0 | – | – | 0 | 0 |
| – | 1 | 0 | 0 | 1 | 0 |
| – | 1 | 1 | 1 | 1 | 1 |
| – | 1 | – | – | 1 | – |
| – | – | 0 | 0 | – | 0 |
| – | 0 | 0 | |||
| – | – | 1 | 1 | 1 | 1 |
| – | – | – | – | – | – |
Аналогичным образом могут быть рассмотрены условия доопределения функций φ(x), f1(x), f2(x) для получения алгебраических разложений по другим выходным функциям, например, таким, как инверсия дизъюнкции, инверсия конъюнкции, исключающее ИЛИ, эквиваленция и т.д.
П р и м е р 1. Приведем пример (табл. 5) такого доопределения частичных функций, заданных таблицами истинности, чтобы выполнялось алгебраическое разложение (2.2). В табл. 5 жирным курсивом выделены замены неопределенных значений функций определенными (0, 1).
Таблица 5.
Доопределения частичных функций (пример 1) для разложения с операцией “&”
| x1 x2 x3 | Исходные функции | Реализующие функции разложения $f_{2}^{*}$$ \prec $ ($f_{1}^{*}\& f_{3}^{*}$) | ||||
|---|---|---|---|---|---|---|
| f2 | f1 | f3 | $f_{2}^{*}$ | $f_{1}^{*}$ | $f_{3}^{*}$ | |
| 0 0 0 | – | – | – | – | – | – |
| 0 0 1 | 1 | – | 1 | 1 | 1 | 1 |
| 0 1 0 | – | 0 | 0 | 0 | 0 | 0 |
| 0 1 1 | – | 1 | 1 | 1 | 1 | 1 |
| 1 0 0 | 1 | 1 | – | 1 | 1 | 1 |
| 1 0 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 1 0 | – | – | – | – | – | – |
| 1 1 1 | 0 | – | 1 | 0 | 1 | 1 |
3. Ортогонализованные формы частичной векторной булевой функции. Интервальная форма задания частичной векторной функции f(x) = (f1(x), …, fm(x)) состоит из троичной матрицы T x задания элементарных конъюнкций и троичной матрицы T f вхождений конъюнкций в ДНФ, представляющих области нулевых и единичных значений компонентных функций. Данная форма задания частичных функций подробно описана в литературе [21]. Если в матричном задании в троичной матрице T x все строки (троичные векторы) ортогональны, то такая матричная форма представления векторной булевой функции называется ортогонализованной. Для ортогонализованной формы строки матрицы T f задают значения функций на соответствующих интервалах булева пространства V x. Алгоритмы получения ортогонализованных форм систем функций по исходным интервальным формам известны из [21, 22]. Более компактной по сравнению с ортогонализованной является обобщенно ортогонализованная форма, когда частичная векторная функция задается на попарно ортогональных ДНФ, а не на попарно ортогональных интервалах (конъюнкциях), как это осуществляется в ортогонализованных формах. Данная форма представления является более компактной и удобной для решения задач, возникающих при доопределении частичных функций, например с целью сокращения сложности BDD [7].
Нахождение обобщенно ортогонализованной формы для частичной векторной булевой функции f(x) = (f1(x), …, fm(x)) сводится к решению задачи нахождения ее минимального дизъюнктивного базиса. Зададим каждую компонентную частичную булеву функцию fi(x) тремя полностью определенными булевыми функциями $\lambda _{i}^{0}$(x), $\lambda _{i}^{1}$(x), $\lambda _{i}^{ - }$(x), такими, что функция $\lambda _{i}^{0}$(x) имеет характеристическое множество $M_{{{{f}_{i}}}}^{0}$, функция $\lambda _{i}^{1}$(x) – характеристическое множество $M_{{{{f}_{i}}}}^{1}$, функция $\lambda _{i}^{ - }$(x) – характеристическое множество $M_{{{{f}_{i}}}}^{ - }$. Минимальным дизъюнктивным базисом для f(x) = (f1(x), …, fm(x)) называется минимальная по мощности система попарно ортогональных полностью определенных булевых функций Π = {Π1(x), …, Π k(x)}, такая, что каждая полностью определенная функция $\lambda _{i}^{0}$(x), $\lambda _{i}^{1}$(x), $\lambda _{i}^{ - }$(x) равна дизъюнкции некоторого подмножества функций системы Π. Частичная булева функция fi(x) задает трехблочное разбиение Ri = {$M_{{{{f}_{i}}}}^{0}$, $M_{{{{f}_{i}}}}^{1}$, $M_{{{{f}_{i}}}}^{ - }$} булева пространства Vx на попарно непересекающиеся подмножества. Нахождение для f(x) = = (f1(x), …, fm(x)) минимального дизъюнктивного базиса (в теоретико-множественной интерпретации) может быть сведено к нахождению произведения разбиений Ri, $i = \overline {1,m} $, [23, с. 12] и составлению из непустых блоков полученного произведения разбиений каждого из исходных блоков $M_{{{{f}_{i}}}}^{0}$, $M_{{{{f}_{i}}}}^{1}$, $M_{{{{f}_{i}}}}^{ - }$. Пусть каждая компонентная функция fi задана тройкой попарно ортогональных ДНФ $D_{{{{f}_{i}}}}^{0}$, $D_{{{{f}_{i}}}}^{1}$, $D_{{{{f}_{i}}}}^{ - }$, данные ДНФ представляют функции $\lambda _{i}^{0}$(x), $\lambda _{i}^{1}$(x), $\lambda _{i}^{ - }$(x) соответственно. В этом случае нахождение минимального дизъюнктивного базиса Π может быть сведено к выполнению операций перемножения, инверсирования и сравнения на равенство ДНФ, алгоритм описан в [24, с. 124]. Он оперирует исходными данными для случая, когда каждая из функций задана элементарной конъюнкцией. Алгоритм пригоден и для случая задания функций $\lambda _{i}^{0}$(x), $\lambda _{i}^{1}$(x), $\lambda _{i}^{ - }$(x) в виде ДНФ. Он программно реализован и использован при решении задачи декомпозиции системы булевых функций. Примеры разбиения булева пространства на непересекающиеся подмножества (характеристические множества попарно ортогональных базисных функций Π1(x), …, Πk(x)) показаны в [7, с. 135; 24, с. 120].
П р и м е р 2. Пусть каждая из частичных компонентных функций f1, f2, f3 векторной булевой функции f(x) = (f1(x), f2(x), f3(x)), x = (x1, x2, x3, x4), задана тремя ДНФ, представляющими области нулевых, единичных и неопределенных значений этой компонентной функции (табл. 6). Чтобы решить задачу нахождения дизъюнктивного разложения (2.1), построим для данных трех функций минимальный дизъюнктивный базис и обобщенно ортогонализованную форму.
Таблица 6.
Задание областей значений функций (пример 2) в виде ДНФ
| Частичная функция | x1 x2 x3 x4 | Значение | Область значений | Функция λ |
|---|---|---|---|---|
| f1 | 0 0 – – | 0 | $M_{{{{f}_{1}}}}^{0}$ | $\lambda _{1}^{0}$ |
| 0 1 0 1 | 0 | |||
| 1 0 – 0 | 1 | $M_{{{{f}_{1}}}}^{1}$ | $\lambda _{1}^{1}$ | |
| 1 – 0 – | 1 | |||
| 0 1 1 1 | 1 | |||
| 1 – 1 1 | 1 | |||
| – 1 1 0 | – | $M_{{{{f}_{1}}}}^{ - }$ | $\lambda _{1}^{ - }$ | |
| 0 1 0 0 | ||||
| f2 | – 1 1 0 | 0 | $M_{{{{f}_{2}}}}^{0}$ | $\lambda _{2}^{0}$ |
| 0 1 0 0 | 0 | |||
| 1 – 0 – | 1 | $M_{{{{f}_{2}}}}^{1}$ | $\lambda _{2}^{1}$ | |
| 0 0 1 – | 1 | |||
| 0 0 0 – | – | $M_{{{{f}_{2}}}}^{ - }$ | $\lambda _{2}^{ - }$ | |
| 0 – 0 1 | – | |||
| 1 0 1 – | – | |||
| 1 – 1 1 | – | |||
| – 1 1 1 | – | |||
| f3 | 0 0 0 – | 0 | $M_{{{{f}_{3}}}}^{0}$ | $\lambda _{3}^{0}$ |
| 0 1 0 1 | 0 | |||
| – 1 1 0 | 1 | $M_{{{{f}_{3}}}}^{1}$ | $\lambda _{3}^{1}$ | |
| 0 1 – 0 | 1 | |||
| 1 – 0 1 | 1 | |||
| 1 – 0 0 | 1 | |||
| – – 1 1 | – | $M_{{{{f}_{3}}}}^{ - }$ | $\lambda _{3}^{ - }$ | |
| – 0 1 0 | – |
Ортогонализованная форма векторной функции f(x) = (f1(x), f2(x), f3(x)) задана в табл. 7. Легко проверить, что каждая пара элементарных конъюнкций, соответствующих троичным векторам из левой части табл. 7, находится в отношении ортогональности (для ортогональных элементарных конъюнкций их произведение равно нулю). Например, рассмотрим первую пару: троичному вектору (0 0 0 –) соответствует элементарная конъюнкция ${{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$, булеву вектору (0 1 0 1) – полная элементарная конъюнкция ${{\bar {x}}_{1}}{{x}_{2}}{{\bar {x}}_{3}}{{x}_{4}}$, они ортогональны по второй компоненте: (${{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$) & & (${{\bar {x}}_{1}}{{x}_{2}}{{\bar {x}}_{3}}{{x}_{4}}$) = 0.
Таблица 7.
Ортогонализованная форма функций (пример 2)
| T x | T f |
|---|---|
| x1 x2 x3 x4 | f1f2f3 |
| 0 0 0 – | 0 – 0 |
| 0 1 0 1 | 0 – 0 |
| 1 – 0 – | 1 1 1 |
| – 1 1 0 | – 0 1 |
| 0 1 0 0 | – 0 1 |
| 0 0 1 – | 0 1 – |
| 1 0 1 – | 1 – – |
| – 1 1 1 | 1 – – |
Представление ДНФ, задающих области значений компонентных функций, в виде дизъюнкций ДНФ минимального дизъюнктивного базиса имеет следующий вид:
Обобщенно ортогонализованная форма частичной векторной функции f(x) = (f1(x), f2(x), f3(x)) дана в табл. 8. Легко видеть, что значения функций на наборах, соответствующих полным элементарным конъюнкциям минимального дизъюнктивного базиса, являются одинаковыми. Теперь легко доопределить функции f1, f2, f3 из табл. 6 так, что возможно провести разложение $f_{3}^{*}$ $ \prec $ ($f_{1}^{*}$ $ \vee $ $f_{2}^{*}$) (табл. 9). Перейдя от ортогонализованной формы (табл. 7) либо от табл. 8 к таблице истинности (табл. 10) частичной векторной функции f(x) = (f1(x), f2(x), f3(x)), можно убедиться, что обобщенно ортогонализованная форма более компактна по сравнению с ортогонализованной формой и значительно более компактна по сравнению с таблицей истинности.
Таблица 8.
Обобщенно ортогонализованная форма функций (пример 2)
| Πi | x1 x2 x3 x4 | f1f2f3 |
|---|---|---|
| Π1 | 0 0 0 – | 0 – 0 |
| 0 1 0 1 | ||
| Π2 | 1 – 0 – | 1 1 1 |
| Π3 | – 1 1 0 | – 0 1 |
| 0 1 0 0 | ||
| Π4 | 0 0 1 – | 0 1 – |
| Π5 | 1 0 1 – | 1 – – |
| – 1 1 1 |
Таблица 9.
Доопределения частичных функций из примера 2 для алгебраического разложения с операцией “$ \vee $”
| Πi | Исходные функции | Реализующие функции разложения $f_{3}^{*}$$ \prec $ ($f_{1}^{*} \vee f_{2}^{*}$) | ||||
|---|---|---|---|---|---|---|
| f1 | f2 | f3 | $f_{1}^{*}$ | $f_{2}^{*}$ | $f_{3}^{*}$ | |
| Π1 | 0 | – | 0 | 0 | 0 | 0 |
| Π2 | 1 | 1 | 1 | 1 | 1 | 1 |
| Π3 | – | 0 | 1 | 1 | 0 | 1 |
| Π4 | 0 | 1 | – | 0 | 1 | 1 |
| Π5 | 1 | – | – | 1 | – | 1 |
Таблица 10.
Таблица истинности функций из примера 2 (строки в таблице истинности переставлены)
| x1 x2 x3 x4 | f1f2f3 |
|---|---|
| 0 0 0 0 | 0 – 0 |
| 0 0 0 1 | 0 – 0 |
| 0 1 0 1 | 0 – 0 |
| 1 0 0 0 | 1 1 1 |
| 1 0 0 1 | 1 1 1 |
| 1 1 0 0 | 1 1 1 |
| 1 1 0 1 | 1 1 1 |
| 0 1 1 0 | – 0 1 |
| 1 1 1 0 | – 0 1 |
| 0 1 0 0 | – 0 1 |
| 0 0 1 0 | 0 1 – |
| 0 0 1 1 | 0 1 – |
| 1 0 1 0 | 1 – – |
| 1 0 1 1 | 1 – – |
| 0 1 1 1 | 1 – – |
| 1 1 1 1 | 1 – – |
У т в е р ж д е н и е 3. Приведенные в табл. 2, 4 доопределения функций для построения разложений (2.1), (2.2) соответственно справедливы для задания функций таблицами истинности, ортогонализованными, обобщенно ортогонализованными формами и графами BDD.
При задании функций BDD проверка возможности доопределения функций, участвующих в разложениях (2.1), (2.2), сводится к логическим операциям над соответствующими BDD: сначала выполняется операция слияния BDD, реализующих f1(x), f2(x), φ(x), т.е. строится BDD векторной функции f = (f1(x), f2(x), φ(x)), затем для листовых вершин, заданных трехкомпонентными троичными векторами, проверяются условия возможности доопределения, приведенные в табл. 2 либо табл. 4.
4. Задача нахождения алгебраически представимых функций. Обозначим через G = {g1, …, gk} множество частичных функций. Найдем в множестве G (если это возможно) максимальное по мощности подмножество Gc функций, которые могут быть выражены через дизъюнкцию либо конъюнкцию пар функций, не вошедших в множество Gc. Это, естественно, происходит при соответствующем доопределении частичных функций, входящих в разложения. Назовем функции из множества Gb = G\Gc основными (базисными), а функции из множества Gc – представимыми. Каждая функция из множества Gc при этом должна задаваться в алгебраическом (дизъюнктивном либо конъюнктивном) разложении своей парой базисных функций, т.е. каждая основная функция может входить в разложение только одной функции из Gc.
З а д а ч а 2. Для заданного множества G = {g1, …, gk} частичных функций требуется найти в G максимальное по мощности подмножество Gc представимых функций (главный критерий) и при этом требуется минимизировать суммарное множество наборов, на которых доопределяются базисные функции (дополнительный критерий оптимизации).
Составим множество всех неупорядоченных пар {gi, gj} функций, i, j = $\overline {1,k} $, i ≠ j. Для каждой пары {gi, gj} проверим выполнение отношения реализации:
т.е. решим задачу 1 нахождения разложений (2.1), (2.2) для троек функций gi, gj, gs (с учетом возможности их доопределения). Если реализация (4.1) возможна, то присвоим ей вес ρ(gi, gj, gs, $ \vee $), равный числу неопределенных значений функций gi, gj, которые надо заменить определенными.Если реализация (4.2) возможна, то присвоим ей вес ρ(gi, gj, gs, &), равный числу неопределенных значений функций gi, gj, которые надо заменить определенными. Составим двудольный неориентированный граф R, вершины первой доли помечены парами {gi, gj}, вершины второй доли – функциями множества G. Число вершин первой доли равно $C_{k}^{2}$, число вершин второй доли – k. Если пара {gi, gj} не реализует gs ни в виде (4.1), ни в виде (4.2), то между вершинами {gi, gj}, gs нет ребра. Если же реализация в виде (4.1) возможна, а реализация (4.2) невозможна, то ребру присваивается вес ρ(gi, gj, gs, $ \vee $); и наоборот, если реализация в виде (4.2) возможна, а реализация (4.1) невозможна, то ребру присваивается вес ρ(gi, gj, gs, &). Если же частичные функции такие, что возможны обе реализации (4.1) и (4.2), то ребру между вершинами {gi, gj} и gs присваивается вес
Каждое ребро 〈{gs, gj}, gs〉 графа R задает тройку функций, реализующих дизъюнктивное (4.1) либо конъюнктивное (4.2) разложение.
Для построения графа R для каждой функции gs, $s = \overline {1,k} $, требуется рассмотреть $C_{k}^{2}$ – (k – 1) вариантов пар проверки возможности дизъюнктивного разложения (исключаются k – 1 пар (gi, gs), i ≠ s;) и столько же $C_{k}^{2}$ – (k – 1) вариантов пар проверки возможности конъюнктивного разложения.
Таким образом, для построения графа R требуется проверить
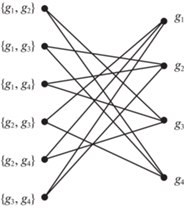
вариантов получения формул (2.1), (2.2) для G = {g1, …, gk}.Двудольный граф для G = {g1, g2, g3, g4} для подсчета числа Z вариантов приведен на рис. 1. В графе на рис. 1 имеется 12 ребер (k = 4) для проверки дизъюнктивного разложения и соответственно столько же ребер для проверки конъюнктивного разложения, поэтому Z = 2 × 4 × ($C_{4}^{2}$ – – (4 – 1)) = 8(6 – 3) = 24.
С использованием графа R решение задачи 2 можно свести к нахождению такого паросочетания графа, которое содержит максимальное количество ребер имеющих минимальный суммарный вес. При этом пометки вершин каждого ребра, вошедшего в паросочетание, должны задавать различные тройки функций. Множество G c представимых функций будут образовывать функции, помечающие вершины второй доли.
4.1. Э в р и с т и ч е с к и й а л г о р и т м р е ш е н и я з а д а ч и 2.
Ш а г 1. Вычислить для каждого ребра 〈{gi, gj}, gs〉 графа R оценку α(gi, gj, gs) – число неизолированных вершин в сокращенном графе R, из которого удалено ребро 〈{gi, gj}, gs〉 и исключены из первой доли графа R вершины-пары (в них входит gi либо gb, либо gj), а из второй доли исключена вершина gs.
Ш а г 2. Найти ребро между вершинами 〈{ga, gb}, gc〉 графа R, которое характеризуется максимальной оценкой α(ga, gb, gc), и включить его в решение. Заметим, что каждое ребро помечено одним из видов разложения (конъюнктивным либо дизъюнктивным). Если таких ребер несколько, то выбрать ребро, характеризуемое минимальным значением веса ρ. Если и таких ребер несколько, то выбрать первое из них.
Ш а г 3. Редуцировать граф, т.е. исключить из первой доли графа R вершины-пары, в которые входит ga либо gb, либо gc, а также исключить вершину gc из второй доли.
Ш а г 4. Выполнять шаги 1, 2 до тех пор, пока в графе R не останется ребер. Перейти на шаг 5.
Ш а г 5. Конец.
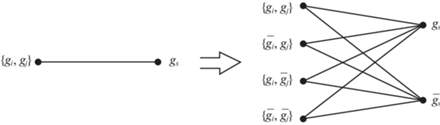
5. Использование инверсий функций при их алгебраическом разложении. Поиск алгебраических разложений может быть осуществлен с учетом инверсирования функций – некоторые функции нельзя представить в виде алгебраических разложений, но их инверсии могут быть представимы. Тогда в уравнение для соответствующей переменной добавляется оператор инверсии. Рассмотрим задачу 2 для случая, когда могут быть использованы для дизъюнктивных либо конъюнктивных разложений функции множества G как в инверсной ${{\bar {g}}_{1}}$, …, ${{\bar {g}}_{k}}$, так и прямой g1, …, gk форме.
Так как каждая из функций gs рассматривается как в прямой gs, так и инверсной ${{\bar {g}}_{s}}$ форме, поэтому в первой (левой) доли графа R будет $C_{{2k}}^{2}$ – k неупорядоченных пар-вершин (пары {gi, gi}, {${{\bar {g}}_{i}}$, ${{\bar {g}}_{i}}$}, {gi, ${{\bar {g}}_{i}}$} не рассматриваются), в правой доли – 2k вершин g1, ${{\bar {g}}_{1}}$, g2, ${{\bar {g}}_{2}}$ ,…, gk, ${{\bar {g}}_{k}}$. По сути, каждое ребро ({gi, gj}, gs) на рис. 1 заменяется подграфом, показанным на рис. 2. Описанный ранее эвристический алгоритм решения задачи 2 подвергается модификации: в шагах 1–3 алгоритма при нахождении оценки α(gi, gj, gs) ребра 〈{gi, gj}, gs〉 и ребра 〈{ga, gb}, gc〉, включаемого в решение, из первой доли графа R исключаются вершины-пары, в которые входит любая функция из множества {ga, ${{\bar {g}}_{a}}$, gb, ${{\bar {g}}_{b}}$, gc, ${{\bar {g}}_{c}}$}, из второй доли исключаются две вершины gc и ${{\bar {g}}_{c}}$.
Очевидно, что комбинаторная сложность решения задачи 2 с учетом возможности инверсирования функций при поиске их алгебраических разложений значительно увеличивается. В данной работе алгебраическое разложение частичных кофакторов основывается на том, что частичный кофактор реализуется выбранной уникальной парой других частичных кофакторов, т.е. один и тот же частичный кофактор не участвует в алгебраическом разложении нескольких частичных кофакторов. Полностью определенные кофакторы, участвующие в алгебраических разложениях, не требуют доопределения, поэтому один и тот же полностью определенный кофактор может использоваться в алгебраических представлениях нескольких кофакторов [17].
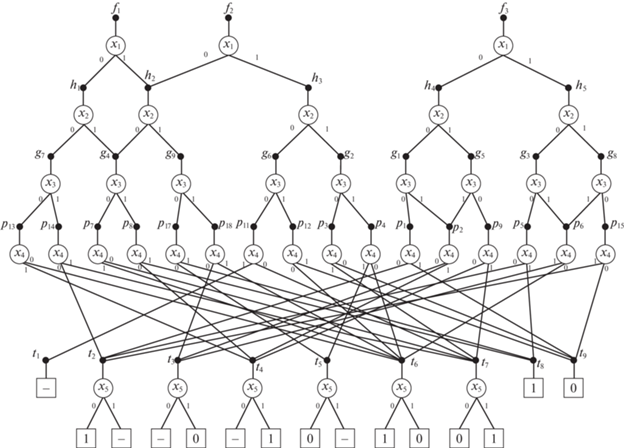
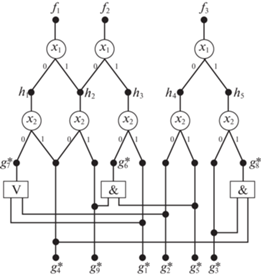
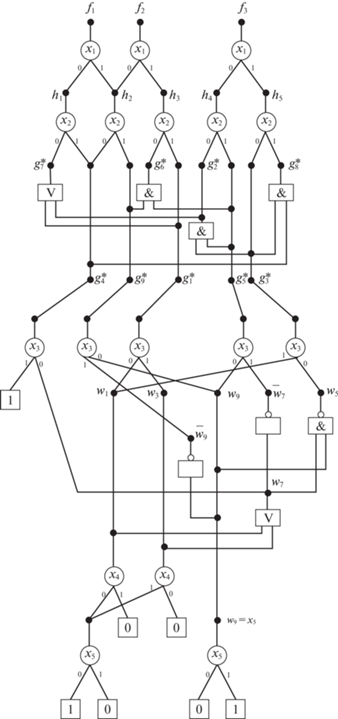
6. Пример BDD для частичной векторной функции. П р и м е р 3. Рассмотрим BDD (рис. 3) для частичной векторной функции f(x) = (f1, f2, f3), заданной таблицей истинности (табл. 11), по перестановке переменных 〈x1, x2, x3, x4, x5〉.
Таблица 11.
Задание частичной векторной функции (пример 3)
| Таблица истинности | Многоуровневое представление (функциональные вершины BDD) | |
|---|---|---|
| x1 x2 x3 x4 x5 | f1f2f3 | |
| 0 0 0 0 0 | 1 0 1 | ${{f}_{1}} = {{\bar {x}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}};{{f}_{2}} = {{\bar {x}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};$ |
| 0 0 0 0 1 | 0 1 – | ${{f}_{3}} = {{\bar {x}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}};$ |
| 0 0 0 1 0 | – 1 0 | |
| 0 0 0 1 1 | 1 0 0 | |
| 0 0 1 0 0 | 1 – – | ${{h}_{1}} = {{\bar {x}}_{2}}{{g}_{7}} \vee {{x}_{2}}{{g}_{4}};\;{{h}_{2}} = {{\bar {x}}_{2}}{{g}_{4}} \vee {{x}_{2}}{{g}_{9}};$ |
| 0 0 1 0 1 | – 1 0 | ${{h}_{3}} = {{\bar {x}}_{2}}{{g}_{6}} \vee {{x}_{2}}{{g}_{2}};$ |
| 0 0 1 1 0 | 0 1 – | ${{h}_{4}} = {{\bar {x}}_{2}}{{g}_{1}} \vee {{x}_{2}}{{g}_{5}};\;{{h}_{5}} = {{\bar {x}}_{2}}{{g}_{3}} \vee {{x}_{2}}{{g}_{8}};$ |
| 0 0 1 1 1 | 1 1 1 | |
| 0 1 0 0 0 | 0 0 – | |
| 0 1 0 0 1 | 1 – 1 | |
| 0 1 0 1 0 | 1 0 0 | ${{g}_{1}} = {{\bar {x}}_{3}}{{p}_{1}} \vee {{x}_{3}}{{p}_{2}};$ |
| 0 1 0 1 1 | 0 1 1 | ${{g}_{2}} = {{\bar {x}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{4}};\;{{g}_{3}} = {{\bar {x}}_{3}}{{p}_{5}} \vee {{x}_{3}}{{p}_{6}};$ |
| 0 1 1 0 0 | – – – | ${{g}_{4}} = {{\bar {x}}_{3}}{{p}_{7}} \vee {{x}_{3}}{{p}_{8}};$ |
| 0 1 1 0 1 | 1 0 0 | ${{g}_{5}} = {{\bar {x}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{2}};\;{{g}_{6}} = {{\bar {x}}_{3}}{{p}_{{11}}} \vee {{x}_{3}}{{p}_{{12}}};$ |
| 0 1 1 1 0 | 1 1 – | ${{g}_{7}} = {{\bar {x}}_{3}}{{p}_{{13}}} \vee {{x}_{3}}{{p}_{{14}}};\;{{g}_{8}} = {{\bar {x}}_{3}}{{p}_{{15}}} \vee {{x}_{3}}{{p}_{6}};$ |
| 0 1 1 1 1 | 1 0 1 | ${{g}_{9}} = {{\bar {x}}_{3}}{{p}_{{17}}} \vee {{x}_{3}}{{p}_{{18}}};$ |
| 1 0 0 0 0 | 0 0 1 | |
| 1 0 0 0 1 | 1 1 – | |
| 1 0 0 1 0 | 1 – 1 | |
| 1 0 0 1 1 | 0 – 1 | ${{p}_{1}} = {{\bar {x}}_{4}}{{t}_{2}} \vee {{x}_{4}}{{t}_{9}} = {{\bar {x}}_{4}}{{t}_{2}};\;{{p}_{2}} = {{\bar {x}}_{4}}{{t}_{3}} \vee {{x}_{4}}{{t}_{4}};$ |
| 1 0 1 0 0 | – 1 1 | ${{p}_{3}} = {{\bar {x}}_{4}}{{t}_{9}} \vee {{x}_{4}}{{t}_{7}} = {{x}_{4}}{{t}_{7}};\;{{p}_{4}} = {{\bar {x}}_{4}}{{t}_{6}} \vee {{x}_{4}}{{t}_{5}};$ |
| 1 0 1 0 1 | 1 0 0 | ${{p}_{5}} = {{\bar {x}}_{4}}{{t}_{2}} \vee {{x}_{4}}{{t}_{8}},{{p}_{6}} = {{\bar {x}}_{4}}{{t}_{6}} \vee {{x}_{4}}{{t}_{3}};$ |
| 1 0 1 1 0 | 1 0 – | ${{p}_{7}} = {{\bar {x}}_{4}}{{t}_{7}} \vee {{x}_{4}}{{t}_{6}};$ |
| 1 0 1 1 1 | 1 0 0 | ${{p}_{8}} = {{\bar {x}}_{4}}{{t}_{4}} \vee {{x}_{4}}{{t}_{8}} = {{\bar {x}}_{4}}{{t}_{4}} \vee {{x}_{4}};\;{{p}_{9}} = {{\bar {x}}_{4}}{{t}_{4}} \vee {{x}_{4}}{{t}_{7}};$ |
| 1 1 0 0 0 | 0 0 0 | ${{p}_{{11}}} = {{\bar {x}}_{4}}{{t}_{7}} \vee {{x}_{4}}{{t}_{1}};\;{{p}_{{12}}} = {{\bar {x}}_{4}}{{t}_{6}} \vee {{x}_{4}}{{t}_{9}} = {{x}_{4}}{{t}_{6}};$ |
| 1 1 0 0 1 | – 0 0 | ${{p}_{{13}}} = {{\bar {x}}_{4}}{{t}_{6}} \vee {{x}_{4}}{{t}_{4}};\;{{p}_{{14}}} = {{\bar {x}}_{4}}{{t}_{2}} \vee {{x}_{4}}{{t}_{7}};$ |
| 1 1 0 1 0 | 0 0 1 | ${{p}_{{15}}} = {{\bar {x}}_{4}}{{t}_{9}} \vee {{x}_{4}}{{t}_{2}} = {{x}_{4}}{{t}_{2}};\;{{p}_{{16}}} = {{\bar {x}}_{4}}{{t}_{6}} \vee {{x}_{4}}{{t}_{3}};$ |
| 1 1 0 1 1 | 1 1 – | ${{p}_{{17}}} = {{\bar {x}}_{4}}{{t}_{5}} \vee {{x}_{4}}{{t}_{7}};\;{{p}_{{18}}} = {{\bar {x}}_{4}}{{t}_{3}} \vee {{x}_{4}}{{t}_{6}}$ |
| 1 1 1 0 0 | – 1 1 | |
| 1 1 1 0 1 | 0 0 0 | |
| 1 1 1 1 0 | 1 0 – | |
| 1 1 1 1 1 | 0 – 0 | |
Алгоритм построения BDD для частичных векторных функций описан в [7, с. 56] и сводится к нахождению одинаковых подфункций, найденных в результате разложения Шеннона по переменной x1 исходных компонентных функций f1, f2, f3, разложением Шеннона по переменной x2 различных частичных подфункций h1, …, h5, полученных на шаге 1 разложения, и т.д. Графу BDD (рис. 3) соответствуют формулы разложений Шеннона, заданные в правом столбце табл. 11, при этом частичные функции t1, …, t9 первого уровня BDD приведены в табл. 12. Кофакторы первого уровня зависят от одной переменной x5 и являются частичными функциями. Число частичных булевых функций, зависящих от n переменных, определяется по формуле ${{3}^{{{{2}^{n}}}}}$. Для n = 1 имеется девять частичных функций, заметим, что все они заданы на первом уровне BDD (рис. 3).
Таблица 12.
Частичные кофакторы первого уровня BDD (рис. 3)
| x5 | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | – | 1 | – | – | 0 | 1 | 0 | 1 | 0 |
| 1 | – | – | 0 | 1 | – | 0 | 1 | 1 | 0 |
На третьем уровне BDD имеется девять кофакторов g1, …, g9, на четвертом – пять кофакторов, на пятом (корневом уровне BDD) – три корневые вершины разлагаемых компонентных частичных функций. Если какая-то дуга BDD пересекает рассматриваемый уровень BDD и заходит в функциональную вершину α более низкого уровня, то считается, что на данном уровне BDD есть кофактор α, зависящий от меньшего числа аргументов. Позже будут представлены примеры таких BDD.
Из BDD можно получить области определения как исходных функций, так и любого из кофакторов, это подробно описано в [7, с. 37]. Каждому пути из корневой вершины BDD, помеченной функцией fj, к листовой вершине 1 соответствует элементарная конъюнкция, включающая дуги (литералы) xi, ${{\bar {x}}_{i}}$ на этом пути. При этом дуге, помеченной символом 0, соответствует отрицательный литерал ${{\bar {x}}_{i}}$; дуге, помеченной символом 1, – положительный литерал xi, а всем путям между указанными вершинами – дизъюнкция получаемых элементарных конъюнкций, образующая ортогонализованную ДНФ $D_{{{{f}_{j}}}}^{1}$. Пути из корневой вершины fj к листовой вершине 0 задают ортогонализованную ДНФ $D_{{{{f}_{j}}}}^{0}$, а пути к вершине “–” – ортогонализованную ДНФ $D_{{{{f}_{j}}}}^{ - }$. При построении ДНФ, описывающих области определения кофактора, вместо корневой вершины BDD рассматривается функциональная вершина данного кофактора.
Например, области нулевых, единичных и неопределенных значений кофактора g1, полученные из графа BDD (рис. 3), задаются следующими ортогонализованными ДНФ:
7. Метод минимизации многоуровневого BDD-представления частичной векторной функции. Исходными данными для предлагаемого метода минимизации многоуровневого представления частичной векторной функции на основе нахождения алгебраических разложений кофакторов является граф BDD. Метод включает пять этапов.
Э т а п 1. Нахождения алгебраически представимых кофакторов.
Выполняется для каждого уровня BDD, начиная с уровня кофакторов, получаемых в результате разложения Шеннона по первой переменной, и исключая последний листовой уровень, на котором расположены константы 0, 1, “–”. Исключается из рассмотрения также первый уровень BDD, соответствующий разложению по последней переменной в заданной перестановке переменных, по которым ведется разложение Шеннона.
З а м е ч а н и е 2. Метод может быть применен с выбранного уровня BDD, двигаясь как вниз, так и вверх по уровням BDD. При движении вверх рассмотрение кофакторов начинается со второго уровня BDD.
На очередном уровне BDD решается задача нахождения наибольшего числа алгебраически представимых частичных кофакторов.
Ш а г 1. Выбор формы представления кофакторов данного уровня BDD (таблица истинности; пара ДНФ, задающая области определения кофактора; подграф BDD) и задание кофакторов в требуемой форме.
Ш а г 2. Нахождение на уровне BDD пар взаимно инверсных кофакторов и выбор одного кофактора из такой пары для получения алгебраических представлений выбранных кофакторов в виде конъюнкции либо дизъюнкции других частичных кофакторов данного уровня.
Ш а г 3. Нахождение максимального по мощности множества частичных кофакторов, которые представимы в виде конъюнкции либо дизъюнкции базисных частичных кофакторов того же уровня BDD – решение задачи 2. Доопределение частичных кофакторов, участвующих в алгебраических разложениях, до полностью определенных.
Ш а г 4. Исключение представимых кофакторов, участвующих в алгебраических разложениях, из шага 5.
Ш а г 5. Построение BDD, реализующей доопределенные базисные кофакторы и неразложенные кофакторы (по той форме их задания, по которой они сравнивались при поиске алгебраически представимых) по старой перестановке переменных либо по новой (лучшей) перестановке переменных, т.е. по той, по которой получается BDD с возможно меньшим числом функциональных вершин.
Ш а г 6. Сокращение BDD на верхних уровнях в случае, если сократилось число кофакторов рассматриваемого уровня за счет доопределения и появления одинаковых функциональных вершин.
Э т а п 2. Доопределение частичной BDD до полностью определенной.
Если после выполнения этапа 1 в BDD остаются листовые вершины “–”, то выполняется замена листовых значений “–” константами 0, 1, т.е. осуществляется доопределение частичной BDD до полностью определенной с возможным выполнением процедуры сокращения BDD [20].
Э т а п 3. Формирование функционального представления системы полностью определенных функций в виде формул разложений Шеннона и формул для представимых кофакторов.
Э т а п 4. Дополнительная оптимизация на основе метода [17] алгебраического разложения полностью определенных кофакторов.
На каждом (из рассматриваемых в методе) уровне BDD, на котором были найдены алгебраические разложения частичных кофакторов, исключаются представимые кофакторы, а для оставшихся решается задача нахождения алгебраических разложений [17], сокращаются множества базисных кофакторов и формируется результирующее многоуровневое представление.
Э т а п 5. Проверка отношения реализации “$ \prec $” между исходной BDD частичной векторной функцией и результирующим многоуровневым представлением.
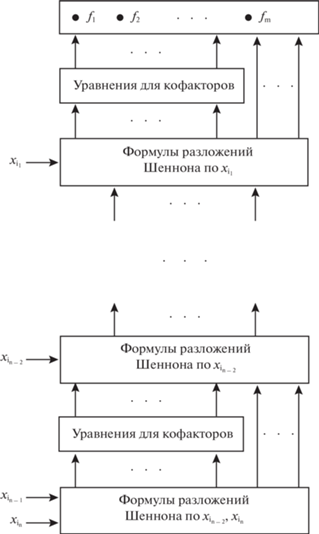
Общий вид многоуровневого представления векторной функции f(x) = (f1(x), …, fm(x)), получаемого предлагаемым методом, показан на рис. 4. Нахождение алгебраически представимых кофакторов может быть выполнено и в процессе построения BDD при задании в виде ДНФ областей определения компонентных функций исходной частичной векторной функции. Кроме того, предлагаемый метод обобщается на случай других выходных функций алгебраических разложений, таких, как исключающее ИЛИ, эквиваленция, а также на случай, когда выходные функции представляют собой n-операндные алгебраические функции дизъюнкции, конъюнкции.
Рис. 4.
Структура многоуровневого представления с использованием алгебраических разложений кофакторов
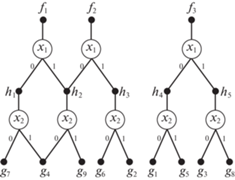
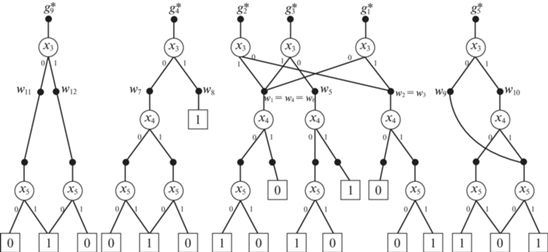
8. Пример применения метода минимизации многоуровневого BDD-представления частичной векторной функции от верхних уровней BDD. Проиллюстрируем метод на примере 3 (рис. 3) векторной булевой функции (табл. 11), начиная с третьего уровня BDD. Подграф BDD, построенный после разложения функций f1, f2, f3 по переменным x1, x2, показан на рис. 5. Данному подграфу соответствуют следующие формулы разложения Шеннона:
Таким образом, на третьем уровне BDD имеются девять кофакторов g1, …, g9.
Э т а п 1. Нахождения алгебраически представимых кофакторов на третьем уровне BDD.
Ш а г 1. Выбор формы представления кофакторов.
Алгебраические разложения кофакторов можно проводить по ортогонализованным ДНФ либо по обобщенно ортогонализованным формам, либо по подграфам BDD. Для удобства изложения примера будем рассматривать таблицу истинности (табл. 13) кофакторов g1, …, g9 (частичных подфункций, зависящих от переменных x3, x4, x5).
Таблица 13.
Частичные кофакторы третьего уровня BDD (рис. 3)
| x3 x4 x5 | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 | g9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 0 0 | 1 | 0 | 1 | 0 | – | 0 | 1 | 0 | 0 |
| 0 0 1 | – | 0 | – | 1 | 1 | 1 | 0 | 0 | – |
| 0 1 0 | 0 | 0 | 1 | 1 | 0 | – | – | 1 | 0 |
| 0 1 1 | 0 | 1 | 1 | 0 | 1 | – | 1 | – | 1 |
| 1 0 0 | – | 1 | 1 | – | – | 1 | 1 | 1 | – |
| 1 0 1 | 0 | 0 | 0 | 1 | 0 | 0 | – | 0 | 0 |
| 1 1 0 | – | 0 | – | 1 | – | 0 | 0 | – | 1 |
| 1 1 1 | 1 | - | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
Ш а г 2. Нахождение на третьем уровне BDD пар взаимно инверсных кофакторов.
В данном примере нет пар взаимно инверсных кофакторов, поэтому на шаге 3 рассматриваются кофакторы g1, …, g9.
Ш а г 3. Решение задачи 2 для кофакторов третьего уровня BDD и доопределение частичных кофакторов, участвующих в алгебраических разложениях, до полностью определенных.
Для третьего уровня BDD множество G = {g1, …, g9} составляют девять (k = 9) кофакторов, $C_{9}^{2}$ = 36 – множество всех неупорядоченных пар кофакторов из такого множества, Z – число перебираемых вариантов проверки существования разложений (4.2), (4.3) для построения графа R:
В качестве одного из решений задачи 2 для множества G = {g1, …, g9} было получено решение (рис. 6) из шести базисных функций g1, g2, g3, g4, g5, g7 с разложениями $g_{7}^{*}$ $ \prec $ ($g_{1}^{*}$ $ \vee $ $g_{2}^{*}$), $g_{8}^{*}$ $ \prec $ ($g_{3}^{*}$ & $g_{4}^{*}$), $g_{6}^{*}$ = ($g_{5}^{*}$ & $g_{9}^{*}$) трех представимых функций $g_{6}^{*}$, $g_{7}^{*}$, $g_{8}^{*}$ и с суммарным числом (девять) замен неопределенных значений определенными. В данном примере число заменяемых неопределенных значений функций определенными подсчитывалось по таблицам истинности функций. Если сравнение функций производится по ортогонализованным формам, то число замен неопределенных значений подсчитывается по таблицам, задающим ортогонализованные формы, если используются подграфы BDD, то – по заменам значений листовых вершин BDD.
Доопределения функций g1, g7, g3, g4, g8, g5, g6, g9 для разложений $g_{7}^{*}$ $ \prec $ ($g_{1}^{*}$ $ \vee $ $g_{2}^{*}$), $g_{8}^{*}$ $ \prec $ ($g_{3}^{*}$ & $g_{4}^{*}$), $g_{6}^{*}$ = $g_{5}^{*}$ & $g_{9}^{*}$ даны в табл. 14–16 соответственно, доопределенные значения выделены жирным курсивом. Выполнять доопределение частичных кофакторов нужно, используя табл. 2, 4. Если для некоторого набора значений переменных (см. последние строки в табл. 2, 4) значения всех кофакторов, участвующих в дизъюнктивном либо конъюнктивном разложениях, не определены, то замена всех значений “–” нулевыми значениями переведет частичные функции в класс полностью определенных и тогда отношение реализации можно заменить отношением равенства. Выполним, не нарушив отношения реализации, доопределения частичных кофакторов из табл. 14–16 следующим образом: $g_{1}^{*}$(1, 0, 0) = 0; $g_{2}^{*}$(1, 1, 1) = 0; $g_{3}^{*}$(1, 1, 0) = 0; $g_{8}^{*}$(1, 1, 0) = 0, получим полностью определенные кофакторы (табл. 17). Теперь отношение реализации в формулах $g_{7}^{*}$ $ \prec $ ($g_{1}^{*}$ $ \vee $ $g_{2}^{*}$) $g_{8}^{*}$ $ \prec $ ($g_{3}^{*}$ & $g_{4}^{*}$) можно заменить отношением равенства и записать формулы алгебраических разложений:
Таблица 14.
Доопределения частичных кофакторов (пример 3) для дизъюнктивного разложения кофактора g7
| x3x4x5 | Исходные функции | Реализующие функции разложения $g_{7}^{*}$$ \prec $($g_{1}^{*}$$ \vee $$g_{2}^{*}$) | ||||
|---|---|---|---|---|---|---|
| g1 | g2 | g7 | $g_{1}^{*}$ | $g_{2}^{*}$ | $g_{7}^{*}$ | |
| 0 0 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 0 1 | – | 0 | 0 | 0 | 0 | 0 |
| 0 1 0 | 0 | 0 | – | 0 | 0 | 0 |
| 0 1 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 0 0 | – | 1 | 1 | – | 1 | 1 |
| 1 0 1 | 0 | 0 | – | 0 | 0 | 0 |
| 1 1 0 | – | 0 | 0 | 0 | 0 | 0 |
| 1 1 1 | 1 | – | 1 | 1 | – | 1 |
Таблица 15.
Доопределения частичных кофакторов (пример 3) для конъюнктивного разложения кофактора g8
| x3 x4 x5 | Исходные функции | Реализующие функции разложения $g_{8}^{*}$$ \prec $ ($g_{3}^{*}$$ \vee $$g_{4}^{*}$) | ||||
|---|---|---|---|---|---|---|
| g3 | g4 | g8 | $g_{3}^{*}$ | $g_{4}^{*}$ | $g_{8}^{*}$ | |
| 0 0 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 0 1 | – | 1 | 0 | 0 | 1 | 0 |
| 0 1 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 1 1 | 1 | 0 | – | 1 | 0 | 0 |
| 1 0 0 | 1 | – | 1 | 1 | 1 | 1 |
| 1 0 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 1 0 | – | 1 | – | – | 1 | – |
| 1 1 1 | 0 | 1 | 0 | 0 | 1 | 0 |
Таблица 16.
Доопределения частичных кофакторов (пример 3) для конъюнктивного разложения кофактора g6
| x3 x4 x5 | Исходные функции | Реализующие функции разложения $g_{6}^{*}$ = $g_{5}^{*}$ & $g_{9}^{*}$ | ||||
|---|---|---|---|---|---|---|
| g5 | g9 | g6 | $g_{5}^{*}$ | $g_{9}^{*}$ | $g_{6}^{*}$ | |
| 0 0 0 | – | 0 | 0 | 0 | 0 | 0 |
| 0 0 1 | 1 | – | 1 | 1 | 1 | 1 |
| 0 1 0 | 0 | 0 | – | 0 | 0 | 0 |
| 0 1 1 | 1 | 1 | – | 1 | 1 | 1 |
| 1 0 0 | – | – | 1 | 1 | 1 | 1 |
| 1 0 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 1 0 | – | 1 | 0 | 0 | 1 | 0 |
| 1 1 1 | 1 | 0 | 0 | 1 | 0 | 0 |
Таблица 17.
Доопределенные кофакторы (пример 3) третьего уровня BDD
| x3 x4 x5 | $g_{1}^{*}$ | $g_{2}^{*}$ | $g_{3}^{*}$ | $g_{4}^{*}$ | $g_{5}^{*}$ | $g_{6}^{*}$ | $g_{7}^{*}$ | $g_{8}^{*}$ | $g_{9}^{*}$ |
|---|---|---|---|---|---|---|---|---|---|
| 0 0 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 0 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 1 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 1 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 0 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 0 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 1 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 1 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
Граф BDD c реализацией кофакторов в виде алгебраических разложений показан на рис. 7. Этому графу соответствуют логические формулы:
(8.1)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}};\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{2}}{{g}_{7}} \vee {{x}_{2}}{{g}_{4}};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}{{g}_{4}} \vee {{x}_{2}}{{g}_{9}};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}{{g}_{6}} \vee {{x}_{2}}{{g}_{2}}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}{{g}_{1}} \vee {{x}_{2}}{{g}_{5}};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}{{g}_{3}} \vee {{x}_{2}}{{g}_{8}};\quad g_{6}^{*} = g_{5}^{*}\& g_{9}^{*};\quad g_{7}^{*} = g_{1}^{*} \vee g_{2}^{*}, \\ g_{8}^{*} = g_{3}^{*}\& g_{4}^{*}. \\ \end{gathered} $Все девять частичных кофакторов доопределились до полностью определенных. Это означает, что произошло доопределение частичной векторной функции до полностью определенной. Позже это доопределение будет показано и проведено его сравнение с доопределениями, полученными другими методами логической оптимизации.
Ш а г 4. Исключение представимых кофакторов из рассмотрения. Кофакторы $g_{6}^{*}$, $g_{7}^{*}$, $g_{8}^{*}$ удаляются из шага 5.
Ш а г 5. Построение BDD, реализующей доопределенные базисные кофакторы.
Дальнейшее построение многоуровневого представления связано с рассмотрением шести полностью определенных кофакторов $g_{1}^{*}$, $g_{2}^{*}$, $g_{3}^{*}$, $g_{4}^{*}$, $g_{5}^{*}$, $g_{9}^{*}$ из табл. 17. Разложение Шеннона по переменной x3, кофакторов, заданных в табл. 17, приводит к следующим формулам (8.2), где кофакторы, зависящие от двух переменных x4 и x5, приведены в табл. 18:
(8.2)
$\begin{gathered} g_{1}^{*} = {{{\bar {x}}}_{3}}{{w}_{1}} \vee {{x}_{3}}{{w}_{2}};\quad g_{2}^{*} = {{{\bar {x}}}_{3}}{{w}_{3}} \vee {{x}_{3}}{{w}_{4}};\quad g_{3}^{*} = {{{\bar {x}}}_{3}}{{w}_{3}} \vee {{x}_{3}}{{w}_{6}}, \\ g_{4}^{*} = {{{\bar {x}}}_{3}}{{w}_{7}} \vee {{x}_{3}}{{w}_{8}};\quad g_{5}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{w}_{{10}}};\quad g_{9}^{*} = {{{\bar {x}}}_{3}}{{w}_{{11}}} \vee {{x}_{2}}{{w}_{{12}}}. \\ \end{gathered} $Таблица 18.
Полностью определенные кофакторы второго уровня BDD, полученные разложением базисных кофакторов по переменной x3
| x4x 5 | w1 | w2 | w3 | w4 | w5 | w6 | w7 | w8 | w9 | w10 | w11 | w12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
На рис. 8 показана BDD, реализующая полностью определенные кофакторы третьего уровня. Если сравнить три нижних уровня исходной BDD (рис. 3) и BDD из рис. 8, то можно легко увидеть, что BDD на рис. 8 не содержит неопределенных листовых вершин “–”.
Шаг 6 не выполняется – одинаковые функциональные вершины в результате преобразования графа BDD не появились.
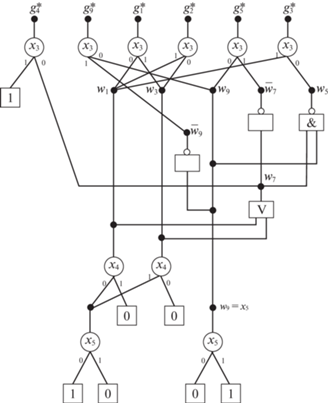
Н а х о ж д е н и е а л г е б р а и ч е с к и п р е д с т а в и м ы х к о ф а к т о р о в н а в т о р о м у р о в н е B D D. Исходной является BDD на рис. 8.
Э т а п 1. Ш а г 1. Выбор формы представления кофакторов.
Будем рассматривать кофакторы, заданные таблицей истинности (табл. 18).
Ш а г 2. Нахождение пар взаимно инверсных кофакторов.
Для неконстантных функций с помощью метода из работы [20] найдем множество функций (табл. 19), к которым (либо к их инверсиям) доопределяются кофакторы из табл. 18. С учетом того, что w8 = 1, w2 = w3, w4 = w1, w6 = w1, w10 = ${{\bar {w}}_{7}}$, w11 = w9, w12 = ${{\bar {w}}_{9}}$, формулы (8.2) перепишутся в виде
(8.3)
$\begin{gathered} g_{1}^{*} = {{{\bar {x}}}_{3}}{{w}_{1}} \vee {{x}_{3}}{{w}_{3}};\quad g_{2}^{*} = {{{\bar {x}}}_{3}}{{w}_{3}} \vee {{x}_{3}}{{w}_{1}};\quad g_{3}^{*} = {{{\bar {x}}}_{3}}{{w}_{5}} \vee {{x}_{3}}{{w}_{1}}, \\ g_{4}^{*} = {{{\bar {x}}}_{3}}{{w}_{7}} \vee {{x}_{3}};\quad g_{5}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{7}};\quad g_{9}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{9}}. \\ \end{gathered} $Таблица 19.
Полностью определенные кофакторы для нахождения их алгебраических представлений
| x4 x5 | w1 | w3 | w5 | w7 | w9 |
|---|---|---|---|---|---|
| 0 0 | 1 | 0 | 1 | 0 | 0 |
| 0 1 | 0 | 0 | 0 | 1 | 1 |
| 1 0 | 0 | 0 | 1 | 1 | 0 |
| 1 1 | 0 | 1 | 1 | 0 | 1 |
Ш а г 3. Нахождение максимального по мощности множества кофакторов из табл. 19, которые представимы в виде конъюнкции либо дизъюнкции кофакторов рассматриваемого уровня BDD.
Будем искать алгебраические разложения полностью определенных кофакторов из табл. 19, используя другие кофакторы из этой же таблицы. Для случая полностью определенных функций не требуется доопределение базисных кофакторов, поэтому один и тот же кофактор может участвовать в разложении нескольких кофакторов. Метод решения этой задачи для полностью определенных кофакторов рассмотрен в [17]. Применяя данный метод, получим, то что инверсии ${{\bar {w}}_{5}}$, ${{\bar {w}}_{7}}$ представимых кофакторов w5, w7 выражаются через основные кофакторы w1, w3, w9 следующим образом: ${{\bar {w}}_{5}} = {{w}_{7}}\& {{w}_{9}}$, ${{\bar {w}}_{7}} = {{w}_{1}}\& {{w}_{3}}$. Последние формулы можно переписать как
Итак, на втором уровне BDD остаются базисные кофакторы w1, w3, w9, реализация которых в виде BDD приводит к формулам w1 = ${{\bar {x}}_{4}}{{\bar {x}}_{5}}$; w3 = x4x5; w9 = x5. Граф BDD, реализующий кофакторы второго уровня BDD с учетом возможности использования их инверсий, показан на рис. 9.
Э т а п 2. Доопределение частичной BDD до полностью определенной.
Выполнение этапа 2 не требуется, так как все полученные кофакторы являются полностью определенными.
Э т а п 3. Формирование функционального представления в виде формул разложений Шеннона и формул для представимых кофакторов.
Логические уравнения после алгебраического разложения кофакторов на третьем и втором уровнях BDD будут иметь следующий вид:
(8.4)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}},\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{1}}g_{7}^{*} \vee {{x}_{2}}g_{4}^{*};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}g_{4}^{*} \vee {{x}_{2}}g_{9}^{*};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}g_{6}^{*} \vee {{x}_{2}}g_{2}^{*}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}g_{1}^{*} \vee {{x}_{2}}g_{5}^{*};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}g_{3}^{*} \vee {{x}_{2}}g_{8}^{*};\quad g_{6}^{*} = g_{5}^{*}\& g_{9}^{*}, \\ g_{7}^{*} = g_{1}^{*} \vee g_{2}^{*};\quad g_{8}^{*} = g_{3}^{*}\& g_{4}^{*},\quad g_{1}^{*} = {{{\bar {x}}}_{3}}{{w}_{1}} \vee {{x}_{3}}{{w}_{3}};\quad g_{2}^{*} = {{{\bar {x}}}_{3}}{{w}_{3}} \vee {{x}_{3}}{{w}_{1}}, \\ g_{3}^{*} = {{{\bar {x}}}_{3}}{{w}_{5}} \vee {{x}_{3}}{{w}_{1}};\quad g_{4}^{*} = {{{\bar {x}}}_{3}}{{w}_{7}} \vee {{x}_{3}};\quad g_{5}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{7}}, \\ g_{9}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{9}};\quad {{w}_{5}} = (\overline {{{w}_{7}}\& {{w}_{9}}} );\quad {{w}_{7}} = (\overline {{{w}_{1}} \vee {{w}_{3}}} ), \\ {{w}_{1}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}};\quad {{w}_{3}} = {{x}_{4}}{{x}_{5}};\quad {{w}_{9}} = {{x}_{5}}. \\ \end{gathered} $Формулы (8.4) содержат 19 внутренних переменных и 70 литералов.
Э т а п 4. Дополнительная оптимизация на основе метода [17] алгебраического разложения полностью определенных кофакторов.
На втором уровне BDD рассматривались полностью определенные кофакторы, поэтому для этого уровня дополнительная оптимизация не выполняется. На третьем уровне BDD располагаются базисные кофакторы $g_{1}^{*}$, $g_{2}^{*}$, $g_{3}^{*}$, $g_{4}^{*}$, $g_{5}^{*}$, $g_{9}^{*}$, которые изначально были частичными, а затем стали полностью определенными. Для них выполняется дополнительная оптимизация, в результате выясняется, что множество базисных кофакторов можно сократить (удалить кофактор $g_{2}^{*}$), так как справедливо конъюнктивное разложение $g_{2}^{*}$ = $g_{3}^{*}$ & $g_{5}^{*}$. Формируется результирующее многоуровневое представление:
(8.5)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}},\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{2}}g_{7}^{*} \vee {{x}_{2}}g_{4}^{*};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}g_{4}^{*} \vee {{x}_{2}}g_{9}^{*};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}g_{6}^{*} \vee {{x}_{2}}g_{2}^{*}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}g_{1}^{*} \vee {{x}_{2}}g_{5}^{*};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}g_{3}^{*} \vee {{x}_{2}}g_{8}^{*};\quad g_{6}^{*} = g_{5}^{*}\& g_{9}^{*}, \\ g_{7}^{*} = g_{1}^{*} \vee g_{2}^{*};\quad g_{8}^{*} = g_{3}^{*}\& g_{4}^{*},\quad g_{1}^{*} = {{{\bar {x}}}_{3}}{{w}_{1}} \vee {{x}_{3}}{{w}_{3}};\quad g_{2}^{*} = g_{3}^{*}\& g_{5}^{*}, \\ g_{3}^{*} = {{{\bar {x}}}_{3}}{{w}_{5}} \vee {{x}_{3}}{{w}_{1}};\quad g_{4}^{*} = {{{\bar {x}}}_{3}}{{w}_{7}} \vee {{x}_{3}};\quad g_{5}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{7}}, \\ g_{9}^{*} = {{{\bar {x}}}_{3}}{{w}_{9}} \vee {{x}_{3}}{{{\bar {w}}}_{9}};\quad {{w}_{5}} = (\overline {{{w}_{7}}\& {{w}_{9}}} );\quad {{w}_{7}} = (\overline {{{w}_{1}} \vee {{w}_{3}}} ), \\ {{w}_{1}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}};\quad {{w}_{3}} = {{x}_{4}}{{x}_{5}};\quad {{w}_{9}} = {{x}_{5}}. \\ \end{gathered} $Формулы (8.5) содержат 19 внутренних переменных и 68 литералов. Результирующий граф BDD, соответствующий формулам (8.5), показан на рис. 10. Алгебраическое представление кофакторов в виде дизъюнкций и конъюнкций на третьем и втором уровнях BDD позволяет уменьшить общее число литералов в результирующем многоуровневом представлении полностью определенной векторной функции, которая реализует частичную векторную функцию из табл. 11. Получение многоуровневого представления системы полностью определенных функций позволяет применить для такого представления еще раз (на этапе 4) метод алгебраических разложений [17], на этот раз уже для полностью определенных кофакторов.
Рис. 10.
Многоуровневое представление после алгебраического разложения кофакторов на втором и третьем уровнях BDD
Э т а п 5. Проверка отношения реализации “$ \prec $” между исходной BDD частичной векторной функцией и многоуровневым представлением.
Доопределение исходной частичной векторной функции до полностью определенной для проверки отношения реализации дано далее (см. табл. 24). Легко видеть, что отношение реализации выполняется.
9. Пример применения метода минимизации многоуровневого BDD-представления частичной векторной функции от нижних уровней BDD. Применять предложенный метод можно не только от верхних, но и от нижних уровней BDD. Опишем вкратце использование метода на том же примере 3 (табл 11, рис. 3), не привязываясь к этапам и шагам выполнения метода.
Рассмотрим частичные кофакторы на втором уровне BDD (табл. 20). С помощью методов из [20] найдем минимальное число кофакторов, к которым доопределяются частичные кофакторы из табл. 20 – это кофакторы p3, p7, p9, p12, p15, p5 = p8 = 1 (табл. 21). При этом частичные кофакторы p9, p15, p5, p8 доопределены, им оставлены прежние обозначения. В нижней строке табл. 21 указаны кофакторы, которые реализуются соответствующими доопределенными кофакторами из верхней части этой таблицы. Найдем BDD-представление кофакторов p3, p7, p9, p12, p15 и выполним сокращение BDD, так как выясняется, что
Таблица 20.
Частичные кофакторы второго уровня BDD (рис. 3)
| x4 x5 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | p11 | p12 | p13 | p14 | p15 | p16 | p17 | p18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 0 | 1 | – | 0 | 1 | 1 | 1 | 0 | – | – | – | 0 | 1 | 1 | 1 | 0 | 1 | 0 | – |
| 0 1 | – | 0 | 0 | 0 | – | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | – | 0 | 0 | – | 0 |
| 1 0 | 0 | – | 0 | 0 | 1 | – | 1 | 1 | 0 | – | – | 0 | – | 0 | 1 | – | 0 | 1 |
| 1 1 | 0 | 1 | 1 | – | 1 | 0 | 0 | 1 | 1 | 1 | – | 0 | 1 | 1 | – | 0 | 1 | 0 |
Таблица 21.
Полностью определенные кофакторы второго уровня BDD
| x4 x5 | p3 | p7 | p9 | p12 | p15 | p5 = p8= 1 |
|---|---|---|---|---|---|---|
| 0 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| Реализуемые кофакторы | p2$ \prec $p3; p10$ \prec $p3; p17$ \prec $p3 | p13$ \prec $${{\bar {p}}_{7}}$; p14$ \prec $${{\bar {p}}_{7}}$; | p11$ \prec $p9 | p1$ \prec $p12; p4$ \prec $p12; p6$ \prec $p12; p16$ \prec $p12 | p18$ \prec $p15 | p5$ \prec $ 1; p8$ \prec $ 1 |
Обозначим u7 = ${{\bar {p}}_{7}}$, тогда многоуровневое представление из табл. 11 принимает вид
(9.1)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}};\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{2}}{{g}_{7}} \vee {{x}_{2}}{{g}_{4}};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}{{g}_{4}} \vee {{x}_{2}}{{g}_{9}};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}{{g}_{6}} \vee {{x}_{2}}{{g}_{2}}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}{{g}_{1}} \vee {{x}_{2}}{{g}_{5}};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}{{g}_{3}} \vee {{x}_{2}}{{g}_{8}};\quad {{g}_{1}} = {{{\bar {x}}}_{3}}{{p}_{{12}}} \vee {{x}_{3}}{{p}_{3}}, \\ {{g}_{2}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{{12}}};\quad {{g}_{3}} = {{{\bar {x}}}_{3}} \vee {{x}_{3}}{{p}_{{12}}}, \\ {{g}_{4}} = {{{\bar {x}}}_{3}}{{p}_{7}} \vee {{x}_{3}};\quad {{g}_{5}} = {{{\bar {x}}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{3}};\quad {{g}_{6}} = {{{\bar {x}}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{{12}}}, \\ {{g}_{7}} = {{u}_{7}};\quad {{g}_{8}} = {{{\bar {x}}}_{3}}{{p}_{{15}}} \vee {{x}_{3}}{{p}_{{12}}};\quad {{g}_{9}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{{15}}};\quad {{p}_{3}} = {{x}_{4}}{{x}_{5}}, \\ {{p}_{7}} = {{{\bar {x}}}_{4}}{{x}_{5}} \vee {{x}_{4}}{{{\bar {x}}}_{5}};\quad {{p}_{9}} = {{x}_{5}};\quad {{p}_{{12}}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}};\quad {{p}_{{15}}} = {{x}_{4}}{{{\bar {x}}}_{5}};\quad {{u}_{7}} = {{{\bar {p}}}_{7}}. \\ \end{gathered} $Сложность формул (9.1): 20 внутренних переменных, 78 литералов. Заметим, что доопределение снизу может потребовать выполнения процедуры сокращения верхней части BDD тогда, когда в результате доопределения появились одинаковые кофакторы.
Перейдем к нахождению алгебраических разложений кофакторов из табл. 21. Заметим, что кофакторы p3 = x4x5, p12 = ${{\bar {x}}_{4}}{{\bar {x}}_{5}}$ , p15 = ${{x}_{4}}{{\bar {x}}_{5}}$ реализуются одной логической операцией “конъюнкция” и нет смысла находить их алгебраические разложения, это касается и кофактора p9 = x5. Кофактор p7 = ${{\bar {x}}_{4}}{{x}_{5}}$ $ \vee $ ${{x}_{4}}{{\bar {x}}_{5}}$ можно представить в виде алгебраического разложения p7 = $\overline {{{p}_{3}} \vee {{p}_{{12}}}} $.
Рассмотрим третий уровень BDD, на котором находятся полностью определенные кофакторы, заданные в табл. 22. По сравнению кофакторами из табл. 17, исходные частичные кофакторы g3 и g9 (табл. 22) доопределены по-другому (эти доопределения в табл. 22 отмечены жирным курсивом), в результате чего только один кофактор g7 может быть алгебраически разложен: g7 = g1$ \vee $ g2.
Таблица 22.
Полностью определенные кофакторы третьего уровня BDD (пример 3)
| x3 x4 x5 | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 | g9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 0 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 0 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 1 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 1 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 0 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 0 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 1 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 1 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
Многоуровневое представление при разложении кофакторов от нижних уровней BDD имеет вид (9.2) и сложность 20 внутренних переменных, 74 литералов:
(9.2)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}};\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{2}}{{g}_{7}} \vee {{x}_{2}}{{g}_{4}};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}{{g}_{4}} \vee {{x}_{2}}{{g}_{9}};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}{{g}_{6}} \vee {{x}_{2}}{{g}_{2}}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}{{g}_{1}} \vee {{x}_{2}}{{g}_{5}};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}{{g}_{3}} \vee {{x}_{2}}{{g}_{8}};\quad {{g}_{1}} = {{{\bar {x}}}_{3}}{{p}_{{12}}} \vee {{x}_{3}}{{p}_{3}}, \\ {{g}_{2}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{{12}}};\quad {{g}_{3}} = {{{\bar {x}}}_{3}} \vee {{x}_{3}}{{p}_{{12}}},\quad {{g}_{4}} = {{{\bar {x}}}_{3}}{{p}_{7}} \vee {{x}_{3}}; \\ {{g}_{5}} = {{{\bar {x}}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{3}};\quad {{g}_{6}} = {{{\bar {x}}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{{12}}},\quad {{g}_{7}} = {{g}_{1}} \vee {{g}_{2}}, \\ {{g}_{8}} = {{{\bar {x}}}_{3}}{{p}_{{15}}} \vee {{x}_{3}}{{p}_{{12}}};\quad {{g}_{9}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{{15}}};\quad {{p}_{3}} = {{x}_{4}}{{x}_{5}}, \\ {{p}_{7}} = \overline {{{p}_{3}} \vee {{p}_{{12}}}} ;\quad {{p}_{9}} = {{x}_{5}};\quad {{p}_{{12}}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}};\quad {{p}_{{15}}} = {{x}_{4}}{{{\bar {x}}}_{5}};\quad {{u}_{7}} = {{{\bar {p}}}_{7}}. \\ \end{gathered} $10. Сравнение с другими методами доопределения частичных векторных функций. 10.1. “Н у л е в о е д о о п р е д е л е н и е”. Если не проводить алгебраические разложения кофакторов, а заменить в табл. 11 все неопределенные значения “–” компонентных функций нулевыми значениями (выполнить “нулевое” доопределение), то получим многоуровневое BDD-представление с 20 внутренними переменными и 79 литералами. Заметим, что при “нулевом” доопределении можно провести алгебраическое разложение только одного полностью определенного кофактора g7 в виде g7 = g1$ \vee $ g2.
10.2. “С о в м е с т н а я м и н и м и з а ц и я в к л а с с е ДНФ”. Совместная минимизация в классе ДНФ исходных частичных функций с помощью программы из [25] приводит к системе ДНФ, содержащей 21 элементарную конъюнкцию. BDD-представление (по найденной лучшей перестановке 〈x1, x3, x2, x4, x5〉) полученной системы полностью определенных функций с помощью программы из [16] содержит 19 внутренних переменных в формулах разложений Шеннона и 76 литералов в этих формулах. Такой результат свидетельствует о том, что целесообразно развивать методы многоуровневой оптимизации для частичных функций, а не минимизировать функции в классе ДНФ и проводить для минимизированных ДНФ оптимизацию в классе BDD.
10.3. “Д о о п р е д е л е н и е B D D”. Доопределение BDD (формул из табл. 11), начинаемое с листьев и выполняемое по правилам (табл. 23), где ti $ \prec $ $t_{i}^{*}$, i = 1, …, 9, c последующим сокращением BDD приводит к нахождению одинаковых функциональных вершин: p17 = p3; p5 = = p8 = 1; p4 = p6 = p12; p2 = p15 и получению следующих уравнений:
(10.1)
$\begin{gathered} {{f}_{1}} = {{{\bar {x}}}_{1}}{{h}_{1}} \vee {{x}_{1}}{{h}_{2}};\quad {{f}_{2}} = {{{\bar {x}}}_{1}}{{h}_{2}} \vee {{x}_{1}}{{h}_{3}};\quad {{f}_{3}} = {{{\bar {x}}}_{1}}{{h}_{4}} \vee {{x}_{1}}{{h}_{5}}, \\ {{h}_{1}} = {{{\bar {x}}}_{2}}{{g}_{7}} \vee {{x}_{2}}{{g}_{4}};\quad {{h}_{2}} = {{{\bar {x}}}_{2}}{{g}_{4}} \vee {{x}_{2}}{{g}_{9}};\quad {{h}_{3}} = {{{\bar {x}}}_{2}}{{g}_{6}} \vee {{x}_{2}}{{g}_{2}}, \\ {{h}_{4}} = {{{\bar {x}}}_{2}}{{g}_{1}} \vee {{x}_{2}}{{g}_{5}};\quad {{h}_{5}} = {{{\bar {x}}}_{2}}{{g}_{3}} \vee {{x}_{2}}{{g}_{8}}, \\ {{g}_{1}} = {{{\bar {x}}}_{3}}{{p}_{1}} \vee {{x}_{3}}{{p}_{2}},\quad {{g}_{2}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{4}};\quad {{g}_{3}} = {{{\bar {x}}}_{3}} \vee {{x}_{3}}{{p}_{{18}}}, \\ {{g}_{4}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}};\quad {{g}_{5}} = {{{\bar {x}}}_{3}}{{p}_{9}} \vee {{x}_{3}}{{p}_{2}};\quad {{g}_{6}} = {{{\bar {x}}}_{3}}{{p}_{{11}}} \vee {{x}_{3}}{{p}_{4}}, \\ {{g}_{7}} = {{{\bar {x}}}_{3}}{{p}_{{13}}} \vee {{x}_{3}}{{p}_{{14}}};\quad {{g}_{8}} = {{{\bar {x}}}_{3}}{{p}_{2}} \vee {{x}_{3}}{{p}_{4}};\quad {{g}_{9}} = {{{\bar {x}}}_{3}}{{p}_{3}} \vee {{x}_{3}}{{p}_{{18}}}, \\ {{p}_{1}} = {{{\bar {x}}}_{4}},\quad {{p}_{2}} = {{x}_{4}};\quad {{p}_{3}} = {{x}_{4}}{{x}_{5}};\quad {{p}_{4}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}};\quad {{p}_{7}} = {{{\bar {x}}}_{4}}{{x}_{5}} \vee {{x}_{4}}{{{\bar {x}}}_{5}}, \\ {{p}_{9}} = {{{\bar {x}}}_{4}} \vee {{x}_{4}}{{x}_{5}};\quad {{p}_{{11}}} = {{{\bar {x}}}_{4}}{{x}_{5}};\quad {{p}_{{13}}} = {{{\bar {x}}}_{4}}{{{\bar {x}}}_{5}} \vee {{x}_{4}}, \\ {{p}_{{14}}} = {{{\bar {x}}}_{4}} \vee {{x}_{4}}{{x}_{5}};\quad {{p}_{{18}}} = {{x}_{4}}{{{\bar {x}}}_{5}}. \\ \end{gathered} $Таблица 23.
Доопределения частичных кофакторов первого уровня BDD (рис. 3)
| Частичные кофакторы | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| x5 | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 |
| 0 | – | 1 | – | – | 0 | 1 | 0 | 1 | 0 |
| 1 | – | – | 0 | 1 | – | 0 | 1 | 1 | 0 |
| Доопределяющие полностью определенные кофакторы | |||||||||
| x5 | $t_{1}^{*}$ | $t_{2}^{*}$ | $t_{3}^{*}$ | $t_{4}^{*}$ | $t_{5}^{*}$ | $t_{6}^{*}$ | $t_{7}^{*}$ | $t_{8}^{*}$ | $t_{9}^{*}$ |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Таблица 24.
Сравнение доопределений частичной векторной функции
| Частичная векторная функция (табл. 11) | Полностью определенная векторная функция – результат доопределения | |||||
|---|---|---|---|---|---|---|
| x1 x2 x3 x4 x5 | f1 f2 f3 | Доопредение BDD “снизу”, формулы (10.1) | “Нулевое” доопределение | Минимизация в классе ДНФ, программа [25] | Алгебраичес-кое разложение кофакторов, сверху BDD, формулы (8.5) | Алгебраичес-кое разложение кофакторов, снизу BDD, формулы (9.2) |
| $f_{1}^{*}f_{2}^{*}f_{3}^{*}$ | $f_{1}^{*}f_{2}^{*}f_{3}^{*}$ | $f_{1}^{*}f_{2}^{*}f_{3}^{*}$ | $f_{1}^{*}f_{2}^{*}f_{3}^{*}$ | $f_{1}^{*}f_{2}^{*}f_{3}^{*}$ | ||
| 0 0 0 0 0 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 |
| 0 0 0 0 1 | 0 1 – | 0 1 1 | 0 1 0 | 0 1 0 | 0 1 0 | 0 1 0 |
| 0 0 0 1 0 | – 1 0 | 1 1 0 | 0 1 0 | 0 1 0 | 0 1 0 | 0 1 0 |
| 0 0 0 1 1 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 |
| 0 0 1 0 0 | 1 – – | 1 1 0 | 1 0 0 | 1 1 1 | 1 1 0 | 1 1 0 |
| 0 0 1 0 1 | – 1 0 | 1 1 0 | 0 1 0 | 0 1 0 | 0 1 0 | 0 1 0 |
| 0 0 1 1 0 | 0 1 – | 0 1 1 | 0 1 0 | 0 1 1 | 0 1 0 | 0 1 0 |
| 0 0 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 |
| 0 1 0 0 0 | 0 0 – | 0 0 1 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 0 1 0 0 1 | 1 – 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 1 1 | 1 0 1 |
| 0 1 0 1 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 |
| 0 1 0 1 1 | 0 1 1 | 0 1 1 | 0 1 1 | 0 1 1 | 0 1 1 | 0 1 1 |
| 0 1 1 0 0 | – – – | 1 0 0 | 0 0 0 | 1 1 1 | 1 1 1 | 1 0 0 |
| 0 1 1 0 1 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 |
| 0 1 1 1 0 | 1 1 – | 1 1 1 | 1 1 0 | 1 1 1 | 1 1 0 | 1 1 0 |
| 0 1 1 1 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 |
| 1 0 0 0 0 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 |
| 1 0 0 0 1 | 1 1 – | 1 1 1 | 1 1 0 | 1 1 1 | 1 1 0 | 1 1 1 |
| 1 0 0 1 0 | 1 – 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 | 1 0 1 |
| 1 0 0 1 1 | 0 – 1 | 0 0 1 | 0 0 1 | 0 0 1 | 0 1 1 | 0 1 1 |
| 1 0 1 0 0 | – 1 1 | 1 1 1 | 0 1 1 | 1 1 1 | 1 1 1 | 1 1 1 |
| 1 0 1 0 1 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 |
| 1 0 1 1 0 | 1 0 - | 1 0 0 | 1 0 0 | 1 0 1 | 1 0 0 | 1 0 0 |
| 1 0 1 1 1 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 | 1 0 0 |
| 1 1 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 1 1 0 0 1 | – 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 1 0 0 | 0 0 0 |
| 1 1 0 1 0 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 | 0 0 1 |
| 1 1 0 1 1 | 1 1 – | 1 1 1 | 1 1 0 | 1 1 0 | 1 1 0 | 1 1 0 |
| 1 1 1 0 0 | – 1 1 | 0 1 1 | 0 1 1 | 1 1 1 | 1 1 1 | 0 1 1 |
| 1 1 1 0 1 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| 1 1 1 1 0 | 1 0 – | 1 0 0 | 1 0 0 | 1 0 1 | 1 0 0 | 1 0 0 |
| 1 1 1 1 1 | 0 – 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 |
| Число литералов в многоуровневом представлении | 89 | 79 | 76 | 68 | 74 | |
Уравнения (10.1) содержат 24 внутренних переменных и 89 литералов.
Приведем в табл. 24 полностью определенные векторные функции, являющиеся доопределениями частичной векторной функции из табл. 11. Жирным курсивом в табл. 24 выделены полностью определенные значения (0, 1) функций, которые заменили неопределенные значения “–” исходных компонентных частичных функций.
Заключение. Предложен метод рационального доопределения систем частичных булевых функций до полностью определенных, позволяющий дополнительно упрощать многоуровневые BDD-представления, используя не только нахождение пар взаимно инверсных подфункций, но и алгебраические разложения подфункций, находящихся на одном уровне BDD. Такая дополнительная технологически независимая оптимизация по числу литералов в результирующих логических уравнениях приводит к более простым функциональным описаниям, по которым осуществляется синтез комбинационных логических схем в различных технологических базисах. Дальнейшие исследования предполагают программную реализацию предложенного метода, экспериментальное исследование программ на различных наборах практических примеров, а также сравнение новых экспериментальных результатов с известными результатами, получаемыми на основе перехода к системам полностью определенных булевых функций и минимизации BDD-представлений в классе полностью определенных функций.
Список литературы
Кнут Д.Э. Искусство программирования. Т. 4, А. Комбинаторные алгоритмы. Ч. 1 / Пер. с англ. М.: Вильямс, 2013.
Карпов Ю.Г. MODEL CHECKING. Верификация параллельных и распределенных программных систем. СПб.: БХВ-Петербург, 2010.
Handbook of Satisfiability / Eds A. Biere, M. Heule, H. Van Maaren, T. Walsh. Amsterdam, Berlin, Oxford, Tokyo, Washington: IOS Press., 2009.
Akers S.B. Binary Decision Diagrams // IEEE Trans. on Computers. 1978. V. C-27. № 6.
Bryant R.E. Graph-based Algorithms for Boolean Functions Manipulation // IEEE Trans. on Computers. 1986. V. C-35. № 8.
Чэнь М., Цинь К., Ку Х.-М., Мишра П. Валидация на системном уровне. Высокоуровневое моделирование и управление тестированием. М.: Техносфера, 2014.
Бибило П.Н. Применение диаграмм двоичного выбора при синтезе логических схем. Минск: Беларус. навука, 2014.
Rudell R. Dynamic Variable Ordering for Ordered Binary Decision Diagrams // Computer-Aided Design: Proc. of the IEEE/ACM Intern. Conf. Santa Clara, Los Alamitos: IEEE Computer Society Press., 1993.
Ebendt R., Gunther W., Drechsler R. An Improved Branch and Bound Algorithm for Exact BDD Minimization // Computer-Aided Design of Integrated Circuits and Systems. 2003. V. 22. № 12.
Ebendt R., Fey G., R. Drechsler R. Advanced BDD Optimization. Dordrech: Springer, 2005.
Drechsler R., Becker B. Binary Decision Diagrams: Theory and Implementation. N. Y.: Springer, 1998.
Bryant R.E., Meinel C. Ordered Binary Decision Diagrams // Logic Synthesis and Verification / Eds S. Hassoun, T. Sasao, R.K. Brayton. Boston, MA: Springer, 2002.
Meinel C., Theobald T. Algorithms and Data Structures in VLSI Design: OBDD – Foundations and Applications. Berlin, Heidelberg: Springer-Verlag, 1998.
Брейтон Р.К., Хэчтел Г.Д., Санджованни-Винчентелли А.Л. Синтез многоуровневых комбинационных логических схем // ТИИЭР. 1990. Т. 78. № 2.
Yang S., Ciesielski M. BDS: a BDD-based Logic Optimization System // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 2002. V. 21. № 7.
Бибило П.Н., Ланкевич Ю.Ю. Использование полиномов Жегалкина при минимизации многоуровневых представлений систем булевых функций на основе разложения Шеннона // Программная инженерия. 2017. № 8.
Бибило П.Н., Романов В.И. Минимизация многоуровневых представлений систем полностью определенных булевых функций с использованием разложений Шеннона и алгебраических представлений кофакторов // Информатика. 2021. Т. 18. № 3.
Бибило П.Н., Романов В.И. Экспериментальное исследование алгоритмов минимизации BDDI-представлений систем булевых функций с использованием алгебраических разложений кофакторов // Программная инженерия. 2022. Т. 13. № 2.
The Tests in the Monograph “Logic Minimization Algorithms for VLSI Synthesis”. Available at: http://www1.cs.columbia.edu/~cs6861/sis/espresso-examples/ex (accessed January 20, 2020).
Бибило П.Н. Минимизация BDDI-представлений систем не полностью определенных булевых функций // Программная инженерия. 2020. Т. 11. № 3.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Логические основы проектирования дискретных устройств. М. : Физматлит, 2007.
Поттосин Ю.В., Шестаков Е.А. Ортогонализация системы полностью определенных булевых функций // Сб. науч. тр. Логическое проектирование. Минск: Ин-т техн. кибернетики НАН Беларуси, 2000. Вып.5.
Романовский И.В. Дискретный анализ: Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. 4-е изд., испр. и доп. СПб.: Невский Диалект; БХВ-Петербург, 2008.
Бибило П.Н., Енин С.В. Синтез комбинационных схем методами функциональной декомпозиции. Минск: Наука и техника, 1987.
Торопов Н.Р. Минимизация систем булевых функций в классе ДНФ // Сб. науч. тр. Логическое проектирование: Минск: Ин-т техн. кибернетики НАН Беларуси, 1999. Вып. 4.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления