Известия РАН. Теория и системы управления, 2022, № 5, стр. 90-101
ОЦЕНКА ПРЕДЕЛЬНЫХ РАСПРЕДЕЛЕНИЙ ПРОПУСКНОЙ СПОСОБНОСТИ В МНОГОПОЛЬЗОВАТЕЛЬСКОЙ СЕТИ ПРИ ПЕРЕДАЧЕ МЕЖУЗЛОВЫХ ПОТОКОВ ПО КРАТЧАЙШИМ МАРШРУТАМ
Ю. Е. Малашенко a, И. А. Назарова a, *
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 07.12.2021
После доработки 24.01.2022
Принята к публикации 28.03.2022
- EDN: BGXIZJ
- DOI: 10.31857/S0002338822040138
Аннотация
В рамках вычислительных экспериментов на модели многопродуктовой сети анализируются две стратегии распределения ресурсов при передаче потоков различных видов. Под ресурсом, выделяемым некоторой паре узлов-корреспондентов, понимается суммарная величина пропускных способностей, требуемых для прохождения данного вида потока по кратчайшему маршруту. Сумма потоков по ребрам, образующим маршрут соединения, трактуется как нагрузка на сеть. Разработанная алгоритмическая схема предполагает последовательное решение цепочки лексикографически упорядоченных задач поиска недискриминирующих распределений ресурсов и межузловых потоков. При реализации вычислительных процедур на каждой итерации часть имеющегося ресурса распределяется поровну между всеми парами узлов-корреспондентов, для которых существует возможность передачи потока. Метод позволяет за конечное число шагов найти финальные уравнительные распределения межузловых потоков и ресурсов сети и достичь предельной загрузки всех ребер. Полученные результаты представлены в виде специальных диаграмм.
Введение. Работа продолжает исследование проблем распределения ресурсов и оценки функциональных характеристик многопользовательских телекоммуникационных систем [1, 2]. При математической формализации используется стандартная запись многопродуктовой потоковой модели, в условия которой в явном виде добавлены переменные, характеризующие пропускную способность каналов связи, выделяемую каждой паре узлов-корреспондентов. В предположениях модели считается, что межузловые потоки различных видов передаются между всеми парами узлов одновременно. Пропускная способность ребер рассматривается как ресурс сети. Под ресурсом для передачи потока определенного вида понимается суммарная величина пропускных способностей ребер на всех маршрутах соединения данной пары узлов. Сумма реберных потоков трактуется как нагрузка на каналообразующие подсистемы сети. В модели результирующая нагрузка численно равна ресурсу для передачи межузлового потока данного вида. В работе сравниваются две стратегии распределения ресурсов сети. Первая стратегия предполагает получение равных межузловых потоков и пропускных способностей ребер для всех корреспондентов, а именно необходимых ресурсов. Согласно второй стратегии, парам узлов-корреспондентов выделяются равные доли ресурсов сети и подсчитываются соответствующие межузловые потоки.
Для проведения вычислительных экспериментов разработана итерационная процедура решения последовательности задач поиска максимальных потоков, передаваемых в монопольном режиме по кратчайшим маршрутам для каждой пары узлов-корреспондентов независимо. На основе найденных реберных нагрузок определяются совместно допустимое распределение межузловых потоков разных видов. Метод позволяет за конечное число шагов получить оценки минимальных удельных затрат ресурсов при предельной загрузке имеющихся ребер сети.
Рассматриваемая постановка задачи лежит в русле исследований, связанных с поиском справедливого или равноправного распределения ресурсов и межузловых потоков в многопользовательских сетях [3–7]. Для анализа прикладных проблем, которые изучаются в рамках многопродуктовой модели, разрабатываются различные численные методы [6–11]. В данной работе используется метод возможных направлений [12] для поиска решения лексикографического максимина для получения многокомпонентных оценок распределения ресурсов и межузловых потоков [1, 2].
1. Математическая модель. Для описания многопользовательской сетевой системы связи воспользуемся следующей математической записью модели передачи многопродуктового потока. Сеть $G$ задается множествами $\langle V,\;R,\;U,P\rangle $: узлов (вершин) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $; ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $; пар узлов-корреспондентов $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $. Предполагается, что в сети отсутствуют петли и сдвоенные ребра.
Ребро ${{r}_{k}} \in R$ соединяет концевые вершины ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Каждому ребру rk ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ из множества U. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют прямое и обратное направления передачи потока по ребру rk между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Каждой паре узлов-корреспондентов ${{p}_{m}}$ из множества $P$ ставится в соответствие: вершина-источник с номером ${{s}_{m}}$, из ${{s}_{m}}$ входной поток m-го вида поступает в сеть; вершина-приемник с номером tm, из tm поток m-го вида покидает сеть. В многопользовательской сети G рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных межузловых потоков различных видов.
Обозначим через zm величину межузлового потока m-го вида, поступающего в сеть из узла с номером ${{s}_{m}}$ и покидающего сеть из узла с номером ${{t}_{m}}$; ${{x}_{{mk}}}$, ${{x}_{{m(k + E)}}}$ – поток m-го вида, который передается по дугам ${{u}_{k}}$ и ${{u}_{{k + E}}}$, согласно направлению передачи, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $; $S({{v}_{n}})$ – множество номеров исходящих дуг, по ним поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по ним поток поступает в узел ${{v}_{n}}$. Состав множеств $S({{v}_{n}})$, $T({{v}_{n}})$ однозначно формируется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами $n$ и $j$, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$, направленная из вершины ${{v}_{n}}$ в ${{v}_{j}}$, считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, а дуга ${{u}_{{k + E}}}$, направленная из ${{v}_{j}}$ в ${{v}_{n}}$, – входящей для ${{v}_{n}}$ и ее номер $k + E$ помещается в список $T({{v}_{n}})$. Дуга uk является входящей для ${{v}_{j}}$ и ее номер k попадает в $T({{v}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ вносится в список исходящих дуг $S({{v}_{j}})$.
Во всех узлах сети ${{v}_{n}} \in V$, $n = \overline {1,N} $, для каждого вида потока должны выполняться условия сохранения потоков:
(1.1)
$\begin{gathered} \sum\limits_{i \in S({{v}_{n}})} {{x}_{{mi}}} - \sum\limits_{i \in T({{v}_{n}})} {{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\quad {{v}_{n}} = {{v}_{{{{s}_{m}}}}}, \hfill \\ - {{z}_{m}},\quad {\text{если}}\quad {{v}_{n}} = {{v}_{{{{t}_{m}}}}}, \hfill \\ 0\quad {\text{в остальных случаях,}} \hfill \\ \end{gathered} \right. \\ n = \overline {1,N} ,\quad m = \overline {1,M} ,\quad {{x}_{{mi}}} \geqslant 0,\quad {{z}_{m}} \geqslant 0. \\ \end{gathered} $Величина ${{z}_{m}}$ равна входному межузловому потоку $m$-го вида, проходящему от источника к приемнику пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.
Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$, определяющее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей – ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектор d задает следующие ограничения на сумму потоков всех видов, передаваемых по ребру ${{r}_{k}}$ одновременно:
(1.2)
$\sum\limits_{m = 1}^M ({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$В рамках данной модели пропускная способность ребер сети измеряется в условных единицах потока и трактуется как ресурсное ограничение. Сумма дуговых потоков (1.2) рассматривается как требование на предоставление ресурсов сети – пропускной способности ребер, необходимой при передаче межузловых потоков по данному ребру.
Для ${{z}_{m}}$, ${{x}_{{mi}}}$, удовлетворяющих условиям (1.1), (1.2), вычисляются суммарные потоки по ребрам сети:
Суммарный реберный поток ${{y}_{m}}$ характеризует нагрузку на сеть при передаче межузлового потока величины ${{z}_{m}}$ из узла-источника ${{s}_{m}}$ в узел-приемник ${{t}_{m}}$. Величина ${{y}_{m}}$ показывает, какая суммарная пропускная способность сети потребуется для передачи межузлового потока ${{z}_{m}}$. В рамках модели отношение реберных и межузловых потоков
можно трактовать как удельные затраты ресурсов сети при передаче единичного потока $m$-го вида между узлами ${{s}_{m}}$ и ${{t}_{m}}$ при соответствующих дуговых потоках ${{x}_{{mi}}}$.Ограничения (1.1)–(1.2) задают множество допустимых значений компонент вектора межузловых потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:
(1.4)
$\mathcal{Z}({\mathbf{d}}) = \{ {\mathbf{z}} \geqslant 0\,{\text{|}}\,\exists \;{\mathbf{x}} \geqslant 0:\;({\mathbf{z}},{\mathbf{x}})\;{\text{удовлетворяют}}\;(1.1){\kern 1pt} - {\kern 1pt} (1.2)\} .$Допустимые распределения реберных потоков принадлежат подмножеству
(1.5)
$Y({\mathbf{d}}) = \{ {\mathbf{y}} \geqslant 0\,|\,({\mathbf{z}},{\mathbf{x}},{\mathbf{y}})\;{\text{удовлетворяют}}\;(1.1){\kern 1pt} - {\kern 1pt} (1.3)\} .$2. Уравнительное распределение межузловых потоков. В рамках модели проводились вычислительные эксперименты для получения многокомпонентных оценок распределения межузловых потоков при предельной загрузке сети. Для экспериментов была разработана специальная PLSR-процедура (от английского peak load shortest route). Выполнение каждой текущей итерации разбивается на несколько этапов. На первом этапе для каждой пары узлов-корреспондентов ищется кратчайший путь, а именно маршрут соединения с минимальным числом ребер. На втором этапе для каждой пары находится максимально допустимый поток при текущих значениях пропускной способности ребер, входящих в кратчайший маршрут соединения. На основе маршрутов и дуговых потоков определяется распределение совместно допустимых межузловых потоков. С учетом остаточных пропускных способностей формируется сеть для проведения следующей итерации. За конечное число итераций, не превосходящее общего количества ребер сети, вычисляются межузловые потоки, при одновременной передаче которых полностью используется пропускная способность всех ребер сети.
На первом шаге (t = 1) PLSR-процедуры для сети $G(1)$ задаются: ${{d}_{k}}(1) = {{d}_{k}}$ – пропускная способность ребра ${{r}_{k}} \in R$, $k = \overline {1,E} $; ${{\Delta }_{k}}(1) = 1$ – длина ребра ${{r}_{k}} \in R$, $k = \overline {1,E} $. Обозначим через ${{H}_{a}}(1)$ кратчайший маршрут соединения для вершин пары pa. Пусть ${{H}_{a}}(1) = \{ {{k}_{1}},{{k}_{2}},...,{{k}_{i}},...,{{k}_{{{{l}_{a}}(1)}}}\} $, где ${{k}_{i}}$ – номер i-го ребра, входящего в кратчайший маршрут ${{H}_{a}}(1)$; ${{h}_{a}}(1)$ – число ребер в маршруте ${{H}_{a}}(1)$; ${{l}_{a}}(1)$ – минимальная длина маршрута :
На первом этапе первого шага последовательно для каждой пары узлов-корреспондентов ${{p}_{a}} \in P$ в сети $G(1)$ решается следующая задача.
Задача 1. В сети $G(1)$ найти кратчайший маршрут передачи ${{H}_{a}}(1)$ из узла-источника ${{{v}}_{{{{s}_{a}}}}}$ в узел-приемник ${{{v}}_{{{{t}_{a}}}}}$.
Маршрут ${{H}_{a}}(1)$ строится с помощью стандартного алгоритма поиска кратчайшего пути между парой вершин во взвешенном графе [13]. Вычисляется максимально допустимый однопродуктовый межузловой поток $z_{a}^{0}(1)$, который можно передать по маршруту ${{H}_{a}}(1)$ только для пары ${{p}_{a}} \in P$ без учета остальных:
Далее $z_{a}^{0}(1)$ будем называть SRM-поток (от английского shortest route max (flow)), а режим передачи потока – монопольным.
При передаче SRM-потока $z_{a}^{0}(1)$ по кратчайшему маршруту ${{H}_{a}}(1)$ для дуговых потоков пары ${{p}_{a}} \in P$ выполняется равенство
Величина реберной нагрузки, согласно (1.3), составляет
Удельные затраты равны числу ребер в кратчайшем маршруте ${{H}_{a}}(1)$:
На основе SRM-потока $z_{a}^{0}(1)$ определяются нормирующие коэффициенты:
На втором этапе указанные коэффициенты используются для поиска текущих совместно допустимых квот на передачу потоков одновременно между всеми парами ${{p}_{m}},m = \overline {1,M} $.
Задача 2. Найти $\alpha {\kern 1pt} *(1) = \mathop {\max }\limits_\alpha \alpha ,$
На основании $\alpha {\kern 1pt} *(1)$ вычисляются дуговые и межузловые потоки:
Таким образом каждой паре корреспондентов на данном этапе выделяется одна и та же квота $\alpha {\kern 1pt} {\text{*}}(1)$ на передачу допустимого потока при заданных кратчайших маршрутах соединения. Решение задачи 2 позволяет получить уравнительное распределение квот на одновременную передачу межузловых потоков различных видов и соответствующие ресурсы, численно равные $y_{m}^{*}(1)$, $m = \overline {1,M} $.
При фиксированных дуговых потоках остаточная пропускная способность всех ребер в сети $G(2)$ равна:
Для следующей итерации t = 2 текущие длины ребер rk для сети $G(2)$ определяются по следующему правилу:
На первом этапе шага $t$ ($t \geqslant 2$) в сети $G(t)$ для каждой пары ${{p}_{a}} \in P$ решается задача 1 – строится кратчайший маршрут ${{H}_{a}}(t) = \{ k_{1}^{'},k_{2}^{'},...,k_{{{{h}_{a}}(t)}}^{'}\} $ длиной
Если длина ${{l}_{a}}(t) \geqslant {{N}^{2}}$, то для пары pa межузловые потоки полагаются равными нулю:
Если же длина ${{l}_{a}}(t) < {{N}^{2}}$, то для пары pa и маршрута ${{H}_{a}}(t)$ (решения задачи 1) вычисляются текущий SRM-поток
дуговые потоки $x_{{ak}}^{0}(t),x_{{a(k + E)}}^{0}(t),\;k \in {{H}_{a}}(t)$, а также коэффициенты:Задача 3. Найти $\alpha {\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\alpha \alpha ,$
На основании решения задачи 3 на шаге $t$ ($t \geqslant 2$) находятся: текущие допустимые значения межузловых потоков, которые могут передаваться в сети $G(t)$ одновременно для всех пар ${{p}_{m}} \in P$:
На заключительном этапе текущего шага $t$ ($t \geqslant 2$) для каждого ребра сети вычисляется остаточная пропускная способность сети $G(t + 1)$:
Если после завершения очередного шага $t$ окажется, что хотя бы для одного ребра ${{r}_{k}} \in R$ остаточная пропускная способность ${{d}_{k}}(t + 1) > 0$, то формируется новая сеть $G(t + 1)$ и производится переход к следующей итерации.
Если же ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то происходит останов, поскольку все пропускные способности ребер исчерпаны и сеть полностью загружена. Финальная итерация обозначается $t: = T$.
Результирующие межузловые и реберные потоки для каждой пары ${{p}_{m}}$, $m = \overline {1,M} $, соответственно равны:
Удельные затраты $w_{m}^{*}(T)$ при передаче межузловых потоков одновременно по всем маршрутам ${{H}_{m}}(1),{{H}_{m}}(2),...,{{H}_{m}}(T)$
Для анализа результатов вычислительных экспериментов формируется несколько массивов данных. Множество пар-корреспондентов P разбивается на два непересекающихся подмножества: смежных узлов-корреспондентов $P({{R}_{ + }})$, расположенных в концевых вершинах ребра ${{r}_{k}}$, $k = \overline {1,E} $, и $P({{R}_{ - }})$ – несмежных пар, кратчайший маршрут соединения для которых содержит более одного ребра:
По завершении последней итерации формируются массивы расчетных данных по следующему правилу:
если ${{p}_{m}} \in P({{R}_{ + }})$, то $z_{m}^{*}(T),$ $y_{m}^{*}(T),$ $w_{m}^{*}(T)$ помещаются в массивы ${\mathbf{Z}}_{ + }^{*}(T)$, ${\mathbf{Y}}_{ + }^{*}(T)$, ${\mathbf{W}}_{ + }^{*}(T)$;
если ${{p}_{m}} \in P({{R}_{ - }})$, то $z_{m}^{*}(T),$ $y_{m}^{*}(T),$ $w_{m}^{*}(T)$ попадают в ${\mathbf{Z}}_{ - }^{*}(T)$, ${\mathbf{Y}}_{ - }^{*}(T)$, ${\mathbf{W}}_{ - }^{*}(T)$.
3. Уравнительное распределение ресурсов. При поиске уравнительного распределения ресурсов (для получения равных нагрузок для всех пар-корреспондентов при передаче межузловых потоков) используется PLSR-процедура, подробно описанная в разд. 2.
При выполнении текущего шага $t$ PLSR-процедуры в сети $G(t)$ при найденных значениях ${{d}_{k}}(t)$ и ${{\Delta }_{k}}(t)$ для каждой пары ${{p}_{a}} \in P$ решением задачи 1 является кратчайший маршрут ${{H}_{a}}(t)$ длиной
Для каждой пары ${{p}_{a}} \in P$ определяются SRM-потоки:
При передаче SRM-потока $z_{a}^{0}(1)$ по кратчайшему маршруту ${{H}_{a}}(1)$ дуговые потоки равны:
По определению (1.3) реберная нагрузка составляет
На основе величины $y_{a}^{0}(t)$ при передаче SPM-потока $z_{a}^{0}(1)$ по кратчайшему пути ${{H}_{a}}(1)$ вычисляются нормирующие коэффициенты:
Коэффициенты $\theta _{a}^{0}(t)$ используются для поиска равных нагрузок при передаче соответствующих межузловых потоков одновременно между всеми парами ${{p}_{a}} \in P$.
Задача 4. Найти $\beta {\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_{\beta > 0} \beta $
при условиях $\beta \sum\limits_{m = 1}^M {\theta _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant {{d}_{k}}(t)} $, $k = \overline {1,E} $.
Для решения задачи 4 $\beta {\kern 1pt} {\text{*}}(t)$ определяются текущие совместно допустимые значения дуговых потоков и реберных нагрузок:
Дуговые потоки $x_{m}^{{**}}(t)$ равны пропускной способности ребра, а нагрузки $y_{m}^{{**}}(t)$ – по построению квоте пропускной способности, которая требуется при передаче межузлового потока:
Решение задачи 4 позволяет на шаге $t$ получить уравнительное распределение ресурсов – одинаковые квоты пропускной способности, равные $\beta {\kern 1pt} {\text{*}}(t)$. Далее вычисляется остаточная пропускная способность ребер в сети $G(t + 1)$:
После завершения очередного шага t осуществляется проверка условий:
если окажется, что хотя бы для одного ребра ${{r}_{k}} \in R$ величина остаточной пропускной способности ${{d}_{k}}(t + 1) > 0$, то формируется новая сеть $G(t + 1)$, определяется длина ребер для $G(t + 1)$:
если же ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то происходит останов, поскольку все пропускные способности ребер исчерпаны и сеть полностью загружена.
Финальная итерация обозначается $t: = T$. Как и в разд. 2, для $t: = T$ вычисляются:
результирующие значения межузловых потоков для каждой пары pm:
финальные реберные нагрузки, которые соответствуют распределению ресурсов сети:Все полученные данные заносятся в массивы по следующему правилу:
если ${{p}_{m}} \in P({{R}_{ + }})$, то $z_{m}^{{**}}(T),$ $y_{m}^{{**}}(T),$ $w_{m}^{{**}}(T)$ помещаются в массивы ${\mathbf{Z}}_{ + }^{{**}}(T)$, ${\mathbf{Y}}_{ + }^{{**}}(T)$, ${\mathbf{W}}_{ + }^{{**}}(T)$;
если ${{p}_{m}} \in P({{R}_{ - }})$, то $z_{m}^{{**}}(T),$ $y_{m}^{{**}}(T),$ $w_{m}^{{**}}(T)$ попадают в ${\mathbf{Z}}_{ - }^{{**}}(T)$, ${\mathbf{Y}}_{ - }^{{**}}(T)$, ${\mathbf{W}}_{ - }^{{**}}(T)$.
4. Вычислительный эксперимент. Описанные ниже результаты вычислительных экспериментов являются продолжением исследований нашей предыдущей статьи. Эксперименты с использованием PLSR-процедуры проводились на моделях сетевых систем, представленных на рис. 1 (слева – базовая сеть, справа – кольцевая). В каждой сети имеется 69 узлов. Пропускные способности ребер dk выбирались случайным образом из отрезка [900, 999] и совпадали для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900.
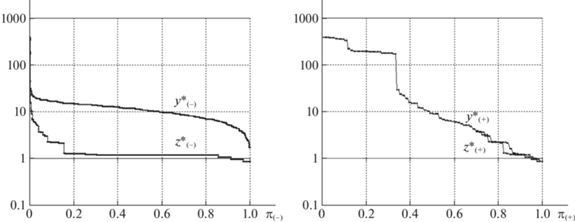
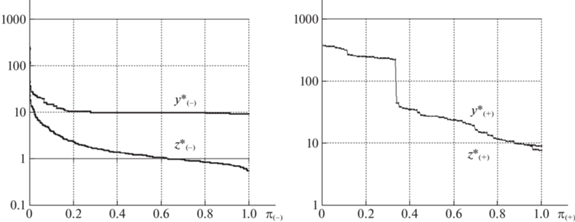
На рис. 2, 3 для базовой, а на рис. 4, 5 для кольцевой сети приведены данные о ходе выполнения PLSR-процедуры. На диаграммах слева указаны суммарные межузловые потоки на каждой итерации, справа – реберные нагрузки, возникающие в сети при передаче соответствующих межузловых потоков. По горизонтальной оси откладываются текущие суммарные значения для смежных пар $P({{R}_{ + }})$, по вертикальной – для пар из множества $P({{R}_{ - }})$. Точки на графиках относятся к очередной итерации и следуют снизу вверх и слева направо, согласно порядку выполнения. Диаграмма слева на рис. 2, 4 отвечает итерациям PLSR-процедуры при уравнительном распределении межузловых потоков в сети, справа указаны реберные нагрузки. На рис. 3, 5 диаграмма справа получена при уравнительном распределении пропускных способностей – ресурсов – для каждой пары корреспондентов, на диаграммах слева представлены межузловые потоки. Точки излома на всех диаграммах свидетельствуют, что за несколько промежуточных итераций резко меняются доли выделенных ресурсов и межузловых потоков для различных групп корреспондентов. На рис. 2–5 видны точки “перегиба”, отвечающие шагу, на котором практически прекращается выделение ресурсов для передачи потоков несмежных пар. Более 25% остаточной пропускной способности распределяется среди 2% смежных корреспондентов. В результате финальные суммарные межузловые потоки для 2% смежных пар оказываются больше или равны суммарным потокам для 97% несмежных пар. Дело в том, что на первых итерациях при исходных значениях пропускной способности удается поддерживать уравнительный принцип распределения. Однако при уменьшении до нуля пропускной способности некоторых ребер происходит разделение сети на отдельные связные компоненты и для большого числа несмежных пар не существует путей передачи потока. На последних итерациях маршруты соединения проходят по смежным ребрам между соответствующими узлами.
Рис. 2.
Межузловые потоки и реберные нагрузки при уравнительном распределении межузловых потоков в базовой сети
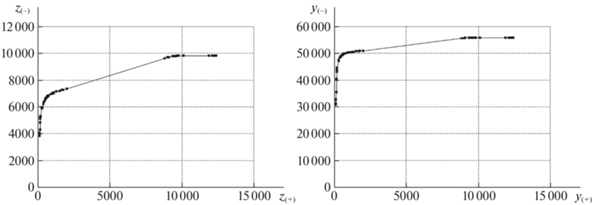
Рис. 3.
Межузловые потоки и реберные нагрузки при уравнительном распределении ресурсов в базовой сети
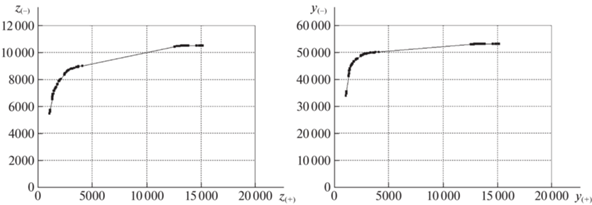
Рис. 4.
Межузловые потоки и реберные нагрузки при уравнительном распределении межузловых потоков в кольцевой сети
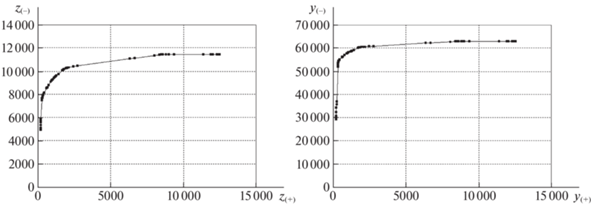
Рис. 5.
Межузловые потоки и реберные нагрузки при уравнительном распределении ресурсов в кольцевой сети
Сравнение диаграмм на рис. 2–5 показывает, что уравнительное распределение пропускной способности (ресурсов) приводит к большим суммарным межузловым потокам для обеих групп корреспондентов. Последнее связано с тем, что распределение ресурсов при передаче потоков только по кратчайшим путям позволяет минимизировать удельные затраты. Результирующие межузловые потоки для близко расположенных корреспондентов получают преимущество даже при формально уравнительном распределении пропускной способности сети.
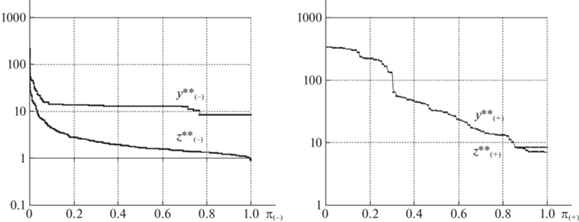
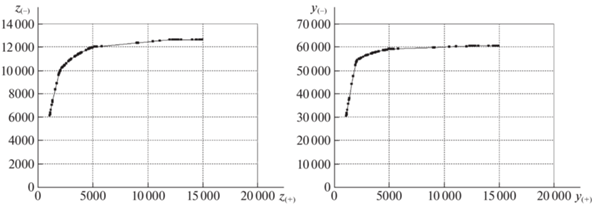
На рис. 6–9 представлены диаграммы финальных распределений межузловых потоков и реберных нагрузок базовой и кольцевой сети. Диаграммы слева относятся к несмежным парам узлов, справа – к смежным корреспондентам ${{p}_{m}} \in P({{R}_{ + }})$. Все полученные ${{z}_{m}}( \cdot )$, ${{y}_{m}}( \cdot )$ упорядочиваются по величине от большего к меньшему (по невозрастанию). По горизонтальной оси указываются относительные порядковые номера корреспондентов в упорядоченных последовательностях:
Рис. 8.
Уравнительное распределение межузловых потоков в кольцевой сети для несмежных и смежных узлов
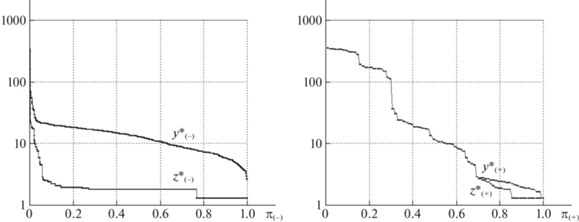
Диаграмма слева на рис. 6 для базовой сети относится к уравнительному распределению межузловых потоков. Кривая сверху иллюстрирует реберные нагрузки. Нижняя почти горизонтальная прямая показывает, что для 82% несмежных пар удается получить практически равные межузловые потоки со средним показателем затрат пропускной способности около 10 единиц. Диаграмма на рис. 7 слева строится при уравнительном распределении ресурсов, а затем вычисляются межузловые потоки. Для 82% несмежных пар удается выделить 10 единиц пропускной способности. Средние значения межузловых потоков при этом оказываются близкими к единице.
Диаграммы на рис. 6, 7 справа относятся к смежным парам узлов-корреспондентов. Результирующие кривые, соответствующие финальным нагрузкам и межузловым потокам, практически совпадают для 97% смежных пар, поскольку кратчайшие маршруты в основном состоят из одного ребра. Небольшие отличия, которые видны на нижней части диаграмм, возникают только для пар, имеющих несколько путей соединения.
Заключение. В [8] сделана попытка классификации методов решения оптимизационных задач на многопродуктовой потоковой модели. Большая часть публикаций, проанализированных в [8], базируется на методах линейного программирования при поиске справедливого или равноправного распределения потоков и ресурсов. В большинстве исследований оценка вычислительных затрат не приводится. При изучении алгоритмических процедур не указаны способы переформирования условий текущих задач линейного программирования и выделения номеров пар узлов, которые исключаются из рассмотрения с фиксированием достигнутых потоков. Согласно классификации, приведенной в [8], предложенный в настоящей работе метод можно отнести к однопутевым процедурам с фиксированной пошаговой маршрутизацией. Оценка числа операций метода равна $O(E{{N}^{5}})$, где $E$ – число ребер сети, $N$ – число узлов [14].
Список литературы
Малашенко Ю.Е., Назарова И.А. Оценки распределения потоков при предельной загрузке многопользовательской сети // Системы и средства информатики. 2020. Т. 30. № 3. С. 4–14.
Малашенко Ю.Е., Назарова И.А. Анализ распределения предельных нагрузок в многопользовательской сети // Информатика и ее применения. 2021. Т. 15. Вып. 4. С. 20–26.
Hahne E.L. Round-Robin Scheduling for Max-Min Fairness in Data Networks // IEEE J. on Selected Areas in Communications. 1991. V. 9. Iss. 7. P. 1024–1039.
Radunovic B., Le Boudec J.-Y. A Unified Framework for Max-Min and Min-Max Fairness With Applications // IEEE/ACM Transactions on Networking. 2007. V. 15. Iss. 5. P. 1073–1083.
Nace D., Doan L.N., Klopfenstein O. et al. Max-min Fairness in Multicommodity Flows // Comput. Oper. Res. 2008. V. 35. Iss. 2. P. 557–573.
Ogryczak W., Luss H., Pioro M. et al. Fair Optimization and Networks: A Survey // J. Appl. Math. 2014. V. 3. P. 1–25.
Luss H. Equitable Resource Allocation: Models, Algorithms, and Applications. Hoboken: John Wiley & Sons, 2012.
Salimifard K., Bigharaz S. The Multicommodity Network Flow Problem: State of the Art Classification, Applications, and Solution Methods // J. Oper. Res. Int. 2020. P. 1–47.
Ros-Giralt J., Tsai W.K. A Lexicographic Optimization Framework to the Flow Control Problem // IEEE Transactions on Information Theory. 2010. V. 56. Iss. 6. P. 2875–2886.
Hajjem M., Bouziri H., Talbi E.-G. A Metaheuristic Framework for Dynamic Network Flow Problems // Recent Developments in Metaheuristics. 2018. P. 285–304.
Masri H., Krichen S., Guitouni A. Metaheuristics for Solving the Bi-objective Single-Path Multicommodity Communication Flow Problem // Int. Trans. Oper. Res. 2019. V. 26. Iss. 2. P. 589–614.
Зойтендейк Г. Методы возможных направлений. М.: Изд-во иностр. лит., 1963.
Берж К. Теория графов и ее применения. М.: Изд-во иностр. лит., 1962.
Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л. и др. Алгоритмы: построение и анализ. М.: Вильямс, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления