Известия РАН. Теория и системы управления, 2022, № 5, стр. 162-176
АДАПТИВНОЕ УПРАВЛЕНИЕ ДВИЖЕНИЕМ МОБИЛЬНОГО КОЛЕСНОГО РОБОТА С УЧЕТОМ НЕИДЕАЛЬНОСТИ ПРИВОДОВ
М. Алхаддад *
* E-mail: alkhaddad.m@phystech.edu
Поступила в редакцию 10.03.2022
После доработки 10.04.2022
Принята к публикации 30.05.2022
- EDN: BCJGGA
- DOI: 10.31857/S0002338822050031
Аннотация
Методом математического моделирования исследуется управляемое движение колесного мобильного робота при наличии параметрических неопределенностей и неконтролируемых погрешностей в формировании приводами управляющих моментов, приложенных к колесам. Предложен алгоритм адаптивного управления, позволяющий роботу с высокой точностью отслеживать заданное программное движение при наличии неопределенностей.
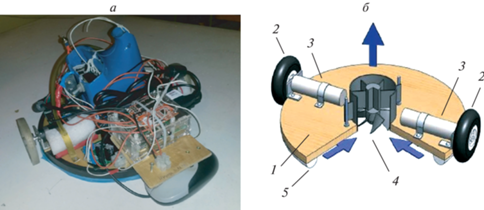
Введение. Данное исследование мотивировано разработкой в лаборатории робототехники и мехатроники Института проблем механики им. А.Ю. Ишлинского РАН мобильного робототехнического комплекса для обслуживания сильно наклонных и вертикальных поверхностей. Комплекс состоит из колесной платформы и малогабаритного колесного робота, который удерживается на вертикальной поверхности за счет разрежения воздуха в полости, отделяющей днище робота от поверхности перемещения. На рис. 1 изображен лабораторный образец робота и показаны его основные компоненты. Робот состоит из жесткого основания 1 круглой формы, на котором крепятся два колеса 2, управляемые независимыми электроприводами 3, и центробежный вакуумный насос 4. Оси вращения колес расположены на одной прямой, проходящей через центр основания. Колеса снабжены шинами, материал которых подбирается так, чтобы обеспечить максимально высокий коэффициент трения колес о поверхность перемещения. Под днищем основания имеется полость 5, в которой создается разрежение воздуха. Благодаря этому робот избыточным внешним атмосферным давлением прижимается к поверхности перемещения с силой, которая позволяет создать трение между колесами и поверхностью, достаточное для удержания робота на поверхности при заблокированных колесах и его движения в любом направлении при включенных приводах. Предусмотрено регулирование степени разреженности воздуха в зависимости от наклона поверхности перемещения и физических условий контакта. Это позволяет экономно расходовать электроэнергию на работу вакуумного насоса. Исследованиям динамических свойств робота, определению состава сенсоров и разработке алгоритмов управления посвящены работы [1–3].
Для описанного робота планируется создать транспортно-манипуляционное устройство, которое доставит робот к месту его использования и приведет в рабочее положение на обслуживаемой поверхности. Устройство изображено на рис. 2 и состоит из колесной транспортной платформы (тележки) и манипулятора. В транспортном положении робот крепится к выходному звену манипулятора днищем вверх. После подъезда платформы к стене, которую будет обслуживать робот, поворотом выходного звена он приводится в положение, в котором днище и колеса обращены к стене, и в контакт со стеной. Затем включается вакуумный насос, робот присасывается к стене, освобождается от закрепления на манипуляторе и начинает функционировать в автономном режиме.
В статье рассматриваются проблемы управления движением транспортной платформы описанного транспортно-манипуляционного устройства по горизонтальной плоскости. Транспортная платформа является колесным мобильным роботом и в дальнейшем обозначается этим термином, поскольку результаты данного исследования применимы не только к транспортной платформе робота вертикального перемещения, но и к широкому классу колесных мобильных роботов различного назначения.
Известны различные схемы адаптивного управления колесными мобильными роботами, математическая модель которых включает неголономные связи. Адаптивные алгоритмы управления отслеживанием движения при наличии параметрических неопределенностей, базирующиеся на кинематических уравнениях, представлены в [4–7]. Робастные адаптивные регуляторы, такие, как адаптивные регуляторы скользящего режима, предназначенные для компенсации непределенностей в конструкции системы и внешних возмущений, исследованы в [8]. Адаптивные нейронные сети, преимущество которых в том, что они не требуют динамической модели робота, обсуждаются в [9]. В [10] для мобильного робота разработана и реализована эталонная модель адаптивного управления, включающая известные и неизвестные динамические параметры. Использование этой модели позволяет увеличить скорость адаптации. Большинство существующих адаптивных регуляторов учитывают неопределенность геометрических или инерционных параметров мобильного робота и не учитывают неидеальности исполнительных механизмов, которая может существенно влиять на точность выполнения роботом программных движений.
В статье предлагается схема адаптивного управления для отслеживания программных движений робота, которая учитывает параметрические неопределенности в конструкции робота, а также неидеальности исполнительных механизмов. Алгоритм управления строится на основе функций Ляпунова. Неидеальность исполнительных механизмов проявляется в различии моментов, реализуемых приводами различных колес, при одном и том же управляющем сигнале. Такое поведение связано прежде всего с трением в трансмиссионных механизмах, передающих вращение от электродвигателей через редукторы к колесам. Алгоритм адаптивного управления позволяет снизить нестабильность угловых скоростей колес при постоянном управляющем напряжении и устранить различия в динамическом поведении колес за счет компенсации неидеальностей этих механизмов средствами управления.
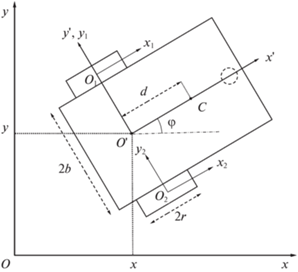
1. Математическая модель мобильного колесного робота. Рассматривается известная модель колесного робота (рис. 3) с двумя приводными колесами, расположенными на одной оси, которая закреплена на жесткой платформе. Кроме приводных колес робот снабжен пассивным рояльным колесом, что обеспечивает роботу трехточечную опору. Предполагается, что рояльное колесо расположено в плоскости, проходящей через середину оси колесной пары и перпендикулярной этой оси. Также предполагается, что трение этого колеса о поверхность перемещения отсутствует. Приводные колеса считаются абсолютно жесткими плоскими круглыми дисками, плоскости которых перпендикулярны оси вращения колес. Робот движется по горизонтальной плоскости без проскальзывания приводных колес. Введем три правые системы координат: неподвижную (инерциальную) систему координат $Oxyz$, систему координат $O{\kern 1pt} 'x{\kern 1pt} 'y{\kern 1pt} 'z{\kern 1pt} '$, жестко связанную с платформой, и системы координат ${{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}$, ${{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}$, жестко связанные с колесами. Оси $z$ и $z{\kern 1pt} '$ направим вертикально вверх, точку $O{\kern 1pt} '$ поместим в середине общей оси колес, точки ${{O}_{1}}$ и ${{O}_{2}}$ расположим в пересечениях оси колес с их плоскостями, ось $x{\kern 1pt} '$ направим горизонтально от точки $O{\kern 1pt} '$ к рояльному колесу, оси ${{y}_{1}}$ и ${{y}_{2}}$ систем координат, связанных с колесами, направим параллельно оси $y{\kern 1pt} '$ системы координат, связанной с платформой. Будем предполагать, что центр масс платформы C находится на оси $x{\kern 1pt} '$.
В качестве обобщенных координат, определяющих конфигурацию системы, будем использовать декартовы координаты $x$ и $y$ точки $O{\kern 1pt} '$ в инерциальной системе отсчета, угол $\varphi $ между осями $x$ и $x{\kern 1pt} '$ и углы ${{\theta }_{1}}$ и ${{\theta }_{2}}$ поворота колес 1 и 2 относительно платформы. Номером 1 помечено колесо, расположенное в “положительном” полупространстве относительно плоскости $x{\kern 1pt} 'z{\kern 1pt} '$; колесо с номером 2 расположено в “отрицательном” полупространстве. Положительным считается полупространство, в котором лежит положительная координатная полуось $y{\kern 1pt} '$.
Обозначим: $2b$ – длина оси колесной пары; $d$ – расстояние от точки $O{\kern 1pt} '$ до центра масс платформы; $r$ – радиус колеса; $M$ – масса платформы; $m$ – масса колеса; $I$ – момент инерции платформы относительно оси, проходящей через центр масс платформы $C$ и параллельной оси $z{\kern 1pt} '$; Jw – момент инерции колеса относительно оси его вращения; ${{A}_{w}}$ – момент инерции колеса относительно его диаметра.
Условие непроскальзывания колес при движении робота (условие равенства нулю скорости точек контакта колес с плоскостью движения) налагает на систему неголономные дифференциальные связи, выражающиеся равенствами
(1.1)
$\begin{gathered} - \dot {x}\sin \varphi + \dot {y}\cos \varphi = 0, \\ \dot {x}\cos \varphi + \dot {y}\sin \varphi - b\dot {\varphi } - r{{{\dot {\theta }}}_{1}} = 0, \\ \dot {x}\cos \varphi + \dot {y}\sin \varphi + b\dot {\varphi } - r{{{\dot {\theta }}}_{2}} = 0. \\ \end{gathered} $Из этих уравнений можно выразить скорости $\dot {x}$, $\dot {y}$ и $\dot {\varphi }$ как функции угла $\varphi $ поворота платформы и угловых скоростей вращения колес относительно платформы ${{\dot {\theta }}_{1}}$ и ${{\dot {\theta }}_{2}}$:
(1.2)
$\begin{gathered} \dot {x} = \frac{r}{2}({{{\dot {\theta }}}_{1}} + {{{\dot {\theta }}}_{2}})\cos \varphi , \\ \dot {y} = \frac{r}{2}({{{\dot {\theta }}}_{1}} + {{{\dot {\theta }}}_{2}})\sin \varphi , \\ \dot {\varphi } = \frac{r}{{2b}}({{{\dot {\theta }}}_{2}} - {{{\dot {\theta }}}_{1}}). \\ \end{gathered} $Уравнения (1.1) и (1.2) эквивалентны.
Уравнения (1.2) можно трактовать как кинематическую модель управления рассматриваемым колесным роботом, считая угловые скорости вращения колес управляющими переменными, а обобщенные координаты x, y и $\varphi $, характеризующие положение платформы относительно неподвижной системы отсчета, – фазовыми переменными.
Введя вместо ${{\dot {\theta }}_{1}}$ и ${{\dot {\theta }}_{2}}$ новые управляющие переменные
(1.3)
$v = \frac{r}{2}({{\dot {\theta }}_{1}} + {{\dot {\theta }}_{2}}),\quad \omega = \frac{r}{{2b}}({{\dot {\theta }}_{2}} - {{\dot {\theta }}_{1}}),$(1.4)
$\begin{gathered} \dot {x} = v\cos \varphi , \\ \dot {y} = v\sin \varphi , \\ \dot {\varphi } = \omega {\kern 1pt} . \\ \end{gathered} $Переменная $v$ есть линейная скорость точки $O{\kern 1pt} '$ платформы. Эта величина может быть как положительной, так и отрицательной; при $v > 0$ платформа движется вперед (скорость направлена от оси колесной пары к рояльному колесу), а при $v < 0$ – пятится.
Запишем теперь уравнения динамики рассматриваемой механической системы в форме уравнений Лагранжа первого рода (с множителями). Кинетическая энергия T имеет вид
(1.5)
$T = \frac{1}{2}[(M + 2m)({{\dot {x}}^{2}} + {{\dot {y}}^{2}}) + (I + 2{{A}_{w}} + M{{d}^{2}} + 2m{{b}^{2}}){{\dot {\varphi }}^{2}} - 2Md\dot {\varphi }(\dot {x}\sin \varphi - \dot {y}\cos \varphi )] + \frac{1}{2}{{J}_{w}}(\dot {\theta }_{1}^{2} + \dot {\theta }_{1}^{2}).$Уравнения связей (1.2) представим в матричной форме
(1.6)
$\begin{gathered} A(q)\dot {q} = 0,\quad q = \left[ {\begin{array}{*{20}{l}} {{{q}_{1}}} \\ {{{q}_{2}}} \end{array}} \right],\quad {{q}_{1}} = \left[ {\begin{array}{*{20}{l}} x \\ y \\ \varphi \end{array}} \right]\quad {{q}_{2}} = \left[ {\begin{array}{*{20}{l}} {{{\theta }_{1}}} \\ {{{\theta }_{2}}} \end{array}} \right], \\ A(q) = [E\;\Gamma (q)],\quad E = \left[ {\begin{array}{*{20}{l}} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}} \right],\quad \Gamma (q) = \left[ {\begin{array}{*{20}{c}} { - \frac{r}{2}\cos \varphi }&{ - \frac{r}{2}\cos \varphi } \\ { - \frac{r}{2}\sin \varphi }&{ - \frac{r}{2}\sin \varphi } \\ {\frac{r}{{2b}}}&{ - \frac{r}{{2b}}} \end{array}} \right]. \\ \end{gathered} $Считаем, что из активных сил на систему действуют только управляющие силы, создающие крутящие моменты ${{\tau }_{1}}$ и ${{\tau }_{2}}$, приложенные к осям соответствующих колес. Эти моменты суть обобщенные силы, отвечающие обобщенным координатам ${{\theta }_{1}}$ и ${{\theta }_{2}}$ соответственно.
Уравнения Лагранжа первого рода для системы с кинетической энергией (1.5) и связями (1.6) в предположении их идеальности можно представить следующим образом:
(1.7)
$\begin{gathered} \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {q}}}_{1}}}} - \frac{{\partial T}}{{\partial {{q}_{1}}}} = \lambda , \\ \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {q}}}_{2}}}} - \frac{{\partial T}}{{\partial {{q}_{2}}}} = {{Q}_{{{{q}_{2}}}}} + {{\Gamma }^{{\text{T}}}}(q)\lambda ,\quad {{Q}_{{{{q}_{2}}}}} = \left[ \begin{gathered} {{\tau }_{1}} \hfill \\ {{\tau }_{2}} \hfill \\ \end{gathered} \right]. \\ \end{gathered} $Здесь $\lambda $ – вектор множителей Лагранжа:
Верхний индекс ${\text{T}}$ обозначает операцию транспонирования матрицы.
Подставляя вместо λ во второе уравнение (1.7) левую часть первого уравнения, получим
(1.8)
$\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {q}}}_{2}}}} - \frac{{\partial T}}{{\partial {{q}_{2}}}} = {{Q}_{{{{q}_{2}}}}} + {{\Gamma }^{{\text{T}}}}(q)\left[ {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {q}}}_{1}}}} - \frac{{\partial T}}{{\partial {{q}_{1}}}}} \right].$После подстановки ${{\dot {q}}_{1}} = - \Gamma (q){{\dot {q}}_{2}}$, ${{\ddot {q}}_{1}} = - \Gamma (q){{\ddot {q}}_{2}} - \dot {\Gamma }(q){{\dot {q}}_{2}}$, вытекающей из уравнений связи (1.6), модель динамики системы с кинетической энергией (1.5) приводится к следующему виду:
(1.9)
$\begin{gathered} {{{\dot {q}}}_{1}} = - \Gamma (q){{{\dot {q}}}_{2}},\quad \bar {M}{{{\ddot {q}}}_{2}} + \bar {C}({{{\dot {q}}}_{2}}){{{\dot {q}}}_{2}} = {{Q}_{{{{q}_{2}}}}}, \\ \bar {M} = \left[ {\begin{array}{*{20}{c}} {{{J}_{w}} + (M + 2m)\frac{{{{r}^{2}}}}{4} + \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}}&{(M + 2m)\frac{{{{r}^{2}}}}{4} - \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \\ {(M + 2m)\frac{{{{r}^{2}}}}{4} - \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}}&{{{J}_{w}} + (M + 2m)\frac{{{{r}^{2}}}}{4} + \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \end{array}} \right], \\ \bar {I} = I + 2{{A}_{w}} + M{{d}^{2}} + 2m{{b}^{2}},\quad \bar {C} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{{Md{{r}^{3}}}}{{4{{b}^{2}}}}({{{\dot {\theta }}}_{2}} - {{{\dot {\theta }}}_{1}})} \\ {\frac{{Md{{r}^{3}}}}{{4{{b}^{2}}}}({{{\dot {\theta }}}_{2}} - {{{\dot {\theta }}}_{1}})}&0 \end{array}} \right]. \\ \end{gathered} $Уравнения (1.9) не учитывают динамику приводов, создающих крутящие моменты ${{\tau }_{1}}$ и ${{\tau }_{2}}$, и не отражают физическую природу этих моментов. В мобильных роботах рассматриваемого типа, как правило, используются электроприводы с двигателями постоянного тока. Уравнение электрической цепи двигателя постоянного тока имеет вид
где $i$ – ток в цепи якоря электродвигателя, $u$ – управляющее электрическое напряжение, $L$ – коэффициент самоиндукции обмотки якоря электродвигателя, $R$ – электрическое сопротивление обмотки якоря электродвигателя, $\dot {\chi }$ – угловая скорость вращения якоря электродвигателя относительно его статора, $k$ – постоянный коэффициент, определяемый конструкцией двигателя. Слагаемое $Ldi{\text{/}}dt$ представляет электродвижущую силу (ЭДС) самоиндукции, наводящуюся в обмотке якоря вследствие изменения тока в ней, а слагаемое $k\dot {\chi }$ – противоЭДС, наводящуюся в обмотке якоря вследствие его вращения в магнитном поле статора. Момент μ электромагнитных сил, приложенных к оси якоря, пропорционален току с коэффициентом k:Будем для простоты считать, что приводы колес робота одинаковы, якорь электродвигателя каждого привода представляет однородный диск, соосный колесу, обслуживаемому данным приводом, а статор жестко закреплен на платформе. Передача вращения от приводов к колесам осуществляется через редукторы с передаточным числом $n$, так что выполнены равенства
(1.12)
${{\dot {\chi }}_{1}} = n{{\dot {\theta }}_{1}},\quad {{\dot {\chi }}_{2}} = n{{\dot {\theta }}_{2}},\quad {{\tau }_{1}} = n{{\mu }_{1}},\quad {{\tau }_{2}} = n{{\mu }_{2}}.$Здесь ${{\tau }_{1}}$ и ${{\tau }_{2}}$ – вращающие моменты, приложенные к колесам; они являются обобщенными силами, отвечающие обобщенным координатам ${{\theta }_{1}}$ и ${{\theta }_{2}}$ соответственно:
(1.13)
${{Q}_{{{{q}_{2}}}}} = \left[ {\begin{array}{*{20}{l}} {{{\tau }_{1}}} \\ {{{\tau }_{2}}} \end{array}} \right].$Выразив токи в якорях двигателей через соответствующие моменты ${{\tau }_{1}}$ и ${{\tau }_{2}}$, используя равенства (1.11) и (1.12), получим
Подставляя выражение (1.14) для токов и выражения (1.12) для скоростей вращения роторов в уравнение (1.10), будем иметь
(1.15)
$L\frac{{d{{\tau }_{\alpha }}}}{{dt}} + R{{\tau }_{\alpha }} + {{n}^{2}}{{k}^{2}}{{\dot {\theta }}_{\alpha }} = nk{{u}_{\alpha }},\quad \alpha = 1,{\kern 1pt} 2.$Для учета динамики привода платформа должна рассматриваться вместе с жестко связанными с ней деталями статоров электродвигателей и редукторов, а в выражение для кинетической энергии надо добавить кинетическую энергию роторов электродвигателей. В результате в (1.9) вместо m, ${{A}_{w}}$, ${{J}_{w}}$ будем иметь $m + {{m}_{a}}$, ${{A}_{w}} + {{A}_{a}}$, ${{J}_{w}} + {{J}_{a}}{{n}^{2}}$, где ${{m}_{a}}$ – масса якоря электродвигателя, ${{A}_{a}}$ и ${{J}_{a}}$ – экваториальный и осевой моменты инерции якоря соответственно.
Таким образом, полная динамическая модель колесного робота с электроприводами включает уравнения (1.2), (1.9), (1.13) и (1.15).
Если выполняется неравенство
где $U$ – характерная (например, максимально допустимая) величина управляющего напряжения, ${{L}_{*}}$ – характерное расстояние, на которое перемещается робот, $r$ – радиус колеса, то можно пренебречь связанными с явлением самоиндукции переходными процессами в цепях якорей электродвигателей приводов и формально положить L = 0. Тогда дифференциальные уравнения (1.15) заменяются конечными уравнениями(1.17)
${{\tau }_{\alpha }} = \frac{{nk}}{R}({{u}_{\alpha }} - nk{{\dot {\theta }}_{\alpha }})\quad \alpha = 1,{\kern 1pt} 2.$Величина $L{\text{/}}R$ имеет размерность времени и характеризует время установления тока в цепи якоря электродвигателя. Величина $nk{{L}_{*}}{\text{/}}(Ur)$ также имеет размерность времени и характеризует время перемещения робота на расстояние ${{L}_{*}}$ с установившейся скоростью, отвечающей управляющему напряжению U. Неравенство (1.16) можно трактовать как малость времени установления тока в цепи якоря электродвигателя по сравнению со временем движения робота. Сделаем числовые оценки. Для рассматриваемого колесного робота имеем $n = 180$, U = 12 В, $k = 0.316$ Нм/А, $L\, = \,0.036$ Гн, $R = 3.6$ Ом, $r = 0.05$ м. Положим ${{L}_{*}} = 1$ м. Тогда получаем $L{\text{/}}R = 0.01{\kern 1pt} $ с, $nk{{L}_{*}}{\text{/}}(Ur)$ = = 9.48 с, и неравенство (1.16) выполнено.
2. Адаптивное отслеживание траектории на основе динамической модели. Разработка адаптивного способа управления, базирующегося на динамической модели колесного робота, необходима для учета инерционных свойств робота и физических процессов в приводах его колес. Адаптивное управление на основе динамической модели позволяет компенсировать неполноту информации об инерционных параметрах (массах и моментах инерции) механических компонент колесного робота, а также неидеальное функционирование приводов, связанное главным образом с трением. Крутящий момент, приложенный к колесам относительно осей их вращения, при наличии трения можно представить следующим образом:
где $\tau $ – крутящий момент, создаваемый двигателем, а $\varepsilon $ – момент сил трения. Таким образом, в соответствии с (1.17) и (2.1) полный крутящий момент, приложенный к колесам, записывается в виде (2.1), где(2.2)
${{\tau }_{w}} = \left[ \begin{gathered} {{\tau }_{{w1}}} \hfill \\ {{\tau }_{{w2}}} \hfill \\ \end{gathered} \right],\quad \tau = \left[ \begin{gathered} {{\tau }_{1}} \hfill \\ {{\tau }_{2}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{nk}}{R}({{u}_{1}} - nk{{{\dot {\theta }}}_{1}})} \\ {\frac{{nk}}{R}({{u}_{2}} - nk{{{\dot {\theta }}}_{2}})} \end{array}} \right],\quad \varepsilon = \left[ \begin{gathered} {{\varepsilon }_{1}} \hfill \\ {{\varepsilon }_{2}} \hfill \\ \end{gathered} \right].$В итоге динамическая модель мобильного робота с учетом динамики приводов представляется следующей системой уравнений:
(2.3)
$\begin{gathered} {{{\dot {q}}}_{1}} = - \Gamma (q){{{\dot {q}}}_{2}}, \\ \bar {\bar {M}}{{{\ddot {q}}}_{2}} + \bar {\bar {C}}({{{\dot {q}}}_{2}}){{{\dot {q}}}_{2}} = u + \bar {\varepsilon },\quad u = [{{u}_{1}},{{u}_{2}}{{]}^{{\text{T}}}}, \\ \bar {\bar {M}} = \frac{R}{{nk}}\left[ {\begin{array}{*{20}{c}} {{{J}_{w}} + (M + 2m)\frac{{{{r}^{2}}}}{4} + \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}}&{(M + 2m)\frac{{{{r}^{2}}}}{4} - \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \\ {(M + 2m)\frac{{{{r}^{2}}}}{4} - \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}}&{{{J}_{w}} + (M + 2m)\frac{{{{r}^{2}}}}{4} + \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \end{array}} \right], \\ \bar {\bar {C}} = \frac{R}{{nk}}\left[ {\begin{array}{*{20}{c}} {\frac{{{{n}^{2}}{{k}^{2}}}}{R}}&{ - \frac{{Md{{r}^{3}}}}{{4{{b}^{2}}}}({{{\dot {\theta }}}_{2}} - {{{\dot {\theta }}}_{1}})} \\ {\frac{{Md{{r}^{3}}}}{{4{{b}^{2}}}}({{{\dot {\theta }}}_{2}} - {{{\dot {\theta }}}_{1}})}&{\frac{{{{n}^{2}}{{k}^{2}}}}{R}} \end{array}} \right],\quad \bar {\varepsilon } = \frac{R}{{nk}}\varepsilon . \\ \end{gathered} $Будем строить режим управления напряжениями, подаваемыми на двигатели приводов, который обеспечивает отслеживание программного движения колесного робота. Пусть ωc = = ${{[{{\omega }_{{c1}}},{{\omega }_{{c2}}}]}^{{\text{T}}}}$ – скорости вращения колес (пока неизвестные), которые обеспечивают отслеживание заданного движения ${{q}_{d}}$. Введем вектор $\zeta = [{{\zeta }_{1}},{{\zeta }_{2}}{{]}^{{\text{T}}}}$, представляющий ошибку отслеживания угловых скоростей колес, следующим образом:
(2.4)
${{\zeta }_{1}} = {{\omega }_{1}} - {{\omega }_{{c1}}},\quad {{\zeta }_{2}} = {{\omega }_{2}} - {{\omega }_{{c2}}},$(2.5)
$\begin{gathered} {{{\dot {q}}}_{1}} = - \Gamma (q)({{\omega }_{c}} + \zeta ), \\ \bar {\bar {M}}\dot {\zeta } + \bar {\bar {C}}(\zeta )\zeta + Yp = u + \bar {\varepsilon }, \\ \end{gathered} $(2.6)
$\begin{gathered} Y = \left[ {\begin{array}{*{20}{c}} {{{{\dot {\omega }}}_{{c1}}}}&{{{{\dot {\omega }}}_{{c2}}}}&{{{\omega }_{{c1}}}}&{\omega {{\omega }_{{c2}}}} \\ {{{{\dot {\omega }}}_{{c2}}}}&{{{{\dot {\omega }}}_{{c1}}}}&{{{\omega }_{{c2}}}}&{ - \omega {{\omega }_{{c1}}}} \end{array}} \right], \\ p = \left[ \begin{gathered} {{p}_{1}} \hfill \\ {{p}_{2}} \hfill \\ {{p}_{3}} \hfill \\ {{p}_{4}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{R}{{nk}}\left( {{{J}_{w}} + (M + 2m)\frac{{{{r}^{2}}}}{4} + \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \right)} \\ {\frac{R}{{nk}}\left( {(M + 2m)\frac{{{{r}^{2}}}}{4} - \bar {I}\frac{{{{r}^{2}}}}{{4{{b}^{2}}}}} \right)} \\ {nk} \\ {\frac{R}{{nk}}\frac{{Md{{r}^{3}}}}{{4{{b}^{2}}}}} \end{array}} \right]. \\ \end{gathered} $Предполагается, что компоненты векторов параметров p и $\bar {\varepsilon }$ неизвестны или известны с погрешностями. Векторы p, $\bar {\varepsilon }$ и $a = [{{a}_{1}},{{a}_{2}}{{]}^{{\text{T}}}}$, где ${{a}_{1}} = r{\text{/}}2$ и ${{a}_{2}} = r{\text{/}}(2b),$ содержат все параметры системы. Поскольку в динамической модели (2.5) имеются неизвестные параметры, будем строить адаптивное управление, которое производит оценку неизвестных параметров в процессе работы. Введем величины $\tilde {p}$, $\tilde {\bar {\varepsilon }}$ и $\tilde {a}$, представляющие разности между реальными значениями неизвестных параметров и их оценками:
(2.7)
$\tilde {p} = p - \hat {p},\quad \tilde {\bar {\varepsilon }} = \bar {\varepsilon } - \hat {\bar {\varepsilon }},\quad \tilde {a} = a - \hat {a},$Пусть нужно, управляя угловыми скоростями колес, обеспечить движение робота по заданной траектории, определяемой функциями $x = {{x}_{d}}(t)$, $y = {{y}_{d}}(t)$, $\varphi = {{\varphi }_{d}}(t)$. Эти функции удовлетворяют уравнениям (1.4), т.е. имеем
(2.8)
$\begin{gathered} {{{\dot {x}}}_{d}} = {{v}_{d}}\cos {{\varphi }_{d}}, \\ {{{\dot {y}}}_{d}} = {{v}_{d}}\sin {{\varphi }_{d}}, \\ {{{\dot {\varphi }}}_{d}} = {{\omega }_{d}}. \\ \end{gathered} $Допустим, что функции $x(t)$, $y(t)$ и $\varphi (t)$ характеризуют реальное движение робота, которое, вообще говоря, отличается от программного, и реальному движению отвечают управления $v(t)$ и $\omega (t)$. Рассогласование реального и программного движений будем характеризовать тремя переменными ${{e}_{1}}$, ${{e}_{2}}$ и ${{e}_{3}}$, определяемыми следующим образом:
(2.9)
$e = \left[ {\begin{array}{*{20}{l}} {{{e}_{1}}} \\ {{{e}_{2}}} \\ {{{e}_{3}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos \varphi }&{\sin \varphi }&0 \\ { - \sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{x}_{d}} - x} \\ {{{y}_{d}} - y} \\ {{{\varphi }_{d}} - \varphi } \end{array}} \right].$Эволюция этих ошибок описывается дифференциальными уравнениями [11]
(2.10)
$\begin{gathered} {{{\dot {e}}}_{1}} = - {{a}_{1}}{{\omega }_{1}} - {{a}_{2}}{{e}_{2}}({{\omega }_{1}} - {{\omega }_{2}}) + {{v}_{d}}\cos {{e}_{3}}, \\ {{{\dot {e}}}_{2}} = {{a}_{2}}({{\omega }_{1}} - {{\omega }_{2}}){{e}_{1}} + {{v}_{d}}\sin {{e}_{3}}, \\ {{{\dot {e}}}_{3}} = {{a}_{2}}({{\omega }_{1}} - {{\omega }_{2}}) + {{\omega }_{d}}. \\ \end{gathered} $Подставляя выражения (2.4) в уравнения (2.10), получим
(2.11)
$\begin{gathered} {{{\dot {e}}}_{1}} = - {{a}_{1}}({{\omega }_{{c1}}} + {{\zeta }_{1}} + {{\omega }_{{c2}}} + {{\zeta }_{2}}) - {{a}_{2}}{{e}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{v}_{d}}\cos {{e}_{3}}, \\ {{{\dot {e}}}_{2}} = {{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}){{e}_{1}} + {{v}_{d}}\sin {{e}_{3}}, \\ {{{\dot {e}}}_{3}} = {{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{\omega }_{d}}. \\ \end{gathered} $Полная система уравнений, определяющая эволюцию всех погрешностей в системе, задается следующим образом:
(2.12)
$\begin{gathered} {{{\dot {e}}}_{1}} = - {{a}_{1}}({{\omega }_{{c1}}} + {{\zeta }_{1}} + {{\omega }_{{c2}}} + {{\zeta }_{2}}) - {{a}_{2}}{{e}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{v}_{d}}\cos {{e}_{3}}, \\ {{{\dot {e}}}_{2}} = {{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}){{e}_{1}} + {{v}_{d}}\sin {{e}_{3}}, \\ {{{\dot {e}}}_{3}} = {{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{\omega }_{d}}, \\ \bar {\bar {M}}\dot {\zeta } + \bar {\bar {C}}(\zeta )\zeta + Yp = u + \bar {\varepsilon }. \\ \end{gathered} $Будем строить законы управления величинами ${{\omega }_{c}}$ и $u$, при которых ошибки ${{\zeta }_{1}},\;{{\zeta }_{2}},\;{{e}_{1}},\;{{e}_{2}}$ и ${{e}_{3}}$ стремятся к нулю с течением времени, несмотря на неопределенности в значениях компонент векторов p, a и $\varepsilon $.
Для системы дифференциальных уравнений (2.12) введем функцию Ляпунова
(2.13)
$V = \frac{{{{\gamma }_{1}}}}{2}(e_{1}^{2} + e_{2}^{2}) + (1 - \cos {{e}_{3}}) + \frac{1}{{2{{\gamma }_{2}}}}\tilde {a}_{1}^{2} + \frac{1}{{2{{\gamma }_{3}}}}\tilde {a}_{2}^{2} + \frac{1}{2}{{\zeta }^{{\text{T}}}}\bar {\bar {M}}\zeta + \frac{1}{2}{{\tilde {p}}^{{\text{T}}}}{{Z}^{{ - 1}}}\tilde {p} + \frac{1}{2}{{\tilde {\bar {\varepsilon }}}^{{\text{T}}}}{{K}^{{ - 1}}}\tilde {\bar {\varepsilon }},$(2.14)
$\dot {V} = {{\gamma }_{1}}{{e}_{1}}{{\dot {e}}_{1}} + {{\gamma }_{1}}{{e}_{2}}{{\dot {e}}_{2}} + \sin {{e}_{3}}{{\dot {e}}_{3}} + \frac{1}{{{{\gamma }_{2}}}}{{\tilde {a}}_{1}}{{\dot {\tilde {a}}}_{1}} + \frac{1}{{{{\gamma }_{3}}}}{{\tilde {a}}_{2}}{{\dot {\tilde {a}}}_{2}} + {{\zeta }^{{\text{T}}}}\bar {\bar {M}}\dot {\zeta } + {{\tilde {p}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{\tilde {\bar {\varepsilon }}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}}.$Подставив в правую часть ((2.14) вместо ${{\dot {e}}_{1}},{{\dot {e}}_{2}},{{\dot {e}}_{3}}$ правые части первых трех уравнений (2.12)), а вместо $\bar {\bar {M}}\dot {\zeta }$ – выражение этого произведения из четвертого уравнения (2.12)), получим
(2.15)
$\begin{gathered} \dot {V} = {{\gamma }_{1}}{{e}_{1}}[ - {{a}_{1}}({{\omega }_{{c1}}} + {{\zeta }_{1}} + {{\omega }_{{c2}}} + {{\zeta }_{2}}) - {{a}_{2}}{{e}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{v}_{d}}\cos {{e}_{3}}] + \\ \, + {{\gamma }_{1}}{{e}_{2}}[{{a}_{2}}{{e}_{1}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{v}_{d}}\sin {{e}_{3}}] + \sin {{e}_{3}}[{{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{\omega }_{d}}] + \\ \, + \frac{1}{{{{\gamma }_{2}}}}{{{\tilde {a}}}_{1}}{{{\dot {\tilde {a}}}}_{1}} + \frac{1}{{{{\gamma }_{3}}}}{{{\tilde {a}}}_{2}}{{{\dot {\tilde {a}}}}_{2}} + {{\zeta }^{{\text{T}}}}[ - \bar {\bar {C}}\zeta - Yp + u + \bar {\varepsilon }] + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}}. \\ \end{gathered} $После преобразований и упрощений имеем
(2.16)
$\begin{gathered} \dot {V} = {{\gamma }_{1}}{{e}_{1}}[ - {{a}_{1}}({{\omega }_{{c1}}} + {{\zeta }_{1}} + {{\omega }_{{c2}}} + {{\zeta }_{2}}) + {{v}_{d}}\cos {{e}_{3}}] + {{\gamma }_{1}}{{e}_{2}}{{v}_{d}}\sin {{e}_{3}} + \sin {{e}_{3}}[{{a}_{2}}({{\omega }_{{c1}}} + {{\zeta }_{1}} - {{\omega }_{{c2}}} - {{\zeta }_{2}}) + {{\omega }_{d}}] + \\ \, + \frac{1}{{{{\gamma }_{2}}}}{{{\tilde {a}}}_{1}}{{{\dot {\tilde {a}}}}_{1}} + \frac{1}{{{{\gamma }_{3}}}}{{{\tilde {a}}}_{2}}{{{\dot {\tilde {a}}}}_{2}} + {{\zeta }^{{\text{T}}}}[ - \bar {\bar {C}}\zeta - Yp + u + \bar {\varepsilon }] + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}}. \\ \end{gathered} $Подстановка $a = \tilde {a} + \hat {a}$, вытекающая из (2.7), в (2.16) дает
(2.17)
$\begin{gathered} \dot {V} = {{\gamma }_{1}}{{e}_{1}}[ - {{{\hat {a}}}_{1}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}) + {{v}_{d}}\cos {{e}_{3}}] + \sin {{e}_{3}}[{{{\hat {a}}}_{2}}({{\omega }_{{c1}}} - {{\omega }_{{c2}}}) + {{\omega }_{d}} + {{\gamma }_{1}}{{e}_{2}}{{v}_{d}}] - {{\gamma }_{1}}{{e}_{1}}{{{\hat {a}}}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \\ \, + \sin {{e}_{3}}{{{\hat {a}}}_{2}}({{\zeta }_{1}} - {{\zeta }_{2}}) - {{\gamma }_{1}}{{e}_{1}}{{{\tilde {a}}}_{1}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}) + \sin {{e}_{3}}{{{\tilde {a}}}_{2}}({{\omega }_{{c1}}} - {{\omega }_{{c2}}}) - {{\gamma }_{1}}{{e}_{1}}{{{\tilde {a}}}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \sin {{e}_{3}}{{{\tilde {a}}}_{2}}({{\zeta }_{1}} - {{\zeta }_{2}}) + \\ \, + \frac{1}{{{{\gamma }_{2}}}}{{{\tilde {a}}}_{1}}{{{\dot {\tilde {a}}}}_{1}} + \frac{1}{{{{\gamma }_{3}}}}{{{\tilde {a}}}_{2}}{{{\dot {\tilde {a}}}}_{2}} + {{\zeta }^{{\text{T}}}}[ - Yp + u + \bar {\varepsilon }] + + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta . \\ \end{gathered} $Будем выбирать ${{\omega }_{{c1}}}$ и ${{\omega }_{{c2}}}$, так, чтобы первые два слагаемых в (2.17) были отрицательными, а именно положим
(2.18)
$\begin{gathered} - {{{\hat {a}}}_{1}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}) + {{v}_{d}}\cos {{e}_{3}} = - {{k}_{1}}{{e}_{1}}, \\ {{{\hat {a}}}_{2}}({{\omega }_{{c1}}} - {{\omega }_{{c2}}}) + {{\omega }_{d}} + {{\gamma }_{1}}{{e}_{2}}{{v}_{d}} = - {{k}_{2}}\sin {{e}_{3}}. \\ \end{gathered} $Здесь ${{k}_{1}}$ и ${{k}_{2}}$ – положительные параметры, подлежащие выбору. Решая уравнения (2.18) относительно ${{\omega }_{{c1}}}$ и ${{\omega }_{{c2}}}$, найдем
(2.19)
$\begin{gathered} {{\omega }_{{c1}}} = \frac{1}{{2{{{\hat {a}}}_{1}}}}({{k}_{1}}{{e}_{1}} + {{v}_{d}}\cos {{e}_{3}}) - \frac{1}{{2{{{\hat {a}}}_{2}}}}({{\omega }_{d}} + {{\gamma }_{1}}{{e}_{2}}{{v}_{d}} + {{k}_{2}}\sin {{e}_{3}}), \\ {{\omega }_{{c2}}} = \frac{1}{{2{{{\hat {a}}}_{1}}}}({{k}_{1}}{{e}_{1}} + {{v}_{d}}\cos {{e}_{3}}) + \frac{1}{{2{{{\hat {a}}}_{2}}}}({{\omega }_{d}} + {{\gamma }_{1}}{{e}_{2}}{{v}_{d}} + {{k}_{2}}\sin {{e}_{3}}). \\ \end{gathered} $Уравнения (2.19) содержат вектор неизвестных параметров $\hat {a}$, для которого будем строить законы адаптации с помощью производной функции Ляпунова (2.17). Подстановка выражений (2.18) в (2.17) дает
(2.20)
$\begin{gathered} \dot {V} = - {{k}_{1}}e_{1}^{2} - {{k}_{2}}\mathop {\sin }\nolimits^2 {{e}_{3}} + {{\gamma }_{1}}{{{\tilde {a}}}_{1}}\left[ { - {{e}_{1}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}) - {{e}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \frac{1}{{{{\gamma }_{1}}{{\gamma }_{2}}}}{{{\dot {\tilde {a}}}}_{1}}} \right] + \\ \, + {{{\tilde {a}}}_{2}}\left[ {\sin {{e}_{3}}({{\omega }_{{c1}}} - {{\omega }_{{c2}}}) + \sin {{e}_{3}}({{\zeta }_{1}} - {{\zeta }_{2}}) + \frac{1}{{{{\gamma }_{3}}}}{{{\dot {\tilde {a}}}}_{2}}} \right] - {{\gamma }_{1}}{{e}_{1}}{{{\hat {a}}}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \\ \, + \sin {{e}_{3}}{{{\hat {a}}}_{2}}({{\zeta }_{1}} - {{\zeta }_{2}}) + {{\zeta }^{{\text{T}}}}( - Yp + u + \bar {\varepsilon }) + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta . \\ \end{gathered} $Будем строить законы адаптации для параметров ${{\hat {a}}_{1}}$ и ${{\hat {a}}_{2}}$ так, чтобы оба выражения в квадратных скобках в (2.20) равнялись нулю, т.е. чтобы выполнялись равенства
(2.21)
$\begin{gathered} - {{e}_{1}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}) - {{e}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \frac{1}{{{{\gamma }_{1}}{{\gamma }_{2}}}}{{{\dot {\tilde {a}}}}_{1}} = 0, \\ \sin {{e}_{3}}({{\omega }_{{c1}}} - {{\omega }_{{c2}}}) + \sin {{e}_{3}}({{\zeta }_{1}} - {{\zeta }_{2}}) + \frac{1}{{{{\gamma }_{3}}}}{{{\dot {\tilde {a}}}}_{2}} = 0. \\ \end{gathered} $Отсюда получаем дифференциальные уравнения, описывающие законы адаптации для оценок ${{\hat {a}}_{1}}$ и ${{\hat {a}}_{2}}$:
(2.22)
$\begin{gathered} {{{\dot {\hat {a}}}}_{1}} = - {{\gamma }_{1}}{{\gamma }_{2}}({{\omega }_{{c1}}} + {{\omega }_{{c2}}}){{e}_{1}} - {{\gamma }_{1}}{{\gamma }_{2}}({{\zeta }_{1}} + {{\zeta }_{2}}){{e}_{1}}, \\ {{{\dot {\hat {a}}}}_{2}} = - {{\gamma }_{3}}({{\omega }_{{c2}}} - {{\omega }_{{c1}}})\sin {{e}_{3}} - {{\gamma }_{3}}({{\zeta }_{2}} - {{\zeta }_{1}})\sin {{e}_{3}}. \\ \end{gathered} $Подстановка выражения (2.21) в (2.20) дает
(2.23)
$\begin{gathered} \dot {V} = - {{k}_{1}}e_{1}^{2} - {{k}_{2}}\mathop {\sin }\nolimits^2 {{e}_{3}} - {{\gamma }_{1}}{{e}_{1}}{{{\hat {a}}}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \sin {{e}_{3}}{{{\hat {a}}}_{2}}({{\zeta }_{1}} - {{\zeta }_{2}}) + \\ \, + {{\zeta }^{{\text{T}}}}( - Yp + u + \bar {\varepsilon }) + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta . \\ \end{gathered} $Заменяя параметры p и $\bar {\varepsilon }$ в (2.23) соответствующими выражениями из (2.7), получим
(2.24)
$\begin{gathered} \dot {V} = - {{k}_{1}}e_{1}^{2} - {{k}_{2}}\mathop {\sin }\nolimits^2 {{e}_{3}} - {{\gamma }_{1}}{{e}_{1}}{{{\hat {a}}}_{1}}({{\zeta }_{1}} + {{\zeta }_{2}}) + \sin {{e}_{3}}{{{\hat {a}}}_{2}}({{\zeta }_{1}} - {{\zeta }_{2}}) + {{\zeta }^{{\text{T}}}}( - Y\hat {p} + u + \hat {\bar {\varepsilon }}) - {{\zeta }^{T}}Y\tilde {p} + {{\zeta }^{T}}\tilde {\bar {\varepsilon }} + \\ \, + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{{\text{T}}}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta = - {{k}_{1}}e_{1}^{2} - {{k}_{2}}\mathop {\sin }\nolimits^2 {{e}_{3}} + {{\zeta }^{{\text{T}}}}\left( {\left[ {\begin{array}{*{20}{c}} { - {{\gamma }_{1}}{{{\hat {a}}}_{1}}{{e}_{1}} + {{{\hat {a}}}_{2}}\sin {{e}_{3}}} \\ { - {{\gamma }_{1}}{{{\hat {a}}}_{1}}{{e}_{1}} - {{{\hat {a}}}_{2}}\sin {{e}_{3}}} \end{array}} \right] - Y\hat {p} + u + \hat {\bar {\varepsilon }}} \right) - \\ \, - {{\zeta }^{T}}Y\tilde {p} + {{\zeta }^{T}}\tilde {\bar {\varepsilon }} + {{{\tilde {p}}}^{{\text{T}}}}{{Z}^{{ - 1}}}\dot {\tilde {p}} + {{{\tilde {\bar {\varepsilon }}}}^{T}}{{K}^{{ - 1}}}\dot {\tilde {\bar {\varepsilon }}} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta . \\ \end{gathered} $Выберем законы управления для напряжений u1 и u2 и законы адаптации для неизвестных параметров $\hat {p}$ и $\hat {\bar {\varepsilon }}$ так, чтобы функция $\dot {V}$ была неположительно определенной, а именно,
(2.25)
$\left[ {\begin{array}{*{20}{c}} {{{u}_{1}}} \\ {{{u}_{2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {Y\hat {p} - \left[ {\begin{array}{*{20}{c}} { - {{\gamma }_{1}}{{{\hat {a}}}_{1}}{{e}_{1}} + {{{\hat {a}}}_{2}}\sin {{e}_{3}}} \\ { - {{\gamma }_{1}}{{{\hat {a}}}_{1}}{{e}_{1}} - {{{\hat {a}}}_{2}}\sin {{e}_{3}}} \end{array}} \right] - \left[ \begin{gathered} {{k}_{3}}{{\zeta }_{1}} \hfill \\ {{k}_{4}}{{\zeta }_{2}} \hfill \\ \end{gathered} \right] - \left[ \begin{gathered} {{{\hat {\bar {\varepsilon }}}}_{1}} \hfill \\ {{{\hat {\bar {\varepsilon }}}}_{2}} \hfill \\ \end{gathered} \right]} \end{array}} \right],$(2.26)
$\begin{gathered} \dot {\hat {p}} = - Z{{Y}^{{\text{T}}}}\zeta , \\ \dot {\hat {\bar {\varepsilon }}} = K\zeta , \\ \end{gathered} $(2.27)
$\dot {V} = - {{k}_{1}}e_{1}^{2} - {{k}_{2}}{{\sin }^{2}}{{e}_{3}} - {{k}_{3}}\zeta _{1}^{2} - {{k}_{4}}\zeta _{2}^{2} - {{\zeta }^{{\text{T}}}}\bar {\bar {C}}\zeta .$Матрица $\bar {\bar {C}}$ – положительно-определенная. Правая часть равенства (2.27) неположительна, поскольку неположительны все ее слагаемые, и, следовательно, $\dot {V} \leqslant 0$. Таким образом, функция V не возрастает вдоль любого решения системы уравнений (2.9)–(2.11). Будучи неотрицательной, функция V ограничена снизу и в силу своего невозрастания имеет конечный предел при $t \to \infty $ вдоль любого решения системы (2.9)–(2.11). Отсюда следует ограниченность переменных ${{e}_{1}}$, ${{e}_{2}}$, ${{e}_{3}}$, ${{a}_{1}} - {{\hat {a}}_{1}}$, ${{a}_{2}} - {{\hat {a}}_{2}}$. Поскольку ${{a}_{1}}$ и ${{a}_{2}}$ – постоянные параметры, хотя и не известные заранее, величины ${{\hat {a}}_{1}}$ и ${{\hat {a}}_{2}}$ также ограничены. Предположим, что функции ${{v}_{d}}(t)$ и ${{\omega }_{d}}(t)$, задающие программное движение, ограничены и непрерывно дифференцируемы. Тогда вторая производная $\ddot {V}$ функции V ограничена. Следовательно, функция $\dot {V}$ равномерно непрерывна и, по лемме Барбалата (Barbalat’s lemma) [12, 13], $\mathop {\lim }\limits_{t \to \infty } \dot {V} = 0$. Отсюда и из выражения (2.13) вытекает, что $e \to 0$ и $\zeta \to 0$ при $t \to \infty $ для (2.12), замкнутой построенным адаптивным управлением.
3. Численное моделирование. Для численного моделирования процесса управления мобильном роботом в соответствии с алгоритмом, описанным в предыдущем разделе, были выбраны следующие значения параметров.
Геометрические параметры робота:
(3.1)
$\begin{array}{*{20}{l}} {r = 0.105\;{\text{м}},\quad b = 0.18\;{\text{м}},\quad d = 0.1\;{\text{м}}.} \end{array}$Инерционные параметры робота:
(3.2)
$\begin{gathered} M = 13.4\;{\text{кг}},\quad m = 1.2\;{\text{кг}}, \\ I = 0.67\;{\text{кг}} \cdot {{{\text{м}}}^{2}},\quad {{A}_{w}} = 0.0066\;{\text{кг}} \cdot {{{\text{м}}}^{2}},\quad {{J}_{w}} = 0.0033\;{\text{кг}} \cdot {{{\text{м}}}^{2}}. \\ \end{gathered} $Предложенный алгоритм управления был реализован в среде MATLAB для модели робота с параметрами, приведенными выше. Результаты моделирования рассмотрены ниже. Все величины, использованные при моделировании, а также результаты этого моделирования представлены в единицах международной системы СИ. Для краткости размерности переменных и параметров в дальнейшем не указываются. При программном движении, которое должен отследить робот, центр оси ведущих колес (точка $O{\kern 1pt} '$) перемещается по окружности радиусом ${{R}_{c}} = 5$ с постоянной линейной скоростью ${{v}_{d}} = 0.5$; угловая скорость вращения робота при этом равна ${{\omega }_{d}} = 0.1$. В начале программного движения точка $O{\kern 1pt} '$ имеет нулевые координаты в неподвижной системе отсчета (${{x}_{d}} = 0,$ ${{y}_{d}} = 0$) и нулевой угол между продольной осью робота и осью x неподвижной системы координат (${{\theta }_{d}} = 0$). Пусть начальное положение робота и его ориентация в отличном от программного моделируемом движении задано следующим образом: x = 0, $y = - 0.6$, $\theta = 0.1$. Начальные значения оцениваемых параметров при этом определяются равенствами ${{\hat {a}}_{1}} = 0.15$, ${{\hat {a}}_{2}} = 0.1$, ${{\hat {p}}_{1}} = 0.1$, ${{\hat {p}}_{2}} = - 0.1$, ${{\hat {p}}_{3}} = 2$, ${{\hat {p}}_{4}} = 0.1$, ${{\hat {\bar {\varepsilon }}}_{1}} = - 1$, ${{\hat {\bar {\varepsilon }}}_{2}} = 0$, а настраиваемые параметры и матрицы законов управления – равенствами ${{k}_{1}} = 10$, ${{k}_{2}} = 1$, ${{\gamma }_{1}} = 5$, ${{\gamma }_{2}} = 0.01$, ${{\gamma }_{3}} = 0.05$, ${{k}_{3}} = 10$, ${{k}_{4}} = 10$, $Z = {\text{diag}}(0.002,0.002,0.002,0.002)$, $K = {\text{diag}}(2,2)$.
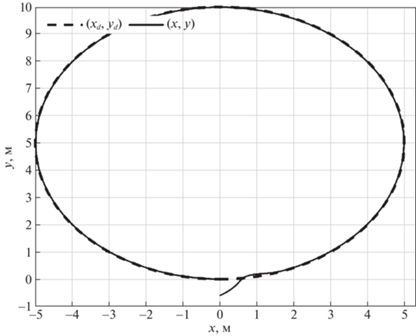
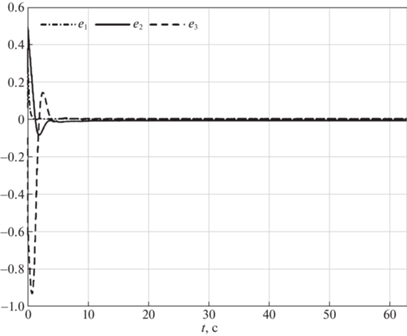
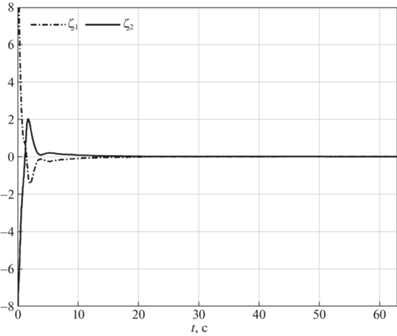
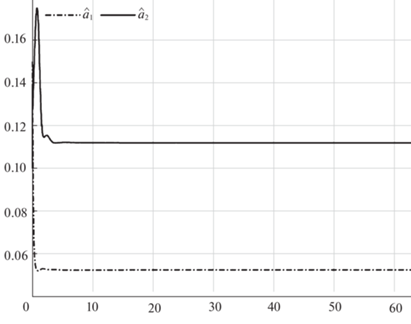
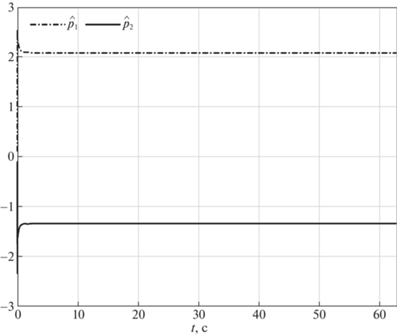
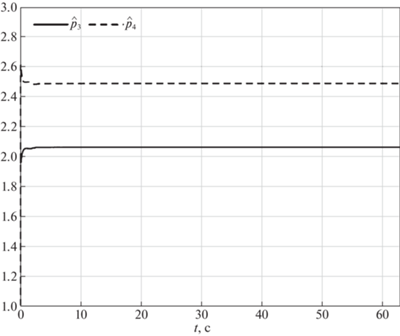
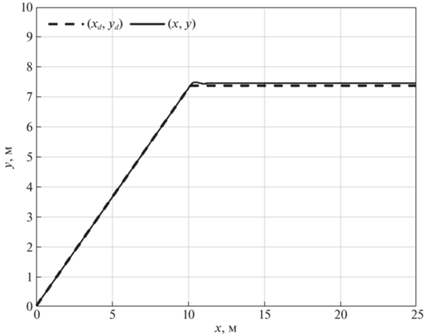
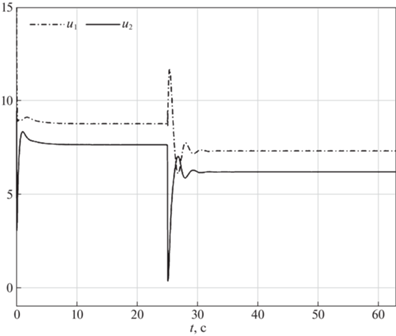
Поведение системы с предложенным алгоритмом управления иллюстрируется на рис. 4–12. На рис. 4 показаны координаты траектории точки $O{\kern 1pt} '$ в моделируемом движении (сплошная кривая) и в номинальном движении (штриховая кривая), а на рис. 5 и 6 изображены зависимости от времени рассогласования сигналов ${{e}_{1}},\;{{e}_{2}},\;{{e}_{3}}$ и $\zeta $ соответственно. Зависимости от времени параметров адаптации $\hat {a}$, $\hat {p}$ и $\hat {\bar {\varepsilon }}$ приведены на рис. 7–10. Из рис. 4 и 5 видно, что ошибки отслеживания роботом программного движения стремятся с течением времени к нулю. Погрешности скоростей также имеют значения, близкие к нулевым (рис. 6). Согласно рис. 7–10, оцениваемые параметры ограничены. На рис. 11 и 12 представлены результаты моделирования отслеживания роботом движения вдоль траектории, состоящей из двух прямолинейных отрезков. Этот численный эксперимент проведен с целью демонстрации влияния неидеальностей (трения) в приводах. Из рис. 12 видно, что при движении вдоль прямолинейных отрезков входные напряжения на приводах правого и левого колес различны. Это различие позволяет выровнять скорости вращения колес.
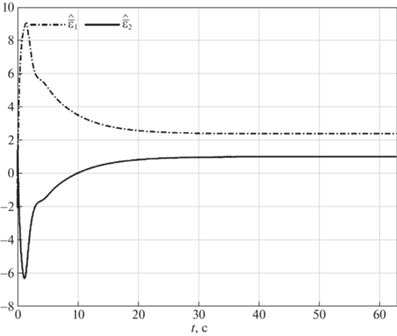
Рис. 10.
Оцениваемые параметры ${{\hat {\bar {\varepsilon }}}_{1}}$ и ${{\hat {\bar {\varepsilon }}}_{2}}$
Заключение. Предложен алгоритм адаптивного управления движением колесного робота с двумя ведущими колесами, расположенными на общей оси. Алгоритм базируется на динамической модели робота и позволяет компенсировать не только неопределенность его геометрических и инерционных параметров, но и неопределенность, связанную с неидеальностью приводов. Моделирование показывает, что данный алгоритм обеспечивает высокую точность отслеживания роботом заданных программных движений.
Список литературы
Нунупаров А.М., Чащухин В.Г. Система управления робота вертикального перемещения с аэродинамическим прижатием // Изв. РАН. ТиСУ. 2020. № 2. С. 168–176.
Chashchukhin V.G. Orientation System of the Aerodynamically Adhesive Wall Climbing Robot // Extreme Robotics. 2019. V. 1. № 1. P. 145–148.
Чащухин В.Г. Исследование параметров движения робота со скользящим уплотнением // Вестн. Нижегородск. ун-та им. Н.И. Лобачевского. 2011. № 4 (2). С. 347–349.
Wang H., Fukao T., Adachi N. An Adaptive Tracking Control Approach for Nonholonomic Mobile Robot // IFAC Proceedings. 1999. V. 32. № 2. P. 8184–8189.
Fukao T., Nakagawa H., Adachi N. Adaptive Tracking Control of a Nonholonomic Mobile Robot // IEEE Transactions on Robotics and Automation. 2000. V. 16. № 5. P. 609–615.
Pourboghrat F., Karlsson M.P. Adaptive Control of Dynamic Mobile Robots with Nonholonomic Constraints // Computers and Electrical Engineering. 2002. V. 28. № 4. P. 241–253.
Koubaa Y., Boukattaya M., Dammak T. An Adaptive Control for Uncertain Mobile Robot Considering Skidding and Slipping Effects // 5th Intern. Conf. on Systems and Control (ICSC). Marrakesh, 2016. P. 13–19.
Wu J., Xu G., Yin Z. Robust Adaptive Control for a Nonholonomic Mobile Robot with Unknown Parameters // J. Control Theory Appl. 2009. V. 7. P. 212–215.
Ye J. Adaptive Control of Nonlinear PID-based Analog Neural Networks for a Nonholonomic Mobile Robot // Neurocomputing. 2008. V. 71. P. 1561–1565.
Canigur E., Ozkan M. Model Reference Adaptive Control of a Nonholonomic Wheeled Mobile Robot for Trajectory Tracking // Intern. Sympos. on Innovations in Intelligent Systems and Applications. Trabzon, 2012. P. 1–5.
Kanayama Y., Kimura Y., Miyazaki F., Noguchi T. A Stable Tracking Control Method for an Autonomous Mobile Robot // Proc. IEEE Intern. Conf. on Robotics and Automation. V. 1. Cincinnati, 1990. P. 384–389.
Slotine J.-J. E., Li W. Applied Nonlinear Control. New Jersey: Prentice-Hall, Inc., 1991.
Astrom K.J., Wittenmark B. Adaptive Control. New Jersey: Pearson Education, Inc., 2006.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления