Известия РАН. Теория и системы управления, 2022, № 5, стр. 152-161

Введение. Мобильные роботы, перемещающиеся в сопротивляющихся средах за счет движения внутренних масс, активно разрабатываются и исследуются в научной литературе. Такие устройства, в частности, предназначены для функционирования в агрессивных средах. Рассматриваются системы как с переменной, так и с неизменяемой геометрией [1–3]. Большим разнообразием отличаются и конструкции корпуса, и схемы организации перемещения внутренних масс [4]. Исследуется перемещение систем, управляемых движением внутренних тел, по твердой поверхности и в жидкости. При этом используются разнообразные математические модели внешних сил [5–8]. Существенно отличаются случаи движения по прямой, по плоскости и в пространстве [9, 10]. Рассматриваются различные задачи управления: ориентация объекта в пространстве, движение вдоль заданной траектории и др. (в ряде работ дополнительно исследуются задачи оптимизации) [6, 11–13].

Разнообразие направлений развития мобильных роботов с подвижными внутренними телами исключительно велико. В настоящей работе остановимся подробнее на одном из них. Будем рассматривать робот с возможностью изменения геометрии (и отдельно проведем сравнение со случаем твердотельного корпуса). Корпус состоит из n звеньев $(n = 1...3)$, соединенных пассивными шарнирами. Аппарат может перемещаться в горизонтальной плоскости. Таким образом, робот относится к змееподобным аппаратам, по конструкции корпуса близким к [14–18], но отличается отсутствием управления в межзвенных шарнирах. Управление осуществляется только посредством одного внутреннего маховика, установленного в головном звене. Ближайшие аналоги – аппараты с двумя/тремя звеньями и одним внутренним маховиком, предложенные и изученные в [19–21]. Подобные однозвенные аппараты исследуются в [22–24].

Модель внешнего воздействия, примененная в работе, принципиально отличается от вышеуказанных статей: рассматривается движение по шероховатой плоскости при наличии анизотропного сухого трения, в то время как в [14, 15] сухое трение изотропно, в [16–20, 22, 23] механическая система является неголономной (по крайней мере, одна из опор представляет собой конек Чаплыгина), в [24] в точке опоры действует анизотропное вязкое трение, а в [21] аппарат движется в жидкости. Можно отметить, что для реальных змей действительно имеет место анизотропия трения при движении [25].

В работе ставится задача формирования установившегося режима, при котором происходит продвижение корпуса в заданном направлении. Проводится параметрический анализ с целью выбора характеристик конструкции (распределения масс между элементами, длин звеньев, коэффициентов жесткости межзвенных пружин), а также параметров закона управления (при наличии фиксированного ограничения на максимальную величину управляющего момента), обеспечивающих как можно более высокую скорость продвижения. При этом сравниваются три конфигурации: аппарат с корпусом неизменяемой геометрии, двухзвенный робот, трехзвенный робот.

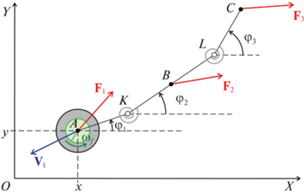
1. Описание системы и постановка задачи. Рассмотрим трехзвенный механизм AK‑KBL‑LC, расположенный в горизонтальной плоскости (рис. 1). Звенья механизма соединены в точках K и L цилиндрическими шарнирами, $AK = KB = BL = LC = r$. Головное звено AK имеет массу ${{m}_{1}}$, центральный момент инерции ${{J}_{1}}$, центр масс звена расположен в точке A. Звено KL имеет массу ${{m}_{2}}$, считаем, что вся масса сосредоточена в точке B. Звено LC имеет массу ${{m}_{3}}$, вся масса сосредоточена в точке C. На головном звене AK в точке A установлен маховик, имеющий массу m₀ и центральный момент инерции ${{J}_{0}}$. Маховик приводится во вращение вокруг вертикальной оси A мотором, статор которого является частью тела AK.

Положение механической системы на неподвижной плоскости OXY задается шестью обобщенными координатами, в качестве которых выберем координаты x и y точки A, углы ${{\varphi }_{i}}$, $i = 1...3$, отклонения звеньев AK, KL, LC от оси OX, угол поворота маховика относительно оси OX (циклическая координата). Здесь и далее индекс i принимает значения 1, 2 и 3, что соответствует первому AK, второму KL и третьему LC звеньям. Обозначим через ${{\omega }_{i}}$ угловые скорости звеньев, ${{\omega }_{f}}$ – угловую скорость маховика относительно первого звена; ${{{\mathbf{V}}}_{i}}$ – векторы скоростей точек A, B, C; ${{V}_{i}}$ – их модули.

Кинетическая энергия системы имеет следующий вид:

В шарнирах K и L установлены спиральные пружины жесткости ${{c}_{1}}$ и ${{c}_{2}}$ соответственно. Пружины находятся в ненапряженном состоянии, когда все точки A, K, B, L, C расположены на одной прямой. Установка пружин в шарнирах для роботов, управляемых перемещением внутренних тел, предложена, например, в [20, 26, 27], для мехатронных устройств преобразования энергии – в [28]. Целесообразность использования пружин обсуждается далее при параметрическом анализе системы. Потенциальная энергия имеет вид

Звенья робота опираются на горизонтальную плоскость в точках A, B, C. В каждой точке опоры действует анизотропное сухое трение ${{{\mathbf{F}}}_{i}}$. Анизотропия связана со свойствами опор, а не поверхности, по которой движется робот. Существуют различные подходы к описанию анизотропного трения [29–33], в данном случае используем модель [29–31]. В соответствии с указанным подходом вводится понятие тензора трения, описывающее зависимость коэффициента сухого трения от направления движения. Пусть ${{{\mathbf{e}}}_{\xi }},{{{\mathbf{e}}}_{\eta }}$ – орты главных осей тензора $\Theta $ трения. Тогда при движении вдоль ${{{\mathbf{e}}}_{\xi }}$ сила трения описывается классическим выражением для сухого трения Кулона с некоторым коэффициентом трения ${{\mu }_{\xi }}$ аналогично для ${{{\mathbf{e}}}_{\eta }}$. При движении в произвольном направлении проекции силы трения F на главные оси тензора трения определяется выражением

где ${{V}_{\xi }},\,\,{{V}_{\eta }}$ – проекции вектора ${\mathbf{V}}$ скорости точки контакта на главные оси тензора трения, N – величина нормальной реакции опоры.

Анизотропию трения можно реализовать на практике, например, используя в качестве опоры жесткосоединенное со звеном (заклиненное) колесо, протектор которого имеет специальный рисунок [30]. Далее для краткости опору с анизотропным трением будем называть “колесо”.

Пусть для i-го звена направления вдоль и поперек звена являются главными для тензора трения. Проекции векторов на эти направления будем обозначать индексами $\xi $ и $\eta $ соответственно, а коэффициенты трения по этим направлениям – ${{\mu }_{{i\xi }}}$ и ${{\mu }_{{i\eta }}} \geqslant {{\mu }_{{i\xi }}}$. Тогда

Момент U, формируемый мотором, – единственное управление, присутствующее в системе. Поскольку рассматриваемая система обладает шестью степенями свободы, имеет место существенный дефицит управляющих воздействий [34, 35]. Считаем, что момент U ограничен по абсолютной величине значением ${{U}_{{\max }}}$.

В качестве основной задачи управления будем рассматривать продвижение робота в направлении, противоположном оси OX. Точнее говоря, цель управления – обеспечить наличие притягивающего установившегося движения робота, при котором средняя (по времени на большом промежутке времени) скорость точки A (а следовательно, и любой другой точки) имеет отрицательную проекцию на ось OX, среднее отклонение точки A от оси OX нулевое, и не происходит “залипания” точек контакта, т.е. их скорости не обращаются в ноль.

2. Уравнения движения. Уравнения, описывающие перемещение аппарата в предположении, что скорости точек опоры ненулевые, запишем в форме уравнений Лагранжа второго рода:

Выражения для кинетической и потенциальной энергий, а также для компонент сил трения приведены выше. Обобщенные силы ${{Q}_{i}}$, соответствующие угловым координатам ${{\varphi }_{i}}$, имеют вид

Управление будем строить следующим образом:

Здесь ${{w}_{0}}$ – частота вынуждающего воздействия, k₀ и k₁ – коэффициенты обратной связи, которые введены для того, чтобы обеспечить нулевое значение среднего отклонения курса от направления против оси OX.

3. Дополнительные предположения и методы решения задачи. В ходе исследования будем считать, что общие габариты робота, параметры маховика и характеристики двигателя фиксированы. Пусть полная масса робота 0.5 кг, масса маховика ${{m}_{0}} = 0.05$ кг, момент инерции маховика ${{J}_{0}} = 0.0005$ кгм², масса первого звена ${{m}_{1}} \geqslant 0.05$ кг, момент инерции первого звена ${{J}_{1}} = 0.002$ кгм², суммарная длина звеньев составляет $4r = 0.2$ м, максимальный модуль управляющего момента ${{U}_{{\max }}} = 0.1$ Н.

Найдем значения коэффициентов ${{w}_{0}}$, ${{k}_{0}}$, ${{k}_{1}}$ закона управления, а также параметры ${{m}_{1}}$, ${{m}_{2}}$, ${{c}_{1}}$, ${{c}_{2}}$ конструкции робота, которые обеспечивают формирование установившегося направленного движения. Проанализируем влияние указанных параметров на среднюю скорость центра масс на таком режиме. При этом будем рассматривать три конфигурации: одно-, двух- и трехзвенный робот. Отметим, что варьирование величин ${{c}_{1}}$, ${{c}_{2}}$ возможно не во всех конфигурациях.

Все описанные далее результаты параметрического анализа получены путем прямого численного интегрирования уравнений движения с различными параметрами и начальными условиями. Поиск аттрактора системы (2.1) выполнялся методом установления. Среди направлений дальнейшего исследования можно выделить применение в данной задаче численно-аналитических методов поиска установившихся решений и исследования их устойчивости, например [36–40].

4. Случай однозвенного робота. В [22] рассмотрено движение саней Чаплыгина с установленным на них управляемым внутренним маховиком и продемонстрировано наличие периодического режима движения, безреверсного по отношению к основному направлению перемещения (т.е. знак проекции скорости центра масс на заданное направление не меняется). Естественно ожидать, что подобный периодический режим существует и для аппарата, в котором конек Чаплыгина заменен на опору с анизотропным трением. В предложенной выше модели такой случай реализуется при следующих условиях на параметры: ${{c}_{1}} = {{c}_{2}} \to \infty $, ${{m}_{2}} = 0$, ${{\mu }_{{1\xi }}} = {{\mu }_{{1\eta }}} = {{\mu }_{{3\xi }}} = \varepsilon \ll 1$, ${{\mu }_{{3\eta }}} \approx 1$. Иными словами, робот представляет собой одно твердое тело, опирающееся на плоскость в точках A и C, причем в точке A трение изотропно, а в точке C – нет. Предположим, что реализуются следующие значения коэффициентов трения: $\varepsilon = 0.025$ (при скольжении стали по льду или некоторым видам пластика), ${{\mu }_{{3\eta }}} = 0.9$ (за счет нанесения на опору микронасечек).

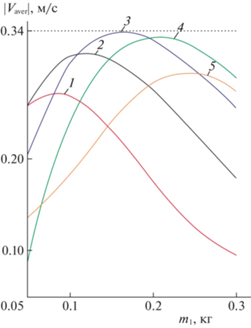
Обозначим модуль средней скорости центра масс на установившемся движении вдоль оси абсцисс через $\left| {{{V}_{{aver}}}} \right|$. На рис. 2 приведены значения $\left| {{{V}_{{aver}}}} \right|$ в зависимости от массы ${{m}_{1}}$ первого звена при различных значениях частоты ${{w}_{0}}$ вынуждающего воздействия. Все значения получены при коэффициентах обратной связи ${{k}_{0}} = - 0.1$ Н, ${{k}_{1}} = 0.1$ Нм. При значениях параметров ${{m}_{1}} \approx 0.15$ кг, ${{w}_{0}} \approx 0.6$ с^–1, на которых достигается максимум $\left| {V_{{aver}}^{{\max }}} \right| \approx 0.34$ м/c, увеличение/уменьшение коэффициентов k₀, k₁, вплоть до двукратного, практически не меняет среднюю скорость перемещения аппарата.

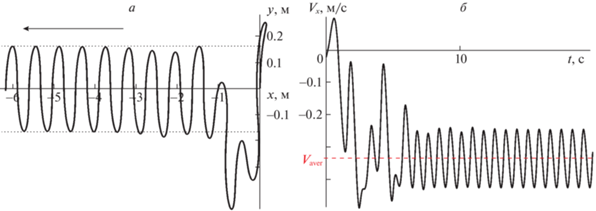
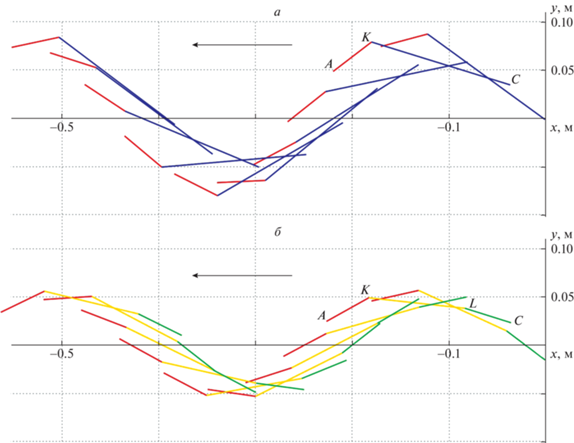
Пример траектории точки A в процессе выхода на установившийся режим при ${{m}_{1}} = 0.15$ кг, ${{w}_{0}} = 0.6$ с^–1, ${{k}_{0}} = - 0.1$ Н, ${{k}_{1}} = 0.1$ Нм приведен на рис. 3, a, начальные значения всех переменных нулевые, кроме $\dot {x}(0)$, $\dot {x}(0) = - 0.02$ м/c. Стрелкой на рисунке показано направление движения. На установившемся режиме знак проекции на ось OX скорости ${{V}_{x}}$ центра масс не меняется, т.е. движение безреверсное (рис. 3, б).

Ширина полосы, необходимой при вышеуказанных параметрах для реализации установившегося движения робота (отрезка АС), составляет около 0.33 м.

В случае, когда в точке А вместо опоры с небольшим изотропным трением установлено “колесо”, аналогичное C (т.е. ${{\mu }_{{1\eta }}} = 0.9$), не удалось найти значения параметров, при которых возможно установившееся направленное продвижение однозвенного робота. В связи с этим отметим, что в “предельном” случае двух коньков Чаплыгина, ориентированных вдоль звена AC, корпус совершает только прямолинейное движение, исключены повороты аппарата, и тем самым нивелируется возможность применения внутреннего маховика для управления.

5. Случай двухзвенного робота. Пусть ${{c}_{2}} \to \infty $, ${{m}_{2}} = 0$. Это соответствует двухзвенному роботу, в котором шарнир (с пружиной) имеется только в точке K. В случае, когда “колесо” установлено только в точке C, а в точке A – опора с небольшим изотропным трением (${{\mu }_{{1\xi }}} = {{\mu }_{{1\eta }}} = {{\mu }_{{3\xi }}} = 0.025$, ${{\mu }_{{3\eta }}} = 0.9$), за счет выбора коэффициента ${{c}_{1}}$ не удалось увеличить максимальную скорость $\left| {{{V}_{{aver}}}} \right|$ по сравнению со значением $\left| {V_{{aver}}^{{\max }}} \right| \approx 0.34$ м/c, полученным для однозвенного робота.

Рассмотрим подробно случай, когда каждая опора (А и С) двухзвенного аппарата представляет собой “колесо”, характеризующееся следующими коэффициентами трения: ${{\mu }_{{1\xi }}} = {{\mu }_{{3\xi }}} = 0.025$, ${{\mu }_{{1\eta }}} = {{\mu }_{{3\eta }}}$ = 0.9. В отличие от однозвенного аппарата, для двухзвенного, благодаря наличию дополнительной степени свободы, такой выбор опор, вообще говоря, не является препятствием к направленному перемещению.

На рис. 4 проиллюстрировано влияние на скорость $\left| {{{V}_{{aver}}}} \right|$ коэффициента ${{c}_{1}}$ жесткости пружины при ${{m}_{1}} = 0.15$ кг, ${{k}_{0}} = - 0.1$ Н, ${{k}_{1}} = 0.1$ Нм и при различных значениях частоты ${{w}_{0}}$ вынуждающего воздействия. При этом удалось реализовать скорость $\left| {V_{{aver}}^{{}}} \right| \approx $ 0.43 м/с. Таким образом, добавление пассивного шарнира, оснащенного пружиной, позволяет увеличить скорость продвижения аппарата более чем на 25%. При этом предпочтительные (с позиций максимизации средней скорости) распределение масс, частота вынуждающего воздействия и тип передней опоры отличаются от случая однозвенного робота.

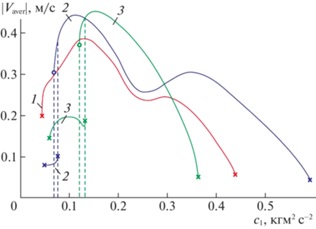
Крестиками на рис. 4 отмечены точки, соответствующие значениям параметров, при которых периодическая траектория системы (2.1) разрушается из-за того, что скорость одной из опор в некоторой точке траектории обращается в нуль. Кружочками обозначены точки, где притягивающее периодическое решение перестает существовать, но скорости опор при этом отделены от нуля: возможно, в этом случае притягивающая траектория разрушается, выходя на некоторое неустойчивое многообразие.

При больших значениях коэффициента жесткости периодические решения системы (2.1) с ненулевым значением $\left| {{{V}_{{aver}}}} \right|$ не обнаружены. Этого следовало ожидать с учетом описанного выше случая однозвенного робота с двумя “колесами”. Интересно отметить, что при относительно малых значениях c₁ режим направленного продвижения также не выявлен. В некотором диапазоне параметров, отвечающих за распределение масс и управление, наблюдается более одного локального максимума скорости $\left| {{{V}_{{aver}}}} \right|$ в зависимости от коэффициента жесткости.

Интересно, что при некоторых значениях параметров существуют единовременно как минимум два притягивающих периодических решения системы (2.1). Границы соответствующих интервалов по параметру ${{c}_{1}}$ отмечены на рис. 4 пунктирными линиями. Не исключено наличие большего числа ветвей бифуркационной диаграммы ${{V}_{{aver}}}({{c}_{1}})$, которые не были обнаружены в ходе прямого численного интегрирования системы (2.1) ввиду узких областей притяжения или неустойчивости соответствующих траекторий.

Пример изменения скорости центра масс при переходе на установившийся режим для набора параметров ${{m}_{1}} = 0.15$ кг, ${{w}_{0}} = 1.1$ с^‑1, ${{c}_{1}} = 0.1$ кгм² c^–2, ${{k}_{0}} = - 0.1$ Н, ${{k}_{1}} = 0.1$ Нм приведен на рис. 5 (начальные значения всех переменных нулевые, кроме $\dot {x}(0) = - 0.01$ м/c). Средняя скорость на режиме составила $\left| {{{V}_{{aver}}}} \right| \approx $ 0.42 м/с.

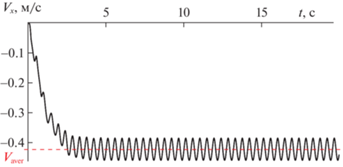
На рис. 6, а показаны положения звеньев робота на полученном установившемся режиме в моменты времени, интервалы между которыми составляют 0.1 с. Масштабы по осям абсцисс и ординат одинаковы. Стрелкой показано направление перемещения.

Отметим, что для двухзвенного робота ширина полосы, необходимой для продвижения в заданном направлении, равна около 0.18 м (что на 45% меньше, чем для однозвенного при максимуме $\left| {{{V}_{{aver}}}} \right|$). Затраты мощности на управление при этом составляют примерно 0.22 Вт (вычисляются как произведение управляющего момента U и относительной угловой скорости маховика ${{\omega }_{f}}$, осредненное по времени на периоде).

6. Трехзвенный робот. Перейдем к исследованию трехзвенного робота. Параметрический анализ системы показывает, что добавление второго шарнира не приводит к существенному увеличению скорости аппарата на установившемся режиме, однако позволяет уменьшить амплитуды отклонений точек корпуса от прямой OX. Для примера рассмотрим случай трехзвенного робота со следующими значениями параметров: ${{m}_{1}} = 0.2$ кг, ${{m}_{3}} = 0.25$ кг, ${{m}_{2}} = 0$, ${{c}_{1}} = {{c}_{2}} = 0.15$ кгм² c^–2, ${{w}_{0}} = 1.2$ с^–1, ${{k}_{0}} = - 0.1$ Н, ${{k}_{1}} = 0.1$ Нм, ${{\mu }_{{1\xi }}} = {{\mu }_{{3\xi }}} = 0.025$, ${{\mu }_{{1\eta }}} = {{\mu }_{{3\eta }}} = 0.9$. Средняя скорость установившегося движения составляет 0.43 м/c. На рис. 6, б приведены положения робота на плоскости в процессе движения по установившейся траектории. Интервалы между моментами времени равны 0.1 с, масштаб тот же, что и на рис. 6, а. Полоса на плоскости, необходимая для продвижения трехзвенного робота, имеет ширину около 0.12 м, т.е. примерно на 30% уже, чем в случае двухзвенного аппарата (рис. 6, а).

Затраты мощности на управление на установившемся режиме – примерно 0.21 Вт.

На рис. 7 проиллюстрировано влияние распределения масс на $\left| {{{V}_{{aver}}}} \right|$ при приведенных выше значениях прочих параметров. Наибольшая средняя скорость получена в случае, когда масса промежуточного звена KL нулевая, а масса третьего звена LC равна массе первого звена вместе с маховиком (на рис. 7 – это пересечение кривой 4 с осью ординат).

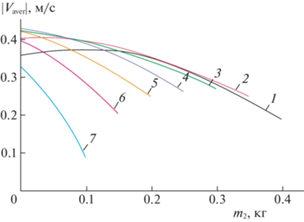
Отметим, что средняя скорость достаточно чувствительна к изменению коэффициента трения ${{\mu }_{{1\xi }}} = {{\mu }_{{3\xi }}} = \varepsilon $ в направлении вдоль звена. Так, при увеличении $\varepsilon $ до 0.05 средняя скорость снижается до 0.27 м/c, при $\varepsilon = 0.06$ она составляет 0.16 м/с, а при $\varepsilon \geqslant 0.07$ режим направленного продвижения не удалось обнаружить.

7. Основные результаты. Рассмотрено движение одно-, двух- и трехзвенного робота при наличии сухого анизотропного трения: коэффициент трения вдоль звена меньше, чем поперек звена. Построено управление внутренним маховиком, обеспечивающее продвижение в заданном направлении.

Показано, что в рамках предложенной модели добавление дополнительных степеней свободы, а именно увеличение числа звеньев при наличии пружин в соединительных шарнирах, позволяет увеличить скорость направленного продвижения робота и уменьшить амплитуды колебаний точек корпуса. В случае, когда корпус не является одним твердым телом, наличие анизотропного трения в передней опорной точке (точнее, увеличение коэффициента трения в направлении поперек звена) способствует значительному увеличению средней скорости движения на установившемся режиме.

Для двухзвенного робота обнаружены диапазоны значений параметров, при которых в системе (2.1) одновременно существуют два аттрактора, соответствующие продвижению аппарата в заданном направлении. Установлено, что для трехзвенного робота в широком диапазоне параметров максимальные значения средней скорости установившегося движения достигаются при нулевой массе промежуточного звена и одинаковых массах первого звена с маховиком и последнего звена.

Заключение. Построена и исследована модель робота-змеи, управляемого движением одного внутреннего маховика, в предположении, что в точках опоры действует сухое анизотропное трение: коэффициент трения поперек звена больше, чем вдоль звена. Построено управление, обеспечивающее продвижение центра масс аппарата, безреверсное по отношению к определенной прямой. Проведено сравнение трех конфигураций – с одним, двумя и тремя звеньями – по критериям максимальной средней скорости установившегося движения и ширины полосы, необходимой для продвижения в заданном направлении. По указанным показателям наиболее предпочтительной оказалась конфигурация с тремя звеньями.