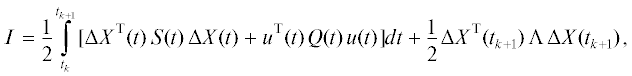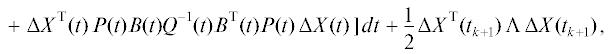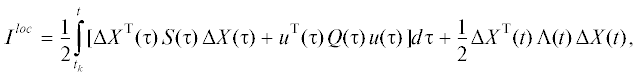Известия РАН. Теория и системы управления, 2022, № 5, стр. 50-75
МУЛЬТИАГЕНТНЫЕ АЛГОРИТМЫ ОПТИМИЗАЦИИ ПУЧКОВ ТРАЕКТОРИЙ ДЕТЕРМИНИРОВАННЫХ СИСТЕМ С НЕПОЛНОЙ МГНОВЕННОЙ ОБРАТНОЙ СВЯЗЬЮ
М. М. С. Каранэ a, А. В. Пантелеев a, *
a МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: avpanteleev@inbox.ru
Поступила в редакцию 20.02.2022
После доработки 19.05.2022
Принята к публикации 30.05.2022
- EDN: TQPEPK
- DOI: 10.31857/S0002338822050080
Аннотация
Рассматривается задача поиска оптимального управления пучками траекторий непрерывных детерминированных систем с неполной обратной связью. К данному классу задач относятся проблемы управления, в которых имеется неопределенность задания начальных условий в виде некоторого множества, а также предполагается, что доступна мгновенная информация только о части координат вектора состояния системы, которая не накапливается. Описано несколько способов параметризации задачи на основе разложений по различным системам базисных функций, применяемых в спектральном методе, включая нестационарные косинусоиды, многочлены Лежандра, финитные функции нулевого, первого, второго и третьего порядков, радиально-базисные функции, а также разложение по полиномам Чебышева, используемое в псевдоспектральных методах. Предложено решать полученную в результате преобразований задачу параметрической оптимизации с помощью двух метаэвристических алгоритмов, в которых реализуются изложенные принципы формирования гибридных мультиагентных алгоритмов, применяя разнообразные процедуры интерполяционного поиска и линейные регуляторы для управления движением агентов. Приведено решение двух модельных примеров, для которых был применен разработанный алгоритм поиска оптимального управления пучками траекторий при наличии неполной информации о векторе состояния, а также прикладная задача управления спутником.
Введение. Предлагается алгоритм решения задачи синтеза оптимального управления нелинейными непрерывными детерминированными динамическими системами. Предполагается, что в начальный момент состояние системы конкретно не задано, а задается множество начальных состояний. Таким образом, это множество при известном законе управления порождает пучок (ансамбль) траекторий. Каждая траектория соответствует одному из начальных состояний из заданного множества. Помимо этого при синтезе оптимального управления учитывается неполнота получаемой информации о координатах вектора состояния. Предполагается, что система управления в текущий момент времени получает мгновенную информацию только о части координат вектора состояния, в то время как значения остальных координат неизвестны. Этот факт является важной особенностью рассматриваемой задачи, так как позволяет решать прикладные задачи, в которых в силу свойств измерительной системы достоверная информация о части координат не доступна, а попытки найти оценки посредством синтеза наблюдателей состояния или фильтров не приводят к желаемому результату. Кроме того, возможны ситуации, когда в процессе управления информация о каких-либо координатах вектора состояния может не поступить в силу технических проблем, и наличие законов управления, зависящих от разного набора координат, может оказаться полезным для обеспечения устойчивости функционирования управляющего комплекса.
В статье рассматривается задача поиска оптимального в среднем управления пучками траекторий непрерывных детерминированных систем с частичной информированностью о векторе состояния. Описано несколько случаев информированности о векторе состояний:
1) информация о векторе состояния отсутствует (ищется оптимальное программное управление);
2) известна только часть координат вектора состояния (ищется управление с неполной обратной связью по известным координатам вектора состояния);
3) известна информация обо всех координатах (ищется управление с полной обратной связью).
Задачи управления пучками траекторий изучались в работах [1–3]. При этом рассматривалась задача нахождения оптимального программного управления для линейных систем, а также решение задач высокой размерности, в которых движение пучка описывается через эллипсоидальные траектории. Для нелинейных систем, определяющих динамику пучков заряженных частиц, задача исследовалась в публикациях [4–8]. В этих работах предложены необходимые условия оптимальности, как программного управления, так и управления с неполной и полной обратной связью. В качестве численных методов применялись градиентные процедуры, в общем случае позволяющие найти локальный экстремум.
В [9] для описания поведения совокупности траекторий при неопределенной информации о начальном состоянии использовался метод эллипсоидов, а в [5, 6, 10–13] – уравнение Лиувилля (уравнение переноса). В [13] сформулированы достаточные условия оптимальности и получены соотношения для нахождения оптимального управления с неполной обратной связью. В [14–16] получены необходимые условия оптимальности для нахождения оптимального в среднем и оптимального гарантирующего программного и позиционного управления пучками траекторий для различных классов систем [14–16].
В [17–20] предложены различные способы решения задачи управления пучками траекторий с помощью перехода к задаче параметрической оптимизации и применения методов поиска экстремума функций. В качестве методов оптимизации использовались интервальные методы, меметические алгоритмы, метод, имитирующий поведение стаи серых волков. Они относятся к метаэвристическим алгоритмам оптимизации, получившим достаточно широкое распространение при решении прикладных задач в разных областях науки и техники [21–30]. Среди метаэвристических алгоритмов можно выделить группы эволюционных и мультистартовых методов, биоинспирированных алгоритмов, методов роевого интеллекта и имитирующих физические процессы, мультиагентных методов. Деление на перечисленные группы является условным, отражая основные идеи, используемые в алгоритмах. В данной работе развиваются мультиагентные алгоритмы, подтвердившие свою эффективность при решении задач оптимизации технических систем и задачах нахождения оптимального программного управления траекториями детерминированных динамических систем [31–33]. На каждой итерации они порождают множество решений (агентов), над которыми проводятся определенные операции, ведущие к результату – достижению окрестности экстремума заданной целевой функции. Сходимость метаэвристических алгоритмов, в том числе и мультиагентных, как правило, не может быть доказана, но они достаточно просты в применении, имеют невысокую вычислительную сложность и позволяют получить результаты хорошего качества за разумное вычислительное время.
В работе изложены принципы формирования мультиагентных алгоритмов, которые реализованы в двух предложенных авторами мультиагентных алгоритмах [34]: алгоритме интерполяционного поиска и алгоритме, основанном на использовании линейных регуляторов управления движением агентов. Эти алгоритмы были применены как в типовых общепринятых задачах оптимизации функций многих переменных, так и в задачах поиска программного управления. Они относятся к гибридным, так как содержат различные эвристики, доказавшие свою эффективность в рамках различных метаэвристических методов, таких, как: самоорганизующийся миграционный алгоритм [35], метод рассеивания [36], методы, имитирующие поведение стаи лягушек [37, 38], стаи криля [39] и распространение сорняков [40], метод роевого интеллекта [41]. Авторами предложено использование кривых Безье, В-сплайнов, кривых Катмулла–Рома для реализации различных режимов в процедуре интерполяционного поиска, а также линейных регуляторов четырех различных типов при управлении движением агентов.
В статье применяется прямой подход к решению задачи, а также параметрическая оптимизация закона управления. Предлагается искать управление в виде функции насыщения, которая гарантирует выполнение параллелепипедных ограничений, наложенных на управление, с помощью разложения по системе базисных функций. В качестве систем базисных функций могут применяться используемые в спектральном методе, включая нестационарные косинусоиды, многочлены Лежандра, финитные функции нулевого, первого, второго и третьего порядков, радиально-базисные функции [42–44], а также разложение по полиномам Чебышева, которое часто употребляется в псевдоспектральных методах [45, 46]. Количество элементов в каждой из базисных систем входит в число неизвестных параметров, как и неизвестные коэффициенты разложений. Таким образом, ставится задача оптимизации с целочисленно-непрерывными переменными, для которой предложена последовательная процедура, включающая линейный поиск по ограниченным целочисленным переменным. За ними следует процесс нахождения коэффициентов разложения с помощью двух мультиагентных метаэвристических алгоритмов оптимизации.
Предложенный подход иллюстрируется на решении двух модельных примеров, для которых ранее находилось оптимальное программное управление при фиксированном начальном состоянии [47] и задаче стабилизации спутника [48].
1. Постановка задачи. Поведение нелинейной непрерывной детерминированной модели объекта управления описывается уравнением
где x – вектор состояния системы, $x \in {{R}^{n}}$; t – непрерывное время, $t \in T = [{{t}_{0}};{{t}_{f}}]$, моменты t0 начала процесса и tf окончания процесса управления считаются заданными; u – вектор управления, $u = {{({{u}_{1}},...,{{u}_{q}})}^{{\text{T}}}} \in U(t) \subseteq {{R}^{q}}$; $U(t)$ – множество допустимых значений управления, представляющее собой прямое произведение отрезков $[{{a}_{j}}(t),{{b}_{j}}(t)]$, $j = \overline {1,q} $; $f(t,x,u) = {{({{f}_{1}}(t,x,u),...,{{f}_{n}}(t,x,u))}^{{\text{T}}}}$ – непрерывно дифференцируемая вектор-функция.Начальные условия заданы компактным множеством $\Omega $ положительной меры с кусочно-гладкой границей:
где множество $\Omega $ характеризует неопределенность задания начальных условий.Предполагается, что при управлении используется информация о времени $t$ и о части координат вектора состояния x (без ограничения общности считается, что это первые m координат). Таким образом, о компонентах вектора ${{x}^{1}} \in {{R}^{m}}$ известна текущая информация, а о компонентах вектора ${{x}^{2}} \in {{R}^{{n - m}}}$ она отсутствует, при этом $x = ({{x}^{1}},{{x}^{2}}) \in {{R}^{n}}$, $m \in \{ \overline {0,n} \} $. Если m = 0, информация о векторе состояния отсутствует, а если m = n, то имеется полная информация о векторе состояния.
Замечание. Если заданы уравнения измерительной системы вида
где $h(t,x)$ – непрерывно дифференцируемая функция по всем переменным, то с учетом (1.1) можно записать дифференциальное уравнениеТогда полученное уравнение вместе с уравнением (1.1) описывают динамическую систему, которую характеризует расширенный вектор состояния $(z,x)$. В нем о координатах вектора $z$ имеется полная информация, а информация о координатах вектора x не известна. В этом случае проблема может быть сведена к рассматриваемой. Альтернативным подходом является синтез наблюдателя состояния, который по выходу измерительной системы z(t) формирует оценку вектора состояния $\hat {x}(t)$, используемую в законе управления [19].
Управление, применяемое в каждый момент времени t, имеет вид управления с неполной обратной связью: $u(t) = u(t,{{x}^{1}}(t))$. Если m = 0, система управления будет разомкнутой по состоянию, а соответствующее управление $u(t)$ – программным, а если m = n, то система управления будет замкнутой с полной обратной связью, определяемой управлением $u(t,x)$. Множество допустимых управлений Um образуют такие функции $u(t,{{x}^{1}})$, что $\forall t \in T$ управление $u(t) = u(t,{{x}^{1}}(t)) \in U(t)$ кусочно-непрерывно, а функция $f(t,x,u(t,{{x}^{1}}))$ такова, что решение уравнения (1.1) с начальным условием (1.2) существует и единственно. Множество допустимых процессов $D({{t}_{0}},{{x}_{0}})$ – множество пар $d = (x( \cdot ),u( \cdot ))$, включающих траекторию $x( \cdot )$ и кусочно-непрерывное допустимое управление $u( \cdot )$, где $\forall t \in T$ $u(t) \in U(t)$, удовлетворяющих уравнению состояния (1.1) и начальному условию (1.2).
На множестве $D({{t}_{0}},{{x}_{0}})$ определен функционал качества управления отдельной траекторией:
(1.3)
$I({{x}_{0}},d) = \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {{{f}^{0}}(t,x(t),u(t))} \,dt + F(x({{t}_{f}})),$(1.4)
$X(t,u(t,{{x}^{1}})) = \cup \{ x(t,u(t,{{x}^{1}}(t)),x({{t}_{0}}))|x({{t}_{0}}) \in \Omega \} ,\quad t \in T,$Качество управления пучком траекторий предлагается оценивать величиной функционала
где mes Ω – мера множества Ω.Требуется найти управление $u{\kern 1pt} *(t,{{x}^{1}}) \in {{U}_{m}}$, минимизирующее функционал (1.5):
(1.6)
$J[u{\kern 1pt} *(t,{{x}^{1}})] = \mathop {\min }\limits_{u(t,{{x}^{1}}) \in {{U}_{m}}} J[u(t,{{x}^{1}})]$.Искомое управление называется оптимальным в среднем, так как минимизируется среднее значение функционала (1.3) на множестве начальных состояний $\Omega $.
2. Переход к задаче параметрической целочисленно-непрерывной оптимизации. Рассмотрим сначала процедуру вычисления критерия оптимальности управления пучком траекторий, а затем возможные варианты параметризации законов управления с неполной обратной связью.
2.1. Приближенное вычисление значения функционала (1.5). Предположим, что множество начальных состояний Ω представляет собой параллелепипед, определенный прямым произведением отрезков $\left[ {{{\alpha }_{i}};{{\beta }_{i}}} \right],\,\,i = \overline {1,n} $, т.е. $\Omega = \left[ {{{\alpha }_{1}};{{\beta }_{1}}} \right] \times ... \times \left[ {{{\alpha }_{n}};{{\beta }_{n}}} \right]$. Все отрезки $\left[ {{{\alpha }_{i}};{{\beta }_{i}}} \right],i = \overline {1,n} $, с помощью шага $\Delta {{x}_{i}}$ разбиваются на Ni отрезков, а параллелепипед Ω делится на $N = {{N}_{1}} \cdots {{N}_{n}}$ элементарных подмножеств ${{\Omega }_{k}},\,\,k = \overline {1,N} $. В каждом элементарном подмножестве ${{\Omega }_{k}}$ задается начальное состояние $x_{0}^{k}$ – центр параллелепипеда ${{\Omega }_{k}}$.
Для каждого начального состояния $x_{0}^{k},k = \overline {1,N} $, из множества начальных состояний $\Omega $ следует проинтегрировать систему дифференциальных уравнений (1.1) с управлением ${{({{u}^{1}}(t,{{x}^{1}}), \ldots ,{{u}^{q}}(t,{{x}^{1}}))}^{{\text{T}}}}$ одним из численных методов, например методом Рунге–Кутты 4-го порядка. В результате получаются пары dk, $k = \overline {1,N} $, образованные и управлением uk(t) = (u1, k(t) = u1(t, x1, k(t)), ... ..., ${{u}^{{q,k}}}(t) = {{u}^{q}}(t,{{x}^{{1,k}}}(t)){{)}^{{\text{T}}}}$, и соответствующими траекториями ${{x}^{k}}(t)$. Следовательно, можно найти приближенное значение критерия качества управления пучком траекторий:
2.2. Параметризация законов управления. Реализуем переход от задачи (1.6) к задаче конечномерной оптимизации, т.е. проблеме поиска наилучших значений параметров, задающих структуру управления. Управление $u(t,{{x}^{1}})$ ищется в параметрическом виде, определяемом числом коэффициентов в разложении управления по выбираемой системе базисных функций и их значениями.
Могут применяться следующие способы параметризации закона управления.
1. Использование ортонормированных систем базисных функций, получивших широкое распространение в спектральном методе [43]. Предлагается искать закон управления в виде функции насыщения sat, гарантирующей выполнение параллелепипедных ограничений на управление [18, 19]:
(2.2)
${{u}_{j}}(t,{{x}^{1}}) = sat\{ {{g}_{j}}(t,{{x}_{1}},...,{{x}_{m}})\} ,\quad j = \overline {1,q} .$Здесь
(2.3)
$sat\,{{v}_{j}}(t) = \left\{ \begin{gathered} {{v}_{j}}(t),\quad {{a}_{j}}\left( t \right) < {{v}_{j}}(t) < {{b}_{j}}\left( t \right), \hfill \\ {{a}_{j}}\left( t \right),\quad {{v}_{j}}(t) \leqslant {{a}_{j}}\left( t \right), \hfill \\ {{b}_{j}}\left( t \right),\quad {{v}_{j}}(t) \geqslant {{b}_{j}}\left( t \right), \hfill \\ \end{gathered} \right.$(2.4)
${{g}_{j}}\left( {t,{{x}_{1}},...,{{x}_{m}}} \right) = \sum\limits_{{{i}_{0}} = 0}^{L_{0}^{j} - 1} {\sum\limits_{{{i}_{1}} = 0}^{L_{1}^{j} - 1} { \ldots \sum\limits_{{{i}_{m}} = 0}^{L_{m}^{j} - 1} {c_{{{{i}_{0}}{{i}_{1}} \ldots {{i}_{m}}}}^{j}\,q\left( {{{i}_{0}},t} \right)} } } {{p}_{1}}\left( {{{i}_{1}},{{x}_{1}}} \right) \cdots {{p}_{m}}\left( {{{i}_{m}},{{x}_{m}}} \right)$,В качестве базисных функций $q({{i}_{0}},t)$, ${{p}_{k}}\left( {{{i}_{k}},{{x}_{k}}} \right),$ $k = \overline {1,m} $, можно, например, взять ортонормированную на отрезке $[0;{{t}_{f}}]$ систему нестационарных косинусоид:
(2.5)
$q({{i}_{0}},t) = \left\{ \begin{gathered} \sqrt {\frac{1}{{{{t}_{f}}}}} ,\quad {{i}_{0}} = 0, \hfill \\ \sqrt {\frac{2}{{{{t}_{f}}}}} \cos \frac{{{{i}_{0}}\pi t}}{{{{t}_{f}}}},\quad {{i}_{0}} = \overline {1,{{L}_{0}} - 1} , \hfill \\ \end{gathered} \right.\quad {{p}_{k}}({{i}_{k}},{{x}_{k}}) = \left\{ \begin{gathered} \sqrt {\frac{1}{{\overline {{{x}_{k}}} - \underline {{{x}_{k}}} }}} ,\quad {{i}_{k}} = 0, \hfill \\ \sqrt {\frac{2}{{\overline {{{x}_{k}}} - \underline {{{x}_{k}}} }}} \cos \frac{{{{i}_{k}}\pi ({{x}_{k}} - \underline {{{x}_{k}}} )}}{{\overline {{{x}_{k}}} - \underline {{{x}_{k}}} }},\quad {{i}_{k}} = \overline {1,{{L}_{k}} - 1} , \hfill \\ \end{gathered} \right.$Неизвестные параметры j-й координаты закона управления: матрица-столбец масштабов усечения ${{L}^{j}} = {{(L_{0}^{j},L_{1}^{j},...,L_{m}^{j})}^{{\text{T}}}}$ и наилучших значений коэффициентов разложения $с_{{{{i}_{0}},{{i}_{1}},...,{{i}_{m}}}}^{j}$, удобно представить в виде блочной гиперстолбцовой матрицы:
Тогда вектор всех неизвестных, подлежащих поиску, можно записать в форме объединенной матрицы-столбца
с ограничениями на компоненты:(2.7)
$0 \leqslant L_{i}^{j} \leqslant L_{{\max }}^{j},\quad L_{i}^{j} - {\text{целые}};\quad j = \overline {1,q} ,$2. Применение финитных базисных систем функций [42]. При m = 0 управление ищется в виде функции насыщения sat, гарантирующей выполнение ограничений на управление:
(2.8)
${{u}_{j}}\left( t \right) = {\text{sat}}\left\{ {{{g}_{j}}\left( t \right)} \right\},\quad j \in \overline {1,q} ,$В качестве базисной системы функций $S(i,t)$ можно использовать сплайны:
$S(i,t) = Sp\left( {{t \mathord{\left/ {\vphantom {t h}} \right. \kern-0em} h} - i} \right),$ $h = {1 \mathord{\left/ {\vphantom {1 {({{L}^{j}} - 1)}}} \right. \kern-0em} {({{L}^{j}} - 1)}}$, $i = \overline {0,{{L}^{j}} - 1} $, – финитные функции, порожденные сплайнами, на отрезке $[0,1]$:
(2.10)
$Sp(t) = \left\{ {\begin{array}{*{20}{l}} {{{2}^{{p - 1}}}{{{(1 + t)}}^{p}},\quad t \in \left[ { - 1, - \frac{1}{2}} \right],} \\ {1 - {{2}^{{p - 1}}}{{{\left| t \right|}}^{p}},\quad t \in \left[ { - \frac{1}{2},\frac{1}{2}} \right],} \\ {{{2}^{{p - 1}}}{{{(1 - t)}}^{p}},\quad t \in \left[ {\frac{1}{2},1} \right],} \\ {0,\quad t \notin [ - 1,1],} \end{array}} \right.$Для преобразования отрезка $[{{t}_{0}},{{t}_{f}}]$ к отрезку $[0,1]$ можно воспользоваться соотношением $t = {{t}_{0}} + ({{t}_{f}} - {{t}_{0}})\tau ,$ $\tau \in [0,1]$. Решение ищется в виде расширенного вектора
(2.11)
${{(\left. {{{L}^{1}},...,{{L}^{q}}} \right|c_{0}^{1},...,c_{{{{L}^{1}} - 1}}^{1},...,c_{0}^{q},...,c_{{{{L}^{q}} - 1}}^{q})}^{{\text{T}}}}$(2.12)
$0 \leqslant L_{{}}^{j} \leqslant L_{{\max }}^{j},\quad L_{{}}^{j} - ~{\text{целые}};\quad j = \overline {1,q} ,$3. Применение радиально-базисных функций [43, 44]. Предлагается использовать функцию Гаусса: $\varphi (r) = {{e}^{{ - {{{(\varepsilon r)}}^{2}}}}},$ мультиквадратичную $\varphi (r) = \sqrt {1 + {{{(\varepsilon r)}}^{2}}} ,$ обратную квадратичную: $\varphi (r)\, = \,1{\text{/(}}1 + {{(\varepsilon r)}^{2}}),$ обратную мультиквадратичную: $\varphi (r) = {1 \mathord{\left/ {\vphantom {1 {\sqrt {1 + {{{(\varepsilon r)}}^{2}}} }}} \right. \kern-0em} {\sqrt {1 + {{{(\varepsilon r)}}^{2}}} }}.$ Здесь $\varepsilon - $ масштабный коэффициент, ${{x}^{i}} - $ базовая точка, $r = \left\| {x - {{x}^{i}}} \right\|.$
Закон управления представляется в форме (2.2)–(2.4), где
(2.13)
${{g}_{j}}\left( {t,{{x}_{1}},...,{{x}_{m}}} \right) = \sum\limits_{{{i}_{0}} = 0}^{L_{0}^{j} - 1} {\sum\limits_{{{i}_{1}} = 0}^{L_{1}^{j} - 1} { \ldots \sum\limits_{{{i}_{m}} = 0}^{L_{m}^{j} - 1} {c_{{{{i}_{0}}{{i}_{1}} \ldots {{i}_{m}}}}^{j}\,} } } \varphi (\left| {t - {{t}_{{{{i}_{0}}}}}} \right|)\varphi (\left| {{{x}_{1}} - {{x}_{{1{{i}_{1}}}}}} \right|) \cdots \varphi (\left| {{{x}_{m}} - {{x}_{{m{{i}_{m}}}}}} \right|,$4. Применение разложений по многочленам Чебышева, используемых в различных вариантах псевдоспектрального метода [45, 46].
А. Можно использовать систему многочленов Чебышева, ортогональных с весом ρ(x) = = ${1 \mathord{\left/ {\vphantom {1 {\sqrt {1 - {{x}^{2}}} }}} \right. \kern-0em} {\sqrt {1 - {{x}^{2}}} }}$ на отрезке $[ - 1,1]$:
(2.14)
${{T}_{0}}(x) = 1,\quad {{T}_{1}}(x) = x,\quad {{T}_{{m + 1}}}(x) = 2x{{T}_{m}}(x) - {{T}_{{m - 1}}}(x),\quad m \geqslant 1.$При этом
Тогда справедливо представление (2.2)–(2.4), где аргументы ${{g}_{j}}\left( {t,{{x}_{1}},...,{{x}_{m}}} \right)$ функции насыщения можно искать в виде линейной комбинации базисных функций:
(2.15)
${{g}_{j}}\left( {t,{{x}_{1}},...,{{x}_{m}}} \right) = \sum\limits_{{{i}_{0}} = 0}^{L_{0}^{j}} {\sum\limits_{{{i}_{1}} = 0}^{L_{1}^{j}} { \ldots \sum\limits_{{{i}_{m}} = 0}^{L_{m}^{j}} {c_{{{{i}_{0}}{{i}_{1}} \ldots {{i}_{m}}}}^{j}\,{{T}_{{{{i}_{0}}}}}\left( t \right)} } } \,{{T}_{{{{i}_{1}}}}}\left( {{{x}_{1}}} \right) \cdots {{T}_{{{{i}_{m}}}}}\left( {{{x}_{m}}} \right).$Здесь $c_{{{{i}_{0}}{{i}_{1}}...{{i}_{m}}}}^{j}$ – неизвестные коэффициенты; $L_{0}^{j},L_{1}^{j},...,L_{m}^{j}$ – масштабы усечения по времени и координатам вектора состояния, используемым в управлении. Решение ищется как расширенная матрица-столбец ${{C}_{N}} = {{(C_{N}^{1},....,C_{N}^{q})}^{{\text{T}}}}$вида (2.6) с ограничениями (2.7).
Для преобразования отрезков $[{{t}_{0}},{{t}_{f}}],[\underline {{{x}_{1}}} ,\overline {{{x}_{1}}} ],...,[\underline {{{x}_{{\,n}}}} ,\overline {{{x}_{n}}} ]$ к стандартному отрезку [–1, 1] можно применить линейные преобразования:
В результате уравнение (1.1) и функционал (1.3) перепишем в следующей форме:
(2.16)
$\begin{gathered} \dot {x}(\tau ) = \frac{{{{t}_{f}} - {{t}_{0}}}}{2}f(\tau ,x(\tau ),u(\tau )), \\ I({{x}_{0}},d) = \frac{{{{t}_{f}} - {{t}_{0}}}}{2}\int\limits_{ - 1}^1 {{{f}^{0}}(\tau ,x(\tau ),u(\tau ))d\tau } + F(x(1)). \\ \end{gathered} $Б. Для случая m = 0 можно использовать многочлены Чебышева, а в качестве узлов интерполяции выбрать положения экстремумов многочлена Чебышева степени ${{N}^{j}}$ и крайние точки отрезка интерполяции: ${{t}_{k}} = \cos \,(\pi k{\text{/}}{{N}^{j}}),$ $k = \overline {0,{{N}^{j}}} $.
На отрезке [–1, 1] они располагаются так: ${{t}_{0}} = 1,{{t}_{1}},...,{{t}_{{{{N}^{j}} - 1}}},{{t}_{{{{N}^{j}}}}} = - 1$ и называются точками CGL(Chebyshev–Gauss–Lobatto). Поскольку многочлены Чебышева можно записать в форме ${{T}_{m}}(t) = \cos (m{\text{arccos}}t),m = \overline {0,{{N}^{j}}} ,$ то их значения в узлах найдем в виде
(2.17)
$\begin{gathered} {{T}_{m}}({{t}_{k}}) = \cos \,(\pi km{\text{/}}{{N}^{j}}),\quad k = \overline {0,{{N}^{j}}} ;\quad j = \overline {1,q} \,, \\ u_{{^{j}}}^{{{{N}^{j}}}}(t) = \sum\limits_{i = 0}^{{{N}^{j}}} {u_{i}^{j}{{\varphi }_{i}}(t)} ,\quad j = \overline {1,q} , \\ \end{gathered} $При этом в узлах выполняются соотношения
В задаче требуется найти координаты расширенного вектора
(2.18)
${{(\left. {{{N}^{1}},...,{{N}^{q}}} \right|\,u_{0}^{1},....,u_{N}^{1},...,u_{0}^{q},....,u_{N}^{q})}^{{\text{T}}}},$Таким образом, при всех описанных способах параметризации закона управления предлагается искать значения координат блочных расширенных векторов (2.6), (2.11), (2.18), содержащих блок целочисленных переменных и блок действительных переменных, на которые наложены интервальные ограничения.
3. Формирование гибридных мультиагентных алгоритмов целочисленно-непрерывной условной оптимизации. Рассмотрим принципы формирования мультиагентных алгоритмов, которые реализованы в двух предложенных авторами алгоритмах.
3.1. Постановка задачи. Все приведенные в разд. 2 способы параметризации управления приводят к необходимости решения смешанной целочисленно-непрерывной задачи условной оптимизации:
где3.1.1. Методика решения целочисленно-непрерывной задачи оптимизации. Для решения задачи (3.1) используются гибридные метаэвристические алгоритмы, относящиеся к группе мультиагентных. Они хорошо зарекомендовали себя при решении задач оптимизации типовых тестовых функций и параметров технических систем [33], а также в задачах поиска оптимального программного управления [31, 32].
Поскольку вектор подбираемых параметров содержит как целочисленные, так и непрерывные координаты, то предлагается последовательная схема решения, включающая:
а) генерирование начального приближения:
б) реализацию процедуры поиска на множестве допустимых решений $Y$ по целочисленным переменным при известных значениях координат вектора x. Применяется процедура целочисленного линейного поиска, являющаяся модификацией предложенной в [36] для решения непрерывных задач оптимизации. При этом значения координат вектора $x$ в блочном векторе $(y,x)$ считаются фиксированными.
1. Упорядочить переменные ${{y}_{i}},i = \overline {1,m} $, случайным образом. Положить New = false – индикатор наличия улучшения, j = 1.
2. Пусть на j-м месте стоит i-я переменная. “Просканировать” множество решений вида $z = y + k{{e}_{i}},$ $k = 0, \pm 1, \pm 2,...,$ $a \leqslant y \leqslant b,$ где ${{e}_{i}} - $ единичный орт, составленный из всех нулей и одной единицы на i-м месте; $a = {{({{a}_{1}},...,{{a}_{m}})}^{{\text{T}}}},$ $b = {{({{b}_{1}},...,{{b}_{m}})}^{{\text{T}}}},$ знак неравенства понимается покоординатно.
3. Если среди полученных в результате сканирования решений имеется наилучшее, удовлетворяющее условию $f(z,x) < f(y,x),$ то заменить y на z и положить $New = true$.
4. Если $j < m,$ то положить $j = j + 1$ и перейти к п. 2. Если $j = m$ и $New = true,$ перейти к п. 1. Иначе завершить процедуру.
в) реализация процедуры поиска на множестве допустимых решений $X$ по непрерывным переменным при фиксированных координатах вектора y. Для этого предлагается применить мультиагентные алгоритмы условной оптимизации (действия, описанные в п. 2 и 3, назовем проходом);
г) если достигнуто максимальное число проходов, процедуру поиска завершить (иначе перейти к следующему проходу, начиная с п. 1, б).
После завершения процедуры целочисленного линейного поиска найденные значения координат вектора $y$ фиксируются.
3.1.2. Гибридные мультиагентные алгоритмы оптимизации. Они объединяют оригинальные приемы (эвристики), используемые в различных эволюционных алгоритмах, методах роевого интеллекта, биоинспирированных и мультистартовых алгоритмах. Эти эвристики управляются алгоритмом более высокого уровня (отсюда термин мета), как правило, с целью преодоления окрестностей локальных экстремумов и получения хорошего приближения к глобальному экстремуму. Мультиагентные алгоритмы являются подмножеством метаэвристических [21–30]. Они основаны на процессах, происходящих в среде, которая имеет множество агентов. Агенты обмениваются информацией для того, чтобы найти решение задачи. В соответствии с постановкой задачи и алгоритмом, изложенными выше, агентом является набор коэффициентов в разложении управления по различным системам базисных функций, а значением целевой функции – значение критерия (2.1).
Агенты принимают решение, учитывая текущее положение, память о своем предыдущем опыте, информацию о положении абсолютных агентов-лидеров и агентов-лидеров подгрупп, в которые могут объединяться.
Мультиагентные методы, как и большинство метаэвристических алгоритмов, начинают свою работу с этапа генерации популяции агентов на множестве допустимых решений задачи. Как правило, при этом используется равномерный закон распределения с учетом принадлежности множеству допустимых решений. Далее популяция делится на группы различными способами:
а) равномерно без учета соответствующих значений целевой функции;
б) равномерно с учетом расстояний между агентами (как в методе рассеивания [36]);
в) равномерно с учетом значений целевой функции. При этом первоначально производится ранжирование агентов по величине целевой функции. Порядок формирования M групп: наилучшее решение помещается в первую стаю, следующее – во вторую, M-е – в M-ю стаю, $\left( {M + 1} \right)$-е – снова в первую стаю и т.д. Такой подход применяется в методе, имитирующем поведение стаи лягушек [37, 38].
Агенты (группы агентов) классифицируются по реализуемым функциям, которые они выполняют на основании получаемой на каждой итерации информации. Предлагается использовать следующие типы:
а) локально-оптимальный агент – реализует движение к лидеру группы или лидеру популяции, но только на текущей итерации;
б) консервативный агент – применяет информацию о своем наилучшем результате, полученном за время поиска;
в) автономный агент – использует текущее положение и изучает только окрестность своего положения;
г) сомневающийся агент – исследует окрестность своей позиции при помощи случайных блужданий разнообразной конфигурации;
д) агент-манипулятор – объявляет себя абсолютным лидером популяции и обеспечивает движение остальных членов популяции к своей текущей позиции;
е) командный, коалиционный агент – организует или входит в состав компактных групп, образованных двумя или тремя лидерами. Командные агенты, как правило, генерируют положение нового агента на основании обработки информации о позициях членов команды.
Движение агентов происходит итерационно в соответствии с операциями, применяемыми к каждому из агентов. В результате агенты меняют свое положение. Совокупность аналогичных операций, реализующих управление движением агентов, образует проход. По окончании прохода производится межгрупповой обмен информацией:
а) из текущей популяции агентов удаляются $q$ наихудших агентов, а на их место генерируются столько же новых тем же способом, как и в начале процесса поиска;
б) из каждой группы удаляются наихудшие агенты и заменяются лидерами из других групп;
в) после реализации процедуры из п. а) и упорядочивания по величине целевой функции можно сформировать группы заново. Порядок формирования M групп такой же, как и при делении на группы начальной популяции.
По окончании очередного прохода агенты могут поменять свой тип, характеризующий поведение агента. Опишем сценарии поведения агентов различных типов.
Поведение локально-оптимального агента.
Сценарий 1. Найти наилучшее текущее решение ${{x}_{{gb}}}$ в популяции агентов, а в рамках группы выбрать наилучшее решение xbest (положение агента) в группе.
Определить новое положение локально-оптимального агента (сначала реализуется движение к лидеру своей группы):
Если при этом значение целевой функции улучшилось, то считать итерацию удачной, иначе сгенерировать решение случайно на множестве $D$ с помощью равномерного закона распределения.
Сценарий 2. Для реализации движения к агенту-лидеру использовать управляемое движение агентов, минимизируя локально-оптимальный критерий близости. При этом применяется управление, минимизирующее величину критерия через достаточно малый промежуток времени управления [31, 33].
Поведение сомневающегося агента.
Сценарий 1. Используя равномерный закон распределения на отрезке $[0;1]$, сгенерировать число u; если $u > 0.5$, то положить $x_{i}^{{j,k + 1}} = x_{i}^{{j,k}} + {\text{rand}}\,[0;{{b}_{i}} - x_{i}^{{j,k}}] \cdot r$; если $u \leqslant 0.5$, то $x_{i}^{{j,k + 1}}$ = = $x_{i}^{{j,k}} - {\text{rand}}\,[0;x_{i}^{{j,k}} - {{a}_{i}}] \cdot r$, где $i = \overline {1,n} $, ${\text{rand}}\,{\kern 1pt} [a;b]$ – случайная величина, равномерно распределенная на отрезке $[a;b]$, $r$ – параметр мутации (рекомендуемое значение 0.01); если $x_{i}^{{j,k + 1}} \notin [{{a}_{i}};{{b}_{i}}]$, то процедуру повторить.
Сценарий 2. Реализовать процедуру локального линейного поиска [36]. Метод имеет параметр – шаг поиска $h$.
Шаг 1. Упорядочить переменные ${{x}_{i}}$, $i = \overline {1,n} $, агента x случайным образом. Положить New = = $false$ – индикатор наличия улучшений, j = 1 – номер переменной в упорядоченном списке.
Шаг 2. Пусть на j-м месте в списке стоит i-я переменная. “Просканировать” множество, т.е. вычислить значение функции приспособленности для особей из множества ls(x, h, i) = = $\{ y \in {{R}^{h}}|y = x + kh{{e}_{i}},k \in Z,a \leqslant y \leqslant b\} $, ${{e}_{i}}$ – единичный орт, состоящий из всех нулей и одной единицы на i-м месте; $a = {{({{a}_{1}},{{a}_{2}},...,{{a}_{n}})}^{{\text{T}}}}$, $b = {{({{b}_{1}},{{b}_{2}},...,{{b}_{n}})}^{{\text{T}}}}$ – векторы соответственно нижних и верхних границ множества $D$.
Шаг 3. Если в результате сканирования находится лучшее положение агента, то агента $x$ заменить агентом $y$ и положить $New = true$.
Шаг 4. Если j < n, то положить $j = j + 1$ и перейти к шагу 2. Если j = n, то при $New = true$ перейти к шагу 1, иначе процесс локального линейного поиска завершить.
Поведение консервативного агента. Основывается на учете своего наилучшего результата за все предыдущие итерации и наилучшего результата среди агентов-соседей. При этом может учитываться эффект забывания текущей позиции.
Новое положение находится по формуле, обобщающей используемую в методе частиц в стае [41]:
Поведение автономного агента. Он использует текущее положение и исследует окрестность своего положения.
Сценарий 1. Генерировать новые положения как в методе распространения сорняков [40]. Количество позиций s j, исследуемых агентом, определяется линейной зависимостью и находится в диапазоне $[{{s}_{{\min }}},{{s}_{{\max }}}]$. Они располагаются вокруг агента, согласно нормальному закону распределения. Математическое ожидание определяется текущим положением агента, а среднеквадратическое отклонение – числом k выполненных итераций, начальным ${{\sigma }_{{initial}}}$ и конечным ${{\sigma }_{{final}}}$ значениями:
Число исследуемых позиций находится по формуле
Сценарий 2. Найти случайное число $NI$ агентов-соседей на отрезке $[N{{I}_{{\min }}},N{{I}_{{\max }}}]$; $N{{I}_{{\min }}} = 5,$ $N{{I}_{{\max }}} = 25$ при помощи равномерного закона распределения с нахождением целой части сгенерированного значения. Далее определить “центр масс” решений, соответствующих агентам-соседям, как взвешенное среднее:
Найти новое положение автономного агента:
Поведение агента-манипулятора. Используется факт объявления текущим абсолютным лидером агента, положению которого соответствует наилучшее значение целевой функции.
Сценарий 1. Члены популяции агентов реализуют процесс миграции в направлении абсолютного лидера, применяя самоорганизующийся метод миграции [35]. При этом обновляются позиции агентов, участвующих в миграции. Они заменяются наилучшими достигнутыми в процессе миграции позициями.
Сценарий 2. Агенты реализуют управляемое движение к абсолютному лидеру с помощью оптимального регулятора с полной обратной связью [31, 33]. При этом управление, используемое агентом, зависит от текущего отклонения положения агента от положения абсолютного лидера. После реализации очередного прохода информация об абсолютном лидере обновляется и формируется новый закон управления с обратной связью по положению агента, применяемый на протяжении следующего прохода. В качестве критерия близости агента к агенту-лидеру используется величина квадратичного критерия, отражающего как степень отклонения от лидера, так и затраты на процесс управления агентом.
Сценарий 3. Может применяться упрощенный по сравнению со сценарием 2 подход. В этом случае все члены группы используют один и тот же найденный закон управления приближением к лидеру, в котором в конце каждого прохода меняется требуемое положение цели, а именно значения координат нового агента-лидера.
Сценарий 4. Агенты реализуют процедуру, описанную в сценарии 2, только в качестве критерия близости к лидеру применяют функционал обобщенной работы, учитывающий затрачиваемую энергию управляемых сигналов [33]. При этом за счет введения полуопределенного критерия упрощается процедура синтеза управления с обратной связью, и процесс выработки решения агентом становится более оперативным.
Поведение командного, коалиционного агента. Он использует идею обмена информацией между членами подгруппы.
Сценарий 1. В популяции случайным образом выбираются четыре агента. Среди них либо выявляется лидер, либо не выявляется в зависимости от способа параметрической интерполяции. Реализуется поиск внутри выпуклой оболочки, образованной выбранными агентами. При этом генерируется положение нового агента. Такой сценарий может быть применен для поиска в новых подобластях множества допустимых решений [31].
Сценарий 2. Среди агентов, ранжированных по величине целевой функции, выбираются два, три или четыре агента-лидера. Решается задача параметрической интерполяции и находится положение нового агента. Применяется для реализации фронтального поиска решения задачи [31, 32]. Линия фронта образуется лидерами процесса поиска экстремума.
Сценарий 3. В конце каждого прохода из группы выделяется агент, которому соответствует наихудшее значение целевой функции. Он исключается из группы и популяции в целом. На его место в группу включается один из лидеров других групп.
Сценарий 4. В конце каждого прохода из популяции исключается фиксированное число наихудших агентов. Команды далее формируются заново с помощью разных вариантов генерирования начальной популяции агентов.
Процедуры выбора агентов друг другом могут быть реализованы несколькими способами.
1. По информации о величине целевой функции, соответствующей положениям агентов.
2. По информации о репутации агента ${{r}_{j}} \in [0,1]$, изменяющейся в процессе поиска. Она формируется на основании показателя доверия ajl агента с номером j к агенту с номером l. В начале поиска все элементы матрицы $A = ({{a}_{{jl}}})$ полагаются равными нулю. Если движение агента с номером j к агенту с номером l сопровождается улучшением значения целевой функции, то показатель доверия к агенту с соответствующим номером увеличивается:
Иначе показатель доверия не изменяется: $a_{{jl}}^{{New}} = {{a}_{{jl}}}$.
Репутация агента с номером l определяется суммой элементов l-го столбца матрицы A:
или ее нормированным значениемВыбор агентов может производиться методом рулетки с учетом значений репутации агентов.
3.1.3. Гибридный мультиагентный метод интерполяционного поиска. Метод основан на процессах, происходящих в среде, которые имеют множество агентов. У агентов есть возможность обмениваться информацией для того, чтобы найти решение задачи.
Стратегия поиска включает интерполяционный поиск, который использует несколько точек текущей популяции и сводит задачу нахождения новых решений к задачам одномерной параметрической минимизации вдоль интерполяционной кривой, например, методом, имитирующим поведение стаи криля [39], а также самоорганизующийся метод [35].
Рассматриваемая целевая функция f(x) называется функцией приспособленности, а вектор параметров $x = {{({{x}_{1}},{{x}_{2}},...,{{x}_{n}})}^{{\text{T}}}}$ целевой функции – агентом. Предполагаемым решением поставленной задачи оптимизации может быть каждый вектор $x = {{({{x}_{1}},{{x}_{2}},...,{{x}_{n}})}^{{\text{T}}}} \in D$. При решении задачи минимизации целевой функции на множестве $D = \{ x\left| {{{x}_{i}} \in [{{a}_{i}},{{b}_{i}}],i = \overline {1,n} } \right.\} $ используются конечные наборы $I = \{ {{x}^{{(j)}}} = {{(x_{1}^{j},x_{2}^{j}, \ldots ,x_{n}^{j})}^{T}},{\kern 1pt} {\kern 1pt} j = \overline {1,NP} \} {\kern 1pt} {\kern 1pt} {\kern 1pt} \subset D$, возможных решений (агентов), называемые популяциями, где ${{x}^{{(j)}}}$ – агент с номером j, NP – размер популяции.
Гибридный мультиагентный метод интерполяционного поиска имитирует эволюцию начальной популяции ${{I}_{0}} = \{ {{x}^{{(j)}}},j = \overline {1,NP} |{{x}^{{(j)}}} = {{(x_{1}^{j},x_{2}^{j}, \ldots ,x_{n}^{j})}^{T}} \in D\} $ и представляет собой итерационный процесс, исследующий множество D. Процедура поиска решения начинается с генерации начальной популяции агентов x(j), $j = \overline {1,NP} $, на множестве $D$ с помощью равномерного закона распределения.
Первой фазой поиска является интерполяционный поиск. Для его реализации в популяции выбираются четыре агента ${{P}_{1}},\;{{P}_{2}},\;{{P}_{3}},\;{{P}_{4}}$, среди них лидер ${{P}_{1}} = {{x}^{{(1)}}}$, а в качестве ${{P}_{2}},\;{{P}_{3}},\;{{P}_{4}}$ – три случайных агента популяции, отличных друг от друга и от x(1). Для их обработки используется кривая Безье. Она проходит внутри выпуклой оболочки, образованной выбранными четырьмя точками (агентами). При t = 0 она проходит через P1, а при t = 1 – через точку P4. Далее находится решение задачи параметрической оптимизации
Для исследования новых областей применяется В-сплайновая кривая, которая формируется по четырем случайным агентам популяции${{P}_{1}},\;{{P}_{2}},\;{{P}_{3}},\;{{P}_{4}}$, отличным друг от друга:
Она, как правило, не проходит ни через одну точку, лежит в выпуклой оболочке, порожденной четырьмя вершинами. В результате популяция пополняется еще одним новым агентом xB.
Второй фазой поиска является миграция популяции [35]. При этом в популяции выбирается агент-лидер (наилучшее решение) x(1). Все остальные агенты популяции ${{x}^{{(j)}}},j = \overline {2,NP} $, двигаются по направлению к лидеру, совершая дискретные шаги, число которых равно $nstep$. Причем половина этих шагов делается к лидеру, а затем в том же направлении совершается еще столько же шагов. Новое положение агента популяции определяется наилучшим достигнутым в ходе этого поиска решением. Направление поиска задается вектором $PRTVector$, координаты которого равны нулю или единице. Если координата равна нулю, поиск по данной координате не проводится, а если единице, то проводится. Таким образом, решение задачи ищется по всем координатам вектора $PRTVector$, равным одновременно единице. Положение лидера в процессе миграции не изменяется.
Третьей фазой является фронтальный поиск, который служит для уточнения итогового решения задачи. При этом используются интерполяционные кривые, для формирования которых учитывается информация о положении трех или четырех лидеров среди агентов популяции.
Среди агентов популяции ${{x}^{{(1)}}},...,{{x}^{{(NP)}}}$, расположенных по возрастанию соответствующего им значения функции приспособленности, выбираются три лидера ${{P}_{1}} = {{x}^{{(1)}}},$ ${{P}_{3}} = {{x}^{{(2)}}},$ ${{P}_{2}} = {{x}^{{(3)}}}$, по которым формируется кривая Безье (при t = 0 проходит через P1, а при t = 1 – через точку P3). Далее решается задача параметрической минимизации
Для продолжения поиска выбираются два лидера, через которых проходит интерполяционная кривая Катмулла–Рома (Catmull–Rom), а также два последующих решения: ${{P}_{1}} = {{x}^{{(3)}}},$ ${{P}_{2}} = {{x}^{{(1)}}},$ ${{P}_{3}} = {{x}^{{(2)}}},$ ${{P}_{4}} = {{x}^{{(4)}}}$ (при t = 0 проходит через P2, а при t = 1 – через P3). Далее решается задача параметрической минимизации
Для аналогичного поиска используется кривая Безье, формируемая по четырем лидерам популяции ${{P}_{1}} = {{x}^{{(1)}}},$ ${{P}_{4}} = {{x}^{{(2)}}},$ ${{P}_{2}} = {{x}^{{(3)}}},$ ${{P}_{3}} = {{x}^{{(4)}}}$ (при t = 0 она проходит через ${{P}_{1}}$, а при t = 1 – через точку ${{P}_{4}}$). Далее решается задача параметрической минимизации
Для фронтального поиска может быть использована В-сплайновая кривая, которая формируется по четырем лидерам популяции ${{P}_{1}} = {{x}^{{(1)}}},$ ${{P}_{4}} = {{x}^{{(2)}}},$ ${{P}_{2}} = {{x}^{{(3)}}},$ ${{P}_{3}} = {{x}^{{(4)}}}$. Кривая не проходит ни через одну выбранную точку, но лежит в выпуклой оболочке, порожденной этими вершинами. Далее находится решение задачи параметрической оптимизации
В результате популяция пополняется еще одним новым агентом xB.
На первой и третьей фазах требуется провести одномерную минимизацию вдоль параметрических кривых. Для этого используется биоинспирированный метод роевого интеллекта – метод, имитирующий поведение популяции криля [39]. Данный алгоритм основан на результатах анализа поведения стай криля – рачков, внешне напоминающих креветок. Их позиции меняются под действием трех факторов: присутствия других членов популяции, необходимости поиска пищи, случайных блужданий. Обычно движение популяции криля определяется двумя целями: увеличением плотности криля и достижением пищи. Задача одномерной параметрической минимизации может быть решена и классическими методами одномерной минимизации: дихотомии, золотого сечения, Фибоначчи и др. [23].
Гибридный мультиагентный метод интерполяционного поиска заканчивает работу после того, как будет исчерпано заданное число итераций. В последней популяции происходит отбор агентов с наименьшим значением целевой функции. Агент с наименьшим значением целевой функции принимается в качестве приближенного решения.
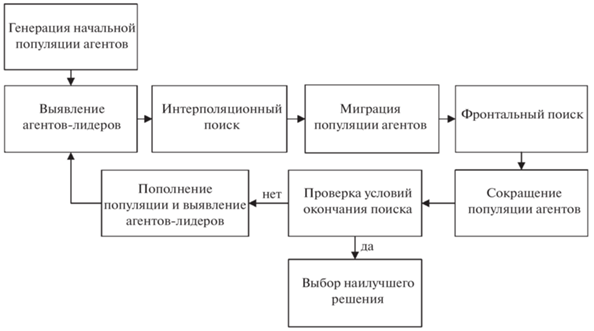
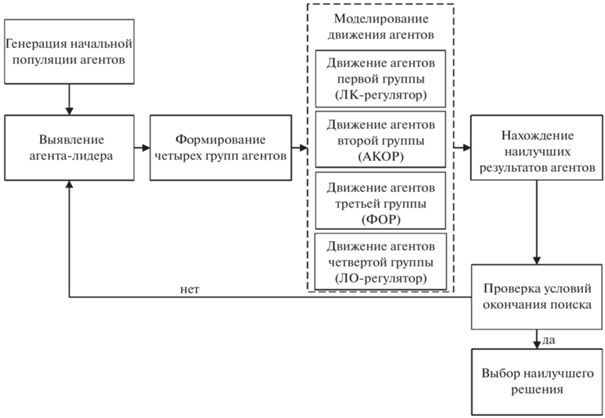
Общая схема работы гибридного мультиагентного метода интерполяционного поиска представлена на рис. 1.
3.1.4. Гибридный мультиагентный метод, основанный на использовании линейных регуляторов управления движением агентов. Метод базируется на процессах, происходящих в среде, которая содержит множество агентов. Агенты имеют возможность обмениваться информацией для того, чтобы найти решение задачи. Стратегия алгоритма основана на применении линейных регуляторов управления движением агентов [31, 33].
На начальном этапе требуется сгенерировать популяцию из NP агентов на множестве допустимых решений D с помощью равномерного закона распределения. Поиск экстремума реализуется за заданное число проходов Pmax. В рамках очередного прохода все агенты двигаются под действием соответствующего управления в течение определенного числа итераций.
Уравнение движения агентов запишем как
(3.2)
$\begin{gathered} \frac{{dx}}{{dt}} = v,\quad x({{t}_{0}}) = {{x}_{0}}, \\ \frac{{dv}}{{dt}} = u,\quad v({{t}_{0}}) = {{v}_{0}}, \\ \end{gathered} $Обозначим через $X = {{({{x}^{{\text{T}}}}\;{{v}^{{\text{T}}}})}^{{\text{T}}}}$ вектор состояния агента и перепишем уравнение (3.2) в форме
(3.3)
$\frac{{dX}}{{dt}} = AX(t) + B\,u(t),\quad X({{t}_{0}}) = {{X}_{0}} = \left( {\begin{array}{*{20}{c}} {{{x}_{0}}} \\ {{{v}_{0}}} \end{array}} \right),\quad A = \left( {\begin{array}{*{20}{c}} {{{O}_{n}}}&{{{E}_{n}}} \\ {{{O}_{n}}}&{{{O}_{n}}} \end{array}} \right),\quad B = \left( {\begin{array}{*{20}{c}} {{{O}_{n}}} \\ {{{E}_{n}}} \end{array}} \right),$В начальной популяции (k = 0), а также в конце каждого k-го прохода требуется определить положение лидера среди агентов популяции и соответствующее ему максимальное значение целевой функции: ${{x}^{{best,k}}},\;f({{x}^{{best,k}}})$. В течение следующего прохода он не изменяет своего положения:
(3.4)
$\begin{gathered} \frac{{d{{x}^{{best}}}}}{{dt}} = o,\quad {{x}^{{best}}}({{t}_{k}}) = {{x}^{{best,k}}}, \\ \frac{{d{{v}^{{best}}}}}{{dt}} = o,\quad {{v}^{{best}}}({{t}_{k}}) = o, \\ t \in [{{t}_{k}},{{t}_{{k + 1}}}),\quad k = \overline {0,{{P}_{{\max }}} - 1} , \\ \end{gathered} $Остальные $(NP - 1)$ агенты делятся на четыре равные группы:
агенты, использующие минимизацию критерия качества управления агентами на конечном промежутке времени;
агенты, применяющие минимизацию критерия качества управления агентами на бесконечном промежутке времени;
агенты, использующие минимизацию полуопределенного критерия качества (критерия обобщенной работы) управления агентами на конечном промежутке времени;
агенты, применяющие минимизацию приращения критерия качества управления агентами (локально-оптимальный подход).
Для всех агентов каждой группы позиции и векторы скорости разные, но находится и используется одно и то же управление с полной обратной связью по вектору состояния, определяемое соотношением для линейного регулятора, матрица коэффициентов усиления которого находится из условия минимизации квадратичного критерия качества управления, характеризующего характер приближения агента к агенту-лидеру на текущей итерации, а также интенсивность применяемого управления.
Введем отклонение от лидера $\Delta X = X - {{X}^{{best}}}$, изменение которого описывается уравнением (вычитая из (3.3) уравнение (3.4))
(3.5)
$\frac{{d\Delta X}}{{dt}} = A\,\Delta X(t) + B\,u(t),\quad \Delta X({{t}_{k}}) = \left( {\begin{array}{*{20}{c}} {x_{{}}^{k} - {{x}^{{best,k}}}} \\ {v_{{}}^{k}} \end{array}} \right),\quad t \in [{{t}_{k}},{{t}_{{k + 1}}}],\quad k = \overline {0,{{P}_{{\max }}} - 1} ,$Движение первой группы агентов. Для всех агентов группы применяется оптимальное управление с конечным горизонтом, т.е. линейно-квадратичный регулятор (ЛК-регулятор). Критерий качества управления траекториями агентов первой группы:
где $S(t),\Lambda $ – неотрицательно определенные симметрические матрицы размеров 2n × 2n, а Q(t) – положительно определенная симметрическая матрица n × nОптимальное управление $u{\kern 1pt} *(t,\Delta X)$ с полной обратной связью для любых начальных состояний имеет вид
Здесь $t \in [{{t}_{k}},{{t}_{{k + 1}}}]$, ${{t}_{0}} = 0,$ значение ${{t}_{{k + 1}}} = {{t}_{k}} + NMAX\,h$, где NMAX – заданное число итераций, h – шаг интегрирования дифференциального уравнения (3.5). Для упрощения решения можно везде положить $A(t) = A,$ $B(t) = B,$ $Q(t) = Q,$ $S(t) = S,$ так как модели (3.4), (3.5) линейные стационарные.
Движение второй группы агентов. Для всех агентов группы применяется оптимальное управление с бесконечным горизонтом, определяемое процедурой аналитического конструирования оптимальных регуляторов (АКОР). Критерий качества управления траекториями агентов второй группы:
Оптимальное управление $u{\kern 1pt} *(\Delta X)$ с полной обратной связью для любых начальных состояний имеет вид
где матрица коэффициентов усиления линейного регулятора $F = {{Q}^{{ - 1}}}{{B}^{T}}P$, а P – положительно определенная симметрическая матрица, удовлетворяющая алгебраическому уравнению Риккати:Решение этого уравнения, удовлетворяющее критерию Сильвестра, единственное.
Движение третьей группы агентов (для всех агентов группы применяется оптимальное управление по функционалу обобщенной работы (ФОР)). Критерий качества управления траекториями агентов третьей группы:
Оптимальное управление ${{u}^{{{\text{о}}{\text{.р}}{\text{.}}}}}(t,\Delta X)$ с полной обратной связью для любых начальных состояний имеет вид
Движение четвертой группы агентов (для всех агентов группы применяется локально-оптимальное управление). Критерий качества управления траекториями агентов четвертой группы:
где $t \in ({{t}_{k}},{{t}_{{k + 1}}}]$, $S(t),\Lambda (t)$ – неотрицательно определенные симметрические матрицы размеров $2n \times 2n$, а $\,Q(t)$ – положительно определенная симметрическая матрица размеров n × n.Локально-оптимальное управление ${{u}^{{loc}}}(t,\Delta X)$ с полной обратной связью для любых начальных состояний имеет вид
Матрицы, использованные в мультиагентном алгоритме, имеют следующую структуру:
Заметим, что матрицы, входящие в функционалы качества управления для всех четырех групп агентов, могут быть заданы независимо, несмотря на одинаковые обозначения.
После выполнения NMAX итераций каждый агент предъявляет наилучший из полученных во время движения результатов. Тем самым завершается очередной проход. Затем среди всех агентов популяции снова выбирается лидер и производится новое деление на группы. Процесс повторения проходов завершается при достижении максимального числа проходов.
Общая схема работы гибридного мультиагентного метода с помощью линейных регуляторов для управления движением агентов представлена на рис. 2.
4. Решение модельных примеров.
Пример 1. Постановка задачи [47] приведена в табл. 1. Использованы следующие параметры алгоритмов [34]: гибридного мультиагентного алгоритма, основанного на применении линейных регуляторов управления движением агентов [47] ($NP = 9$, $NMAX = 10$, ${{P}_{{\max }}} = 5$, ${{k}_{s}} = 0.1$, ${{k}_{l}} = 5$, $h = 0.0001$), гибридного мультиагентного алгоритма интерполяционного поиска (NP = 30, ${{I}_{{\max }}} = 10$, ${{M}_{1}} = 5$, ${{M}_{2}} = 5$, $PRTVector = 0.01$, $nstep = 5$, b2 = 8). В качестве базисных функций использовалась система нестационарных косинусоид (2.5). Представлены ограничения, положенные на значения $с_{i}^{j}$ коэффициентов в управлении: ${{c}_{{\min }}} = - 5,{\text{ }}{{c}_{{\max }}} = 5$. Множество начальных состояний $\Omega = \left[ { - 0.05;0,05} \right] \times \left[ { - 0.05;0.05} \right],$ ${{N}_{1}} = {{N}_{2}} = 5$.
Таблица 1.
Постановка задачи (пример 1)
| Размерность вектора состояния | n = 2 |
|---|---|
| Временной интервал | $t \in [0;1]$ |
| Ограничения на управление | $ - 1 \leqslant u \leqslant 1$ |
| Система дифференциальных уравнений | $\left\{ \begin{gathered} {{{\dot {x}}}_{1}} = {{x}_{2}} + \sin {{x}_{1}} + u \hfill \\ {{{\dot {x}}}_{2}} = {{x}_{1}}\cos {{x}_{2}}u \hfill \\ \end{gathered} \right.$ |
| Функционал (1.3) | $I({{x}_{0}},d) = x{}_{2}(1)$ |
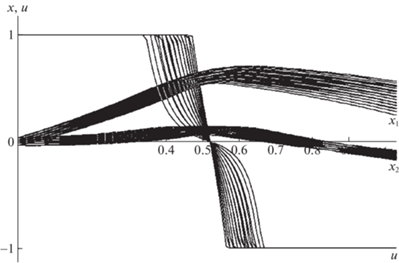
В задаче минимизировалось среднее значение функционала (1.5) на множестве начальных состояний $\Omega $. Решены задачи синтеза оптимального управления с полной и неполной обратной связью, включая случай m = 0. Для каждого случая определялось оптимальное количество коэффициентов в разложении ${{L}_{0}},\;{{L}_{1}},\;{{L}_{2}}$ и значения коэффициентов. Результаты решения задачи приведены в табл. 2, 3. Исходя из численных результатов, лучшее значение критерия получается при управлении с полной обратной связью. Примененные мультиагентные алгоритмы не уступают друг другу в точности. Найденные наилучшие пучок траекторий и управление для случая $m = 2$ изображены на рис. 3.
Таблица 2.
Решение примера 1 методом интерполяционного поиска
| Метод интерполяционного поиска | $u(t)$ | $u(t,{{x}_{1}})$ | $u(t,{{x}_{2}})$ | $u(t,{{x}_{1}},{{x}_{2}})$ |
|---|---|---|---|---|
| Масштаб усечения | ${{L}_{0}} = 2,{{L}_{1}} = 0,$L2 = 0 | ${{L}_{0}} = 2,{{L}_{1}} = 2$, L2 = 0 | ${{L}_{0}} = 2,{{L}_{1}} = 0$, L2 = 1 | ${{L}_{0}} = 2,{{L}_{1}} = 2$, L2 = 1 |
| Отрезки значений координат x1(1), x2(1) | [0.2667; 0.6172], [–0.176; –0.0914] | [0.3989; 0.4436], [–0.1756; –0.0927] | [0.281; 0.6315], [–0.1763; –0.0923] | [0.4646; 0.5038], [–0.1768; –0.0922] |
| Значение функционала (2.1) | –0.1337 | –0.13435 | –0.1343 | –0.13467 |
| Вектор коэффициентов в разложении (2.4) | 0.02; 3.51 | 0.27; 2.18; 2.26; 2.34 | 0.06; 3.51 | 0.89; 2.4; 2.47; 2.5 |
Таблица 3.
Решение примера 1 методом, основанным на использовании линейных регуляторов
| Метод линейных регуляторов | $u(t)$ | $u(t,{{x}_{1}})$ | $u(t,{{x}_{2}})$ | $u(t,{{x}_{1}},{{x}_{2}})$ |
|---|---|---|---|---|
| Масштаб усечения | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 2,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 1$ | ${{L}_{0}} = 2,{{L}_{1}} = 2,{{L}_{2}} = 1$ |
| Отрезки значений координат x1(1), x2(1) | [0.2706; 0.6212], [–0.1758; –0.0914] | [0.4444; 0.485], [–0.1766; –0.0925] | [0.2797; 0.6302], [–0.1764; –0.0923] | [0.4277; 0.469], [–0.1769; –0.0932] |
| Значение функционала (2.1) | –0.13356 | –0.13472 | –0.134326 | –0.13522 |
| Вектор коэффициентов в разложении (2.4) | 0.05; 3.38 | 0.7; 2.5; 2.5; 2.5 | 0.06; 3.54 | 0.65; 2.5; 2.5; 2.5 |
Пример 2. Постановка задачи [47] рассмотрена в табл. 4. Представлены следующие параметры алгоритмов [34]: гибридного мультиагентного алгоритма, основанного на использовании линейных регуляторов управления движением агентов ($NP = 9$, $NMAX = 10$, ${{P}_{{\max }}} = 5$, ${{k}_{s}} = 0.1$, ${{k}_{l}} = 5$, $h = 0.0001$), гибридного мультиагентного алгоритма интерполяционного поиска ($NP = 20$, ${{I}_{{\max }}} = 10$, ${{M}_{1}} = 2$, ${{M}_{2}} = 5$, $PRTVector = 0.01$, $nstep = 5$, ${{b}_{2}} = 8$). В качестве базисных функций применялась система нестационарных косинусоид (2.5). Приведены ограничения, наложенные на значения $с_{i}^{j}$ коэффициентов в управлении: ${{c}_{{\min }}} = 0,{\text{ }}{{c}_{{\max }}} = 350$. Множество начальных состояний $\Omega = [0.95;1.05] \times [ - 0.05;0.05],$ ${{N}_{1}} = {{N}_{2}} = 5$.
Таблица 4.
Постановка задачи (пример 2)
| Размерность вектора состояния | $n = 2$ |
|---|---|
| Временной интервал | $t \in [0,\;1.6]$ |
| Ограничения на управление | $ - 2 \leqslant u \leqslant 1$ |
| Система дифференциальных уравнений | $\left\{ \begin{gathered} {{{\dot {x}}}_{1}} = \frac{1}{{\cos {{x}_{1}} + 2}} + 3\sin {{x}_{2}} + u \hfill \\ {{{\dot {x}}}_{2}} = {{x}_{1}} + {{x}_{2}} + u \hfill \\ \end{gathered} \right.$ |
| Функционал (1.3) | $I({{x}_{0}},d) = - x{}_{1}(1.6) + \frac{1}{2}{{x}_{2}}(1.6)$ |
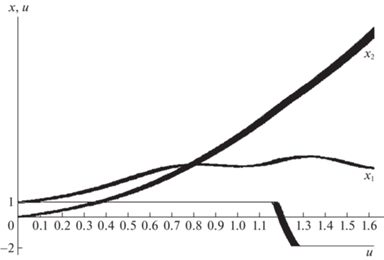
В задаче минимизировалось среднее значение функционала (1.5) на множестве начальных состояний. Решены задачи синтеза оптимального управления с полной и неполной обратной связью, включая случай m = 0. Для каждого случая определялось наилучшее количество коэффициентов в разложении ${{L}_{0}},{{L}_{1}},{{L}_{2}}$ и значения коэффициентов. Результаты решения задачи рассмотрены в табл. 5, 6. Исходя из численных результатов, лучшее значение критерия получается при управлении с полной обратной связью. При применении алгоритма, основанного на использовании линейных регуляторов управления движением агентов, был получен наилучший результат. Найденные наилучшие пучок траекторий и управление для случая m = 2 изображены на рис. 4.
Таблица 5.
Решение примера 2 методом интерполяционного поиска
| Метод интерполяционного поиска | u(t) | $u(t,{{x}_{1}})$ | $u(t,{{x}_{2}})$ | $u(t,{{x}_{1}},{{x}_{2}})$ |
|---|---|---|---|---|
| Масштаб усечения | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 1,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 1$ | ${{L}_{0}} = 2,{{L}_{1}} = 1,{{L}_{2}} = 1$ |
| Отрезки значений координат x1(1), x2(1) | [3.3645; 3.4519], [12.2765; 13.1466] | [3.4124; 3.5214], [12.3914; 13.264] | [3.406; 3.5109], [12.3426; 13.2172] | [3.4628; 3.6002], [12.5276; 13.4027] |
| Значение функционала (2.1) | –2.96042 | –2.96212 | –2.94643 | –2.96575 |
| Вектор коэффициентов в разложении (2.4) | 13.76; 13.83 | 22.87; 31.52 | 24.41; 35.29 | 117.21; 151.69 |
Таблица 6.
Решение примера 2 методом, основанным на использовании линейных регуляторов
| Метод линейных регуляторов | $u(t)$ | $u(t,{{x}_{1}})$ | $u(t,{{x}_{2}})$ | $u(t,{{x}_{1}},{{x}_{2}})$ |
|---|---|---|---|---|
| Масштаб усечения | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 1,{{L}_{2}} = 0$ | ${{L}_{0}} = 2,{{L}_{1}} = 0,{{L}_{2}} = 1$ | ${{L}_{0}} = 2,{{L}_{1}} = 1,{{L}_{2}} = 1$ |
| Отрезки значений координат x1(1), x2(1) | [3.3241; 3.3962], [12.1768; 13.0449] | [3.3559; 3.4395], [12.2688; 13.1369] | [3.4008; 3.5048], [12.3812; 13.2519] | [3.4187; 3.5315], [12.4304; 13.3018] |
| Значение функционала (2.1) | –2.95377 | –2.96564 | –2.970204 | –2.97337 |
| Вектор коэффициентов в разложении (2.4) | 30.69; 31.16 | 173.756; 239.405 | 71.40; 96.33 | 216.79; 284.65 |
5. Решение задачи о стабилизации спутника. Рассматривается задача гашения вращательного движения спутника с помощью установленных на нем двигателей [48]. Движение твердого тела относительно центра инерции после перехода к безразмерным переменным имеет следующий вид:
Функционал качества управления отдельной траекторией характеризует затраты топлива при работе реактивных двигателей и степень выполнения конечных условий:
(5.1)
$I({{x}_{0}},d) = \underbrace {\int\limits_{{{t}_{0}}}^{{{t}_{f}}} {[\left| {{{u}_{1}}(t)} \right| + \left| {{{u}_{2}}(t)} \right| + \left| {{{u}_{3}}(t)} \right|]} dt}_{{{I}_{0}}({{x}_{0}},d)} + {{R}_{1}}p{{({{t}_{f}})}^{2}} + {{R}_{2}}q{{({{t}_{f}})}^{2}} + {{R}_{3}}r{{({{t}_{f}})}^{2}},$Требуется найти оптимальное программное управление и соответствующий ему пучок траекторий, минимизирующие функционал (1.5) с учетом (5.1). Приближенное значение критерия качества управления пучком траекторий вычисляется по формуле (2.1).
Задача была решена с использованием двух рассмотренных в разд. 3.1.3 и 3.1.4 мультиагентных алгоритмов с помощью сплайн-интерполяции (2.9), (2.10). При решении применялись кусочно-постоянный, кусочно-линейный, квадратичный и кубический сплайны. В каждом случае определялось наилучшее количество коэффициентов в разложении $L_{0}^{{{{u}_{1}}}},L_{0}^{{{{u}_{2}}}},L_{0}^{{{{u}_{3}}}}$ для каждого управления ${{u}_{1}}$, ${{u}_{2}}$, ${{u}_{3}}$, а также значения коэффициентов разложения (2.9).
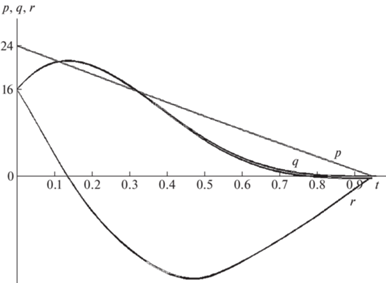
Для гибридного мультиагентного алгоритма, основанного на применении линейных регуляторов управления движением агентов, были подобраны следующие параметры: $NP = 101$, $NMAX = 8$, ${{P}_{{\max }}} = 12$, ${{k}_{s}} = 1$, ${{k}_{l}} = 5$, $h = 0.0001$. Коэффициенты штрафной функции (5.1): ${{R}_{1}} = {{R}_{2}} = {{R}_{3}}$ = 1000. Результаты, полученные этим методом, приведены в табл. 7. На рис. 5 и 6 представлены графики траекторий и координат программного управления для случая кубического сплайна.
Таблица 7.
Результаты решения задачи о стабилизации спутника. Гибридный мультиагентный алгоритм, основанный на использовании линейных регуляторов управления движением агентов
| Тип сплайна | Отрезки значений координат p(t1), q(t1), r(t1) | Количество коэффициентов в разложении для u1(t), u2(t), u3(t) | Коэффициенты разложения для u1(t), u2(t), u3(t) | Значение функциона-ла J |
|---|---|---|---|---|
| Кусочно-постоянный сплайн | [0.0782; 0.2282], [–0.1996; 0.1048], [–0.5772; 0.1065] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 8 \hfill \\ L_{0}^{{{{u}_{2}}}} = 8 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–132; –132; –148; –148; –148; –141.0195; –148; –141.242), (–15.9096; –1.8506; –50; 50; 40.9225; 49.8753; 25.0656; 50), (0.0077; 0.0949) | 175.75168 |
| Кусочно-линейный сплайн | [–0.0219; 0.1281], [–0.2079; 0.0823], [–0.6238 ;0.0785] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 4 \hfill \\ L_{0}^{{{{u}_{2}}}} = 6 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–147.5634; –136.6439; –146.6189; –148), (–19.6645; –12.5656; 10.7914; 30.8425; 48.6036; 50), (0.1; 0) | 170.38687 |
| Квадратичный сплайн | [–0.0597; 0.0903], [–0.1974; 0.1157], [–0.5481; 0.0786] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 3 \hfill \\ L_{0}^{{{{u}_{2}}}} = 3 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–144.3531; –141.6404; –148), (–42.588; 35.2651; 31.7664), (0.1; 0.0821) | 173.72941 |
| Кубический сплайн | [0.0079; 0.1579], [–0.2102; 0.097], [–0.5339; 0.0997] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 2 \hfill \\ L_{0}^{{{{u}_{2}}}} = 4 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–140.7678; –146.2378), (–49.9956; 19.9524; 28.9641; 43.4511), (0.0846; 0.1) | 169.48431 |
Рис. 5.
Графики координат программного управления u1(t), u2(t), u3(t), полученные при решении задачи о стабилизации спутника мультиагентным алгоритмом, основанным на использовании линейных регуляторов управления движением агентов (кубический сплайн)
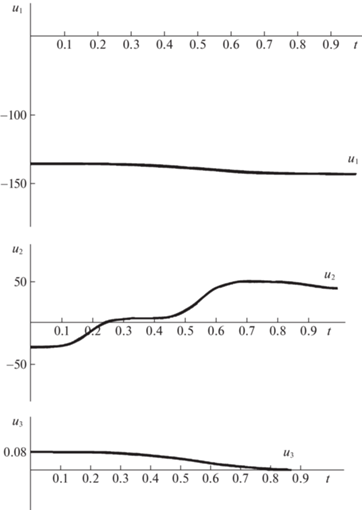
Рис. 6.
Графики поведения пучка траекторий p(t), q(t), r(t), полученные при решении задачи о стабилизации спутника методом линейных регуляторов (кубический сплайн)
Для гибридного мультиагентного алгоритма интерполяционного поиска подобраны следующие параметры: $NP = 40$, ${{I}_{{\max }}} = 500$, ${{M}_{1}} = 5$, ${{M}_{2}} = 10$, $PRTVector = 1$, $nstep = 5$, ${{b}_{2}} = 20$. Коэффициенты штрафной функции (5.1): ${{R}_{1}} = {{R}_{2}} = {{R}_{3}} = 1000.$ Результаты, найденные этим методом, рассмотрены в табл. 8.
Таблица 8.
Результаты решения задачи о стабилизации спутника. Гибридный алгоритм интерполяционного поиска
| Тип сплайна | Отрезки значений координат p(t1), q(t1), r(t1) | Количество коэффициентов в разложении для u1(t), u2(t), u3(t) | Коэффициенты разложения для u1(t), u2(t), u3(t) | Значение функционала J |
|---|---|---|---|---|
| Кусочно-постоянный сплайн | [0.1303; 0.2803], [–0.2345; 0.0645], [–0.5413; 0.1252] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 6 \hfill \\ L_{0}^{{{{u}_{2}}}} = 5 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–145.3921; –145.9129; –148; –137.2779; –138.4453; –135.8569), (–13.6532; –35.8449; 50; 50; 16.2456), (0.027; 0.0785) | 187.32285 |
| Кусочно-линейный сплайн | [0.0696; 0.2196], [–0.1709; 0.1221], [–0.5854; 0.0829] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 5 \hfill \\ L_{0}^{{{{u}_{2}}}} = 4 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–147.5928; –146.1051; –147.9969; –134.2685; –140.7262), (–44.5223; 11.5358; 34.9848; 47.5463), (0.0439; 0.098) | 176.46869 |
| Квадратичный сплайн | [–0.0062; 0.1438], [–0.2246; 0.0948], [–0.5577; 0.0438] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 4 \hfill \\ L_{0}^{{{{u}_{2}}}} = 3 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–141.2904; –146.5011; –145.2951; –136.6422), (–49.8131; 41.0978; 21.9337), (0.057; 0.0691) | 173.18994 |
| Кубический сплайн | [0.0192; 0.1692], [–0.2157; 0.1149], [–0.4574; 0.1184] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 3 \hfill \\ L_{0}^{{{{u}_{2}}}} = 3 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–137.7344; –146.6208; –142.7623), (–50; 43.5601; 15.245), (0.0002; 0) | 170.13441 |
В ходе решения задачи были получены данные о вычислительных затратах (времени решения задачи), приведенные в табл. 9. Используется процессор 11th Gen Intel(R) Core(TM) i7-1165G7 с частотой 2.80 GHz.
Таблица 9.
Вычислительные затраты при решении задачи о стабилизации спутника
| Метод | Тип сплайна | Значение функционала | Затраченное время t, c |
|---|---|---|---|
| Гибридный алгоритм интерполяционного поиска | Кусочно-постоянный сплайн | 187.32285 | 2819 |
| Кусочно-линейный сплайн | 176.46869 | 1150 | |
| Квадратичный сплайн | 173.18994 | 1945 | |
| Кубический сплайн | 170.13441 | 1412 | |
| Гибридный мультиагентный алгоритм, основанный на использовании линейных регуляторов управления движением агентов | Кусочно-постоянный сплайн | 175.75168 | 130 |
| Кусочно-линейный сплайн | 170.38687 | 99 | |
| Квадратичный сплайн | 173.72941 | 317 | |
| Кубический сплайн | 169.48431 | 306 |
Анализ результатов, представленных в табл. 7–9, позволяет сделать вывод о том, что для данной задачи применение гибридного мультиагентного алгоритма, основанного на использовании линейных регуляторов управления движением агентов, приводит к лучшим результатам. При этом с ростом степени сплайна минимальное значение функционала уменьшается, за исключением квадратичного сплайна в случае гибридного мультиагентного алгоритма, базирующегося на применении линейных регуляторов управления движением агентов. Также полученные результаты сравниваются с решением задачи методом, имитирующим поведение стаи криля [39] (табл. 10).
Таблица 10.
Результаты решения задачи о стабилизации спутника. Метод, имитирующий поведение стаи криля
| Тип сплайна | Отрезки значений координат p(t1), q(t1), r(t1) | Количество коэффициентов в разложении для u1(t), u2(t), u3(t) | Коэффициенты разложения для u1(t), u2(t), u3(t) | Значение функциона-ла J | Затрачен-ное время t, c |
|---|---|---|---|---|---|
| Кусочно-постоянный сплайн | [–0.0007; 0.1493], [–0.2057; 0.0862], [–0.7656; –0.0485] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 6 \hfill \\ L_{0}^{{{{u}_{2}}}} = 6 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–142.63; –133.95; –145.94; –144.13; –145.14; –147.36), (15.64; –33.95; 7.26; 43.89; 47.95; 48.65), (0.07; 0.09) | 191.26713 | 262 |
| Кусочно-линейный сплайн | [0.0586; 0.2086], [–0.1992; 0.1074], [–0.5253; 0.1166] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 6 \hfill \\ L_{0}^{{{{u}_{2}}}} = 4 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–137.77; –144.66; –144.06; –142.31; –147.34; –137.43), (–46.52; 12.53; 43.75; 28.82), (0.07; 0.07) | 173.2539 | 200 |
| Квадратичный сплайн | [–0.0205; 0,1295], [–0.1988; 0,1165], [–0.5284; 0,096] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 4 \hfill \\ L_{0}^{{{{u}_{2}}}} = 3 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–136.03; –144.01; –145.50; –146.97), (–41.23; 35.57; 31.16), (0.08; 0.02) | 170.01691 | 205 |
| Кубический сплайн | [–0.0018; 0.1482], [–0.2114; 0.0875], [–0.5573; 0.0986] | $\begin{gathered} L_{0}^{{{{u}_{1}}}} = 2 \hfill \\ L_{0}^{{{{u}_{2}}}} = 4 \hfill \\ L_{0}^{{{{u}_{3}}}} = 2 \hfill \\ \end{gathered} $ | (–142.5836; –144.5378), (–42.9706; 15.1389; 29.766; 49.0521), (0.0166; 0.0322) | 169.4311 | 340 |
Заключение. Рассмотрена задача поиска оптимального управления пучками траекторий в условия неопределенности задания начальных условий при наличии неполной информации о векторе состояния. Для решения этой задачи предложены различные структуры, которые определяют закон управления, основанные на разложениях управления по различным системам базисных функций. Предложена методика решения поставленной смешанной целочисленно-непрерывной параметрической задачи условной оптимизации. В качестве процедуры нахождения целочисленных параметров использовалась модифицированная процедура линейного поиска, а для определения коэффициентов разложения – два гибридных мультиагентные метода: алгоритм интерполяционного поиска и алгоритм на базе линейных регуляторов управления движением агентов. Эффективность представленного подхода исследована на модельных примерах и прикладной задаче стабилизации спутника.
Список литературы
Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.: Наука, 1977. 392 с.
Куржанский А.Б., Месяц А.И. Управление эллипсоидальными траекториями. Теория и вычисления // ЖВМ и МФ. 2014. Т. 54. № 3. С. 404–414.
Kurzhanski A.B., Filippova T.F. On the Theory of Trajectory Tubes — A Mathematical Formalism for Uncertain Dynamics, Viability and Control. Advances in Nonlinear Dynamics and Control: A Report from Russia. Progress in Systems and Control Theory. V. 17. Boston, MA: Birkhäuser, 1993.
Зубов В.И. Синтез многопрограммных устойчивых управлений // Докл. АН СССР. 1991. Т. 318. № 2. С. 274–277.
Овсянников Д.А. Математические методы управления пучками. Л.: Изд-во ЛГУ, 1980. 228 с.
Овсянников Д.А. Моделирование и оптимизация динамики пучков заряженных частиц. Ленинград: Изд-во ЛГУ, 1990, 312 с.
Овсянников Д.А., Егоров Н.В. Математическое моделирование систем формирования электронных ионных пучков. СПб: Изд-во СПбГУ, 1998. 276 с.
Овсянников Д.А., Мизинцева М.А., Балабанов М.Ю., Дуркин А.П., Едаменко Н.С., Котина Е.Д., Овсянников А.Д. Оптимизация динамики пучков траекторий c использованием гладких и негладких функционалов. Ч. 1 // Вестн. СПбГУ. Сер. 10. Прикладная математика. Информатика. Процессы управления. 2020. Т. 16. № 1. С. 73–84.
Черноусько Ф.Л. Оценивание фазового состояния динамических систем. М.: Наука, 1988. 320 с.
Brockett R.W. Optimal Control of the Liouville Equation // AMS IPStudies in Advanced Mathematics. 2007. V. 39. P. 23–35.
Henrion D., Korda M. Convex Computation of the Region of Attraction of Polynomial Control Systems // European Control Conf, (ECC). Zurich, 2013. P. 676–681.
Halder A., Bhattacharya R. Dispersion Analysis in Hypersonic Flight During Planetary Entry Using Stochastic Liouville Equation // J. Guidance, Control, and Dynamics. 2011. V. 34. № 2. P. 459–474.
Пантелеев А.В., Семенов В.В. Синтез оптимальных систем управления при неполной информации. М.: Изд-во МАИ, 1992. 192 с.
Бортаковский А.С. Оптимальное и субоптимальное управления пучками траекторий детерминированных логико-динамических систем // Изв. РАН. ТиСУ. 2009. № 6. С. 29–46.
Бортаковский А.С. Оптимальное и субоптимальное управления пучками траекторий детерминированных систем автоматного типа // Изв. РАН. ТиСУ. 2016. № 1. С. 5–26.
Бортаковский А.С., Немыченков Г.И. Оптимальное в среднем управление детерминированными переключаемыми системами при наличии дискретных неточных измерений // Изв. РАН. ТиСУ. 2019. № 1. С. 52–57.
Пановский В.Н., Пантелеев А.В. Метаэвристические интервальные методы поиска оптимального в среднем управления нелинейными детерминированными системами при неполной информации о ее параметрах // Изв. РАН. ТиСУ. 2017. № 1. С. 53–64.
Пантелеев А.В., Письменная В.А. Применение меметического алгоритма в задаче оптимального управления пучками траекторий нелинейных детерминированных систем с неполной обратной связью // Изв. РАН. ТиСУ. 2018. № 1. С. 27–38.
Давтян Л.Г., Пантелеев А.В. Метод параметрической оптимизации нелинейных непрерывных систем совместного оценивания и управления // Изв. РАН. ТиСУ. 2019. № 3. С. 34–47.
Пантелеев А.В. Метаэвристические алгоритмы оптимизации законов управления динамическими системами. М.: Факториал, 2020. 564 с.
Handbook of Metaheuristics / Eds M. Gendreau, J-Y. Potvin. N.Y.: Springer, 2019. P. 604.
Handbook of Metaheuristics / Eds F.W. Glover, G.A. Kochenberger. Boston, MA: Kluwer Acad. Publ., 2003. P. 557.
Encyclopedia of Optimization / Eds C.A. Floudas, P.M. Pardalos. N.Y.: Springer, 2009. P. 4626.
Floudas C.A. Pardalos P.M., Adjiman C.S. Handbook of Test Problems in Local and Global Optimization. Dordrecht: Kluwer Acad. Publ., 1999. P. 447.
Practical Handbook of Genetic Algorithms. Applications / Ed. D.L. Chambers N.Y.: Chapman and Hall; CRC Press, 2001. P. 520.
Handbook of Memetic Algorithms / Eds F. Neri, C. Cotta, P. Moscato. N.Y.: Springer, 2012. P. 309.
Yang X.S. Nature-Inspired Metaheuristic Algorithms. Frome, UK: Luniver Press, 2010. P. 148.
Гладков В.А., Курейчик В.В. Биоинспирированные методы в оптимизации. М.: Физматлит, 2009. 384 с.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 446 с.
Пантелеев А.В., Скавинская Д.В. Метаэвристические алгоритмы глобальной оптимизации. М.: Вузовская книга, 2019. 232 с.
Panteleev A., Karane M. Application of Multi-agent Optimization Methods Based on the Use of Linear Regulators and Interpolation Search for a Single Class of Optimal Deterministic Control Systems // Applied Mathematics and Computational Mechanics for Smart Applications. Singapore: Springer, 2021.
Panteleev A., Karane M. Multi-agent Optimization Algorithms for a Single Class of Optimal Deterministic Control Systems // Advances in Theory and Practice of Computational Mechanics. Singapore: Springer, 2020.
Karane M., Panteleev A. Benchmark Analysis of Novel Multi-agent Optimization Algorithm Using Linear Regulators for Agents Motion Control // IOP Conf. Series: Materials Science and Engineering. Alushta, 2020.
Каранэ М.С. Программный комплекс мультиагентных алгоритмов условной оптимизации // Федеральная служба по интеллект. собственности. Св-во о гос. регистрации программы для ЭВМ № 2021662276. 2021.
Davendra D., Zelinka I. Self-Organizing Migrating Algorithm. Methodology and Implementation // Studies in Computational Intelligence. V. 626. Springer, 2016.
Duarte A., Marti R., Glover F., Gortazar F. Hybrid Scatter Tabu Search for Unconstrained Global Optimization // Annals of Operations Research. 2011. V. 183. 31. № 1. P. 95–123.
Elbeltagi E., Hegazy T., Grierson D. A Modified Shuffled Frog-leaping Optimization Algorithm // Structure and Infrastructure Engineering. 2007. URL: http// www.tandf.co.uk/J.s.
Eusuff M.M., Lansey K.E., Pasha F. Shuffled Frog-leaping Algorithm: a Memetic Meta-heuristic for Discrete Optimization // Engineering Optimization. 2006. V. 38. № 2. P. 129–154.
Gandomi A.H., Alavi A.H. Krill herd: A New Bio-inspired Optimization Algorithm// Commun. Nonlinear Sci. Numer. Simulat. 2012. V. 17. № 12. P. 4831–4845.
Mehrabian A.R., Lucas C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization // Ecological Informatics. 2006. V. 1. P. 355–366.
Kennedy J., Eberhart R. Particle Swarm Optimization // URL: http://www.engr.iupui.edu/ ~shi/ Coference/psopap4.html.
Rybakov K.A. Applying Spectral Form of Mathematical Description for Representation of Iterated Stochastic Integrals // Differencialnie Uravnenia i Protsesy Upravlenia. 2019. № 4. P. 1–31.
Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. Radial Basis Function Interpolation // Numerical Recipes: The Art of Scientific Computing (3rd ed.). N.Y.: Cambridge University Press, 2007. P. 1256.
Buhmann M.D. Radial Basis Functions: Theory and Implementations. N.Y.: Cambridge University Press, 2003. P. 260.
Fahroo F., Ross I.M. Direct Trajectory Optimization by a Chebyshev Pseudospectral Method // J. Guidance, Control, and Dynamics. 2002. V. 25. № 1. P. 160–166.
Garg D., Patterson M.A., Hager W.W., Rao A.V., Benson D., Huntington G.T. A Unified Framework for the Numerical Solution of Optimal Control Problems Using Pseudospectral Methods // Automatica. 2010. V. 46. № 11. P. 1843–1851.
Финкельштейн Е.А. Вычислительные технологии аппроксимации множества достижимости управляемой системы: автореф. дис. … канд. техн. наук: 05.13.01. Иркутск: Сиб. аэрокосм. акад. им. акад. М.Ф. Решетнева, 2018. 19 с.
Крылов И.А. Численное решение задачи об оптимальной стабилизации спутника // ЖВМ и МФ. 1968. Т. 8. № 1. С. 203–208.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления