Известия РАН. Теория и системы управления, 2022, № 5, стр. 40-49

Введение. Рассматривается задача оптимальной фильтрации в стохастических системах наблюдения с непрерывным и дискретным временем. Эта задача состоит в оценивании траектории ненаблюдаемого случайного процесса по наблюдениям другого случайного процесса, доступным к текущему моменту времени [1]. Математическая модель стохастической системы наблюдения состоит из двух уравнений, одно из которых описывает ненаблюдаемый случайный процесс (объект наблюдения), а другое – наблюдаемый случайный процесс (измерительная система). Оценивание проводится с помощью динамической системы, называемой фильтром, преобразующей измерения в оценку вектора состояния объекта наблюдения. Синтез фильтра осуществляется в соответствии с заданным критерием качества.

Цель работы состоит в сравнении фильтров частиц для систем наблюдения с непрерывным [2] и дискретным временем [2–4]. Такие фильтры основаны на методе статистических испытаний, или методе Монте-Карло. Их достаточно просто реализовать на практике в виде прикладных программ, однако метод статистических испытаний требует значительных вычислительных ресурсов для достижения приемлемой точности. С развитием вычислительной техники и технологий параллельного программирования фильтры частиц все чаще привлекают внимание инженеров, так как появилась возможность их реализации в реальном масштабе времени даже для сложных динамических систем [5].

По-видимому, одной из первых работ, в которой сформированы алгоритмы фильтров частиц для стохастических систем наблюдения с непрерывным и дискретным временем, была [6]. В настоящее время по фильтрам частиц существует обширная литература, включающая журнальные публикации и монографии, обзор которых здесь не приводится. В этой статье сравнение фильтров частиц проводится в контексте их практической реализации.

Отличие рассматриваемых стохастических систем наблюдения состоит в математическом аппарате, который применяется для их описания. Для систем с непрерывным и дискретным временем – это стохастические дифференциальные и разностные уравнения соответственно. Нахождение аналитических решений стохастических дифференциальных уравнений представляет собой сложную задачу, используемые для этого приемы применимы в довольно ограниченном числе частных случаев [7]. Даже если аналитическое решение найдено, то возникает задача моделирования траекторий такого решения. Наиболее часто для приближенного нахождения решений стохастических дифференциальных уравнений осуществляется переход к разностным уравнениям, т.е. применяются численные методы решения. Это уменьшает различия между стохастическими системами наблюдения с непрерывным и дискретным временем. И здесь возникает закономерный вопрос о том, какой алгоритм для решения задачи фильтрации выбрать: алгоритм непрерывного  фильтра частиц с учетом дискретизации по времени или алгоритм дискретного фильтра частиц. При некоторых допущениях оба алгоритма являются эквивалентными, однако с точки зрения практической реализации предпочтительнее оказывается алгоритм дискретного фильтра частиц. Это продемонстрировано на тестовой задаче оценивания погрешности показаний навигационной системы о координатах объекта с использованием корректирующих измерений [8, 9].

1. Задачи оптимальной фильтрации для стохастических систем наблюдения с непрерывным и дискретным временем. Будем рассматривать скрытую марковскую модель стохастической системы наблюдения с непрерывным временем, которая включает уравнение модели объекта наблюдения и уравнение измерительной системы:

Уравнение (1.1) – стохастическое дифференциальное уравнение в смысле Ито (если записать его в интегральном виде, то стохастический интеграл в правой части следует понимать как интеграл Ито [10]). В нем используются следующие обозначения: $X \in {{\mathbb{R}}^{n}}$ – $n$-мерный вектор состояния, $t \in {\text{T}} = [0,T]$, T – заданный отрезок времени функционирования системы; f(t, x) : ${\text{T}} \times {{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{n}}$, $\sigma (t,x):{\text{T}} \times {{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{{n \times s}}}$; $W(t)$ – s-мерный стандартный винеровский случайный процесс, X₀ и $W(t)$ независимы. Закон распределения начального вектора состояния X₀ задан, в частном случае X₀ – детерминированный $n$-мерный вектор.

Уравнение (1.2) – также  стохастическое  дифференциальное уравнение, в нем $Y \in {{\mathbb{R}}^{m}}$ – $m$-мерный вектор измерений; $c(t,x):{\text{T}} \times {{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{m}}$, $\zeta (t):{\text{T}} \to {{\mathbb{R}}^{{m \times d}}}$; $V(t)$ – $d$-мерный стандартный винеровский случайный процесс, не зависящий от винеровского процесса $W(t)$. Здесь важно, что слагаемое, содержащее $dV(t)$, не включает случайных процессов $X(t)$ и $Y(t)$. При этом предполагается, что матрица $\eta (t) = \zeta (t){{\zeta }^{{\text{T}}}}(t)$ невырождена, т.е. $\det \eta (t) \ne 0$ и существует обратная матрица ${{\eta }^{{ - 1}}}(t)$ при любом $t \in {\text{T}}$.

Перечисленные функции $f(t,x)$, $\sigma (t,x)$, $c(t,x)$ и $\zeta (t)$ удовлетворяют условиям существования и единственности решений стохастических дифференциальных уравнений (условия линейного роста и Липшица по x), кроме того, ${\text{E|}}{{X}_{0}}{{{\text{|}}}^{2}} < \infty $, где E означает математическое ожидание. Более подробно эти условия изложены, например, в [10, 11].

Задача оптимальной фильтрации для стохастической системы наблюдения (1.1), (1.2) заключается в нахождении оценки $\hat {X}(t)$ вектора состояния по доступным к текущему моменту времени t измерениям $Y_{0}^{t} = \left\{ {Y(\tau ),~\tau \in [0,t]} \right\}$ в виде $\hat {X}(t) = \Phi (t,Y_{0}^{t})$, т.е. требуется синтезировать фильтр, который определяется функцией $\Phi (t,Y_{0}^{t})$, преобразующий измерения $Y_{0}^{t}$ в оценку вектора состояния объекта наблюдения.

Синтез фильтра осуществляется по заданному критерию качества, обеспечивающему минимум среднего риска в каждый момент времени $t \in {\text{T}}$: ${\text{E}}\Pi (t,\mathcal{E}(t)) \to \min $, где минимум берется по всем допустимым функциям $\Phi (t,Y_{0}^{t})$, $\Pi (t,\varepsilon )$ – функция потерь, $\mathcal{E}(t) = X(t) - \hat {X}(t)$ – вектор ошибки оценивания [1]. Ограничимся наиболее часто используемой в приложениях квадратичной функцией потерь $\Pi (t,\varepsilon ) = {{\varepsilon }^{{\text{T}}}}L(t)\varepsilon $, для которой $L(t)$ – положительно определенная матрица весовых коэффициентов размеров n × n. Например, при $L(t) = E$, где E – единичная матрица, функция потерь равна сумме квадратов координат вектора ошибки оценивания.

Известно [1], что для квадратичной функции потерь оптимальная оценка вектора состояния задается выражением

т.е. оптимальная оценка представляет собой апостериорное математическое ожидание вектора состояния. Эта оценка помимо того, что обеспечивает минимум среднеквадратического отклонения ошибки, является еще и несмещенной, т.е. ${\text{E}}\mathcal{E}(t) = {\text{E}}[X(t) - \hat {X}(t)]$ = 0.

Далее запишем уравнения скрытой марковской модели стохастической системы наблюдения с дискретным временем. Эти уравнения, как и для непрерывного случая, представлены уравнением модели объекта наблюдения и уравнением измерительной системы (стохастическое разностное уравнение, уравнение регрессии):

где $X \in {{\mathbb{R}}^{n}}$ – $n$-мерный вектор состояния, $Z \in {{\mathbb{R}}^{m}}$ – m-мерный вектор измерений, $k \in {\text{K}} = \{ \overline {1,N} \} $ – дискретное время; ${{f}_{k}}(x):{{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{n}}$, ${{\sigma }_{k}}(x):{{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{{n \times s}}}$, ${{c}_{k}}(x):{{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{m}}$, ${{\zeta }_{k}}$ – числовая матрица размеров $m \times d$; ${{W}_{k}}$ и ${{V}_{k}}$ – $s$- и $d$-мерный случайные векторы, координаты которых независимы в совокупности и имеют стандартное нормальное распределение. При этом предполагается, что матрица ${{\eta }_{k}} = {{\zeta }_{k}}\zeta _{k}^{{\text{T}}}$ невырождена, т.е. $\det {{\eta }_{k}} \ne 0$ и существует обратная матрица $\eta _{k}^{{ - 1}}$ при любом $k \in {\text{K}}$. Закон распределения начального вектора состояния X₀ задан, X₀ не зависит от ${{W}_{k}}$ и ${{V}_{k}}$. В частном случае X₀ – детерминированный $n$-мерный вектор.

Задача оптимальной фильтрации для стохастической системы наблюдения (1.3), (1.4) заключается в нахождении оценки ${{\hat {X}}_{k}}$ вектора состояния по доступным к текущему моменту времени k измерениям $Z_{1}^{k} = \{ {{Z}_{i}},~i = \overline {1,k} \} $ в виде ${{\hat {X}}_{k}} = {{\Psi }_{k}}(Z_{1}^{k})$. Другими словами, требуется синтезировать фильтр, который определяется функцией ${{\Psi }_{k}}(Z_{1}^{k})$, преобразующий измерения $Z_{1}^{k}$ в оценку вектора состояния объекта наблюдения.

Как и для системы с непрерывным временем, фильтр необходимо синтезировать в соответствии с заданным критерием качества, который обеспечивает минимум среднего риска в каждый момент времени $k \in {\text{K}}$: ${\text{E}}{{\Pi }_{k}}({{\mathcal{E}}_{k}}) \to \min $. Выберем квадратичную функцию потерь ${{\Pi }_{k}}(\varepsilon ) = {{\varepsilon }^{{\text{T}}}}{{L}_{k}}\varepsilon $, где L_k – положительно определенная матрица весовых коэффициентов размеров n × n, например ${{L}_{k}} = E$, и ${{\mathcal{E}}_{k}} = {{X}_{k}} - {{\hat {X}}_{k}}$ – вектор ошибки оценивания. Тогда [3]

т.е. оптимальная оценка представляет собой апостериорное математическое ожидание вектора состояния. Эта оценка обеспечивает минимум среднеквадратического отклонения ошибки и также является несмещенной, т.е. ${\text{E}}{{\mathcal{E}}_{k}} = {\text{E}}[{{X}_{k}} - {{\hat {X}}_{k}}] = 0$.

Отметим, что уравнения модели стохастической системы наблюдения с дискретным временем записаны таким образом, чтобы такую модель можно было согласовать с уравнениями модели стохастической системы наблюдения с непрерывным временем. Именно этим обусловлено то, что векторы W_k и V_k имеют нормальное распределение, а ${{\zeta }_{k}}$ – числовая матрица. Вообще говоря, обе математические модели могут иметь более общий вид [12], однако в этой работе ограничимся именно такой постановкой задачи.

2. Связь моделей стохастических систем наблюдения с непрерывным и дискретным временем. Получим аналоги уравнений (1.1), (1.2) с дискретным временем. Для этого определим точки $\{ {{t}_{k}}\} $ на отрезке T таким образом, что

где $h$ – заданное положительное число, $h \ll T$, и воспользуемся разностной схемой метода Эйлера–Маруямы [13]: т.е. $({{X}_{k}},{{Y}_{k}})$ – дискретная аппроксимация пары случайных процессов $(X(t),Y(t))$, пара $({{X}_{k}},{{Y}_{k}})$ при фиксированном k соответствует моменту времени ${{t}_{k}}$. Кроме того, с помощью обозначения ${{Z}_{{k - 1}}} = \left( {{{Y}_{k}} - {{Y}_{{k - 1}}}} \right){\text{/}}h$ перепишем соотношение (2.2) в виде

Сравнивая уравнения (1.3), (1.4) с (2.1), (2.3), имеем

с учетом того, что для модели (2.1), (2.3) происходит запаздывание на один такт в части измерений. Последнее обстоятельство обусловлено применением явного численного метода, в результате для модели (1.1), (1.2) требуется измерять начальный вектор состояния X₀ в отличие от модели (1.3), (1.4). Тогда где $Z_{0}^{{k - 1}} = \{ {{Z}_{i}},~i = \overline {0,k - 1} \} $.

Отметим, что для получения аналога уравнений (1.1), (1.2) с дискретным временем выбран наиболее простой и наименее точный метод численного решения стохастических дифференциальных уравнений, имеющий порядок p = 0.5 сильной сходимости [13]. Однако именно разностная схема метода Эйлера–Маруямы с последующим предельным переходом по $h \to 0$ применяется при доказательстве утверждений для решений стохастических дифференциальных уравнений [10], и эта схема позволяет получить уравнения, которые наиболее близки по структуре к уравнениям (1.3), (1.4). Другие методы могут усложнить аналоги уравнений (1.1), (1.2) с дискретным временем. Использование методов, имеющих порядок сильной сходимости $p \geqslant 0.5$ (методы типа Рунге–Кутты [13, 14], Розенброка [15, 16], Мильштейна [17], Кузнецова [18, 19] и др.), может привести к модели стохастической системы наблюдения другого класса, например, уравнение измерительной системы будет содержать не только ${{V}_{k}}$, но и ${{W}_{k}}$. Это характерно для разностных схем “предиктор-корректор” или для схем, в которых используется регуляризация, они обеспечивают лучший результат с точки зрения приближенного моделирования траекторий стохастической системы наблюдения с непрерывным временем, но усложняют задачу фильтрации для системы с дискретным временем. Для некоторых разностных схем в уравнения вводятся дополнительные случайные величины с распределением, отличным от нормального.

Здесь нужно указать, что усложнения задачи фильтрации можно избежать, если применять приведенные численные методы только для уравнения объекта наблюдения, а для уравнения измерительной системы ограничиться методом Эйлера–Маруямы. Это оправдано тем, что вектор измерений не входит в уравнение объекта наблюдения, а также в правую часть уравнения измерительной системы. В качестве варианта можно предложить использование неявного численного метода Эйлера–Маруямы для уравнения измерительной системы, тогда при ${{Z}_{k}} = ({{Y}_{k}} - {{Y}_{{k - 1}}}){\text{/}}h$ не будет эффекта запаздывания на один такт в части измерений.

3. Непрерывные и дискретные фильтры частиц. Фильтры частиц – название для целого семейства методов и алгоритмов решения задачи оптимальной фильтрации для стохастических систем наблюдения с непрерывным и дискретным временем, а также гибридных систем. Такие методы основаны на моделировании объекта наблюдения с учетом априорной информации, т.е. известных уравнения модели объекта наблюдения и закона распределения начального вектора состояния. Оптимальная оценка вычисляется с помощью результатов моделирования и доступных измерений в соответствии с заданным критерием качества.

Под частицей понимается пара $(X(t),\omega (t))$ для модели (1.1), (1.2) или $({{X}_{k}},{{\omega }_{k}})$ для модели (1.3), (1.4), где $\omega (t)$ или ${{\omega }_{k}}$ называют весом, или весовым коэффициентом [2, 3]. Поскольку для модели (1.1), (1.2) используется ее аналог (2.1), (2.3) с дискретным временем, в приведенной далее методике указаны только составляющие пары $({{X}_{k}},{{\omega }_{k}})$.

Случайный процесс $\omega (t)$ для модели (1.1), (1.2) определяется соотношением [2]

а при переходе от модели (1.1), (1.2) к модели (2.1), (2.3), т.е. при дискретизации с шагом h,

Случайная последовательность ${{\omega }_{k}}$ для модели (1.3), (1.4) удовлетворяет следующему рекуррентному соотношению [3]:

где ${{p}_{k}}(x)$ – плотность распределения вероятностей случайного вектора ${{\zeta }_{k}}{{V}_{k}}$ (она выполняет роль функции правдоподобия [2]): так как этот вектор имеет гауссовское распределение с нулевым математическим ожиданием и ковариационной матрицей ${{\eta }_{k}}$. Для модели (2.1), (2.3) имеем

Оптимальная оценка для фиксированных измерений $Y_{0}^{t}$ в модели (1.1), (1.2) выражается следующим образом:

Если рассматривается модель (1.3), (1.4), то для фиксированных измерений $Z_{1}^{k}$

где ${{\omega }_{k}}$ удовлетворяет (3.3). Для модели (2.1), (2.3) формула оптимальной оценки аналогична с учетом того, что ${{\omega }_{k}}$ удовлетворяет (3.2) и используются измерения $Z_{0}^{{k - 1}}$.

Покажем, что формулы (3.2) и (3.4) эквиваленты (эквивалентность состоит в том, что оптимальная оценка не зависит от выбора соотношения для весового коэффициента (3.2) или (3.4), но эти соотношения определяют разные случайные последовательности весовых коэффициентов). Поскольку измерения зафиксированы, то числитель и знаменатель правой части выражения (3.5) можно умножить на одну и ту же детерминированную величину ${{\Gamma }_{k}}$ и внести ее под знак математического ожидания.

Рассмотрим подробнее выражение ${{p}_{k}}({{Z}_{k}} - {{c}_{k}}({{X}_{k}}))$:

следовательно,

Таким образом, если в качестве детерминированной величины ${{\Gamma }_{k}}$ выбрать

и умножить на нее числитель и знаменатель правой части выражения (3.5), то оптимальная оценка останется неизменной, но случайная последовательность весовых коэффициентов будет определяться формулой (3.2), а не (3.4). Здесь, однако, нужно подчеркнуть, что при использовании разностной схемы для (3.1), отличной от приведенной выше, так просто согласовать правила нахождения весовых коэффициентов вряд ли удастся.

Подводя итог этого раздела, кратко опишем методику решения задачи фильтрации. Она состоит в последовательном моделировании реализаций вектора состояния ${{X}_{k}}$, согласно уравнению модели объекта наблюдения (реализации начального вектора состояния X₀ моделируются, согласно заданному закону распределения), т.е. формировании траекторий объекта наблюдения (формулы (2.1) и (1.3)), моделировании соответствующих весовых коэффициентов ${{\omega }_{k}}$ с учетом доступных измерений, позволяющих преобразовать априорные оценки моментов вектора состояния или его распределения в апостериорные (фильтрация) для каждого момента времени (см. формулы (3.2) и (3.3)), вычислении оценки ${{\hat {X}}_{k}}$ по реализациям вектора состояния ${{X}_{k}}$ и весовых коэффициентов ${{\omega }_{k}}$. Возможны дополнительные шаги, например перевыборка при вырождении апостериорного распределения.

4. Практическая реализация непрерывных и дискретных фильтров частиц. Непосредственная реализация в виде прикладных программ описанных выше фильтров частиц включает моделирование пар $(X_{k}^{i},\omega _{k}^{i})$, где i – номер реализации, и статистическую обработку результатов моделирования. Таким образом, моделируется объект наблюдения и весовые коэффициенты методом статистических испытаний, или методом Монте-Карло. Общее количество реализаций M задается заранее, его выбор определяется компромиссом между допустимым временем расчетов и их точностью. Время расчетов зависит от M линейно. Точность оценивания подчиняется более сложному закону. Во-первых, при синтезе оптимального фильтра, преобразующего измерения в оценку вектора состояния объекта наблюдения, минимизируется среднеквадратическое отклонение ошибки, но, как правило, эта характеристика больше нуля. Во-вторых, если задача фильтрации рассматривается для стохастической системы наблюдения с непрерывным временем, то численное моделирование траекторий объекта наблюдения сопряжено с применением численных методов решения стохастических дифференциальных уравнений, каждый из которых имеет свою методическую погрешность. В-третьих, есть и статистическая погрешность метода, она, как известно, обратно пропорциональна величине $\sqrt M $. Кроме того, есть погрешности, обусловленные применением псевдослучайных последовательностей и машинной арифметики.

Пары $(X_{k}^{i},\omega _{k}^{i})$ для стохастической системы наблюдения с непрерывным временем при дискретизации с шагом $h$ определяются рекуррентными соотношениями (2.1), (3.2), а для стохастической системы наблюдения с дискретным временем – (1.3), (3.3). Формула для оценки вектора состояния, которая получается из (3.5) заменой математического ожидания выборочным средним, при этом записывается следующим образом:

причем для каждого шага необходимо дополнительно проводить нормировку весовых коэффициентов, т.е. при начальном условии $\omega _{0}^{i} = 1{\text{/}}M$.

Такая нормировка выполняет важную функцию, а именно при ее использовании минимизируются ошибки переполнения, поскольку иначе величины $\omega _{k}^{i}$ при ${{p}_{k}}(0) > 1$ могут возрастать с ростом k для некоторых номеров i. Это замечание относится к рекуррентным соотношениям (3.3) и (3.4). Однако при использовании соотношения (3.2), как показано в работе [20], такой нормировки может оказаться недостаточно. Ошибки переполнения могут возникать из-за того, что число ${{{\text{e}}}^{\mu }}$, где для фиксированного $k$

оказывается больше допустимой максимальной величины, которую может обрабатывать процессор при операциях с числами с плавающей точкой. Например, при одинарной точности (для хранения в памяти числа требуется 32 бита) значение $\mu $ ограничено сверху величиной 88.722, а при двойной точности (для хранения в памяти числа требуется 64 бита) – величиной 706.893 с учетом округления.

В [20] была предложена модификация алгоритма непрерывного фильтра частиц, основанного на вычислении весовых коэффициентов по формуле (3.2). Эта модификация заключалась в том, что вместо формулы (3.2) использовалось следующее рекуррентное соотношение:

где параметр ${{\gamma }_{k}}$ определяется для каждого момента времени из условия равенства нулю максимума выражения в фигурных скобках по всем имеющимся реализациям.

Напомним, что умножение числителя и знаменателя правой части выражения (3.5) на одну и ту же детерминированную величину ${{\Gamma }_{k}}$ не влияет на результат оценивания. Здесь за исходное правило нахождения весовых коэффициентов взята формула (3.2), а в качестве такого множителя выступает ${{\Gamma }_{k}} = {{{\text{e}}}^{{ - {{\gamma }_{k}}}}}$.

Наиболее эффективно при практической реализации непрерывных и дискретных фильтров частиц использовать рекуррентное соотношение

вместо (3.2) и (3.4) и ${{\omega }_{k}} = {{\omega }_{{k - 1}}}p_{k}^{*}({{Z}_{k}} - {{c}_{k}}({{X}_{k}}))$ вместо (3.3), где

Такие соотношения гарантируют отсутствие ошибок переполнения: они порождают невозрастающую последовательность весовых коэффициентов, поскольку по сравнению с соотношениями (3.3) и (3.4) отсутствует коэффициент ${{[{{(2\pi )}^{{n{\text{/}}2}}}\sqrt {\det {{\eta }_{k}}} ]}^{{ - 1}}}$, не влияющий на результат оценивания, хотя проблема вырождения весовых коэффициентов остается. В отличие от соотношения (4.2) не требуется находить максимальный элемент по множеству реализаций, что сокращает время вычислений и упрощает формирование параллельного алгоритма фильтрации.

5. Вычислительный эксперимент. Для сравнения фильтров частиц в классе стохастических систем с непрерывным и дискретным временем рассмотрим тестовую задачу оценивания погрешности показаний навигационной системы о координатах объекта с использованием корректирующих измерений (данных карты геофизического поля) [8, 9].

Будем полагать, что объект движется прямолинейно с заданной постоянной скоростью, т.е. координата объекта описывается функцией $x(t) = {{x}_{0}} + Vt$, где ${{x}_{0}} = 8{\mkern 1mu} $ км – начальная координата, $V = 0.005{\mkern 1mu} $ км/с – скорость движения, T = 200 c.

Измерения (показания навигационной системы) имеют вид $z(t) = x(t) + \Delta _{z}^{*}$, где $\Delta _{z}^{*}$ – реализация гауссовской центрированной случайной величины ${{\Delta }_{z}}$ с дисперсией $\sigma _{z}^{2}$ (ошибка навигационной системы), σ_z = 1 км. Дополнительно имеются измерения аномалий силы тяжести, представленные в виде $y(t) = c(x(t)) + {{\Delta }_{y}}(t)$, где $c(x)$ – полином заданной степени q с известными коэффициентами:

в котором:

при q = 1: ${{F}_{0}} = 31{\mkern 1mu} $ мГал, ${{F}_{1}} = 0.08$ мГал/км;

при q = 2: ${{F}_{0}} = 45$ мГал, ${{F}_{1}} = - 3$ мГал/км, ${{F}_{2}} = 0.15$ мГал/км²;

при q = 3: ${{F}_{0}} = 65{\mkern 1mu} $ мГал, ${{F}_{1}} = - 10{\mkern 1mu} $ мГал/км, ${{F}_{2}} = 1.0$ мГал/км², ${{F}_{3}} = - 0.03$ мГал/км³,

т.е. рассматриваются три варианта аппроксимации геофизического поля полиномами первой, второй и третьей степеней. Далее, ${{\Delta }_{y}}(t)$ – центрированный гауссовский белый шум интенсивности r², r = 1 мГал/$\sqrt {{\text{Гц}}} $, ${{\Delta }_{z}}$ и ${{\Delta }_{y}}(t)$ независимы.

Задача состоит в оценивании величины $\Delta _{z}^{*}$ по измерениям $z(t)$ и $y(t)$ на заданном отрезке времени [0, T]. Следуя постановке и общей методике решения задачи навигации по геофизическим полям в рамках байесовской теории нелинейной фильтрации [8, 9], дифференциальное уравнение (1.1) запишем в форме $dX(t) = 0$, где ${{X}_{0}} = X(0)$ – гауссовская случайная величина с нулевым математическим ожиданием и дисперсией $\sigma _{z}^{2}$, т.е. $X(t) = {{\Delta }_{z}}$, а дифференциальное уравнение (1.2) – в форме $dY(t) = c(z(t) - X(t))dt + rdV(t)$, ${{X}_{0}}$ и $V(t)$ независимы. Таким образом, $n = m = d = 1$.

Соответствующие разностные уравнения (2.1)–(2.3) имеют вид ${{X}_{k}} = {{X}_{{k - 1}}}$, Y_k = Y_k – 1 = = $hc(z({{t}_{{k - 1}}}) - {{X}_{{k - 1}}}) + \sqrt h r{{V}_{k}}$ и ${{Z}_{{k - 1}}} = c\left( {z({{t}_{{k - 1}}}) - {{X}_{{k - 1}}}} \right) + (r{\text{/}}\sqrt h ){{V}_{k}}$, где ${{V}_{k}}$ – случайные величины, которые независимы в совокупности и имеют стандартное нормальное распределение, h – шаг численного интегрирования.

Особенность этой задачи состоит в том, что уравнение измерительной системы здесь параметризовано величиной $\Delta _{z}^{*}$, каждому значению этой величины соответствует свое уравнение. Поэтому при $q = 2,3, \ldots $, когда уравнение измерительной системы нелинейно, математическое ожидание ошибки оценивания отлично от нуля (не выполняется свойство несмещенности оценки).

Для нахождения весовых коэффициентов применялись рекуррентные соотношения (4.2) и (4.3). Рекуррентное соотношение (3.2) приводит к ошибкам переполнения при условии $h{\text{/}}{{r}^{2}}$ > > 0.17 для одинарной точности и $h{\text{/}}{{r}^{2}} > 1.4$ при двойной точности, где усредненные значения 0.17 и 1.4 получены по результатам вычислительного эксперимента. В этой тестовой задаче при условии $h{\text{/}}{{r}^{2}} \ll 0.17$ при одинарной точности вычислений и $h{\text{/}}{{r}^{2}} \ll 1.4$ при двойной точности допустимо применение соотношения (3.2). Оценка ошибки навигационной системы вычислялась по формуле (3.5).

Программное обеспечение для решения этой задачи разработано с использованием компилятора C++ из пакета Intel Parallel Studio. Оно позволяет на одной реализации последовательности случайных величин (начальных ошибок, шумов измерительной системы) получать оценки с помощью фильтров частиц для стохастических систем наблюдения с непрерывным и дискретным временем для всех вариантов описания геофизического поля. Реализованы также модифицированный непрерывный фильтр частиц, фильтры Калмана и Калмана–Бьюси, однако они не использовались в сравнении (сравнительный анализ двух вариантов непрерывных фильтров частиц и фильтра Калмана–Бьюси представлен в [21]).

Результаты оценивания совпадают, что вполне ожидаемо. Отметим выигрыш по времени расчетов с помощью рекуррентного соотношения (4.3) вместо (4.2) для нахождения весовых коэффициентов. Для числа частиц $M = {{10}^{6}}$ при h = 0.1 время вычислений при использовании (4.2) составляет 14 с ($h = 0.01$–133 с, $h = 0.001$–1316 с), а при использовании (4.3)–10 с ($h = 0.01$–100 с, $h = 0.001$–1089 с). Время указано для процессора Intel Core i7 4930 K и двойной точности вычислений. Таким образом, при той же точности оценивания применение рекуррентного соотношения (4.3) для нахождения весовых коэффициентов дает определенный выигрыш по времени расчетов.

Приведем примеры оценивания величины $\Delta _{z}^{*}$ при аппроксимации геофизического поля полиномами первой, второй и третьей степеней для числа частиц M = 10⁵ при h = 1. На рис. 1 сплошной линией показана оцениваемая ошибка навигационной системы $\Delta _{z}^{*} = 2$ км, результаты ее оценивания при $q = \overline {1.3} $ показаны соответственно пунктирной, штриховой и штрихпунктирной линиями. Здесь при q = 2 результат значительно хуже остальных за счет того, что начальная координата объекта с учетом ошибки навигационной системы совпадает с локальным минимумом полинома $c(x)$. В окрестности этого локального минимума x* измерения для координат $x{\kern 1pt} {\text{*}} \pm \delta $ отличаются только за счет возмущений ${{\Delta }_{y}}(t)$, и точность оценивания возрастает только после прохождения объектом окрестности x*.

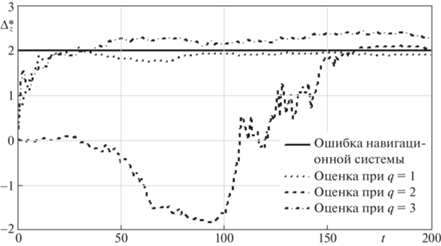
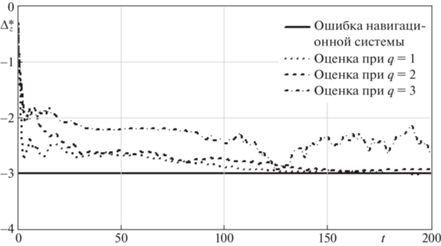
Рисунок 2 соответствует ошибке навигационной системы $\Delta _{z}^{*} = - 3$ км, обозначения такие же, как и для рис. 1. В данном случае худший результат имеет место при q = 3 по тем же причинам, а именно начальная координата объекта с учетом ошибки навигационной системы близка к локальному минимуму полинома $c(x)$.

Точность оценивания для каждой степени q полинома $c(x)$ в этой задаче зависит от величины $\Delta _{z}^{*}$ именно из-за параметризации уравнения измерительной системы этой величиной. Однако в среднем по множеству реализаций $\Delta _{z}^{*}$ в соответствии с заданным распределением этой величины результаты оценивания ранжируются в соответствии со степенью q полинома $c(x)$: чем больше q, тем выше точность оценивания [21].

Заключение. Рассмотрена задача оптимальной фильтрации в стохастических системах наблюдения как c непрерывным, так и с дискретным временем. Показано, что фильтры частиц в обоих случаях дают практически один результат при условии, что в случае непрерывного времени для моделирования траекторий объекта наблюдения используется простейший численный метод решения стохастических дифференциальных уравнений, а именно метод Эйлера–Маруямы (однако возможна реализация непрерывного фильтра частиц без перехода к дискретному времени [22]). В качестве тестовой задачи выбрана задача оценивания погрешности показаний навигационной системы о координатах объекта с помощью корректирующих измерений, при решении которой обнаружен интересный эффект смещения оценки за счет того, что уравнение измерительной системы параметризовано оцениваемой величиной.