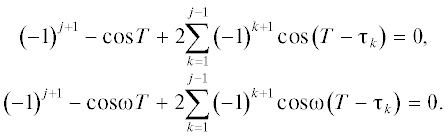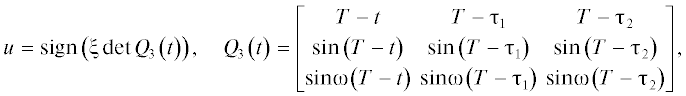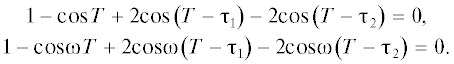Известия РАН. Теория и системы управления, 2022, № 6, стр. 38-55

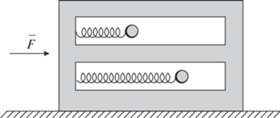
Введение. Рассматривается система, состоящая из несущего твердого тела и прикрепленных к нему линейными пружинами двух материальных точек (рис. 1). Пружины параллельны горизонтальной оси, вдоль которой несущее тело движется поступательно. Единственная управляющая сила $\overline F $ приложена к этой платформе и ограничена по модулю наперед заданной величиной. Подобная модель может приближенно описывать малые перемещения платформы с упругими звеньями или сосуда, частично заполненного жидкостью. Постановки задач управления такими объектами известны давно [1], но многие из них до сих пор актуальны. Проблема – в дефиците управляющих воздействий, когда одной силой требуется погасить колебания нескольких взаимосвязанных тел. Известно, что платформа с $n$ осцилляторами при действии горизонтальной силы управляема, если частоты собственных колебаний осцилляторов попарно различны [1, 2]. Практическая невозможность аналитического решения задачи наибыстрейшего перемещения такой системы стимулировала поиски методов квазиоптимального управления. В [3] предложен поэтапный алгоритм синтеза ограниченного управления, где сочетаются метод [4] аппроксимации множества достижимости (для больших энергий системы) и применение общей функции Ляпунова [5, 6] (для построения обратной связи в окрестности требуемого положения равновесия). Подход развивался в работе [7], где исследовались проблемы существования и единственности движения под действием предлагаемого управления, а также в [8], где подробно рассмотрен случай платформы с двумя осцилляторами. Для этой же системы были построены алгоритмы, достигающие цели при действии неизвестных возмущений и при неизмеряемых состояниях осцилляторов [9, 10]. В работе [11] указан закон управления, переводящего платформу с n осцилляторами за конечное время в требуемое состояние покоя при неполной информации о состоянии и возмущениях, причем для некоторого типа начальных состояний найдена асимптотика времени движения в зависимости от числа $n$.

Далее речь пойдет о задаче оптимального быстродействия, когда трение отсутствует, а фазовое состояние системы в каждый момент измеримо. Ранее с помощью принципа максимума Понтрягина [12] была решена задача наибыстрейшего перемещения платформы с одним осциллятором, где оптимальное управление оказалось кусочно-постоянным с тремя переключениями [1, 13].

В [14] на основе учета симметрий задачи предложена структура управления, удовлетворяющего необходимым условиям оптимального быстродействия для перемещения платформы с n осцилляторами. В его записи участвуют значения первых $n$ моментов переключения, что требует предварительного решения системы нелинейных уравнений. Показано, что искомое управление является кусочно-постоянным с нечетным числом переключений. Для случая $n = 2$ численные решения иллюстрировались на фазовой плоскости одного из осцилляторов, и, в частности, доказано, что для малых значений дальности перемещения количество переключений равно пяти.

1. Постановка задачи. Повторяя использованные в [14] преобразования координат и времени, приведем уравнения движения платформы с двумя осцилляторами (рис. 1) к форме с безразмерными переменными и временем:

где $u$ – управляющая сила, параметр ${{\omega }} > 1$ растет с увеличением отношения собственных частот осцилляторов. Переменные ${{x}_{0}}$, ${{x}_{1}}$, ${{x}_{2}}$ являются линейными комбинациями горизонтальных координат платформы и осцилляторов. Одновременное обращение в нуль значений ${{x}_{1}}$ и ${{x}_{2}}$ соответствует ненапряженным состояниям пружин. Полагая, что при требуемом перемещении платформы переменная x₀ меняется на величину 2b, назначим в середине этого отрезка начало отсчета координаты x₀. Аналогичную “удвоенную” запись введем и для искомого общего времени $2T$ движения системы, что придаст краевым условиям симметричный вид.

Задача оптимального по быстродействию перемещения платформы с двумя осцилляторами формулируется следующим образом: требуется определить управление $u\left( t \right)$, $t \in \left[ {0,~\,2{\kern 1pt} {\kern 1pt} T} \right]$, переводящее систему (1.1) из состояния

за наименьшее время $2T$ (заранее неизвестное) в состояние

Как и в работе [14], поставленную задачу быстродействия будем рассматривать для взаимной вариационной задачи на максимум дальности 2b при заданном времени $2T$. При этом исследуем эволюцию функций оптимального управления $u\left( t \right)$, $t \in \left[ {0,~\,2{\kern 1pt} {\kern 1pt} T} \right]$ с изменением параметра Т. Для наглядного представления этой эволюции введем изображение, которое назовем диаграммой функций оптимального управления. Поскольку каждая такая функция однозначно задается чередованием участков с постоянными значениями “+1” и “–1”, то поставим ей в соответствие отрезок длиной $2T$, составленный из серых и белых фрагментов, повторяющих длительности положительных и отрицательных участков на графике. Таким способом за счет двух цветов графический образ функции $u\left( t \right)$, $t \in \left[ {0,~\,2{\kern 1pt} {\kern 1pt} T} \right]$ станет одномерным. Далее из составных отрезков (как из горизонтальных слоев) на плоскости с вертикальной координатой Т соберем двумерную диаграмму, отражающую эволюцию функции управления с изменением T. Если при этом использовать смещенное время $\tilde {t} = t - T$, $\tilde {t} \in \left[ { - T,\,\,T} \right]$, то диаграмма для функций $u\left( {\tilde {t}} \right)$ окажется симметричной относительно вертикальной оси.

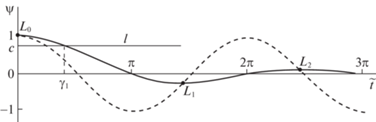
На рис. 2 построена такая диаграмма для решенной в [1, 13] задачи наибыстрейшего перемещения платформы с одним осциллятором. Каждое горизонтальное сечение диаграммы символизирует одну функцию $u\left( {\tilde {t}} \right)$, $\tilde {t} \in \left[ { - T,\,\,T} \right]$, с тремя моментами переключения.

Поставим задачу исследования закономерностей, позволяющих строить диаграммы функций управления в задаче оптимального по быстродействию перемещения платформы с двумя осцилляторами.

2. Свойства движений, удовлетворяющих необходимым условиям оптимальности. На основе принципа максимума Понтрягина было показано [14], что в задаче оптимального быстродействия (1.1)–(1.3) в смещенном времени $\tilde {t} = t - T$, $\tilde {t} \in \left[ { - T,\,\,T} \right]$, оптимальное управление $u\left( {\tilde {t}} \right)$, а также решения ${{x}_{i}}\left( {\tilde {t}} \right)$, $i = \overline {0,2} $, будут нечетными функциями, а ${{\dot {x}}_{i}}\left( {\tilde {t}} \right)$, $i = \overline {0,2} $, – четными функциями. В конце оптимальной полутраектории выполняются соотношения

Оптимальное управление будет кусочно-постоянным с конечным числом переключений, число которых нечетно. Особые управления здесь невозможны в силу линейной независимости известных решений сопряженной системы принципа максимума.

Моменты времени переключения управления будем обозначать через ${{\tau }_{k}}$, увеличивая индексы k с ростом значений времени. Их общее количество заранее не известно, но всегда в середине списка – момент времени Т. Если его номер равен  j (т.е. ему предшествуют моменты переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$), то в конце оптимальной полутраектории выполняется [14] система двух уравнений:

Использование моментов переключения управления как корней системы (2.2) (при заданном значении T) лежит в основе дальнейших рассуждений. Для достаточно малых T имеет место [14] следующее утверждение.

Замечание 1. При каждом значении $T \in \left( {0,{\text{\;}}{{T}_{s}}} \right]$, где ${{T}_{s}} = 2\pi {\text{/}}\omega $, в задаче оптимального быстродействия (1.1)–(1.3) существует режим движения с пятью переключениями управления в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$.

Можно показать [14], что если число ${{\omega }}$ – рациональное, представимое несократимой дробью

то в задаче оптимального быстродействия (1.1)–(1.3) выполняются следующие свойства.

Свойство 1. Существует оптимальное движение с одним переключением управления при $T = {{T}_{*}}$, где ${{T}_{*}} = 2m{{\pi }}$.

Свойство 2. Если управление с моментами переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T удовлетворяет краевым условиям (2.2), то управление с моментами переключения ${{{{\tau }}}_{1}} + {{T}_{*}}$, ${{{{\tau }}}_{2}} + {{T}_{*}}$, …, ${{{{\tau }}}_{{j - 1}}} + {{T}_{*}}$, $T + {{T}_{*}}$ тоже им удовлетворит.

Свойство 3. Если управление с моментами переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T при $T < {{T}_{*}}{\text{/}}2$ удовлетворяет краевым условиям (2.2), то управление с моментами переключения ${{{{\tau }}}_{1}} + \Delta $, ${{{{\tau }}}_{2}} + \Delta $, …, ${{{{\tau }}}_{{j - 1}}} + \Delta $, $T + \Delta $ (где $\Delta = {{T}_{*}} - 2T$) тоже им удовлетворит.

Заметим, что в случае иррационального значения ${{\omega }}$ свойства 1–3 уже не выполняются, так как в системе (2.2) не будет общего периода ${{T}_{*}}$ всех функций. В этом случае зависимость дальности перемещения системы от времени не сможет быть предъявлена в каком-либо завершенном виде ввиду бесконечного чередования все новых типов движений с ростом времени 2T.

Далее ограничимся случаями, когда число ${{\omega }}$ имеет вид (2.3).

Из [14] следуют замечания 2–4.

Замечание 2. Если в задаче (1.1)–(1.3) траектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с пятью переключениями управления (в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$), то управляющая функция имеет вид

где знак константы ξ определяется известным (по условию) значением управления u(t) при $t \in [0,{{{{\tau }}}_{1}})$.

Для сценария, описанного в замечании 2, значения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$ (при заранее заданной длительности полутраектории Т) находятся из системы (2.2), принимающей при  j = 3 вид

Замечание 3. Если в задаче (1.1)–(1.3) траектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с количеством переключений большим, чем пять, то вид управляющей функции будет тот же (2.4).

Это замечание относится к ситуации, когда неизвестных значений ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, ${{{{\tau }}}_{3}}$, … больше, чем уравнений (2.2). Здесь проверить оптимальность конкретного набора моментов переключений можно путем интегрирования уравнений движения (1.1)–(1.2): расписание должно подтвердиться автоматически при действии управления (2.4), иначе оно не оптимально.

Замечание 4. Если в задаче (1.1)–(1.3) траектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с тремя переключениями (в моменты времени ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$), то управляющая функция имеет вид

Для сокращения записей каждому значению ${{\tau }_{k}}$ момента времени переключения управления будем ставить в соответствие разность

3. Режимы с тремя переключениями управления. Далее будет показано, что при построении диаграмм функций оптимального управления важную роль играют режимы с тремя переключениями. Их моменты времени ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$ соответствуют корням системы (2.2), принимающей при $j = 2$ вид

Необходимое условие оптимальности режима, описанного в замечании 4, выражается в том, что действующая по закону (2.6) функция управления не должна обратиться в нуль при других значениях времени, кроме ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$. Для исследования этого условия используем смещенное время $\tilde {t} = t - T$, $\tilde {t} \in \left[ { - T,\,\,T} \right]$, обозначения (2.7) и преобразуем определитель (2.6) к виду

Здесь введено обозначение функции

которую доопределим значением $\psi \left( 0 \right) = 1$.

Функция $\psi \left( {\tilde {t}} \right)$ – четная. При $\tilde {t} > 0$ условие ее экстремумов

соответствует точкам пересечения графиков функции $\psi \left( {\tilde {t}} \right)$ (на рис. 3 – сплошная линия) и функции $\cos \left( {\tilde {t}} \right)$ (пунктирная линия). Такими точками являются, например, ${{L}_{1}}$ ($\tilde {t} \approx 1.4303\pi $, $\psi \approx - 0.21723$), ${{L}_{2}}$ ($\tilde {t} \approx 2.4590\pi $, $\psi \approx 0.12837$) и т.д. С увеличением номера i аргумент i-го экстремума монотонно приближается к значению $(2i + 1)\pi {\text{/}}2$.

Чтобы удовлетворить необходимому условию оптимальности, управление (2.6) должно обращаться в нуль только при $\tilde {t} = 0$ и $\tilde {t} = \pm {{\gamma }_{1}}$. Геометрически это равносильно следующему требованию.

Условие 1. Горизонталь l, проведенная на уровне $c = \psi \left( {{{\gamma }_{1}}} \right)$, должна иметь ровно одну общую точку с графиком функции $\psi \left( {\tilde {t}} \right)$ при $\tilde {t} > 0$.

Тогда на рис. 3 она должна пройти либо через точку ${{L}_{1}}$, либо между точками ${{L}_{0}}$ и ${{L}_{2}}$.

Утверждение 1. Для любого ${{\omega }} \ne {\text{2}}$ в задаче оптимального быстродействия (1.1)–(1.3) существует такое значение дальности перемещения $2b$, при котором управление будет иметь ровно три момента переключения: ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$. Эти значения удовлетворят не только системе (3.1), но и неравенству

Доказательство. В силу монотонной зависимости $T(b)$ поиск значения b заменим варьированием $T$. Первое уравнение системы (3.1) представим в виде

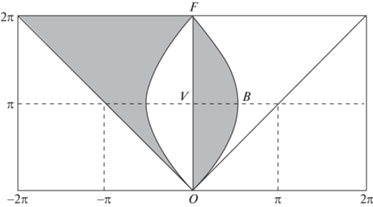
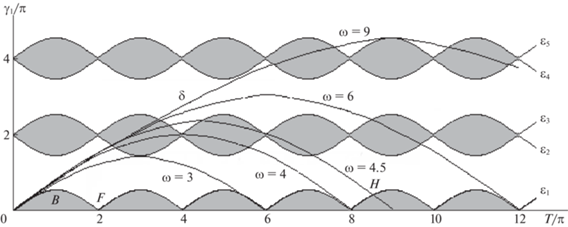
Множество его корней изображается (рис. 4) на координатной плоскости ($T$, ${{\gamma }_{1}}$) бесконечной фигурой из горизонтальных цепочек ${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$, ${{\varepsilon }_{3}}$, …, составленных из одинаковых дуг. Левая нижняя дуга $OBF$ служит графиком функции

Ранее эта же дуга встречалась на рис. 2. Она является симметричной относительно оси VB ($T = \pi $) и выпуклой вверх, так как ${{d}^{2}}{{\gamma }_{1}}{\text{/}}d{{T}^{2}} < 0$. Производная $d{{\gamma }_{1}}{\text{/}}dT$ в точках $T = 0$, $T = \pi $, $T = 2\pi $ имеет значения соответственно $\sqrt 2 {\text{/}}2$, 0, $ - \sqrt 2 {\text{/}}2$.

Из всего множества решений уравнения (3.5) условию 1 удовлетворяют только те, которые на рис. 4 изображены несвязным множеством $\Omega $, полученным из цепочки ${{\varepsilon }_{1}}$ путем удаления из нее точек оси ${{\gamma }_{1}} = 0$. Эти корни удовлетворяют неравенству $0 < {{\gamma }_{1}} < \pi {\text{/}}2$, равносильному (3.4).

Для решения системы (3.1) при условии (3.4) достаточно найти такие корни T, ${{\gamma }_{1}}$ уравнения (3.5), которые удовлетворят ему и при замене на $\omega T$, $\omega {{\gamma }_{1}}$. Графически это соответствует точкам пересечения всей совокупности цепочек ${{\varepsilon }_{i}}$, $i \in N$, и несвязной линии $\delta $, полученной из множества $\Omega $ при растяжении в $\omega $ раз (т.е. при гомотетии плоскости с коэффициентом $\omega $ и центром O(0, 0)).

Если число $\omega $ – целое, то линия $\delta $ (в силу отсутствия у нее точек на оси ${{\gamma }_{1}} = 0$) не имеет общих точек с множеством ${{\varepsilon }_{1}}$. При этом линия $\delta $ пересечет ближайшую цепочку ${{\varepsilon }_{2}}$ только при $\omega \geqslant 3$ (рис. 4). Отсюда следует, что при $\omega = 2$ система (3.1) не имеет решений. Если же число $\omega $ – не целое, то у множеств $\delta $ и $\Omega $ всегда имеются пересечения. Тем самым доказано не только утверждение 1, но и его следствие.

Следствие. Если при некотором $T$ нашлось значение ${{{{\tau }}}_{1}}$, удовлетворяющее системе (3.1) и неравенству (3.4), то управление с тремя переключениями в моменты ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$ будет удовлетворять необходимым условиям оптимальности.

4. Контрольная кривая и ее свойства. Рассматривая функцию оптимального управления (2.4) в смещенном времени $\tilde {t} = t - T$, $\tilde {t} \in \left[ { - T,\,\,T} \right]$, преобразуем определитель из (2.4) к виду

где используется ранее введенная функция (3.3).

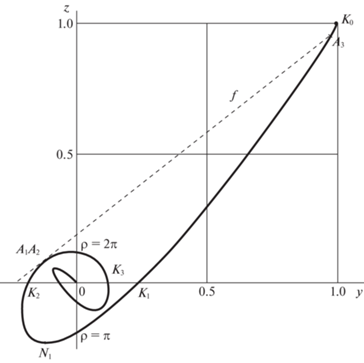
Определитель (4.1) составлен из трех векторов-столбцов ${\mathbf{p}}(\tilde {t})$, ${\mathbf{p}}({{\gamma }_{1}})$, ${\mathbf{p}}({{\gamma }_{2}})$ с однотипной структурой ${\mathbf{p}}(\theta ) = {{\left( {1,{\text{\;}}\psi \left( \theta \right),\psi \left( {\omega \theta } \right)} \right)}^{{\text{T}}}}$. Условие $\det {{Q}_{3}}\left( {\tilde {t}} \right) = 0$ переключения оптимального управления выполняется либо при $\tilde {t} = 0$, либо при компланарности трех векторов, что имеет место, в частности, при $\tilde {t} = {{\gamma }_{1}}$ или $\tilde {t} = {{\gamma }_{2}}$. Постоянные векторы ${\mathbf{p}}({{\gamma }_{1}})$ и ${\mathbf{p}}({{\gamma }_{2}})$ не коллинеарны, поэтому при откладывании от начала координат в пространстве $(x,y,z)$ порождают конкретную плоскость. Она пересечет плоскость $x = 1$ по некоторой прямой, чью проекцию на плоскость $yOz$ обозначим $g$. На эту же плоскость конец переменного вектора ${\mathbf{p}}(\tilde {t})$ проецируется в точку $M$ с координатами $y = \psi \left( {\tilde {t}} \right)$, $z = \psi \left( {\omega \tilde {t}} \right)$. Линию на плоскости $yOz$, по которой точка $M$ движется с изменением параметра $\tilde {t} \in \left[ { - T,\,\,T} \right]$, назовем контрольной кривой. Для рассматриваемого случая (2.3) ввиду свойств 2 и 3 ограничимся рассмотрением диапазона $T \in (0,{{T}_{*}}{\text{/}}2]$. Таким образом, контрольную кривую зададим параметрическим уравнением

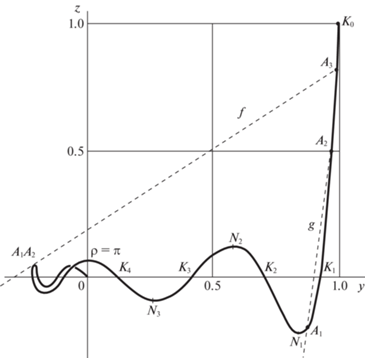
Форма этой кривой зависит от значения константы $\omega $, но всегда кривая начинается в точке ${{K}_{0}}(1,1)$ (при $\rho = 0$), пересекает ось $Oz$ при $\rho = k\pi $, $k \in N$ и приходит в точку $O(0,0)$ при $\rho = {{T}_{*}}{\text{/}}2$. На рис. 5 показана контрольная кривая для $\omega = 9{\text{/}}2$ (при $\rho \in [0,2\pi ]$); на рис. 6 – для $\omega = 5{\text{/}}4$ (при $\rho \in [0,4\pi ]$).

Наряду с параметром $\rho $ введем пропорциональный ему параметр

Его натуральным значениям соответствуют точки пересечения контрольной кривой с горизонтальной осью $Oy$, которые последовательно обозначим через ${{K}_{i}}$. В частности, если $\omega $ – целое, то при $i = \omega $ точка K_i совпадет с $O(0,0)$.

Экстремумы функций $z(y)$ и $\psi \left( {\tilde {t}} \right)$ численно равны, а параметры ${{\sigma }_{i}} = i + 0.5$ точек N_i, $i = 1,2,...$, на рис. 5 мало отличаются от соответствующих значений $\tilde {t}{\text{/}}\pi $, вычисленных для экстремальных точек ${{L}_{i}}$ на рис. 3. Можно показать, что внутри каждой дуги ${{K}_{i}}{{K}_{{i + 1}}}$, $i = ~1,2,...$, контрольной кривой есть единственная точка перегиба ${{P}_{i}}$, расположенная ближе к точке ${{K}_{{i + 1}}}$.

С помощью контрольной кривой можно геометрически интерпретировать необходимые условия оптимальности, выраженные формулами (2.4) и (4.1). Например, сочетание корней ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$ системы (2.5) будет соответствовать оптимальному управлению с пятью переключениями, согласно замечанию 2, лишь при условии, что определитель (2.4) не обратится в нуль при других значениях времени t, кроме ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$. Это условие соответствует тому, что прямая g, проведенная через точки ${{A}_{1}}$ и ${{A}_{2}}$ (с параметрами $\rho = {{\gamma }_{1}}$ и $\rho = {{\gamma }_{2}}$), не имеет других общих точек с контрольной кривой (рис. 5). Действительно, если параметру $\rho = T$ соответствует точка W, то в смещенном времени $\tilde {t} \in \left[ { - T,\,\,T} \right]$ изображающая точка $M$ с координатами $(\psi \left( {\tilde {t}} \right),\psi \left( {\omega \tilde {t}} \right))$, двигаясь по контрольной кривой из W в ${{K}_{0}}$ и обратно, дважды пройдет дугу $W{{K}_{0}}$. При этом знак управления $u\left( {\tilde {t}} \right)$, согласно формулам (2.4) и (4.1), меняется последовательно в точках ${{A}_{1}}$, ${{A}_{2}}$, ${{K}_{0}}$, ${{A}_{2}}$ и ${{A}_{1}}$.

На контрольной кривой выявляется оптимальность режимов, упомянутых в замечании 1, так как при $T \in \left( {0,{{T}_{s}}} \right]$ положения точек W (с параметрами $\sigma \in \left( {0,{\text{2}}} \right]$) не выходят за пределы дуги ${{K}_{0}}{{K}_{2}}$. В силу неравенств

точки ${{A}_{1}}$ и ${{A}_{2}}$ окажутся внутри вогнутой части этой дуги, поэтому прямая $g = {{A}_{1}}{{A}_{2}}$ не имеет других пересечений с контрольной кривой.

5. Эволюция функций оптимального управления в задаче (1.1)–(1.3). Исследуем изменение функций оптимального управления $u\left( t \right)$, $t \in \left[ {0,~\,2{\kern 1pt} {\kern 1pt} T} \right]$ в задаче (1.1)–(1.3) при непрерывном возрастании дальности перемещения платформы, что равносильно непрерывному увеличению параметра T. Для определенности ограничимся случаем $\omega \geqslant 3$, когда качественный вид контрольной кривой соответствует рис. 5. К случаю $1 < \omega < 3$ вернемся позже.

Итак, в диапазоне $T \in \left( {0,{\text{\;}}{{T}_{s}}} \right]$ оптимальное управление имеет ровно пять переключений в моменты ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$, удовлетворяющие системе (2.5). В обозначениях (2.7) эта система примет вид

Дифференцируя соотношения (5.1) по T, разрешим полученную систему уравнений относительно производных

Здесь

где использованы координаты ${{y}_{i}} = \psi \left( {{{\gamma }_{i}}} \right)$, ${{z}_{i}} = \psi \left( {\omega {{\gamma }_{i}}} \right)$, $i = 1,2$, точек ${{A}_{1}}$ и ${{A}_{2}}$ на контрольной кривой. Аналогично вычисляются определители с помощью координат точки W в виде ${{y}_{0}} = \psi \left( T \right)$, ${{z}_{0}} = \psi \left( {\omega T} \right)$ и ориентированных площадей параллелограммов построенных на векторах $\overline {O{{A}_{1}}} = ({{y}_{1}},{{z}_{1}})$, $\overline {O{{A}_{2}}} = ({{y}_{2}},{{z}_{2}})$, $\overline {OW} = ({{y}_{0}},{{z}_{0}})$.

Эволюции режимов с пятью переключениями управления (при увеличении параметра $T \in \left( {0,{\text{\;}}{{T}_{s}}} \right]$) соответствует перемещение точек W, ${{A}_{1}}$ и ${{A}_{2}}$ по контрольной кривой (рис. 5) с соблюдением порядка следования (4.4). При всех положениях точки W на дуге ${{K}_{0}}{{N}_{1}}$ повороты векторов $\overline {O{{A}_{1}}} \to \overline {OW} $, $\overline {O{{A}_{2}}} \to \overline {OW} $, $\overline {O{{A}_{2}}} \to \overline {O{{A}_{1}}} $ осуществляются по часовой стрелке, поэтому ${{S}_{{10}}} < 0$, ${{S}_{{20}}}$ < 0, ${{S}_{{21}}} < 0$. В силу (5.2) имеем ${{\dot {\gamma }}_{1}} > 0$, ${{\dot {\gamma }}_{2}} > 0$, т.е. монотонный рост ${{\gamma }_{1}}(T)$, ${{\gamma }_{2}}(T)$. При дальнейшем продвижении (до состояния K₂) точка W пройдет через некоторое положение, при котором $\overline {OW} $||$\overline {O{{A}_{1}}} $. Это следует из того, что в состоянии K₂ (при $T = {{T}_{s}}$) точка $W$ окажется выше точки ${{A}_{1}}$, для которой ${{\gamma }_{1}} > {{T}_{s}}{\text{/}}2$ [14], т.е. $\sigma > 1$. В состоянии, когда $\overline {OW} $||$\overline {O{{A}_{1}}} $, определитель ${{S}_{{10}}}$ (а значит, и ${{D}_{2}}$) меняет знак, т.е. функция ${{\gamma }_{2}}(T)$ достигает максимума. Далее с ростом $T$ получим ${{S}_{{10}}} > 0$, ${{S}_{{20}}} < 0$, ${{S}_{{21}}} < 0$, т.е. ${{\dot {\gamma }}_{1}} > 0$, ${{\dot {\gamma }}_{2}} < 0$, что на контрольной кривой соответствует росту параметра ${{\gamma }_{1}}(T)$ точки ${{{\text{A}}}_{1}}$ и убыванию ${{\gamma }_{2}}(T)$, т.е. движению “вспять” точки A₂. Эти неравенства, порожденные направлениями вращения векторов $\overline {OW} $, $\overline {O{{A}_{1}}} $, $\overline {O{{A}_{2}}} $, сохранят свой смысл вплоть до достижения точкой ${{A}_{2}}$ положения ${{K}_{0}}$ (рис. 5) при ${{\gamma }_{2}} = 0$, когда $u\left( t \right)$ выродится в функцию с тремя моментами переключения ${{{{\tau }}}_{1}}$, T, $2T - {{{{\tau }}}_{1}}$. Ее параметры $T = {{T}_{1}}$, ${{{{\tau }}}_{1}} = T - {{\lambda }_{1}}$ соответствуют (рис. 4) координатам $(\omega {{T}_{1}},\omega {{\lambda }_{1}})$ точки, в которой линия $\delta $ пересекла цепочку ${{\varepsilon }_{2}}$, входя в закрашенную область. Обозначим через $(\omega {{T}_{2}},\omega {{\lambda }_{2}})$ координаты на выходе (где $\delta $ пересекает ${{\varepsilon }_{3}}$).

Замечание 5. При всех значениях $T \in (0,{{T}_{1}})$ прямая g не имеет других общих точек с контрольной кривой, кроме ${{A}_{1}}$ и ${{A}_{2}}$, поскольку они расположены на вогнутой части дуги ${{K}_{0}}{{K}_{2}}$ (рис. 5). Следовательно, при $T \in (0,{{T}_{1}})$ функция оптимального управления будет иметь ровно пять моментов переключения.

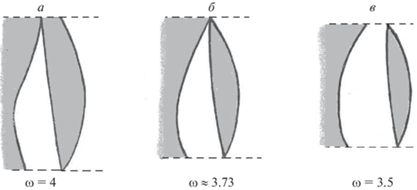
Можно показать, что на контрольной кривой при $T = {{T}_{1}}$ у точки ${{A}_{1}}$ параметр ${{\gamma }_{1}} = {{\lambda }_{1}}$ будет меньше, чем у точки ${{P}_{1}}$ перегиба, т.е. ${{A}_{1}}$ останется на вогнутой части дуги ${{K}_{1}}{{K}_{2}}$. При $T = {{T}_{1}} + \Delta T$ (где $\Delta T$ – мало) продолжение режимов с пятью переключениями неосуществимо в силу ${{\gamma }_{2}} = 0$, ${{\dot {\gamma }}_{2}} < 0$. Далее непрерывная эволюция оптимальной функции $u\left( t \right)$ возможна лишь путем добавления двух новых сколь угодно близких моментов переключения, что на графике соответствует “игольчатой вариации” (рис. 7). В этом состоянии на контрольной кривой прямая g должна пройти через точку ${{A}_{1}}$, но не должна быть секущей к этой кривой, иначе в графике u(t) возникли бы скачкообразные изменения. Поэтому через точку с параметром ${{\lambda }_{1}}$ прямая $g$ пройдет как касательная l к дуге ${{P}_{1}}{{N}_{2}}$ (на рис. 8, а показан такой случай для $\omega = 4$). Точка касания получит статус “сдвоенной” ${{A}_{1}} = {{A}_{2}}$ (с параметрами ${{\gamma }_{1}} = {{\gamma }_{2}}$), а прежняя точка ${{A}_{1}}$ переименуется в ${{A}_{3}}$ (с параметром ${{\gamma }_{3}} = {{\lambda }_{1}}$). На рис. 7 эта же ситуация показана на графике функции u(t) при $\omega = 4$, где T = = ${{T}_{1}} \approx 2.01371$, ${{\tau }_{1}} \approx {{\tau }_{2}} \approx 0.45324$, ${{\tau }_{3}} \approx 0.73266$, т.е. ${{\gamma }_{1}} \approx {{\gamma }_{2}} \approx 1.56047$, ${{\gamma }_{3}} = {{\lambda }_{1}} \approx 1.28104$.

Значения ${{\gamma }_{1}}$, ${{\gamma }_{2}}$, ${{\gamma }_{3}}$ будут корнями системы (2.2) при $j = 4$:

и будут меняться с увеличением параметра T. Скорости ${{\dot {\gamma }}_{1}}$, ${{\dot {\gamma }}_{2}}$, ${{\dot {\gamma }}_{3}}$ можно выразить, дифференцируя по T как соотношения (5.4), так и равенство вытекающее из необходимого условия оптимальности (2.4). Разрешив полученную систему трех уравнений относительно производных, получим

Использованные здесь определители приводятся к виду

где обозначения ${{S}_{{ij}}}$, $i,j = \overline {0,3} $, $i \ne j$, имеют прежний смысл (5.3), а частные производные H₂, H₃ получаются из записи круговой перестановкой индексов.

Можно показать, что совпадавшие при $T = {{T}_{1}}$ значения ${{\gamma }_{1}}$, ${{\gamma }_{2}}$ в силу (5.6) “расходятся”, т.е. далее начинается эволюция режимов с семью переключениями управления в моменты ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, ${{{{\tau }}}_{3}}$, $T$, $2T - {{{{\tau }}}_{3}}$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$.

Замечание 6. При всех значениях $T \in ({{T}_{1}},{{T}_{2}})$ прямая $g$, проходящая через ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$, не может иметь еще одну общую точку с контрольной кривой.

Для доказательства покажем, что точки ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ при всех $T \in ({{T}_{1}},{{T}_{2}})$ не могут выйти за пределы дуги ${{N}_{1}}{{N}_{2}}$. Если бы точка ${{A}_{1}}$ совместилась с N₂, то получили бы ${\text{cos}}\left( {\omega {{\gamma }_{1}}} \right) = 0$ и отрицательность левой части уравнения (5.4) в силу ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) < {\text{cos}}\left( {\omega {{\gamma }_{2}}} \right)$. Это неравенство выполнялось бы при расположении точки ${{A}_{2}}$ как на дуге ${{K}_{2}}{{N}_{1}}$ (ввиду $\pi {\text{ < }}\omega {{\gamma }_{3}} < \omega {{\gamma }_{2}} < 2\pi $), так и на дуге ${{K}_{2}}{{N}_{2}}$, где ${\text{cos}}\left( {\omega {{\gamma }_{2}}} \right) > 0$. В последнем случае ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) < 0$, поскольку точка ${{A}_{3}}$ лежала бы на дуге ${{K}_{1}}{{N}_{1}}$ выше, чем точка пересечения прямой ${{K}_{2}}{{N}_{2}}$ и контрольной кривой. Расчеты показывают, что параметр $\sigma $ этой точки пересечения монотонно убывает при $\omega \in (3,\,\infty )$ от $\sigma \approx 1.25884$ до $\sigma \approx 1.18418$. Аналогично доказывается невозможность совмещения точек ${{A}_{3}}$ и ${{N}_{1}}$, так как из условия ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) = 0$ следует отрицательность левой части уравнения (5.4) в силу ${\text{cos}}\left( {\omega {{\gamma }_{1}}} \right) < {\text{cos}}\left( {\omega {{\gamma }_{2}}} \right)$. Это неравенство выполнится как в случае ${{A}_{2}} \in {{K}_{2}}{{N}_{2}}$ (когда $2\pi < \omega {{\gamma }_{2}} < \omega {{\gamma }_{1}} < 3\pi $), так и в случае ${{A}_{2}} \in {{K}_{2}}{{N}_{1}}$ (где ${\text{cos}}\left( {\omega {{\gamma }_{2}}} \right) > 0$, причем ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) < 0$ ввиду ${{A}_{1}} \in {{K}_{3}}{{N}_{2}}$).

Эволюция режимов с семью переключениями управления завершится при $T = {{T}_{2}}$, когда из трех общих точек ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ прямой g и контрольной кривой две совместятся в виде точки касания (и “исчезнут”). В зависимости от значения $\omega $ совместятся

1) либо точки ${{A}_{1}}$, ${{A}_{2}}$, если $3 < \omega < {{\omega }_{*}}$,

2) либо точки ${{A}_{2}}$, ${{A}_{3}}$, если $\omega > {{\omega }_{*}}$.

Критическим является значение ${{\omega }_{*}} \approx 3.73$, при котором параметр ${{\lambda }_{2}}$ соответствует точке ${{P}_{1}}$ перегиба на дуге ${{N}_{1}}{{N}_{2}}$ контрольной кривой. В случае 1) оставшаяся третья точка ${{A}_{3}}$, лежащая ниже ${{P}_{1}}$, переименуется в точку ${{A}_{1}}$ с параметром ${{\gamma }_{1}} = {{\lambda }_{2}}$. В случае 2) останется точка ${{A}_{1}}$, лежащая выше ${{P}_{1}}$ (рис. 8, б). Итак, при $T = {{T}_{2}}$ совпадут моменты переключения ${{{{\tau }}}_{1}}$ и ${{{{\tau }}}_{2}}$ (случай 1) либо ${{{{\tau }}}_{2}}$ и ${{{{\tau }}}_{3}}$ (случай 2) на графике функции $u\left( t \right)$, так что она вновь станет функцией с тремя моментами переключения.

Из следствия и замечаний 5, 6 следует утверждение.

Утверждение 2. Для любого $\omega \geqslant 3$ в задаче оптимального быстродействия (1.1)–(1.3) функция $u\left( t \right)$, $t \in \left[ {0,~\,2T} \right]$ имеет:

а) пять переключений при $T \in (0,{\text{\;}}{{T}_{1}})$;

б) три переключения при $T = {{T}_{1}}$;

в) семь переключений при $T \in ({{T}_{1}},{{T}_{2}})$;

г) три переключения при $T = {{T}_{2}}$.

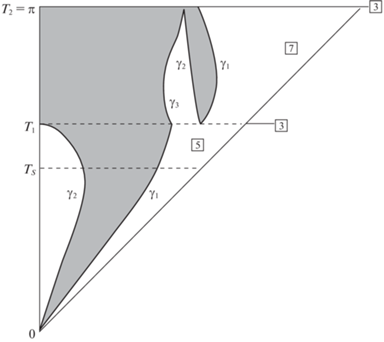
Заметим, что перечисленный список сценариев а)–г) окажется завершающим в диапазоне $T \in (0,{{T}_{*}}{\text{/}}2]$ для случая $\omega = 4$, так как для него ${{T}_{2}} = \pi $. На рис. 9 для $\omega = 4$ показана лишь правая часть диаграммы функций оптимального управления (ее левая часть – зеркальная, но с переменой местами белого и серого цветов). В каждом слое диаграммы цифрой указано соответствующее количество переключений.

На рис. 10, а–в сравниваются фрагменты из горизонтального слоя диаграммы при $T \in ({{T}_{1}},{{T}_{2}})$ для значений $\omega = 4$, $\omega = {{\omega }_{*}}$ и $\omega = 3.5$.

Замечание 7. Для всех случаев $\omega \geqslant 3$, $\omega \ne 4$ найдется $\Delta T$, такое, что при каждом значении $T \in \left( {{{T}_{2}},{{T}_{2}} + \Delta T} \right]$ в задаче (1.1)–(1.3) оптимальное управление будет кусочно-постоянным с пятью моментами переключения.

Такой режим последует непосредственно за сценариями в), г). После “исчезновения” двух совместившихся при $T = {{T}_{2}}$ точек на контрольной кривой, прямая g может быть проведена лишь через оставшуюся точку, наделяемую ролью ${{A}_{1}}$, и новую ${{A}_{2}}$, начинающую движение из состояния K₀ при $T > {{T}_{2}}$. В начальном (при $T = {{T}_{2}}$) положении ${{K}_{0}}{{A}_{1}}$ прямая g не имеет других общих точек с дугой ${{K}_{3}}{{K}_{4}}$ контрольной кривой, поскольку этой дуги не задевает даже проходящая выше прямая ${{K}_{0}}{{N}_{2}}$. Можно показать, что при $\omega \geqslant 3$ ее угловой коэффициент превосходит угловой коэффициент касательной, проведенной из ${{N}_{2}}$ к дуге ${{K}_{3}}{{K}_{4}}$ (в пределе при $\omega \to \infty $ отношение этих угловых коэффициентов монотонно убывает и стремится к значению $ \approx 1.943215$).

Упомянутому в замечании 7 диапазону параметров $T$ соответствует такое расположение векторов, что повороты $\overline {O{{A}_{1}}} \to \overline {OW} $, $\overline {O{{A}_{2}}} \to \overline {OW} $, $\overline {O{{A}_{2}}} \to \overline {O{{A}_{1}}} $ осуществляются по часовой стрелке, поэтому ${{S}_{{10}}} < 0$, ${{S}_{{20}}} < 0$, ${{S}_{{21}}} < 0$, т.е. ${{\dot {\gamma }}_{1}} > 0$, ${{\dot {\gamma }}_{2}} > 0$. С ростом параметра ${{\gamma }_{1}}(T)$ точка ${{A}_{1}}$, пройдя положение ${{N}_{2}}$, попадет в зону, где прямая ${{A}_{1}}{{A}_{2}}$ может коснуться дуги ${{K}_{3}}{{N}_{3}}$. Из точки касания выйдут “новые” ${{A}_{1}}$ и ${{A}_{2}}$, а прежние точки ${{A}_{1}}$ и ${{A}_{2}}$ переименуются в ${{A}_{3}}$ и ${{A}_{4}}$. Тогда начнется режим с девятью переключениями в моменты ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, ${{{{\tau }}}_{3}}$, ${{{{\tau }}}_{4}}$, $T$, $2T - {{{{\tau }}}_{4}}$, $2T - {{{{\tau }}}_{3}}$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$. В обозначениях (2.7) параметры ${{\gamma }_{1}}$, ${{\gamma }_{2}}$, ${{\gamma }_{3}}$, ${{\gamma }_{4}}$ будут корнями системы (2.2) при $j = 5$:

Кроме необходимого условия оптимальности (5.5), они также должны удовлетворить аналогичному уравнению:

Дифференцируя по $T$ соотношения (5.5), (5.9), (5.10), разрешим полученную систему уравнений относительно производных:

Здесь

где ${{V}_{{ij}}} = \omega {{\gamma }_{i}}{{\gamma }_{j}}{{S}_{{ij}}}$, обозначения ${{S}_{{ij}}}$, $i,j = \overline {0,4} $, $i \ne j$, имеют прежний смысл (5.3), выражения ${{\eta }_{i}}$, $i = \overline {1,4} $, вычисляются по формулам (5.7), а частные производные ${{R}_{i}} = \partial R{\text{/}}\partial {{\gamma }_{i}}$, i = 1, 2, 4, получаются из ${{H}_{i}}$, $i = \overline {1,3} $, (5.8) формальной заменой индексов 3 на 4.

Уравнения (5.11) описывают эволюцию корней ${{\gamma }_{i}}(T)$ системы (5.9), определяющих при каждом значении T моменты ${{\tau }_{i}}$, $i = \overline {1,4} $, переключения управления. На контрольной кривой этой эволюции соответствует перемещение коллинеарных точек ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$, ${{A}_{4}}$.

Замечание 8. В режиме с девятью переключениями управления, начатом при расположении точек ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ внутри дуги ${{N}_{2}}{{N}_{3}}$ (и точки ${{A}_{4}}$ внутри ${{K}_{0}}{{K}_{1}}$), прямая g не может иметь еще одну общую точку с контрольной кривой.

Для доказательства покажем, что в этом режиме точки ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ останутся внутри дуги ${{N}_{2}}{{N}_{3}}$. Если бы точка ${{A}_{1}}$ совпала с ${{N}_{3}}$, то получили бы ${\text{cos}}\left( {\omega {{\gamma }_{1}}} \right) = 0$ и противоречие во втором уравнении (5.9), где выражение в левой части превзошло бы значение 1, а в правой – нет. Во-первых, потому, что ${\text{cos}}\left( {\omega {{\gamma }_{2}}} \right) < {\text{cos}}\left( {\omega {{\gamma }_{3}}} \right)$ как в случае ${{A}_{2}} \in {{K}_{3}}{{N}_{2}}$ (где $2\pi < \omega {{\gamma }_{3}} < \omega {{\gamma }_{2}} < 3\pi $), так и в случае ${{A}_{2}} \in {{K}_{3}}{{N}_{3}}$ (где ${\text{cos}}\left( {\omega {{\gamma }_{2}}} \right) < 0$, причем ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) > 0$, ибо ${{A}_{3}} \in {{K}_{2}}{{N}_{2}}$, поскольку точка ${{N}_{2}}$ лежит выше прямой ${{K}_{3}}{{N}_{3}}$). Во-вторых, потому, что ${\text{cos}}\left( {\omega {{\gamma }_{4}}} \right) < 0$, так как точка ${{A}_{4}}$ на дуге ${{K}_{0}}{{K}_{1}}$ была бы ниже, чем точка $E$ пересечения дуги ${{K}_{0}}{{K}_{1}}$ с касательной, проведенной из ${{N}_{3}}$ к дуге ${{K}_{3}}{{N}_{2}}$ (расчеты показывают, что параметр $\sigma $ этой точки $E$ на промежутке $\omega \in (4,\,\infty )$ монотонно растет от $\sigma \approx 0.60873$ до $\sigma \approx 0.71015$). Аналогичное противоречие возникло бы при совмещении точек ${{A}_{3}}$ и ${{N}_{2}}$, когда ${\text{cos}}\left( {\omega {{\gamma }_{3}}} \right) = 0$ и ${\text{cos}}\left( {\omega {{\gamma }_{2}}} \right) < {\text{cos}}\left( {\omega {{\gamma }_{1}}} \right)$, поскольку обе точки ${{A}_{1}}$ и ${{A}_{2}}$ оказались бы на дуге ${{K}_{3}}{{N}_{3}}$ (где $3\pi {\text{ < }}\omega {{\gamma }_{2}} < \omega {{\gamma }_{1}} < 3.5\pi $). При этом ${\text{cos}}\left( {\omega {{\gamma }_{4}}} \right) < 0$, так как точка ${{A}_{4}}$ на дуге ${{K}_{0}}{{K}_{1}}$ была бы ниже, чем точка $G$ пересечения дуги ${{K}_{0}}{{K}_{1}}$ с касательной, проведенной из ${{N}_{2}}$ к дуге ${{K}_{3}}{{N}_{3}}$ (параметр точки $G$ на промежутке $\omega \in (4,\,\infty )$ монотонно растет от $\sigma \approx 0.59170$ до $\sigma \approx 0.67535$).

В силу замечания 8 упомянутый в нем режим с девятью переключениями управления удовлетворяет необходимым условиям оптимальности. При совпадении на контрольной кривой точек ${{A}_{1}}$ и ${{A}_{2}}$ (либо ${{A}_{2}}$ и ${{A}_{3}}$) этот режим может трансформироваться в режим с пятью переключениями управления, вновь описываемый соотношениями (5.2).

6. Построение диаграммы функций оптимального управления в задаче (1.1)–(1.3). На рис. 11 для случая $\omega = 6$ показана правая (зеркальная) часть диаграммы функций оптимального управления в диапазоне $T \in (0,\,\pi ]$. Перечисленным в утверждении 2 сценариям б) и г) здесь соответствуют значения ${{T}_{1}} \approx 1.29464$, ${{T}_{2}} \approx 1.86017$. При $T \in (0,\,{{T}_{1}})$ (сценарий а) функции ${{\gamma }_{i}}(T)$, $i = \overline {1,2} $, являются решениями системы (5.2), а при $T \in ({{T}_{1}},{{T}_{2}})$ (сценарий в) функции ${{\gamma }_{i}}(T)$, $i = \overline {1,3} $, – решения системы (5.6). На горизонтали $T = {{T}_{1}}$ (рис. 11) точкам ${{A}_{3}}$ (${{\gamma }_{3}} = {{\lambda }_{1}} \approx 0.88107$) и ${{A}_{1}}$, ${{A}_{2}}$ (γ₁ = = ${{\gamma }_{2}} \approx 1.01064$) соответствует случай (рис. 8, а) касательной из точки ${{A}_{3}}$ к дуге ${{P}_{1}}{{N}_{2}}$ контрольной кривой, после чего начинается режим с семью переключениями. Он завершается на горизонтали $T = {{T}_{2}}$ (рис. 11) в момент совмещения точек ${{A}_{3}}$ и ${{A}_{2}}$ – случай касательной из точки ${{A}_{1}}$ (${{\gamma }_{1}} = {{\lambda }_{2}} \approx 1.20540$) к дуге ${{P}_{1}}{{N}_{1}}$. При $T > {{T}_{2}}$, согласно замечанию 7, начинаются режимы с пятью переключениями, сменяемые режимами с девятью переключениями при $T \in (2.070,\,2.452)$ и при $T \in (2.753,\,\pi ]$ (в соответствии с поведением прямой $g$ на контрольной кривой).

На диаграмме (рис. 11) можно выделить три слоя, отделяемые горизонталями $T = {{T}_{1}}$ и $T = {{T}_{2}}$. В общем случае таких слоев может быть больше. Их количество (внутри диапазона $T \in (0,{{T}_{*}}{\text{/}}2]$, ${{T}_{*}} = 2m\pi $, отвечающего несократимой дроби ${{\omega }} = l{\text{/}}m$) определяется числом пересечений первых m фрагментов линии $\delta $ (рис. 4) с семейством цепочек ${{\varepsilon }_{j}}$, $j \in N$. С ростом значений ${{\omega }}$ и m количество слоев растет.

На рис. 4 пронумеруем координаты $(\omega {{T}_{i}},\omega {{\lambda }_{i}})$, $i = 1,2,...$, упомянутых точек пересечения в порядке возрастания ${{T}_{i}}$, так что нечетным значениям i будут соответствовать точки “входа” линии $\delta $ в закрашенные области (рис. 4), а четным значениям i – точки “выхода”. В случае прохождения линии $\delta $ через “узловую точку” цепочки (или касания с ней) положим ${{T}_{i}} = {{T}_{{i + 1}}}$.

Из вышеизложенного следует, что при $T \in ({{T}_{i}},{{T}_{{i + 1}}})$ ($i$ – нечетные) реализуются режимы с семью переключениями оптимального управления. В начале и в конце диапазонов $T \in ({{T}_{i}},{{T}_{{i + 1}}})$ (i – четные) – режимы с пятью переключениями, между которыми возможны (если прямая g заденет еще одну дугу контрольной кривой) режимы с девятью переключениями. В результате диаграмма функций оптимального управления вдоль вертикальной оси $T \in (0,{{T}_{*}}{\text{/}}2]$ составится из чередующихся слоев, отделяемых горизонталями $T = {{T}_{i}}$, символизирующими режимы с тремя переключениями управления. При этом для каждого слоя справедливы следующие обобщения замечаний 6 либо 8.

Замечание 9. Прямая g, пересекающая контрольную кривую в правой полуплоскости ($y > 0$) в точках ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ при $T \in ({{T}_{i}},{{T}_{{i + 1}}})$ (i – нечетное), не может иметь еще одну общую точку с контрольной кривой.

Доказательство аналогично обоснованию замечания 6: точки ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ на контрольной кривой не могут выйти за пределы дуги ${{N}_{i}}{{N}_{{i + 1}}}$ (i – нечетное), внутри которой они появились в начале диапазона $T \in ({{T}_{i}},{{T}_{{i + 1}}})$. Можно показать, что в таких положениях прямая g не задевает ближайшей дуги ${{K}_{{i - 1}}}{{N}_{{i - 2}}}$.

Замечание 10. В режиме с девятью переключениями управления, начатом при ${{A}_{4}} \in {{K}_{0}}{{K}_{1}}$ с точками ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ внутри дуги ${{N}_{i}}{{N}_{{i + 1}}}$ (i – четное, $i < \omega {\text{/}}2$), прямая g не может иметь еще одну общую точку с контрольной кривой.

Доказательство аналогично обоснованию замечания 8: точки ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ на контрольной кривой не могут выйти за пределы этой дуги ${{N}_{i}}{{N}_{{i + 1}}}$.

Отметим, в частности, что при $3 < \omega < 4$ линия $\delta $ (рис. 4) целиком лежит в диапазоне значений $\sigma < 2$, что соответствует таким завершениям режимов с семью переключениями, когда точка ${{A}_{1}}$ на контрольной кривой находится внутри дуги ${{K}_{1}}{{K}_{2}}$. По этой причине при $3 < \omega < 4$ режимы с девятью переключениями оптимального управления невозможны.

Алгоритм построения диаграммы функций оптимального управления начинается с определения корней системы (3.1) и изображения горизонталей $T = {{T}_{i}}$, $i = 1,2,...$, отделяющих слои. Затем внутри каждого слоя строятся графики функций ${{\gamma }_{k}}(T)$, $k = 1,2,...$, путем интегрирования соответствующих уравнений. Система (5.6) – для режимов с семью переключениями при $T \in ({{T}_{i}},{{T}_{{i + 1}}})$ (i – нечетное). Система (5.2) – для режимов с пятью переключениями в начале и в конце диапазонов при $T \in ({{T}_{i}},{{T}_{{i + 1}}})$ (i – четное). На каждом шаге интегрирования системы (5.2) проверяется, нет ли касания прямой ${{A}_{1}}{{A}_{2}}$ с контрольной кривой, чтобы в таком случае перейти к уравнениям (5.11) – с девятью переключениями.

В начале и в конце промежутков интегрирования в формулах (5.2), (5.6) возникает неопределенность вида “$0{\text{/}}0$”, но она преодолевается вычислением соответствующих пределов (подробности опускаем).

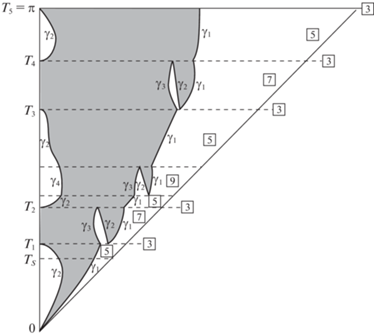
На рис. 12 показана правая (зеркальная) часть диаграммы функций оптимального управления для случая ω = 9 при $T \in (0,{{T}_{*}}{\text{/}}2]$. Здесь корни системы (3.1) ${{T}_{1}} \approx 0.852783$, ${{T}_{2}} \approx 1.204395$, ${{T}_{3}} \approx 2.163081$, ${{T}_{4}} \approx 2.628611$. Последний корень ${{T}_{5}} = \pi $ совпадает (ввиду целочисленности $\omega $) с ${{T}_{*}}{\text{/}}2$ и задает граничную горизонталь.

Оба замечания 9 и 10 относились к случаям, когда упоминаемые в них дуги ${{N}_{i}}{{N}_{{i + 1}}}$ контрольной кривой при $\omega \geqslant 3$ располагались в правой полуплоскости $y > 0$, отвечающей диапазону параметров $0 < T < \pi $. В частности, для целых значений $\omega > 1$ имеем ${{T}_{*}}{\text{/}}2 = \pi $. Поскольку при $\omega = 2$ оптимальное управление имеет [14] либо одно переключение (если $T$ кратно $2\pi $), либо пять (в остальных случаях), то справедливо следующее утверждение.

Утверждение 3. Для любого целого значения ω > 1 в задаче оптимального быстродействия (1.1)–(1.3) функция u(t), $t \in \left[ {0,~\,2{\kern 1pt} {\kern 1pt} T} \right]$ не может иметь другого количества переключений, кроме 1, 3, 5, 7, 9.

При этом свойства контрольной кривой гарантируют также следующие симметрии, порождаемые свойствами 2 и 3.

Утверждение 4. Для любого целого значения ω > 1 в задаче оптимального быстродействия (1.1)–(1.3) если функция управления с моментами переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T при $T < {{T}_{*}}{\text{/}}2$ удовлетворяет необходимым условиям оптимальности, то им также удовлетворят функции управления:

1) с моментами переключения ${{{{\tau }}}_{1}} + \Delta $, ${{{{\tau }}}_{2}} + \Delta $, …, ${{{{\tau }}}_{{j - 1}}} + \Delta $, $T + \Delta $ (где $\Delta = {{T}_{*}} - 2T$);

2) с моментами переключения ${{{{\tau }}}_{1}} + {{T}_{*}}$, ${{{{\tau }}}_{2}} + {{T}_{*}}$, …, ${{{{\tau }}}_{{j - 1}}} + {{T}_{*}}$, $T + {{T}_{*}}$.

Доказательство следует из того, что при одинаковом увеличении всех значений T и ${{\tau }_{k}}$, $k = \overline {1,j - 1} $, останутся неизменными все параметры ${{\gamma }_{k}}$ (2.7) и положения соответствующих точек ${{A}_{k}}$, $k = \overline {1,j - 1} $, на контрольной кривой. Она содержит точку $O(0,0)$ с параметром $\rho = \pi $, т.е. расположена в правой полуплоскости $y > 0$ для всех значений $0 < T < \pi $. Относя, как и прежде, точке $W$ параметр T, обозначим через ${{W}_{2}}$ и ${{W}_{1}}$ точки с параметрами $(T + {{T}_{*}})$ и $(T + \Delta )$ (где $\Delta = {{T}_{*}} - 2T$). Ввиду соотношений $\overline {O{{W}_{1}}} = {{\mu }_{1}}\overline {OW} $, ${{\mu }_{1}} = T{\text{/}}(T - 2\pi )$ и $\overline {O{{W}_{2}}} = {{\mu }_{2}}\overline {OW} $, ${{\mu }_{2}} = T{\text{/}}(T + 2\pi )$ имеем коллинеарность векторов. Поэтому приведенные выше обоснования замечаний 5–10, гарантировавших отсутствие дополнительных общих точек прямой g и контрольной кривой, сохранят свой смысл, если вместо точки W взять ${{W}_{1}}$ либо ${{W}_{2}}$.

Из п. 1) и 2) утверждения 4 вытекают свойства симметрии диаграмм функций оптимального управления при целых значениях $\omega > 1$. На рис. 9, 11, 12 изображенная правая (зеркальная) часть диаграммы дополнялась неизображенной левой (с заменой знаков управления на противоположные). Согласно п. 1), внутренность объединенного треугольника продолжится симметрично, отразившись относительно горизонтали $T = \pi $. Сдвоенная таким образом фигура (внутренность квадрата) затем будет периодически повторяться, согласно п. 2), с увеличением вертикальной координаты T до бесконечности.

В отличие от целочисленных ${{\omega }}$, для случая несократимой дроби ${{\omega }} = l{\text{/}}m$ возникает дополнительный сценарий, отвечающий пересечению линии $\delta $ с цепочкой ${{\varepsilon }_{1}}$ при $(l - 1)\pi < \omega T < (l + 1)\pi $. На рис. 4 для $\omega = 9{\text{/}}2$ эта точка пересечения обозначена $H$. Ей соответствует начало такого режима с семью переключениями управления, когда из точки, расположенной в верхней части дуги ${{K}_{0}}{{K}_{1}}$, строится касательная  f к крайней слева дуге контрольной кривой (рис. 5). Возможность (или невозможность) пересечения прямой f еще одной дуги контрольной кривой (в левой полуплоскости) требует дополнительного исследования. По крайней мере, диапазон значений T для точек, предшествующих точке $H$ вдоль линии $\delta $ (рис. 4), включает промежуток

В этом промежутке функция оптимального управления не может иметь более девяти переключений.

Для случаев $1 < \omega < 2$ свойства контрольной кривой отличаются тем, что точки ${{K}_{2}}$ и ${{K}_{1}}$ лежат по разные стороны от оси $Oz$, которую контрольная кривая пересекает последовательно в точках с параметрами $\rho = k\pi $, $k = \overline {1,m} $. На рис. 6 для $\omega = 5{\text{/}}4$ показан сценарий касания прямой  f  к крайней слева дуге контрольной кривой при ${{T}_{1}} \approx 5.65644$, ${{\gamma }_{3}} = {{\lambda }_{1}} \approx 0.43949$. Этому сценарию предшествовали, согласно свойству 4, режимы с пятью переключениями управления, когда функции ${{\gamma }_{i}}(T)$, $i = 1,2$, были решениями системы (5.2) при $T \in \left( {0,{\text{\;}}{{T}_{s}}} \right]$. Значению ${{T}_{s}} = 2\pi {\text{/}}\omega $ (т.е. $\sigma = 2$) соответствует совмещение точки $W$ с точкой ${{K}_{2}}$. При движении точки $W$ по контрольной кривой (рис. 6) в диапазоне $\pi < T < {{T}_{s}}$ последовательно осуществится коллинеарность сначала векторов $\overline {OW} $ и $\overline {O{{A}_{2}}} $ (меняющая знаки ${{S}_{{20}}}$ и ${{\dot {\gamma }}_{1}}$), затем векторов $\overline {OW} $ и $\overline {O{{A}_{1}}} $ (со сменой знаков ${{S}_{{10}}}$ и ${{\dot {\gamma }}_{2}}$). После этого обе точки ${{A}_{1}}$ и ${{A}_{2}}$ будут двигаться вверх по дуге ${{K}_{0}}{{K}_{1}}$ вплоть до совмещения ${{A}_{2}}$ и ${{K}_{0}}$, причем у прямой ${{A}_{1}}{{A}_{2}}$ и контрольной кривой не появится новых общих точек. Прямая f коснется дуги ${{K}_{2}}{{K}_{3}}$ (рис. 6) раньше, чем точка W достигнет положения с параметром $T = 2\pi $. Поэтому в диапазоне $T \in \left( {0,{\text{2}}\pi } \right]$ для случаев $1 < \omega < 2$ возможны лишь режимы с пятью или семью переключениями управления.

Для случаев $2 < \omega < 3$ дуга ${{K}_{2}}{{K}_{3}}$ контрольной кривой лежит выше оси $Oy$, но рассекается осью $Oz$. Здесь для режимов с пятью переключениями, начатых при $T \in \left( {0,{\text{\;}}{{T}_{s}}} \right]$, точки $W$, ${{A}_{1}}$, ${{A}_{2}}$ будут смещаться по кривой так, что (в отличие от случаев $1 < \omega < 2$) сначала осуществится коллинеарность векторов $\overline {OW} $ и $\overline {O{{A}_{1}}} $ (меняющая знак ${{\dot {\gamma }}_{2}}$), затем векторов $\overline {OW} $ и $\overline {O{{A}_{2}}} $ (со сменой знака ${{\dot {\gamma }}_{1}}$), после чего точка ${{A}_{1}}$ будет двигаться “вспять” (в отличие от сценария а) случаев $\omega \geqslant 3$). Поэтому в момент совмещения ${{A}_{2}}$ и ${{K}_{0}}$ точка ${{A}_{1}}$ окажется выше оси $Oy$, касательная из нее к контрольной кривой может строиться лишь к “крайней слева” дуге (аналогично прямой  f  на рис. 6). В этот момент параметры ${{T}_{1}}$ и ${{\lambda }_{1}}$ точек $W$и ${{A}_{1}}$ будут соответствовать на рис. 4 пересечению линии $\delta $ с цепочкой ${{\varepsilon }_{1}}$. Таким образом, для случаев $2 < \omega < 3$ режиму (при $T = {{T}_{1}}$) с тремя переключениями предшествуют только режимы с пятью переключениями, в том числе в диапазоне (6.1).

Вышеизложенное можно обобщить для любых $\omega $ в следующем виде.

Утверждение 5. В задаче оптимального быстродействия (1.1)–(1.3) функция u(t), $t \in \left[ {0,~\,2\,T} \right]$ в диапазоне (6.1) не может иметь другого количества переключений, кроме 3, 5, 7, 9.

Заключение. Рассмотрена задача оптимального по быстродействию перемещения (на заданное расстояние) платформы с двумя осцилляторами из одного состояния покоя в другое. На основе свойств [14] функций оптимального управления введено графическое представление (в виде контрольной кривой), позволившее исследовать эволюцию таких функций в зависимости от дальности перемещения. Предложен наглядный образ этой зависимости в виде диаграммы, для построения которой указан алгоритм.

Наиболее простыми для исследования оказались случаи, когда значения $\omega $ – целые. Им соответствуют не только простейшая форма (всего из одной арки) линии $\delta $ на рис. 4, но и актуальность лишь части контрольной кривой, лежащей в правой полуплоскости, а также наименьший период для функций ${{\gamma }_{k}}(T)$, $k = 1,2,...$, чьи графики порождают контуры диаграммы. В частности, показано, что при целочисленных $\omega $ в задаче быстродействия (1.1)–(1.3) оптимальное управление не может иметь другого количества переключений, кроме 1, 3, 5, 7 или 9.

Заметим, что с увеличением значения ω растет количество корней системы (3.1), демонстрируемых точками пересечения линий на рис. 4 и отвечающих режимам с тремя переключениями управления. При этом на диаграмме функций оптимального управления становится все больше горизонтальных слоев и уменьшаются их толщины. Поскольку эти же корни являются координатами точек и на дуге $OBF$ (рис. 2), то в среднем фигура на диаграмме для платформы с двумя осцилляторами приближается к виду диаграммы для платформы с одним осциллятором, отличаясь от нее все меньшими амплитудами флуктуаций. Это соответствует асимптотическому поведению системы (1.1), в которой при $\omega \to \infty $ третье уравнение вырождается.