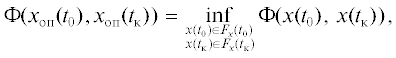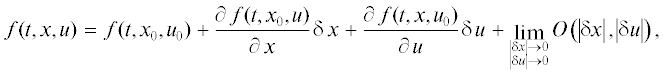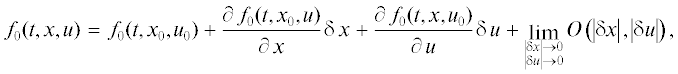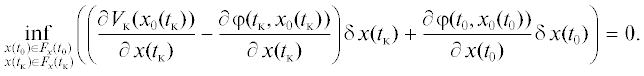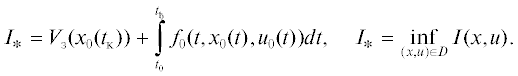Известия РАН. Теория и системы управления, 2022, № 6, стр. 20-37
ПРИБЛИЖЕННО-ОПТИМАЛЬНЫЙ СИНТЕЗ СИСТЕМ ОПЕРАТИВНОГО УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ НА ОСНОВЕ КВАЗИЛИНЕАРИЗАЦИИ И ДОСТАТОЧНЫХ УСЛОВИЙ ОПТИМАЛЬНОСТИ
А. В. Данеев a, *, В. Н. Сизых a, **
a Иркутский государственный ун-т путей сообщения
Иркутск, Россия
* E-mail: daneev@mail.ru
** E-mail: sizykh_vn@mail.ru
Поступила в редакцию 24.03.2022
После доработки 13.04.2022
Принята к публикации 30.05.2022
- EDN: YCZOSU
- DOI: 10.31857/S0002338822060063
Аннотация
Изложен новый подход к аналитическому конструированию линейных и нелинейных иерархических по контурам управления, многофункциональных систем автоматического управления реального (ускоренного) масштаба времени, базирующийся на совместном использовании технологий динамического программирования и метода квазилинеаризации. Для непрерывных динамических систем приведены основы теории нелинейного синтеза в формулировке, которая допускает формирование оптимальной, приближенно-оптимальной и субоптимальных стратегий управления относительно заранее неизвестной, но определяемой на малых длинах оптимизации вектор-функции оптимального управления.
Введение. Управление – создание в каждый текущий момент времени целенаправленных воздействий на объект управления в зависимости от доступной информации о поведении объекта и действующих на него возмущений. В теории управления рассматриваются три принципа управления: 1) по разомкнутому контуру, 2) по замкнутому контуру, 3) в реальном или в ускоренном времени (времени, на которое прогнозируется движение объекта [1, 2]). При использовании первого принципа до начала процесса управления по априорной информации строится программа (программное управление), которая в процессе управления не корректируется. При втором принципе управления текущие управляющие воздействия (позиционные управления) создаются по заранее (до начала процесса управления) составленным правилам, определенным на всевозможной информации, которая может появиться о поведении объекта и действующих на него возмущений в процессе управления. Эти правила реализуются в форме прямых, обратных и комбинированных связей. При использовании третьего принципа управления перечисленные связи заранее не создаются, их текущие (потребные будущие) значения вычисляются в реальном (ускоренном) масштабе времени в процессе функционирования объекта. Здесь эти связи являются гомеостатическими (нежесткими), как у обычных систем автоматического управления (САУ). Они создаются и обновляются в процессе функционирования объекта в управляющем устройстве.
Подход к проблеме синтеза непрерывных динамических систем, ориентированный на принцип оптимального управления (ОУ) в реальном или в ускоренном времени, был предложен в начале 70-х годов В.С. Шендриком (по инициативе Б.Н. Петрова) и развит А.А. Красовским и его учениками [1]. Наибольший вклад в развитие данного направления теории ОУ внес В.Н. Буков [2]. В начале 90-х годов принцип управления в реальном времени был “переоткрыт” Р. Габасовым и Ф.М. Кирилловой и успешно развивается в белорусской школе математиков [3].
Известно, что на традиционные алгоритмы последовательных улучшений накладываются достаточно жесткие условия по сходимости и выбору начальных приближений [8, 9]. На пути использования только достаточных условий оптимальности или теории квазилинеаризации простых и надежных (гарантирующих поточечную сходимость) методов, как отмечалось еще Р. Беллманом [4], создать не удалось. Для преодоления этих трудностей в статье развивается многометодная технология, основанная на сочетании метода квазилинеаризации с достаточными условиями оптимальности. Предлагается применить квазилинеаризацию для локальной оптимизации в окрестности стационарности точек функции Гамильтона, а достаточные условия оптимальности – для интервальной оптимизации. Основная идея предлагаемой двухметодной технологии: за счет интервальной оптимизации осуществлять грубый поиск начального приближения по достаточным условиям, а затем итерационным путем уточнять полученное приближение по условиям локальной оптимальности (стационарности или в форме принципа минимума).
Для организации минимизирующих последовательностей слабой минимали формулируется вспомогательная (вырожденная по формулировке) задача приближенно-оптимального синтеза. Вырожденность здесь заложена в саму постановку проблемы управления и проявляется особым образом: исходная (невырожденная) задача синтеза доопределяется до сингулярной с целью включения предельных функций управления в множество допустимых, но таким образом, чтобы преобразованная задача содержала оптимальное решение. Если в традиционных постановках вырожденных задач управления сингулярная кривая подлежит определению, то в преобразованной задаче она известна: ею является оптимальная траектория исходной задачи.
Таким образом, в отличие от известных подходов к решению задачи приближенно-оптимального синтеза регуляторов, когда в методе решения используется имеющаяся неоднозначность в выборе производящих функций со свойствами функции Ляпунова, в данном случае существует место другое продолжение теории достаточных условий: путем фазовой линеаризации уравнений динамической системы и интегранта функционала исходной задачи нелинейного синтеза относительно заранее неизвестных, но определяемых в процессе функционирования объекта постоянных на малых интервалах времени оптимальных значений вектор-функций управления (квазилинеаризации) и через формирование градиентной стратегии ньютоновского типа по вариациям управлений на тех же интервалах последовательно определяются и уточняются точки стационарности искомой минимали. С целью фиксации предельных элементов минимизирующих последовательностей поиска оптимального решения по условиям стационарности предлагается использовать функционал обобщенной работы А.А. Красовского.
Разработаны эффективный метод совмещенного синтеза и процедуры решения двухточечной краевой задачи по схеме дифференциального динамического программирования (ДП), обеспечивающие поинтервальную монотонно убывающую (релаксационную) сходимость процессов управления по необходимым условиям локальной оптимальности. Сформулированы основные теоремы и приводится один из вариантов алгоритмической реализации метода. Необходимость в такой разработке обусловлена фактическим отсутствием надежных методов нелинейного синтеза цифровых регуляторов, гарантирующих высокую точность и устойчивость решения при приемлемых вычислительных затратах.
1. Постановка задачи приближенно-оптимального синтеза управлений. Под оптимизацией непрерывных процессов управления будем понимать решение задачи выбора на отрезке времени $T = [{{t}_{0}},{{t}_{{\text{к}}}}]$ позиционного управления
для динамической системы такого, чтобы на траектории движения объекта $x(t)$, удовлетворяющей заданным ограничениям на множествах начального и конечного состояний(1.3)
$\mu ({{t}_{0}},x({{t}_{0}}),{{t}_{{\text{к}}}},x({{t}_{{\text{к}}}})) = 0,\quad \mu \in {{R}^{p}},$В дальнейшем будем рассматривать менее общую постановку задачи оптимизации – постановку задачи нелинейного синтеза, для которой условие (1.3) без потери общности может учитываться в конструкции модифицированного лагранжиана; а скалярная функция ${{V}_{{\text{з}}}}(x({{t}_{{\text{к}}}}))\,\, = \,\,{{V}_{{\text{з}}}}({{t}_{{\text{к}}}},x({{t}_{{\text{к}}}}))$ определяет граничные условия только на правом конце траектории (терминальное множество). Граничные условия на левом конце траектории $x({{t}_{0}}) = {{x}^{0}} \in {{R}^{n}}$ выбираются произвольными. Конечные ограничения на граничные условия и на значения управляющих функций и траектории процесса (1.3) будем записывать как
где $F(t) \subset {{G}_{x}} \times {{G}_{u}},$ ${{G}_{x}} = X,$ ${{G}_{u}} = U$ является декартовым произведением множеств топологической степени $(n + m)$, зависящим от времени $t$.Множество пар вектор-функций $\{ x(t),u(t)\} $, удовлетворяющих дифференциальной связи (1.2) и конечным ограничениям (1.5), называют множеством допустимых D. Предполагается, что $D \ne \emptyset $.
Пару функций $\{ {{x}_{{{\text{оп}}}}}(t),{{u}_{{{\text{оп}}}}}(t)\} \in D$ будем называть оптимальным процессом (минималью) для I на D, если
Здесь $d = \mathop {\inf }\limits_D I(x(t),u(t))$ – нижняя точная грань функционала (1.4).
Нижнюю точную грань функционала (1.4) в общей теории экстремальных задач называют опорным функционалом (опорой) [5].
Последовательность $\{ {{x}_{s}}(t),{{u}_{s}}(t)\} \in D$, на которой
является минимизирующей для функционала I на множестве D.2. Квазилинеаризация и достаточные условия оптимальности. Введем непрерывную и достаточно гладкую (дифференцируемую или абсолютно непрерывную) функцию $\varphi (t,x) \in \Phi $ и рассмотрим следующие конструкции [5, с. 263]:
(2.1)
$R(t,x,u) = \frac{{\partial \,\varphi (t,x)}}{{\partial \,t}} + \frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}f(t,x,u) + {{f}_{0}}(t,x,u),$(2.2)
$\Phi (x({{t}_{0}}),x({{t}_{{\text{к}}}})) = {{V}_{{\text{з}}}}(x({{t}_{{\text{к}}}})) - \varphi ({{t}_{{\text{к}}}},x({{t}_{{\text{к}}}})) + \varphi ({{t}_{0}},x({{t}_{0}}))$.Для того чтобы пара $({{x}_{{{\text{оп}}}}},{{u}_{{{\text{оп}}}}}) \in D$ была минималью в задаче (1.1)–(1.5), достаточно существования такой гладкой функции $\varphi (t,x)$, чтобы выполнялись условия [6]
(2.3)
$\mu (t) = R(t,{{x}_{{{\text{оп}}}}},{{u}_{{{\text{оп}}}}}) = \mathop {\inf }\limits_{(x,u) \in F(t)} R(t,x,u)\quad {\text{для любого}}\quad t \in [{{t}_{0}},{{t}_{{\text{к}}}}],$Учтем в исходных конструкциях (2.3), (2.4) тейлоровское разложение функций f, f0 в малой окрестности локальной минимали $({{x}_{0}}(t),{{u}_{0}}(t)) = ({{x}_{{{\text{оп}}}}}(t),{{u}_{{{\text{оп}}}}}{{(t,\tau )}_{{|\tau = t}}})$:
где для краткости обозначимЗдесь $O\left( {\left| {\delta x} \right|,\left| {\delta u} \right|} \right)$представляет члены более высокого порядка малости [7, c. 19], чем модули $\left| {\delta x} \right|$ и $\left| {\delta u} \right|$ (т.е.  ) на длинах оптимизации Δt с точностью определения погрешностей вычислений 5–7% в точках стационарности функции
Гамильтона, причем в (2.5) остаточный член представляет собой вектор, а в (2.6) –
скаляр. Так как предполагается, что члены разложения выше второго порядка пренебрежительно
малы, и принимается, что незначимая функция времени $\mu (t) = R(t,{{x}_{{{\text{оп}}}}},{{u}_{{{\text{оп}}}}}) = \mathop {\inf }\limits_{(x,u) \in F(t)} R(t,x,u)$ = 0, то достаточные условия (2.3), (2.4) с учетом (2.5), (2.6) перепишутся в виде
) на длинах оптимизации Δt с точностью определения погрешностей вычислений 5–7% в точках стационарности функции
Гамильтона, причем в (2.5) остаточный член представляет собой вектор, а в (2.6) –
скаляр. Так как предполагается, что члены разложения выше второго порядка пренебрежительно
малы, и принимается, что незначимая функция времени $\mu (t) = R(t,{{x}_{{{\text{оп}}}}},{{u}_{{{\text{оп}}}}}) = \mathop {\inf }\limits_{(x,u) \in F(t)} R(t,x,u)$ = 0, то достаточные условия (2.3), (2.4) с учетом (2.5), (2.6) перепишутся в виде
(2.7)
$\begin{gathered} \mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\frac{{\partial \,\varphi (t,x)}}{{\partial \,t}} + \frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}f(t,{{x}_{0}},{{u}_{0}}) + {{f}_{0}}(t,{{x}_{0}},{{u}_{0}})} \right) + \mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\left[ {\frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}\frac{{\partial \,f}}{{\partial \,x}} + \frac{{\partial \,{{f}_{0}}}}{{\partial \,x}}} \right]\delta \,x} \right) + \\ \, + \mathop {\inf }\limits_{u \in U} \left( {\left[ {\frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}\frac{{\partial \,f}}{{\partial \,u}} + \frac{{\partial \,{{f}_{0}}}}{{\partial \,u}}} \right]\delta \,u} \right) = 0, \\ \end{gathered} $Выражения в квадратных скобках формулы (2.7) могут быть записаны через скалярную функцию$H(t,x,{{\varphi }_{x}},u) = \partial \,\varphi (t,x){\text{/}}\partial \,x \cdot f + {{f}_{0}}$. Тогда формулу (2.8) можно представить как
(2.9)
$\begin{gathered} \mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\frac{{\partial \,\varphi (t,x)}}{{\partial \,t}} + \frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}f(t,{{x}_{0}},{{u}_{0}}) + {{f}_{0}}(t,{{x}_{0}},{{u}_{0}})} \right) + \mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\frac{{\partial \,H(t,{{x}_{0}},{{\varphi }_{x}},u)}}{{\partial \,x}}\delta \,x} \right) + \\ \, + \mathop {\inf }\limits_{u \in U} \left( {\frac{{\partial \,H(t,x,{{\varphi }_{x}},{{u}_{0}})}}{{\partial \,u}}\delta \,u} \right) = 0. \\ \end{gathered} $Соотношение (2.9) будет характеризовать четыре различные ситуации, каждой из которых соответствуют свои конструкции алгоритмов оптимального управления.
Первая ситуация типична при решении задач ОУ на основе принципа минимума, где постулируется сам факт существования экстремали Понтрягина: $x = {{x}_{0}}(t),$ ${{u}_{{{\text{оп}}}}}(t,t) = {{u}_{0}}(t),$ ${{\varphi }_{x}} = {{\psi }^{{\text{Т}}}}(t)$. Тогда при фиксированных начальных условиях $(\delta \,x({{t}_{0}}) = 0)$ из (2.9) можно формально выписать уравнение сопряженной системы (уравнение импульсов), а из формулы (2.8) определить условия его трансверсальности.
Вторая ситуация имеет место при решении задач синтеза ОУ методом дифференциального ДП [8], когда об оптимальности траектории $x = {{x}_{0}}(t)$ можно косвенно судить по условиям оптимальности отдельных ее участков (интервалов $[t,{{t}_{{\text{к}}}}]$) при ненулевой вариации управления ($\delta \,u \ne 0$) на этих участках. Такой способ вычислений не связан с непосредственным варьированием управления и траектории и, как следует из формулы (2.9), сводится к поиску минимизирующей последовательности (к организации процедуры слабого локального улучшения) ${{u}_{{{\text{оп}}}}}(t,\tau )\mathop \to \limits_{\tau \to t} {{u}_{{{\text{оп}}}}}(t,t) = {{u}_{0}}(t)$, где локально-оптимальное управление ${{u}_{0}}(t)$ определяется по условию стационарности. При $x = {{x}_{0}}(t)$ функция $\varphi (t,x)$ является функцией Беллмана $S(t,x)$ (${{S}_{x}} = {{\psi }^{{\rm T}}}(t)$).
Третья ситуация соответствует случаю $x \ne {{x}_{0}}(t),$ ${{u}_{{{\text{оп}}}}}(t,t) = {{u}_{0}}(t)$, допускает и фактически рекомендует тип приближения, называемый приближением в пространстве политик [4], который также отсутствует в классическом анализе. Политика (процедура сильного локального улучшения) $x(\tau )\mathop \to \limits_{\tau \to t} {{x}_{0}}(t)$, согласно (2.7), (2.8), формируется по условию
(2.10)
$\mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\left[ {\frac{{\partial \,\varphi (t,x)}}{{\partial \,x}}\frac{{\partial \,f}}{{\partial \,x}} + \frac{{\partial \,{{f}_{0}}}}{{\partial \,x}}} \right]\delta \,x} \right) = \mathop {\inf }\limits_{x \in {{F}_{x}}} \left( {\frac{{\partial \,H(t,{{x}_{0}},{{\varphi }_{x}},{{u}_{0}})}}{{\partial \,x}}\delta \,x} \right) = 0,$(2.11)
$\frac{{\partial \,H(t,{{x}_{0}},{{\varphi }_{x}},{{u}_{{\text{0}}}})}}{{\partial \,x}} \equiv 0$Четвертая ситуация формально напоминает классическую постановку решения вариационных задач, так как в ней за счет квазилинеаризации предполагается использовать ненулевые вариации траектории и управления: $x \ne {{x}_{0}}(t),$ $u \ne {{u}_{0}}(t)$. Через соотношения $\partial H(t,x,{{\varphi }_{x}},{{u}_{{\text{0}}}}){\text{/}}\partial u \equiv 0,$ $\partial H(t,{{x}_{0}},{{\varphi }_{x}},u){\text{/}}\partial x\, \equiv \,0$ здесь организуются итерационные процедуры улучшения ${{u}_{{{\text{оп}}}}}(t,\tau )\mathop \to \limits_{\tau \to t} {{u}_{{{\text{оп}}}}}(t,t)$ = = u0(t), $x(\tau )\mathop \to \limits_{\tau \to t} {{x}_{0}}(t)$, обеспечивающие выполнение необходимого условия абсолютного локального минимума функционала (1.4): при $\delta \,x \to 0,$ $\delta \,u \to 0$ ожидается сходимость
Определим множества
Определение 1 [9]. Пара функций $({{x}_{0}}(t),\,{{u}_{0}}(t)) \in D$ называется сильной (слабой) локальной минималью, если существует такое число ε > 0, что $I({{x}_{0}},\,{{u}_{0}}) \leqslant I(x,\,u)$ для всех (x(t), $u(t)) \in {{D}_{1}}(\varepsilon )({{D}_{2}}(\varepsilon ))$.
Сформулируем теперь ряд теоретических положений о слабой минимали, которые формально следуют из анализа формул (2.8), (2.9).
Теорема 1 (условия локальной оптимальности в форме принципа минимума11). Если в задаче (1.1)–(1.5) существует локальная минималь $({{x}_{0}},{{u}_{0}})$, то в каждой точке стационарности выполняются следующие условия:
1) $\frac{{\partial \,\varphi (t,{{x}_{0}})}}{{\partial \,t}} + \bar {H}(t,{{x}_{0}},\psi ) = 0,$ $\frac{{\partial \,\varphi (t,{{x}_{0}})}}{{\partial \,x}} = {{\psi }^{{\rm T}}}(t)$,
2) ${{V}_{{\text{з}}}}({{x}_{0}}({{t}_{{\text{к}}}})) = \varphi ({{t}_{{\text{к}}}},{{x}_{0}}({{t}_{{\text{к}}}})) - \varphi ({{t}_{0}},{{x}_{0}}({{t}_{0}})),$
3) $\bar {H}(t,{{x}_{{\text{0}}}},\psi ) = H(t,{{x}_{{\text{0}}}},\psi ,{{u}_{{\text{0}}}}) = \mathop {\inf }\limits_{u \in U} H(t,{{x}_{0}},\psi ,u).$
Здесь условиям 1), 2) соответствует канонически сопряженная система уравнений, формирующая двухточечную краевую задачу:
(2.12)
${{\dot {x}}_{0}} = \frac{{\partial \,{{{\bar {H}}}^{{\rm T}}}(t,{{x}_{0}},\psi )}}{{\partial \,\psi }} = f(t,{{x}_{0}},{{u}_{0}}),\quad {{x}_{0}}({{t}_{0}}) = {{x}^{0}},$(2.13)
$\dot {\psi } = - \frac{{\partial \,{{{\bar {H}}}^{{\rm T}}}(t,{{x}_{0}},\psi )}}{{\partial \,x}} = - \frac{{\partial \,{{f}^{{\rm T}}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,x}}\psi - \frac{{\partial \,f_{0}^{{\rm T}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,x}},\quad {{\psi }^{{\rm T}}}({{t}_{{\text{к}}}}) = \frac{{\partial \,{{V}_{{\text{з}}}}({{x}_{{\text{0}}}}({{t}_{{\text{к}}}}))}}{{\partial \,x({{t}_{{\text{к}}}})}}.$Из условия 3) определяется вектор управления ${{u}_{0}}(t) = {{u}_{{{\text{оп}}}}}(t,\,\,t) = \mathop {\arg \min }\limits_{u \in U} H(t,{{x}_{0}},\psi ,u)$, в локальном смысле доставляющий минимум функционалу (1.4):
Таким образом, в рассмотренной выше первой ситуации локальная минималь (оптимальная программа) и опорный функционал ${{I}_{*}}$ вычисляются через решение двухточечной краевой задачи (2.12), (2.13).
Отметим, что предположение теоремы 1 о том, что пара $({{x}_{0}},\,\,{{u}_{0}})$ – локальная минималь в задаче (1.1)–(1.5), несколько эвристично, пока не доказан факт ее существования [7, c. 24–26]. Этот факт устанавливается путем такой переформулировки исходной задачи ОУ, при которой имеется возможность организации процедур поиска минимизирующих последовательностей, монотонно сходящихся по u к локальной минимали.
Теорема 2 (условия первого порядка локального минимума22). Для того чтобы пара $({{x}_{0}},\,{{u}_{0}})$ была слабой локальной минималью задачи (1.1)–(1.6), необходимо и достаточно выполнения следующих условий:
1) $\frac{{\partial \,\varphi (t,{{x}_{0}})}}{{\partial \,t}} + \frac{{\partial \,\varphi (t,{{x}_{0}})}}{{\partial \,x}}f(t,{{x}_{0}},{{u}_{0}}) + {{f}_{0}}(t,{{x}_{0}},{{u}_{0}}) = 0,$ $\frac{{\partial \,\varphi (t,{{x}_{0}})}}{{\partial \,x}} = \frac{{\partial \,S(t,{{x}_{0}})}}{{\partial \,x}} = {{\psi }^{{\rm T}}}(t),$
2) ${{V}_{{\text{з}}}}({{x}_{0}}({{t}_{{\text{к}}}})) = \varphi ({{t}_{{\text{к}}}},{{x}_{0}}({{t}_{{\text{к}}}})) - \varphi ({{t}_{0}},{{x}_{0}}({{t}_{0}})),$
3) $\partial \,H(t,{{x}_{0}},\psi ,{{u}_{0}}){\text{/}}\partial \,u \equiv 0$ для $u \in \operatorname{int} U$ или $U = {{R}^{m}}$ и при ненулевой допустимой вариации управления $\delta \,u$.
Замечание 1. По-видимому, на границах множества U следующее из анализа (2.9) равенство $\mathop {\inf }\limits_{u \in U} (\partial \,H(t,x,{{\varphi }_{x}},{{u}_{0}}){\text{/}}\partial \,u \cdot \delta \,u) = 0$ уступит место соотношению $\mathop {\inf }\limits_{u \in U} (H(t,{{x}_{0}},\psi ,\,u)\,\varepsilon \,\xi (t)) = 0$, где $\varepsilon $ – малое число, $\xi (t)$ – непрерывная и кусочно-гладкая на множестве малой меры функция. Тогда условие 3) теоремы 2 можно заменить на условие $\mathop {\inf }\limits_{u \in U} H(t,{{x}_{0}},\psi ,u) \equiv 0.$
Теорема 2 соответствует случаю решения задачи локально-оптимального синтеза ОУ по схеме дифференциального ДП [8]. Здесь локальное улучшение управления осуществляется через квазилинеаризацию дифференциальной связи (1.3) и интегранта функционала качества (1.4) в окрестности ${{u}_{0}}(t)$, т.е.
(2.16)
$I(u( \cdot )) = {{V}_{{\text{з}}}}({{x}_{0}}({{t}_{{\text{к}}}})) + \int\limits_{{{t}_{0}}}^{{{t}_{{\text{к}}}}} {({{f}_{0}}} (t,{{x}_{0}}(t),{{u}_{0}}(t)) + \frac{{\partial \,{{f}_{0}}}}{{\partial \,u}}\delta \,u)dt = {{I}_{*}} + \int\limits_{{{t}_{0}}}^{{{t}_{{\text{к}}}}} {\left( {\frac{{\partial \,{{f}_{0}}}}{{\partial \,u}}\delta \,u} \right)} {\kern 1pt} {\kern 1pt} dt.$Непосредственно из формул (2.15), (2.16) видно, что при организации процедуры приближений ${{u}_{{{\text{оп}}}}}(t,\tau )\mathop \to \limits_{\tau \to t} {{u}_{{{\text{оп}}}}}(t,t) = {{u}_{0}}(t)$ значения функционала (2.16) стремятся к нижней точной грани ${{I}_{*}}$ функционала исходной задачи (1.1)–(1.5).
Аналогичные теореме 2 утверждения сформулированы в [11, 12] для схемы приближения в пространстве политик и аналога вариационной схемы в задаче локализации и улучшения.
3. Метод решения двухточечных краевых задач для непрерывных динамических систем по схеме дифференциального ДП. 3.1. Релаксационное расширение пространства состояний. Следующий конструктивный шаг к практической реализации рассмотренных выше схем решения задачи (1.1)–(1.5) состоит в определении стратегии приближенного синтеза оптимальных в локальном смысле управлений через релаксационное расширение пространства состояний. Релаксационное расширение связано с исследованием свойств предельных элементов минимизирующих последовательностей поиска управлений, которые определяют исходную постановку задачи синтеза для дифференциальной системы (1.3).
В основу организации поиска предельных элементов положены [13]:
идея квазилинеаризации – фазовой линеаризации процесса (1.3) и интегранта функционала (1.4) относительно оптимальных, определяемых в процессе функционирования объекта, и постоянных на конечном числе малых длин оптимизации $\Delta t$ параметров ${{u}_{0}} = u{\kern 1pt} *$ по формулам (2.15), (2.16);
предположение о допустимости выбора управлений и/или траекторий, мало отличающихся от оптимальных на конечном числе длин $\Delta t$, что дает возможность организовать приближенную стратегию синтеза на паре (u, u0) по схеме дифференциального ДП:
где $\vartheta $ – “новый” $m$-вектор управления.Если длины оптимизации $\Delta t$ малы, то производные в (3.1) с достаточной степенью точности описываются соотношением
которое может быть реализовано в виде итерационной процедуры ньютоновского типа для определения локальной минимали: при $\vartheta \to 0$ в каждой точке стационарности обеспечивается выполнение условия $u(t)\, \to {{u}_{0}}(t).$ Поэтому выбор градиентной стратегии типа (3.1) естественен, соответствует идеологии квазилинеаризации и идее нелинейного синтеза в процессе функционирования объекта (1.3) (совмещенного синтеза) на малых длинах $\Delta t$. Этим самым и сама задача синтеза представляется в линеаризованном виде: множество всех точек $x({{t}_{{\text{к}}}})$ терминального члена функционала (1.5) становится близко к выпуклому [14].3.2. Применение функционала обобщенной работы в задаче приближенно-оптимального синтеза регуляторов. Суть градиентной стратегии (3.1) – релаксационное расширение пространства состояний (1.3): $y = (x,\,\delta \,u)$ для схемы дифференциального ДП. Поэтому требуется таким образом переформулировать исходную постановку задачи оптимизации (1.1)–(1.5), чтобы была возможность зафиксировать предельные элементы минимизирующих последовательностей в точках стационарности $u = {{u}_{0}}$. Для этого предлагается применить функционал обобщенной работы (ФОР) [1]
(3.2)
$I(y( \cdot )) = {{S}_{{\text{з}}}}(y({{t}_{{\text{к}}}})) + \int\limits_{{{t}_{0}}}^{{{t}_{{\text{к}}}}} {[{{Q}_{р}}(\theta ,y) + {{L}_{{{\text{з1}}}}}(\vartheta ) + {{L}_{{{\text{з1}}}}}({{\vartheta }_{0}})]\,d\theta } ,$Переменная ${{\vartheta }_{0}}$ на длинах $\Delta t$ является постоянным, не варьируемым параметром: ${{\vartheta }_{0}} = \vartheta {\kern 1pt} *$.
Задача получения оптимального решения линеаризованного на малых длинах оптимизации $\Delta t$ процесса (1.3) формулируется следующим образом: организовать итерационные процедуры поиска слабой минимали (теорема 2), обеспечивающие инфимум ФОР (3.2) при дифференциальных связях (1.3).
Сформулированная задача приближенно-оптимального синтеза решается методом характеристических полос [1]. Основной результат формулируется в виде следующей теоремы.
Теорема 3. Для процесса (1.3) оптимальное в смысле достижения локального минимума функционала (1.3) и ФОР (3.2) управление определяется процедурой слабого улучшения ${{u}_{{{\text{оп}}}}}(t,\tau )\mathop \to \limits_{\tau \to t} {{u}_{{{\text{оп}}}}}(t,t) = {{u}_{{\text{0}}}}(t)$, получаемой из канонически сопряженной системы: дифференциальной связи (2.15) и уравнений
(3.3)
${{\dot {p}}_{x}} = - \frac{{\partial \,f_{0}^{{\text{T}}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,x}} - \frac{{\partial \,{{f}^{{\text{T}}}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,x}}\,{{p}_{x}} + \frac{{\partial \,(\delta \,{{u}^{{\rm T}}}\dot {p}_{{\delta u}}^{{}})}}{{\partial \,x}},$(3.4)
${{\dot {p}}_{{\delta u}}} = - \frac{{\partial \,f_{0}^{{\rm T}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,u}} - \frac{{\partial \,{{f}^{{\rm T}}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,u}}{{p}_{x}},$(3.6)
$\dot {S}(t,x,\delta \,u) = - {{f}_{0}}(t,{{x}_{0}},{{u}_{0}}) - \frac{{\partial \,{{f}_{0}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial \,u}}\delta \,u,$Доказательство теоремы 3 осуществляется через прямое преобразование условий оптимальности к более простым условиям в форме уравнения Ляпунова для расширенного пространства состояний с последующим его решением методом характеристик и приведено в Приложении.
4. Алгоритмы с прогнозирующей моделью. Известны и получили развитие различные варианты и редакции алгоритмов с прогнозирующей моделью [1, 2]. Базовыми из них являются алгоритм модифицированный и алгоритм с матрицей чувствительности, программную реализацию первого из которых покажем на примере использования схемы дифференциального ДП (теорема 3).
Алгоритм основан на непосредственном вычислении градиентов px, pδu по формулам (3.3), (3.4) и реализует процедуру слабого локального улучшения через последовательность следующих операций.
Шаг 1. Прогнозируется состояние объекта на интервале [tu, tк] с помощью модели
(4.1)
${{\dot {x}}_{{\text{м}}}} = \chi {{F}_{{\text{м}}}}(\tau ,{{x}_{{\text{м}}}},{{u}_{{\text{м}}}}),$Шаг 2. Определяются значения вектора xм(τк) и на основе предварительно продифференцированной по xм и по uм функции Sз вычисляются ее градиенты в конечный момент времени τк = tк:
(4.2)
${{p}_{{\text{к}}}}\left( {{{\tau }_{{\text{к}}}}} \right) = - \frac{{\partial \,S_{{\text{з}}}^{{\text{T}}}({{x}_{{\text{м}}}}\left( {{{\tau }_{{\text{к}}}}} \right),\delta \,u\left( {{{\tau }_{{\text{к}}}}} \right))}}{{\partial \,{{x}_{{\text{м}}}}\left( {{{\tau }_{{\text{к}}}}} \right)}},\quad {{p}_{{\delta \,u}}}\left( {{{\tau }_{{\text{к}}}}} \right) = - \frac{{\partial \,S_{{\text{з}}}^{{\text{T}}}({{x}_{{\text{м}}}}\left( {{{\tau }_{{\text{к}}}}} \right),\delta \,u\left( {{{\tau }_{{\text{к}}}}} \right))}}{{\partial \,\delta \,u\left( {{{\tau }_{{\text{к}}}}} \right)}}.$Шаг 3. С начальными условиями (4.2) на интервале [τ0, τк] с шагом Δτ при j = 0 интегрируется в ускоренном обратном времени система уравнений (2.15), (3.3)–(3.6):
Здесь Tп – время прогнозирования.
Замечание 2. При организации итерационной процедуры в уравнениях прогнозирующей модели (ПМ) вместо вектора u0 рассматривается модельное управление предыдущей итерации uмj.
Дополнительно вместе с соотношениями (4.3) вычисляется функция Беллмана для задачи с расширенным вектором состояния
(4.4)
$\dot {S}(\tau ,{{x}_{{\text{м}}}},\delta u) = \chi {{Q}_{{\text{p}}}}(\tau ,{{x}_{{\text{м}}}},\delta u),\quad \delta u = {{u}_{{{\text{м}}j + 1}}} - {{u}_{{{\text{м}}j}}}.$Матрицы частных производных векторной и скалярной функций Fм, Qp по компонентам xм, δu вычисляются на основе прогнозов (4.1).
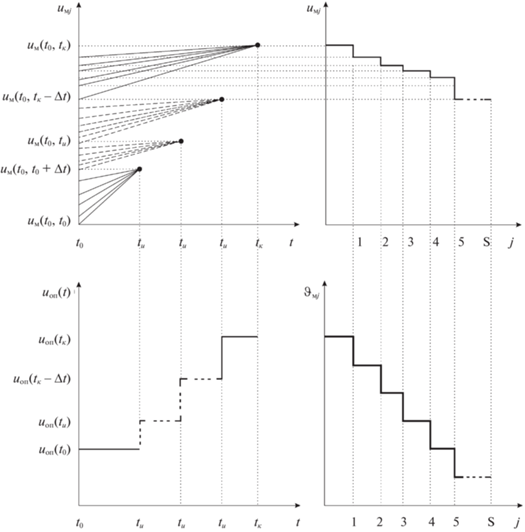
Шаг 4. На длинах оптимизации Δt организуется итерационная процедура уточнения точек стационарности локальной минимали (рис. 1) при $j = \overline {1,{{N}_{{\text{з}}}}} $ по формулам (4.3), (4.4). Условием останова итерационной процедуры является выполнение неравенства $\delta \,u \leqslant {{\varepsilon }_{{\text{з}}}}$ или при более грубой оценке по точности вычислений: $j \leqslant {{N}_{{\text{з}}}}$.
Шаг 5. При выполнении условия останова вновь полученное управление принимается за оптимальное управление ${{u}_{{{\text{м}}j + 1}}} = {{u}_{0}}$ и подается на объект (1.3). Через промежуток времени Δt шаги 1 – 4 алгоритма повторяются (рис. 1). При этом на каждом участке Δt в модели (4.3) с заданной точностью выполняется условие: ${{\vartheta }_{{{\text{м}}j}}} = {{\vartheta }_{0}} = 0$.
5. Свойства сходимости алгоритмов с прогнозирующей моделью. Недостатком всех современных численных методов, используемых в прямых методах (например, метода обратных задач динамики [15]) и в непрямых методах интервальной оптимизации в точной формулировке, служит отсутствие строго математического доказательства их сходимости. Процедуры прямых методов являются градиентными и позволяют определить только локальный экстремум, а не минимизировать функционал (1.4) во всей области его определения. Для рассмотренных же выше методов интервальной оптимизации зачастую характерна “овражная” ситуация: застревание процесса в окрестности одной из точек локального экстремума, в силу чего задача (1.1)–(1.5) или имеет решение, далекое от истинного, или же вообще может наблюдаться расходимость процессов управления.
Для преодоления этих трудностей предлагается применить процедуру дифференциального ДП для получения грубого начального приближения точек стационарности локальной минимали, а градиентную процедуру квазилинеаризации – для последующего уточнения этих точек. Поэтому доказательство сходимости алгоритмов, построенных на основе формул (2.15), (3.3), (3.4) теоремы 3, должно состоять из двух этапов: доказательства сходимости процессов по условиям стационарности к решению исходной задачи (1.1) – (1.5), доказательства сходимости к локальной минимали в окрестности точек стационарности по методу квазилинеаризации. Рассмотрим оба эти этапа.
5.1. Свойства сходимости алгоритмов с прогнозирующими моделями при интервальной оптимизации процессов управления. Доказательство сходимости по рассмотренной выше схеме дифференциального ДП основывается на рассмотрении свойств предельных элементов минимизирующих последовательностей поиска локальной минимали (x0, u0). Для выявления этих свойств введем понятие множества достижимости [16–18].
Определение 2. Множеством достижимости X(t, X0, τ) в момент времени τ систем (2.15), (3.3), (3.4) называется множество, порожденное в момент времени t множеством начальных состояний X0 этих систем.
Множество достижимости при τ → t оценивается результатом минимизации функционала (3.2) – приближенно вычисленным через итерационную процедуру улучшения ${{u}_{{{\text{оп}}}}}(t,\tau )\mathop \to \limits_{\tau \to t} {{u}_{{{\text{оп}}}}}(t,t)$ = = u0(t) значением опорного функционала ${{I}_{*}}$ в момент времени t (t ∈ [t0, tк]), равного значению оптимального в локальном смысле функционала (1.4) исходной задачи синтеза (1.1)–(1.5).
Определение 3. Предельным множеством достижимости X*(t, X0, τ) систем (2.15), (3.3), (3.4) будем называть фиксированное в момент времени τ = t множество, порожденное множеством начальных состояний X0 этих систем.
Предельное множество достижимости при uоп(t, t) = u0(t) определяет одинаковый результат минимизации ФОР (3.2) в расширенной формулировке (теорема 3) и функционала (1.4) в исходной постановке задачи нелинейного синтеза (1.1)–(1.5).
Теорема 4 (об определении элементов предельного множества достижимости). Если управление u = u0(t) соответствует локальному минимуму функционала (1.4) и определяет локальную минималь процесса (1.3) на незамкнутых множествах u ∈ Rm, x ∈ Rn, то существуют такие векторная, ненулевая и непрерывная функция px и скалярная функция φ, которые удовлетворяют следующим условиям:
1) управляемой прогнозирующей модели – решаемой в ускоренном времени системе канонически сопряженных уравнений: дифференциальной связи (1.3) и векторному уравнению
(5.1)
${{\dot {p}}_{x}} = - \frac{{\partial f_{0}^{T}(t,{{x}_{0}},{{u}_{0}})}}{{\partial x}} - \frac{{\partial {{f}^{T}}(t,{{x}_{0}},{{u}_{0}})}}{{\partial x}}{{p}_{x}},\quad p\left( {{{t}_{{\text{к}}}}} \right) = \frac{{\partial V_{{\text{з}}}^{{\text{T}}}(x\left( {{{t}_{{\text{к}}}}} \right))}}{{\partial x\left( {{{t}_{{\text{к}}}}} \right)}},$2) условию стационарности точек функции Гамильтона по u:
(5.2)
$\frac{{\partial \,H_{{}}^{{\text{T}}}}}{{\partial \,\delta \,u}} = {{\dot {p}}_{{\delta \,u}}} = \frac{{\partial \,f_{0}^{{\text{T}}}\left( {t,{{x}_{0}},{{u}_{0}}} \right)}}{{\partial \,u}} - \frac{{\partial \,f_{{}}^{{\text{T}}}\left( {t,{{x}_{0}},{{u}_{0}}} \right)}}{{\partial \,u}}{{p}_{x}} = 0,$3) условию равенства нулю предельных элементов минимизирующей последовательности по u в градиентной процедуре (3.5):
4) условию минимума локального функционала, определяемого через вычисление функции Ляпунова:
(5.4)
$\dot {I}(t) = \dot {\varphi }(t,{{x}_{0}}) = - {{f}_{0}}(t,{{x}_{0}},{{u}_{0}}),\quad \varphi ({{t}_{{\text{к}}}},{{x}_{0}}({{t}_{{\text{к}}}}) = {{V}_{{\text{з}}}}({{x}_{0}}({{t}_{{\text{к}}}})).$Доказательство теоремы 4 приведено в Приложении.
Таким образом, теорема 4 завершает доказательство сходимости алгоритмов с прогнозирующей моделью по условиям стационарности. Основное свойство слабой локальной минимали состоит в том, что при отсутствии ограничений на управление она определяется стационарными точками функции Гамильтона, которые удовлетворяют векторному уравнению $\partial H{\text{/}}\partial \delta \,u = 0$.
Заметим, что один и тот же результат минимизации ФОР (3.2) в постановке задачи синтеза ОУ с релаксационным расширением пространства состояний и функционала (1.4) в исходной постановке позволяет сделать вывод о том, что предельные множества достижимости для расширенной задачи совпадают с множеством достижимости задачи (1.1)–(1.5). Главное отличие расширенной формулировки задачи нелинейного синтеза заключается в том, что она определяет минимизирующую последовательность по u поиска слабой локальной минимали, тогда как в исходной формулировке только констатируется факт ее существования. Если управление можно однозначно определить (синтезировать) в виде обратных связей u = u0(t, x, px), то решение исходной задачи (1.1)–(1.5) сводится к решению двухточечной краевой задачи для дифференциальной системы (1.3), (5.1), (5.2).
По-видимому, слабая локальная минималь существует только тогда, когда при выполнении необходимого условия (стационарности или принципа минимума) одновременно (как в теории устойчивости) выполняется и достаточное условие оптимальности, но не наоборот. В задаче нелинейного синтеза это не совсем очевидно.
5.2. Свойства сходимости алгоритмов с прогнозирующей моделью в окрестности точек стационарности локальной минимали. Процедура дифференциального ДП позволяет получить грубое начальное приближение точек стационарности локальной минимали на длинах оптимизации Δt (рис. 1). Для уточнения данного решения используется квазилинеаризация – градиентная процедура (3.1) последовательного улучшения точек стационарности. Поэтому можно утверждать, что в алгоритмах с прогнозирующей моделью метод квазилинеаризации есть просто применение метода Ньютона–Рафсона–Канторовича в функциональном пространстве [4, 19]. Так как сходимость метода имеет место для начальных приближений из какой-либо окрестности точек стационарности слабой локальной минимали, то градиентная процедура (3.1) является локально сходящейся.
Известно [4], что метод квазилинеаризации имеет основные свойства – монотонность и квадратичную сходимость. Докажем аналогичные свойства локальной сходимости алгоритмов с прогнозированием, следуя методике Беллмана.
1. Монотонность.
Определение 4 [20]. Если при реализации градиентной процедуры (3.1) значения функционала (3.2) на итерациях uj монотонно убывают, то последовательность uj → u0 называется релаксационной, а параметр ϑ – релаксационным параметром.
Различают два вида сходимости градиентных процедур: сходимость по функционалу и сильную сходимость (сходимость).
Определение 5. Градиентная процедура (3.1) называется сходящейся, если
Очевидно, сходимость процедур влечет сходимость по функционалу. Обратное, вообще говоря, не верно.
Свойство монотонности в алгоритмах с прогнозирующей моделью подразумевает сходимость градиентной процедуры (3.1), которая в свою очередь зависит от начальных приближений в окрестности точек стационарности слабой локальной минимали и выбранного релаксационного параметра. Так как начальные приближения вычисляются по схеме дифференциального ДП, то для доказательства монотонности итерационных процедур остается определить свойство релаксационного параметра $\vartheta $. Этот параметр имеет функциональный смысл и вычисляется по формуле (3.5): $\vartheta = - r\partial {{\varphi }^{{\text{T}}}}{\text{/}}\partial \delta u = - r{{p}_{{\delta u}}}$.
На длинах оптимизации Δt в каждой точке стационарности слабой локальной минимали параметр $\vartheta $ обращается в нуль (см. Приложение). В силу чего можно утверждать, что при $r > {\rm O}$ градиент ${{p}_{{\delta \,u}}}$ является убывающей положительной функцией времени, а переменная u по шагам итераций подчинена условию
Это условие характеризует свойство монотонности процесса (3.1) и для процедуры квазилинеаризации по вычисленному начальному приближению локально-оптимального управления поясняется рис. 2.
2. Квадратичная сходимость.
Второе важное и не так очевидное свойство градиентной процедуры (3.1) – это квадратичная сходимость.
Утверждение 1. Для градиентной процедуры (3.1) справедлива следующая оценка:
(5.5)
${\text{|}}u_{0}^{{j + 1}} - {{u}_{0}}{\text{|}} \leqslant {{k}_{1}}{\text{||}}u_{0}^{j} - {{u}_{0}}{\text{|}}{{{\text{|}}}^{2}},\quad {\text{|}}u_{0}^{{j + 1}} - u_{0}^{j}{\text{|}} \leqslant {{k}_{2}}{\text{||}}u_{0}^{j} - u_{0}^{{j - 1}}{\text{|}}{{{\text{|}}}^{2}},$Доказательство утверждения 1 приведено в Приложении.
Вторая оценка в формуле (5.5) получается путем непосредственного преобразования рекуррентного соотношения (см. Приложение)
(5.6)
$u_{{0i}}^{{j + 1}} - u_{{0i}}^{j} = {{\xi }^{1}}_{i}(u_{{0i}}^{j}) - {{\xi }^{1}}_{i}(u_{{0i}}^{{j - 1}}) = (u_{{0i}}^{j} - u_{{0i}}^{{j - 1}})\,{{\dot {\xi }}^{1}}_{i}(u_{0}^{{j - 1}}) + \frac{{{{{(u_{{0i}}^{j} - u_{{0i}}^{{j - 1}})}}^{2}}}}{2}\,{{\ddot {\xi }}^{1}}_{i}(\theta ),$С другой стороны, $\dot {u}_{{0i}}^{j} = \dot {u}_{{0i}}^{{j - 1}} + {{\dot {\vartheta }}_{i}}(u_{{0i}}^{{j - 1}})\Delta t$ (см. Приложение). Тогда $\dot {\xi }{{_{{}}^{1}}_{i}}(u_{{0i}}^{{j - 1}}) = \dot {u}_{{0i}}^{j} = (u_{{0i}}^{j} - u_{{0i}}^{{j - 1}}){\text{/}}\Delta t$ и уравнение (5.6) запишется в виде
(5.7)
$u_{{0i}}^{{j + 1}} - u_{{0i}}^{j} = {{(u_{{0i}}^{j} - u_{{0i}}^{{j - 1}})}^{2}}\left( {\frac{1}{{\Delta t}} + \frac{1}{2}{{{\ddot {\xi }}}^{1}}_{i}(\theta )} \right),$(5.8)
${\text{|}}u_{{0i}}^{{j + 1}} - u_{{0i}}^{j}{\text{|}} \leqslant {{k}_{{2i}}}{\text{|}}u_{{0i}}^{j} - u_{0}^{{j - 1}}{{{\text{|}}}^{2}},$Уравнение (5.8), записанное в векторной форме, является второй искомой оценкой в формулах (5.5). Свойство, выражаемое вторыми оценками в выражениях (5.5), называется квадратичной сходимостью [4]. Очевидно, что сходимость метода квазилинеаризации значительно ускоряется по мере приближения ($x_{0}^{j}$, $u_{0}^{j}$) → (x0, u0). Получается, что каждый следующий шаг асимптотически удваивает число правильных знаков в данном приближении. Следовательно, свойство квадратичной сходимости оказывается особенно полезным при решении многомерных задач, и не только потому, что время расчета прямо пропорционально числу итераций, но и в силу возрастания ошибок округления при этих итерациях.
Пример. Управление колебательным процессом на скользящем интервале оптимизации.
Рассмотрим управление квазилинейным колебательным звеном в задаче слежения (${{t}_{{\text{к}}}} = t + {{T}_{{\text{п}}}}$):
(5.9)
$\begin{gathered} {{{\dot {x}}}_{1}} = {{x}_{2}}, \\ {{{\dot {x}}}_{2}} = {{a}_{1}}{{x}_{1}} + {{a}_{2}}x_{3}^{3} + bu, \\ \end{gathered} $Цель управления состоит в стабилизации заданного состояния ${{х}_{{\text{з}}}} = - 0.4$ при ограничении на управление |u| = 2 и выбранных начальных условиях: x1(0) = 2, x2(0) = 0.
Требуется решить задачу синтеза оптимального управления: через минимизацию ФОР (3.2):
(5.10)
$I = \int\limits_{{\text{t}}{}_{{\text{0}}}}^{{\text{t}} + {{{\text{T}}}_{{\text{п}}}}} {\{ 0.5\beta {{{\left( {{{x}_{1}}\left( t \right) - {{x}_{{\text{з}}}}} \right)}}^{2}} + {{u}_{{{\text{оп}}}}}{{k}^{{ - 1}}}u + 0.5{{r}^{{ - 1}}}({{\vartheta }^{2}} + \vartheta _{{{\text{оп}}}}^{{\text{2}}})\} {\kern 1pt} {\kern 1pt} d\theta ,} $(5.11)
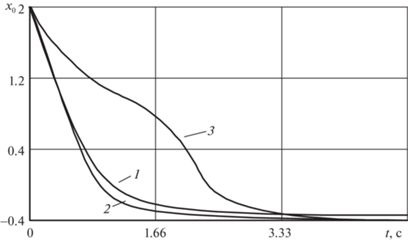
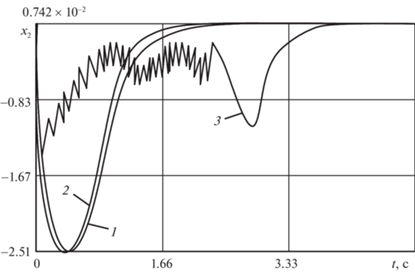
$I = \int\limits_{t{}_{{\text{0}}}}^{t + {{T}_{{\text{п}}}}} {\{ 0.5\beta {{{\left( {{{x}_{1}}\left( t \right) - {{x}_{{\text{з}}}}} \right)}}^{2}} + {{u}_{{{\text{оп}}}}}{{k}^{{ - 1}}}u\} d\theta ,} $Результаты минимизации ФОР (5.10) и КВОР (5.11) на основе так называемого “алгоритма модифицированного” (рис. 1) приведены на рис. 3–5.
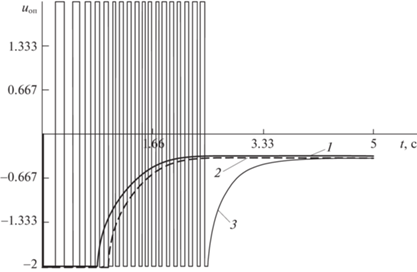
Для проверки работоспособности алгоритма при стратегии совмещенного синтеза u → uоп (кривые 2) и при субоптимальных стратегиях управления (кривые 1, 3) проводился сравнительный анализ численных расчетов.
Моделирование проводилось при шаге оптимизации Δt = 0.05c, ${{\varepsilon }_{{\text{з}}}}$ = 0.01 и при выбранных эмпирическим путем значениях параметров ФОР (5.10) и КВОР (5.11): ${{T}_{{\text{п}}}} = 1.6,$ $\beta = 1.5,$ $k = 1.2,$ $r = 0.4$.
Сравнительный анализ численных расчетов показывает, что по точности и затратам на управление наиболее предпочтительна приближенно-оптимальная стратегия управления (кривые 2). Точность вычислений здесь обеспечивается за счет поинтервального уточнения точек стационарности локальной минимали при среднем числе итераций $j = 4{\kern 1pt} - {\kern 1pt} 6$ на каждой длине оптимизации.
Качественно близкие результаты моделирования получаются при использовании комбинированной стратегии управления (кривые 1). Однако стабилизация заданного движения ${{х}_{{\text{з}}}} = - 0.4$ при применении релейно-линейного закона происходит с постоянной статической ошибкой $\Delta {{x}_{1}} = 0.1$, что не всегда приемлемо с точки зрения выдерживания точностных характеристик регулятора.
Организация скользящего режима работы квазиоптимального регулятора относительно поверхности переключения – вычисляемой функции Ляпунова $V(t,\,{{x}_{0}})$ – обеспечивается релейным законом управления (рис. 5). Использование релейного закона позволяет точно стабилизировать заданную выходную координату системы (5.9). Однако при этом заметно ухудшаются показатели качества переходных процессов и увеличиваются затраты на управление.
Заключение. Таким образом, совместное использование процедур интервальной и локальной оптимизации позволяет существенно упростить алгоритмы управления. Вместо того, чтобы для обеспечения ожидаемой квадратичной сходимости одновременно использовать характеристики первого и второго порядков (уравнения сопряженной системы и матричное нелинейное уравнение типа Риккати), предлагается применять только характеристики первого порядка, точки стационарности которых уточняются путем квазилинеаризации на длинах Δt, а грубое начальное приближение локальной минимали определяется из процедуры по схеме дифференциального динамического программирования.
На основе условий теорем 3, 4 разработано алгоритмическое обеспечение интегрированной САУ, стратифицированное по уровням управления воздушным судном (например, [22–26]), которое проверено на модельных задачах динамики перспективных автоматизированных систем предупреждения столкновений и преодоления сдвига ветра при заходе на посадку самолета среднего класса.
Список литературы
Справочник по теории автоматического управления / Под ред. А.А. Красовского. М.: Наука, 1987.
Буков В.Н. Адаптивные прогнозирующие системы управления полетом. М.: Наука, 1987.
Габасов Р., Кириллова Ф.М. Принципы оптимального управления // Докл. НАН Беларуси. 2004. Т. 48. С. 15–18.
Беллман Р., Калаба Р. Квазилинеаризация и нелинейные краевые задачи. М.: Мир, 1968.
Атанс М.М., Фалб П. Оптимальное управление / Под ред. Ю.И. Топчеева. М.: Машиностроение, 1968.
Хрусталев М.М. О достаточных условиях абсолютного минимума // Докл. АН СССР. 1967. Т. 174. № 5. С. 1026–1029.
Москаленко А.И. Оптимальное управление моделями экономической динамики. Новосибирск: Наука. СО, 1999.
Jacobson D.H. Differential Dynamic Programming Methods for Solving Bang-bang Control Problems // IEEE Trans. On Autom. Control. 1968. V. AC-13. № 6. P. 661–675.
Батурин В.А., Урбанович Д.Е. Приближенные методы оптимального управления, основанные на принципе расширения. Новосибирск: Наука. СО, 1997.
Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. М.: Наука, 1973.
Сизых В.Н., Данеев А.В. Квазилинеаризация и достаточные условия оптимальности в задаче улучшения и локализации // Изв. Самарского научного центра РАН. 2016. Т. 18. № 4 (6). С. 1250–1260.
Sizykh V.N., Daneev A.V., Dambaev J.G. Methodology of Approximately Optimal Synthesis of Fuzzy Controllers for Circuit of Improvement and Localization // Far East J. of Mathematical Sciences. 2017. V. 101. № 3. P. 487–506.
Сизых В.Н. Итерационно-релаксационный метод приближенно-оптимального синтеза регуляторов // Докл. РАН. 2000. Т. 371. № 5. С. 571–574.
Болтянский В.Г. Отделимость выпуклых конусов – общий метод решения экстремальных задач // Оптимальное управление. М.: Знание, 1978.
Диль В.Ф., Сизых В.Н. Методика синтеза законов управления летательным аппаратом на основе траекторного прогнозирования и метода обратных задач динамики // Современные технологии, системный анализ, моделирование. 2015. № 4 (48). С. 134–138.
Константинов Г.Н. Нормирование воздействий на динамические системы. Иркутск: Изд-во Иркутского ун-та, 1983.
Черноусько Ф.Л., Баничук В.П. Вариационные задачи механики и управления. М.: Наука, 1973.
Моисеев Н.Н. Элементы теории оптимальных систем. М.: Наука, 1974.
Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.–Л.: Физматгиз, 1962.
Бобылев Н.А., Емельянов С.В., Коровин С.К. Геометрические методы в вариационных задачах. М.: Изд-во Магистр, 1998.
Буков В.Н., Сизых В.Н. Приближенный синтез оптимального управления в вырожденной задаче аналитического конструирования // АиТ. 1999. № 12. С. 16–32.
Диль В.Ф., Сизых В.Н. Синтез оптимального управления воздушным судном на основе уравнений нелинейной динамики // Научный вестник МГТУ ГА. 2017. Т. 20. № 3. С. 139–148.
Данеев А.В., Диль В.Ф., Сизых В.Н. Оптимизация процессов управления пространственным движением воздушного судна на основе уравнений нелинейной динамики // Изв. Самарского научного центра РАН. 2017. Т. 19. № 1. С. 195–200.
Буков В.Н., Сизых В.Н. Метод и алгоритмы решения сингулярно-вырожденных задач аналитического конструирования // Изв. РАН. ТиСУ. 2001. № 5. С. 43–51.
Сизых В.Н. Итерационно-релаксационный метод нелинейного синтеза регуляторов // АиТ. 2005. № 6. С. 108–119.
Данеев А.В., Сизых В.Н. Методология проектирования алгоритмического обеспечения интегрированных систем управления авиационными транспортными средствами на основе уравнений нелинейной динамики. М.: Наука, 2021. 295 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления