Известия РАН. Теория и системы управления, 2022, № 6, стр. 11-19

Введение. Современные наземные, морские и воздушные объекты обладают высокоразвитыми эффективными системами информационного противодействия управлению беспилотных летательных аппаратов (БПЛА) [1–4].

Информационное противодействие создается с помощью маскирующих помех, предназначенных для “подавления” приемных устройств систем наведения БПЛА, и имитационных помех, способных дезориентировать БПЛА. Для защиты от противодействия кроме технических и алгоритмических способов и средств распознавания помех и соответствующего изменения технических характеристик систем наведения применяются различные тактические приемы, одним из которых является наведение группы взаимодействующих БПЛА [5].

Для повышения эффективности противодействия, а также из-за ограничений по электромагнитной совместимости при выполнении других задач объект осуществляет резкую внезапную и, как правило, скрытую перестройку параметров и характеристик противодействия, что приводит к возникновению случайных скачкообразных процессов в системах наведения БПЛА.

В настоящей статье рассматривается задача построения алгоритмов взаимодействия БПЛА в группе при распознавании помеховой ситуации и оценивании координат объектов и расстояния между соседними участниками группы БПЛА. Задача решается на основе теории систем со случайной скачкообразной структурой (ССС) [3, 4, 6–13].

1. Постановка задачи. Группа БПЛА наводится на некоторый объект. С учетом ложных целей число одновременно наблюдаемых объектов i в системе наведения каждого БПЛА равно m; число классов объектов $j$ равно $n$, из них первый класс – цель (Ц), остальные – различные помехи (П). В системе наведения производится разделение сигналов от пространственно разнесенных источников излучения и сигналов по информационным признакам различия по каналам. Предварительный анализ информации осуществляется отдельно в каждом канале, а затем выполняется ее комплексирование, в результате чего происходит распознавание текущей ситуации противодействия и оценивание пространственных координат объекта.

В зависимости от конкретных условий (тип системы наведения, класс объектов и пр.) в качестве используемых признаков могут быть выбраны различные пространственные, геометрические, кинематические, спектральные и энергетические информационные различительные признаки. При выборе признака различия основную роль играют три фактора: сложность определения признака, точность его оценивания и инвариантность к условиям применения. Идеальным вариантом является независимость характеристик признака от условий применения, приемлемым – незначительная зависимость от тех условий, которые в системе не определяются.

Выбранные признаки делятся на две группы: 1) континуальные (принадлежащие к непрерывному множеству значений) и 2) принадлежащие конечному множеству значений. Первая группа наблюдается с помощью измерителей, вторая – с помощью индикаторов. Число возможных ситуаций противодействия (состояний структуры $s(t)$), составляющих полную группу несовместных случайных событий, равно $N$: $s = \overline {1,N} $.

Состояния структуры представляют собой различные сочетания наблюдаемых объектов $i$ и классов $j$. Например, множество возможных ситуаций противодействия (состояний структуры $s$), составляющих полную группу несовместных случайных событий для $m = 2$, $n = 2$, представлено в табл. 1.

Как видно из таблицы, $s$-я ситуация при $s = \overline {1,3} $ состоит в том, что $i$-й объект принадлежит $j$‑му классу ($j = 1$ – цель, $j = 2$ – ложная цель (помеха)), $i = 1,{\kern 1pt} 2$; $j = 1,{\kern 1pt} 2$. Ситуация $s = 4$ означает, что система наведения подавлена мощной шумовой помехой. Ситуации, когда подавлен только один из каналов ($i = 1$ или 2), а другой – нет, принципиально возможны, но их вероятность по сравнению с вероятностями перечисленных в таблице ситуаций ничтожно мала.

Динамика и измерение непрерывнозначных различительных признаков описываются линейными уравнениями (в дискретной форме), позволяющими применить фильтры Калмана для синтеза алгоритмов, что широко используется на практике при конструрировании систем управления летательных аппаратов:

где ${{x}_{k}}(j)$ – вектор континуальных различительных признаков  j-го класса объектов; $z_{k}^{{(i)}}\left( j \right)$ – вектор континуальных измерений различительных признаков i-го объекта; ${{\xi }_{k}}(j)$ и ${{\zeta }_{k}}(j)$ – векторы возмущений и помех – последовательности независимых случайных величин с нулевыми математическими ожиданиями и с ковариациями ${{G}_{k}}(j)$ и ${{Q}_{k}}(j)$ соответственно; ${{u}_{k}}(j)$ – вектор управляющих сигналов; ${{w}_{k}}(j)$ – вектор известных функций времени $k$; ${{A}_{k}}(j)$, ${{B}_{k}}(j)$, ${{H}_{k}}(j)$, ${{F}_{k}}(j)$ – матрицы известных коэффициентов соответствующих размерностей.

Различительные признаки, принадлежащие к конечному множеству, распознаются с помощью индикаторов признаков, которые используются для составления формул, описывающих индикаторы структуры ${{s}_{k}}$:

где ${{s}_{k}}$ – состояние структуры – марковская цепь, заданная вероятностями переходов из ${{s}_{k}}$ в ${{s}_{{k + 1}}}$: ${{q}_{k}}({{s}_{{k + 1}}}\,{\text{|}}\,{{s}_{k}})$; ${{r}_{k}}$ – состояние индикатора структуры, описываемое формулой (1.3); $l$ – число индикаторов; $\Delta t = {{t}_{{k + 1}}} - {{t}_{k}}$; $T$ – параметр инерционности индикатора; ${{\pi }_{{k + 1}}}(r_{{k + 1}}^{{(\nu )}}\,{\text{|}}\,r_{k}^{{(\nu )}},{{s}_{{k + 1}}})$ – вероятность показаний $\nu $-го индикатора структуры, представляющего собой условную марковскую цепь, которая описывается вероятностью перехода состояния индикатора из ${{r}_{k}}$ в ${{r}_{{k + 1}}}$ при фиксированном состоянии структуры ${{s}_{{k + 1}}}$; ${{\bar {\pi }}_{{k + 1}}}({{r}_{{k + 1}}}\,{\text{|}}\,{{s}_{{k + 1}}})$ – известные установившиеся значения вероятностей правильных (при ${{r}_{{k + 1}}} = {{s}_{{k + 1}}}$) и ошибочных (при ${{r}_{{k + 1}}} \ne {{s}_{{k + 1}}}$) показаний индикатора.

Индикаторы структуры применяются в системах наведения для обнаружения и распознавания ситуаций противодействия и помех. Например, индикаторы скачков мощности и амплитуды предназначены для обнаружения факта отстрела инфракрасных и радиолокационных ловушек, а также включения форсажа двигателей истребителя при маневре, указывающего на увеличение его ускорения. Индикаторы, измеряющие отношение “сигнал–шум”, используются для обнаружения шумовых маскирующих помех, гребенчатые доплеровские фильтры – для разрешения целей в группе. Индикаторы таких геометрических признаков, как, например, площадь или конфигурация изображения объектов применяются в фокальной плоскости приемников телевизионных и тепловизионных систем, индикаторы эффективной площади рассеивания электромагнитного излучения – в радиолокационных системах наведения и др. [1, 4, 14].

Основными алгоритмическими характеристиками индикаторов являются вероятность обнаружения или распознавания и время обработки информации от момента поступления входного сигнала до момента принятия решения, характеризуемое параметром инерционности T.

В научно-технической литературе используются такие хорошо известные специалистам по теории и системам управления общепринятые понятия, как, например, “вероятность пропуска сигнала” и “вероятность ложной тревоги” в задачах различения двух альтернативных гипотез [4, 5, 15, 16].

Требуется построить алгоритм взаимосвязанного распознавания помеховых ситуаций, оценивания координат объекта и определения расстояния между соседними участниками группы БПЛА.

2. Алгоритм распознавания помеховых ситуаций, оценивания координат объекта и управления БПЛА. Информационно-управляющий алгоритм, основанный на теории ССС, состоит из пяти блоков [3, 4, 6–8]:

классификатор структуры,

идентификатор структуры,

фильтр Калмана,

дисперсиометр,

регулятор,

которые описываются следующими формулами.

1. Классификатор структуры:

где индекс $k + 1$ у квадратной скобки ${{[ \cdot ]}_{{k + 1}}}$ относится ко всем переменным внутри ее (т.е. z, $\tilde {x}$, $\Theta $ и s); $j{\kern 1pt} *(s) = \overline {1,{\kern 1pt} n} $ – номер объекта $j = \overline {1,{\kern 1pt} n} $, соответствующего номеру структуры $s = \overline {1,{\kern 1pt} N} $; $\beta = \overline {1,b} $ – номер непрерывнозначного различительного признака; где ${{\hat {p}}_{k}}({{s}_{k}})$ и ${{\tilde {p}}_{k}}({{s}_{k}})$ – соответственно апостериорная и прогнозируемая на один шаг вперед вероятности состояния структуры; $\tilde {x}_{k}^{{j{\kern 1pt} *({{s}_{k}})\beta }}$ – прогнозируемая оценка $\beta $-го различительного признака $j{\kern 1pt} *({{s}_{k}})$-го объекта; $\tilde {R}_{k}^{{j{\kern 1pt} *({{s}_{k}})\beta }}$ – прогнозируемая дисперсия оценивания $\beta $-го признака $j{\kern 1pt} *({{s}_{k}})$-го объекта; $Q_{k}^{{j{\kern 1pt} *({{s}_{k}})\beta }}$ – дисперсия ошибки измерения $\beta $-го признака $j{\kern 1pt} *({{s}_{k}})$-го объекта.

Например, для частного случая, приведенного в табл. 1 ($m = 2$, $n = 2$, $N = 4$) и при двух (b = 2) непрерывнозначных различительных признаках $\beta = 1,2$, формула (2.3) принимает следующий вид:

2. Идентификатор структуры:

3. Фильтр Калмана:

где $\hat {X}$, $\tilde {X}$, Z – блочные векторы с элементами соответственно $\hat {x}(j)$, $\tilde {x}(j)$, $z(j)$, описываемые формулами (1.1), (1.2); $A$, $B$, $H$ – блочные диагональные матрицы с элементами $A(j)$, $B(j)$ , $H(j)$ из (1.1); $\tilde {R}$ и $\Theta $ – блочные диагональные матрицы с элементами ${{\tilde {R}}^{{j{\kern 1pt} *\beta }}}$ и ${{\Theta }^{{j{\kern 1pt} *\beta }}}$ из (2.5).

4. Дисперсиометр:

где ${{F}_{k}}$, ${{G}_{k}}$ – блочные диагональные матрицы с элементами соответственно ${{F}_{k}}(j)$, ${{G}_{k}}(j)$ из (1.1); ${{\hat {R}}_{k}}$ – блочная диагональная матрица с элементами $\hat {R}_{k}^{{j{\kern 1pt} *\beta }}$ (апостериорными дисперсиями оценивания $\beta $-го признака j*-го объекта).

5. Регулятор. Представляет собой закон управления БПЛА $u{\kern 1pt} _{k}^{*}$, зависящий от $\hat {x}_{k}^{{\text{Ц}}}$, ${{\hat {L}}_{k}}$ и их производных, где $\hat {x}_{k}^{{\text{Ц}}}$ – оценка вектора пространственных координат цели; ${{\hat {L}}_{k}}$ – оценка расстояния между двумя соседними БПЛА. Вектор $x_{k}^{{\text{Ц}}}$ – это часть общего вектора различительных признаков x_k, описываемого уравнением (1.1).

В зависимости от условий конкретной задачи (типы и характеристики объектов и БПЛА) закон управления может иметь различный вид. Оценка расстояния ${{\hat {L}}_{k}}$ также может иметь различную форму зависимости от $\hat {x}_{k}^{{{\text{Ц1}}}}$ и $\hat {x}_{k}^{{{\text{Ц2}}}}$, вычисляемых в системах управления двух соседних БПЛА (см. п. 3).

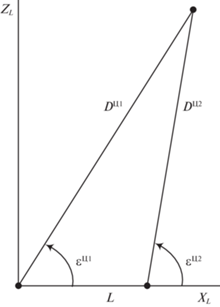
3. Пример. В горизонтальной плоскости декартовой прямоугольной системы координат $({{z}_{L}},{{x}_{L}})$, ось ${{x}_{L}}$ которой совпадает с направлением ${{L}_{k}}$, с различных направлений на одну цель, прикрываемую одной ложной целью (“помехой”), наводится два БПЛА (рис. 1 ).

Непрерывнозначными различительными признаками являются: $D_{k}^{{\text{Ц}}}$ – дальность до цели; $D_{k}^{{\text{П}}}$ – дальность до помехи; $\varepsilon _{k}^{{\text{Ц}}}$ – угол пеленга цели; $\varepsilon _{k}^{{\text{П}}}$ – угол пеленга помехи. Различительные признаки принадлежат конечному множеству: “геометрические” ${{\sigma }^{{\text{Ц}}}}$, ${{\sigma }^{{\text{П}}}}$ и “спектральные” ${{\lambda }^{{\text{Ц}}}}$, ${{\lambda }^{{\text{П}}}}$ (${{\sigma }^{{\text{Ц}}}}$, ${{\sigma }^{{\text{П}}}}$, ${{\lambda }^{{\text{Ц}}}}$, ${{\lambda }^{{\text{П}}}}$ – константы). Таким образом, m = 2, n = 2, $b = 2$, $l = 2$.

Множество возможных помеховых ситуаций (состояний структуры $s$) представлено в табл. 2.

Системы наведения обоих БПЛА по двухсторонней линии связи обмениваются информацией об оценках дальностей и углов. На основании этой информации в обеих системах вычисляется расстояние ${{L}_{k}}$ между БПЛА, которое затем регулируется в заданных пределах.

Число состояний структуры $N = 3$ (см. табл. 1). В общем случае структура ${{s}_{k}}$ – марковская цепь с вероятностями переходов ${{q}_{k}}({{s}_{{k + 1}}}\,{\text{|}}\,{{s}_{k}})$, которые учитывают возможность пересечения трасс объектов в фокальной плоскости приемного устройства в промежутке времени между двумя соседними измерениями. При малом $\Delta t$ пересечение трасс фиксируется с высокой вероятностью. Тогда происходит обмен номерами каналов $L$, и это равносильно тому, что пересечения как бы не произошло. Математически это формулируется в следующем виде: при ${{s}_{k}},{\kern 1pt} {{s}_{{k + 1}}} = 1,{\kern 1pt} 2$

а при ${{s}_{k}} = 3$

Представим математическую модель изменения дальностей, углов пеленга и угловых скоростей линии визирования до Ц и до П, также спектральных (λ) и геометрических (σ) информационных различительных признаков и всех их измеряемых значений уравнениями [3]

Здесь символом ˘ обозначены измеряемые значения соответствующих переменных: $D_{k}^{j}$ – дальности БПЛА до Ц и до П; $\varepsilon _{k}^{j}$ – углы пеленга Ц и П; $\omega _{k}^{j}$ – скорости изменения углов пеленга; ${{u}_{k}}$ – сигнал управления БПЛА; $w_{k}^{j}$ – известные детерминированные функции $k$; $\xi _{k}^{{Dj}}$, $\xi _{k}^{{\varepsilon j}}$ – возмущения – последовательности независимых случайных величин с нулевыми математическими ожиданиями и с дисперсиями соответственно ${{G}^{{Dj}}}$ и ${{G}^{{\varepsilon j}}}$; ${{{v}}_{k}}$ – априорная оценка скорости сближения БПЛА с объектами – известная функция времени; $\zeta _{k}^{{Dj}}$, $\zeta _{k}^{{\varepsilon j}}$ – ошибки измерений – последовательности независимых случайных величин с нулевыми математическими ожиданиями и с дисперсиями соответственно ${{Q}^{{Dj}}}$, ${{Q}^{{\varepsilon j}}}{\text{/}}{{(\tau _{k}^{j})}^{2}}$; $\tau _{k}^{j} = D_{k}^{j}{\text{/}}{{{v}}_{k}}$ – время, оставшееся до конца наведения БПЛА соответственно на цель и на помеху.

Символ Кронекера

описывает перерывы поступления информации при подавлении приёмного устройства маскирующей помехой. Вероятности $\pi (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\lambda } _{k}^{i}\,{\text{|}}\,{{\lambda }^{j}})$, $\pi (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } _{k}^{i}\,{\text{|}}\,{{\sigma }^{j}})$ – соответственно вероятности ошибочных (при ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\lambda } }^{i}} \ne {{\lambda }^{j}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }^{i}} \ne {{\sigma }^{j}}$) и правильных (при ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\lambda } }^{i}} = {{\lambda }^{j}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }^{i}} = {{\sigma }^{j}}$) показаний индикаторов в первом и во втором каналах наблюдения спектрального $\lambda $ и геометрического $\sigma $ признаков; $i = 1,{\kern 1pt} 2$; $j = {\text{Ц,П}}$.

Как видно из выражений для дисперсий ошибок измерения углов пеленга, они обратно пропорциональны квадратам дальностей до Ц и до П. Это объясняется тем, что в активных и полуактивных радиолокационных системах, а также в корреляционных оптико-электронных системах ошибки измерения угла пеленга – так называемое “блуждание центра отражения” – зависят от линейного размера объекта [12].

Информационно-управляющий алгоритм, согласно (2.1)–(2.12), с учетом (3.1) имеет следующий вид.

Классификатор структуры:

Идентификатор структуры:

Фильтр дальности:

Фильтр углов пеленга:

Фильтр угловых скоростей пеленга:

При $j = {\text{Ц}}$

при $j = {\text{П}}$

В формулах (3.11)–(3.13): $u_{k}^{{^{*}}}$ – оптимальное управление БПЛА, зависящее от оценок координат цели (см. блок Регулятор), $K_{k}^{{\beta j}}$ – так называемый коэффициент доверия, $\beta = D,\varepsilon ,\omega $; j = Ц, П (см. блок Дисперсиометр).

Как видно из рисунка, расстояние ${{L}_{k}}$ между соседними БПЛА определяется как

откуда следует выражение для оценки ${{\hat {L}}_{k}}$:

Дисперсиометр. Алгоритм дисперсиометра состоит из формул для коэффициентов $K_{k}^{{\beta j}}$, полученных в результате решений уравнений (2.10)–(2.12) для ${{\hat {R}}_{k}}$ в установившемся режиме (т.е. при ${{\hat {R}}_{{k + 1}}} = {{\hat {R}}_{k}} = \hat {R}$) [3]:

где $\Delta {{\omega }^{j}}$ – ширина спектра дискретного белого шума $\xi _{k}^{{Dj}}$ в (3.3).

Как видно из (3.16), чем меньше дисперсия ошибки измерения ${{Q}^{{\beta j}}}$ ($\beta = D,\;{\kern 1pt} \varepsilon ,{\kern 1pt} \;\omega $;  j = Ц, П), тем больше коэффициент доверия ${{K}^{{\beta j}}}$ и тем самым, как следует из (3.11)–(3.13), меньше разность между оценкой ${{\hat {X}}_{k}}$ и измерением ${{Z}_{k}}$ (${{\hat {X}}_{k}} = \hat {D}_{k}^{j},\varepsilon _{k}^{j},\hat {\omega }_{k}^{j}$; ${{Z}_{k}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }_{k}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }_{k}}$).

Регулятор. Регулятор – это закон управления движением БПЛА. В зависимости от конкретной задачи (типы и характеристики объектов и БПЛА и другие условия наведения) закон управления может иметь тот или иной вид из перечня известных стандартных методов наведения. Например, можно применить закон управления, задаваемый формулой [3]

где ${{\bar {\varepsilon }}_{k}}$, ${{\bar {\omega }}_{k}}$, ${{\bar {L}}_{k}}$, ${{{\bar {v}}}_{k}}$ – требуемые значения переменных ${{\varepsilon }_{k}}$, ${{\omega }_{k}}$, ${{L}_{k}}$, ${{{v}}_{k}}$; ${v} \triangleq \dot {L}$, $\hat {\nu } = \dot {\hat {L}}$; ${{c}^{\varepsilon }}$, ${{c}^{\omega }}$, ${{c}^{L}}$, ${{c}^{\nu }}$ – коэффициенты усиления обратной связи, определяемые способом параметрической оптимизации в процессе имитационного математического моделирования.

В целом, информационно-управляющий алгоритм каждого из соседних взаимодействующих БПЛА описывается замкнутой системой рекуррентных уравнений (3.6)–(3.18).

Заключение. Представлены взаимосвязанные информационно-управляющие алгоритмы соседних участников группы БПЛА, наводящихся на группу объектов, часть из которых – ложные цели, создаваемые с помощью имитационных помех. Кроме того, противодействие осуществляется путем постановки маскирующих помех, приводящих к перерывам информации в системах управления.

Алгоритмы, основанные на теории систем со случайной скачкообразной структурой [3, 5–11], осуществляют распознавание помеховых ситуаций, оценивание координат объектов и соседних участников группы БПЛА и управление БПЛА, обеспечивающее требуемые точность наведения и дистанцию между соседними БПЛА.

Приведен пример наведения двух соседних взаимодействующих БПЛА на одну и ту же цель, прикрываемую одной имитационной помехой, которая дезориентирует систему управления БПЛА, и маскирующей помехой, вызывающей перерывы информации в двух каналах наблюдения. В каждом из информационных каналов измеряются координаты объектов – дальности и углы пеленга, а также спектральные и геометрические различительные признаки наблюдаемых объектов.

Представлены взаимосвязанные информационно-управляющие алгоритмы двух соседних участников группы БПЛА.