Известия РАН. Теория и системы управления, 2022, № 6, стр. 112-122
АНАЛИЗ РАСПРЕДЕЛЕНИЯ НАГРУЗКИ И МЕЖУЗЛОВЫХ ПОТОКОВ ПРИ РАЗЛИЧНЫХ СТРАТЕГИЯХ МАРШРУТИЗАЦИИ В МНОГОПОЛЬЗОВАТЕЛЬСКОЙ СЕТИ
Ю. Е. Малашенко a, И. А. Назарова a, *
a ФИЦ ИУ РАН
Москва, Россия
* E-mail: irina-nazar@yandex.ru
Поступила в редакцию 28.03.2021
После доработки 02.06.2022
Принята к публикации 01.08.2022
- EDN: DLVLJD
- DOI: 10.31857/S0002338822060130
Аннотация
В рамках вычислительных экспериментов на многопродуктовой сетевой модели изучаются функциональные возможности телекоммуникационной системы по обеспечении связи для заданных пар узлов-корреспондентов. Анализируются две стратегии распределения пропускной способности и различные правила маршрутизации. При реализации первой стратегии осуществляется поиск распределения ресурсов, при котором межузловые потоки равны друг другу. Вторая стратегия предполагает получение недискриминирующего распределения ресурсов сети между всеми корреспондентами. При использовании каждой стратегии сравниваются различные правила маршрутизации. Оценка минимальных удельных затрат производится при передаче каждого вида потока по кратчайшим маршрутам с минимальным числом ребер. При поиске различных путей соединения предварительно определяется максимальный однопродуктовый поток для данной пары и маршруты прокладываются по всем ребрам соответствующего минимального разреза. Вычислительные эксперименты проводились для различных сетей с одинаковым набором узлов-корреспондентов.
Введение. В рамках многопродуктовой сетевой модели рассматриваются различные стратегии распределения ресурсов и правила построения маршрутов передачи. Оценки функциональных возможностей сети опираются на вектор совместно допустимых межузловых потоков. Под ресурсом для некоторой пары узлов-корреспондентов понимается суммарная величина пропускных способностей, необходимых для обеспечения связи данного вида. Сумма соответствующих реберных потоков трактуется как нагрузка, возникающая при передаче заданного межузлового потока. Изучаются две стратегии распределения пропускной способности. При реализации первой осуществляется поиск распределения, при котором межузловые потоки равны друг другу. Вторая предполагает поиск недискриминирующего распределения ресурсов сети между всеми корреспондентами при равных нагрузках. В ходе выполнения вычислительных экспериментов на каждой текущей итерации часть имеющегося ресурса распределяется строго поровну между всеми парами источник-сток при условии, что для них существует путь соединения. Для оценки минимальных удельных затрат для передачи каждого вида потока выбираются кратчайшие маршруты с минимальным числом ребер. Для определения затрат ресурсов при соединении корреспондентов по различным путям для каждой пары узлов вычисляется максимальный однопродуктовый поток. Маршруты передачи потоков каждого вида прокладываются по ребрам соответствующих минимальных разрезов и подсчитываются допустимые нагрузки. Эксперименты проводились для дальнейшего изучения функциональных характеристик, допустимых распределений ресурсов и межузловых потоков в многопользовательских сетях связи [1, 2].
В настоящее время для создания, развития и эксплуатации систем связи используются потоковые модели и специальные методы решения [3]. Математические модели передачи многопродуктового потока применяются для поиска недискриминирующих правил распределения ресурсов в многопользовательских системах связи [4]. На основе формализма многокритериальной оптимизации создаются методы анализа сетевых систем с учетом вектора требований всех равноправных и невзаимозаменяемых пользователей [5]. В рамках методологии исследования операций и теории игр рассматриваются справедливые правила распределения потоков и ресурсов: решается задача на максимин и/или находятся гарантированные оценки [6–9]. В русле указанных работ лежат алгоритмические схемы получения уравнительных распределений межузловых потоков и выравнивания нагрузок, которые приведены в разд. 3 и 4. В разд. 5 обсуждаются результаты экспериментов и сравниваются достижимые межузловые потоки при маршрутизации по кратчайшим путям и результирующие распределения при расщепленной SPLIT-маршрутизации [10–15]. Для решения оптимизационных многопродуктовых сетевых задач предлагаются специально разработанные алгоритмы [16–18]. В работе используется метод возможных направлений с полиномиальной оценкой вычислительных затрат [19–21].
1. Математическая модель. Для описания многопользовательской сетевой системы связи воспользуемся следующей математической записью модели передачи многопродуктового потока. Сеть $G$ задается множествами $\langle V,\;R,\;U,P\rangle $: узлов (вершин) сети $V = \{ {{v}_{1}},{{v}_{2}},...,{{v}_{n}},...,{{v}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $; ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $; пар узлов-корреспондентов $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $. Предполагается, что в сети отсутствуют петли и сдвоенные ребра.
Ребро ${{r}_{k}} \in R$ соединяет концевые вершины ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Каждому ребру ${{r}_{k}}$ ставятся в соответствие две ориентированные дуги ${{u}_{k}}$, ${{u}_{{k + E}}}$ из множества U. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют прямое и обратное направления передачи потока по ребру ${{r}_{k}}$ между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$. Каждой паре узлов-корреспондентов ${{p}_{m}}$ из множества $P$ ставится в соответствие: вершина-источник с номером ${{s}_{m}}$, из ${{s}_{m}}$ входной поток m-го вида поступает в сеть; вершина-приемник с номером ${{t}_{m}}$, из ${{t}_{m}}$ поток m-го вида покидает сеть. Множество пар-корреспондентов $P$ разбивается на два непересекающихся подмножества: смежных узлов-корреспондентов $P({{R}_{ + }})$, расположенных в концевых вершинах ребра ${{r}_{k}}$, $k = \overline {1,E} $, и $P({{R}_{ - }})$ – несмежных пар, для которых кратчайший маршрут соединения содержит более одного ребра:
Далее изучается распределение ресурсов для пар-корреспондентов из множества $P({{R}_{ - }})$.
В многопользовательской сети $G$ рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных межузловых потоков различных видов. Обозначим через ${{z}_{m}}$ величину межузлового потока $m$-го вида, поступающего в сеть из узла с номером ${{s}_{m}}$ и покидающего сеть из узла с номером ${{t}_{m}}$; ${{x}_{{mk}}}$, ${{x}_{{m(k + E)}}}$ – поток $m$-го вида по дугам ${{u}_{k}}$ и ${{u}_{{k + E}}}$, согласно направлению передачи, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $; $S({{v}_{n}})$ – множество номеров исходящих дуг, по ним поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по ним поток поступает в узел ${{v}_{n}}$. Состав множеств $S({{v}_{n}})$, $T({{v}_{n}})$ однозначно формируется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами $n$ и j, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{v}_{n}},{{v}_{j}})$, направленная из вершины ${{v}_{n}}$ в ${{v}_{j}}$, считается исходящей из вершины ${{v}_{n}}$ и ее номер k заносится в множество $S({{v}_{n}})$, а дуга ${{u}_{{k + E}}}$, направленная из ${{v}_{j}}$ в ${{v}_{n}}$, – входящей для ${{{v}}_{n}}$ и ее номер $k + E$ помещается в список $T({{v}_{n}})$. Дуга ${{u}_{k}}$ является входящей для ${{v}_{j}}$ и ее номер k попадает в $T({{v}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ вносится в список исходящих дуг $S({{v}_{j}})$.
Во всех узлах сети ${{v}_{n}} \in V$, $n = \overline {1,N} $, для каждого вида потока должны выполняться условия сохранения потоков:
(1.1)
$\sum\limits_{i \in S({{v}_{n}})} {{x}_{{mi}}} - \sum\limits_{i \in T({{v}_{n}})} {{x}_{{mi}}} = \left\{ \begin{gathered} {{z}_{m}},\quad {\text{если}}\;\;{{v}_{n}} = {{v}_{{{{s}_{m}}}}}{\text{,}} \hfill \\ - {{z}_{m}},\quad {\text{если}}\;\;{{v}_{n}} = {{v}_{{{{t}_{m}}}}}{\text{,}} \hfill \\ 0\quad {\text{в остальных случаях,}} \hfill \\ \end{gathered} \right.$Величина ${{z}_{m}}$ равна входному межузловому потоку $m$-го вида, проходящему от источника к приемнику пары ${{p}_{m}}$ при распределении потоков ${{x}_{{mi}}}$ по дугам сети.
Каждому ребру ${{r}_{k}} \in R$ приписывается неотрицательное число ${{d}_{k}}$, определяющее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа ${{d}_{k}} > 0$. Вектор ${\mathbf{d}}$ задает следующие ограничения на сумму потоков всех видов, передаваемые по ребру ${{r}_{k}}$ одновременно:
(1.2)
$\sum\limits_{m = 1}^M ({{x}_{{mk}}} + {{x}_{{m(k + E)}}}) \leqslant {{d}_{k}},\quad {{x}_{{mk}}} \geqslant 0,\quad {{x}_{{m(k + E)}}} \geqslant 0,\quad k = \overline {1,E} .$В рамках данной модели пропускная способность ребер сети измеряется в условных единицах потока и трактуется как ресурсное ограничение. Сумма дуговых потоков (1.2) рассматривается как требование на предоставление ресурсов сети – пропускной способности ребер, необходимой при передаче межузловых потоков по данному ребру.
Для ${{z}_{m}}$, ${{x}_{{mi}}}$, удовлетворяющих условиям (1.1), (1.2), вычисляются суммарные потоки по ребрам сети:
Суммарный реберный поток ${{y}_{m}}$ характеризует нагрузку на сеть при передаче межузлового потока величины ${{z}_{m}}$ из узла-источника ${{s}_{m}}$ в узел-приемник ${{t}_{m}}$. Величина ${{y}_{m}}$ показывает, какая суммарная пропускная способность сети потребуется для передачи межузлового потока ${{z}_{m}}$. В рамках модели отношение реберных и межузловых потоков
можно трактовать как удельные затраты ресурсов сети при передаче единичного потока m-го вида между узлами ${{s}_{m}}$ и ${{t}_{m}}$ при соответствующих дуговых потоках ${{x}_{{mi}}}$.Ограничения (1.1), (1.2) задают множество допустимых значений компонент вектора межузловых потоков ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$:
(1.4)
$\mathcal{Z}({\mathbf{d}}) = \{ {\mathbf{z}} \geqslant 0\,{\text{|}}\,\exists \;{\mathbf{x}} \geqslant 0:\;({\mathbf{z}},{\mathbf{x}})\;{\text{удовлетворяют}}\;(1.1),(1.2)\} .$Допустимые распределения реберных потоков принадлежат подмножеству
(1.5)
$Y({\mathbf{d}}) = \{ {\mathbf{y}} \geqslant 0\,{\text{|}}\,({\mathbf{z}},{\mathbf{x}},{\mathbf{y}})\;{\text{удовлетворяют}}\;(1.1){\kern 1pt} - {\kern 1pt} (1.3)\} .$2. Маршрутизация межузловых потоков по кратчайшем путям. В рамках первой группы экспериментов проводится оценка минимальных удельных затрат. Для получения допустимых распределений межузловых потоков, передаваемых одновременно по кратчайшим маршрутам, используется следующая процедура. Выполнение каждой итерации разбивается на несколько этапов. На предварительном этапе шага $t$ при заданных текущих значениях пропускной способности ${{d}_{k}}(t)$ для каждой пары несмежных узлов-корреспондентов ${{p}_{m}} \in P({{R}_{ - }})$ определяется максимально допустимый однопродуктовый поток $z_{m}^{0}(t)$, который можно передать по кратчайшему маршруту $H_{m}^{0}(t)$, состоящему из минимального числа ребер $h_{m}^{0}(t)$ [22]. Маршрут $H_{m}^{0}(t)$ задается списком номеров ребер: $H_{m}^{0}(t) = \{ {{k}_{1}},{{k}_{2}},...,{{k}_{m}}\} $.
При поиске максимально допустимого потока $z_{m}^{0}(t)$ на ребрах минимального маршрута $H_{m}^{0}(t)$ определяются дуговые потоки: $(x_{{mk}}^{0}(t),x_{{m(k + E)}}^{0}(t))$, ${{p}_{m}} \in P({{R}_{ - }})$, $m = \overline {1,M} $, $k \in H_{m}^{0}(t)$, и результирующая реберная нагрузка:
Вычисляются коэффициенты нормировки:
Коэффициенты $\theta _{a}^{0}(t)$ используются для поиска равных нагрузок при передаче совместно допустимых дуговых потоков одновременно между всеми парами ${{p}_{m}} \in P({{R}_{ - }})$.
Задача 1. Найти $\beta {\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\beta \beta $
при условиях $\beta \sum\limits_{m \in {{R}_{ - }}} {\theta _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant } $ ${{d}_{k}}(t),k = \overline {1,E} $.
На основании $\beta {\kern 1pt} *(t)$ (решения задачи 1) для несмежных пар определяются совместно допустимые дуговые потоки:
Полученные значения запоминаются и используются в дальнейшем при вычислении текущих и финальных распределений. Подсчитываются текущие реберные нагрузки:
Таким образом определенная часть ресурса (пропускной способности сети) делится строго поровну между всеми корреспондентами, для которых существует маршрут передачи в сети $G(t)$ при текущих значениях ${{d}_{k}}(t)$, $k = \overline {1,E} $. Вычисляется остаточная пропускная способность ребер:
Если в сети $G(t + 1)$ при поиске максимальных потоков окажется, что $z_{m}^{0}(t + 1) = 0$ для всех ${{p}_{m}} \in P({{R}_{ - }})$, то происходит останов. Формируются массивы финальных данных $Y_{y}^{*}(T)$, $Z_{y}^{*}(T)$, где нижний индекс y указывает на распределение финальных нагрузок $y_{m}^{*}(T)$. Элементы множества $Y_{y}^{*}(T)$
численно равны ресурсам сети (пропускной способности) для передачи межузловых потоков:Описанная стратегия названа SRMF-процедурой от английского short – route – max – flow (получение максимально возможного потока $z_{m}^{0}(t)$, передаваемого по кратчайшему пути).
Для анализа функциональных возможностей сети в ходе выполнения второй серии экспериментов изучается уравнительное распределение межузловых потоков при передаче по кратчайшим маршрутам. При проведении экспериментов с помощью SRMF-процедуры на предварительном этапе каждой итерации $t$ при заданных значениях пропускных способностей ${{d}_{k}}(t)$ определяется максимальный поток $z_{m}^{0}(t)$, который можно передать по кратчайшему маршруту $H_{m}^{0}(t)$.
Для каждой пары ${{p}_{m}} \in P({{R}_{ - }})$ вычисляются нормирующие коэффициенты:
Коэффициенты $\xi _{m}^{0}(t)$ используются далее для поиска текущих совместно допустимых квот на передачу межузловых потоков одновременно между всеми парами ${{p}_{m}} \in P({{R}_{ - }})$.
Задача 2. Найти $\alpha {\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\alpha \alpha $
при условиях $\alpha \sum\limits_{m \in {{R}_{ - }}} {\xi _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant {{d}_{k}}(t)} $, $k = \overline {1,E} $.
На основании α*(t) (решения задачи 2) для каждого $m = \overline {1,M} $ находятся совместно допустимые дуговые потоки:
Полученные значения фиксируются и подсчитывается остаточная пропускная способность ребер в сети $G(t + 1)$:
Если на шаге $(t + 1)$ при поиске максимального потока на предварительном этапе в сети $G(t + 1)$ все $z_{m}^{0}(t + 1) = 0$ для всех ${{p}_{m}} \in P({{R}_{ - }})$, то происходит останов и формируются массивы финальных значений $Y_{z}^{*}(T)$, $Z_{z}^{*}(T)$, $D_{z}^{*}(T)$, где индекс z указывает на распределение межузловых потоков $z_{m}^{*}(T)$. Элементы массива $D_{z}^{*}(T)$ – значения остаточной пропускной способности $d_{k}^{*}(T) = {{d}_{k}}(t + 1)$ для всех $k = \overline {1,E} $; элементы $Z_{z}^{*}(T)$ – межузловые потоки
3. Маршрутизация межузловых потоков через минимальные разрезы. Третья серия экспериментов проводилась для оценки затрат ресурсов при передаче каждого межузлового потока одновременно по нескольким маршрутам. Для формирования различных маршрутов передачи использовались решения стандартной задачи поиска максимального однопродуктового потока и минимального разреза [19] для каждой пары узлов-корреспондентов. При реализации процедуры выполнение каждого шага разбивается на несколько этапов. На предварительном этапе шага t в сети $G(t)$ при заданных значениях пропускной способности ребер ${{d}_{k}}(t)$ для каждой пары узлов-корреспондентов ${{p}_{m}} \in P({{R}_{ - }})$ определяется максимально допустимый однопродуктовый поток $z_{m}^{0}(t)$, соответствующие дуговые потоки $(x_{{mk}}^{0}(t),x_{{m(k + E)}}^{0}(t)),$ ${{p}_{m}} \in P({{R}_{ - }})$, и суммарная реберная нагрузка
Для каждой пары ${{p}_{m}} \in P({{R}_{ - }})$ вычисляются коэффициенты нормировки:
Коэффициенты $\theta _{m}^{0}(t)$ используются далее для поиска совместно допустимых дуговых потоков для всех ${{p}_{m}} \in P({{R}_{ - }})$.
Задача 3. Найти $\beta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\beta \beta $
при условиях $\beta \sum\limits_{m \in {{R}_{ - }}} {\theta _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant {{d}_{k}}(t),} $ $k = \overline {1,E} $.
С помощью $\beta {\kern 1pt} *{\kern 1pt} *(t)$ (решения задачи 3) для каждого $m = \overline {1,M} $ находятся текущие допустимые значения дуговых потоков:
Таким образом на каждом шаге определенная часть имеющегося ресурса (пропускной способности) делится строго поровну между всеми корреспондентами, для которых существует путь передачи в G(t).
Вычисляется остаточная пропускная способность ребер в сети $G(t + 1)$:
Если на предварительном этапе шага $(t + 1)$ окажется, что все $z_{m}^{0}(t + 1) = 0$ для вех ${{p}_{m}} \in P({{R}_{ - }})$, то по аналогии с разд. 2 формируются массивы: $D_{y}^{{**}}(T)$ финальных значений остаточной пропускной способности
$Y_{y}^{{**}}(T)$ финальных значений реберной нагрузки численно равные ресурсам сети, необходимым для передачи межузловых потоков:Финальные значения $z_{m}^{{**}}(T)$ образуют массив $Z_{y}^{{**}}(T)$.
Описанная стратегия названа MFMC-процедурой от английского max – flow – min – cut (получение максимально возможного потока $z_{m}^{0}(t)$, передаваемого по всем возможным путям, проходящим через минимальный разрез).
Четвертая серия экспериментов проводилась с помощью MFMC-стратегии для оценки функциональных возможностей системы при передаче межузловых потоков по нескольким маршрутам. На предварительном этапе шага t в сети $G(t)$ при заданных значениях пропускной способности ребер ${{d}_{k}}(t)$ для каждой пары узлов-корреспондентов ${{p}_{m}} \in P({{R}_{ - }})$ определяется максимально допустимый однопродуктовый поток $z_{m}^{0}(t)$, соответствующие дуговые потоки $(x_{{mk}}^{0}(t),x_{{m(k + E)}}^{0}(t)),$ ${{p}_{m}} \in P({{R}_{ - }})$, и коэффициенты нормировки
Коэффициенты $\xi _{m}^{0}(t)$ используются для поиска текущих совместно допустимых квот на передачу потоков одновременно между всеми парами ${{p}_{m}} \in P({{R}_{ - }})$.
Задача 4. Найти $\alpha {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(t) = \mathop {\max }\limits_\alpha \alpha $
при условиях $\alpha \sum\limits_{m \in {{R}_{ - }}}^{} {\xi _{m}^{0}(t)(x_{{mk}}^{0}(t) + x_{{m(k + E)}}^{0}(t)) \leqslant {{d}_{k}}(t),} $ $k = \overline {1,E} $.
На основании α*(t) (решения задачи 4) вычисляются совместно допустимые дуговые потоки:
Если на предварительном этапе шага (t + 1) окажется, что $z_{m}^{0}(t + 1) = 0$ для всех ${{p}_{m}} \in P({{R}_{ - }})$, то происходит останов и формируются массивы финальных данных. По аналогии с разд. 2 значения остаточных пропускных способностей $d_{k}^{{**}}(T) = {{d}_{k}}(t + 1)$ для всех $k = \overline {1,E} $ помещаются в массив $D_{z}^{{**}}(T)$. Найденные значения межузловых потоков
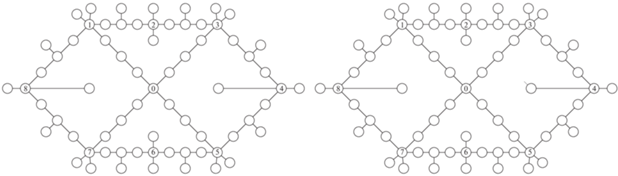
4. Вычислительный эксперимент. Вычислительные эксперименты проводились на моделях сетевых систем, представленных на рис. 1 (слева – базовая сеть, справа – кольцевая). В каждой сети имеется 69 узлов. Пропускные способности ребер dk выбираются случайным образом из отрезка [900, 999] и совпадают для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900.
Далее на диаграммах и в табл. 1 для обозначения элементов массивов $Y_{y}^{*}(T)$ введена запись y*; $Z_{y}^{*}(T)$ – $z(y{\kern 1pt} *)$ (поскольку значения межузловых потоков подсчитывается с учетом распределения $y_{m}^{*}(T)$); $Y_{z}^{*}(T)$ – $y(z{\kern 1pt} *)$; $Z_{z}^{*}(T)$ – $z{\kern 1pt} *$; $Y{\kern 1pt} *{\kern 1pt} *(T)$ – $y{\kern 1pt} *{\kern 1pt} *$; $Z_{y}^{{**}}(T)$ – $z(y{\kern 1pt} *{\kern 1pt} *)$; $Y_{z}^{{**}}(T)$ – $y(z{\kern 1pt} *{\kern 1pt} *)$; $Z_{z}^{{**}}(T)$ – $z{\kern 1pt} *{\kern 1pt} *$.
Таблица 1
| Сеть | Базовая | Кольцевая | ||||||
|---|---|---|---|---|---|---|---|---|
| Значения | SRMF-стратегия | MFMC-стратегия | SRMF-стратегия | MFMC-стратегия | ||||
| Медиан | z* | z(y*) | z** | z(y**) | z* | z(y*) | z** | z(y**) |
| потоков | 1.2 | 1.2 | 1 | 1.1 | 1.8 | 1.7 | 1.4 | 1.4 |
| Медиан | y(z*) | y* | y(z**) | y** | y(z*) | y* | y(z**) | y** |
| нагрузок | 11.2 | 9.9 | 11.1 | 10.8 | 12.9 | 13.2 | 12.5 | 12.6 |
| Удельные | y(z*)/z* | y*/z(y*) | y(z**)/z** | y**/z(y**) | y(z*)/z | y*/z(y*) | y(z**)/z** | y**/z(y**) |
| значения | 9.3 | 8.3 | 10.8 | 9.8 | 7.2 | 7.8 | 8.9 | 9.0 |
На рис. 2, 3 представлены финальные значения межузловых потоков и соответствующих нагрузок, полученных в результате выполнения SRMF- и MFMC-процедур, для базовой сети. Значения финальных потоков и нагрузок упорядочиваются от большего к меньшему (по невозрастанию). По горизонтальной оси указываются относительные порядковые номера корреспондентов в упорядоченных последовательностях:
Рис. 2.
Маршрутизация межузловых потоков в базовой сети по кратчайшим путям и через минимальные разрезы

Рис. 3.
Межузловые нагрузки при маршрутизации межузловых потоков в базовой сети по кратчайшим путям и через минимальные разрезы
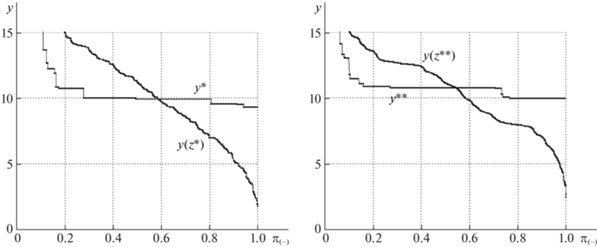
Диаграммы на рис. 3 свидетельствуют, что нагрузку для 80% несмежных пар корреспондентов удается распределить почти равномерно при использовании как SRMF-, так и MFMC-стратегии. Аналогичная зависимость наблюдается и на рис. 2 для потоков.
На всех диаграммах слева для 20% пар корреспондентов наблюдаются нарушения уравнительного распределения. Дело в том, что при выполнении как SRMF-, так и MFMC-процедуры после 30-й итерации пропускная способность многих ребер становится равной нулю, текущая сеть $G(t)$ распадается на несколько связных компонент. Вследствие этого для многих пар максимальный поток оказывается равным нулю, а остаточная пропускная способность распределяется между оставшимися корреспондентами. При уравнительном распределении остаточной пропускной способности среди небольшого числа пар результирующие финальные значения потоков и нагрузок резко возрастают.
Из сравнения диаграмм на рис. 2 для межузловых потоков следует, что медианные значения для SRMF-процедуры практически совпадают, как и для MFMC-стратегии. При этом медианные значения потоков для SRMF-процедуры превосходят медианные значения для MFMC-стратегии. Таким образом распределение по кратчайшим путям позволяет достичь бóльших значений межузловых потоков для бóльшего числа пар. MFMC-стратегия при передаче каждого межузлового потока использует бóльшее число путей и требует бóльших удельных затрат пропускной способности.
Последнее иллюстрируют диаграммы распределения нагрузок (рис. 3). В рамках модели величины нагрузок численно равны суммарным значениям пропускных способностей на всех маршрутах передачи каждого межузлового потока. Результирующие затраты ресурсов больше для MFMC-стратегии и распределении межузловых потоков по всем ребрам минимальных разрезов.
В таблице собраны значения медиан нагрузок и межузловых потоков при различных стратегиях маршрутизации. Для базовой сети и SRMF-стратегии достигнутые значения потоков оказываются чуть выше, чем для MFMC-стратегии, а удельные затраты – меньше для кратчайших маршрутов передачи. Удельные затраты выше при передаче межузловых потоков по большему числу путей. Для кольцевой сети из таблицы следует, что увеличение пропускной способности и структурной связности в центральной части сети позволяет увеличить медианные значения межузловых потоков и снизить удельные затраты ресурсов при передаче. Предлагаемые методы позволяют оценить соответствующие изменения функциональных характеристик при смене маршрутизации.
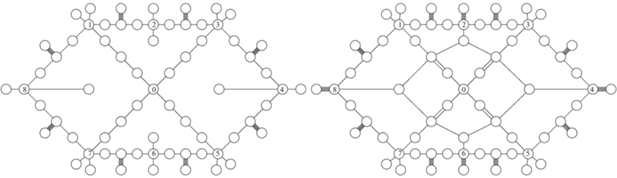
На рис. 4 указана загрузка ребер сети $G(t)$ после выполнения 41 итерации как SRMF-, так и MFMC-процедуры. Тонкими линиями изображены ребра, остаточная пропускная способность которых не превышает 3% от исходной: ${{d}_{k}}(41) \leqslant 0.03{{d}_{k}}(1)$. Жирными линиями изображены ребра с остаточной пропускной способностью более 70% от исходной: $0.7{{d}_{k}}(1) \leqslant {{d}_{k}}(41)$. Таким образом узким местом сети при одновременной передаче всех потоков для всех пар ${{p}_{m}} \in P({{R}_{ - }})$ являются все ребра центральной части сети.
На рис. 5, 6 представлены результаты расчетов для кольцевой сети. Из диаграмм рис. 5, 6 следует, что использование SRMF-стратегии не позволяет получить распределения межузловых потоков и нагрузок, соответствующих уравнительному правилу. Ступенчатые диаграммы с большим шагом показывают, что уже на начальных итерациях происходит разрыв сети на отдельные компоненты и для значительного числа пар в сетях $G(t)$ не существует путей передачи потока.
Рис. 5.
Маршрутизация межузловых потоков в кольцевой сети по кратчайшим путям и через минимальные разрезы

Рис. 6.
Межузловые нагрузки при маршрутизации межузловых потоков в кольцевой сети по кратчайшим путям и через минимальные разрезы
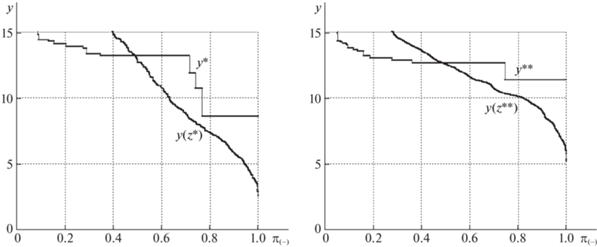
Заключение. Изучались распределения межузловых потоков разных видов. Предполагалось, что все пары корреспондентов равноправны, соответствующие потоки невзаимозаменяемы, а требования пользователей неизвестны. В условиях указанной неопределенности проводилась оценка характеристической величины допустимого потока, одинакового для всех пар корреспондентов. В ходе экспериментов для определения оценок характеристических величин анализировались финальные значения потоков при последовательном уравнительном предельном распределении ресурсов. На каждом шаге при выполнении вычислительной процедуры остаточный ресурс распределялся строго поровну между парами-корреспондентов. В рамках модели пропускные способности ребер рассматривались как вектор ресурсов различных типов, которые распределяются между корреспондентами при передаче потоков различных видов. Полученные значения медиан распределений как потоков, так и пропускных способностей можно интерпретировать как представительные оценки функциональных возможностей сети в условиях неопределенности и однородности корреспондентов. Все межузловые потоки, не превышающие медианных значений, можно передать в сети одновременно. Для последних наблюдается небольшой разброс при разных правилах маршрутизации. Финальные потоки при предельных распределениях для 80% пар практически равны медианным, хотя средние показатели сильно отличаются. Для 20% пар финальные значения при предельных распределениях на порядок, а для 2% пар – на два порядка превышают медианные значения. Выделенная группа привилегированных пользователей и большая остаточная пропускная способность на ребрах, ведущих к висячих вершинам, указывают на возможное несоответствие структуры сети эффективному использованию ресурсов при передаче однородных межузловых потоков в стационарном режиме. Полученные медианы являются представительной оценкой распределений с равными значениями потоков в условиях неопределенности. В рамках модели указанные медианы можно трактовать как нормативные характеристики при работе сети в стационарном режиме при однородных нагрузках в заданном диапазоне. Анализ всех промежуточных результатов экспериментов позволяет априори предложить рекомендации по рандомизации маршрутов передачи для всех корреспондентов.
Список литературы
Малашенко Ю.Е., Назарова И.А. Оценки распределения потоков при предельной загрузке многопользовательской сети // Системы и средства информатики. 2020. Т. 30. № 3. С. 4–14.
Малашенко Ю.Е., Назарова И.А. Анализ распределения предельных нагрузок в многопользовательской сети // Информатика и ее применения. 2021. Т. 15. Вып. 4. С. 20–26.
Salimifard K., Bigharaz S. The Multicommodity Network Flow Problem: State of the Art Classification, Applications, and Solution Methods // J. Oper. Res. Int. 2020. V. 22. Iss. 2. P. 1–47.
Luss H. Equitable Resource Allocation: Models, Algorithms, and Applications. Hoboken: John Wiley & Sons, 2012.
Balakrishnan A., Li G., Mirchandani P. Optimal Network Design with End-to-End Service Requirements // Oper. Res. 2017. V. 65. Iss. 3. P. 729–750.
Hahne E.L. Round-Robin Scheduling for Max-Min Fairness in Data Networks // IEEE J. on Selected Areas in Communications. 1991. V. 9. Iss. 7. P. 1024–1039.
Radunovic B., Le Boudec J.-Y. A Unified Framework for Max-Min and Min-Max Fairness With Applications // IEEE/ACM Transactions on Networking. 2007. V. 15. Iss. 5. P. 1073–1083.
Nace D., Doan L.N., Klopfenstein O. et al. Max-min Fairness in Multicommodity Flows // Comput. Oper. Res. 2008. V. 35. Iss. 2. P. 557–573.
Ros-Giralt J., Tsai W.K. A Lexicographic Optimization Framework to the Flow Control Problem // IEEE Transactions on Information Theory. 2010. V. 56. Iss. 6. P. 2875–2886.
Ramaswamy R., Orlin J.B., Chakravarti N. Sensitivity Analysis for Shortest Path Problems and Maximum Capacity Path Problems in Undirected Graphs // Math. Prog. 2005. V. 102. Iss. 2. P. 355–369.
Masri H., Krichen S., Guitouni A. A Multi-start Variable Neighborhood Search for Solving the Single Path Multicommodity Flow Problem // Appl. Math. Comput. 2015. V. 251. P. 132–142.
Masri H., Krichen S., Guitouni A. Metaheuristics for Solving the Bi-objective Single-Path Multicommodity Communication Flow Problem // Int. Trans. Oper. Res. 2019. V. 26. Iss. 2. P. 589–614.
Baier G., Kohler E., Skutella M. The k-Splittable Flow Problem // Algorithmica. 2005. V. 42. Iss. 3–4. P. 231–248.
Kabadurmus O., Smith A.E. Multicommodity k-Splittable Survivable Network Design Problems with Relays // Telecommun. Syst. 2016. V. 62. Iss. 1. P. 123–133.
Bialon P. A Randomized Rounding Approach to a k-Splittable Multicommodity Flow Problem with Lower Path Flow Bounds Affording Solution Quality Guarantees // Telecommun. Syst. 2017. V. 64. Iss. 3. P. 525–542.
Ogryczak W., Luss H., Pioro M. et al. Fair Optimization and Networks: A Survey // J. Appl. Math. 2014. V. 3. P. 1–25.
Hajjem M., Bouziri H., Talbi E.-G. A Metaheuristic Framework for Dynamic Network Flow Problems // Recent Developments in Metaheuristics. Operations Research/Computer Science Interfaces Series. V. 62. Cham: Springer, 2018. P. 285–304.
Leighton T., Makedon F., Plotkin S. et al. Fast Approximation Algorithms for Multicommodity Flow Problems // J. Comput. Syst. Sci. 1995. V. 50. Iss. 2. P. 228–243.
Йенсен П., Барнес Д. Потоковое программирование. М.: Радио и связь, 1984.
Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л. и др. Алгоритмы: построение и анализ. М.: Вильямс, 2005.
Зойтендейк Г. Методы возможных направлений. М.: Изд-во иностр. лит., 1963.
Берж К. Теория графов и ее применения. М.: Изд-во иностр. лит., 1962.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления