Известия РАН. Теория и системы управления, 2022, № 6, стр. 95-102
МАТРИЦА НЕЧЕТКИХ КОРРЕСПОНДЕНЦИЙ МОДЕЛИ АВИАЦИОННЫХ ПЕРЕВОЗОК
В. А. Нестеров a, *, В. А. Судаков a, b, c, **, К. И. Сыпало d, ***, Ю. П. Титов c, ****
a МАИ (национальный исследовательский ун-т)
Москва, Россия
b ИПМ им. М.В. Келдыша РАН
Москва, Россия
c ФГБОУ ВО РЭУ им. Г.В. Плеханова
Москва, Россия
d Центральный аэрогидродинамический ин-т им. проф. Н.Е. Жуковского
Жуковский, Россия
* E-mail: nesterov46@inbox.ru
** E-mail: sudakov@ws-dss.com
*** E-mail: ksypalo@tsagi.ru
**** E-mail: kalengul@mail.ru
Поступила в редакцию 25.04.2022
После доработки 15.05.2022
Принята к публикации 30.05.2022
- EDN: LOSEFT
- DOI: 10.31857/S0002338822060154
Аннотация
Предложен новый метод поддержки принятия решений при планировании авиаперевозок с использованием неопределенностей в форме нечетких чисел. Он позволяет определить такие изменения транспортного графа, чтобы они в большей мере соответствовали текущим потребностям населения и доступному парку воздушных судов. Это особенно актуально в условиях существенной трансформации транспортных потоков и доступных типов летательных аппаратов в современных реалиях. Задача решается путем восстановления нечеткой матрицы корреспонденций по данным об авиаперевозках за предыдущие периоды. Часто неизвестно, какая часть пассажиров перемещается между заданными пунктами вынуждено, используя в качестве промежуточных крупные транспортные хабы. Для определения истиной матрицы корреспонденций строится ряд оптимизационных моделей определения функции принадлежности нечеткого числа перевезенных пассажиров. Создано алгоритмическое и программное обеспечение поиска нечетких корреспонденций и нечеткого ранжирования потенциально перспективных маршрутов. Возможности метода показаны на примере задачи выбора новых маршрутов между аэропортами.
Введение. Эффективность современных авиатранспортных систем во многом обеспечивается не только возможностями конкретных моделей воздушных судов, но и рациональным подходом к планированию и управлению комплексами авиационного транспорта. Создание интеллектуальных решений по стратегическому планированию транспортных потоков и систем поддержки принятия оперативных решений в логистике обеспечивает достижение целей по занятию лидерских позиций в освоении и использовании воздушного пространства, Мирового океана, Арктики и Антарктики. Для повышения связанности территории Российской Федерации, в силу больших расстояний и большого количества малых населенных пунктов с плохой дорожной инфраструктурой, необходимо решать высокоразмерные задачи планирования авиатранспортных потоков.
Моделирование транспортных потоков и оценка результатов моделирования затрудняется существенной долей неопределенных факторов. Это и пандемии, и фундаментальные изменения в экономике, и непрогнозируемые политические и военные изменения. Вероятностные оценки этих неопределенностей не всегда возможны в силу уникальностей ситуаций, отсутствия необходимых статистических данных.
Первоочередной задачей, с которой приходится сталкиваться при создании транспортных моделей, выступает формирование матрицы корреспонденций (origin–destination matrix). Данная задача обычно решается классическими способами, предложенными исследователями для автомобильного транспорта, – это методы на базе гравитационной и энтропийной моделей [1]. В гравитационной модели ищется аналогия между классическими физическими силами притяжения масс и притяжением людей к определенным районам проживания или работы [2]. Однако применение такого подхода к авиационным перевозкам вызывает сомнения. Для перемещения в городе естественно считать, что притяжение к легкодоступным районам больше, но на больших расстояниях работают другие критерии. Нет оснований считать, что популярность курортного города имеет обратную квадратичную зависимость от затрат на его посещение. Другим критерием определения корреспонденций является использование подхода на базе максимизации энтропии, что соответствует попытке найти аналогию c термодинамикой, когда система пытается прийти в равновесное состояние с максимальной энтропией [3]. Для “условно хаотического” движения машин, возможно, такие соображения и справедливы, но в авиационных перевозках мы сталкиваемся с большей “регулярностью”, которая обусловлена системой ценностей авиакомпаний и регулирующих органов. Часто матрицу корреспонденций находят путем проведения маркетинговых опросов, но подобные опросы затрагивают ограниченный круг лиц.
В авиации есть подробная статистика по авиационным перевозкам между отдельными аэропортами. В России в форме “Сведения об объемах перевозок между пунктами полета” (код формы N 14-ГА утвержден Росстатом), в США (в T-100 базе данных) эти данные собираются ежемесячно авиационными властями. Однако по ним нельзя определить, сколько пассажиров вынуждены лететь транзитом. Для определенного процента пассажиров можно использовать данные посадочных купонов, но обычно это закрытая и/или сильно зашумленная информация, кроме того, подобная выборка не является полной [4]. Классические методы для решения данной задачи хоть и дают ответ, но не позволяют оценить степень неопределенности этого ответа.
В работе предлагается новый метод получения нечетких оценок корреспонденций путем формализации и решения ряда оптимизационных задач линейного программирования. Этот метод позволяет осуществлять поддержку принятия решений по совершенствованию транспортной инфраструктуры с учетом возможной степени неопределенности ситуации и хорошо масштабируется при программной реализации на современных вычислительных комплексах.
1. Постановка задачи. Пусть дан связный ориентированный граф. Для каждой дуги известен поток в заданную единицу времени: для текущей прикладной задачи авиационного транспорта – это число пассажиров в месяц между заданными аэропортами, вершины графа – это аэропорты. Требуется найти матрицу корреспонденций между вершинами графа: сколько человек переместились между заданными вершинами.
Введем обозначения: D = {d} – множество дуг графа, ${{x}_{{ij}}}$ – число пассажиров в месяц, переместившихся из аэропорта i в аэропорт j (${{x}_{{ij}}} \geqslant 0$). Между пунктами i и j может не быть прямого маршрута, поэтому ${{x}_{{ij}}}$ – это суммарный поток из i в j по всем маршрутам за месяц. Если i = j, то xij = 0 и Vd – известный нам поток по дуге d.
Решение задачи должно удовлетворять системе уравнений
(1.1)
$\mathop \sum \limits_i \mathop \sum \limits_j p_{{ij}}^{d}{{x}_{{ij}}} = {{V}_{d}},\quad \forall d \in D,$2. Метод решения. Вышеуказанная система из |D| уравнений давала бы однозначное решение, если бы число уравнений было бы равно числу неизвестных, но на практике обычно переменных больше, чем уравнений. Поэтому однозначное решение отсутствует.
Пусть ${{X}_{{ij}}}$ определяет поток из вершины i в вершину $j$ в виде нечеткого числа. Мы не знаем этих значений, но хотим их найти. Поскольку известно точное значение потока ${{V}_{d}}$ на каждой дуге d текущей транспортной сети, возможно, что реальная величина потребности в перевозках из вершины i в вершину $j$ принадлежит некоторому интервалу $[x_{{ij}}^{{{\text{min}}}},x_{{ij}}^{{{\text{max}}}}]$, где $x_{{ij}}^{{{\text{min}}}}$ – минимально возможный поток из вершины i в вершину $j$, $x_{{ij}}^{{{\text{max}}}}$ – максимально возможный поток из вершины i в вершину $j$.
Для поиска решений предлагается определить нечеткую корреспонденцию в форме треугольной функции принадлежности:
(2.1)
${{X}_{{ij}}} = \langle x_{{ij}}^{{{\text{min}}}},{{\bar {x}}_{{ij}}},x_{{ij}}^{{{\text{max}}}}\rangle .$Левые границы находятся путем решения линейных оптимизационных задач (2.2) c ограничениями (1.1) для каждой комбинации значений i и $j$:
(2.2)
$\begin{array}{*{20}{c}} {x_{{ij}}^{{{\text{min}}}} = \mathop {\min }\limits_{i,j = \overline {1,n} ,i \ne j} {{x}_{{ij}}},} \\ {\mathop \sum \limits_i \mathop \sum \limits_j p_{{ij}}^{d}{{x}_{{ij}}} = {{V}_{d}}{\text{\;}}\quad \forall d \in D,} \end{array}$(2.3)
$\begin{array}{*{20}{c}} {x_{{ij}}^{{{\text{max}}}} = \mathop {\max }\limits_{i,j = \overline {1,n} ,i \ne j} {{x}_{{ij}}},} \\ {\mathop \sum \limits_i \mathop \sum \limits_j p_{{ij}}^{d}{{x}_{{ij}}} = {{V}_{d}}{\text{\;\;}}\forall d \in D.} \end{array}$Для графа, если число вершин равно n, необходимо решить n(n – 1) оптимизационных задач. Для некоторых корреспонденций может получиться, что
В этом случае
так какЕсли $x_{{ij}}^{{{\text{min}}}} < x_{{ij}}^{{{\text{max}}}}$, то необходимо выбрать некое наиболее возможное значение ${{\bar {x}}_{{ij}}}$ из диапазона $[x_{{ij}}^{{{\text{min}}}},x_{{ij}}^{{{\text{max}}}}]$, такое, что $\mu \left( {{{{\bar {x}}}_{{ij}}}} \right) = 1$, где $\mu $ обозначает функцию принадлежности треугольного числа ${{X}_{{ij}}}$. Этот выбор обусловлен априорной информацией о миграции населения. Информация может быть представлена в экспертном виде, причем допустимо применить подходы к согласованию экспертных оценок, в качестве “экспертов” могут выступать и стратегические соображения, которыми оперирует лицо, принимающее решения. Предположим “обобщенный сценарий”, такой, что
(2.7)
${{\bar {x}}_{{ij}}} \cong {{\alpha }_{{ij}}}x_{{ij}}^{{{\text{max}}}} + {{\beta }_{{ij}}}x_{{ij}}^{{{\text{min}}}}.$Знак $ \cong $ означает примерное равенство, так как выбранные ${{\bar {x}}_{{ij}}}$ могут быть несовместны с точки зрения основного ограничения (1.1). При этом предполагаем, что ${{\bar {x}}_{{ij}}}$ должны быть наиболее возможны. Из условия (2.6) следует, что ${{\alpha }_{{ij}}} + {{\beta }_{{ij}}} = 1$. Задача на повышение связности регионов допускает рассмотрение сценария ${{\alpha }_{{ij}}} \to 0$, когда ${{\bar {x}}_{{ij}}} \cong x_{{ij}}^{{{\text{min}}}}$ для j, соответствующего крупному транспортному хабу, нагрузку на который мы хотим снизить, и ${{\alpha }_{{ij}}} \to 1$ ${{\bar {x}}_{{ij}}} \cong x_{{ij}}^{{{\text{max}}}}$, для i вершины графа, связность которых хотим увеличить. Если какие-либо соображения отсутствуют, то можно выбрать ${{\alpha }_{{ij}}} = {{\beta }_{{ij}}} = 1{\text{/}}2$.
Обозначим наиболее возможную оценку:
(2.8)
${{\tilde {x}}_{{ij}}} = {{\alpha }_{{ij}}}x_{{ij}}^{{{\text{max}}}} + {{\beta }_{{ij}}}x_{{ij}}^{{{\text{min}}}}.$Окончательные оценки ${{\bar {x}}_{{ij}}}$ вычисляются путем решения оптимизационной задачи:
(2.9)
$\begin{array}{*{20}{c}} {\mathop {\min }\limits_{{{{\bar {x}}}_{{ij}}}} \mathop \sum \limits_i \mathop \sum \limits_j \left| {{{{\bar {x}}}_{{ij}}} - {{{\tilde {x}}}_{{ij}}}} \right|,} \\ {\mathop \sum \limits_i \mathop \sum \limits_j p_{{ij}}^{d}{{{\bar {x}}}_{{ij}}} = {{V}_{d}}{\text{\;}}\forall d \in D.} \end{array}$Целевая функция (2.9) не линейна, однако задачу можно привести к линейному виду, для этого введем два класса технических дополнительных переменных:
Добавим ограничение
А целевую функцию (2.9) перепишем в виде
(2.12)
$\mathop {\min }\limits_{y_{{ij}}^{ + },y_{{ij}}^{ - }} \mathop \sum \limits_i \mathop \sum \limits_j (y_{{ij}}^{ + } + y_{{ij}}^{ - }).$Полученная задача эквивалентна исходной, алгоритм оптимизации будет всегда получать либо $y_{{ij}}^{ + }$, либо $y_{{ij}}^{ - }$ равным нулю и минимизировать оставшуюся ненулевую переменную.
Альтернативная постановка ориентирована на минимизацию не суммарного, а наибольшего отклонения от “идеального” решения:
(2.13)
$\begin{array}{*{20}{c}} {\mathop {\min }\limits_{{{{\bar {x}}}_{{ij}}}} \mathop {{\text{max}}}\limits_{i,j} \left| {{{{\bar {x}}}_{{ij}}} - {{{\tilde {x}}}_{{ij}}}} \right|,} \\ {\mathop \sum \limits_i \mathop \sum \limits_j p_{{ij}}^{d}{{{\bar {x}}}_{{ij}}} = {{V}_{d}}{\text{\;}}\forall d \in D.} \end{array}$Она тоже может быть сведена к линейному виду путем добавления бинарных переменных, таким образом можно получить смешанно-целочисленную линейную задачу. Выбор вида целевой функции (2.9) или (2.13) обусловлен требованиями лица, принимающего решения, к дальнейшему применению результатов расчетов.
3. Алгоритмическая и программная реализация. Программная реализация данной математической модели расчета нечетких корреспонденций была разработана на языке Python 3. В качестве пакета оптимизации использовался SCIP Optimization Suite [6]. Данный пакет предоставляет возможности решать задачи линейного смешанно-целочисленного программирования. Он бесплатен для некоммерческого использования и поставляется с открытыми исходными текстами. Модуль интеграции PySCIPOpt с открытыми исходными текстами позволил объединить подготовку исходных данных с применением быстродействующих генераторных выражений Python и запуск решения оптимизационных задач в единой программе.
Программная реализация была размещена на портале веб-методов поддержки принятия решений WS-DSS [7]. Данный портал разработан одним из авторов статьи и позволяет запускать программную реализацию математических моделей, строя последовательные и параллельные цепочки запуска модулей с передачей параметров межу ними. Портал написан на языке Ruby, для организации вызова расчетных модулей используется менеджер задач Sidekiq на базе NoSQL базы данных Redis, что обеспечивает высокую производительность. Помимо модулей на Python реализован запуск модулей на Ruby, R, С++. С помощью открытого каркаса Ruby on Rail реализована возможность асинхронного запуска моделей через RESTful API. Входные и выходные параметры передаются в форматах JSON и CSV. Результаты сохраняются в базе данных PostgreSQL. Такая реализация обеспечивает независимость от зарубежных поставщиков системного программного обеспечения в условиях санкционного давления.
Общий алгоритм работы программного обеспечения, состоит из следующих шагов.
Шаг 1. На веб-сервер WS-DSS поступает HTTP запрос POST с исходными данными для решаемой задачи. В ответ клиенту возвращается уникальный ID созданной задачи.
Шаг 2. WS-DSS формирует задачу для расчета в Sidekiq.
Шаг 3. Рабочий процесс Sidekiq запускает расчетный модуль на Python.
Шаг 4. Формируется массив объемов перевозок ${{V}_{d}}$ по всем дугам d.
Шаг 5. С помощью пакета NetworkX, используя алгоритм Дейкстры, рассчитываются все кратчайшие пути между всеми вершинами.
Шаг 6. Заполнение параметров $p_{{ij}}^{d}$. Для всех d проверяется, входит ли она в кратчайший путь из вершины i в вершину j. Если ответ да, то $p_{{ij}}^{d} = 1{\text{/}}k$, где k – общее число кратчайших путей из i в j.
Шаг 7. Формирование ограничений (1.1).
Шаг 8. Расчет $x_{{ij}}^{{{\text{min}}}}$. Формирование целевой функции (2.2), решение полученной оптимизационной задачи для всех комбинаций значений $i$ и $j$.
Шаг 9. Расчет $x_{{ij}}^{{{\text{min}}}}$. Формирование целевой функции (2.3), решение полученной оптимизационной задачи для всех комбинаций значений $i$ и $j$.
Шаг 10. Расчет параметров ${{\tilde {x}}_{{ij}}}$ по формуле (2.8).
Шаг 11. Формирование ограничений (2.11).
Шаг 12. Поиск ${{\bar {x}}_{{ij}}}$ путем решения оптимизационной задачи (2.12) при ограничениях (2.11) и (1.1).
Шаг 13. Сохранение полученных $x_{{ij}}^{{{\text{min}}}},{{\bar {x}}_{{ij}}},x_{{ij}}^{{{\text{max}}}}$ в базе данных PostgreSQL.
Шаг 14. Возврат полученного решения по HTTP (hypertext transfer protocol) запросу GET клиента с ID задачей. Если решение в момент запроса еще не получено, то будет возвращен специальный статус ожидания результата.
Шаг 15. В случае необходимости клиент может обратиться с HTTP-запросом PUT с измененными данными для повторного расчета.
4. Применение предложенного подхода. Апробирование системы проводилось по данным с авиаперевозками по России между семью городами:
1) Екатеринбург,
2) Минеральные Воды,
3) Москва,
4) Омск,
5) Самара,
6) Сыктывкар,
7) Махачкала.
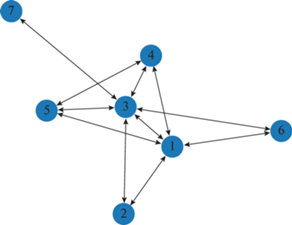
В качестве периода был выбран июль 2019 г., так как июль – достаточно насыщенный месяц для проведения репрезентативного анализа. На рис. 1 представлен граф существующих маршрутов между городами. Номера вершин графа i соответствуют порядковым номерам городов в списке.
Как видно из рис. 1, на текущий момент не все города из этого списка соединены прямыми рейсами. При этом известно, что в 80-е годы прошлого века существовали дополнительные прямые рейсы, которые в настоящее время отсутствуют. Информация из матрицы корреспонденций позволит оценить как необходимость возрождения данных рейсов, так и определить, какие типы воздушных судов целесообразней развивать. Полученная в результате решения оптимизационных задач корреспонденция между заданными городами показана в таблице 1.
Таблица 1.
Результаты решения
| i | j | $x_{{ij}}^{{\min }}$ | ${{\bar {x}}_{{ij}}}$ | $x_{{ij}}^{{\max }}$ |
|---|---|---|---|---|
| 1 | 2 | 1025 | 2479 | 3933 |
| 4 | 2 | 0 | 179 | 359 |
| 5 | 2 | 0 | 1052 | 2105 |
| 6 | 2 | 0 | 222 | 444 |
| 1 | 3 | 42 897 | 83 211 | 96 707 |
| 1 | 7 | 0 | 13 495 | 53 810 |
| 1 | 4 | 0 | 97 | 293 |
| 2 | 4 | 0 | 146 | 293 |
| 6 | 4 | 0 | 48 | 293 |
| 1 | 5 | 0 | 772 | 1693 |
| 2 | 5 | 0 | 846 | 1693 |
| 6 | 5 | 0 | 74 | 444 |
| 1 | 6 | 0 | 86 | 439 |
| 2 | 6 | 0 | 219 | 439 |
| 4 | 6 | 0 | 59 | 359 |
| 5 | 6 | 0 | 73 | 439 |
| 7 | 3 | 0 | 8531 | 51 188 |
| 7 | 1 | 0 | 12 724 | 51 188 |
| 7 | 2 | 0 | 8531 | 51 188 |
| 7 | 4 | 0 | 6808 | 40 848 |
| 7 | 5 | 0 | 8531 | 51 188 |
| 7 | 6 | 0 | 6061 | 12 123 |
| 2 | 1 | 1648 | 2860 | 4073 |
| 2 | 3 | 17 810 | 62 651 | 71 620 |
| 2 | 7 | 0 | 8968 | 53 810 |
| 3 | 1 | 42 571 | 81 034 | 93 759 |
| 3 | 7 | 0 | 8968 | 53 810 |
| 4 | 7 | 0 | 6857 | 41 144 |
| 5 | 7 | 0 | 8968 | 53 810 |
| 6 | 7 | 0 | 6552 | 13 104 |
| 3 | 2 | 25 462 | 68 118 | 76 650 |
| 3 | 4 | 0 | 34 040 | 40 848 |
| 3 | 5 | 10 776 | 53 432 | 61 964 |
| 3 | 6 | 0 | 6061 | 12 123 |
| 4 | 1 | 0 | 119 | 359 |
| 4 | 3 | 0 | 34 286 | 41 144 |
| 4 | 5 | 212 | 212 | 212 |
| 5 | 1 | 0 | 979 | 2105 |
| 5 | 3 | 8747 | 53 588 | 62 557 |
| 5 | 4 | 149 | 149 | 149 |
| 6 | 1 | 0 | 99 | 444 |
| 6 | 3 | 0 | 6552 | 13 104 |
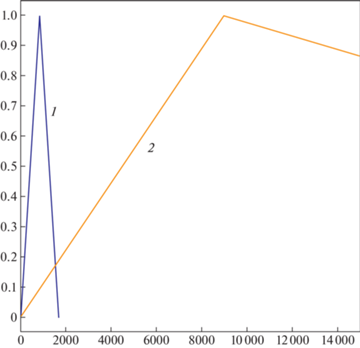
Рассмотрим в качестве примера анализа нечетких корреспонденций два новых маршрута из города 2 – (2, 7) и (2, 5). Из таблицы видно, что для маршрутов (2, 7) и (2, 5) наиболее возможный пассажиропоток составляет 8968 и 846 человек в месяц соответственно. Значит маршрут (2, 7), скорей всего, более приоритетен с точки зрения открытия. Но степень неопределенности достаточно велика и должна быть учтена при планировании управленческих решений на основе полученных результатов. В данном случае маршрут (2, 5) может содержать пассажиропоток от 0 до 1693 человек, а (2, 7) может содержать пассажиропоток от 0 до 53810 человек, и сохраняется небольшая возможность большего пассажиропотока для маршрута (2, 5). Уровень уверенности в этом составляет 0.17 и соответствует точке пресечения треугольных функций принадлежности, показанных на рис. 2.
Рис. 2.
Функции принадлежности для нечеткого значения пассажиропотока: 1 – города 2–5, 2 – города 2–7
Основное преимущество метода по сравнению с аналогами заключается в том, что он позволяет находить нечеткую матрицу корреспонденций даже при отсутствии экспертных оценок. Еще одним преимуществом является использование модели в виде линейных целевых функций и ограничений, которые достаточно легко вычислить. Изначально решается ряд самостоятельных задач математического программирования, поэтому часть трудоемкого вычислительного процесса легко организовать в параллельные потоки. Программная реализация для поиска по нечеткой матрице корреспонденций и нечеткого ранжирования размещена на портале веб-сервисов поддержки принятия решений WS-DSS. Она доступна для использования широким кругом разработчиков приложений транспортных и логистических систем.
Заключение. Полученная в настоящей работе нечеткая матрица корреспонденций позволяет решать следующие задачи:
1) составление оптимальных маршрутов,
2) составление рационального расписания,
3) оценка перспектив импортозамещения авиационной техники,
4) анализ возможностей по замене устаревшей авиационной техники,
5) поддержка принятия решений по модернизации существующей транспортной инфраструктуры.
Решив задачи поиска корреспонденций в разных временных периодах, можно строить прогнозы на основе нечетких регрессионных моделей, проводить нечеткое сглаживание колебаний корреспонденций для поиска рациональных моделей развития транспортно-логистических систем. Результат полезен для разработчиков моделей исследования транспортных операций. Полученные нечеткие оценки можно рассматривать как параметры моделей оптимального расписания, а также использовать при решении задачи распределения воздушных судов.
Метод подходит для случаев, когда мы не можем установить реальные пункты отправления и назначения конкретных пассажиров, но знаем количество пассажиров, перевезенных по конкретным дугам транспортного графа. Это обычная ситуация, когда задачи стратегического планирования приходится решать не на уровне отдельных авиакомпаний, а на уровне государства.
В условиях появления большого количества неопределенных факторов, влияющих на авиаперевозки, проектировщики транспортно-логистических систем могут решать задачи планирования маршрутов перевозок, выбора самолетов и проектирования новых аэропортов, используя эту модель как источник информации о возможном транспорте. Ученые в области исследования транспортных операций могут верифицировать экспертные суждения и правила, чтобы проверить их близость к возможным значениям элементов матрицы корреспонденций.
Предложенный алгоритм поиска нечеткой матрицы корреспонденций позволяет осуществлять планирование стратегического развития транспортной инфраструктуры. Используя методы поддержки принятия решений в нечеткой информационной среде, можно определить как предпочтения в развитии новых маршрутов авиаперевозок, так и степень уверенности в данном решении.
Апробация метода показала, что он может быть успешно применен для определения корреспонденций между заданным набором городов с учетом высокой степени неопределенности. В дальнейшем экспертные оценки могут использоваться в сочетании с этим методом для точного предсказания нечетких корреспонденций в графе. Предложенный алгоритм актуален как для авиационного, так и для автомобильного транспорта. Рассмотренный пример добавления новых транспортных маршрутов в виде новых дуг к существующему графу позволяет предложить рациональные варианты улучшения транспортной ситуации в случае отсутствия необходимого количества зарубежных магистральных самолетов и планировать перевозки на модифицированном нечетком графе с помощью отечественных воздушных судов ИЛ-114, SSJ-100, ТУ-214, Ил-96-400М, МС‑21.
Список литературы
Profillidis V.A., Botzoris G.N. Modeling of Transport Demand – Analyzing, Calculating and Forecasting Transport. Amsterdam, Netherlands: Elsevier Eds., 2018.
Ekowicaksono I., Bukhari F., Aman A. Estimating Origin-Destination Matrix of Bogor City Using Gravity Model // IOP Conf. Series: Earth and Environmental Science. V. 31. Workshop and International Seminar on Science of Complex Natural Systems. Bogor, Indonesia, 2016.
Wilson A.G. A Statistical Theory of Spatial Distribution Models // Transportation Research. 1967. V. 1. P. 253–270.
Park Y., O’Kelly M.E. Origin–Destination Synthesis for Aviation Network Data: Examining Hub Operations in the Domestic and International US Markets // J. Adv. Transp. 2016. V. 50. P. 2288–2305.
Dutov A.V., Nesterov V.A., Sudakov V.A., Sypalo K.I. Fuzzy Preference Domains and Their Use for Selecting an Electronic Flight Bag for Flight Crews // J. of Computer and Systems Sciences International. 2018. V. 57. № 2. P. 230–238.
Vigerske S., Gleixner A. SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework // Optimization Methods and Software. 2018. V. 33. № 3. P. 563–593.
Sudakov V., Nesterov V., Kurennykh A. Integration of Decision Support Systems “Kosmos” and WS-DSS with Computer Models // Tenth Intern. Conf. Management of Large-Scale System Development (MLSD). M., 2017. P. 1–4.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления