Известия РАН. Теория и системы управления, 2022, № 6, стр. 85-94

Введение. Качели – это механический объект, которым управляет человек. Проблемы управления подобными объектами можно отнести как к теории управления колебаниями, так и к биомеханике. Таким образом, задача синтеза управления качелями представляет интерес с различных точек зрения.

При рассмотрении задачи о синтезе управления раскачиванием качелей следует различать случаи, когда человек раскачивается, стоя на них или сидя. В каждом из этих случаев приходится исследовать свою модель. В статье анализируется задача раскачивания качелей стоящим на них человеком. На самом деле, человек, стоящий на качелях, в определенные моменты времени приседает, а в другие моменты встает и выпрямляется. При этом его центр масс то опускается, то поднимается. Поэтому во многих работах, например [1–8], при рассмотрении задачи о раскачивании качелей человеком, стоящим на них, изучается модель качелей в виде маятника переменной длины. В этом случае в большинстве публикаций при синтезе управления используется подход, при котором длина качелей выбирается в виде периодической функции времени и задача синтеза управления рассматривается как задача параметрического возбуждения колебаний. Менее распространен подход, при котором управление строится в виде обратной связи, хотя, как представляется авторам статьи, именно этот подход является естественным для задачи синтеза управления качелями. В виде обратной связи строится управление качелями в [8, 9].

В работе продолжаются начатые в [10–12] исследования, посвященные задаче оптимального раскачивания качелей стоящим на них человеком. Задача о раскачивании качелей человеком, сидящим на них, обсуждается в [13, 14]. В настоящей статье управление строится в виде обратной связи, подобно тому, как это делается в [14] для человека, сидящего на качелях.

Вначале здесь рассматривается нелинейная математическая модель качелей с одной степенью свободы. В этой модели управляющим параметром считается расстояние материальной точки, расположенной в центре масс человека, от точки подвеса качелей. Раскачивание качелей со стоящим на них человеком происходит именно путем перемещения его центра масс вдоль качелей при приседании и вставании. Для этой модели построено в виде обратной связи оптимальное управление, при котором по окончании каждого полуколебания угол отклонения качелей от вертикали достигает максимума, а свободный конец качелей в этот момент поднимается на максимально возможную высоту. При таком управлении амплитуда колебаний качелей возрастает максимально быстро. Оптимальное перемещение материальной точки происходит скачкообразно и описывается кусочно-постоянной функцией фазовых переменных.

После модели качелей с одной степенью свободы рассматривается более реалистичная модель качелей – с двумя степенями свободы. В этой модели управляющим параметром является сила, которая прикладывается к центру масс человека. Эта сила призвана отслеживать при помощи сервосистемы оптимальный закон перемещения центра масс, построенный для модели с одной степенью свободы.

В модели качелей с двумя степенями свободы есть только одно управляющее воздействие – сила, приложенная к материальной точке. Шарнир в точке подвеса качелей является пассивным, в нем прикладывается только момент сил вязкого трения. Поэтому в изучаемой здесь системе с двумя степенями свободы количество управляющих воздействий на единицу меньше количества степеней свободы, т.е. имеет место дефицит управляющих воздействий. Для подобных систем с произвольным количеством степеней свободы в [15–17] предложен общий метод поиска оптимального управления амплитудой колебаний по пассивной степени свободы.

1. Математическая модель качелей с человеком на них. На рис. 1 показана схема качелей, представляющих собой маятник OB, в котором O – неподвижная точка подвеса, B – свободный конец. Через $\varphi $ обозначен угол отклонения маятника от вертикали, С – центр масс маятника, m – его масса, g – ускорение силы тяжести, М – материальная точка, масса которой равна массе человека, эта точка расположена в центре масс человека. Буквой M будем обозначать одновременно и материальную точку, и ее массу, $\rho = OM$ – расстояние от точки подвеса качелей O до точки M, постоянные величины ${{\rho }_{{\min }}} > 0$ и ${{\rho }_{{\max }}} > 0$ – соответственно минимально и максимально возможные расстояния центра масс M от точки подвеса O, т.е.:

Будем рассматривать качели как механическую систему с одной степенью свободы, в которой обобщенной координатой является угол $\varphi $. Этот угол равен нулю, когда качели висят вертикально вниз, и положителен, когда они отклоняются от этого положения, поворачиваясь против хода часовой стрелки. Расстояние $\rho = OM$ считаем управляющим параметром, который ограничен условиями (1.1). Кусочно-непрерывную функцию $\rho \left( {\varphi {\text{,}}\dot {\varphi }} \right),$ удовлетворяющую неравенствам (1.1), будем называть допустимым управлением. Множество допустимых управлений обозначим через Ω.

Уравнение движения качелей запишем в виде

Здесь $I$ – момент инерции маятника относительно точки подвеса O, $b = OC = {\text{const}}$, $\chi > 0$ – коэффициент вязкого трения в шарнире О. Обозначим момент количества движения качелей относительно точки O буквой K:

Уравнение (1.2) описывает изменение кинетического момента K, происходящее под влиянием моментов сил тяжести и вязкого трения относительно точки O. Из соотношения (1.3) следует, что $K = 0$ тогда и только тогда, когда $\dot {\varphi } = 0$, и, кроме того, ${\text{sign}}K = {\text{sign}}\dot {\varphi }$, поскольку $I + M{{\rho }^{2}} > 0$ при любом значении ${{\rho }}$.

Уравнения (1.2), (1.3) можно представить в виде системы двух уравнений первого порядка с неизвестными переменными ${{\varphi }}$ и K:

При условии $K \ne 0$, наряду с системой уравнений (1.4), можно рассматривать уравнение

которое описывает движение качелей на фазовой плоскости $(\varphi {\text{,}}K)$ (или на фазовом цилиндре).

2. Оптимальное управление раскачиванием качелей. Зададим начальное, в момент $t = 0$, состояние системы (1.4) в виде

При начальных условиях (2.1) и допустимом управлении $\rho = {\text{const}}$ качели, как обычный маятник (с вязким трением в точке подвеса O), вращаются и в некоторый момент времени $\theta > 0$ оказываются в состоянии

При этом момент количества движения, а значит, и угловая скорость не обращаются в нуль: $K\left( t \right) \ne 0$, $\dot {\varphi }\left( t \right) \ne 0$ ни при каком значении $0 < t < \theta $.

Описанное выше движение качелей представляет собой пример полуколебания, во время которого они поворачиваются из одного состояния, когда кинетический момент $K\left( 0 \right) = 0$ $\left( {\dot {\varphi }\left( 0 \right) = 0} \right)$, в другое, когда кинетический момент, а значит, и угловая скорость в следующий раз снова обращаются в нуль. В действительности, каждое полуколебание качелей, его размах, длительность зависят от управления $\rho \left( t \right)$.

Целью управления качелями является их раскачивание. Это означает, что требуется построить допустимое управление как функцию времени $\rho = \rho \left( t \right)$ или как функцию фазовых координат $\rho = \rho \left( {\varphi ,\dot {\varphi }} \right)$, при котором амплитуда колебаний качелей возрастает.

Допустим, что начальные условия (2.1), параметры системы (1.4), в том числе коэффициент вязкого трения χ, ограничения ${{\rho }_{{\min }}}$, ${{\rho }_{{\max }}}$, наложенные на управление $\rho $ (см. неравенства (1.1)), таковы, что ни при каком управлении $\rho \left( t \right) \in \Omega $ соответствующая фазовая траектория не попадает в область

Другими словами, качели не могут пройти через верхнее положение $\varphi = \pi $ и тем самым совершить ротацию (переворот). В этом случае при всяком управлении $\rho \left( t \right) \in \Omega $ траектория движения качелей, начинающаяся из состояния (2.1), попадает в область

и в течение какого-то времени остается в области (2.4). При этом свободный конец B качелей в течение некоторого времени поднимается вверх, т.е. $\dot {\varphi }\left( t \right) > 0$. В какой-то момент времени $t = \theta $ качели “на мгновение замирают”, т.е. при $t = \theta $ угловая скорость $\dot {\varphi }\left( t \right)$ обращается в нуль – $\dot {\varphi }\left( \theta \right) = 0$, поскольку траектория движения, по предположению, не может попасть в область (2.3). Затем при $t \geqslant \theta $ качели начинают и в течение некоторого времени продолжают вращаться в другую сторону – по ходу часовой стрелки.

Таким образом, при $t = \theta $ угол $\varphi $ достигает локального максимума. Высота подъема конца B качелей в этот момент $t = \theta $ также достигает своего локального максимума. Движение качелей в течение времени $0 \leqslant t \leqslant \theta $ является полуколебанием.

Поставим теперь задачу синтеза оптимального управления $\rho = \rho \left( {\varphi ,\dot {\varphi }} \right)$ раскачиванием качелей следующим образом. Пусть задано начальное при $t = 0$ состояние (2.1) системы. Требуется найти управление $\rho \left( {\varphi ,\dot {\varphi }} \right) \in \Omega $, при котором достигается максимум угла $\varphi \left( t \right)$, в момент времени $t = \theta > 0$, когда кинетический момент $K\left( t \right)$, а следовательно, и скорость $\dot {\varphi }\left( t \right)$ обращаются в нуль. Причем момент $t = \theta $ является первым после момента $t = 0$, когда эти величины обращаются в нуль. Сформулированную задачу запишем символически таким образом:

Другими словами, задача (2.5) состоит в отыскании оптимального управления, при котором по окончании полуколебания, начинающегося из состояния (2.1), свободный конец B качелей поднимается на максимально возможную высоту.

Рассматривая уравнение (1.5), нетрудно убедиться в том, что управление, решающее задачу (2.5), должно максимизировать производную при каждом текущем значении угла [11, 12, 14]. Пользуясь формулой (1.5) для производной, находим оптимальное управление

При выводе формулы (2.6) используется следующее равенство, вытекающее из соотношения (1.3):

Картина синтеза управления (2.6) показана на рис. 2.

Заметим, что задача максимизации позиционной координаты в момент, когда ее производная обращается в нуль, рассматривается для систем второго порядка в [18]. В монографии [1] исследуется задача раскачивания качелей стоящим на них человеком. При этом считается известным из наблюдений, что человек встает на качелях, когда их свободный конец B проходит через низшую точку, и приседает, когда этот конец B оказывается на максимально возможной высоте. Однако в [1] не решается описанная выше или какая-нибудь другая задача оптимальности и не объясняется, почему человек ведет себя на качелях указанным образом.

Выражение (2.6) для оптимального управления $\rho \left( {\varphi ,\dot {\varphi }} \right)$ означает, что при условии

центр масс человека M должен находиться на максимально возможном расстоянии ${{\rho }_{{\max }}}$ от точки подвеса O, т.е. человек должен присесть на качелях. В этом случае момент силы тяжести, приложенный к качелям, будет максимальным и они, начав свое движение из состояния (2.1), достигнут в некоторый момент времени своего нижнего положения

Когда траектория системы (1.4) пересекает прямую (2.8), неравенство (2.7) меняется на противоположное:

В соответствии с формулой (2.6) расстояние $\rho $ при условии (2.9) должно стать минимальным – $\rho = {{\rho }_{{\min }}}$, т.е. человек должен встать на качелях в полный рост. При мгновенном уменьшении расстояния $\rho $ кинетический момент K, как следует из уравнений (1.2), (1.3), остается без изменения. Что касается момента инерции $I + M{{\rho }^{2}}$, то он мгновенно уменьшается с максимально возможного значения $I + M\rho _{{\max }}^{2}$ до минимально возможного $I + M\rho _{{\min }}^{2}$. Из соотношения (1.3) вытекает, что в это мгновение угловая скорость $\dot {\varphi }$ скачкообразно увеличивается и приобретает значение

Заметим также, что после этого мгновения во время подъема качелей уменьшается (по абсолютной величине) до минимально возможного значения и направленный по ходу часовой стрелки момент силы тяжести – момент, который препятствует дальнейшему повороту качелей против хода часовой стрелки и тем самым достижению их свободным концом B максимально возможной высоты по окончании этого полуколебания.

Нетрудно проверить, что при вращении качелей в противоположном направлении, т.е. по ходу часовой стрелки, расстояние $\rho $ будет меняться в той же последовательности, как и при вращении против хода часовой стрелки. В соответствии с законом управления (2.6) в тот момент времени, когда угловая скорость качелей $\dot {\varphi }$ обращается в нуль, центр тяжести человека M должен мгновенно переместиться от точки подвеса качелей O на максимальное расстояние, т.е. человек должен присесть, увеличив (по абсолютной величине) приложенный к качелям момент силы тяжести до максимального. Иначе говоря, в начале движения по ходу часовой стрелки будет иметь место равенство $\rho = {{\rho }_{{\max }}}$, затем после прохождения качелями низшего положения – равенство $\rho = {{\rho }_{{\min }}}$. При таком управлении по окончании второго полуколебания конец B качелей также поднимется на максимально возможную в этом полуколебании высоту.

Легко убедиться в том, что при управлении (2.6) свободный конец B качелей достигает максимально возможной высоты не только по окончании каждого полуколебания, но также и по окончании каждого полного колебания. Более того, при этом управлении максимально возможная высота достигается после каждых n колебаний, где n – произвольное целое число. Тем самым если начальные условия таковы, что при управлении (2.6) амплитуда колебаний возрастает, то можно утверждать, что при этом происходит максимально быстрый рост амплитуды. Если же амплитуда колебаний убывает, то это происходит наиболее медленно.

Управление, при котором свободный конец B качелей по окончании каждого полуколебания оказывается на минимально возможной высоте, получается путем замены знаков неравенств в формуле (2.6) на противоположные. При таком управлении происходит максимально быстрое гашение колебаний качелей.

3. Численные исследования системы с одной степенью свободы. Предположим, что маятник представляет собой однородный стержень и рассмотрим следующие значения параметров системы (1.4):

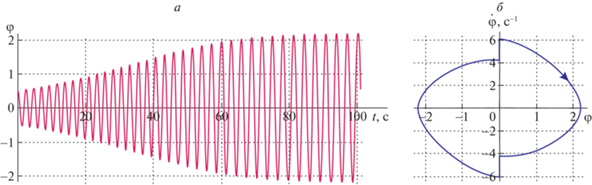
На рис. 3,a показано решение $\varphi \left( t \right)$ системы (1.4) при управлении (2.6), значениях параметров (3.1), коэффициенте $\chi = 30\;{\text{Н}} \cdot {\text{м}} \cdot {\text{с}}$ вязкого трения в точке подвеса О и начальных условиях $\varphi \left( 0 \right) = 0.5$, $\dot {\varphi }(0) = 0$. Из рассмотрения рис. 3,а следует, что амплитуда колебаний качелей монотонно возрастает и при $t \to \infty $ стремится к постоянной величине, т.е. движение качелей выходит на стационарный режим. Соответствующая фазовая траектория стремится к предельному циклу, изображенному на рис. 3,б.

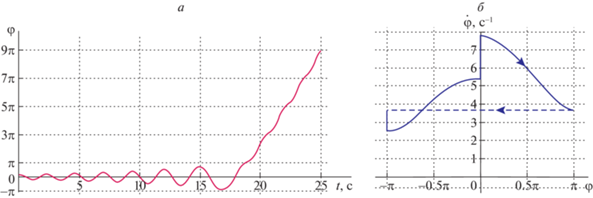
На рис. 4,а показано решение $\varphi \left( t \right)$ при тех же значениях параметров и начальных условиях, что и на рис. 3,а, за исключением величины коэффициента вязкого трения $\chi $, который в отличие от предыдущего случая принимает значение $\chi = 20\;{\text{Н}} \cdot {\text{м}} \cdot {\text{с}}$. Соответствующая фазовая траектория стремится к изображенному на рис. 4,б предельному циклу, охватывающему цилиндр. Пунктир на развертке фазового цилиндра соответствует формальному уменьшению угла $\varphi $ на $2\pi $ при переходе маятника через верхнее положение. В этом примере вращение качелей происходит против хода часовой стрелки.

Таким образом, численные исследования показывают, что если коэффициент вязкого трения $\chi $ достаточно велик, то качели при построенном управлении (2.6) колеблются. При $t \to \infty $ траектория, отвечающая этим колебаниям, стремится к орбитально асимптотически устойчивому циклу. Если же коэффициент вязкого трения не слишком велик, то качели при управлении (2.6) выходят на ротационное движение. При $t \to \infty $ это движение стремится к орбитально асимптотически устойчивому вращению с постоянным периодом.

Заметим, что в [1] не рассматривается режим ротации качелей вокруг их точки подвеса.

4. Математическая модель качелей с двумя степенями свободы. При составлении математической модели (1.4) предполагается, что расстояние ρ от точки подвеса качелей O до материальной точки M (центра масс человека) является управляющим параметром. Допустимым считается, что управляющая функция может претерпевать разрывы. Найденное оптимальное управление (2.6) действительно изменяется скачкообразно. Однако человек, стоящий на качелях, приседая и вставая, развивает ограниченные по величине усилия, при которых перемещение его центра масс (материальной точки M) происходит непрерывно. Поэтому в настоящем параграфе, в отличие от предыдущих, поведение качелей моделируется системой с двумя степенями свободы. При этом одной из обобщенных координат остается, как и в уравнениях (1.4), угол φ, а другой координатой становится расстояние ${{\rho }}{\text{.}}$ Используя уравнение (1.2), можно получить следующую математическую модель системы с двумя степенями свободы:

Будем строить управляющие силы ${{F}_{с}},$ ${{F}_{{{\rho }}}}$ и $\Delta {{F}_{{{\rho }}}}$ так, чтобы функция ${{\rho }}\left( t \right)$, полученная при решении уравнений (4.1), (4.2), была, по возможности, близкой к кусочно-непрерывной функции времени, полученной при помощи управления (2.6).

Пусть сила ${{F}_{с}}$ компенсирует центробежную силу $M{{\rho }}{{{{\dot {\varphi }}}}^{2}}$ и проекцию $Mg\cos {{\varphi }}$ силы тяжести, приложенные к центру масс человека:

Управляющую силу ${{F}_{\rho }}$ выберем в виде линейной обратной связи по разности ${{\rho }} - {{{{\rho }}}_{{{\text{prog}}}}}$ и ее производной ${{\dot {\rho }}}$ с постоянными коэффициентами ${{c}_{1}},{{c}_{2}} = {\text{const}}$ и ограничением ${{F}_{{{{\rho 0}}}}} = {\text{const}}$:

Программное значение ${{{{\rho }}}_{{{\text{prog}}}}}$ определим в соответствии с выражением (2.6):

Обратная связь, описываемая выражением (4.4), призвана отслеживать изменение во времени программной величины ${{{{\rho }}}_{{{\text{prog}}}}}$, вычисляемой по формуле (4.5).

Силу $\Delta {{F}_{{{\rho }}}}$ выберем в виде

для того чтобы вместе с силой ${{F}_{{{\rho }}}}$, по возможности, минимизировать время, в течение которого происходит нарушение неравенств (1.1). С этой целью коэффициент ${{k}_{S}}$ выберем “большим”. При этом выражения ${{k}_{S}}\left( {{{\rho }_{{\max }}} - \rho } \right)$ и ${{k}_{S}}\left( {{{\rho }_{{\min }}} - \rho } \right)$ описывают силы, развиваемые как бы односторонними “жесткими” пружинами. Когда неравенства (1.1) нарушаются, эти силы стремятся вернуть величину $\rho $ в диапазон (1.1). Перемещения центра масс человека вдоль качелей происходят благодаря усилиям, развиваемым в его коленных и тазобедренных суставах. В силу анатомических свойств человека углы в его суставах могут изменяться лишь в ограниченных пределах. Эти ограничения реализуются, в частности, связками, сухожилиями, которые могут развивать большие усилия. Равенство (4.6) можно трактовать как модель сил, развиваемых в суставах человека. Модель такого вида рассматривается в работах [14, 19].

Таким образом, математическая модель системы с двумя степенями свободы состоит из уравнений (4.1)–(4.6).

Предположим, что имеют место неравенства (1.1), тогда в соответствии с равенством (4.6) сила $\Delta {{F}_{\rho }} = 0$. Подставив в уравнение (4.2) выражение (4.3), а также среднюю строчку из формулы (4.4), получим дифференциальное уравнение

В соответствии с выражением (4.5) величина ${{{{\rho }}}_{{{\text{prog}}}}}$ принимает постоянное значение ${{{{\rho }}}_{{\max }}}$ или ${{{{\rho }}}_{{\min }}}$. Если ${{{{\rho }}}_{{{\text{prog}}}}} = {\text{const}}$, то линейное дифференциальное уравнение (4.7) имеет стационарное решение:

Для того, чтобы решение (4.8) было асимптотически устойчивым, необходимо и достаточно, чтобы коэффициенты c₁ и c₂ характеристического уравнения

были положительными. При изменении величины ${{{{\rho }}}_{{{\text{prog}}}}}$ со значения ${{{{\rho }}}_{{\max }}}$ на значение ${{{{\rho }}}_{{\min }}}$ и наоборот в решениях уравнения (4.7) возникают переходные процессы. Желательно, чтобы эти переходные процессы были апериодическими и, по возможности, короткими. Процессы будут апериодическими, если корни характеристического уравнения (4.9) действительные, т.е. при условии

5. Численные исследования системы с двумя степенями свободы. Пусть в системе (4.1), (4.2) с параметрами (3.1) действует управление вида (4.3)–(4.6) с коэффициентами

Отметим, что при значениях параметров (3.1), (5.1) неравенство (4.10) выполняется.

На рис. 5,а иллюстрируется процесс раскачивания качелей с начальными условиями $\varphi (0)$ = = 0.5, $\dot {\varphi }(0) = 0$ (как и в разд. 3), $\rho \left( 0 \right) = 1.2$ м, $\dot {\rho }(0) = 0$ при значении $\chi = 8\;{\text{Н}} \cdot {\text{м}} \cdot {\text{с}}$ коэффициента вязкого трения. Амплитуда колебаний монотонно возрастает и стремится к постоянной величине, т.е. система выходит на стационарный режим. В фазовом пространстве этому режиму соответствует орбитально асимптотически устойчивый предельный цикл, проекция которого на плоскость $\left( {\varphi ,\dot {\varphi }} \right)$ представлена на рис. 5,б.

Отметим, что амплитуда установившихся колебаний близка к амплитуде колебаний, показанных на рис. 3,а. Такая близость амплитуд достигается путем подбора значения коэффициента вязкости $\chi $. Причем этот коэффициент оказывается в несколько раз меньше, чем в случае, рассмотренном в разд. 3. Дело в том, что в системе (4.1), (4.2) с управлением (4.3)–(4.6) учитывается динамика перемещения центра масс M, наложены дополнительные ограничения на управление и в результате описываемое формулой (4.5) программное положение ${{{{\rho }}}_{{{\text{prog}}}}}$ точки M не точно отслеживается сервосистемой.

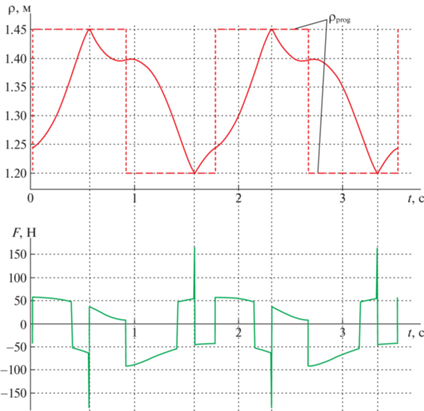
На рис. 6 для одного полного колебания в установившемся режиме иллюстрируется изменение положения центра масс M человека и для сравнения пунктиром показана функция ${{{{\rho }}}_{{{\text{prog}}}}}$, а также построено суммарное управляющее воздействие $F = {{F}_{с}} + {{F}_{{{\rho }}}} + \Delta {{F}_{{{\rho }}}}$.

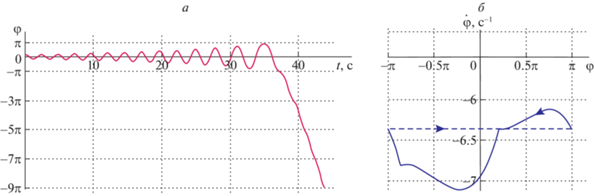
На рис. 7,а иллюстрируется процесс раскачивания с начальными условиями $\varphi \left( 0 \right) = 0.5$, $\dot {\varphi }(0) = 0$ (как и в предыдущих примерах) при значении $\chi = 4\;{\text{Н}} \cdot {\text{м}} \cdot {\text{с}}$. В этом случае качели выходят на установившийся ротационный режим, которому соответствует орбитально асимптотически устойчивый предельный цикл. Этот цикл спроектирован на полосу $ - \pi \leqslant \varphi < \pi $ фазовой плоскости $\left( {\varphi ,\dot {\varphi }} \right)$ и показан на рис. 7,б. В этом примере вращение качелей происходит по ходу часовой стрелки.

Итак, построенное управление (4.3)–(4.6) решает задачу раскачивания качелей. При относительно небольшом коэффициенте трения (а также при нулевом) качели выходят на установившийся ротационный режим. При относительно большом трении качели выходят на режим установившихся колебаний. Если же трение слишком велико, то качели совершают затухающие колебания, несмотря на приложенное управляющее воздействие. Интересно отметить, что в некотором диапазоне параметров существуют и колебательный, и ротационный установившиеся режимы: система выходит на один из них в зависимости от начальных условий.

Заключение. Исследуется модель качелей, которые раскачивает стоящий на них человек. Учитываются силы вязкого трения, действующие в точке подвеса качелей. Механическая модель системы имеет одну степень свободы. Математическая модель системы содержит два нелинейных дифференциальных уравнения первого порядка. В качестве управляющего воздействия рассматривается расстояние между точкой подвеса качелей и центром масс человека. Это расстояние может меняться в некоторых пределах, которые определяются положениями центра масс, когда человек стоит на качелях в полный рост и когда он приседает на них. Построен оптимальный закон управления, при котором свободный конец качелей поднимается на максимально возможную высоту по окончании каждого полуколебания и каждого полного колебания. Численные исследования показывают, что в случае достаточно большого трения в точке подвеса движение качелей при построенном управлении стремится к орбитально асимптотически устойчивому режиму колебаний с постоянной амплитудой. Амплитуда колебаний, как следует из теоретических результатов, возрастает с максимально возможной скоростью. В случае достаточно малого трения движение качелей стремится к орбитально асимптотически устойчивому режиму ротаций с постоянным периодом. Построен также закон управления, обеспечивающий максимально быстрое гашение колебаний качелей.

Наряду с моделью, которая имеет одну степень свободы, исследуется и более реалистичная модель – с двумя степенями свободы. В ней, кроме угла отклонения качелей от вертикали, в качестве обобщенной координаты выступает также расстояние между точкой подвеса и центром масс человека (в модели с одной степенью свободы это расстояние – управляющий параметр). Управлением является сила, приложенная к центру масс человека и направленная вдоль качелей. В этой модели при помощи сервосистемы отслеживается оптимальное изменение расстояния между точкой подвеса и центром масс человека, найденное теоретически для модели с одной степенью свободы. При численных исследованиях так же, как и в модели с одной степенью свободы, построены режимы колебаний и ротаций.