Известия РАН. Теория и системы управления, 2023, № 1, стр. 164-176

Введение. Существует класс устройств, способных передвигаться в пространстве за счет неравномерного периодического движения внутренних элементов и сил взаимодействия различной природы между корпусом и внешней средой. Вопрос о возможности создания таких аппаратов возник в 1964 г. в связи с попыткой дискредитации ньютоновой механики, но систематические научные его исследования начались только в последнее время, например с работы [1], и продолжаются до сих пор.

С физической точки зрения способ движения таких устройств близок к виброперемещениям. Теория вибрационной механики была введена в [2]. Будем называть такие устройства вибрационными роботами. Изолированность их двигающихся частей от внешних воздействий делает актуальным применение таких роботов в условиях агрессивных сред, например, в глубине водоемов, в экстремальных климатических условиях Арктики, пустынь или на других планетах, а также в медицине [3, 4].

В [5] рассмотрена двумерная задача о наиболее быстром вращении твердого тела при перемещении внутренней массы. Способ управления ориентацией твердого тела при помощи вспомогательных масс, движущихся относительно тела, предложен в [6]. В [7] аналитически и экспериментально исследуется движение по шероховатой горизонтальной плоскости мобильного робота капсульного типа, управляемого периодической упругой силой. Результаты модельных и экспериментальных исследований согласуются между собой.

Среди подобных механических систем особое место занимают мобильные роботы, состоящие из нескольких тел [8, 9], и роботы, перемещающиеся в жидкой среде [10–13]. В частности, в [10] изучается движение в идеальной жидкости произвольного двумерного тела с подвижной внутренней массой и можно добиться перемещения тела в заданную точку. В [14] показано, что мобильные роботы могут использовать высокочастотные параметрические колебания внутренней массы для создания быстрого и эффективного движения по шероховатой поверхности.

Описаны схемы, реализующие прямолинейное и плоское движение [15–18] в сопротивляющейся среде с вязким и сухим трением. Скольжение по шероховатой плоскости параллелепипеда с внутренними маховиком и подвижной точкой приведено в [19]. Показано наличие эффекта поворота тела вокруг вертикальной оси вследствие неравномерности нормального напряжения в области контакта. В [20] рассмотрено плоское движение твердого тела при перемещении двух внутренних масс. Возможен периодический режим движения, состоящий из нескольких фаз: покой, скольжение, отрыв, свободное движение над горизонтальной плоскостью, безударный контакт с плоскостью и скольжение по ней до остановки.

В [21] была представлена плоская модель вибрационного робота с несбалансированным внутренним ротором, опирающегося плоским дном на шероховатую плоскость. Предложен метод построения алгоритма управления вращением ротора, реализующий возможность корпуса оторваться от поверхности на практически нулевую высоту и в таком режиме полета совершить поступательное движение. Подобный метод был применен в [22–24] в задаче о плоском движении инерционного робота с одним дебалансом и одним маховиком. Маховик использовался для сохранения горизонтальной ориентации корпуса в режиме полета.

Непрямолинейное движение вибрационного робота по шероховатой плоскости рассмотрено в ряде работ [25–33]. В [25, 27, 28] для поворота использован однородный вращающийся ротор, установленный внутри полости твердого тела, а для линейного смещения – материальная точка с одной степенью свободы. В [26, 29, 32, 33] рассчитаны схемы робота с двумя осциллирующими вдоль заданных направлений материальными точками. В [9, 10] показана модель вибрационной системы с двумя роторами, вращающимися с переменной угловой скоростью. Движение робота вызвано силами инерции и трением между плоскостью и опорными частями корпуса.

В статье рассматривается режим полета пространственной конструкции робота с одним дебалансом и двумя маховиками. Этот режим реализуется посредством ускоренного движения дебаланса. Ось вращения дебаланса смещена от горизонтали на некоторый угол, что позволяет корпусу в режиме “полета” отклоняться от прямолинейного движения и поворачивать на определенный угол вокруг вертикали. Предполагается, что маховики обеспечивают стабилизацию горизонтальной ориентации корпуса в таком режиме. Их вращение в данной работе детально не приводится.

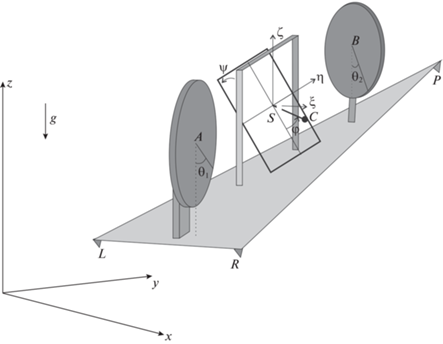
1. Описание системы и постановка задачи. Рассматривается движение по шероховатой горизонтальной плоскости вибрационного робота (рис. 1), корпус массы m₁ которого содержит невесомую рамку с дебалансом – материальной точкой C массой m₂ и два маховика, представляющих собой однородные диски массой m₃, m₄ соответственно. Дно корпуса – плоская платформа с тремя точками опоры: P, L, R. Дебаланс движется по окружности в плоскости рамки вокруг точки S, являющейся центром масс корпуса (SC = l). Рамка наклонена на установочный угол $\psi \in ( - \pi {\text{/}}2,\pi {\text{/}}2)$ по отношению к плоскости, перпендикулярной платформе. Маховики вращаются вокруг своих осей динамической симметрии, проходящих через их центры A и B. Центры маховиков расположены на одинаковой высоте в плоскости, перпендикулярной дну корпуса и проходящей через его продольную ось. Ось вращения ротора A параллельна продольной оси дна, а ось ротора B перпендикулярна продольной оси дна.

На систему действуют следующие внешние силы: сила тяжести на каждый элемент системы: ${{m}_{1}}\vec {g},\;{{m}_{2}}\vec {g},\;{{m}_{3}}\vec {g},\;{{m}_{4}}\vec {g}$ ($\vec {g}$ – ускорение силы тяжести), а также в случае контакта с опорой силы реакций ${{\vec {F}}_{P}}$, ${{\vec {F}}_{L}}$ и ${{\vec {F}}_{R}}$ в точках P, L, R соответственно. Силы реакции опоры имеют вертикальные ${{\vec {N}}_{P}}$, ${{\vec {N}}_{L}}$ и ${{\vec {N}}_{R}}$ и горизонтальные ${{\overrightarrow R }_{P}}$, ${{\overrightarrow R }_{L}}$ и ${{\overrightarrow R }_{R}}$ составляющие. При скольжении тела по опоре они связаны между собой по закону Кулона: $\left| {{{{\overrightarrow R }}_{P}}} \right| = \mu \left| {{{{\overrightarrow N }}_{P}}} \right|$, $\left| {{{{\overrightarrow R }}_{L}}} \right| = \mu \left| {{{{\overrightarrow N }}_{L}}} \right|$, $\left| {{{{\overrightarrow R }}_{R}}} \right| = \mu \left| {{{{\overrightarrow N }}_{R}}} \right|$, где µ – коэффициент трения между телом и опорной плоскостью. Аэродинамическими силами пренебрегаем. В дальнейшем можно учесть влияние воздействия на объект среды, в которой происходит движение, (воздуха/жидкости). Такое усложнение модели можно реализовать, опираясь на квазистатический подход к описанию взаимодействия твердого тела со средой, а также можно принимать во внимание эффекты, связанные с так называемыми присоединенными массами (см. [34]), или, используя феноменологические модели, например, вводить присоединенный осциллятор [35]. Учет воздействия среды не внесет принципиальных изменений в подход, применяемый далее для построения алгоритма управления.

Опишем внутренние силы, воздействующие на элементы системы:

момент от двигателя ${{\overrightarrow M }_{{12}}}$ влияет со стороны корпуса 1 на дебаланс 2, а со стороны дебаланса 2 на корпус 1 – момент ${{\overrightarrow M }_{{21}}}$;

момент от двигателя ${{\overrightarrow M }_{{13}}}$ действует со стороны корпуса 1 на маховик 3, а со стороны маховика 3 на корпус 1 – момент ${{\overrightarrow M }_{{31}}}$;

момент от двигателя ${{\overrightarrow M }_{{14}}}$ поступает со стороны корпуса 1 на маховик 4, а со стороны маховика 4 на корпус 1 действует момент ${{\overrightarrow M }_{{41}}}$;

сила реакции от корпуса 1 на дебаланс 2 ${{\overrightarrow F }_{{12}}} = - {{\overrightarrow F }_{{21}}}$, здесь ${{\overrightarrow F }_{{ij}}}$ – сила, с которой i-тое тело действует на j-тое; сила реакции от корпуса 1 на маховик 3 ${{\overrightarrow F }_{{13}}} = - {{\overrightarrow F }_{{31}}}$;

сила реакции от корпуса 1 на маховик 4 ${{\overrightarrow F }_{{14}}} = - {{\overrightarrow F }_{{41}}}$.

Введем неподвижную систему координат Oxyz: ось z направлена вертикально вверх, а плоскость xy параллельна опорной поверхности.

Пусть Sξηζ – подвижная система координат, оси которой направлены по главным осям инерции корпуса: Sζ перпендикулярна плоскости платформы, Sη лежит в плоскости, перпендикулярной плоскости платформы, и направлена ортогонально Sζ, Sξ дополняет систему до правой. Положение системы описывается следующими обобщенными координатами: x, y, z – координаты точки S, α, β, γ – углы тангажа, крена и рыскания для корпуса соответственно, θ_A, θ_B – углы поворотов маховиков относительно корпуса (циклические координаты), φ – угол поворота дебаланса относительно корпуса, отсчитываемый от положения, максимально приближенного к платформе.

Ориентацию системы Sξηζ зададим углами Крылова:

Угловая скорость подвижной системы координат

Считаем, что в любой момент времени мы можем задавать необходимые угловые ускорения маховиков и дебаланса. Контролируя вращение дебаланса, можно изменять нормальные реакции в точках опоры, в том числе добиваться обнуления этих реакций. Задача маховиков состоит в том, чтобы поддерживать платформу горизонтальной, обеспечивая нулевой крен и тангаж. В отличие от [6], где для задания ориентации тела используются подвижные материальные точки, и от [36], где ориентация объектов стабилизируется магнитными моментами, горизонтальную стабилизацию платформы осуществляем маховиками. Для реализации этого в системе есть два управляющих ускорения маховиков, поэтому такая задача разрешима. В рамках настоящей работы будем считать, что движение маховиков организовано должным образом, и рассматривать только плоскопараллельное движение корпуса, при котором $\alpha (t) \equiv 0,$ $\beta (t) \equiv 0,$ $\vec {\omega } = \dot {\gamma }{{\vec {e}}_{z}}$.

2. Математическая модель. Для каждого элемента механической системы определим уравнения, описывающие их движение.

2.1. Корпус. Запишем для корпуса теорему о движении центра масс и теорему об изменении кинетического момента относительно центра масс:

Здесь ${{\vec {v}}_{S}}$ – скорость центра масс корпуса, ${{\mathbb{J}}_{S}}$ – тензор инерции корпуса, имеющий в связанных осях $S\xi \eta \zeta $ диагональный вид ${{\mathbb{J}}_{S}} = {\text{diag}}({{J}_{{S\xi }}},{{J}_{{S\eta }}},{{J}_{{S\zeta }}})$.

2.2. Дебаланс. Получим систему уравнений, описывающую движение дебаланса:

Ускорение точки C запишем в следующей форме:

Здесь ${{\vec {\omega }}_{C}} = \vec {\omega } + \dot {\varphi }(\cos \psi {{\vec {e}}_{\xi }} + \sin \psi {{\vec {e}}_{\zeta }})$ – угловая скорость дебаланса, ${{\vec {K}}_{S}} = [\overrightarrow {SC} ,{{\vec {v}}_{C}}]$ – момент количества движения дебаланса относительно центра масс, ${{\vec {v}}_{C}}$ – скорость точки С, вектор $\overrightarrow {SC} $ можно представить в виде $\overrightarrow {SC} = l\left( {\cos \varphi \sin \psi {{{\vec {e}}}_{\xi }} + \sin \varphi {{{\vec {e}}}_{\eta }} - \cos \varphi \cos \psi {{{\vec {e}}}_{\zeta }}} \right).$

2.3. Маховики. Следующая система уравнений описывает движение маховиков:

Здесь ${{\vec {K}}_{A}} = {{\mathbb{J}}_{A}}{{\vec {\omega }}_{A}}$, где ${{\vec {\omega }}_{A}} = \vec {\omega } + {{\dot {\theta }}_{A}}{{\vec {e}}_{\xi }}$ – угловая скорость маховика 3, ${{\vec {K}}_{B}} = {{\mathbb{J}}_{B}}{{\vec {\omega }}_{B}}$, где ${{\vec {\omega }}_{B}}$ = $\vec {\omega } + {{\dot {\theta }}_{B}}{{\vec {e}}_{\eta }}$ – угловая скорость маховика 4, ${{\mathbb{J}}_{A}} = {\text{diag}}({{J}_{{A\xi }}},{{J}_{{A\eta }}},{{J}_{{A\zeta }}}),$ ${{\mathbb{J}}_{B}} = {\text{diag}}({{J}_{{B\xi }}},{{J}_{{B\eta }}},{{J}_{{B\zeta }}})$ – центральные тензоры инерции маховиков в связанных осях $A\xi \eta \zeta $ и $B\xi \eta \zeta $. Ускорение центров масс маховиков ${{\vec {a}}_{A}},\;{{\vec {a}}_{B}}$ может быть найдено по формулам

Для упрощения предположим, что маховики имеют одинаковую массу ${{m}_{3}} = {{m}_{4}} = m$, а также что их центры расположены симметрично относительно точки S, т.е. $\overrightarrow {SA} = - \overrightarrow {SB} = {{\eta }_{A}}{{\vec {e}}_{\eta }}$. Тогда

так как

Обозначим через M суммарную массу всех элементов системы. Далее подставим в систему (2.1) выражения для ${{\vec {F}}_{{13}}},{{\vec {F}}_{{14}}}$ с учетом ${{\vec {a}}_{A}},{{\vec {a}}_{B}}$ и ${{\vec {a}}_{C}},{{\vec {M}}_{{12}}},{{\vec {M}}_{{13}}},{{\vec {M}}_{{14}}}$, после чего перегруппируем слагаемые в уравнениях (2.1) и получим систему, описывающую движение робота:

3. Проекция уравнений движения на вертикаль. 3.1. Отсутствие контакта корпуса с опорой. Спроектируем первое уравнение системы (2.2) на ось $z$:

Здесь через N обозначена суммарная нормальная реакция $\langle {{\vec {F}}_{P}} + {{\vec {F}}_{L}} + {{\vec {F}}_{R}},{{\vec {e}}_{z}}\rangle $. Рассмотрим состояние механической системы, при котором нормальные реакции в опорах равны нулю. Принципиальная возможность такого состояния показана в работах [21–24]. В частности, для случая $\psi = 0$ была описана так называемая фаза полета, при которой $N = 0$ и корпус не совершает движения вдоль вертикали. И хотя в данной системе рамка дебаланса установлена под углом к вертикали, соответствующее уравнение имеет тот же вид, что и в [23], но с поправкой на установочный угол $\psi $

По аналогии с [24] для реализации описанного плоскопараллельного движения необходимо, чтобы положение $\varphi $ и угловая скорость $\dot {\varphi }$ дебаланса удовлетворяли соотношению (частному интегралу уравнения 3.1)

Предполагаются две основные фазы движения.

Фаза разгона. Корпус неподвижен за счет силы трения покоя, при этом дебаланс набирает необходимое количество движения, чтобы величины угла его поворота $\varphi $ и скорости его вращения $\dot {\varphi }$ могли достичь значений, удовлетворяющих зависимости (3.2). Вид зависимости (3.2) на фазовой плоскости $(\varphi ,\dot {\varphi })$ и алгоритмы осуществления фазы разгона описаны в [23, 24, 29] и не рассматриваются в рамках настоящей статьи. На этой фазе, в частности, возможны изменение угла $\psi $ рамки и уменьшение угловых скоростей (разгрузка) маховиков.

Фаза полета. В этой фазе движения угол $\varphi $ и угловая скорость $\dot {\varphi }$ удовлетворяют соотношению (3.2). Дебаланс вначале ($\varphi < \pi $) замедляется и изменяет количество движения и кинетический момент корпуса, в результате чего нормальные реакции уменьшаются до нуля. Корпус устремляется за дебалансом и совершает перемещение с вращением вокруг вертикали. После прохождения положения $\varphi = \pi $ дебаланс снова ускоряется, из-за чего замедляется вращение корпуса. Как было показано в [23], в начальный (t = 0) и конечный моменты ($t = {{t}_{*}}$) фазы полета угловая скорость дебаланса одинакова.

Пусть в начальный момент фазы полета состояние дебаланса следующее: $\varphi = {{\varphi }_{0}};$ $\dot {\varphi } = {{\dot {\varphi }}_{0}}$. Найдем программное управление дебаланса, обеспечивающее N = 0. Для этого проинтегрируем выражение (3.1) с начальными условиями ${{\dot {\varphi }}_{0}},{{\varphi }_{0}}$:

Частный вид траектории (3.3) для случая $\psi = 0$ был определен в работе [37]. Отметим, что существуют и другие технические способы управления мотором дебаланса, реализующие фазу полета. Например, формула (3.2) представляет собой обратную связь угловой скорости дебаланса по его положению.

Кроме того, подставим (3.2) в (3.1) и определим обратную связь для ускорения дебаланса от угла поворота:

Формулы (3.2)–(3.4), а также следуемые из них зависимости $\dot {\varphi }(t),\ddot {\varphi }(t),\ddot {\varphi }(\dot {\varphi })$ могут быть использованы для управления дебалансом при реализации вибрационного робота, исходя из конструкционных особенностей управляющего мотора.

Вычислим время ${{t}_{*}}$, которое затрачивается на фазу полета. Из (3.3) вытекает, что

3.2. Поворот корпуса вокруг вертикали. Спроектируем второе уравнение системы (2.2) на вертикаль и проинтегрируем его с начальными условиями $\dot {\gamma }(0) = 0,$ $\gamma (0) = 0$, ${{J}_{{S\zeta }}}\dot {\gamma } = - {{m}_{3}}{{l}^{2}}(\dot {\varphi }{\text{sin}}\psi $ + $\dot {\gamma }({\text{si}}{{{\text{n}}}^{2}}\varphi + {\text{co}}{{{\text{s}}}^{{\text{2}}}}\varphi {\text{si}}{{{\text{n}}}^{2}}\psi )) - {{J}_{{A\zeta }}}\dot {\gamma } - {{J}_{{B\zeta }}}\dot {\gamma } - 2m\eta _{A}^{2}\dot {\gamma } + {{m}_{2}}{{l}^{2}}{{\dot {\varphi }}_{0}}{\text{sin}}\psi ,$ откуда заключаем, что

Таким образом, с учетом подстановок (3.2) и (3.3) получаем

Замечание. Корпус вибрационного робота имеет нулевую угловую скорость после поворота, так как $\dot {\varphi }({{t}_{*}}) = {{\dot {\varphi }}_{0}}$.

Утверждение 1. Функция $\gamma (t)$ может быть вычислена в квадратурах.

Доказательство. Из (3.2) следует, что

Подставим это выражение в (3.6):

Введем обозначения:

Тогда вычисление интеграла (3.7) сводится к нахождению двух интегралов:

После подстановок $u = \cos \frac{\varphi }{2}$ и ${{\cos }^{2}}\varphi = {{(2{{u}^{2}} - 1)}^{2}}$

где I₂ вычисляется с помощью подстановки $v = {\text{tg}}\varphi $: где C определяется как

Таким образом,

Утверждение 1 доказано.

4. Горизонтальное смещение. 4.1. Смещение центра масс. По теореме о сохранении количества движения, во время фазы полета первое уравнение системы (2.2) допускает два первых интеграла:

На практике наличие горизонтальной скорости, которую приобретет центр масс корпуса в момент завершения фазы полета, является нежелательным, поскольку она может привести к скольжению вибрационного робота по опорной поверхности. Определим условия, позволяющие обеспечить полную остановку корпуса после поворота:

Утверждение 2. При совершении поворота корпуса на ненулевой угол ${{\gamma }_{*}}$, отличный от $\pi $, условия равенства нулю боковой и продольной скорости в момент приземления эквивалентны. При повороте на угол ${{\gamma }_{*}} = \pi $ общая скорость центра масс корпуса будет нулевой, если и только если начальное положение дебаланса ${{\varphi }_{0}} = \pi {\text{/}}2$.

Доказательство. Если ψ = 0, то из (3.5) следует, что $\gamma (t) \equiv 0 = {{\gamma }_{*}}$, т.е. поворота не происходит, и система (4.2) выполняется тождественно. Проведем доказательство для случая, когда рамка дебаланса отклонена на некоторый угол от вертикали.

Из первого уравнения системы (4.2)

Таким образом, при ${{\gamma }_{*}} \ne \pi $ первое и второе условия системы (4.2) эквивалентны. Если же ${{\gamma }_{*}} = \pi $, то первое условие системы (4.2) выполняется тождественно, а второе принимает вид $\cos {{\varphi }_{0}} = 0$ и, следовательно, выполняется при ${{\varphi }_{0}} = \pi {\text{/}}2$. Утверждение 2 доказано.

4.2. Траектория центра масс. Система (4.2) может быть представлена в виде

Пусть начальное положение корпуса таково, что $x(0) = 0,$ $y(0) = 0$. Тогда

Система (4.3) описывает траекторию центра масс корпуса S в горизонтальной плоскости.

4.3. Максимальный угол поворота. Оценим наибольший угол поворота корпуса, после которого его центр масс S останавливается. Для этого запишем первое уравнение системы (4.2) в следующей форме:

Это уравнение задает двумерную поверхность в пространстве ${{\gamma }_{*}},\;{{\varphi }_{0}},\;\psi $. Интересующие нас движения лежат на пересечении этой поверхности с поверхностью всевозможных поворотов, которая задается формулой (3.8) при подстановке $\varphi = 2\pi - {{\varphi }_{0}}$. Из физических соображений ясно, что максимальный угол поворота корпуса достигается при стремлении $\psi \to \pi {\text{/}}2$, так как в этом положении рамка горизонтальна, и весь кинетический момент дебаланса направлен на поворот. (Также это можно увидеть из уравнения (3.5), однако оговоримся, что при $\psi = \pi {\text{/}}2$ не может быть организовано управление $\varphi (t)$, обеспечивающее отсутствие контакта корпуса с опорой (3.3).) Поэтому наибольший угол поворота должен удовлетворять соотношению:

С другой стороны, угол поворота должен быть реализован вибрационным роботом и удовлетворять уравнению (3.8) при $\psi \to \pi {\text{/}}2$:

Вышесказанное рассуждение можно сформулировать в следующем виде.

Утверждение 3. Максимальный угол поворота корпуса при полной остановке центра масс после завершения фазы полета равен ${{\gamma }_{{{\text{max}}}}} = 2\varphi {\kern 1pt} *$, где φ* определяется из уравнения

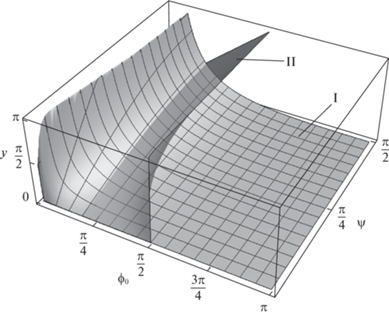
5. Численное моделирование движения. 5.1. Поворот робота. Зафиксируем параметры системы следующим образом: $M = 15$ кг, ${{m}_{2}} = 10$ кг, ${{\eta }_{A}} = 1;$ ${{({{J}_{{S\zeta }}} + {{J}_{{A\zeta }}} + {{J}_{{B\zeta }}} + 2m\eta _{A}^{2})} \mathord{\left/ {\vphantom {{({{J}_{{S\zeta }}} + {{J}_{{A\zeta }}} + {{J}_{{B\zeta }}} + 2m\eta _{A}^{2})} {{{m}_{2}}{{l}^{2}}}}} \right. \kern-0em} {{{m}_{2}}{{l}^{2}}}}$ = 5. На рис. 2 поверхность I описывает зависимость возможных углов поворота корпуса ${{\gamma }_{*}}$ от параметров ${{\varphi }_{0}}$, $\psi $. Она построена по формуле (3.8) при подстановке $\varphi = 2\pi - {{\varphi }_{0}}$. Поверхность II задана уравнением (4.4) – пересечение этих множеств соответствует таким поворотам вибрационного робота, после которых корпус будет иметь нулевую скорость. Согласно утверждению 3, наибольший угол поворота при условии остановки корпуса составляет 71.1°.

Из общего вида поверхностей можем заключить, что они пересекаются по прямой ${{\gamma }_{*}} = 0;$ $\psi = 0$, которая соответствует смещению корпуса в продольном направлении без поворота, а также некоторой кривой в пространстве ${{\varphi }_{0}},\psi ,\gamma $. Эта кривая обладает следующим свойством: переменная $\psi $ растет и убывает одновременно с переменной ${{\varphi }_{0}}$. Поэтому справедливо следующее утверждение.

Утверждение 4. Для каждого установочного угла рамки $\psi \ne 0$ существует единственное начальное положение дебаланса ${{\varphi }_{0}}$, при котором корпус останавливается после поворота. Угол этого поворота возрастает с увеличением $\psi ,$ а ${{\varphi }_{0}}$ лежит в диапазоне (34.7; 35.7°).

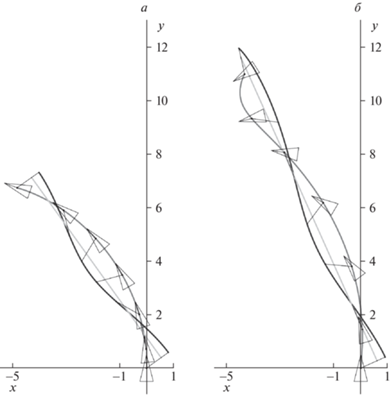
5.2. Траектория корпуса. Рассмотрим траекторию центра масс на плоскости $xy$ во время фазы полета. Рисунки 3, 4 иллюстрируют движение вибрационного робота в горизонтальной и вертикальных плоскостях соответственно при:

а) ${{\varphi }_{0}} = 35.69^\circ ,$ $\psi = 88^\circ $, выбранных из условий (3.8) и (4.4); угол поворота корпуса при этих параметрах составляет 70°;

б) ${{\varphi }_{0}} = 24^\circ ,$ $\psi = 86^\circ $, не соответствующих условиям (3.8) и (4.4); в этом случае корпус поворачивает вокруг вертикали на 127.5°.

Черным цветом представлены траектории центра масс корпуса S, серым – траектории дебаланса C, пунктиром – траектории центра масс системы. При отсутствии контакта с опорой на систему действует единственная внешняя по отношению к ней сила – сила тяжести. Однако проекция этой силы на горизонтальную плоскость нулевая, в связи с чем центр масс системы в плоскости $xy$ движется по инерции равномерно и прямолинейно.

Еще одна особенность рассматриваемой системы заключается в том, что выбор параметров, отвечающих остановке вибрационного робота после поворота, обеспечивает постоянную ориентацию корпуса вдоль касательной к траектории точки $S$ (рис. 3, a). Результат проверен численно для возможных углов поворотов ${{\gamma }_{*}}$ в диапазоне (0, 71.1°].

Однако если параметры ${{\varphi }_{0}},\psi $ не соответствуют условиям (3.8) и (4.4), то корпус будет отклоняться от касательной к траектории точки S и в конце фазы полета направление скорости его центра масс будет отлично от ориентации вибрационного робота (рис. 3, б).

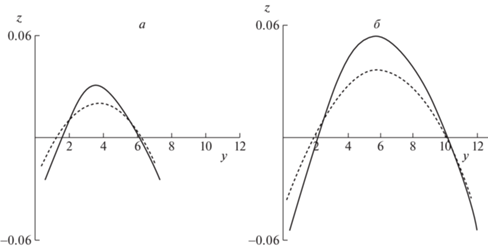
На рис. 4 представлены проекции точек системы на вертикальную плоскость. Под действием силы тяжести центр масс системы движется по параболе с ускорением $ - g{{\vec {e}}_{z}}$. Наивысшая точка траектории достигается в момент прохождения дебалансом положения $\varphi = \pi $.

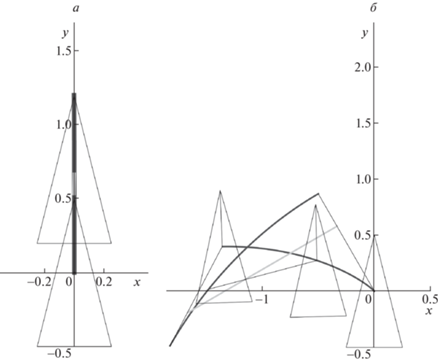
Любопытно, что если ${{\varphi }_{0}} > \pi {\text{/}}2$, то центр масс всей системы движется назад относительно корпуса, а сам корпус смещается в положительном направлении по оси $y$, хотя и на малое расстояние. Так, наибольшее смещение достигается при вертикальном положении рамки (рис. 5, а), а наибольший угол поворота не превосходит 8° и реализуется при горизонтальном положении рамки (рис. 5, б). Из вида поверхности на рис. 2 следует, что на описанном классе движений поворот робота несовместим с остановкой после завершения фазы полета.

Заключение. Рассмотрено плоскопараллельное движение в поле силы тяжести вибрационного робота, представленного корпусом, дебалансом, закрепленным в центре корпуса, и двумя однородными маховиками. Плоскость вращения дебаланса может быть отклонена от вертикали на фиксированный угол. Управление роботом происходит за счет выбора углового ускорения дебаланса и маховиков. В результате работы была построена математическая модель движения робота, и для него были найдены шесть режимов управления, которые реализуют поворот робота на некоторый угол.

Представлен параметрический анализ системы, в рамках которого продемонстрирована зависимость угла поворота корпуса от начального положения дебаланса и установочного угла рамки в фазе полета. Показано, что поворот корпуса сопряжен с общим смещением корпуса в продольном и боковом направлениях. При этом возможность выбора параметров, обеспечивающих полную остановку корпуса после поворота, доказана аналитически. Также оценен максимальный угол поворота робота, после которого его корпус останавливается.