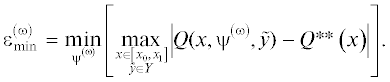Известия РАН. Теория и системы управления, 2023, № 1, стр. 56-71

Введение. Задачи управления не полностью определенными динамическими объектами относятся в настоящее время к числу приоритетных и представляют значительный теоретический и прикладной интерес [1–8]. Большинство работ в этом направлении относится к системам с сосредоточенными параметрами (ССП), для которых известные результаты получены в основном с использованием аппарата функций Ляпунова и линейных матричных неравенств при ограниченной неопределенности модельных представлений [2–4] либо с помощью модифицированных аналогов принципа максимума Понтрягина [5, 6], главным образом, в линейно-квадратичных задачах оптимизации со свободным правым концом фазовой траектории процесса управления.

Применительно к системам с распределенными параметрами (СРП), в рамках моделей которых описывается широкий круг управляемых процессов самой различной физической природы [9], задачи управления в условиях неопределенности принципиально усложняются бесконечной размерностью пространственно распределенной управляемой величины [7, 8]. Их решение разработанными для ССП методами становится затруднительным, особенно при типичных для приложений равномерных оценках целевых множеств конечных состояний СРП, на негладкой границе которых неприменимы классические условия трансверсальности [7, 8, 10–13].

В настоящей работе предлагается конструктивный метод решения линейно-квадратичной задачи оптимального управления СРП с заданной точностью равномерного приближения конечного состояния системы к требуемому пространственному распределению управляемой величины в условиях интервальной неопределенности неизменных во времени параметрических характеристик объекта. Разработанный метод опирается на установленные ранее в этих условиях альтернансные свойства параметризуемых оптимальных программных управляющих воздействий, распространяющие на рассматриваемые задачи оптимального управления известные результаты теории нелинейных чебышевских приближений [7, 8, 10–13].

1. Постановка задачи. Пусть управляемая величина $Q\left( {x,t} \right)$ объекта с распределенными параметрами описывается в зависимости от пространственной координаты $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$ и времени $t \in \left[ {0,{{t}_{1}}} \right]$ линейным уравнением второго порядка в частных производных параболического типа:

с начальными и граничными условиями при пространственно-временном кусочно-непрерывном [13] внутреннем управляющем воздействии $u\left( {x,t} \right)$, заданных достаточно гладких функциях $a\left( x \right)$, $b\left( x \right)$, $c\left( x \right)$ и постоянных коэффициентах ${{\alpha }_{0}}$, ${{\alpha }_{1}} \geqslant 0$; ${{\beta }_{0}}$, ${{\beta }_{1}} > 0$.

Здесь для простоты без потери общности получаемых далее основных результатов предполагается равномерное распределение $Q\left( {x,0} \right)$ по пространственной координате в (1.2) и управляющие воздействия не стесняются никакими дополнительными ограничениями.

Эквивалентное (1.1)–(1.3) представление модели объекта управления может быть получено в форме бесконечной системы обыкновенных дифференциальных уравнений первого порядка относительно коэффициентов (временных мод) ${{\bar {Q}}_{n}}\left( t \right)$ разложения $Q\left( {x,t} \right)$ в сходящийся в среднем ряд по ортонормированной с весом r(x) системе собственных функций ${{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right)$, $n = 1,2,...$, определяемых вместе с собственными числами $\mu _{n}^{2}$ известными методами конечных интегральных преобразований [9, 13, 14]:

Здесь ${{\bar {u}}_{n}}\left( t \right)$ – временные моды разложения $u\left( {x,t} \right)$ в ряд вида (1.5):

рассматриваемые далее в качестве бесконечного числа автономных, независимых друг от друга и нестесняемых ограничениями сосредоточенных управляющих воздействий, и ${{\bar {Q}}^{{\left( 0 \right)}}}\left( {{{\mu }_{n}}} \right)$ – моды ${{Q}_{0}}\left( x \right)$.

При этом поведение каждой из модальных составляющих ${{\bar {Q}}_{n}}$ управляемой величины определяется только “своим” управляющим воздействием ${{\bar {u}}_{n}}$, согласно решению каждого из уравнений (1.4) в отдельности независимо от других, обеспечивая в итоге требуемое состояние $Q\left( {x,t} \right)$, описываемое рядом (1.5).

Можно показать [15, 16], что в малостеснительных условиях выполнения усиленных условий Коши–Липшица система уравнений (1.4) имеет единственное решение при заданных воздействиях ${{\bar {u}}_{n}}\left( t \right)$, которое с любой требуемой точностью при необходимости аппроксимируется решением “укороченной” системы, образуемой достаточно большим конечным числом $N$ первых уравнений (1.4) при ${{\bar {Q}}_{n}}\left( t \right) = 0$ для всех $n > N$. В итоге оказывается допустимой конечномерная аппроксимация модели (1.4) при $n = \overline {1,N} $, $N < \infty $. Всюду далее на этом основании учитывается ${{N}_{1}}$ мод ${{\bar {Q}}_{n}}$, $n = \overline {1,{{N}_{1}}} $, в (1.4), где ${{N}_{1}} = \infty $ или ${{N}_{1}} = N < \infty $ в зависимости от используемой схемы анализа и возможностей практической реализации исследуемых алгоритмов управления. Конкретный выбор числа N₁ должен производиться при проектировании системы управления, исходя из практически требуемой точности описания модели объекта N₁уравнениями (1.4).

В характерных условиях интервальной неопределенности начального состояния объекта ${{Q}_{0}}$ и вектора w его неизменных во времени параметрических характеристик, с точностью до которых определены ограниченные в этих условиях своими заданными максимально и минимально возможными величинами значения ${{\alpha }_{0}}$, ${{\alpha }_{1}}$, ${{\beta }_{0}}$, ${{\beta }_{1}}$ в (1.3), вся информация о величинах ${{Q}_{0}}$ и w исчерпывается сведениями об их принадлежности заданным компактным множествам $\Omega $ и $W$:

Поскольку собственные числа находятся в зависимости от коэффициентов $\alpha $ и $\beta $ в граничных условиях (1.3) [14], то ${{\mu }_{n}}$ в (1.4), (1.5) также оказываются заданными с точностью до известного интервала их возможных изменений.

Каждой реализуемой, согласно (1.7), паре $y = \left( {{{Q}_{0}},w} \right) \in Y = \Omega \times W$ значений неопределенных факторов при любом допустимом управлении $u\left( {x,t} \right)$ соответствует определяемая решением системы уравнений (1.4) траектория процесса $\bar {Q}\left( {\bar {u},t,y} \right) = \left( {{{{\bar {Q}}}_{n}}\left( {{{{\bar {u}}}_{n}},t,y} \right)} \right)$, $\bar {u} = \left( {{{{\bar {u}}}_{n}}} \right)$, $n = \overline {1,{{N}_{1}}} $, $t \in \left[ {0,{{t}_{1}}} \right]$. Их объединение по всем $y \in Y$ при одном и том же управляющем воздействии образует ансамбль траекторий [1]:

описывающий поведение управляемой функции состояния вида (1.5) на множестве $Y \in y$ не полностью определенных параметрических характеристик объекта:

Пусть необходимо обеспечить за фиксируемое априори время t₁ при управлении ансамблем (1.8) заданную точность $\varepsilon $ равномерного приближения конечного пространственного распределения управляемой величины $Q\left( {x,\bar {u},{{t}_{1}},y} \right)$ к требуемому состоянию, описываемому кусочно-непрерывной функцией $Q{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(x) > {{Q}_{0}}$, $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$, для всех $y \in Y$, согласно соотношению

которое определяет оцениваемое в типичной для приложений равномерной метрике целевое множество конечных состояний распределенной системы [10–13].

Пусть далее эффективность процесса управления объектом (1.1)–(1.3) оценивается квадратичным функционалом качества

Переход к описанию объекта в терминах модальных переменных приводит в силу ортонормированности семейства собственных функций к представлению критерия (1.11) в следующем виде [13]:

а требования (1.10) к конечному состоянию объекта определяются в форме условия

В соответствии со стратегией управления по принципу наилучшего гарантированного результата рассмотрим следующую минимаксную задачу робастной оптимизации поведения ансамбля траекторий (1.8) [7]. Обозначим через $u\left( {Q,x,t} \right)$ управляющее воздействие с обратной связью по управляемой величине Q.

Требуется найти оптимальное управление $u{\kern 1pt} {\text{*}}(Q,x,t)$ обеспечивающее перевод не полностью определенного в условиях (1.7) объекта (1.4) в требуемое конечное состояний (1.13) при минимально возможном значении критерия оптимальности:

Решение сформулированной задачи существует при достижимых значениях ε в (1.13) [1].

2. Программное оптимальное управление ансамблем траекторий. 2.1. Структура оптимального управления для детерминированной модели объекта. При некотором фиксированном значении $y = \tilde {y} = {\text{const}} \in Y$ задача (1.13), (1.14) приводится к рассмотренному в [13] виду

для детерминированной модели объекта.

Как показано в [13], стандартные процедуры принципа максимума Понтрягина приводят к представлению оптимальных модальных управлений $\bar {u}_{n}^{*}\left( t \right)$ в форме явной функции от сопряженной переменной $\psi _{n}^{*}\left( t \right)$, соответствующей оптимальному процессу, независимо от других составляющих вектора $\bar {u}{\kern 1pt} * = (\bar {u}_{n}^{*})$, $n = \overline {1,{{N}_{1}}} $:

2.2. Краевая задача принципа максимума для детерминированной модели объекта. Уравнения (1.4) с подстановкой управляющего воздействия в форме (2.3) образуют в рассматриваемом случае совместно с уравнениями для сопряженных переменных ${{\psi }_{n}}\left( t \right)$ линейную программно-управляемую систему второго порядка относительно двух переменных ${{\bar {Q}}_{n}}$, ${{\psi }_{n}}$ для каждого $n = \overline {1,{{N}_{1}}} $ [13]:

Система (2.4) замыкается требованиями к ее конечному состоянию, которые считаются определенными, исходя из общего для всех $n = \overline {1,{{N}_{1}}} $ условия (2.1).

Решение уравнений (2.4) может быть получено в векторно-матричной форме [13]:

Здесь ${{A}_{n}}$ – $2 \times 2$-матрица коэффициентов системы (2.4), ${{e}^{{{{A}_{n}}t}}}$ – $2 \times 2$-матрица (матричная экспонента)

где ${{A}_{{nij}}}\left( t \right)$; i, $j = 1,2$ известные в соответствии со структурой системы уравнений (2.4) элементы ${{e}^{{{{A}_{n}}t}}}$ [13].

2.3. Параметризация управляющих воздействий при полном объеме информации о характеристиках объекта. Согласно (2.5), $\psi _{n}^{*}\left( t \right)$, а следовательно, и программное управление (2.3) определяются для каждой известной величины ${{\bar {Q}}_{n}}\left( 0 \right)$ с точностью до начальных значений $\psi _{n}^{*}\left( 0 \right)$, совокупность которых для всех $n = \overline {1,{{N}_{1}}} $ выступает таким образом, в роли параметрического представления $u{\kern 1pt} {\text{*}}\left( {x,t} \right)$ в соответствии с (1.6), (2.3), (2.4) [17, 18]. Однако для систем с распределенными параметрами такой подход оказывается неконструктивным, прежде всего, в силу бесконечной размерности вектора $\psi \left( 0 \right) = (\psi _{n}^{{}}\left( 0 \right))$, $n = \overline {1,{{N}_{1}}} $ при ${{N}_{1}} = \infty $. В работе [12] применительно к требованиям (2.1), предъявляемым к конечному состоянию объекта $\bar {Q}\left( {{{t}_{1}}} \right) = \left( {{{{\bar {Q}}}_{n}}\left( {{{t}_{1}}} \right)} \right)$, $n = \overline {1,{{N}_{1}}} $, предложен конструктивный способ последовательной конечномерной параметризации управляющих воздействий (“ψ – параметризация”) на множестве M‑мерных векторов ${{\psi }^{{\left( M \right)}}} = \left( {{{{\tilde {\psi }}}_{i}}} \right)$, $i = \overline {1,M} $; ${{\tilde {\psi }}_{i}} = {{\psi }_{i}}\left( {{{t}_{1}}} \right)$, $M < {{N}_{1}}$, финишных значений ${{\tilde {\psi }}_{i}}$ первых M сопряженных функций в (2.4) при равных нулю всех остальных значениях ${{\psi }_{i}}\left( {{{t}_{1}}} \right)$:

С возрастанием $M$ обеспечивается попадание под действием параметризуемых на множестве параметров (2.7) управляющих воздействий вида (2.3) в сужающееся к началу координат в пространстве $\bar {Q}\left( t \right)$ целевое множество, гарантируя выполнение условий (2.1) для достижимых значений $\varepsilon $ при некотором конечном значении $M \geqslant 1$ [12].

Явная форма $\psi $-параметризованного управления (2.3) может быть получена в результате прогонки начальных условий в (2.5) к моменту $t = {{t}_{1}}$ в виде следующей линейной зависимости от определяемого, согласно (2.7), конечного значения $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ в оптимальном процессе и начального состояния ${{\bar {Q}}_{n}}\left( 0 \right)$ объекта управления [13]:

где $\tilde {\psi }_{n}^{*}$ – значения ${{\tilde {\psi }}_{n}}$ в (2.7), соответствующие оптимальному процессу. Здесь [13] ${{\hat {A}}_{{nij}}}$, i, $j = 1,2$, подобные (2.6) блоки обратной матрицы ${{e}^{{ - {{A}_{n}}\left( {{{t}_{1}} - t} \right)}}}$ и

Последующая подстановка (2.8) в (1.6), где следует учесть ${{N}_{1}} \leqslant \infty $ слагаемых бесконечной суммы, приводит к ψ-параметризованной форме оптимального программного управления $u{\kern 1pt} {\text{*}}(x,t)$:

Таким образом, $u{\kern 1pt} {\text{*}}(x,t)$ находится, согласно (2.11), с точностью до выбора оптимального вектора параметров $\psi _{*}^{{\left( M \right)}} = (\tilde {\psi }_{i}^{*})$, $i = \overline {1,M} $, в (2.7). К его определению применительно к задаче (1.13), (1.14) управления ансамблем траекторий (1.8) и сводится дальнейшая задача.

2.4. Редукция к не полностью определенной минимаксной задаче полубесконечной оптимизации. В зависимости от реализуемой величины $\tilde {y} \in Y$ оптимальное управление $\bar {u}_{n}^{*}\left( {t,\tilde {y}} \right)$ определяется в форме (2.8)–(2.10):

где ${{A}_{{nij}}}$, ${{\hat {A}}_{{nij}}}$, i, $j = 1,2$, находятся в соответствии со структурой системы уравнений (2.4) при ${{\mu }_{n}} = {{\mu }_{n}}\left( {\tilde {y}} \right)$. На этом основании, согласно (2.11),

Интегрирование уравнений системы (1.4) с $\psi $-параметризованным управляющим воздействием вида (2.12)–(2.14) позволяет получить в форме (1.9) зависимости $Q(x,{{\psi }^{{\left( M \right)}}},\tilde {y})$ управляемой величины в конце оптимального процесса и критерия оптимальности ${{J}_{1}}({{\psi }^{{\left( M \right)}}},\tilde {y})$ в (1.12) для каждого значения $\bar {Q}\left( 0 \right)$ в (2.12) в виде явных функций x, ${{\psi }^{{\left( M \right)}}}$ и $\tilde {y}$. В результате осуществляется точная редукция исходной задачи оптимального управления (1.12)–(1.14) к минимаксной задаче полубесконечной оптимизации (ЗПО) [10, 11]:

на экстремум функции ${{J}_{2}}({{\psi }^{{\left( M \right)}}})$ конечного числа M переменных ${{\tilde {\psi }}_{i}}$, $i = \overline {1,M} $, в (2.7) с бесконечным числом ограничений (2.17). Эти ограничения порождаются требованиями выполнения условия (1.13), записываемого в форме (1.10), для всех $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$, $\tilde {y} \in Y$ и заменяются одним эквивалентным ограничением на ошибку равномерного приближения $Q(x,{{\psi }^{{\left( M \right)}}},\tilde {y})$ к $Q{\kern 1pt} *{\kern 1pt} *\left( x \right)$ в области $G = \left[ {{{x}_{0}},{{x}_{1}}} \right] \times Y$.

ЗПО (2.16), (2.17) существенно усложняется по сравнению с ее частным случаем для детерминированной модели объекта управления [13], во-первых, ограничением на функцию максимума в (2.17), определяемую на расширенном множестве аргументов, которое включает кроме пространственной переменной $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$ все допустимые реализации неопределенных факторов $y \in Y$, и, во-вторых, вычислением ${{J}_{2}}({{\psi }^{{\left( M \right)}}})$ в (2.16) по максимальной величине ${{J}_{1}}$ на множестве Y.

Аналогично детерминированному варианту вида (2.1), (2.2), к которому сводится задача (2.16), (2.17) с фиксируемыми значениями $\tilde {y}$, размерность M вектора $\psi _{*}^{{\left( M \right)}} = (\tilde {\psi }_{n}^{*})$, $n = \overline {1,M} $, однозначно определяется в зависимости от заданной величины $\varepsilon $ в (2.17) соотношением [10–13]

где

Значения $\varepsilon _{{\min }}^{{\left( \omega \right)}}$, $\omega = \overline {1,\rho } $, образуют, как правило, убывающую с возрастанием ω цепочку неравенств [10–13]. Задача (2.16), (2.17) оказывается разрешимой, если $\varepsilon \geqslant {{\varepsilon }_{{\inf }}}$. Здесь точная нижняя грань ${{\varepsilon }_{{\inf }}}$ достижимых значений $\varepsilon $ становится равной минимаксу $\varepsilon _{{\min }}^{{\left( \rho \right)}}$, где $\rho = \infty $ при ${{\varepsilon }_{{\inf }}} = 0$ и $\rho < \infty $ при ${{\varepsilon }_{{\inf }}} > 0$ соответственно для управляемых и неуправляемых относительно $Q{\kern 1pt} *{\kern 1pt} {\text{*}}(x)$ объектов [10].

2.5. Решение минимаксной задачи полубесконечной оптимизации. Решение ЗПО (2.16), (2.17) относительно вектора параметров ${{\psi }^{{\left( M \right)}}}$, а также априори неизвестной величины $\varepsilon _{{\min }}^{{\left( M \right)}}$ в (2.18) в случае, когда по исходным условиям задачи должно быть выполнено равенство $\varepsilon = \varepsilon _{{\min }}^{{\left( M \right)}}$ в (2.17), может быть получено альтернансным методом [10, 11, 13]. Метод базируется на специальных альтернансных свойствах искомого решения $\psi _{*}^{{\left( M \right)}} = (\tilde {\psi }_{i}^{*})$, $i = \overline {1,M} $, задачи (2.16), (2.17) и диктуемой закономерностями предметной области дополнительной информации о характере и формах распределения результирующего состояния $Q(x,{{\psi }^{{\left( M \right)}}},y) - Q{\kern 1pt} *{\kern 1pt} *\left( x \right)$ управляемой величины в области $G\, = \,[{{x}_{0}},{{x}_{1}}]\, \times \,Y$, $\left( {x,y} \right) \in G$, и значения критерия оптимальности ${{I}_{1}}(\psi _{*}^{{\left( M \right)}},y)$ в области $Y \mathrel\backepsilon y$. Можно показать [10], что в рассматриваемой ЗПО, согласно альтернансным свойствам $\psi _{*}^{{\left( M \right)}}$, в условиях малостеснительных допущений равные допустимой величине ε значения $\mathop {\max }\limits_{x,\tilde {y}} {\text{|}}Q(x,\psi _{*}^{{(M)}},\tilde {y})\, - \,Q{\kern 1pt} *{\kern 1pt} {\text{*}}(x){\text{|}}$ и совпадающие с ${{J}_{2}}(\psi _{*}^{{\left( M \right)}})$ в (2.16) значения $\mathop {\max }\limits_{\tilde {y}} {{J}_{1}}(\psi _{*}^{{\left( M \right)}},\tilde {y})$ достигаются соответственно в некоторых точках $(x_{j}^{0}$, $\tilde {y} = y_{j}^{0}) \in G$, $j = \overline {1,{{R}_{x}}} $, и $y_{{ei}}^{0} \in Y$, $i = \overline {1,{{R}_{y}}} $:

В общем случае значения $y_{j}^{0}$ неопределенных факторов в (2.21) заранее не определены и процедура их поиска существенно затрудняет дальнейшее решение задачи [5, 6]. Ограничимся далее типичной для прикладных задач возможностью предварительной фиксации этих величин, как правило, на границе $\partial Y$ области Y, которые считаются известными, исходя из физических закономерностей конкретных оптимизируемых процессов [7, 10, 19–22].

Числа ${{R}_{x}}$ и ${{R}_{y}}$ в (2.20), (2.21) определяются следующими соотношениями в зависимости от значения $\varepsilon $ в (2.20), замыкающими систему равенств (2.20), (2.21) относительно искомых параметров оптимального процесса:

где M находится по правилу (2.18). Вариант (2.24) исключается далее из рассмотрения, поскольку он отвечает решению ${{\bar {\psi }}^{{\left( M \right)}}}$ задачи (2.16) без учета ограничения (2.17).

При наличии информации из предметной области о форме распределений $Q(x,\psi _{*}^{{\left( M \right)}},y)$ на $G \mathrel\backepsilon \left( {x,y} \right)$ и ${{J}_{1}}(\psi _{*}^{{\left( M \right)}},y)$ на $Y \mathrel\backepsilon y$, которая позволяет идентифицировать точки $x_{j}^{0}$, $y_{j}^{0}$, $y_{{ei}}^{0}$ и знаки разности $Q(x_{j}^{0},\psi _{*}^{{\left( M \right)}},y_{j}^{0}) - Q{\kern 1pt} *{\kern 1pt} {\text{*}}(x_{j}^{0})$, равенства (2.20), (2.21), дополненные условиями существования экстремума функций $Q(x,\psi _{*}^{{\left( M \right)}},y) - Q{\kern 1pt} *{\kern 1pt} {\text{*}}(x)$ и ${{J}_{1}}(\psi _{*}^{{\left( M \right)}},y)$ соответственно в принадлежащих $\operatorname{int} \left[ {{{x}_{0}},{{x}_{1}}} \right]$ точках $x_{{jg}}^{0} \in \left\{ {x_{j}^{0}} \right\}$ при $y = y_{{jg}}^{0} \in \left\{ {y_{j}^{0}} \right\}$, $g = \overline {1,{{R}_{{1x}}}} $, ${{R}_{{1x}}} \leqslant {{R}_{x}}$, и внутренних точках $y_{{eip}}^{0} \in \left\{ {y_{{ei}}^{0}} \right\}$ множества $Y$, $p = \overline {1,{{R}_{{1y}}}} $, ${{R}_{{1y}}} \leqslant {{R}_{y}}$, переводятся в случае (2.22) в замкнутую систему уравнений:

с известными числами ${{R}_{{1x}}}$, ${{R}_{{1y}}}$ и однозначно определяемым знаком ε в (2.25) для каждой пары значений $x_{j}^{0}$, $y_{j}^{0}$.

Совместное решение в условиях (2.22) ${{R}_{x}} + {{R}_{y}} + {{R}_{{1x}}} + {{R}_{{1y}}} = M + 1 + {{R}_{{1x}}} + {{R}_{{1y}}}$ уравнений (2.25)–(2.28) относительно $M + 1 + {{R}_{{1x}}} + {{R}_{{1y}}}$ неизвестных $\psi _{*}^{{\left( M \right)}} = (\psi _{i}^{*})$, $i = \overline {1,M} $; ${{J}_{2}}(\psi _{*}^{{\left( M \right)}})$: $x_{{jg}}^{0}$, $g = \overline {1,{{R}_{{1x}}}} $; $y_{{eip}}^{0}$, $p = \overline {1,{{R}_{{1y}}}} $, при заданных величинах $y_{j}^{0}$ позволяет определить все искомые параметры в ЗПО (2.16), (2.17) применительно к варианту (2.22).

В случае (2.23) получаем систему $M + 1 + {{R}_{{1x}}}$ уравнений (2.25), (2.27), разрешаемую относительно $M + 1 + {{R}_{{1x}}}$ неизвестных $\psi _{*}^{{\left( M \right)}} = (\psi _{i}^{*})$, $i = \overline {1,M} $; $\varepsilon _{{\min }}^{{\left( M \right)}}$; $x_{{jg}}^{0}$, $g = \overline {1,{{R}_{{1x}}}} $.

Для выпуклого минимизируемого функционала качества (1.12) значения $\mathop {\max }\limits_{\tilde {y}} {{J}_{1}}(\psi _{*}^{{\left( M \right)}},\tilde {y})$ в (2.16) достигаются в точках $y_{{ei}}^{0} \in \partial Y$, $i = \overline {1,{{R}_{y}}} $ [6]. Ограничимся далее типичным случаем наличия при ${{R}_{y}} = 1$ в (2.26) только одной такой заранее фиксируемой (подобно $y_{j}^{0}$) точки $y_{{e1}}^{0} \in \partial Y$, соответствующей единственной “наихудшей” реализации значений неопределенных величин $y \in Y$, на которой достигается $\mathop {\max }\limits_{\tilde {y}} {{J}_{1}}(\psi _{*}^{{\left( M \right)}},\tilde {y})$. При этом точки $y_{{eip}}^{0} \in \operatorname{int} Y$ отсутствуют и уравнения (2.28) исключаются из системы (2.25)–(2.28), которая принимает в итоге следующий вид:

где, как правило, $y_{{e1}}^{0} \in \left\{ {y_{j}^{0}} \right\}$ в (2.29). Согласно (2.22), при ${{R}_{y}} = 1$, $\varepsilon _{{\min }}^{{\left( M \right)}} < \varepsilon < \varepsilon _{{\min }}^{{\left( {M - 1} \right)}}$ будем иметь ${{R}_{x}} = M$. Система ${{R}_{x}} + {{R}_{{1x}}} = M + {{R}_{{1x}}}$ уравнений (2.29), (2.31) может быть решена известными численными методами относительно ${{R}_{x}} + {{R}_{{1x}}}$ неизвестных $\psi _{*}^{{\left( M \right)}} = (\tilde {\psi }_{i}^{*})$, $i = \overline {1,M} $; $x_{{jg}}^{0}$, $g = \overline {1,{{R}_{{1x}}}} $, независимо от значений ${{J}_{1}}(\psi _{*}^{{\left( M \right)}},y_{{e1}}^{0})$. По найденной таким образом величине $\psi _{*}^{{\left( M \right)}}$ определяется ${{J}_{2}}(\psi _{*}^{{\left( M \right)}})$ из уравнения (2.30).

Состояние управляемой величины $Q(x,\psi _{*}^{{\left( M \right)}},\tilde {y})$ в конце оптимального процесса при любом реализуемом значении $\tilde {y} \in Y$ описывается рядом вида (1.9):

с вектором $\bar {Q}(\psi _{*}^{{\left( M \right)}},\tilde {y}) = ({{\bar {Q}}_{n}}(\psi _{*}^{{\left( M \right)}},\tilde {y}))$ конечных значений модальных переменных ${{\bar {Q}}_{n}}$. Здесь, подобно (2.12), можно получить следующее выражение для ${{\bar {Q}}_{n}}(\psi _{*}^{{\left( M \right)}},\tilde {y})$ в форме линейной функции начального состояния объекта ${{\bar {Q}}_{n}}\left( 0 \right)$ и конечных значений $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ вектора сопряженных переменных [13]: где $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ по-прежнему определяется, согласно (2.7), ${{B}_{n}}\left( {{{t}_{1}},\tilde {y}} \right)$, ${{B}_{{1n}}}\left( {{{t}_{1}},\tilde {y}} \right)$ вычисляются по формулам (2.14) и, следовательно, $Q\left( {x_{j}^{0},\psi _{*}^{{\left( M \right)}},y_{j}^{0}} \right)$ в системе уравнений (2.29), (2.31) находится в форме (2.32), (2.33) с заменой $\tilde {y}$ на $y_{j}^{0}$.

Таким образом, значения $\psi _{*}^{{\left( M \right)}}$ в задаче (2.16), (2.17) находятся в результате решения системы уравнений (2.29), (2.31), учитывающей конечное состояние всего ансамбля траекторий управляемой системы. Зависимость ${{J}_{1}}(\psi _{*}^{{\left( M \right)}},\tilde {y})$ от $\tilde {y}$ создается за счет включения в подынтегральную функцию критерия (1.12) значений ${{\bar {Q}}_{n}}$ и ${{\bar {u}}_{n}}$, зависящих от y.

При заранее фиксируемом известными закономерностями предметной области значении y* величины $y_{{e1}}^{0}$ в (2.30) в силу соотношений (2.16), (2.17), (2.30) выполняются равенства для найденного вектора $\psi _{*}^{{\left( M \right)}}$:

Отсюда в соответствии с представлением критерия оптимальности ${{J}_{1}}\left( {\bar {u},y} \right)$ в форме (1.12) следует, что искомое $\psi $-параметризованное оптимальное программное управление $\bar {u}{\kern 1pt} {\text{*}}(t)$ ансамблем траекторий (1.8) совпадает с $\bar {u}{\kern 1pt} *\left( {t,y{\kern 1pt} *} \right) = (\bar {u}_{n}^{*}\left( {t,y{\kern 1pt} *} \right))$, $n = \overline {1,{{N}_{1}}} $, где $\bar {u}_{n}^{*}\left( {t,y{\kern 1pt} *} \right)$ определяется, согласно (2.12), при $\tilde {y} = y{\kern 1pt} *$.

В итоге программное оптимальное управление ансамблем (1.8) определяется в форме (2.15) с подстановкой (2.12)–(2.14), где $\tilde {\psi }_{*}^{{\left( M \right)}}$, $n = \overline {1,M} $, находятся в результате решения системы уравнений (2.29)–(2.31), а $\tilde {y}$ выбирается равным y*.

2.6. Учет ограничений на характер пространственного распределения программного управления ансамблем траекторий. При характерных для приложений затруднениях в технической реализации пространственного распределения управлений $u{\kern 1pt} *\left( {x,t} \right)$ вида (2.15) они ищутся в форме взвешенной суммы заранее фиксируемых проектными решениями объекта и заведомо исполнимых стандартными инженерными средствами зависимостей (чаще всего, кусочно-постоянных) ${{F}_{m}}\left( x \right)$, $m = \overline {1,s} $; $s \geqslant 1$, от пространственной координаты с весовыми коэффициентами, в роли которых выступает искомые сосредоточенные управляющие воздействия ${{\upsilon }_{m}}\left( t \right)$ [13]:

Конечное интегральное преобразование равенства (2.35) приводит к следующему выражению для модальных управляющих воздействий ${{\bar {u}}_{n}}\left( t \right)$ в (1.4) [13]:

где ${{\bar {F}}_{{mn}}}$ – $n$-я мода разложения ${{F}_{m}}\left( x \right)$ в ряд вида (1.5) по собственным функциям начально-краевой задачи (1.1)–(1.3).

В типичной для приложений ситуации, когда можно ограничиться учетом только ${{N}_{1}} = N$ мод ${{\bar {Q}}_{n}}$ в (1.5) и возможен выбор $s = N$ в (2.35), равенства (2.36) при $n = \overline {1,N} $, $N = s$ образуют линейную систему уравнений относительно $\upsilon _{m}^{*}\left( t \right)$, $m = \overline {1,s} $, для заданных значений $\bar {u}_{n}^{*}\left( t \right)$ в (2.8), решение которой определяется формулами Крамера непосредственно по решению задачи с автономными модальными управлениями:

Здесь $D = \det \left[ {{{{\bar {F}}}_{{mn}}}} \right]$, m, $n = \overline {1,s} $; ${{D}_{{mn}}}$ – алгебраическое дополнение n-го элемента m-го столбца D и $D \ne 0$ при линейно-независимых функциях $F\left( x \right)$.

В результате искомое программное управление ансамблем траектории $u{\text{*}}(x,t)$ восстанавливается в виде (2.35) с подстановкой (2.37):

где $\bar {u}_{n}^{*}\left( t \right)$ находятся по схеме (2.12)–(2.34) в форме (2.12) при $\tilde {y} = y{\kern 1pt} *$. В более общем случае $s < {{N}_{1}} = N$ в (2.35) задача определения многоканального сосредоточенного управления $\upsilon _{m}^{*}\left( t \right)$, $m = \overline {1,s} $, решается распространением полученных в (2.3)–(2.9) результатов на подобную (2.4) программно-управляемую систему теперь уже N-го порядка путем, указанным в [13].

3. Синтез оптимального управления с модальными управляющими воздействиями. Применение известных процедур аналитического конструирования оптимальных регуляторов в рассматриваемой не полностью определенной линейно-квадратичной задаче оптимизации существенно усложняется трудностями реализации алгоритмов позиционного управления ансамблем траекторий движения объекта [1, 6] и отсутствием классических условий трансверсальности на негладкой границе целевого множества (1.10) [8, 13]. В настоящем разделе предлагается метод синтеза управляющих воздействий $u{\kern 1pt} {\text{*}}(Q,x,t)$ с обратной связью, осуществляемый по принципу наилучшего гарантированного результата с использованием, подобно [8, 13], в качестве условий трансверсальности на правом конце оптимальной траектории известных конечных значений управляемых и сопряженных переменных, которые определяются предварительным расчетом программного управления. Рассмотрим сначала задачу синтеза для детерминированной модели объекта при $\tilde {y} = y{\kern 1pt} *$ в (2.12)–(2.14), для которой управляющее воздействие $u{\kern 1pt} {\text{*}}(x,t)$ совпадает, как показано в разд. 2, с оптимальным программным управлением ансамблем траекторий (1.8) в форме (2.15) с заменой $\tilde {y}$ на y*.

Перенос (прогонка) начальных значений ${{\psi }_{n}}\left( 0 \right)$, ${{Q}_{n}}\left( 0 \right)$ в (2.5) в конечный момент времени t₁ приводит при $\tilde {y} = y{\kern 1pt} *$ к решению системы уравнений (2.4) в следующем виде [13]:

где $\psi _{n}^{*}\left( t \right)$, $\bar {Q}_{n}^{*}\left( {t,y{\kern 1pt} *} \right)$ соответствуют оптимальному процессу и конечные значения $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$, $\bar {Q}_{n}^{*}\left( {{{t}_{1}},y{\kern 1pt} *} \right)$ фиксируются решением задачи программного управления описанным в разд. 2 способом. После умножения равенств (3.1), (3.2) соответственно на известные значения $\bar {Q}_{n}^{*}\left( {{{t}_{1}},y{\kern 1pt} *} \right) = \bar {Q}_{n}^{*}(\psi _{*}^{{\left( M \right)}},y{\kern 1pt} *)$ и $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ в (2.33) и (2.7) левые части соотношений (3.1), (3.2) становятся одинаковыми. Последующее вычитание этих уравнений приводит к зависимости сопряженных переменных от наблюдаемых мод $\bar {Q}_{n}^{*}\left( {t,y{\kern 1pt} *} \right)$ в случае, когда на множестве $Y$ реализуется именно изначально фиксируемое значение $y = y{\kern 1pt} *$:

Выражения (3.3)–(3.5) однозначным образом определяют зависимость $\psi _{n}^{*}$ от своих аргументов. При этом зависимость $\psi _{n}^{*}$ от ${{\bar {Q}}_{n}}\left( 0 \right)$ в (3.3) характеризуется представлением $\bar {Q}_{n}^{*}\left( {{{t}_{1}},y{\kern 1pt} *} \right)$ в (3.4), (3.5) в виде (2.33).

Подстановка (3.3) в выражение (2.3) для модального управления приводит к линейному закону синтеза оптимального регулятора с нестационарными коэффициентами обратных связей по измеряемому состоянию $\bar {Q}\left( t \right) = \left( {{{{\bar {Q}}}_{n}}\left( t \right)} \right)$, $n = \overline {1,{{N}_{1}}} $, в форме (1.6) в условиях реализации значения y = y*:

Здесь значения ${{T}_{{n1}}}$, ${{T}_{{n2}}}$ представляются, согласно (3.4), (3.5), известными функциями времени с фиксируемыми на протяжении процесса управления величинами ${{\bar {Q}}_{n}}\left( 0 \right)$ в (2.33), которые находятся по результатам наблюдения $\bar {Q}\left( t \right)$ в момент t = 0.

При наблюдении вектора $\bar {Q}\left( {t,y} \right)$ в условиях неопределенности величин $y \in Y$ при некотором заранее неизвестном значении $y = \tilde {y} = {\text{const}} \ne y{\kern 1pt} *$ реализуемый алгоритм обратной связи сохраняется в виде (3.6) с заменой $\bar {Q}\left( {t,y{\kern 1pt} *} \right)$ на $\bar {Q}\left( {t,\tilde {y}} \right)$:

в отличие от оптимального который определяется, подобно (3.6), для всех $\tilde {y} \in Y$. Однако оптимальный регулятор (3.8) нереализуем в рассматриваемой задаче робастной оптимизации, не предусматривающей использование идентификаторов значений $\tilde {y}$, из-за невозможности предварительного вычисления ${{T}_{{n1}}}\left( {t,\tilde {y}} \right)$, ${{T}_{{n2}}}\left( {t,\tilde {y}} \right)$ и ${{\varphi }_{n}}\left( {{{\mu }_{n}}\left( {\tilde {y}} \right),x} \right)$ для заведомо непредсказуемых величин $\tilde {y}$.

Поскольку алгоритму (3.6) соответствует оптимальное программное управление (2.15) ансамблем траекторий при $\tilde {y} = y{\kern 1pt} *$, то на основании (3.7), (3.8) и соотношений (2.34) выполняются неравенства:

согласно которым величина ${{J}_{1}}\left( {u\left( {\bar {Q}\left( {t,\tilde {y}} \right),y{\kern 1pt} *,x,t} \right),y{\kern 1pt} *} \right)$, определяемая законом обратной связи (3.7), не превышает верхней оценки достижимых значений J₂ при управлении (3.6) детерминированной моделью объекта. Отсюда следует, что синтез оптимального регулятора (3.7) можно считать гарантированным решением рассматриваемой задачи управления ансамблем траекторий управляемого процесса.

Переход в (3.7) от $\bar {Q}\left( {t,\tilde {y}} \right)$ к измеряемому выходу объекта ${{Q}_{u}}\left( {{{x}_{u}},t,\tilde {y}} \right) = \left( {Q\left( {{{x}_{{uj}}},t,\tilde {y}} \right)} \right)$ в r точках ${{x}_{{uj}}} \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$, $j = \overline {1,r} $, определяется в соответствии с (1.5) векторно-матричным уравнением наблюдения

В условиях $r < {{N}_{1}}$ неполного измерения состояния для восстановления вектора $\bar {Q}\left( {t,\tilde {y}} \right)$ по значениям ${{Q}_{u}}\left( {{{x}_{u}},t,\tilde {y}} \right)$ требуется построение наблюдателя точного или пониженного порядка [23]. Если по условиям требуемой точности моделирования объекта (1.4) можно ограничиться учетом только M первых слагаемых $\bar {Q}\left( {t,\tilde {y}} \right) = \left( {{{{\bar {Q}}}_{n}}\left( {t,\tilde {y}} \right)} \right)$, $n = \overline {1,M} $, с минимальным их числом $M < {{N}_{1}}$, необходимым для решения системы уравнений (2.29), (2.31) относительно вектора $\psi _{*}^{{\left( M \right)}}$, то $\bar {Q}\left( {t,\tilde {y}} \right)$ непосредственно определяется решением уравнения (3.10) относительно $\bar {Q}\left( {t,\tilde {y}} \right)$ при r = M, N₁ = = N = M:

Подстановка (3.11) в (3.7) приводит к линейному алгоритму синтеза с обратными связями по измеряемому выходу объекта:

где $\Phi _{u}^{{ - 1}}\left( {\tilde {y}} \right){{Q}_{u}}\left( {{{x}_{u}},t,\tilde {y}} \right)$ – матрица-строка; $\varphi \left( {y{\kern 1pt} *,x,t} \right)$ – матрица-столбец.

Аналогично (3.8) регулятор (3.12) нереализуем ввиду невозможности предварительного вычисления $\Phi _{u}^{{ - 1}}\left( {\tilde {y}} \right)$ для непредсказуемых заранее конкретных значений $\tilde {y} \in Y$. Замена $\Phi _{u}^{{ - 1}}\left( {\tilde {y}} \right)$ на $\Phi _{u}^{{ - 1}}\left( {y{\kern 1pt} *} \right)$ в (3.12) приводит в силу неравенств вида (3.9) к реализуемому гарантированному алгоритму управления

не превышающему верхней оценки критерия качества J₂ в (3.9).

В условиях (2.35)–(2.37) при ${{N}_{1}} = N = s$ управление $u{\kern 1pt} *\left( {x,t} \right)$ представляется в форме (2.38). Подстановка $\bar {u}_{n}^{*}\left( t \right)$ в (2.38) в виде (2.3), (3.3)–(3.5) приводит в таком случае вместо (3.7) и (3.13) к следующим алгоритмам синтеза оптимального регулятора с обратными связями по $\bar {Q}\left( {t,\tilde {y}} \right)$:

и по измеряемому выходу объекта: где аналогично (3.12) ${{\varphi }_{{0m}}}\left( {y{\kern 1pt} *,t} \right)$ – матрица-столбец.

4. Синтез оптимального регулятора для не полностью определенного объекта технологической теплофизики. В качестве примера, представляющего самостоятельный интерес, рассмотрим задачу синтеза оптимального управления температурным режимом нагрева неограниченной пластины в условиях интервальной неопределенности характеристик объекта [7, 10, 19–22].

Пусть температурное поле Q(x, t) неограниченной пластины описывается в процессе ее нагрева в зависимости от пространственной координаты x и времени t линейным неоднородным уравнением теплопроводности вида (1.1)–(1.3) в относительных единицах [19–21]:

где граничные условия (4.2) учитывают тепловые потери в окружающую среду с нулевой температурой на границе пластины x = 1 по закону конвективной теплопередачи с заданным значением $\alpha $ критерия Био. Здесь $u\left( {x,t} \right)$ в (4.1) – нестесняемое дополнительными ограничениями кусочно-непрерывное пространственно-временное воздействие по мощности внутреннего тепловыделения.

В характерной ситуации, когда вся информация о неизменных во времени величинах Q₀ и α в (4.2) исчерпывается сведениями об их предельно допустимых значениях ${{Q}_{{0\min }}}$, ${{Q}_{{0\max }}}$, ${{\alpha }_{{\min }}}$, ${{\alpha }_{{\max }}}$, получаем следующий вектор $y$ неопределенных факторов в (1.8), (1.9):

При этом управляемая величина $Q\left( {x,\bar {u},t,y} \right)$ представляется в форме ее разложения в ряд (1.9) по собственным функциям ${{\varphi }_{n}}\left( {x,y} \right) = \cos \left( {{{\mu }_{n}}\left( y \right),x} \right)$ [19–21]:

где ${{\mu }_{n}}$ – бесконечно возрастающая последовательность корней трансцендентного уравнения вычисляемых в зависимости от заданного значения α в условиях (4.3), а ${{\bar {Q}}_{n}}\left( {{{{\bar {u}}}_{n}},t,y} \right)$ определяется решением системы уравнений вида (1.4): где ${{\bar {Q}}^{{\left( 0 \right)}}}\left( {{{\mu }_{n}}} \right)$ – моды Q₀ в (4.2).

Зависимости ${{\mu }_{n}}\left( \alpha \right)$ в (4.5) и ${{\bar {Q}}^{{\left( 0 \right)}}}\left( {{{\mu }_{n}},{{Q}_{0}}} \right)$ в (4.6) определяют $Q\left( {x,\bar {u},t,y} \right)$ как сложную функцию y.

Требуется найти управление $u{\kern 1pt} *\left( {Q,x,t} \right)$ с обратной связью, являющееся решением минимаксной задачи оптимизации (1.12)–(1.14) при $Q{\kern 1pt} *{\kern 1pt} *\left( x \right) = Q{\kern 1pt} *{\kern 1pt} * = {\text{const}} > {{Q}_{0}}$.

4.1. Решение задачи программного управления. Процедура $\psi $-параметризации приводит к представлению $\psi {\kern 1pt} *\left( {{{t}_{1}}} \right)$ в форме (2.7). Для типичного в приложениях случая $\varepsilon = \varepsilon _{{\min }}^{{\left( 2 \right)}}$ в (2.17), (2.19) здесь следует принять M = 2, согласно (2.18), и тогда в соответствии с (2.7)

Примем здесь и всюду далее для большей простоты и наглядности получаемых результатов ${{N}_{1}} = N = 2$ в (4.4), ограничиваясь учетом только двух модальных переменных в сумме (4.4). При $\varepsilon = \varepsilon _{{\min }}^{{\left( 2 \right)}}$ получаем ${{R}_{x}} = M + 1 = 3$ в (2.29) в соответствии с правилом (2.23), образуя замкнутую систему равенств (2.29), (2.31) относительно неизвестных $\psi _{*}^{{\left( M \right)}}$; $x_{{jg}}^{0}$, $j = 1,2,3$, $g = \overline {1,{{R}_{{1x}}}} $, при заданных величинах $y_{{jg}}^{0}$ в (2.31).

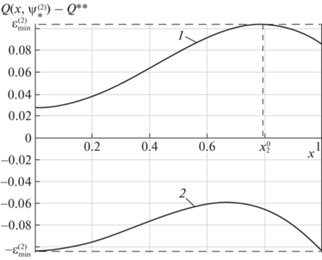
Физические закономерности поведения нестационарных температурных полей в оптимальном процессе нагрева пластины и альтернансные свойства $\psi _{*}^{{\left( 2 \right)}}$ однозначным образом определяют в рассматриваемом примере, подобно [19–21], при M = 2, $\varepsilon = \varepsilon _{{\min }}^{{\left( 2 \right)}}$, ${{Q}_{0}} = {\text{const}}$, $Q{\kern 1pt} *{\kern 1pt} * = {\text{const}}$ форму кривых результирующего распределения температуры $Q(x,\psi _{*}^{{(M)}},y)\, - \,Q{\kern 1pt} *{\kern 1pt} *$ по пространственной координате (рис. 1) для всех значений $y = \left( {{{Q}_{0}},\alpha } \right) \in Y$. Это позволяет заведомо идентифицировать в (2.29), (2.31) при ${{R}_{{1x}}} = 1$ координаты точек $x_{1}^{0} = 0$, $x_{2}^{0} = x_{{2g}}^{0} = x_{{21}}^{0} \in \left( {0,1} \right)$, $x_{3}^{0} = 1$; значения $y_{1}^{0} = \left( {{{Q}_{{0\min }}},{{\alpha }_{{\max }}}} \right)$, $y_{2}^{0}\,\, = \,\,y_{{2g}}^{0}\,\, = \,\,y_{{21}}^{0}\,\, = \,\,({{Q}_{{0\max }}},{{\alpha }_{{\min }}})$; $y_{3}^{0} = y_{1}^{0}$ и знаки $Q(x_{j}^{0},\psi _{*}^{{(2)}},y_{j}^{0})$ – Q**, $j = \overline {1,3} $. В результате равенства (2.29), (2.31) редуцируются к замкнутой системе линейных по $\tilde {\psi }_{1}^{*}$, $\tilde {\psi }_{2}^{*}$ уравнений:

разрешаемой относительно $\psi _{*}^{{\left( 2 \right)}} = (\tilde {\psi }_{1}^{*},\tilde {\psi }_{2}^{*})$ и $x_{2}^{0}$ при $x_{1}^{0} = 0$, $x_{3}^{0} = 1$. Здесь $Q(x,\psi _{*}^{{\left( 2 \right)}},y)$ при $y = y_{j}^{0}$, j = 1, 2, 3, находится в форме (4.4) при t = t₁ с подстановкой ${{\bar {Q}}_{n}}\left( {{{{\bar {u}}}_{n}},{{t}_{1}},y} \right)$ в виде ${{\bar {Q}}_{n}}(\psi _{*}^{{\left( 2 \right)}},y)$ в (2.33). Значения ${{B}_{n}}$ и ${{B}_{{1n}}}$ вычисляются по выражениям (2.14) в зависимости от блочных компонентов матричной экспоненты (2.6) системы уравнений (2.4), которые в свою очередь определяются по описанной в [13] схеме для $y = y_{j}^{0}$.

В силу базовых свойств температурного распределения $Q(x,\psi _{*}^{{\left( 2 \right)}},y)$ значение $y_{{e1}}^{0}$ в (2.30), на котором достигается оптимальная величина ${{J}_{2}}(\psi _{*}^{{\left( 2 \right)}})$ квадратичного критерия качества, оказывается равной, подобно [19–21], величине $y{\kern 1pt} * = y_{2}^{0} = \left( {{{Q}_{{0\max }}},{{\alpha }_{{\min }}}} \right)$. В таком случае ${{J}_{2}}(\psi _{*}^{{\left( 2 \right)}})$ непосредственно находится из уравнения (2.30) при найденном значении $\psi _{*}^{{\left( 2 \right)}}$.

В итоге оптимальное программное управление определяется в виде (2.15) с подстановкой (2.13), (2.14) при $\tilde {y} = y{\kern 1pt} * = y_{2}^{0} = \left( {{{\alpha }_{{\min }}},{{Q}_{{0\max }}}} \right)$ и известных значениях ${{A}_{{nij}}}$, ${{\hat {A}}_{{nij}}}$; $i,j = 1,2$.

4.2. Аналитическое конструирование оптимального регулятора. Согласно (3.7), (4.3), получаем линейный с нестационарными коэффициентами алгоритм оптимального управления с обратными связями по реализуемому состоянию $\bar {Q}\left( {t,\tilde {y}} \right) = \left( {{{{\bar {Q}}}_{n}}\left( {t,\tilde {y}} \right)} \right)$, $n = 1,2$:

с известными функциями ${{T}_{{n1}}}\left( {y{\kern 1pt} *,t} \right)$, ${{T}_{{n2}}}\left( {y{\kern 1pt} *,t} \right)$ в (3.4), (3.5); значениями $\psi _{*}^{{\left( 2 \right)}} = (\tilde {\psi }_{1}^{*},\tilde {\psi }_{2}^{*})$, найденными в условиях ${{N}_{1}} = N = 2$ в (4.4), и собственными функциями ${{\varphi }_{n}}\left( {{{\mu }_{n}}\left( {y{\kern 1pt} *} \right),x} \right) = {{\varphi }_{n}}\left( {{{\mu }_{n}}\left( {{{\alpha }_{{\min }}}} \right),x} \right)$, определяемыми, согласно (4.4), (4.5), в следующем виде: где ${{\mu }_{n}}\left( {{{\alpha }_{{\min }}}} \right)$ – корни уравнения (4.5) при $\alpha = {{\alpha }_{{\min }}}$.

При наличии двух измерителей выхода объекта в точках ${{x}_{{u1}}}$, ${{x}_{{u2}}} \in \left[ {0,1} \right]$ получаем систему двух линейных уравнений (3.10) при $\tilde {y} = y{\kern 1pt} *$:

разрешаемую относительно ${{\bar {Q}}_{1}}\left( {t,y{\kern 1pt} *} \right)$, ${{\bar {Q}}_{2}}\left( {t,y{\kern 1pt} *} \right)$ по известным значениям наблюдаемых величин ${{Q}_{u}}\left( {{{x}_{u}},t,y{\kern 1pt} *} \right)$.

Подстановка решения системы уравнений (4.9) в (4.7) определяет искомый алгоритм синтеза оптимального регулятора с обратными связями по наблюдаемому выходу объекта в форме (3.13), где в данном примере ${{x}_{u}} = \left( {{{x}_{{u1}}},{{x}_{{u2}}}} \right)$, $\Phi _{u}^{{ - 1}}\left( {y{\kern 1pt} *} \right)$ – 2 × 2-матрица и матрица-столбец $\varphi \left( {y{\kern 1pt} *,x,t} \right)$, состоит из двух элементов при n = 1, 2 в (3.12).

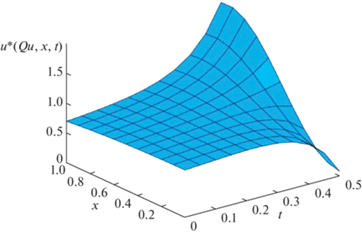
На рис. 1, 2 представлены некоторые расчетные результаты, полученные при $Q{\kern 1pt} *{\kern 1pt} * = 0.5$; ${{\alpha }_{{\min }}} = 0.3$; ${{\alpha }_{{\max }}} = 0.7$; ${{Q}_{{0\min }}} = 0$; ${{Q}_{{0\max }}} = 0.15$; ${{t}_{1}} = 0.5$ при ${{x}_{{u1}}} = 1$, ${{x}_{{u2}}} = 0$.

На рис. 1 показано результирующее состояние ансамбля траекторий оптимального процесса (1 – $\alpha = {{\alpha }_{{\min }}}$; ${{Q}_{0}} = {{Q}_{{0\max }}}$; 2 – $\alpha = {{\alpha }_{{\max }}}$; ${{Q}_{0}} = {{Q}_{{0\min }}}$; $\tilde {\psi }_{1}^{*} = 2.12$; $\tilde {\psi }_{2}^{*} = - 1.40$; $\varepsilon _{{\min }}^{{\left( 2 \right)}} = 0.104$).

Рисунок 2 иллюстрирует в условиях реализации неизменных во времени значений $\tilde {y} = y{\kern 1pt} * = \left( {{{\alpha }_{{\min }}},{{Q}_{{0\max }}}} \right)$ поведение управляющих воздействий $u\left( {{{Q}_{u}}\left( {{{x}_{u}},t,y{\kern 1pt} *} \right),y{\kern 1pt} *,x,t} \right)$ на пространственно-временной плоскости, изменяющихся во времени по алгоритму (3.13) в зависимости от текущих значений измеряемых сигналов обратной связи в точках ${{x}_{{u1}}} = 1$, ${{x}_{{u2}}} = 0$ с нестационарными коэффициентами передачи.

Заключение. Предлагаемые методы решения линейно-квадратичных задач робастной оптимизации пространственно-временного управления системами с распределенными параметрами параболического типа в условиях интервальной неопределенности параметрических характеристик объекта разработаны применительно к характерным для приложений оценкам целевых множеств конечных состояний ансамбля траекторий управляемой системы в равномерной метрике. Полученные уравнения субоптимальных регуляторов, сводимые к линейным алгоритмам обратной связи по измеряемому состоянию объекта с нестационарными коэффициентами передачи, характеризуются достигаемыми значениями критерия оптимальности, не превышающими их максимально возможные величины в исследуемых условиях неопределенности, и тем самым реализуют стратегию управления по принципу наилучшего гарантированного результата.