Известия РАН. Теория и системы управления, 2023, № 1, стр. 44-55
ВОССТАНОВЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
О. Н. Корсун a, *, А. В. Стуловский a
a ФАУ “ГосНИИАС”
Москва, Россия
* E-mail: marmotto@rambler.ru
Поступила в редакцию 05.08.2022
После доработки 21.09.2022
Принята к публикации 26.09.2022
- EDN: JAAOFU
- DOI: 10.31857/S0002338823010055
Аннотация
Рассмотрен метод решения задачи восстановления сигналов, основанный на прямом поиске оптимального программного управления. Его основу составляет параметризация искомых сигналов и нахождение решения путем численной оптимизации в конечномерном пространстве с использованием какого-либо генетического или популяционного алгоритма. В целях проверки работоспособности метода приводится задача нахождения угловых скоростей и углов ориентации летательного аппарата по имеющимся на борту данным при отсутствии прямых измерений. Проводится сравнение различных вариантов параметризации сигналов на основе Эрмитовых кубических сплайнов.
Введение. Миниатюризация приемников систем спутниковой навигации и рост вычислительных мощностей микроконтроллеров позволили малоразмерным беспилотным летательным аппаратам за последние несколько лет достигнуть уровня автономных систем [1]. Высокий уровень автоматизации накладывает строгие требования на точность оценки пространственного положения объекта управления. Вместе с тем малый размер таких летательных аппаратов (ЛА) ограничивает возможность установки дополнительного оборудования.
Существуют разные способы преодоления данного противоречия. Предлагается рассмотреть подход, заключающийся в восстановлении измерительных сигналов отсутствующих датчиков [2–7] на основе известных из динамики полета математических моделей, связывающих различные полетные параметры.
Восстановление сигналов основано на прямом методе оптимального управления, в котором искомые сигналы представляются в виде полиномиальных или сплайн-аппроксимаций. Параметры сигналов находятся путем решения оптимизационной задачи в конечномерном пространстве. В качестве метода оптимизации используется алгоритм роя частиц [8, 9], а для аппроксимации сигналов применяются Эрмитовы сплайны 3-го порядка дефектов 1 и 2 [10]. Отметим, что традиционно под задачей восстановления данных и проверки совместимости с помощью дифференциальных уравнений движения ЛА [11] понимается более простая задача, которая предполагает, что все основные полетные параметры измеряются непосредственно. Это означает, что входные сигналы известны и решение получается путем численного интегрированием соответствующих дифференциальных уравнений [12, 13].
1. Постановка задачи восстановления параметров полета. Рассмотрим две задачи, связанные с оценкой значений угловых скоростей и углов ориентации ЛА. В первой из них требуется найти оценки угловых скоростей в предположении, что измеряются только значения углов ориентации. Соотношения, связывающие эти величины, хорошо известны [11]. Это кинематические уравнения Эйлера:
(1.1)
$\begin{gathered} \dot {\vartheta } = {{\omega }_{y}}\sin \gamma + {{\omega }_{z}}\cos \gamma , \\ \dot {\gamma } = {{\omega }_{x}} - tg\vartheta ({{\omega }_{y}}\cos \gamma - {{\omega }_{z}}\sin \gamma ), \\ \dot {\psi } = \frac{1}{{\cos \vartheta }}({{\omega }_{y}}\cos \gamma - {{\omega }_{z}}\sin \gamma ), \\ \end{gathered} $Отметим, что для данной задачи известно простое решение, основанное на численном дифференцировании значений углов ориентации [14, 15]. При этом существенно усиливаются случайные составляющие погрешностей измерений, поэтому его практическое применение ограничено. В предлагаемом методе этот недостаток отсутствует.
Во второй задаче требуется восстановить углы ориентации и угловые скорости ЛА при отсутствии на борту соответствующих датчиков, т.е. без использования прямых измерений. Для ее решения используются измерения перегрузок в связанной системе координат и три компоненты скорости ЛА в земной системе координат, измеряемые навигационной системой, спутниковой или инерциальной.
Пусть известны значения перегрузок в связанной системе координат. Это позволяет определить проекции ускорения на ее оси [14]:
(1.2)
$\begin{gathered} {{a}_{x}} = g({{n}_{x}} - \sin \vartheta ), \\ {{a}_{y}} = g({{n}_{y}} - \cos \vartheta \cos \gamma ), \\ {{a}_{z}} = g({{n}_{z}} + \cos \vartheta \sin \gamma ), \\ \end{gathered} $Воспользовавшись матрицей перехода [11], проекции ускорений можно пересчитать из связанной системы в нормальную земную. Далее, проинтегрировав проекции ускорения в земной системе координат, получим значения проекций скорости:
(1.3)
$\begin{gathered} {{V}_{{xg}}}(t) = {{V}_{{xg}}}({{t}_{0}}) + \int\limits_{{{t}_{0}}}^t {{{a}_{{xg}}}(\tau )d\tau ,} \\ {{V}_{{yg}}}(t) = {{V}_{{yg}}}({{t}_{0}}) + \int\limits_{{{t}_{0}}}^t {{{a}_{{yg}}}(\tau )d\tau } , \\ {{V}_{{zg}}}(t) = {{V}_{{zg}}}({{t}_{0}}) + \int\limits_{{{t}_{0}}}^t {{{a}_{{zg}}}(\tau )d\tau } , \\ \end{gathered} $Выражения (1.2) и (1.3) определяют связи между перегрузками и проекциями скорости, которые зависят от угловой ориентации ЛА, в первую очередь от углов тангажа и крена. Благодаря этому можно найти оценки угловых величин, т.е. углов Эйлера и угловых скоростей, которые, согласно принятому допущению, не измеряются.
2. Общий метод решения задачи. В работе используется метод нахождения сигналов, аналогичный прямому методу решения задач оптимального управления [9, 16, 17]. Он основан на параметризации искомого сигнала и сведении решаемой задачи к задаче численной оптимизации [18].
Пусть требуется вычислить значения угловых скоростей на рассматриваемом промежутке времени. Предполагается, что искомый сигнал – угловые скорости, которые являются достаточно гладкими функциями времени, чтобы их можно было с хорошей точностью приблизить кубическими сплайнами. В таком случае определение параметров сплайнов позволит восстановить искомые сигналы.
Отличие приведенной задачи от задачи аппроксимации состоит в том, что за исключением класса рассматриваемых функций о самом сигнале ничего не известно. Поэтому для их восстановления используются соотношения динамики полета, зависящие от измеряемых сигналов. Очевидно, что в летном эксперименте измерения всех параметров движения ЛА содержат погрешности, в первую очередь постоянные. Их влияние на результат восстановления полетных параметров необходимо исследовать отдельно. Однако следует отметить, что для восстанавливаемых сигналов предлагаемый метод решает проблему погрешностей измерения кардинальным образом. Действительно, если при получении конечного результата данные какого-либо измерительного канала не используются, то и его погрешности на этот результат не влияют.
2.1. Математическая модель. Сформулированная таким образом задача нахождения параметров сплайнов является примером задачи численной параметрической оптимизации и в общем виде может быть записана как
где x – вектор фазовых координат или выходных сигналов; u – вектор управления, или входной сигнал, который однозначно определяется вектором параметров ${\mathbf{a}}$; $U$ – множество допустимых значений вектора управления. При этом полагаем, что нелинейная модель объекта управления, связывающая входные и выходные сигналы, задана как и начальные условия ${\mathbf{x}}({{t}_{0}}) = {{{\mathbf{x}}}_{{\mathbf{0}}}}$ принимаются известными.Из постановки задачи следует, что искомое управление должно обеспечивать минимальные отклонения выходных сигналов системы от заданных на рассматриваемом интервале времени. Это позволяет составить целевой функционал (2.1) следующим образом:
(2.3)
$J({\mathbf{x}},{\mathbf{u}}({\mathbf{a}})) = J({\mathbf{x}},{\mathbf{\tilde {x}}},{\mathbf{u}}({\mathbf{a}})) = \int\limits_{{{t}_{0}}}^T {{{{({\mathbf{x}}(t) - {\mathbf{\tilde {x}}}(t))}}^{T}}{\mathbf{K}}(} {\mathbf{x}}(t) - {\mathbf{\tilde {x}}}(t))\,dt,$Поскольку в общем случае размерность вектора ${\mathbf{a}}$ может быть достаточно велика, решать сформулированную задачу (2.1)–(2.3) предлагается численно [19] с помощью популяционных или эволюционных алгоритмов [8, 20–24]. В работе использовался метод роя частиц [20, 21, 25–27].
Конкретный вид математических моделей динамических систем, рассматриваемых в данной
работе, и детальное описание двух решаемых задач представлены выше в разд. 1. Для
первой задачи – это дифференциальные уравнения (1.1). В обозначениях функционала (2.3) вектору фазовых координат соответствуют углы ориентации
ЛА 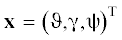 , вектору управления – угловые скорости ${\mathbf{u}} = {{({{{{\omega }}}_{x}}{\text{,}}{{{{\omega }}}_{y}}{\text{,}}{{{{\omega }}}_{z}})}^{{\text{T}}}}$. Для второй задачи – это дифференциальные уравнения (1.1) и (1.3) с учетом алгебраических соотношений (1.2). В этом случае фазовые координаты представляют
собой проекции скорости ${\mathbf{x}} = {{({{V}_{{xg}}}{\text{,}}{{V}_{{yg}}}{\text{,}}{{V}_{{zg}}})}^{{\text{T}}}}$, а вектор управления – проекции перегрузок u = = ${{({{n}_{x}}{\text{,}}{{n}_{y}}{\text{,}}{{n}_{z}})}^{{\text{T}}}}$. В обеих задачах желаемыми фазовыми координатами ${\mathbf{\tilde {x}}}$ являются измеренные в эксперименте значения фазовых координат. Роль вектора параметров
${\mathbf{a}}$ исполняют коэффициенты сплайнов, обсуждению которых посвящен следующий раздел.
, вектору управления – угловые скорости ${\mathbf{u}} = {{({{{{\omega }}}_{x}}{\text{,}}{{{{\omega }}}_{y}}{\text{,}}{{{{\omega }}}_{z}})}^{{\text{T}}}}$. Для второй задачи – это дифференциальные уравнения (1.1) и (1.3) с учетом алгебраических соотношений (1.2). В этом случае фазовые координаты представляют
собой проекции скорости ${\mathbf{x}} = {{({{V}_{{xg}}}{\text{,}}{{V}_{{yg}}}{\text{,}}{{V}_{{zg}}})}^{{\text{T}}}}$, а вектор управления – проекции перегрузок u = = ${{({{n}_{x}}{\text{,}}{{n}_{y}}{\text{,}}{{n}_{z}})}^{{\text{T}}}}$. В обеих задачах желаемыми фазовыми координатами ${\mathbf{\tilde {x}}}$ являются измеренные в эксперименте значения фазовых координат. Роль вектора параметров
${\mathbf{a}}$ исполняют коэффициенты сплайнов, обсуждению которых посвящен следующий раздел.
2.2. Эрмитовы сплайны. Предлагаемый метод использует параметризацию искомого сигнала. Поскольку угловые скорости являются достаточно гладкими сигналами, перспективным выглядит представить их в виде сплайнов. Этому способствуют достигнутые результаты в решении задач сплайн-аппроксимации сигналов.
Учитывая характеристики рассматриваемых сигналов, в качестве их модели были предложены кубические сплайны, прежде всего так называемые кубические сплайны дефекта 2, именуемые также эрмитовыми. Особенностью данного вида сплайнов является, как следует из названия, разрывность второй производной, что приводит к необходимости задавать в узлах сплайна значения как самой функции, так и ее первой производной. Кратко приведем здесь их формулы [10].
Пусть на некотором интервале $t \in [{{t}_{1}},\;{{t}_{M}}]$ заданы М значений ${{t}_{i}},\;i = \overline {1,M} $, которые называются узлами сплайна. Тогда для точки t из отрезка $[{{t}_{i}},\;{{t}_{{i + 1}}}]$ значение сплайна рассчитывается по формуле
Значения коэффициентов ${{f}_{i}},\;{{f}_{{i + 1}}},\;f_{i}^{'},\;f_{{i + 1}}^{'}$ могут быть определены с помощью численной оптимизации. В рассматриваемой задаче для этой цели применялся популяционный алгоритм роя частиц.
В качестве материала для сравнения использовался вариант кубических сплайнов, называемый интерполяционным кубическим сплайном. От приведенного выше сплайна он отличается дополнительным требованием непрерывности второй производной в узлах и, следовательно, меньшим дефектом:
Это требование позволяет получить систему из M – 2 уравнений, которая может быть разрешена относительно значений производных сплайна в узлах методом “прогонки” [10].
Неизвестными параметрами для этого сплайна являются только значения самой функции в узлах сплайна и ее производной на концах участка, что позволяет существенно сократить размерность пространства поиска. Недостатком выступает возрастающее требование к гладкости функций и более узкий класс приближаемых сигналов.
2.3. Метод роя частиц. Для решения задачи численной параметрической оптимизации был выбран алгоритм, называемый методом роя частиц (particle swarm optimization) [25, 26].
Общую концепцию алгоритмов роя можно описать следующим образом. Сначала формируется пространство поиска, имеющее размерность, которая равна числу искомых параметров. Таким образом каждой точке этого пространства соответствует единственное решение рассматриваемой задачи. Затем в пространство поиска “вбрасываются” частицы – случайным образом выбирается несколько точек пространства. Кроме того, для каждой из них задается вектор скорости, величина и направление которого выбираются случайным образом. Для каждой частицы определяется соответствующее решение и вычисляется значение целевого функционала.
На каждом последующем шаге алгоритма частицы смещаются в поисковом пространстве, причем направления и модуль этого смещения определяются как изначальной скоростью, которой располагала частица, так и положением частиц роя, имеющих лучшие значения целевого функционала. Учет таких влияний с помощью весовых коэффициентов позволяет добиться от алгоритма требуемого сочетания между покрытием пространства поиска и тщательностью исследования областей перспективных решений [20].
Вычисления прекращаются, если на протяжении определенного времени не происходит заметного улучшения качества получаемых решений.
Если распространенным представлением для градиентных методов является шар, движущийся под действием силы тяжести на поверхности, кривизна которой определяется значением минимизируемого функционала, то для алгоритма роя таких шаров оказывается несколько и их движение определяется начальными условиями и информацией о положении других шаров, а не потенциалом некого единого поля.
Очевидным недостатком метода роя частиц, впрочем, как всего семейства алгоритмов популяционной оптимизации, является субоптимальность получаемых решений [10, 28]. Его достоинство – простота формализации задачи и малое время, требуемое для получения решения.
Выбор данного метода в рассматриваемой задаче определяется, прежде всего, предполагаемой областью применения, а также тем, что для приближения сигналов с достаточной точностью требуется задание значительного числа параметров (от 16 до 24 для каждого сигнала), что придает задаче большую размерность, затрудняя ее решение градиентными методами.
Более подробное описание применявшегося метода приводится в Приложении.
3. Описание экспериментов. Эксперимент проводился в несколько этапов. Первоначально определялись требования к сплайнам, такие, как необходимое количество узлов сплайнов и требования к пространству поиска. Затем решалась задача восстановления значений угловых скоростей с привлечением модели (1.1) и сравнение возможных параметризаций сплайнов. Наконец, аналогичное сравнение выполнялось для второй задачи при помощи математической модели (1.2)–(1.3). В качестве матрицы весовых коэффициентов K (2.3) была выбрана единичная матрица, хотя в общем случае она может иметь и более сложную структуру.
Эксперименты показали, что на персональном компьютере, оснащенном процессором Intel Core 2 Duo с частотой 2.4 ГГц и оперативной памятью 1.99 Гб, определение 72 параметров (в случае трех сигналов с 12 узлами для каждого) занимало порядка 30–40 мин.
3.1. Определение параметров сплайнов. На предварительном этапе эксперимента требовалось убедиться, что выбранная параметризация позволяет с достаточной точностью описывать искомые сигналы, подбирая необходимое число узлов на участке аппроксимации.
При решении этой проблемы необходимо учитывать характеристики рассматриваемого сигнала. Например, сигналы угловых скоростей являются более высокочастотными, чем сигналы углов ориентации. Угловые скорости крена и тангажа подвержены более динамичным изменениям, чем угловая скорость угла рыскания, что связано с разделением на движения центра масс и относительно центра масс.
Задача аппроксимации решалась для каждого рассматриваемого сигнала. По ее результатам было определено необходимое количество узлов сплайна, а также параметры пространства поиска, которые позволяли восстановление сигнала с достаточной точностью. На участок времени длиной 7 с для угловых скоростей тангажа и крена использовалось 12 узлов и 8 узлов для угловой скорости рыскания.
Полученные решения задачи аппроксимации приводятся на рис. 1 и 2.
Рис. 1.
Значения угловой скорости рыскания на рассматриваемом участке, исходные данные (сплошная линия) и полученные при решении задачи аппроксимации с 8 узлами (штрихпунктирная линия)
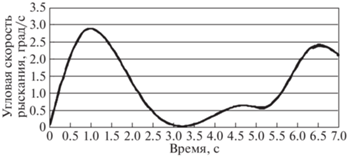
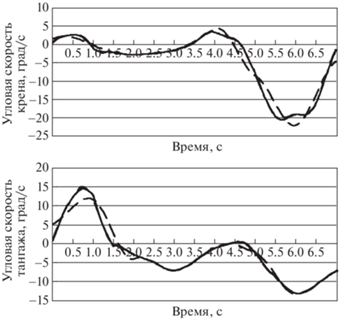
Рис. 2.
Значения угловых скоростей тангажа и крена, исходные данные (сплошная линия) и полученные при решении задачи аппроксимации с 8 (штриховая линия) и 12 узлами (штрихпунктирная линия)
Из рис. 1 видно, что уже для 8 узлов решение с достаточной точностью воспроизводит исходный сигнал угловой скорости рыскания. Поэтому увеличение числа узлов для угловой скорости рыскания является нецелесообразным.
Для двух других угловых скоростей (как можно видеть на рис. 2) для достаточно точного воспроизведения сигнала требуется 12 узлов, тогда как при меньшем их количестве возникают заметные погрешности. Этот вывод подтверждается и данными табл. 1, где приводятся соответствующие среднеквадратические отклонения (СКО) рассогласований. При выбранном количестве узлов истинное значение и аппроксимация на графиках уже практически не различимы визуально.
Таблица 1.
Значения СКО рассогласований для угловых скоростей тангажа и крена ЛА при аппроксимации их сплайнами с разным количеством узлов
| Измеряемая величина, град/с | Для сплайна с 12 узлами | Для сплайна с 8 узлами |
|---|---|---|
| Угловая скорость крена | 0.17 | 1.47 |
| Угловая скорость тангажа | 0.21 | 1.37 |
По результатам решения задачи аппроксимации можно заметить, что в отсутствие шумов проявляется очевидное соответствие между ростом количества узлов и улучшением качества получаемого приближения.
3.2. Восстановление значений угловых скоростей на основе кинематических уравнений Эйлера. После того как были определены условия, позволяющие добиться достаточного качества аппроксимации, решалась основная задача – восстановление сигналов угловых скоростей при заданных значениях углов ориентации на основе модели (1.1) (уравнений Эйлера).
Поиск сигналов производился в классе Эрмитовых сплайнов со значениями дефектов 1 и 2. Сравнение двух видов сплайнов производилось при одинаковом числе узлов. Как можно видеть на рис. 3, Эрмитов сплайн дефекта 2 обеспечивает более точное приближение, чем интерполяционный кубический сплайн.
Рис. 3.
Значения угловых скоростей (сплошная линия), воспроизведенные с помощью интерполяционного кубического сплайна (штриховая линия) и Эрмитова кубического сплайна (штрихпунктирная линия)
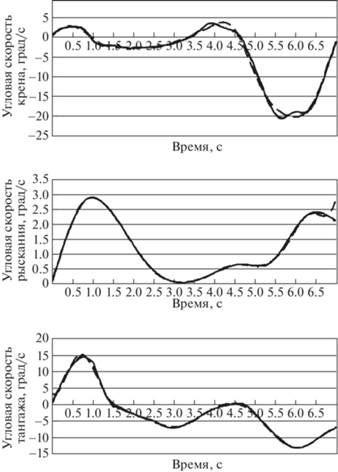
Если рассмотреть полученные при решении задачи СКО, приведенные в табл. 2, то можно видеть, что Эрмитов кубический сплайн позволяет добиться меньшего отклонения, особенно явно в случае угловой скорости крена.
Таблица 2.
Значения СКО для угловых скоростей ЛА при поиске сигналов по значениям углов ориентации
| Измеряемая величина, град/с | Эрмитов кубический сплайн дефекта 2 | Кубический интерполяционный сплайн дефекта 1 |
|---|---|---|
| Угловая скорость крена | 0.17 | 0.7 |
| Угловая скорость рыскания | 0.02 | 0.07 |
| Угловая скорость тангажа | 0.21 | 0.51 |
Объяснением может служить то, что он представляет более широкий класс функций за счет отсутствия требования непрерывности второй производной и является более вариативным благодаря большему числу изменяемых параметров. В свою очередь большее число коэффициентов увеличивает размерность решаемой задачи, затрудняя сходимость решения и увеличивая время на вычисления. Заметное преимущество применения интерполяционного кубического сплайна заключается в необходимости задавать в узлах только значения самой функции. За счет этого количество искомых параметров снижается примерно вдвое.
3.3. Восстановление значений углов ориентации по информации о проекциях перегрузки и скорости. В данном случае используется модель (1.2), (1.3). Задача несколько усложняется, так как одних выходных сигналов – проекций скорости в земной системе координат – оказывается недостаточно для определения значения угла рыскания, а оценки углов тангажа и крена имеют существенные погрешности (рис. 4).
Рис. 4.
Значения углов ориентации ЛА, заданные (сплошная линия) и полученные при решении задачи оптимизации (штриховая линия)
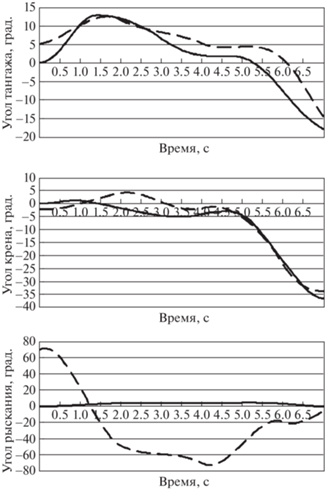
Для повышения точности приближения требуется дополнительная информация, например, значения угла скольжения. Как можно видеть на рис. 5, учет угла скольжения позволяет существенно улучшить качество оценок.
Рис. 5.
Значения углов ориентации при известном угле скольжения, исходные данные (сплошная линия), полученные при использовании интерполяционного сплайна (штриховая линия) и Эрмитова кубического сплайна
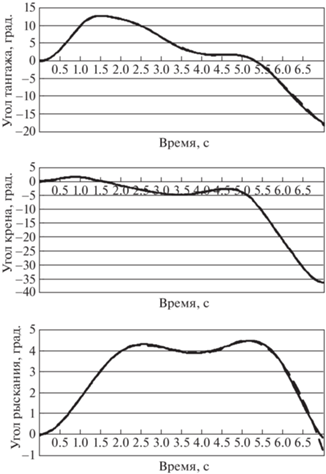
Сравнение сплайнов осуществлялось, как и в предыдущем случае, для равного числа узлов. Угол скольжения считался известным. В условиях рассматриваемой задачи оба сплайна дают сходные результаты (рис. 5).
Полученные СКО приводятся в табл. 3.
Таблица 3.
Значения СКО для углов ориентации и угловых скоростей ЛА при поиске сигналов по перегрузкам и проекциям скорости
| Измеряемая величина | Эрмитов кубический сплайн дефекта 2 | Кубический интерполяционный сплайн дефекта 1 |
|---|---|---|
| Угол тангажа, град. | 0.2 | 0.18 |
| Угол крена, град. | 0.11 | 0.17 |
| Угол рыскания, град. | 0.1 | 0.03 |
| Угловая скорость крена, град/с | 0.55 | 0.96 |
| Угловая скорость рыскания, град/с | 0.14 | 0.09 |
| Угловая скорость тангажа, град/с | 1.03 | 0.94 |
Визуальный анализ графиков и данных таблицы показывает, что вид сплайна существенного влияния на точность не оказывает.
Итак, проведенные эксперименты показали, что предложенный метод обеспечивает восстановление полетных параметров, для которых отсутствуют прямые измерения. Положительный эффект достигается за счет использования моделей динамики полета, задающих связь между параметрами движения. Установлено также, что точность результатов существенно зависит от задаваемого числа узлов сплайнов.
Полученные по результатам моделирования погрешности в основном не превышают 0.2 град. для углов ориентации ЛА и 1 град/с для угловых скоростей. Очевидно, что эта точность существенно уступает прямым измерениям (погрешность измерения углов ориентации обычно не превышает угловой минуты, угловых скоростей – 0.1 град/с). Таким образом, метод имеет смысл применять при отсутствии прямых измерений полетных параметров.
Заключение. Рассматривается метод восстановления входных сигналов системы при условии, что математическая модель системы задана. Он опирается на идеи прямого метода решения задач оптимального управления, а именно на параметризацию искомого сигнала и сведение приведенной задачи к задаче численной оптимизации.
В качестве примера применения метода описываются задачи восстановления угловых скоростей ЛА по известным значениям углов ориентации и углов ориентации и угловых скоростей по значениям перегрузок в связанной системе координат и проекций скорости в земной системе координат. Кроме того, в этих задачах проводится сравнение двух различных параметризаций: Эрмитовых сплайнов дефектов 1 и 2. Основываясь на полученных результатах, делается вывод о целесообразности использования Эрмитового сплайна дефекта 2, в случае если дополнительные расходы времени на вычисление и памяти допустимы.
Проведенные экспериментальные исследования также показали, что точность метода восстановления уступает точности прямых измерений. Поэтому преимущества данного подхода проявляются при отказах датчиков или в случае отсутствия на борту соответствующих датчиков, что особенно характерно для беспилотных ЛА. Итоговые рекомендации по применению предложенного подхода – следует сформировать практическое решение нескольких конкретных навигационных задач.
Список литературы
Биард Р.У., МакЛэйн Т.У. Малые беспилотные летательные аппараты: теория и практика. М.: Техносфера, 2015. 311 с.
Корсун О.Н., Данеко А.И., Мотлич П.А., Ом М.Х. Оценка углов атаки и скольжения беспилотного летательного аппарата при отсутствии датчиков аэродинамических углов // Мехатроника, автоматизация, управление. 2022. № 5. С. 274–280.
Пушков С.Г., Ловицкий Л.Л., Корсун О.Н. Методы определения скорости ветра при проведении летных испытаний авиационной техники с применением спутниковых навигационных систем // Мехатроника, автоматизация, управление. 2013. № 9. С. 65–70.
Харьков В.П. Дискретно-непрерывный алгоритм определения высотно-скоростных параметров полета ЛА // Инновационные, информационные и коммуникационные технологии. 2019. № 1. С. 330–333.
Падерин Ф.Г. Комплексная обработка информации в бортовом навигационном комплексе БПЛА с использованием метода одновременной навигации и составления карты (SLAM) // Труды МИЭА. Навигация и управление летательными аппаратами. 2017. № 19. С. 79–87.
Жарков М.В., Веремеенко К.К., Антонов Д.А., Кузнецов И.М. Вычисление параметров ориентации по интерферометрическим неоднозначным фазовым измерениям спутниковых навигационных систем и измерениям абсолютной угловой скорости // Гироскопия и навигация. 2018. № 3(102). С. 54–68.
Богдановский С.В., Симонов А.Н., Севидов В.В. Поляризационный способ определения ориентации БЛА // Успехи современной радиоэлектроники. 2017. № 10. С. 15–19.
Davis L. Handbook of Genetic Algorithms. N. Y., USA: Van Nostrand Reinhold, 1991. 385 p.
Методы классической и современной теории автоматического управления / Под ред. К.А. Пупкова, Н.Д. Егупова. М.: Изд. МГТУ им. Баумана, 2004. 656 с.
Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. 352 с.
ГОСТ 20058-80. Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. М.: Изд-во стандартов, 1981. 54 с.
Klein V., Morelli E. Aircraft System Identification. Theory and Practice. Reston: AIAA, 2006. 484 p.
Корсун O.H., Мотлич П.А. Оценка погрешностей бортовых измерений на основе уравнений движения самолета // Вестник метролога. 2019. № 1. С. 5–8.
Аэродинамика, устойчивость и управляемость сверхзвуковых самолетов / Под ред. Г.С. Бюшгенса. М.: Наука. Физмалит, 1998. 816 с.
Овчаренко В.Н. Аэродинамические характеристики летательных аппаратов: идентификация по полетным данным. М.: ЛЕНАНД, 2019. 236 с.
Rao A.V. Survey of Numerical Methods for Optimal Control // Advances Astronautical Sciences. 2010. V. 135. P. 497–528.
Корсун О.Н., Стуловский А.В. Прямой метод формирования оптимального программного управления летательным аппаратом // Изв. РАН. ТиСУ. 2019. № 2. С. 75–89.
Hull D.G. Conversion of Optimal Control Problems into Parameter Optimization Problems // J. Guidance, Control, Dynamics. 1997. V. 20. № 1. P. 57–60.
Conway B.A. A Survey of Methods Available for Numerical Optimization of Continuous Dynamic Systems // J. Optimization Theory Appl. 2012. V. 152. № 2. P. 271–306.
Nature-inspired Optimizers: Theories, Literature Reviews and Applications / Eds S. Mirjalili, J.S. Dong, A. Lewis. Switzerland, AG: Springer Nature, 2020. 239 p.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд. МГТУ им. Баумана, 2016. 448 с.
Степанов Д.В. Популяционные алгоритмы в задачах оптимального управления // Системы управления и обработки информации. 2013. № 26. С. 118–127.
Дивеев А.И. Гибридный эволюционный алгоритм для решения задачи оптимального управления // Вопросы теории безопасности и устойчивости систем. 2021. № 23. С. 3–12.
Diveev A., Shmalko E. Comparison of Direct and Indirect Approaches for Numerical Solution of the Optimal Control Problem by Evolutionary Methods // Communications in Computer and Information Science. 2020. V. 1145 CCIS. P. 180–193.
Eberhardt R.C., Kennedy J.A. Particle Swarm Optimization // Proceedings of the IEEE Intern. Conf. on Neural Networks. Piscataway, NJ, 1995. P. 1942–1948.
Olsson A.E. Particle Swarm Optimization: Theory, Techniques and Applications. Hauppage, USA: Nova Science Publishers, 2011. 305 p.
Курейчик В.М., Каланчук С.А. Обзор и состояние проблемы роевых методов оптимизации // Информатика, вычислительная техника и инженерное образование. 2016. № 1(25). С. 1–13.
Clerc M. Guided Randomness in Optimization. Hoboken, USA: John Wiley & Sons, Inc., 2015. 320 p.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


