Известия РАН. Теория и системы управления, 2023, № 1, стр. 18-27
СИНТЕЗ ПАРАМЕТРОВ ПРОПОРЦИОНАЛЬНО-ИНТЕГРИРУЮЩИХ И ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИРУЮЩИХ РЕГУЛЯТОРОВ ДЛЯ СТАЦИОНАРНЫХ ЛИНЕЙНЫХ ОБЪЕКТОВ С НЕНУЛЕВЫМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ
a ИПУ РАН
Москва, Россия
b МФТИ
Долгопрудный, Россия
* E-mail: dvshatov@gmail.com
Поступила в редакцию 07.06.2022
После доработки 29.07.2022
Принята к публикации 26.09.2022
- EDN: JALDCC
- DOI: 10.31857/S0002338823010080
Аннотация
Рассматривается задача синтеза пропорционально-интегрирующих и пропорционально-интегрально-дифференцирующих регуляторов в нестандартной постановке. Для линейного одномерного объекта управления с ненулевыми начальными условиями требуется найти регулятор, который является оптимальным в смысле квадратичного функционала от состояния объекта с регуляризационной добавкой по управлению. Процедура синтеза представляет собой решение соответствующей квадратичной задачи оптимизации с помощью метода, подобного методу сопряженных градиентов (направление на каждом шаге вычисляется по методу сопряженных градиентов, а длина шага – по правилу Армихо). Численные примеры иллюстрируют эффективность предложенного алгоритма при синтезе регуляторов для моделей объектов управления, распространенных на практике.
Введение. Пропорционально-интегрирующие (ПИ) и пропорционально-интегрально-дифференцирующие (ПИД) регуляторы возникли как естественное развитие центробежных регуляторов, использовавшихся для регулирования скорости вращения в паровых машинах XIX в. Их параметры настраивались выбором физических характеристик конструкции: масс, жесткости пружин или вязкости смазочных материалов. Единственным критерием качества регулирования выступала устойчивость [1, 2]. В первой половине XX в. ПИ- и ПИД-регуляторы развились в конструктивно обособленные, универсальные устройства, позволяющие менять параметры закона управления в некоторых фиксированных диапазонах настройки. Несмотря на значительный технологический прогресс, существовал серьезный недостаток простых и эффективных методов настройки параметров регуляторов. В 40-е годы XX в. были предложены два, пожалуй, самых популярных эмпирических метода настройки ПИД-регуляторов [3]. Исходно предназначавшиеся для контроля давления данные методы настройки носят универсальный характер, впоследствии они получили теоретическое обоснование [4]. Во второй половине XX в. был достигнут значительный прогресс в исследовании ПИ- и ПИД-регуляторов как в теоретическом плане, так и учитывая специфику конкретных производственных отраслей [4–6]. Значительное число известных методов и подходов к синтезу ПИ- и ПИД-регуляторов собрано в сборнике “рецептов” для настройки [7].
Широкое применение ПИ- и ПИД-регуляторов связано в первую очередь с их простотой – необходимо выбрать всего три (или два для ПИ-случая) коэффициента. До сих пор, несмотря на обилие методов, в реальных установках ПИД-регуляторы часто настраиваются вручную, исходя из интуитивного понимания технологического процесса и влияния на него отдельных составляющих ПИД-закона управления.
У ПИД-регуляторов есть и недостатки: если посмотреть на модели объектов управления в [7], то все они имеют невысокий порядок. Такой выбор обусловлен естественным ограничением применимости ПИД-регуляторов – из-за их простоты они не предназначены для управления сложными объектами. Ряд современных подходов направлен на преодоление этого ограничения, например, адаптивное ПИД-управление [8], ${\text{П}}{{{\text{И}}}^{{{\lambda }}}}{{{\text{Д}}}^{{{\mu }}}}$-регуляторы дробного порядка [9], оптимизация [10, 11] и др. Большинство методов рассматривают задачи синтеза ПИД-регуляторов для одномерных (SISO – single-input single-output) систем (с одним входом и одним выходом), но существуют подходы и к их многомерному синтезу [12, 13].
Все описанные выше подходы предназначены для синтеза следящих систем управления, цель которых обеспечить минимальную ошибку между некоторым эталонным задающим сигналом (уставкой) и выходным сигналом объекта. При этом предполагается, что начальные условия в объекте нулевые. Настоящая статья рассматривает обратную ситуацию, когда на объект не действуют внешние возмущения (ни уставка, ни возмущения), а движение в ней вызвано ненулевыми начальными условиями. Целью управления выбирается минимизация их влияния на объект управления с помощью ПИ- или ПИД-регулятора. Подобная задача является нестандартной для ПИД-регуляторов, однако в теории управления она рассматривалась давно и может считаться классической. Так синтез линейных квадратичных регуляторов (ЛКР-задача) [14, 15] представляет собой близкую задачу: поиск статического оптимального регулятора по состоянию (или выходу). В последние годы новый подход к ЛКР-задачам был предложен в [16, 17], в них синтез регулятора рассматривается как задача матричной оптимизации, в которой переменной является матрица коэффициентов обратной связи. В постановке задачи и общем подходе к ее решению будем следовать работе [17]. В настоящей статье обсуждается вычислительный аспект этого подхода применительно к практическим задачам синтеза ПИ- и ПИД-регуляторов при ненулевых начальных условиях.
В разд. 1 демонстрируется, как с помощью расширения пространства состояний можно свести поиск коэффициентов ПИ- и ПИД-регуляторов к ЛКР-задаче. Раздел 2 описывает алгоритм синтеза регулятора, который представляет собой процедуру решения задачи оптимизации методом, схожим с методом сопряженных градиентов. В разд. 3 приведены ряд примеров синтеза регуляторов, обсуждаются практические аспекты применимости найденных регуляторов в классической следящей системе и предлагаются модификации, позволяющие улучшить показатели качества систем.
1. Постановка задачи. Рассмотрим полностью управляемый и наблюдаемый объект управления, описываемый уравнениями состояния:
(1.1)
$\left\{ {\begin{array}{*{20}{l}} {\dot {x}(t) = Ax(t) + Bu(t),} \\ {y(t) = Cx(t),} \end{array}\quad x(0) = {{x}_{0}} \ne 0} \right.,$Объект (1.1) замыкается идеальным ПИ-/ПИД-регулятором, формирующим управляющий сигнал:
(1.2)
$u(t) = - {{k}_{P}}y(t) - {{k}_{I}}\int\limits_0^t {y({{\tau }})} d{{\tau }} - {{k}_{D}}\dot {y}(t),$Рассматриваемая система (1.1), (1.2) является системой стабилизации, а не слежения как в классических постановках, когда есть внешний задающий сигнал (уставка). Единственным возмущением в системе являются ненулевые начальные условия, влияние которых необходимо подавить, используя сигнал управления, оптимальный по квадратичному критерию.
Покажем, каким образом задача синтеза сводится к ЛКР-задаче. Для этого введем в рассмотрение вспомогательную переменную
принимая во внимание, что $\dot {z}(t) = y(t) = Cx(t)$, уравнение регулятора (1.2) можно представить в следующем виде:Выделив управление из последнего уравнения, окончательно получим
Уравнения замкнутой системы (1.1), (1.2) можно найти, подставив найденное $u(t)$ в (1.1). Обозначая расширенный вектор состояния как $\tilde {x}(t) = {{\left[ {x(t){\text{ }}z(t)} \right]}^{{\text{T}}}} \in {{R}^{{n + 1}}}$, перепишем (1.1) в следующем виде:
Обозначим через ${{S}_{k}} = \{ K:\operatorname{Re} \{ \max {{\lambda }}(\tilde {A}(K))\} < 0\} $ (где ${{\lambda }}( \cdot )$ – собственные числа матрицы) множество стабилизирующих регуляторов K, которые обеспечивают устойчивость объекта (1.1). Тогда предлагается свести задачу синтеза ПИ-/ПИД-регулятора к решению оптимизационной задачи:
где $J(K)$ – целевая функция, которая представляет собой квадратичный критерий:(1.4)
$J(K) = \int\limits_0^\infty {{{{\tilde {x}}}^{{\text{T}}}}(t)Q\tilde {x}(t)dt} + {{\rho |}}K{{{\text{|}}}^{2}},$В [16, 17] исследуются свойства функции (1.4) и доказано, что задача (1.3), (1.4) может рассматриваться как задача матричной оптимизации, к которой применимы соответствующие классические методы. Единственным дополнительным предположением служит существование известного стабилизирующего регулятора ${{K}_{0}} \in {{S}_{k}}$.
Задача синтеза состоит в поиске оптимального ПИ-/ПИД-регулятора K*, который доставляет минимум критерию (1.3) при известном объекте управления (1.1) и начальных условиях ${{x}_{0}}$.
2. Процедура синтеза. Синтез регулятора сводится к решению задачи (1.3). Предлагается использовать метод, подобный методу сопряженных градиентов [18]: выбор направления выполняется в соответствии с правилами метода сопряженных градиентов, но полная релаксация по длине шага заменяется линейным поиском по правилу Армихо [19]. В данном разделе описывается алгоритм решения задачи оптимизации и некоторые технические детали, упрощающие ее численное решение.
2.1. Алгоритм синтеза. Вначале приведем исходные данные, которые используются при синтезе:
матрицы объекта управления $A,B,C$ и его ненулевые начальные условия ${{x}_{0}}$;
весовые параметры: положительно-определенная матрица $Q \in {{R}^{{n + 1{\text{ }} \times {\text{ }}n + 1}}}$ и скалярные параметр ${{\rho }}$;
известный стабилизирующий регулятор ${{K}_{0}} \in {{S}_{k}}$, который является “стартовой точкой” для оптимизационного процесса; для такого поиска можно воспользоваться готовыми решениями для синтеза ПИД-регуляторов (например, PID Tuner в MATLAB) или известными аналитическими выражениями для расчета по моделям параметров ПИ- и ПИД-регуляторов [7];
настраиваемые параметры процедуры оптимизации: стартовый шаг ${{{{\alpha }}}_{0}}$, который выбирается достаточно большим вещественным числом и число ${{\tau }} \in \left( {0,1} \right)$, используемые в правиле Армихо, ${{\varepsilon }} > {\text{0}}$ – достаточно малое число, определяющее точность решения задачи оптимизации, ${{N}_{{{\text{max}}}}}$ – максимальное число итераций, после достижения которого процедура синтеза завершается.
Процесс оптимизации носит итеративный характер с улучшением значения целевой функции на каждой итерации. Каждая j-я итерация процедуры оптимизации состоит из следующих этапов.
1. Проверить ограничения на число итераций $j < {{N}_{{{\text{max}}}}}$: если оно нарушается, то процесс останавливается на текущем найденном регуляторе с параметрами ${{K}_{{j - 1}}}$ в качестве решения задачи (1.3). Здесь и далее ${{K}_{{j - 1}}}$ – вектор параметров ПИД-регулятора, найденный на предыдущей итерации (при j = 1 предыдущим является стартовый регулятор ${{K}_{0}}$).
2. Определить направление ${{s}_{j}}$ на текущей итерации, согласно соотношению
где ${{r}_{j}} = \nabla J({{K}_{{j - 1}}})$ – градиент целевой функции, а коэффициент ${{{{\beta }}}_{j}}$ находится следующим образом:3. Вычислить величину шага ${{{{\alpha }}}_{j}}$ на текущей итерации. Для этого используется поиск с остановкой по правилу Армихо: выбирается значение ${{{{\alpha }}}_{j}} = {{{{\alpha }}}_{0}}$ и проверяется условие
(2.1)
$J({{K}_{{j - 1}}} + {{{{\alpha }}}_{j}}{{s}_{j}}) < J({{K}_{{j - 1}}}) + {{\tau }}{{{{\alpha }}}_{j}}\left\langle {J({{K}_{{j - 1}}}),{{s}_{j}}} \right\rangle .$Если условие выполнено, то текущий шаг допустим и рассчитывается текущий вектор параметров регулятора:
В противном случае, когда условие (2.1) нарушается, необходимо уменьшить величину шага ${{{{\alpha }}}_{j}} = {{{{\alpha }}}_{j}}{\text{/}}2$ и снова проверить условие (2.1), продолжая до тех пор, пока не будет получено допустимое значение ${{{{\alpha }}}_{j}}$. Сокращение шага выполняется также в случаях, когда условие (2.1) не может быть проверено, потому что промежуточный вектор Kj приводит к неустойчивости замкнутой системы.
4. Проверить условие остановки синтеза:
Если оно выполняется, то процедура оптимизации завершена и решением является текущий регулятор $K{\kern 1pt} * = {{K}_{j}}$. В противном случае необходимо перейти к следующей итерации процедуры синтеза.
2.2. Вычисление целевой функции и ее градиента. Целевая функция (1.4) может быть вычислена в явном виде для любого заданного вектора параметров $K \in {{S}_{k}}$ на основе леммы 1.2.3 из [20], в которой доказано, что уравнение Ляпунова
имеет единственное положительно-определенное решение тогда и только тогда, когда матрица $A$ гурвицева.Для регулятора $K \in {{S}_{k}}$, соответствующей матрицы замкнутой системы $\tilde {A}(K)$, весовой матрицы $Q \in {{R}^{{n + 1 \times n + 1}}}$ и параметра ${{\rho }}$ значение функции (1.4) вычисляется, используя аналитическое выражения для решения уравнения Ляпунова, с помощью соотношения
где матрица $P \in {{R}^{{n + 1{\text{ }} \times {\text{ }}n + 1}}}$ является решением сопряженного уравнения Ляпунова:Вычисление градиента $\nabla J(K)$ также основано на решении уравнений Ляпунова и использует подход, предложенный в работах [16, 17]. Для этого требуется представить матрицу $\tilde {A}(K)$ в виде линейной комбинации:
(2.3)
$\tilde {A}(K) = {{\tilde {A}}_{0}} + \left[ {\begin{array}{*{20}{c}} {{{{\tilde {A}}}_{P}}}&{{{{\tilde {A}}}_{I}}}&{{{{\tilde {A}}}_{D}}} \end{array}} \right]K = {{\tilde {A}}_{0}} + {{k}_{P}}{{\tilde {A}}_{P}} + {{k}_{I}}{{\tilde {A}}_{I}} + {{k}_{D}}{{\tilde {A}}_{P}}.$Учитывая, что в общем случае элементами матрицы $\tilde {A}(K)$ могут быть дробно-рациональные функции от параметров регуляторов K, представление (2.3) без введения новых переменных и усложнения вычислений, возможно, только в случае ортогональности векторов C и $B$. Также условие CB = 0 гарантирует, что в формуле для $\tilde {A}(K)$ знаменатель $1 + {{k}_{D}}CB \ne 0$. Следующее утверждение описывает достаточное условие ортогональности.
Утверждение. Для ортогональности векторов $C$ и $B$ достаточно, чтобы объект (1.1) имел относительный порядок больше 1, т.е. при записи в форме передаточной функции степень числителя $m$ должна быть меньше или равна n – 2.
Доказательство. Запишем объект (1.1) в канонической управляемой форме, что всегда возможно сделать для управляемого и наблюдаемого объекта. Матрицы $B,\;C$ в этом случае имеют фиксированную структуру [21]:
(2.4)
$w(s) = \frac{{{{c}_{0}}{{s}^{m}} + {{c}_{1}}{{s}^{{m - 1}}} + \ldots + {{c}_{{m - 1}}}s + {{c}_{m}}}}{{{{s}^{n}} + {{a}_{1}}{{s}^{{n - 1}}} + \ldots + {{a}_{{n - 1}}}s + {{a}_{n}}}}.$Произведение $CB = 0$ при ${{b}_{0}} = {{b}_{1}} = 0$. Из постановки задачи предполагается, что у объекта (1.1) нет прямой связи между $u(t)$ и $y(t)$, что соответствует моделям реальных физических процессов. Поэтому в (2.4) коэффициент ${{c}_{0}} = {{b}_{0}} = 0$, а для выполнения ${{b}_{1}} = 0$ требуется также, чтобы ${{c}_{1}} = 0$, что означает выполнение условия, описанного в утверждении: $n - m \geqslant 2$. Утверждение доказано.
Достаточно широкий класс моделей объектов, используемых на практике, подходит под критерии утверждения (см., например, [22]). Далее в примерах предлагаемый алгоритм синтеза будет применен для поиска ПИ- и ПИД-регуляторов только для таких объектов.
Согласно результатам [17], обозначим первое слагаемое в (1.4) как функцию
Вычислить ее градиент можно с помощью следующего соотношения:
(2.5)
${{\tilde {A}}^{{\text{T}}}}(K)Y + Y\tilde {A}(K) + R = 0,\quad R = \tilde {x}(0)\tilde {x}_{{}}^{{\text{T}}}(0).$Окончательно компоненты вектора градиента $\nabla J(K)$ вычисляются как
3. Примеры. Предложенный алгоритм синтеза ПИ- и ПИД-регуляторов применяется к нескольким моделям объектов управления, используемым в реальной инженерной практике. Начальные условия x0 объекта (1.1) во всех примерах выбираются вектором, состоящим из единиц.
Общие параметры синтеза во всех примерах заданы следующими: весовая матрица $Q \in {{R}^{{5 \times 5}}}$ выбрана как единичная, а регуляризационный параметр ρ = 1, точность решения задачи оптимизации ${{\varepsilon }} = {\text{1}}{{{\text{0}}}^{{ - {\text{8}}}}}$, максимальное число итераций ${{N}_{{{\text{max}}}}} = 200$.
3.1. Синтез ПИ-регулятора. Объект управления взят из [22] и описывается передаточной функцией с кратными единичными полюсами и без нулей:
которая при записи в пространстве состояний (1.1) в канонической управляемой форме имеет матрицы $A,B,C$ следующего вида:Начальные условия объекта выбраны как ${{x}_{0}} = {{\left[ {1{\text{ 1 1 1}}} \right]}^{{\text{T}}}}$, тогда в (2.5) матрица
Стартовый ПИ-регулятор задан ${{K}_{0}} = {{\left[ {\begin{array}{*{20}{c}} 1&{{\text{0}}{\text{.8}}} \end{array}} \right]}^{{\text{T}}}}$. Параметры, используемые при линейном поиске по правилу Армихо, ${{{{\alpha }}}_{0}} = 20$ и ${{\tau }} = {\text{0}}{\text{.6}}$. В результате синтеза за N = 28 итераций был найден оптимальный ПИ-регулятор, за ним указан показатель качества (1.4), который он обеспечивает:
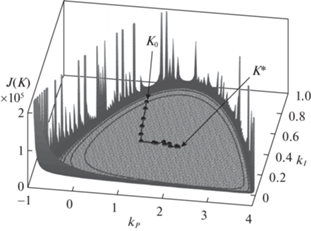
В случае ПИ-регулятора есть возможность проиллюстрировать поведение решения задачи в пространстве параметров ${{k}_{P}}$ и ${{k}_{I}}$. На рисунке 1 черным цветом изображена траектория изменения значений ${{K}_{j}}$. Она начинается в точке ${{K}_{0}}$ и заканчивается в точке оптимума K*. Поверхность, показанная градациями серого цвета с выделенными на ней линиями уровня, отвечает значениям целевой функции (1.4). В данном примере видно, что функция $J(K)$ в области Sk – выпуклая, с единственной точкой минимума, которая находится в процессе синтеза ПИ-регулятора.
Дополнительно укажем инженерные свойства синтезированной замкнутой системы: частота среза ${{{{\omega }}}_{{{\text{ср}}}}} = 0.666$ рад/с позволяет оценить быстродействие системы – величина $3{\text{/}}{{{{\omega }}}_{{{\text{ср}}}}} = {\text{4}}{\text{.5}}$ с дает оценку времени установления до 5% при реакции на единичное ступенчатое воздействие, запасы устойчивости по модулю и фазе равны $L = 1.59$ и ${{{{\varphi }}}_{{\text{з}}}} = 28.6^\circ $ соответственно. При этом обычно на практике требуется обеспечить выполнение неравенств $L > 2$ и ${{{{\varphi }}}_{{\text{з}}}} > 30^\circ $, чтобы система обладала достаточными робастными свойствами. Найденный оптимальный ПИ-регулятор малопригоден в классическом инженерном смысле для слежения за уставкой, так как малые запасы устойчивости приводят к значительному перерегулированию и колебательности в переходном процессе при ступенчатом задающем сигнале. Такие результаты объясняются ограниченностью возможностей ПИ-регулятора при управлении объектом 4-го порядка.
3.2. Синтез ПИД-регулятора. Объект управления задается следующей передаточной функцией [22]:
(3.1)
${{G}_{1}}(s) = \frac{1}{{(1 + s)(1 + {{\delta }}s)(1 + {{{{\delta }}}^{{\text{2}}}}s)(1 + {{{{\delta }}}^{{\text{3}}}}s)}};\quad {{\delta }} = {\text{0}}{\text{.1;0}}{\text{.2;0}}{\text{.5;1}}{\text{.}}$При δ = 1 она совпадает с объектом управления в предыдущем примере, а при δ = 0.1 передаточная функция ${{G}_{1}}(s)$ представляет собой объект с разнотемповой динамикой, который практически неуправляем с помощью ПИ-регулятора. Параметры синтеза выбраны такими же, как в случае ПИ-регулятора и для краткости опущены.
Результаты синтеза представлены в табл. 1: первая строка которой содержит значения параметра ${{\delta }}$ из (3.1); вторая строка содержит ${{t}_{{{{G}_{1}}}}}$ – время установления до 5% при подаче на объект (3.1) единичной ступенчатой функции (на эту величину можно ориентироваться при анализе быстродействия замкнутой системы – найденный ПИД-регулятор обычно должен обеспечивать сравнимое быстродействие); третья строка – стартовые ПИД-регуляторы, которые были определены с помощью PID Tuner в MATLAB. Далее указаны число итераций N, найденный ПИД-регулятор K* и значение целевой функции, обеспечиваемое оптимальным регулятором. Последние две строки имеют те же инженерные показатели, что приведены в примере с ПИ-регулятором, причем в предпоследней строке сначала указана частота среза, далее, в скобках – оценка длительности переходного процесса $3{\text{/}}{{{{\omega }}}_{{{\text{ср}}}}}$.
Таблица 1.
Результаты численных экспериментов для ${{G}_{1}}(s)$
| ${{\delta }}$ | 0.1 | 0.2 | 0.5 | 1 |
| ${{t}_{{{{G}_{1}}}}}$, с | 3.11 | 3.27 | 4.1 | 7.75 |
| ${{K}_{0}}$ | $\left[ {\begin{array}{*{20}{c}} {{\text{1}}{\text{.74}} \times {{{10}}^{6}}} \\ {2.69 \times {{{10}}^{6}}} \\ {1.897 \times {{{10}}^{5}}} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {3.13 \times {{{10}}^{4}}} \\ {3.97 \times {{{10}}^{4}}} \\ {5950} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {133.8} \\ {90.8} \\ {49.27} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.13} \\ {0.5} \\ {2.26} \end{array}} \right]$ |
| $J({{K}_{0}})$ | $1.031 \times {{10}^{{13}}}$ | $2.586 \times {{10}^{9}}$ | 28760.15 | 177.32 |
| N | 34 | 33 | 18 | 34 |
| K* | $\left[ {\begin{array}{*{20}{c}} { - 0.004} \\ {72.09} \\ { - 0.018} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} { - 0.007} \\ {20.78} \\ { - 0.07} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {0.32} \\ {5.45} \\ { - 0.45} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.82} \\ {1.22} \\ {3.55} \end{array}} \right]$ |
| J(K*) | 35812.28 | 2607.12 | 143 | 139.26 |
| ${{{{\omega }}}_{{{\text{ср}}}}}{\text{, рад/с}}$ (3/ωср, c) | $7.21 \times {{10}^{{ - 5}}}{\text{ (4}}{\text{.16}} \times {{10}^{4}}{\text{)}}$ | $1.33 \times {{10}^{{ - 3}}}{\text{ (}}2.26 \times {{10}^{3}}{\text{)}}$ | 0.085 (35.29) | 0.926 (3.24) |
| [$L$, ${{{{\varphi }}}_{{\text{з}}}}$] | $[1.36 \times {{10}^{5}}\,\,90^\circ ]$ | $[3.48 \times {{10}^{3}}\,\,89.9^\circ ]$ | $\left[ {\begin{array}{*{20}{c}} {18}&{81.2^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.81}&{43.8^\circ } \end{array}} \right]$ |
Данные табл. 1 демонстрируют, что для всех ${{\delta }}$ найденные оптимальные ПИД-регуляторы естественно оказываются лучше стартовых, причем разница в показателях растет по мере уменьшения ${{\delta }}$ (усложнения объекта с точки зрения управления). Такой результат объясняется тем, что исходный регулятор ${{K}_{0}}$ был синтезирован для классической следящей системы и дал заметно худшие значения показателя качества при оценке по другому критерию $J(K)$.
С другой стороны, анализ классических инженерных показателей систем с найденными оптимальными регуляторами $K{\kern 1pt} *$ при использовании их в следящей системе демонстрирует их практическую неприменимость (за исключением случая δ = 1). При больших запасах устойчивости найденные регуляторы имеют очень низкое быстродействие – при ${{\delta }} = {\text{0}}{\text{.5}}$ длительность реакции на ступенчатую уставку можно приблизительно оценить как $3{\text{/}}{{{{\omega }}}_{{{\text{ср}}}}} = {\text{35}}{\text{.29}}$ с, а для остальных случаев оценка длительности переходных процессов достигает тысячи секунд. Отдельно отметим, что при δ = 1, когда объект управления совпадает с передаточной функцией объекта $G(s)$ из разд. 3.1, ПИД-регулятор обеспечивает улучшение всех рассматриваемых показателей качества ($J(K{\kern 1pt} *)$, ${{{{\omega }}}_{{{\text{ср}}}}}$ и [$L$, ${{{{\varphi }}}_{{\text{з}}}}$]) по сравнению с ПИ-регулятором, который, как уже было сказано выше, имеет ограниченные возможности.
Найденные предложенным методом ПИД-регуляторы решают поставленную задачу – подавить влияние ненулевых начальных условий. Но иногда они оказываются малопригодны для практического применения, особенно по показателю быстродействия замкнутой системы. Исправить данный недостаток можно, добавив ограничение на множество стабилизирующих регуляторов следующего вида:
(3.2)
${{S}_{{k{{\sigma }}}}} = \{ K: - \operatorname{Re} \{ \max {{\lambda }}(\tilde {A}(K))\} > {{\sigma }}{\kern 1pt} *\} ,$Существенным недостатком приведенного приема служит ухудшение значения целевой функции. Также некоторой проблемой может быть поиск стартового ПИД-регулятора K0, обеспечивающего устойчивость ${{\tilde {A}}_{{{\sigma }}}}({{K}_{0}})$.
Использование предложенного приема проиллюстрируем для значения параметра ${{\delta }} = {\text{0}}{\text{.2}}$ в (3.1): задавшись стартовым ПИД-регулятором $K_{{{\sigma }}}^{*} = {{\left[ {\begin{array}{*{20}{c}} {3 \times {{{10}}^{4}}}&{4.2 \times {{{10}}^{4}}}&{5350} \end{array}} \right]}^{{\text{T}}}}$, проведем синтез для нескольких значений ${{\sigma }}{\kern 1pt} *$. Результаты представлены в табл. 2: первая строка содержит заданную степень устойчивости замкнутой системы, вторая – найденный регулятор, третья – фактическую степень устойчивости замкнутой системы ${{\sigma (}}\tilde {A}(K{\kern 1pt} *))$. Далее указано фактическое время установления ${{t}_{{{\sigma }}}}$ до 5% при подаче единичной ступенчатой уставки, остальные строки имеют такую же структуру как в табл. 1.
Таблица 2.
Результаты численных экспериментов для ${{G}_{1}}(s)$ при разных σ*
| σ* | 0 | 0.05 | 0.1 | 0.2 | 0.3 |
| $K_{{{\sigma }}}^{*}$ | $\left[ {\begin{array}{*{20}{c}} { - 0.007} \\ {20.78} \\ { - 0.07} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} { - 35.9} \\ {734.93} \\ {1.66} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} { - 138.4} \\ {1360.3} \\ {12.8} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} { - 456.4} \\ {2284.9} \\ {90.5} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} { - 833.4} \\ {2771.4} \\ {246.9} \end{array}} \right]$ |
| ${{\sigma (}}\tilde {A}(K{\text{*}}))$ | $1.3 \times {{10}^{{ - 3}}}$ | 0.0503 | 0.1002 | 0.2004 | 0.3009 |
| ${{t}_{{{\sigma }}}}$, с | 2250 | 61 | 31.5 | 17.05 | 12.9 |
| $J(K_{{{\sigma }}}^{*})$ | 2607.12 | $5.43 \times {{10}^{5}}$ | $1.87 \times {{10}^{6}}$ | $5.44 \times {{10}^{6}}$ | $8.44 \times {{10}^{6}}$ |
| ${{{{\omega }}}_{{{\text{ср}}}}}{\text{ (3/}}{{{{\omega }}}_{{{\text{ср}}}}}{\text{)}}$ | $1.33 \times {{10}^{{ - 3}}}{\text{ (}}2.26 \times {{10}^{3}}{\text{)}}$ | $0.047{\text{ (}}6{\text{3}}.83{\text{)}}$ | ${\text{0}}{\text{.087 (34}}{\text{.6)}}$ | ${\text{0}}{\text{.145 (20}}{\text{.7)}}$ | ${\text{0}}{\text{.174 (17}}{\text{.2)}}$ |
| [$L$, ${{{{\varphi }}}_{{\text{з}}}}$] | $[3.48 \times {{10}^{3}}\,\,89.9^\circ ]$ | $\left[ {\begin{array}{*{20}{c}} {82}&{86.5^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {37}&{83.3^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {17.4}&{78.1^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {11.7}&{74.6^\circ } \end{array}} \right]$ |
Данные табл. 2 демонстрируют, что с увеличением параметра σ* происходит рост значений $J(K_{{{\sigma }}}^{*})$, увеличение частоты среза (растет быстродействие) и немного сокращаются запасы устойчивости. Выбор конкретного значения σ* может осуществляться, исходя из требуемого быстродействия, по формуле ${{\sigma }}{\kern 1pt} * = 3{\text{/}}t{\kern 1pt} *$, где $t{\kern 1pt} *$ – желаемое время установления. Нужно отметить, что последняя формула для σ* носит эвристический характер. Фактическое быстродействие системы может оказаться как выше заданного, так и ниже. Например, в рассмотренном примере в табл. 2 при ${{\sigma }}{\kern 1pt} * = 0.3$ соответствующее желаемое время составит $t{\kern 1pt} * = 10$ с, однако фактическое время установления ${{t}_{{{\sigma }}}} = {\text{12}}{\text{.9}}$ с.
Важно отметить, что увеличение σ* приводит к сокращению запасов устойчивости и снижению робастных свойств замкнутой системы. Это нужно учитывать, задавая желаемое быстродействие: найденный регулятор должен обеспечивать $L > 2$ и ${{{{\varphi }}}_{{\text{з}}}} > 30^\circ $.
Второй пример, для которого проводится синтез ПИД-регуляторов, описывается передаточной функцией [22]:
Это неминимально-фазовый объект с кратными единичными полюсами и неустойчивым нулем, величина которого является параметром с заданным набором значений. Параметры синтеза оставлены без изменений.
Данные табл. 3 демонстрируют, что найденный оптимальный ПИД-регулятор K* дает некоторый небольшой выигрыш по сравнению с исходным регулятором K0, который, напомним, был определен как оптимальный для следящей системы. По мере увеличения ${{\delta }}$ задача управления усложняется, что видно по увеличению значения целевой функции (как для стартового ПИД-регулятора, так и для синтезированного). Показатели запасов устойчивости уменьшаются с ростом ${{\delta }}$, однако остаются допустимыми, с инженерной точки зрения, для всех значений ${{\delta }}$. Показатель быстродействия, оцениваемый через ${{{{\omega }}}_{{{\text{ср}}}}}$, уменьшается с ростом ${{\delta }}$, но остается достаточно высоким (для ${{\delta }} = {\text{2}}{\text{.5}}$ оценка длительности переходного процесса дает $3{\text{/}}{{{{\omega }}}_{{{\text{ср}}}}} = {\text{1}}6.76$ c). При необходимости увеличить быстродействие можно использовать прием, описанный выше. Однако следует учитывать, что в неминимально-фазовом случае частота среза системы ограничена, поэтому даже выбор большой степени устойчивости может не обеспечивать желаемого быстродействия [23]. Для всех случаев ${{\delta }}$ качество замкнутых систем с синтезированными ПИД-регуляторами, с инженерной точки зрения, достаточно хорошее.
Таблица 3.
Результаты численных экспериментов для ${{G}_{2}}(s)$
| ${{\delta }}$ | 0.1 | 0.2 | 0.5 | 1 | 2.5 |
| ${{K}_{0}}$ | $\left[ {\begin{array}{*{20}{c}} {2.22} \\ {0.841} \\ {1.42} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.11} \\ {0.762} \\ {1.46} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {1.41} \\ {0.526} \\ {0.947} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {0.628} \\ {0.276} \\ {0.187} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {0.293} \\ {0.143} \\ 0 \end{array}} \right]$ |
| $J({{K}_{0}})$ | 41.83 | 48.45 | 73.23 | 134.8 | 311.16 |
| N | 22 | 21 | 27 | 43 | 40 |
| K* | $\left[ {\begin{array}{*{20}{c}} {2.15} \\ {0.965} \\ {1.41} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {1.95} \\ {0.899} \\ {1.5} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {1.39} \\ {0.665} \\ {1.37} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {0.876} \\ {0.399} \\ {0.916} \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {0.417} \\ {0.167} \\ {0.416} \end{array}} \right]$ |
| J(K*) | 41.51 | 47.83 | 71.84 | 121.15 | 286.52 |
| ${{{{\omega }}}_{{{\text{ср}}}}}{\text{, рад/с}}$ | 0.818 | 0.755 | 0.559 | 0.373 | 0.179 |
| [L, ${{{{\varphi }}}_{{\text{з}}}}$] | $\left[ {\begin{array}{*{20}{c}} {10.5}&{56.8^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {5.77}&{58.5^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {3.04}&{59.8^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.42}&{58.5^\circ } \end{array}} \right]$ | $\left[ {\begin{array}{*{20}{c}} {2.19}&{61.2^\circ } \end{array}} \right]$ |
Заключение. Предложен алгоритм синтеза ПИ- и ПИД-регуляторов для подавления эффекта ненулевых начальных условий. Описанная процедура синтеза продолжает новый подход к таким задачам, который предлагает рассмотреть задачу синтеза как задачу оптимизации по параметрам обратной связи и решать ее методами оптимизации. Численные примеры демонстрируют применимость найденных регуляторов для управления моделями объектов, используемых в инженерной практике, хоть и с некоторыми ограничениями, которые можно обойти введением желаемой заданной степени устойчивости замкнутой системы (см. разд. 3.1).
Дальнейшим развитием предложенного подхода служит применение алгоритма синтеза к задаче подавления импульсных внешних возмущений, которые можно свести к действию ненулевых начальных условий, с учетом инженерных требований к качеству управления замкнутой системы при действии ступенчатой уставки. Другим возможным направлением развития предложенного подхода будет исследование задачи синтеза для других более сложных форм ПИД-регуляторов: с фильтром, двумя степенями свободы и т.п.
Список литературы
Maxwell J.C. On Governors // Proceedings of the Royal Society of London. 1868. V. 16. P. 270–283.
Айзерман М.А. Краткий очерк становления и развития классической теории регулирования и управления // АиТ. 1993. № 7. С. 6–18.
Ziegler J.G., Nichols N.B. Optimum Settings for Automatic Controllers // Transactions of ASME. 1942. V. 64. P. 759–768.
Åström K.J., Hägglund T. Advanced PID Control. NC: ISA, 2006. 460 p.
Visioli A. Practical PID Control. London: Springer-Verlag, 2006. 310 p.
Wang L. PID Control System Design and Automatic Tuning using MATLAB/Simulink. Wiley-IEEE Press, 2020. 368 p.
O’Dwyer A. Handbook of PI and PID Controller Tuning Rules: 3rd edition. London: Imperial College Press, 2009. 608 p.
Александров А.Г., Паленов М.В. Состояние и перспективы развития адаптивных ПИД-регуляторов // АиТ. 2014. № 2. С. 16–30.
Podlubny I. Fractional-order Systems and $P{{I}^{{{\lambda }}}}{{D}^{{{\mu }}}}$-controllers // IEEE Transactions on Automatic Control. 1999. V. 44. №. 1. P. 208–214.
Hast M., Åström K.J., Bernhardsson B., Boyd S. PID Design by Convex-Concave Optimization // Proc. Europ. Control Conf. (ECC-2013). Zurich, Switzerland, 2013. P. 4460–4465.
Han S., Keel L.H., Bhattacharyya S.P. PID Controller Design with an ${{H}_{\infty }}$ Criterion // IFAC PapersOnLine. 2018. V. 51. №. 4. P. 400–405.
Wang Q.-G., Ye Z., Cai W.-J., Hang C.-C. PID Control for Multivariable Processes. Berlin: Springer-Verlag, 2008. 273 p.
Boyd S., Hast M., Åström K.J. MIMO PID Tuning via Iterated LMI Restriction // Intern. J. Robust and Nonlinear Control. 2016. V. 26. P. 1718–1731.
Kwakernaak H., Sivan R. Linear Optimal Control Systems. First Edition. London: Wiley-Interscience, 1972. 575 p.
Anderson B.D.O., Moore J.B. Optimal Control. Linear Quadratic Methods. New Jersey: Prentice-Hall, 1989. 380 p.
Fatkhullin I., Polyak B. Optimizing Static Linear Feedback: Gradient Method // SIAM J. on Control and Optimization. 2021. V. 59. № 51. P. 3887–3911.
Поляк Б.Т., Хлебников М.В. Новые критерии настройки ПИД-регуляторов // АиТ. 2022. № 11.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983. 384 с.
Armijo L. Minimization of Functions Having Lipschitz Continuous First Partial Derivatives // Pacific J. Mathematics. 1966. V. 16. № 1. P. 1–3.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными системами при внешних возмущениях: Техника линейных матричных неравенств. М.: ЛЕНАНД, 2014. 560 с.
Ким Д.П. Теория автоматического управления. Т. 2. Многомерные, нелинейные, оптимальные и адаптивные системы. М.: Физматлит, 2004. 464 с.
Åström K.J., Hägglund T. Benchmark Systems for PID Control // IFAC Proceedings Volumes. 2000. V. 33. №. 4. P. 165–166.
Åström K.J. Limitations on Control System Performance // European Journal of Control. 2000. V. 6. Iss.1. P. 2–20.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления