Известия РАН. Теория и системы управления, 2023, № 1, стр. 28-43

Введение. На практике часто возникает задача сопровождения подвижных объектов, например воздушных судов по локационным измерениям параметров их траекторий. Для решения задачи оценивания при определении параметров движения и организации сопровождения объектов широкое распространение получил линейный фильтр Калмана (ФК) [1, 2]. Однако в статистически неопределенных ситуациях в условиях маневра подвижного объекта, вызванных резким изменением траектории, например при смене эшелонов полета воздушного судна, и/или неопределенных измерений, обусловленных помехами (искусственного или естественного происхождения) и влиянием других объектов, уточнение траектории движения объекта может происходить по измерениям, не содержащим полезной информации об этом маневрирующем объекте [3–5]. В результате вычисляемая в алгоритме ковариационная матрица ошибок оказывается излишне оптимистической и значительно ухудшаются характеристики точности оценивания и условия сопровождения (вплоть до срыва сопровождения). Поэтому широко используются различные модификации ФК, пригодные для оценивания в условиях неопределенных измерений траектории маневрирующего объекта [6, 7]. В этих алгоритмах оценки параметров движения объекта формируются на выходах двух или более параллельно работающих ФК по поступающим результатам измерений. Каждый из ФК соответствует своему виду маневра и основан на представлении маневра объекта в виде стохастического процесса. Итоговая оценка находится путем объединения соответствующих оценок по каждому виду маневра с учетом их весов, что эквивалентно гауссовской аппроксимации апостериорной плотности вероятности параметров движения объекта на каждом такте. Эффективным средством синтеза модифицированных ФК является марковская теория оценивания [8, 9].

Кроме того, для повышения потенциальной точности и достоверности результатов сопровождения маневрирующих объектов широко используется комплексирование разнотипных измерителей с совпадающими зонами наблюдения и имеющими разную физическую природу, например активными радиолокационными и пассивными оптико-электронными [10–13].

Развитие средств вычислительной техники позволяет реализовать комплексную обработку информации (КОИ) в цифровой форме при достаточно большом числе уровней квантования аналого-цифровых преобразователей и разрядов для представления чисел [14]. Максимального выигрыша от комплексирования можно достичь, решив задачу синтеза, что позволяет определить оптимальную структуру и характеристики системы комплексной обработки информации [8].

Для решения задачи КОИ при сопровождении маневрирующего объекта в условиях противодействия среды может быть использован математический аппарат дискретно-непрерывных марковских процессов (ДНМП) в дискретном времени [14], адекватный решаемой задаче при реализации синтезированных алгоритмов на ЭВМ.

1. Постановка задачи оценивания дискретно-непрерывного марковского процесса в дискретном времени. Пусть вектор состояния сопровождаемого динамического маневрирующего объекта описывается линейным векторно-матричным стохастическим дифференциальным уравнением (СДУ) с постоянными во времени коэффициентами, зависящим от изменяющегося во времени случайного дискретного параметра A_k, который характеризует виды маневров объекта [15]:

где ${\mathbf{X}}(t)$ – ${{n}_{x}}$-мерный вектор фазовых координат ДНМП; ${{{\mathbf{X}}}_{0}}$ – вектор начальных фазовых координат, имеющий гауссовское распределение; ${\mathbf{F}}$ – матрица коэффициентов усиления состояния размером (${{n}_{x}}\, \times \,{{n}_{x}}$); ${\mathbf{G}}$ – матрица интенсивностей шумов размером (${{n}_{x}}\, \times \,{{n}_{\xi }}$); ${\mathbf{Q}} = {\mathbf{GG}}_{{}}^{{\text{T}}}$ – матрица коэффициентов диффузии вектора ${\mathbf{X}}(t)$; Т – операция транспонирования; ${{{\mathbf{N}}}_{\xi }}(t)$ – ${{n}_{\xi }}$-мерный вектор белого гауссовского шума (БГШ) с нулевым математическим ожиданием и единичной матрицей интенсивностей; ${{A}_{k}} \equiv A({{t}_{k}})$ – дискретный конечномерный марковский процесс, который может принимать значения ${{a}_{j}},\,j = \overline {1,{{M}_{1}}} $, – марковская цепь с матрицей вероятностей переходов смена состояний которой может происходить только в фиксированные моменты времени ${{t}_{k}} = {{t}_{0}} + k\Delta $, k = 1, 2, …, разделенные постоянным интервалом $\Delta = {{t}_{k}} - {{t}_{{k - 1}}}$; Р – оператор вероятности; ${{M}_{1}}$ – число значений дискретного параметра a_k.

Решение уравнения (1.1) имеет вид [16]

где фундаментальная матрица решений ${\mathbf{\Phi }}$ удовлетворяет уравнению

Интеграл в правой части равенства (1.2) представляет собой векторный процесс с нулевым математическим ожиданием и матрицей центральных моментов второго порядка:

где I, 0 – единичная и нулевая матрицы соответственно.

Так как для неперекрывающихся интервалов времени значения этого процесса статистически независимы, аналогично [16] уравнение состояния (1.1) может быть представлено в статистически эквивалентной форме в виде разностного уравнения с шагом дискретизации $\Delta = {{t}_{k}} - {{t}_{{k - 1}}}$:

где ${{{\mathbf{X}}}_{k}} \equiv {\mathbf{X}}\left( {{{t}_{k}}} \right)$, ${\mathbf{\Gamma }}({{A}_{k}})$ – нижняя треугольная матрица, которая определяется соотношением ${\mathbf{\Xi }}$ – n_x-мерный вектор независимых гауссовских случайных величин с нулевыми математическими ожиданиями и единичными дисперсиями; ${\mathbf{X}}_{0}^{*}$ = $\mathcal{N}\left\{ {{\mathbf{X}} - {{{\mathbf{m}}}_{0}};{{{\mathbf{B}}}_{0}}} \right\}$ – вектор начальных фазовых координат, имеющий нормальное распределение с вектором математических ожиданий m₀ и корреляционной матрицей B₀.

Эквивалентное дискретное представление (1.3) непрерывных моделей вектора состояния маневрирующего объекта (1.1) является абсолютно точным в том смысле, что для любых ${{t}_{k}} - {{t}_{{k - 1}}} > 0$ оно позволяет получить случайные процессы с теми же статистическими характеристиками, как и решение СДУ (1.1), без погрешностей аппроксимации [8].

Пусть в дискретные моменты времени ${{t}_{k}} = {{t}_{0}} + k\Delta $, k = 1, 2, …, уравнение измерений имеет вид

где ${{{\mathbf{Y}}}_{k}} = {{\left[ {{\mathbf{Y}}_{k}^{{(1){\text{T}}}},{\mathbf{Y}}_{k}^{{(2){\text{T}}}}} \right]}^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}}$, ${\mathbf{Y}}_{k}^{{(1)}}$ – ${{n}_{{y1}}}$-мерный вектор наблюдений активного канала измерений, использующего отраженные от объекта зондирующие сигналы; ${\mathbf{Y}}_{k}^{{(2)}}$ – ${{n}_{{y2}}}$-мерный вектор наблюдений пассивного канала измерений, применяющего собственное электромагнитное излучение объекта; ${{{\mathbf{\Xi }}}_{k}}$, ${{{\mathbf{\Psi }}}_{k}} = {{\left[ {{\mathbf{\Psi }}_{k}^{{(1){\text{T}}}},{\mathbf{\Psi }}_{k}^{{(2){\text{T}}}}} \right]}^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}}$ – выборки независимых векторных БГШ с нулевыми математическими ожиданиями и единичными корреляционными матрицами соответствующей размерности; ${\mathbf{H}}\left( {{{B}_{k}},{{C}_{k}}} \right) = {{\left[ {\begin{array}{*{20}{c}} {{\mathbf{H}}_{1}^{{\text{T}}}\left( {{{B}_{k}}} \right)}&{{\mathbf{H}}_{2}^{{\text{T}}}\left( {{{C}_{k}}} \right)} \end{array}} \right]}^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}}$; ${\mathbf{V}}\left( {{{B}_{k}},{{C}_{k}}} \right) = {\text{diag}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{V}}}_{1}}\left( {{{B}_{k}}} \right)}&{{{{\mathbf{V}}}_{2}}\left( {{{C}_{k}}} \right)} \end{array}} \right]$ – матрица известных коэффициентов и матрица диагональных элементов, характеризующих погрешности измерений соответственно; ${{B}_{k}}$, ${{C}_{k}}$ – дискретные марковские процессы нарушений в каналах измерений, описываемые цепями Маркова на ${{M}_{2}}$- и ${{M}_{3}}$-положений соответственно, с матрицами вероятностей переходов: смена состояний которых может происходить только в фиксированные моменты времени k = 1, 2, …; ${{M}_{2}}$, ${{M}_{3}}$ – число значений дискретных параметров ${{b}_{m}}$, ${{c}_{d}}$ соответственно.

Применительно к решаемой задаче синтеза вектор состояния представляет собой ДНМП $\left[ {{\mathbf{X}}_{k}^{{\text{T}}},{{A}_{k}},{{B}_{k}},{{C}_{k}}} \right]{{\,}^{{\text{T}}}} \equiv \left[ {{\mathbf{X}}_{k}^{{\text{T}}},{\mathbf{S}}_{k}^{{\text{T}}}} \right]{{\,}^{{\text{T}}}}$, где ${{{\mathbf{X}}}_{k}}$ – непрерывная ${{n}_{x}}$-мерная компонента ДНМП, описывающий в пространстве состояний динамику фазовых координат объекта; ${{{\mathbf{S}}}_{k}} = \left[ {{{A}_{k}},{{B}_{k}},{{C}_{k}}} \right]{{\,}^{{\text{T}}}}$ – дискретная компонента ДНМП – трехкомпонентный дискретный марковский процесс, причем марковские цепи ${{B}_{k}}$ и ${{C}_{k}}$ не зависят от ${{{\mathbf{X}}}_{k}}$ и ${{A}_{k}}$.

По условию задачи известны матрицы ${\mathbf{\Phi }}$, ${\mathbf{\Gamma }}$, ${\mathbf{H}}$, ${\mathbf{V}}$, а также начальные распределения марковского вектора, причем компоненты марковской цепи ${{A}_{k}}$, ${{B}_{k}}$ и ${{C}_{k}}$, характеризующие маневр объекта и нарушения в каналах измерений соответственно, не зависят друг от друга.

Цель работы – на основе марковской теории оценивания случайных процессов разработать оптимальные (квазиоптимальные) алгоритмы комплексной обработки ДНМП $\left[ {{\mathbf{X}}_{k}^{{\text{T}}},{{A}_{k}},{{B}_{k}},{{C}_{k}}} \right]{{\,}^{{\text{T}}}}$, характеризующего сопровождение маневрирующего объекта, по наблюдаемым в дискретном времени выходным сигналам измерителей ${{{\mathbf{Y}}}_{k}} = {{\left[ {{\mathbf{Y}}_{k}^{{(1){\text{T}}}},{\mathbf{Y}}_{k}^{{(2){\text{T}}}}} \right]}^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}}$ в статистически неопределенных ситуациях.

2. Закон распределения смешанного вектора состояния дискретно-непрерывного марковского процесса. Обозначим апостериорное распределение смешанного вектора состояния $\left[ {{\mathbf{X}}_{k}^{{\text{T}}},{\mathbf{S}}_{k}^{{\text{T}}}} \right]{{\,}^{{\text{T}}}}$ по наблюдаемой последовательности измерений ${\mathbf{y}}_{1}^{k} = \left\{ {{{{\mathbf{y}}}_{1}},{{{\mathbf{y}}}_{2}},...,{{{\mathbf{y}}}_{k}}} \right\}$ как ${{w}_{{jmd}}}({\mathbf{x}}_{k}^{{}})$. Величина ${{w}_{{jmd}}}({\mathbf{x}}_{k}^{{}})d{\mathbf{x}}_{k}^{{}}$ равна вероятности одновременного выполнения условий ${\mathbf{X}}_{k}^{{}} \in ({\mathbf{x}}_{k}^{{}},{\mathbf{x}}_{k}^{{}} + d{\mathbf{x}}_{k}^{{}})$, ${{A}_{k}} = {{a}_{j}}$, ${{B}_{k}} = {{b}_{m}}$, ${{C}_{k}} = {{c}_{d}}$, где x_k – детерминированное значение случайной величины X_k при условии ${\mathbf{Y}}_{1}^{k} = {\mathbf{y}}_{1}^{k}$. На основании свойств марковских процессов в дискретном времени запишем рекуррентное уравнение:

где ${{f}_{j}}\left( {{{{\mathbf{x}}}_{k}}\,{\text{|}}\,{{{\mathbf{x}}}_{{k - 1}}}} \right) = f\left( {{{{\mathbf{x}}}_{k}}\,{\text{|}}\,{{{\mathbf{x}}}_{{k - 1}}},{{A}_{k}} = {{a}_{j}}} \right)$ – условная плотность вероятности (ПВ), определяемая с помощью уравнения (1.3); $w_{{ine}}^{*}\left( {{{{\mathbf{x}}}_{{k - 1}}}} \right)$ – апостериорное распределение, полученное на предыдущем k – 1-м шаге по последовательности измерений ${\mathbf{y}}_{1}^{{k - 1}}$ = $\{ {{{\mathbf{y}}}_{1}},{{{\mathbf{y}}}_{2}},...,{{{\mathbf{y}}}_{{k - 1}}}\} $; ${{f}_{{md}}}({{{\mathbf{y}}}_{k}}\,{\text{|}}\,{{{\mathbf{x}}}_{k}})$ = $f({{{\mathbf{y}}}_{k}}\,{\text{|}}\,{{{\mathbf{x}}}_{k}},{{B}_{k}}\, = \,{{b}_{m}}$, C_k = c_d) – одношаговая функция правдоподобия; $f({{{\mathbf{y}}}_{k}}\,{\text{|}}\,{\mathbf{y}}_{1}^{{k - 1}})$ – нормирующий коэффициент,

В (2.1) и далее для простоты записи аргументы k, $k{\text{--}}1$ всех функций, где это возможно и не вызывает сомнений, опущены, а интегрирование по переменной x ведется в области ${{\Re }^{{{{n}_{x}}}}}$.

Выражение (2.1) по своей сути – интегрально-рекуррентная формула Стратоновича–Бухалева [17, 18] апостериорного распределения смешанного вектора состояния ${{[{\mathbf{X}}_{k}^{{\text{T}}},{\mathbf{S}}_{k}^{{\text{T}}}]}^{{\text{T}}}}$ в дискретном времени и представляет собой решение задачи оценивания этого вектора состояния. Оптимальный алгоритм является рекуррентным и описывает эволюцию апостериорного распределения $w_{{jmd}}^{*}\left( {{{{\mathbf{x}}}_{k}}} \right)$ на каждом k-м шаге. Начальное условие $w_{{jmd}}^{*}\left( {{{{\mathbf{x}}}_{0}}} \right)$ равно известному априорному совместному распределению случайных величин ${\mathbf{X}}_{0}^{{}}$, ${{A}_{0}}$, ${{B}_{0}}$, ${{C}_{0}}$.

Вводя обозначение $\tilde {w}_{{jmd}}^{{}}({\mathbf{x}}_{k}^{{}})$ (экстраполированного по измерениям ${\mathbf{y}}_{1}^{{k - 1}} = \left\{ {{{{\mathbf{y}}}_{1}},{{{\mathbf{y}}}_{2}},...,{{{\mathbf{y}}}_{{k - 1}}}} \right\}$ распределения смешанного вектора состояния ${{[{\mathbf{X}}_{k}^{{\text{T}}},{\mathbf{S}}_{k}^{{\text{T}}}]}^{{\text{T}}}}$), перепишем (2.1) в виде цепочки из двух формул:

Уравнение (2.2) описывает преобразование апостериорного распределения предыдущего шага в экстраполированное распределение ${{\tilde {w}}_{{jmd}}}\left( {{{{\mathbf{x}}}_{k}}} \right)$. С помощью соотношения (2.3) производится уточнение экстраполированного распределения на основе полученного измерения ${{{\mathbf{y}}}_{k}}$ и определяется апостериорное распределение $w_{{jmd}}^{*}\left( {{{{\mathbf{x}}}_{k}}} \right)$.

Для нахождения апостериорной вероятности дискретной компоненты ДНМП на текущем k-м шаге ${\text{P}}_{{jmd}}^{*}\left( k \right)$ проинтегрируем (2.1) по переменным ${{{\mathbf{x}}}_{k}}$, ${{{\mathbf{x}}}_{{k - 1}}}$, в результате получим систему рекуррентных уравнений:

где – условная ПВ одношагового предсказания наблюдаемых сигналов, а нормирующий множитель $f({{{\mathbf{y}}}_{k}}\,{\text{|}}\,{\mathbf{y}}_{1}^{{k - 1}})$ определяется как

Для нахождения условной ПВ непрерывной компоненты ДНМП $f_{{jmd}}^{*}\left( {{{{\mathbf{x}}}_{k}}} \right)$ = f(x_k | A_k = a_j, ${{B}_{k}} = {{b}_{m}},{{C}_{k}} = {{c}_{d}},{\mathbf{y}}_{1}^{k})$ введем в рассмотрение условную экстраполированную ПВ непрерывной компоненты ДНМП ${{\tilde {f}}_{{jmd}}}\left( {{{{\mathbf{x}}}_{k}}} \right) = f({{{\mathbf{x}}}_{k}}\,{\text{|}}\,{{A}_{k}} = {{a}_{j}},{{B}_{k}} = {{b}_{m}},{{C}_{k}} = {{c}_{d}},{\mathbf{y}}_{1}^{{k - 1}})$ и применим свойство условных распределений. В результате из (2.2) и (2.3) получим систему рекуррентных уравнений:

где ${{\tilde {f}}_{{jmd}}}\left( {{{{\mathbf{x}}}_{k}}} \right)$ – условная экстраполированная ПВ вектора X_k при условии ${{A}_{k}} = {{a}_{j}}$, ${{B}_{k}} = {{b}_{m}}$, ${{C}_{k}} = {{c}_{d}}$; $f_{{jmd}}^{*}\left( {{{{\mathbf{x}}}_{k}}} \right)$ – условная апостериорная ПВ вектора X_k при условии ${{A}_{k}} = {{a}_{j}}$, ${{B}_{k}} = {{b}_{m}}$, ${{C}_{k}} = {{c}_{d}}$; $f_{{ine}}^{*}\left( {{{{\mathbf{x}}}_{{k - 1}}}} \right)$ – условная апостериорная ПВ вектора ${{{\mathbf{X}}}_{{k - 1}}}$ при условии ${{A}_{{k - 1}}} = {{a}_{i}}$, ${{B}_{{k - 1}}} = {{b}_{n}}$, ${{C}_{{k - 1}}} = {{c}_{e}}$, полученная на предыдущем $k{\text{--}}1$-м шаге (вывод уравнений (2.1)–(2.8) приводится в Приложении).

Синтезированный алгоритм совместной фильтрации компонент ДНМП (2.5)–(2.8) является нелинейным даже для линейных априорных уравнений (1.3), (1.4). Нелинейные операции выполняются при вычислении условной ПВ (2.6), используемой для определения апостериорных вероятностей (2.5). Особенность синтезированного алгоритма состоит в неразрывной связанности уравнений фильтрации и экстраполяции дискретного и непрерывного компонентов между собой.

3. Квазиоптимальный алгоритм оценивания вектора состояния дискретно-непрерывного марковского процесса. Практическая реализация синтезированного оптимального алгоритма совместной фильтрации компонент ДНМП (2.5)–(2.8) встречает значительные трудности. Они обусловлены требованием больших объемов памяти и быстродействия вычислителя при выполнении численного интегрирования многомерных ПВ. Поэтому представляет большой интерес синтез квазиоптимальных алгоритмов фильтрации и экстраполяции [8, 19].

Существует большое количество различных методов синтеза квазиоптимальных алгоритмов нелинейного оценивания [17, 18]. Наибольшее распространение получил метод гауссовской аппроксимации, который требует минимальных вычислительных затрат по сравнению с остальными методами и во многих случаях позволяет задать требуемое качество оценивания, несмотря на приближенное нахождение компонент ДНМП. Для этого необходимо выполнить двухмоментную параметрическую гауссовскую аппроксимацию апостериорного распределения $w_{{ine}}^{*}\left( {{{{\mathbf{x}}}_{{k - 1}}}} \right)$. Эта аппроксимация состоит в замене этой неизвестной функции некоторыми известными функциями, в частности условными математическим ожиданием и ковариационной функцией, случайные значения которых определяются так:

Применяя, таким образом, на каждом k-м шаге гауссовскую аппроксимацию для условного апостериорного распределения $w_{{ine}}^{*}\left( {{{{\mathbf{x}}}_{{k - 1}}}} \right)$, можно показать, что квазиоптимальный алгоритм фильтрации непрерывного компонента ДНМП описывается системой рекуррентных уравнений, вывод которых приводится в Приложении.

Вектор текущей условной оценки непрерывного компонента ДНМП и ковариационная матрица ее погрешностей

определяется по результатам текущих измерений ${\mathbf{Y}}_{k}^{{(1)}}$ и ${\mathbf{Y}}_{k}^{{(2)}}$:

Здесь

1) ${\mathbf{K}}_{{jmd}}^{{(1)}}\left( k \right)$ и ${\mathbf{K}}_{{jmd}}^{{(2)}}\left( k \right)$ – оптимальные коэффициенты передачи:

2) ${{{\mathbf{\tilde {X}}}}_{{jmd}}}(k)$ – условно-прогнозная оценка непрерывного компонента ДНМП при условии A_k = a_j, ${{B}_{k}} = {{b}_{m}}$, ${{C}_{k}} = {{c}_{d}}$ и ${{{\mathbf{\tilde {R}}}}_{{jmd}}}\left( k \right)$ – ковариационная матрица погрешностей предсказания:

3) ${\mathbf{\tilde {Y}}}_{{jmd}}^{{(1)}}\left( k \right)$, ${\mathbf{\tilde {Y}}}_{{jmd}}^{{(2)}}\left( k \right)$ – прогнозируемые значения векторов измерений и ${{{\mathbf{\tilde {W}}}}_{{jmd}}}\left( k \right)$ – условная блочная ковариационная матрица погрешностей предсказания измерений:

При этом начальные условия для квазиоптимального алгоритма КОИ (2.4), (2.5), (3.1)–(3.13):

Уравнения оценивания апостериорной вероятности дискретной компоненты ДНМП (2.4), (2.5) остаются без изменения, а условная ПВ одношагового предсказания наблюдаемых сигналов (2.6) имеет вид [15]

Задача КОИ при сопровождении маневрирующего объекта считается решенной, если на выходе оптимального фильтра на каждом k-м шаге формируется оптимальная оценка, соответствующая определенному критерию оптимальности. Байесовское решение может быть получено на основе минимизации апостериорного риска [20], который применительно к решаемой задаче имеет вид

где ${{g}_{{jmd\mu \nu \eta }}}\left( {{{{\mathbf{x}}}_{k}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }}}}_{k}}} \right)$ – функция потерь; ${\mathbf{u}}_{k}^{o}$ – оптимальное решение.

При решении многих практических задач малым ошибкам непрерывного компонента соответствуют меньшие потери. В таких случаях применяется функция потерь [15], простая по дискретному и квадратичная по непрерывному компонентам:

где $\alpha $, $\beta $ – коэффициенты потерь; ${{{{\delta }}}_{{jmd\mu \nu \eta }}}$ – символ Кронекера:

Функция потерь (3.16) означает, что при любом неправильном определении значений дискретного компонента потери равны коэффициенту α, а при правильном принятии решения потери пропорциональны сумме квадратов ошибок оценки непрерывного компонента. Подставляя выражение (3.16) в (3.15) и выполняя минимизацию апостериорного риска, можно показать, что решающее правило имеет следующий вид:

где ${\text{Tr}}\left\{ {\mathbf{A}} \right\}$ – след матрицы А.

Таким образом, в качестве безусловной оценки непрерывного компонента ДНМП выступает условное апостериорное математическое ожидание ${\mathbf{X}}_{{jmd}}^{*}\left( k \right)$. Из (3.17) следует, что принятие решения сводится к максимизации взвешенных апостериорных вероятностей дискретных компонент ДНМП. При этом следует отметить, что с увеличением погрешности оценки непрерывного компонента ДНМП уменьшаются веса погрешностей оценки дискретных компонент ДНМП. В результате может приниматься гипотеза с меньшей апостериорной вероятностью, но и с меньшими погрешностями оценки непрерывного компонента ДНМП, т.е. может отвергаться гипотеза с большей апостериорной вероятностью.

Условная ковариационная матрица ${\mathbf{R}}_{{jmd}}^{*}\left( k \right)$ характеризует качество оценки при правильном определении значений дискретных компонент ${{A}_{k}} = {{a}_{j}}$, ${{B}_{k}} = {{b}_{m}}$, ${{C}_{k}} = {{c}_{d}}$. Безусловная ковариационная матрица ${\mathbf{R}}{\kern 1pt} {\text{*}}(k)$ погрешностей оценки непрерывного компонента ДНМП определяется по формуле

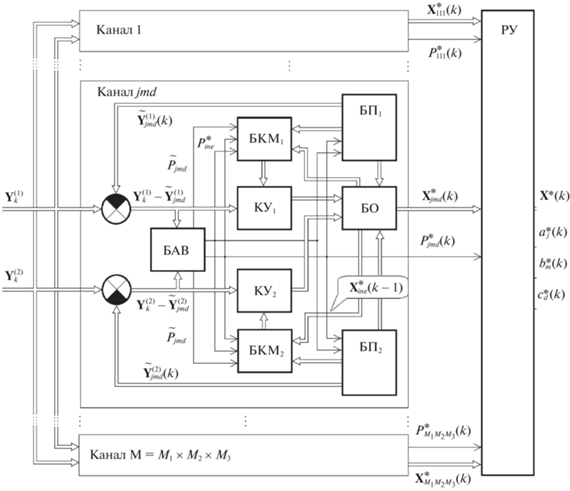
Квазиоптимальный цифровой фильтр КОИ (рис. 1), реализующий алгоритм (2.4), (2.5)–(3.14), (3.16)–(3.18), является многоканальным с числом каналов $M = {{M}_{1}} \times {{M}_{2}} \times {{M}_{3}}$ и в основном сохраняет структуру и все обратные связи, присущие оптимальному устройству. Каждый канал состоит из блоков КУ₁ и КУ₂ – вычисления коэффициентов усиления ${\mathbf{K}}_{{jmd}}^{{(1)}}\left( k \right)$ и ${\mathbf{K}}_{{jmd}}^{{(2)}}\left( k \right)$; блока оценки (БО), в котором рассчитываются ${\mathbf{X}}_{{jmd}}^{*}\left( k \right)$, ${\mathbf{X}}_{{ine}}^{*}\left( {k - 1} \right)$; блоков прогноза БП₁ и БП₂, в которых вычисляются ${{{\mathbf{\tilde {X}}}}_{{jmd}}}\left( k \right)$, ${\mathbf{\tilde {Y}}}_{{jmd}}^{{(1)}}\left( k \right)$, ${\mathbf{\tilde {Y}}}_{{jmd}}^{{(2)}}\left( k \right)$; блока апостериорных вероятностей (БАВ), в котором рассчитываются ${\text{P}}_{{jmd}}^{*}(k)$, ${\text{P}}_{{ine}}^{*}(k - 1)$, ${{{{\tilde {P}}}}_{{jmd}}}(k)$, и блоков вычисления корреляционных матриц БКМ₁ и БКМ₂, в которых вычисляются ${{{\mathbf{\tilde {R}}}}_{{jmd}}}\left( k \right)$, ${{{\mathbf{\tilde {W}}}}_{{jmd}}}\left( k \right)$, ${\mathbf{R}}_{{jmd}}^{*}\left( k \right)$ и ${\mathbf{R}}_{{ine}}^{*}(k - 1)$. Окончательное решение о принятии безусловных оценок ${\mathbf{X}}_{k}^{*} = {\mathbf{X}}_{{jmd}}^{*}\left( k \right)$, ${{A}_{k}} = a_{j}^{*}$, ${{B}_{k}} = b_{m}^{*}$, ${{C}_{k}} = c_{d}^{*}$ производится в решающем устройстве (РУ).

4. Пример. Приведены результаты моделирования алгоритма сопровождения маневрирующей цели в горизонтальной плоскости в условиях нарушений в каналах измерений угла пеленга. По условиям постановки задачи исходные вектор состояния ${\mathbf{X}}(t)$ и коэффициенты матриц априорного уравнения (1.1) определяются из системы СДУ:

где $\varphi $ – угол пеленга на объект; $\omega $ – угловая скорость линии визирования; D – дальность до объекта; $V$ – скорость сближения с объектом; J – ускорение сближения с объектом; $1{\text{/}}{{\alpha }_{\omega }} = D{\kern 1pt} {\text{*/}}2V$ – время, оставшееся до конца сопровождения, $\chi $ – коэффициент, характеризующий математическое ожидание флуктуаций угловой скорости линии визирования; ${{\alpha }_{J}}$ – коэффициент, характеризующий ширину спектральной плотности флуктуаций ускорения сближения с объектом; $\psi = 1{\text{/}}D{\kern 1pt} *$; D* – текущая оценка дальности до объекта (считается, что измеряется без погрешностей даже в статистически неопределенных ситуациях), $1{\text{/}}\chi _{J}^{{}} = {{\tau }_{{\text{м}}}}$ – среднее время маневра; $\sigma _{\omega }^{2}$ – дисперсия флуктуаций угловой скорости линии визирования; $\sigma _{J}^{2}$ – дисперсия флуктуаций ускорения сближения с объектом; ${{\xi }_{1}}\left( t \right)$, ${{\xi }_{1}}\left( t \right)$ – стандарные БГШ.

Исходный вектор наблюдения ${\mathbf{Y}}(k)$ и коэффициенты матриц априорного уравнения (1.4) определяются как

где ненулевые элементы матрицы ${\mathbf{H}}\left( {{{C}_{k}}} \right)$: ${{h}_{{11}}} = {{h}_{{24}}} = 1$, ${{h}_{{31}}} = {{C}_{k}}$.

Проверка качества квазиоптимального алгоритма проведена с помощью статистического моделирования на электронно-вычислительной машине для случая, когда параметры уравнений (4.1), (4.2) равны: ${{\tau }_{{\text{м}}}}$ = 10 c, $\chi $ = 0.16 рад/с, $\Delta $ = 1 с, $\sigma _{{y11}}^{{}}$ = 0.01 рад; $\sigma _{{y12}}^{{}}$ = 0.02 рад; $\sigma _{{y2}}^{{}}$ = 0.5 м/с; а цепи Маркова принимают значения ${{a}_{1}}$ = 1, ${{a}_{2}}$ = 5; ${{b}_{1}}$ = 1, ${{b}_{2}}$ = 10; ${{c}_{1}}$ = 1, ${{c}_{2}}$ = 10. Вероятности перехода $\pi _{{11}}^{a}$ = $\pi _{{11}}^{b}$ = $\pi _{{11}}^{c}$ = 0.8; $\pi _{{12}}^{a}$ = $\pi _{{12}}^{b}$ = $\pi _{{12}}^{c}$ = 0.2. В целях повышения наглядности функционирования алгоритма была сформирована тестовая реализация для дискретных компонент ${{B}_{k}}$, ${{C}_{k}}$. При этом было принято, что длина реализации $k = \overline {1,200} $, а цепи Маркова запишем как

Ускорение объекта изменяется по следующему закону:

Определение статистических характеристик квазиоптимальных алгоритмов КОИ проводилось методом Монте-Карло, при этом тестовая реализация дискретной цепи Маркова $A\left( k \right)$ сохранялась неизменной, а независимые гауссовские последовательности ${{\Xi }_{1}}(k)$, ${{\Xi }_{2}}(k)$, ${{\Psi }_{1}}(k)$ – ${{\Psi }_{3}}(k)$ формировались с помощью датчика случайных чисел. Для определения оценок дискретного и непрерывного компонентов использовалось решающее правило (3.16)–(3.17), для которого коэффициенты потерь принимали значения $\alpha = 1$, $\beta = 0$.

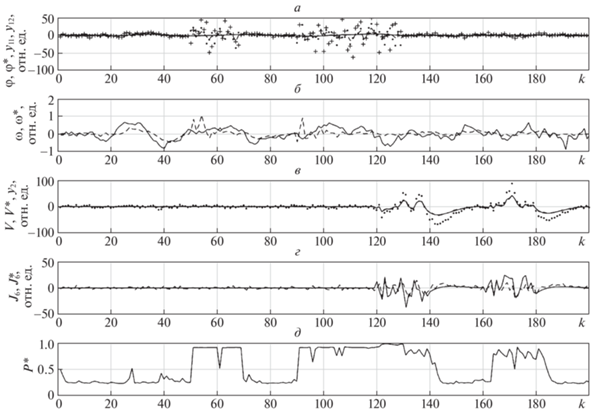
Результаты моделирования приведены на рис. 2, где показаны зависимости от дискретного времени: а) φ(k) – угла визирования объекта (сплошная), φ*(k) – оценки угла визирования объекта (пунктир), ${{y}_{{11}}}(k)$ – измерений активным каналом (точки), ${{y}_{{12}}}(k)$ – измерений пассивным каналом (крестики); б) $\omega \left( k \right)$ – угловой скорости линии визирования (сплошная), ω*(k) – оценки угловой скорости линии визирования (пунктир); в) V – скорости объекта, V* – оценки скорости объекта (пунктир), ${{y}_{2}}(k)$ – измерений скорости объекта (точки); г) ${{J}_{{\text{б}}}}$ – бокового ускорения объекта (сплошная), $J_{{\text{б}}}^{*}$ – оценки бокового ускорения объекта (пунктир); д) $P{\kern 1pt} *$ – совместной вероятности правильного обнаружения нарушений в каналах измерений и маневров объекта.

Данные рис. 2 показывают работоспособность квазиоптимального алгоритма (2.4)–(3.14), (3.16)–(3.18) при оценке угловой скорости линии визирования, что особенно важно в случае, когда одновременно наблюдается как маневр объекта, так и скачкообразные нарушения в каналах измерений. Необходимо также отметить, что при реализации квазиоптимального алгоритма отсутствует рост числа каналов фильтра, как в случае байесовского алгоритма адаптивного оценивания [8], что обусловлено марковским свойством ДНМП.

Заключение. Методами теории условных марковских процессов решена задача оптимального оценивания ненаблюдаемых компонент векторной марковской последовательности ДНМП при двухканальном векторном наблюдении. Синтезированные алгоритмы основаны на разложении смешанной апостериорной плотности вероятности вектора состояния ${{\left[ {{\mathbf{X}}_{k}^{{\text{T}}},{{A}_{k}},{{B}_{k}},{{C}_{k}}} \right]}^{{\,{\text{T}}}}}$ и являются алгоритмами с обратными связями по дискретному процессу ${\mathbf{S}}_{k}^{{\text{T}}} = \left[ {{{A}_{k}},{{B}_{k}},{{C}_{k}}} \right]$. На базе квазиоптимального алгоритма разработана соответствующая структурная схема цифрового фильтра КОИ.

Особенность синтезированного квазиоптимального алгоритма комплексирования состоит в неразрывной связанности уравнений фильтрации и экстраполяции дискретного и непрерывного компонентов ДНМП между собой, что потребует дополнительных вычислительных затрат по сравнению с известными алгоритмами. Однако современная высокопроизводительная вычислительная техника позволяет построить практически реализуемый цифровой фильтр КОИ в статистически неопределённых ситуациях.